A General Technique to Train Language
Models on Language Models
Mark-Jan Nederhof
University of Groningen
∗
We show that under certain conditions, a language model can be trained on the basis of a
second language model. The main instance of the technique trains a finite automaton on the
basis of a probabilistic context-free grammar, such that the Kullback-Leibler distance between
grammar and trained automaton is provably minimal. This is a substantial generalization of
an existing algorithm to train an n-gram model on the basis of a probabilistic context-free
grammar.
1. Einführung
In diesem Artikel, the term language model is used to refer to any description that assigns
probabilities to strings over a certain alphabet. Language models have important
applications in natural language processing, and in particular, in speech recognition
Systeme (Manning and Sch ¨utze 1999).
Language models often consist of a symbolic description of a language, wie zum Beispiel
a finite automaton (FA) or a context-free grammar (CFG), extended by a probability
assignment to, Zum Beispiel, the transitions of the FA or the rules of the CFG, by which
we obtain a probabilistic finite automaton (PFA) or probabilistic context-free grammar
(PCFG), jeweils. For certain applications, one may first determine the symbolic part
of the automaton or grammar and in a second phase try to find reliable probability
estimates for the transitions or rules. The current article is involved with the second
Problem, that of extending FAs or CFGs to become PFAs or PCFGs. We refer to this
process as training.
Training is often done on the basis of a corpus of actual language use in a certain
Domain. If each sentence in this corpus is annotated by a list of transitions of an
FA recognizing the sentence or a parse tree for a CFG generating the sentence, Dann
training may consist simply in relative frequency estimation. This means that we estimate
probabilities of transitions or rules by counting their frequencies in the corpus, relative
to the frequencies of the start states of transitions or to the frequencies of the left-hand
side nonterminals of rules, jeweils. By this estimation, the likelihood of the corpus
is maximized.
The technique we introduce in this article is different in that training is done on
the basis not of a finite corpus, but of an input language model. Our goal is to find
estimations for the probabilities of transitions or rules of the input FA or CFG such that
∗ Faculty of Arts, Humanities Computing, P.O. Kasten 716, NL-9700 AS Groningen, Die Niederlande.
Email: markjan@let.rug.nl.
Einreichung erhalten: 20th January 2004; Revised submission received: 5th August 2004; Accepted for
Veröffentlichung: 19th September 2004
© 2005 Verein für Computerlinguistik
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
l
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
/
3
1
2
1
7
3
1
7
9
8
1
1
1
0
8
9
1
2
0
1
0
5
4
2
2
3
9
8
6
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Computerlinguistik
Volumen 31, Nummer 2
the resulting PFA or PCFG approximates the input language model as well as possible,
or more specifically, such that the Kullback-Leibler (KL) Distanz (or relative entropy)
between the input model and the trained model is minimized. The input FA or CFG to
be trained may be structurally unrelated to the input language model.
This technique has several applications. One is an extension with probabilities
of existing work on approximation of CFGs by means of FAs (Nederhof 2000). Der
motivation for this work was that application of FAs is generally less costly than
application of CFGs, which is an important benefit when the input is very large, als
is often the case in, Zum Beispiel, speech recognition systems. The practical relevance of
this work was limited, Jedoch, by the fact that in practice one is more interested in
the probabilities of sentences than in a purely Boolean distinction between grammatical
and ungrammatical sentences.
Several approaches were discussed by Mohri and Nederhof (2001) to extend this
work to approximation of PCFGs by means of PFAs. A first approach is to directly map
rules with attached probabilities to transitions with attached probabilities. Obwohl
this is computationally the easiest approach, the resulting PFA may be a very inaccurate
approximation of the probability distribution described by the input PCFG. In particu-
lar, there may be assignments of probabilities to the transitions of the same FA that lead
to more accurate approximating language models.
A second approach is to train the approximating FA by means of a corpus. Wenn
the input PCFG was itself obtained by training on a corpus, then we already possess
training material. Jedoch, this may not always be the case, and no training material
may be available. Außerdem, as a determinized approximating FA may be much
larger than the input PCFG, the sparse-data problem may be more severe for the
automaton than it was for the grammar.1 Hence, even if sufficient material was available
to train the CFG, it may not be sufficient to accurately train the FA.
A third approach is to construct a training corpus from the PCFG by means of
A (pseudo)random generator of sentences, such that sentences that are more likely
according to the PCFG are generated with greater likelihood. This has been proposed
by Jurafsky et al. (1994), for the special case of bigrams, extending a nonprobabilistic
technique by Zue et al. (1991). It is not clear, Jedoch, whether this idea is feasible
for training of finite-state models that are larger than bigrams. The reason is that
very large corpora would have to be generated in order to obtain accurate probability
estimates for the PFA. Note that the number of parameters of a bigram model is
bounded by the square of the size of the lexicon; such a bound does not exist for
general PFAs.
The current article discusses a fourth approach. In the limit, it is equivalent to the
third approach above, as if an infinite corpus were constructed on which the PFA is
trained, but we have found a way to avoid considering sentences individually. Der Schlüssel
idea that allows us to handle an infinite set of strings generated by the PCFG is that we
construct a new grammar that represents the intersection of the languages described by
the input PCFG and the FA. Within this new grammar, we can compute the expected
frequencies of transitions of the FA, using a fairly standard analysis of PCFGs. Diese
expected frequencies then allow us to determine the assignment of probabilities to
transitions of the FA that minimizes the KL distance between the PCFG and the resulting
PFA.
1 In Nederhof (2000), several methods of approximation were discussed that lead to determinized
approximating FAs that can be much larger than the input CFGs.
174
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
l
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
/
3
1
2
1
7
3
1
7
9
8
1
1
1
0
8
9
1
2
0
1
0
5
4
2
2
3
9
8
6
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Nederhof
Training Models on Models
The only requirement is that the FA to be trained be unambiguous, by which we
mean that each input string can be recognized by at most one computation of the FA.
The special case of n-grams has already been formulated by Stolcke and Segal (1994),
realizing an idea previously envisioned by Rimon and Herz (1991). An n-gram model is
here seen as a (P)FA that contains exactly one state for each possible history of the n − 1
previously read symbols. It is clear that such an FA is unambiguous (even deterministic)
and that our technique therefore properly subsumes the technique by Stolcke and Segal
(1994), although the way that the two techniques are formulated is rather different. Auch
note that the FA underlying an n-gram model accepts any input string over the alphabet,
which does not hold for general (unambiguous) FAs.
Another application of our work involves determinization and minimization of
PFAs. As shown by Mohri (1997), PFAs cannot always be determinized, and no practical
algorithms are known to minimize arbitrary nondeterministic (P)FAs. This can be a
problem when deterministic or small PFAs are required. We can, Jedoch, always
compute a minimal deterministic FA equivalent to an input FA. The new results in this
article offer a way to extend this determinized FA to a PFA such that it approximates
the probability distribution described by the input PFA as well as possible, in terms of
the KL distance.
Although the proposed technique has some limitations, insbesondere, that the model
to be trained is unambiguous, it is by no means restricted to language models based on
finite automata or context-free grammars, as several other probabilistic grammatical
formalisms can be treated in a similar manner.
The structure of this article is as follows. We provide some preliminary definitions
in Section 2. Abschnitt 3 discusses how the expected frequency of a rule in a PCFG can be
computed. This is an auxiliary step in the algorithms to be discussed below. Abschnitt 4
defines a way to combine a PFA and a PCFG into a new PCFG that extends a well-known
representation of the intersection of a regular and a context-free language. Thereby
we merge the input model and the model to be trained into a single structure. Das
structure is the foundation for a number of algorithms, presented in section 5, welche
erlauben, jeweils, training of an unambiguous FA on the basis of a PCFG (section 5.1),
training of an unambiguous CFG on the basis of a PFA (section 5.2), and training of an
unambiguous FA on the basis of a PFA (section 5.3).
2. Preliminaries
Many of the definitions on probabilistic context-free grammars are based on Santos
(1972) and Booth and Thompson (1973), and the definitions on probabilistic finite
automata are based on Paz (1971) and Starke (1972).
A context-free grammar G is a 4-tuple (Σ, N, S, R), where Σ and N are two finite
disjoint sets of terminals and nonterminals, jeweils, S ∈ N is the start symbol, Und
R is a finite set of rules, each of the form A → α, where A ∈ N and α ∈ (Σ ∪ N)
. A
probabilistic context-free grammar G is a 5-tuple (Σ, N, S, R, pG ), where Σ, N, S and R
are as above, and pG is a function from rules in R to probabilities.
∗
In what follows, symbol a ranges over the set Σ, symbols w, v range over the
set Σ∗
, symbols A, B range over the set N, symbol X ranges over the set Σ ∪ N,
∗
symbols α, β, γ range over the set (Σ ∪ N)
, symbol ρ ranges over the set R, Und
∗
symbols d, e range over the set R
. With slight abuse of notation, we treat a rule
∗
ρ = (A → α) ∈ R as an atomic symbol when it occurs within a string dρe ∈ R
.
The symbol (cid:5) denotes the empty string. String concatenation is represented by
operator · or by empty space.
175
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
l
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
/
3
1
2
1
7
3
1
7
9
8
1
1
1
0
8
9
1
2
0
1
0
5
4
2
2
3
9
8
6
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Computerlinguistik
Volumen 31, Nummer 2
.
∗
∗
∗
∗
∗
(cid:2)
(cid:2)
(cid:2)
∗
∈ R
ρ1⇒ α1
and δ ∈ (Σ ∪ N)
· · · ρm, m ≥ 0, such that α0
For a fixed (P)CFG G, we define the relation ⇒ on triples consisting of two strings
and a rule ρ ∈ R by α ρ⇒ β, if and only if α is of the form wAδ and β
α, β ∈ (Σ ∪ N)
is of the form wγδ, for some w ∈ Σ∗
, and ρ = (A → γ). A leftmost
ρ2⇒ · · · ρm⇒ αm, für
derivation (in G) is a string d = ρ1
some α0, . . . , αm
; d = (cid:5) is always a leftmost derivation. In the remainder
of this article, we let the term derivation refer to leftmost derivation, unless spec-
ified otherwise. If α0
, then we say that
∗
∈ (Σ ∪ N)
d = ρ1
from itself. A derivation d such that S d⇒ w, for some w ∈ Σ∗
, is called a complete
derivation. We say that G is unambiguous if for each w ∈ Σ∗
, S d⇒ w for at most
∗
one d ∈ R
· · · ρm derives αm from α0, and we write α0
ρ1⇒ · · · ρm⇒ αm for some α0, . . . , αm
d⇒ αm; (cid:5) derives any α0
∈ (Σ ∪ N)
∈ (Σ ∪ N)
and d = ρ1
is defined to be
Let G be a fixed PCFG (Σ, N, S, R, pG ). For α, β ∈ (Σ ∪ N)
,
(cid:1)
m ≥ 0, we define pG (α d⇒ β) =
M
i=1 pG (ρi) if α d⇒ β, and pG (α d⇒ β) = 0 ansonsten. Der
probability pG (w) of a string w ∈ Σ∗
d pG (S d⇒ w).
PCFG G is said to be proper if
ρ,α pG (A ρ⇒ α) = 1 for all A ∈ N, das ist, wenn die
probabilities of all rules ρ = (A → α) with left-hand side A sum to one. PCFG G is said to
w pG (w) = 1. Consistency implies that the PCFG defines a probability
be consistent if
distribution on the set of terminal strings. There is a practical sufficient condition for
consistency that is decidable (Booth and Thompson 1973).
, and β ∈ (Σ ∪ N)
A PCFG is said to be reduced if for each nonterminal A, there are d1, d2
∗
∈ R
,
such that pG (S d1⇒ w1Aβ) · pG (w1Aβ d2⇒ w1w2) > 0. In
w1, w2
Wörter, if a PCFG is reduced, then for each nonterminal A, there is at least one derivation
d1d2 with nonzero probability that derives a string w1w2 from S and that includes
some rule with left-hand side A. A PCFG G that is not reduced can be turned into
one that is reduced and that describes the same probability distribution, provided that
(cid:2)
w pG (w) > 0. This reduction consists in removing from the grammar any nonterminal
A for which the above conditions do not hold, together with any rule that contains
such a nonterminal; see Aho and Ullman (1972) for reduction of CFGs, which is very
ähnlich.
· · · ρm
A finite automaton M is a 5-tuple (Σ, Q, q0, qf , T), where Σ and Q are two
∈ Q are the initial and final
finite sets of terminals and states, jeweils, q0, qf
A(cid:11)→ s, Wo
Staaten, jeweils, and T is a finite set of transitions, each of the form r
r ∈ Q − {qf
}, s ∈ Q, and a ∈ Σ.2 A probabilistic finite automaton M is a 6-tuple (Σ, Q,
q0, qf , T, pM), where Σ, Q, q0, qf , and T are as above, and pM is a function from transitions
in T to probabilities.
∈ Σ∗
∗
In what follows, symbols q, R, s range over the set Q, symbol τ ranges over the set T,
and symbol c ranges over the set T
∗
.
(cid:4)
τ
(cid:3) (S, w
(cid:4)
) if and only if w is of the form aw
For a fixed (P)FA M, we define a configuration to be an element of Q × Σ∗
, and we
define the relation (cid:15) on triples consisting of two configurations and a transition τ ∈ T
A(cid:11)→ s).
von (R, w)
τ1(cid:3) (r1, w1)
A computation (in M) is a string c = τ1
τ2(cid:3) · · · τm(cid:3) (rm, wm), for some (r0, w0), . . . , (rm, wm) ∈ Q × Σ∗
; c = (cid:5) is always a compu-
· · ·
Station. Wenn (r0, w0)
∗
(cid:3) (qf , (cid:5)).
τm
τ1(cid:3) · · · τm(cid:3) (rm, wm) for some (r0, w0), . . . , (rm, wm) ∈ Q × Σ∗
(cid:3) (rm, wm). We say that c recognizes w if (q0, w)
· · · τm, m ≥ 0, such that (r0, w0)
, for some a ∈ Σ, and τ = (R
, then we write (r0, w0)
and c = τ1
∈ T
C
C
2 That we only allow one final state is not a serious restriction with regard to the set of strings we can
Verfahren; only when the empty string is to be recognized could this lead to difficulties. Lifting the
restriction would encumber the presentation with treatment of additional cases without affecting,
Jedoch, the validity of the main results.
176
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
l
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
/
3
1
2
1
7
3
1
7
9
8
1
1
1
0
8
9
1
2
0
1
0
5
4
2
2
3
9
8
6
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Nederhof
Training Models on Models
C
C
∗
C[(q, w)
(cid:3) (qf , (cid:5)) for at most one c ∈ T
(cid:4)
, there is at most one combination of τ ∈ T and (S, w
Let M be a fixed FA (Σ, Q, q0, qf , T). The language L(M) accepted by M is
defined to be {w ∈ Σ∗ | ∃
(cid:3) (qf , (cid:5))]}. We say M is unambiguous if for each
w ∈ Σ∗
. We say M is deterministic if for each
, (q0, w)
(R, w) ∈ Q × Σ∗
solch
Das (R, w)
). Turning a given FA into one that is deterministic and accepts the
same language is called determinization. All FAs can be determinized. Turning a given
(deterministic) FA into the smallest (deterministic) FA that accepts the same language
is called minimization. There are effective algorithms for minimization of deterministic
FAs.
) ∈ Q × Σ∗
(cid:4)
τ
(cid:3) (S, w
Let M be a fixed PFA (Σ, Q, q0, qf , T, pM). Für (R, w), (S, v) ∈ Q × Σ∗
(cid:1)
∗
∈ T
, we define pM((R, w)
C
(cid:3) (S, v)) =
M
i=1 pM(τi) Wenn (R, w)
C
(cid:3) (S, v)) = 0 ansonsten. The probability pM(w) of a string w ∈ Σ∗
Und
C
(cid:3) (S, v), Und
is defined
· · · τm
c = τ1
pM((R, w)
(cid:2)
to be
c pM((q0, w)
C
(cid:3) (qf , (cid:5))).
PFA M is said to be proper if
(cid:2)
τ,A,S: τ=(R
A(cid:5)→s)∈T pM(τ) = 1 for all r ∈ Q − {qf
}.
3. Expected Frequencies of Rules
Let G be a PCFG (Σ, N, S, R, pG ). We assume without loss of generality that S does not
occur in the right-hand side of any rule from R. For each rule ρ, we define
E(ρ) =
(cid:3)
D,D(cid:1),w
pG (S
(cid:1)
dρd
⇒ w)
(1)
If G is proper and consistent, (1) is the expected frequency of ρ in a complete derivation.
(cid:4)
Each complete derivation dρd
(cid:4)(cid:4)
can be written as dρd
(cid:4)(cid:4)(cid:4)
D
, with d
(cid:4)(cid:4)
(cid:4) = d
(cid:4)(cid:4)(cid:4)
D
(cid:4)
d⇒ w
S
Aβ, A
(cid:1)(cid:1)
ρ⇒ α, α d
(cid:4)(cid:4)
⇒ w
(cid:1)(cid:1)(cid:1)
, β d
⇒ w
(cid:4)(cid:4)(cid:4)
(cid:4)
for some A, α, β, w
(cid:4)(cid:4)
, w
(cid:4)(cid:4)(cid:4)
, and w
. daher
E(ρ) = outer(A) · pG (ρ) · inner(α)
where we define
outer(A) =
(cid:3)
pG (S
(cid:4)
d⇒ w
Aβ) · pG (β d
⇒ w
(cid:4)(cid:4)(cid:4)
)
(cid:1)(cid:1)(cid:1)
D,w(cid:1),β,D(cid:1)(cid:1)(cid:1),w(cid:1)(cid:1)(cid:1)
(cid:3)
(cid:1)(cid:1)
pG (α d
(cid:4)(cid:4)
⇒ w
)
inner(α) =
D(cid:1)(cid:1),w(cid:1)(cid:1)
, Wo
(2)
(3)
(4)
(5)
for each A ∈ N and α ∈ (Σ ∪ N)
following equations:
∗
. From the definition of inner, we can easily derive the
inner(A) = 1
inner(A) =
(cid:3)
ρ,α:
ρ=(A→α)
pG (ρ) · inner(α)
inner(Xβ) = inner(X) · inner(β)
(6)
(7)
(8)
177
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
l
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
/
3
1
2
1
7
3
1
7
9
8
1
1
1
0
8
9
1
2
0
1
0
5
4
2
2
3
9
8
6
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Computerlinguistik
Volumen 31, Nummer 2
This can be taken as a recursive definition of inner, assuming β (cid:18)= (cid:5) In (8). Ähnlich, Wir
can derive a recursive definition of outer:
outer(S) = 1
outer(A) =
(cid:3)
ρ,B,α,β:
ρ=(B→αAβ)
outer(B) · pG (ρ) · inner(α) · inner(β)
(9)
(10)
for A (cid:18)= S.
Allgemein, there may be cyclic dependencies in the equations for inner and outer;
das ist, for certain nonterminals A, inner(A) and outer(A) may be defined in terms
of themselves. There may even be no closed-form expression for inner(A). Jedoch,
one may approximate the solutions to arbitrary precision by means of fixed-point
iteration.
4. Intersection of Context-Free and Regular Languages
We recall a construction from Bar-Hillel, Perles, and Shamir (1964) that computes the
intersection of a context-free language and a regular language. The input consists of a
CFG G = (Σ, N, S, R) and an FA M = (Σ, Q, q0, qf , T); note that we assume, without loss
of generality, that G and M share the same set of terminals Σ.
The output of the construction is CFG G∩ = (Σ, N∩, S∩, R∩), where N∩ = Q ×
(Σ ∪ N) × Q, S∩ = (q0, S, qf ), and R∩ consists of the set of rules that is obtained as
follows:
(cid:1)
(cid:1)
· · · Xm) ∈ R, m ≥ 0, and each sequence of states
∈ Q, let the rule ρ∩ = ((r0, A, rm) → (r0, X1, r1) · · · (rm−1, Xm, rm))
For each rule ρ = (A → X1
r0, . . . , rm
be in R∩; for m = 0, R∩ contains a rule ρ∩ = ((r0, A, r0) → (cid:5)) für jede
state r0.
For each transition τ = (R
in R∩.
A(cid:11)→ s) ∈ T, let the rule ρ∩ = ((R, A, S) → a) Sei
Note that for each rule (r0, A, rm) → (r0, X1, r1) · · · (rm−1, Xm, rm) from R∩, there is a
· · · Xm from R from which it has been constructed by the above.
unique rule A → X1
A(cid:11)→ s. This means that if
Ähnlich, each rule (R, A, S) → a uniquely identifies a transition r
we take a derivation d∩ in G∩, we can extract a sequence h1(d∩) of rules from G and a
sequence h2(d∩) of transitions from M, where h1 and h2 are string homomorphisms that
we define pointwise as
h1(ρ∩) = ρ if ρ∩ = ((r0, A, rm) → (r0, X1, r1) · · · (rm−1, Xm, rm))
and ρ = (A → X1
(cid:5) if ρ∩ = ((R, A, S) → a)
· · · Xm)
h2(ρ∩) = τ if ρ∩ = ((R, A, S) → a) and τ = (R
A(cid:11)→ s)
(cid:5) if ρ∩ = ((r0, A, rm) → (r0, X1, r1) · · · (rm−1, Xm, rm))
(11)
(12)
(13)
(14)
178
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
l
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
/
3
1
2
1
7
3
1
7
9
8
1
1
1
0
8
9
1
2
0
1
0
5
4
2
2
3
9
8
6
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Nederhof
Training Models on Models
C
C
d∩⇒ w, then for the same w, we have S d⇒ w and (q0, w)
We define h(d∩) = (h1(d∩), h2(d∩)). It can be easily shown that if h(d∩) = (D, C) Und
(cid:3) (qf , (cid:5)). Umgekehrt, if for some
S∩
w, D, and c we have S d⇒ w and (q0, w)
(cid:3) (qf , (cid:5)), then there is precisely one derivation d∩
such that h(d∩) = (D, C) and S∩
It was observed by Lang (1994) that G∩ can be seen as a parse forest, das ist, A
compact representation of all parse trees according to G that derive strings recognized
by M. The construction can be generalized to, Zum Beispiel, tree-adjoining grammars
(Vijay-Shanker and Weir 1993) and range concatenation grammars (Boullier 2000;
Bertsch and Nederhof 2001). The construction for the latter also has implications for
linear context-free rewriting systems (Seki et al. 1991).
d∩⇒ w.
The construction has been extended by Nederhof and Satta (2003) to apply to a
PCFG G = (Σ, N, S, R, pG ) and a PFA M = (Σ, Q, q0, qf , T, pM). The output is a
PCFG G∩ = (Σ, N∩, S∩, R∩, p∩), where N∩, S∩, and R∩ are as before, and p∩ is
defined by
p∩((r0, A, rm) → (r0, X1, r1) · · · (rm−1, Xm, rm)) = pG (A → X1
· · · Xm)
p∩((R, A, S) → a) = pM(R
A(cid:11)→ s)
(15)
(16)
If d∩, D, and c are such that h(d∩) = (D, C), then clearly p∩(d∩) = pG (D) · pM(C).
5. Training Models on Models
We restrict ourselves to a few cases of the general technique of training a model on the
basis of another model.
5.1 Training a PFA on a PCFG
Let us assume we have a proper and consistent PCFG G = (Σ, N, S, R, pG ) and an FA
M = (Σ, Q, q0, qf , T) that is unambiguous. This FA may have resulted from (nonprob-
abilistic) approximation of CFG (Σ, N, S, R), but it may also be totally unrelated to G.
Note that an FA is guaranteed to be unambiguous if it is deterministic; any FA can be
determinized. Our goal is now to assign probabilities to the transitions from FA M to
obtain a proper PFA that approximates the probability distribution described by G as
well as possible.
Let us define 1 as the function that maps each transition from T to one. Das heisst
C
C
(cid:3) (S, (cid:5))) = 0
(cid:3) (S, (cid:5))) = 1 Wenn (R, w)
(cid:3) (S, (cid:5)), Und 1((R, w)
C
that for each r, w, c and s, 1((R, w)
ansonsten.
Of the set of strings generated by G, a subset is recognized by computations of M;
note again that there can be at most one such computation for each string. The expected
frequency of a transition τ in such computations is given by
E(τ) =
(cid:3)
w,C,C(cid:1)
pG (w) · 1((q0, w)
(cid:1)
cτc
(cid:15) (qf , (cid:5)))
(17)
Now we construct the PCFG G∩ as explained in section 4 from the PCFG G and the
A(cid:11)→ s) ∈ T and ρ = ((R, A, S) → a). On the basis of the
PFA (Σ, Q, q0, qf , T, 1). Let τ = (R
179
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
l
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
/
3
1
2
1
7
3
1
7
9
8
1
1
1
0
8
9
1
2
0
1
0
5
4
2
2
3
9
8
6
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Computerlinguistik
Volumen 31, Nummer 2
properties of function h, we can now rewrite E(τ) als
E(τ) =
(cid:3)
pG (S
d⇒ w) · 1((q0, w)
(cid:1)
cτc
(cid:15) (qf , (cid:5)))
D,w,C,C(cid:1)
(cid:3)
pG (S
d⇒ w) · 1((q0, w)
(cid:1)
cτc
(cid:15) (qf , (cid:5)))
(cid:1)
e,D,w,C,C
:
H(e)=(D,cτc
(cid:3)
(cid:1)
)
p∩(S∩
(cid:1)
eρe
⇒ w)
=
=
e,e(cid:1),w
= E(ρ)
(18)
Hereby we have expressed the expected frequency of a transition τ = (R
A(cid:11)→ s) In
terms of the expected frequency of rule ρ = ((R, A, S) → a) in derivations in PCFG G∩.
It was explained in section 3 how such a value can be computed. Note that since
by definition 1(τ) = 1, also p∩(ρ) = 1. Außerdem, for the right-hand side a of ρ,
inner(A) = 1. daher,
E(τ) = outer((R, A, S)) · p∩(ρ) · inner(A)
= outer((R, A, S))
(19)
To obtain the required PFA (Σ, Q, q0, qf , T, pM), we now define the probability
function pM for each τ = (R
A(cid:11)→ s) ∈ T as
pM(τ) =
(cid:2)
outer((R, A, S))
(cid:1)
A
(cid:5)→s(cid:1) )∈T
outer((R, A(cid:4), S(cid:4)))
A(cid:1),S(cid:1):(R
(20)
That such a relative frequency estimator pM minimizes the KL distance between pG and
pM on the domain L(M) is proven in the appendix.
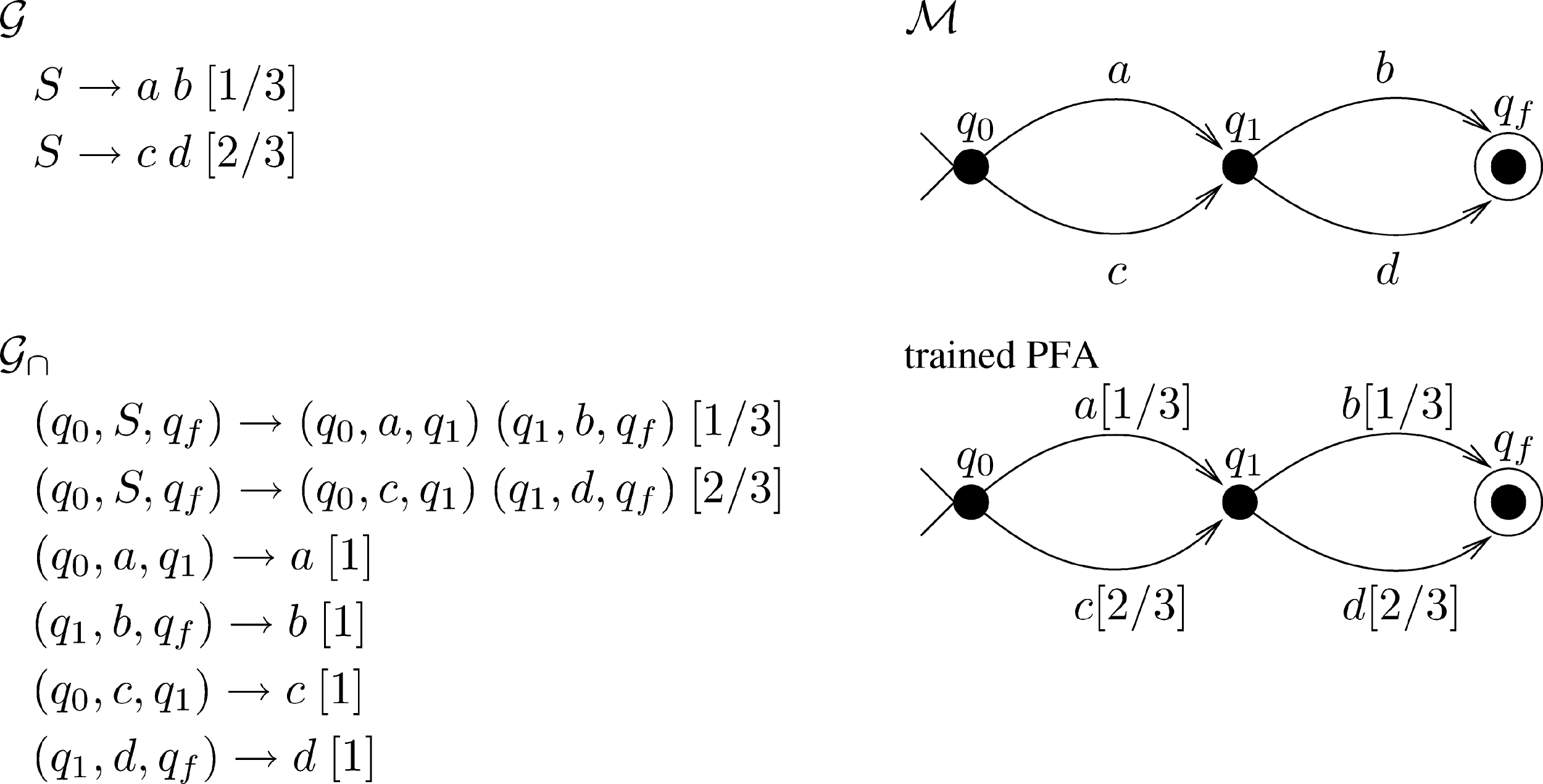
An example with finite languages is given in Figure 1. Wir haben, Zum Beispiel,
pM(q0
A(cid:11)→ q1) =
outer((q0, A, q1))
outer((q0, A, q1)) + outer((q0, C, q1))
=
1
3
3 + 2
1
3
= 1
3
(21)
5.2 Training a PCFG on a PFA
Similarly to section 5.1, we now assume we have a proper PFA M = (Σ, Q, q0,
qf , T, pM) and a CFG G = (Σ, N, S, R) that is unambiguous. Our goal is to find a
function pG that lets proper and consistent PCFG (Σ, N, S, R, pG ) approximate M as
well as possible. Although CFGs used for natural language processing are usually
ambiguous, there may be cases in other fields in which we may assume grammars are
unambiguous.
180
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
l
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
/
3
1
2
1
7
3
1
7
9
8
1
1
1
0
8
9
1
2
0
1
0
5
4
2
2
3
9
8
6
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Nederhof
Training Models on Models
Figur 1
Example of input PCFG G, with rule probabilities between square brackets, input FA M, Die
reduced PCFG G∩, and the resulting trained PFA.
Let us define 1 as the function that maps each rule from R to one. Of the set of
strings recognized by M, a subset can be derived in G. The expected frequency of a rule
ρ in those derivations is given by
E(ρ) =
(cid:3)
D,D(cid:1),w
pM(w) · 1(S
(cid:1)
dρd
⇒ w)
(22)
Now we construct the PCFG G∩ from the PCFG G = (Σ, N, S, R, 1) und das
PFA M as explained in section 4. Analogously to section 5.1, we obtain for each
ρ = (A → X1
· · · Xm)
(cid:3)
E(ρ) =
r0,r1,…,rm
(cid:3)
r0,r1,…,rm
=
E((r0, A, rm) → (r0, X1, r1) · · · (rm−1, Xm, rm))
outer((r0, A, rm)) · inner((r0, X1, r1) · · · (rm−1, Xm, rm))
(23)
To obtain the required PCFG (Σ, N, S, R, pG ), we now define the probability function
pG for each ρ = (A → α) als
pG (ρ) =
(cid:2)
E(ρ)
ρ(cid:1)=(A→α(cid:1) )∈R E(ρ(cid:4))
(24)
The proof that this relative frequency estimator pG minimizes the KL distance between
pM and pG on the domain L(G) is almost identical to the proof in the appendix for a
similar claim from section 5.1.
5.3 Training a PFA on a PFA
We now assume we have a proper PFA M
M
1 = (Σ, Q1, q0,1, qf,1, T1, p1) and an FA
2 = (Σ, Q2, q0,2, qf,2, T2) that is unambiguous. Our goal is to find a function p2 so that
181
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
l
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
/
3
1
2
1
7
3
1
7
9
8
1
1
1
0
8
9
1
2
0
1
0
5
4
2
2
3
9
8
6
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Computerlinguistik
Volumen 31, Nummer 2
proper PFA (Σ, Q2, q0,2, qf,2, T2, p2) approximates M
the KL distance between p1 and p2 on the domain L(M
2).
1 as well as possible, minimizing
One way to solve this problem is to map M
2 to an equivalent right-linear CFG G and
then to apply the algorithm from section 5.2. The obtained probability function pG can
be translated back to an appropriate function p2. For this special case, the construction
from section 4 can be simplified to the “cross-product” construction of finite automata
(sehen, z.B., Aho and Ullman 1972). The simplified forms of the functions inner and outer
from section 3 are commonly called forward and backward, jeweils, und sie sind
defined by systems of linear equations. Infolge, we can compute exact solutions, als
opposed to approximate solutions by iteration.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
l
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
/
3
1
2
1
7
3
1
7
9
8
1
1
1
0
8
9
1
2
0
1
0
5
4
2
2
3
9
8
6
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Appendix
We now prove that the choice of pM in section 5.1 is such that it minimizes the Kullback-
Leibler distance between pG and pM, restricted to the domain L(M). Without this
restriction, the KL distance is given by
D(pG(cid:19)pM) =
(cid:3)
w
pG (w) · log
pG (w)
pM(w)
(25)
This can be used for many applications mentioned in section 1. Zum Beispiel, an FA M
approximating a CFG G is guaranteed to be such that L(M) ⊇ L(G) in the case of most
practical approximation algorithms. Jedoch, if there are strings w such that w /∈ L(M)
and pG (w) > 0, Dann (25) is infinite, regardless of the choice of pM. We therefore restrict
pG to the domain L(M) and normalize it to obtain
pG|M(w) =
pG (w)
Z
, if w ∈ L(M)
0, ansonsten
(26)
(27)
(cid:2)
where Z =
show that our choice of pM minimizes
w:w∈L(M) pG (w). Note that pG|M = pG if L(M) ⊇ L(G). Our goal is now to
D(pG|M(cid:19)pM) =
(cid:3)
w:w∈L(M)
pG|M(w) · log
pG|M(w)
pM(w)
= log 1
Z
+ 1
Z
(cid:3)
w:w∈L(M)
pG (w) · log
pG (w)
pM(w)
As Z is independent of pM, it is sufficient to show that our choice of pM minimizes
(cid:3)
w:w∈L(M)
pG (w) · log
pG (w)
pM(w)
(cid:4)
τ
pM(τ)E(τ)
Now consider the expression
182
(28)
(29)
(30)
Nederhof
Training Models on Models
By the usual proof technique with Lagrange multipliers, it is easy to show that our
choice of pM in section 5.1, given by
pM(τ) =
(cid:2)
E(τ)
(cid:1)
A
(cid:5)→s(cid:1) )∈T
τ(cid:1),A(cid:1),S(cid:1):τ(cid:1)=(R
E(τ(cid:4))
(31)
A(cid:11)→ s) ∈ T, is such that it maximizes (30), under the constraint of
for each τ = (R
properness.
For τ ∈ T and w ∈ Σ∗
, we define #τ(w) to be zero, if w /∈ L(M), and otherwise to be
the number of occurrences of τ in the (unique) computation that recognizes w. Formally,
#τ(w) =
(cid:3) (qf , (cid:5))). We rewrite (30) als
(cid:2)
cτc
(cid:1)
C,C(cid:1) 1((q0, w)
(cid:4)
pM(τ)E(τ) =
(cid:4)
(cid:2)
w pG (w)·#τ(w)
pM(τ)
τ
τ
(cid:4)
(cid:4)
pM(τ)pG (w)·#τ(w)
=
=
=
=
=
=
w
(cid:4)
τ
(cid:5)
(cid:4)
w
τ
(cid:4)
(cid:6)
pG (w)
pM(τ)#τ(w)
pM(w)pG (w)
w:pM(w)>0
(cid:4)
w:pM(w)>0
(cid:4)
w:pM(w)>0
(cid:4)
w:pM(w)>0
2pG (w)·log pM(w)
2pG (w)·log pM(w)−pG (w)·log pG (w)+pG (w)·log pG (w)
−pG (w)·log
2
pG (w)
pM (w) +pG (w)·log pG (w)
(cid:2)
−
= 2
w:pM (w)>0 pG (w)·log
pG (w)
pM (w) · 2
(cid:2)
w:pM (w)>0 pG (w)·log pG (w)
(32)
We have already seen that the choice of pM that maximizes (30) is given by (31), Und
(31) implies pM(w) > 0 for all w such that w ∈ L(M) and pG (w) > 0. Since pM(w) > 0 Ist
impossible for w /∈ L(M), the value of
(cid:2)
2
w:pM (w)>0 pG (w)·log pG (w)
(33)
is determined solely by pG and by the condition that pM(w) > 0 for all w such that
w ∈ L(M) and pG (w) > 0. Das impliziert das (30) is maximized by choosing pM such
Das
(cid:2)
−
2
w:pM (w)>0 pG (w)·log
pG (w)
pM (w)
(34)
183
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
l
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
/
3
1
2
1
7
3
1
7
9
8
1
1
1
0
8
9
1
2
0
1
0
5
4
2
2
3
9
8
6
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Computerlinguistik
Volumen 31, Nummer 2
is maximized, or alternatively that
(cid:3)
w:pM(w)>0
pG (w) · log
pG (w)
pM(w)
(35)
is minimized, under the constraint that pM(w) > 0 for all w such that w ∈ L(M) Und
pG (w) > 0. For this choice of pM, (29) equals (35).
Umgekehrt, if a choice of pM minimizes (29), we may assume that pM(w) > 0 für
all w such that w ∈ L(M) and pG (w) > 0, since otherwise (29) is infinite. Wieder, for this
choice of pM, (29) equals (35). It follows that the choice of pM that minimizes (29) concurs
with the choice of pM that maximizes (30), which concludes our proof.
Danksagungen
Comments by Khalil Sima’an, Giorgio Satta,
Yuval Krymolowski, and anonymous
reviewers are gratefully acknowledged. Der
author is supported by the PIONIER Project
Algorithms for Linguistic Processing, funded
by NWO (Dutch Organization for Scientific
Forschung).
Verweise
Aho, Alfred V. and Jeffrey D. Ullman. 1972.
Parsing, Volumen 1 of The Theory of Parsing,
Translation and Compiling. Prentice Hall,
Englewood Cliffs, NJ.
Bar-Hillel, Yehoshua, M. Perles, Und
E. Shamir. 1964. On formal properties of
simple phrase structure grammars. In
Yehoshua Bar-Hillel, editor, Language and
Information: Selected Essays on Their Theory
and Application. Addison-Wesley, Reading,
MA, pages 116–150.
Bertsch, Eberhard and Mark-Jan Nederhof.
2001. On the complexity of some
extensions of RCG parsing. In Proceedings
of the Seventh International Workshop on
Parsing Technologies, pages 66–77, Peking,
Oktober.
Booth, Taylor L. and Richard A. Thompson.
1973. Applying probabilistic measures to
abstract languages. IEEE Transactions on
Computers, C-22(5):442–450.
Boullier, Pierre. 2000. Range concatenation
grammars. In Proceedings of the Sixth
International Workshop on Parsing
Technologies, pages 53–64, Trient, Italien,
Februar.
Jurafsky, Daniel, Chuck Wooters, Gary
Tajchman, Jonathan Segal, Andreas
Stolcke, Eric Fosler, and Nelson Morgan.
1994. The Berkeley Restaurant Project. In
Proceedings of the International Conference on
Spoken Language Processing (ICSLP-94),
pages 2139–2142, Yokohama, Japan.
184
Lang, Bernard. 1994. Recognition can be
harder than parsing. Rechnerisch
Intelligence, 10(4):486–494.
Manning, Christopher D. and Hinrich
Sch ¨utze. 1999. Foundations of Statistical
Natural Language Processing. MIT Press,
Cambridge, MA.
Mohri, Mehryar. 1997. Finite-state
transducers in language and speech
Verarbeitung. Computerlinguistik,
23(2):269–311.
Mohri, Mehryar and Mark-Jan Nederhof.
2001. Regular approximation of
context-free grammars through
transformation. In J.-C. Junqua and G. Transporter
Noord, editors, Robustness in Language and
Speech Technology. Kluwer Academic,
pages 153–163.
Nederhof, Mark-Jan. 2000. Practical
experiments with regular approximation
of context-free languages. Rechnerisch
Linguistik, 26(1):17–44.
Nederhof, Mark-Jan and Giorgio Satta. 2003.
Probabilistic parsing as intersection. In
Proceedings of the Eighth International
Workshop on Parsing Technologies, Seiten
137–148, Laboratoire Lorrain de recherche
en informatique et ses applications
(LORIA), Nancy, Frankreich, April.
Paz, Azaria. 1971. Introduction to Probabilistic
Automata. Academic Press, New York.
Rimon, Mori and J. Herz. 1991. Der
recognition capacity of local syntactic
constraints. In Proceedings of the Fifth
Conference of the European Chapter of the
ACL, pages 155–160, Berlin, April.
Santos, Eugene S. 1972. Probabilistic
grammars and automata. Information and
Kontrolle, 21:27–47.
Seki, Hiroyuki, Takashi Matsumura,
Mamoru Fujii, and Tadao Kasami.
1991. On multiple context-free grammars.
Theoretical Computer Science,
88:191–229.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
l
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
/
3
1
2
1
7
3
1
7
9
8
1
1
1
0
8
9
1
2
0
1
0
5
4
2
2
3
9
8
6
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Nederhof
Training Models on Models
Starke, Peter H. 1972. Abstract Automata.
North-Holland, Amsterdam.
Stolcke, Andreas and Jonathan Segal. 1994.
Precise N-gram probabilities from
stochastic context-free grammars. In
Proceedings of the 32nd Annual Meeting
of the ACL, pages 74–79, Las Cruces,
NM, Juni.
Vijay-Shanker, K. and David J. Wehr.
1993. The use of shared forests in
tree adjoining grammar parsing. In
Proceedings of the Sixth Conference of the
European Chapter of the ACL, pages 384–393,
Utrecht, Die Niederlande, April.
Zue, Victor, James Glass, David Goodine,
Hong Leung, Michael Phillips, Joseph
Polifroni, and Stephanie Seneff. 1991.
Integration of speech recognition and
natural language processing in the MIT
Voyager system. In Proceedings of the
ICASSP-91, Toronto, Volumen 1, Seiten
713–716.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
l
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
/
3
1
2
1
7
3
1
7
9
8
1
1
1
0
8
9
1
2
0
1
0
5
4
2
2
3
9
8
6
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
185