Construction of a Biological - IA de Investigación especializada en el MIT

Construction of a Biological
Tissue Model Based on
a Single-Cell Model:
A Computer Simulation
of Metabolic Heterogeneity
in the Liver Lobule

Abstract An enormous body of information has been obtained by
molecular and cellular biology in the last half century. Sin embargo, incluso
these powerful approaches are not adequate when it comes to
higher-level biological structures, such as tissues, organs, y
individual organisms, because of the complexities involved. De este modo,
accumulation of data at the higher levels supports and broadens
the context for that obtained on the molecular and cellular levels.
Under such auspices, an attempt to elucidate mesoscopic and
macroscopic subjects based on plentiful nanoscopic and microscopic
data is of great potential value. Por otro lado, fully realistic
simulation is impracticable because of the extensive cost entailed and
enormous amount of data required. Abstraction and modeling that
balance the dual requirements of prediction accuracy and manageable
calculation cost are of great importance for systems biology. Tenemos
constructed an ammonia metabolism model of the hepatic lobule,
a histological component of the liver, based on a single-hepatocyte
model that consists of the biochemical kinetics of enzymes and
transporters. To bring the calculation cost within reason, el
porto-central axis, which is an elemental structure of the lobule, es
defined as the systems biological unit of the liver, and is accordingly
modeled. A model including both histological structure and
position-specific gene expression of major enzymes largely represents
the physiological dynamics of the hepatic lobule in nature. Además,
heterogeneous gene expression is suggested to have evolved to
optimize the energy efficiency of ammonia detoxification at the
macroscopic level, implying that approaches like this may elucidate
how properties at the molecular and cellular levels, such as regulated
gene expression, modify higher-level phenomena of multicellular
tejido, organs, and organisms.

Hiroshi Ohno**,y
Keio University

Yasuhiro Naito*,**,y,z
Keio University

Hiromu Nakajima§
Osaka Medical Center
for Cancer and
Cardiovascular Diseases

Masaru Tomita**,y,z
Keio University

Palabras clave
Zonal metabolic heterogeneity, hepatic
lobule, biological simulation, ammonia
metabolism

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
a
r
t
yo
/

a
r
t
i
C
mi
–
pag
d

F
/

1
4
1
3
1
6
6
2
4
6
6
a
r
t
yo
.

2
0
0
8
1
4
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

* Contact author.

** Institute for Advanced Biosciences, Keio University, 14-1 Baba-cho, Tsuruoka, 997-0035, Japón. Correo electrónico: n02139ho@sfc.keio.ac.jp
y Bioinformatics Program, Graduate School of Media and Governance, Keio University, 5322 Endo, Fujisawa, 252-8520, Japón.
z Department of Environmental Information, Keio University, 5322 Endo, Fujisawa, 252-8520, Japón. Correo electrónico: ynaito@sfc.keio.ac.jp (Y.N.);

mt@sfc.keio.ac.jp (M.T.)

§ Clinical Laboratory, Osaka Medical Center for Cancer and Cardiovascular Diseases, 1-3-3 Nakamichi, Higashinariku, Osaka, 537-0025,

Japón. Correo electrónico: nakajima-hi@mc.pref.osaka.jp

norte 2008 Instituto de Tecnología de Massachusetts

Artificial Life 14: 3 – 28 (2008)

h. Ohno et al.

Construction of a Biological Tissue Model Based on a Single-Cell Model

1 Introducción

Systems biology is intended to elucidate the dynamics of the biological cell based on a compendium
of data carried out by what might be called the ‘‘ome’’ and the ‘‘omics’’ sciences, such as the genome
and genomics, the proteome and proteomics, or the metabolome and metabolomics [21, 26]. Significar-
mientras, biological life, which it is hoped will come to be understood, is rarely restricted to a single cell,
or unicellular organism. The human being is a representative multicellular organism, consisting of
aproximadamente 60 trillion cells, and undoubtedly the subject that we would like to investigate most
intensively. Actualmente, the greater part of the data that support systems biology is information at the
molecular and cellular (nanoscopic and microscopic) niveles. While the explosive development of
molecular and cellular biology has yielded both copious and precise information at the subcellular
nivel, biology for higher-level (mesoscopic and macroscopic) structures has lagged far behind. Anat-
omy and histology represent an organism in a hierarchical classification scheme, namely of tissues,
organs, and individual, going from the microscopic to macroscopic. The store of knowledge built up
at each level of the hierarchy is at present disproportionate. The knowledge accumulated in the last
decade at higher levels than the cell is undoubtedly less than that at the cellular and subcellular levels.
A major constraint is the currently limited technology, which for the tissue or organ level presents
greater difficulties in all aspects of sample preparation, cultivation, and measurement than required
for the single-cell level.

Hasta ahora, nanoscopic and microscopic mathematical models for the life sciences have been
isolated from mesoscopic and macroscopic ones in most cases, while mesoscopic and macroscopic
entities inevitably consist of macroscopic entities. Here we report an effort to expand the knowledge
of cellular, subcellular, and molecular levels to higher levels such as tissues and organs through
biological simulation, which is one of the main contributions of systems biology. We are aware that
such a bottom-up approach is not always appropriate; por ejemplo, a description of solid-body mo-
tion with quantum mechanics is almost always pointless. Sin embargo, given the overwhelming shortage
of quantitative information at the mesoscopic and macroscopic levels, a serious effort to elucidate
higher-level behaviors of life based on the abundant molecular and cellular data collected is of value
whatever the difficulty entailed. To construct a tissue or organ model based on a single-cell model,
simple aggregation of the cell model into a higher-level model is essentially inadequate. Not only
organs of complicated structure such as the heart and brain, but those of comparatively simple
structure such as the liver and kidney, are impossible to model by simple multiplication of single cells,
because each tissue or organ has its own intrinsic and exquisitely specific structure. The spatio-
temporal position of the cells in the tissue or organ structure influences the behavior of each cell, y
the total of the cellular behaviors naturally affects the behaviors of the higher structures— the tissue,
organ, or organism —in turn. Por lo tanto, how to effectively assemble the single-cell model(s),
a saber, how to represent the mesoscopic and macroscopic structure, is critically important for the
modeling of tissues and/or organs.

For this study the rodent liver was selected as the subject of modeling because of (1) its com-
paratively simple histological structure among mammalian tissues and organs [37], y (2) el
availability of data from previous investigations, including a great deal of kinetic data. The liver
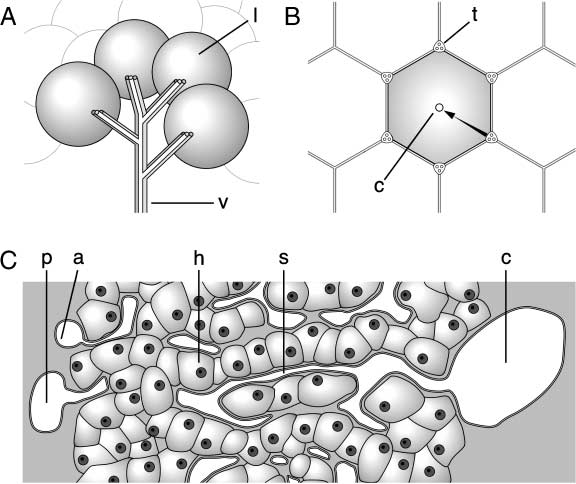
consists of a huge structure consisting of repetitions of a fundamentally simple structural unit, el
hepatic lobule. The entire liver looks the like a bunch of grapes, in which the portal tracts (influx
vessels) and the central vein (efflux vessel) supply each bunch (Figura 1A). The portal tracts are a
bundle of small branches of the hepatic portal vein, which carries the absorbed food products
directly from the gut to the liver, and the hepatic artery, which supplies oxygen to support liver
metabolism. The central veins are confluent and form the hepatic vein. The hepatic lobule is roughly
hexagonal in sectional configuration and is centered on a central vein. The portal tracts are posi-
tioned at the corners of the hexagon. The blood from the portal vein and hepatic artery branches in
the portal tracts flows to a central vein (Figura 1B, C). The overwhelmingly predominant component
of the liver is the parenchymal liver cell, called the hepatocyte. The hepatocytes form branching

Artificial Life Volume 14, Número 1

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
a
r
t
yo
/

a
r
t
i
C
mi
–
pag
d

F
/

1
4
1
3
1
6
6
2
4
6
6
a
r
t
yo
.

2
0
0
8
1
4
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

h. Ohno et al.

Construction of a Biological Tissue Model Based on a Single-Cell Model

Cifra 1. Schematic drawings of the connection of the hepatic lobules in the liver (A), hexagonal shape of a hepatic
structure in section (B), and the porto-central axis (C). yo, a hepatic lobule; v, influx and efflux vessels consist of terminal
branches of the portal vein, hepatic artery, and hepatic vein; t, periportal tracts; C, central vein; pag, terminal portal vein; a,
terminal hepatic artery; s, sinusoid; h, hepatocyte. The arrow indicates the direction of sinusoidal blood flow.

cords of cells between capillary vessels, which are known as sinusoids in the hepatic lobule. Blood
flow into the sinusoids comes from terminal branches of the portal tracts, bringing nutrient-rich
blood from the portal vein and oxygen-rich blood from the hepatic artery. Blood from the portal
vein and the hepatic artery passes through the sinusoids, where it comes into intimate contact with
the hepatocytes for the exchange of nutrients and metabolic products. The blood then flows into
branches of the hepatic vein and thence into the inferior vena cava. Por lo tanto, the liver can be
described histologically as a rough hierarchy of the hepatocyte (cell), the hepatic lobule (tejido), y
the liver (organ).

Concentrations of nutrients and metabolites in the periportal zone (the upper reach of the
sinusoid) are inevitably different from those in the perivenous zone (the lower reach) even if the
properties of all the hepatocytes are homogeneous, because the downstream hepatocytes accept
nutrients and metabolites already taken up and put there by the upstream hepatocytes. Thus a liver
model constructed by multiplying single hepatocytes by the number of hepatocytes in the liver
would not be representative, but it may be possible to investigate the global behavior of the liver by
a simple multiplication of the hepatic lobule, since the liver is a repetitive accumulation of the
hepatic lobules as functioning units. Sin embargo, since a human hepatic lobule consists of
approximately one million hepatocytes (there are approximately 100 billion hepatocytes and
100,000 lobules in a human liver), simulation of the hepatic lobule at the molecular level is far
from realizable with the computational resources currently available. Thereupon, we consider a
sinusoid along the porto-central axis (the line between the portal tracts and the central vein) y el
surrounding hepatocytes, known as hepatic cords (Figura 1C), to be the primary histological unit for
modelado. Since the hepatic lobule has a point symmetry in which the center point is the central vein,
the overall behavior of the hepatic lobule and the liver can be derived from that of the porto-central
axis. The porto-central axis is the minimal unit preserving the proportionality with the dynamics of the
mayor que, macroscopic structure. Through model construction of the porto-central axis, it becomes
possible to investigate the behavior of the liver, at the organ level, based on molecular-level simu-
lations of single hepatocytes.

Artificial Life Volume 14, Número 1

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
a
r
t
yo
/

a
r
t
i
C
mi
–
pag
d

F
/

1
4
1
3
1
6
6
2
4
6
6
a
r
t
yo
.

2
0
0
8
1
4
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

h. Ohno et al.

Construction of a Biological Tissue Model Based on a Single-Cell Model

A multitude of hepatocyte zonal heterogeneities are known [19, 23 –25]. Fatty acid oxidation,
gluconeogenesis, ureagenesis, amino acid conversion to glucose, cholesterol synthesis, and glutathi-
one peroxidation and conjugation are predominant in the periportal zone; Glycolysis, liponeogenesis,
glutamine formation from ammonia, monooxygenation, and glucuronidation are predominant in
the perivenous zone. In addition to the heterogeneity generated by the structural constraints de-
scribed above, enzyme activities regulated by the substrate concentrations in blood, the circulating
hormone levels, the autonomic hepatic nerves, and the biomatrix are known to actively modify the
conditions of the zonal heterogeneities. Such active regulation of heterogeneities must result from
some gain in evolutionary fitness. Since fitness is necessarily the property not of molecules, genes,
cells, tissues, or organs, but of classes of organisms [34], the advantage generated by heterogeneous
regulation within an organ at the subcellular level must be measured to elucidate the functional ac-
tivity of the organ that the regulation has evolved. Actualmente, it is extremely hard for the experi-
mental biosciences to measure the properties of an organism simultaneously at multiple levels such as
the cell, tejido, and organism. en este estudio, we constructed a model of the porto-central axis, y
obtained insight into the origin of one of the regulated heterogeneities in metabolism, ammonia
detoxification.

Ammonia metabolism is one of the most important metabolic pathways for a mammal, desde
the accumulation of ammonia induces lethal uremia. Ammonia is detoxified exclusively by the
hepatocyte in mammals. Respectivamente, appropriate ammonia metabolism in the mammalian liver is
directly reflected in the health of the organism. The efficiency of ammonia metabolism should
therefore link directly with fluctuations of fitness. The fitness fluctuation related to ammonia
metabolism may be captured and analyzed through calculation of the efficiency of ammonia
detoxification in the porto-central axis unit. The pathway structure of ammonia metabolism around
the core of the urea cycle is relatively simple among the major metabolic pathways, and there are a
number of biological investigations and several mathematical models for single hepatocytes. El
metabolism of ammonia and amino acids is also heterogeneous in the hepatic lobule. The periportal
zone is characterized by a high capacity for uptake and catabolism of amino acids (except glutamate
and aspartate) as well as for urea synthesis and gluconeogenesis. Por otro lado, glutamine
synthesis, ornithine transamination, and the uptake of vascular glutamate, aspartate, malate, y un-
ketoglutarate are restricted to a small perivenous hepatocyte population [20]. Respectivamente, en el
hepatic lobule the major pathways for ammonia detoxification and urea and glutamine synthesis are
anatomically separated from each other and represent in functional terms the sequence of a
periportal
low-affinity system (urea synthesis) and a perivenous high-affinity system (glutamine
synthesis) for ammonia detoxification [13 – 18, 20]. Perivenous glutamine synthase-containing
hepatocytes act as high-affinity scavengers for the ammonia that escapes the upstream urea-
synthesizing compartment.

Three major enzymes involved in ammonia metabolism — carbamoyl phosphate synthase (CPS),
ornithine aminotransferase (OAT), and glutamine synthase (GS) —have been characterized as being
heterogeneously expressed (synthesized at different rates) in particular locations within the hepatic
lobule [5, 9, 10, 22 – 24]. The regulation of gene expression of these enzymes may be mainly deter-
mined not by the substrate concentrations, the hormone levels, or neural regulation, but rather by
the histological position of the hepatocyte in the lobule [12, 20, 36, 43, 44]. Además,
ornithine aminotransferase is demonstrated to be coexpressed with glutamine synthase in perivenous
intestine,
hepatocytes in adult mouse liver, while there is no such coexpression in the kidney,
and brain [30, 31]. One possible explanation of this phenomenon is that the colocalized enzymes
lead to more efficient removal of ammonia because ornithine aminotransferase produces glutamate,
which is a substrate for glutamine synthase [31]. Sin embargo, these are still matters of speculation
and only subjected to thought experiments. Positional regulation, such as regulation of gene
expresión, can modulate the pattern of intralobular heterogeneity. Such heterogeneity may appear
to be dispensable, but for some reason it is actually present. This raises the question of the pur-
pose for which heterogeneous gene expressions exist. While various possible determinants of the
positional regulation of gene expression have been proposed (gradual change in the concentrations

Artificial Life Volume 14, Número 1

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
a
r
t
yo
/

a
r
t
i
C
mi
–
pag
d

F
/

1
4
1
3
1
6
6
2
4
6
6
a
r
t
yo
.

2
0
0
8
1
4
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

h. Ohno et al.

Construction of a Biological Tissue Model Based on a Single-Cell Model

of blood constituents, the extracellular matrix produced by the endothelium of the central venule,
intrahepatic cell-cell interaction, etc.), the regulative function of heterogeneous gene expression has been
developed evolutionally and has preserved whichever determinants are selected for over time.

Here we show that the positional regulation of gene expression may improve the energy efficiency
of ammonia metabolism at the tissue and organ levels, using computer simulation of the porto-
central axis unit. Improvement of ammonia detoxification in the liver means increased efficiency at
the individual organism level, and this could very well amount to a gain in evolutionary fitness. Este
suggests that these particular forms of gene expression regulation may reasonably be characterized as
advantageous adaptations evolved through natural selection.

2 The Model

We hypothesized that the heterogeneous expression of carbamoyl phosphate synthase, glutamine
synthase, and ornithine aminotransferase improves the energy efficiency of ammonia clearance, y
therefore increases the evolutionary fitness of the liver, as well as that of the organism. El número
of ATP molecules required to eliminate one molecule of ammonia in the hepatic lobule is certainly
an appropriate indicator of the energy efficiency of ammonia detoxification. Because ammonia is
eliminated by multiple pathways, mainly urea synthesis and glutamine synthesis, the stoichiometry of
total ammonia degradation is variable. To calculate the ATP consumption by ammonia metabolism,
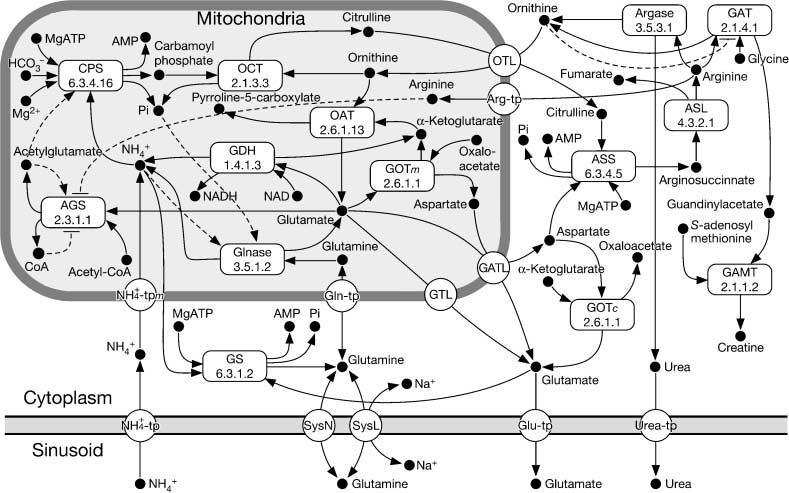
a simple model of the hepatic lobule was constructed, through a two-step procedure. In the first step,
a single-compartment model that consisted of the hepatocyte and the sinusoid, named the zone model,
was built (Cifra 2), and unknown parameters were predicted, as will be described later. En el
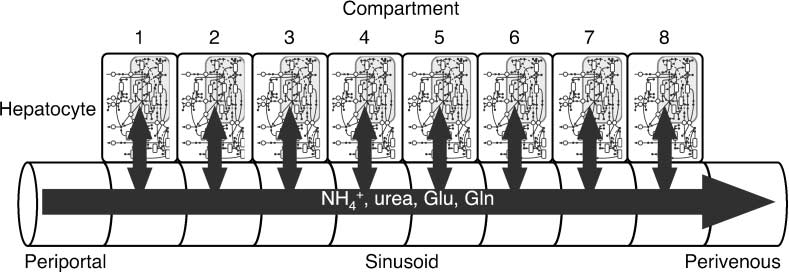
second step, we modeled the hepatic lobule as a simple compartment model in which eight modeled
compartments were connected in series.

The zone model included 67 substances and 29 total reactions consisting of chemical reactions
and transportations. Almost all of the known enzymes in the mammalian ammonia metabolism have
been described by rate equations. Mathematical models for four enzymes were developed for a urea
cycle model developed by Kuchel and his colleagues [29]. Carbamoyl phosphate synthase [7, 8],
glutamine synthase [40], phosphate-dependent glutaminase (Glnase) [35, 41], N-acetyl glutamate
synthetase (AGS) [2, 3], system N (the sodium-dependent glutamine transport system) [32], sistema
l (the sodium-independent glutamine transport system) [32], the ammonia transport system
(between the sinusoid and the hepatocellular cytoplasm), the glutamate transport system [11], y
the urea transport system (from the hepatocellular cytoplasm to the sinusoid) were modeled using
kinetic information obtained from previous publications (see Appendix 1 and Web supplements).
The rest of the models, eso es, the six enzymes and three transporters, were quoted from a
ureagenesis model using a MetaNet graph (see Appendix A1.1) [28]. While MetaNet cannot be
guaranteed to reproduce accurate enzyme kinetics [28], it was used with the expectation that it is able
to estimate the rates of reactions roughly but sufficiently well.

The metabolite concentrations were determined mainly based on Kohn and his colleagues’ work
(see Web supplements, Table S1) [28]. The volume ratio of cytoplasm to mitochondria was assumed
to be four to one [28], and that between the cytoplasm and the sinusoidal space one to one. Certain
kinetic parameters were adjusted under an assumption of steady state. If the model is held in steady
estado, the following equations are adequately assumed:

vCPS ¼ vOCT ¼ vOTL ¼ vASS ¼ vASL

vGAMT ¼ vGAT ¼ vASL (cid:6) vArgase

vGOTm ¼ vGATL ¼ vASS ¼ vGOTc

Artificial Life Volume 14, Número 1

ð1Þ

ð2Þ

ð3Þ

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
a
r
t
yo
/

a
r
t
i
C
mi
–
pag
d

F
/

1
4
1
3
1
6
6
2
4
6
6
a
r
t
yo
.

2
0
0
8
1
4
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

h. Ohno et al.

Construction of a Biological Tissue Model Based on a Single-Cell Model

Cifra 2. Schematic representation of the model describing ammonia metabolism in single zone model. Filled circles,
open rounded rectangles, and open circles represent substances, enzymes, and transporters, respectivamente. Solid line
arrows represent reactions and transportations. Broken lines with a triangular arrowhead and with a bar at one end
represent positive and negative feedback, respectivamente. AGS, N-acetyl glutamate synthetase; Argase, arginase; ASL,
argininosuccinate lyase; ASS, argininosuccinate synthetase; CPS, carbamoyl phosphate synthetase; GAMT, guanidino-
acetate methyltransferase; GAT, arginine:glycine amidinotransferase; GDH, glutamate dehydrogenase; Glnase, phosphate-
dependent glutaminase; GOTc, glutamate:oxaloacetate transaminase in the cytoplasm; GOTm, glutamate:oxaloacetate
transaminase in the mitochondria; GS, glutamine synthetase; OAT, ornithine aminotransferase, OCT, ornithine carba-
moyltransferase; Arg-tp, arginine transporter; GATL, glutamate-aspartate translocase; Gln-tp, glutamine transporter in
+-tp, ammonia transporter in
mitochondrial membrane; Glu-tp, glutamate transporter; GTL, glutamate translocase; NH4
+-tpm, ammonia transporter in the mitochondrial membrane; OTL, ornithine-citrulline trans-
the cell membrane; NH4
locase; SysL, system L; SysN, system N; Urea-tp, urea transporter. The entity abbreviation may be used with an index
variable that represents the location of the entity. The indices c, metro, and s indicate the cytoplasm, mitochondria, y
sinusoid, respectivamente. Numbers in the rounded rectangles represent EC numbers.

De este modo, [CPS], [OCT], [OTL], [ASS], [GAMT], [GAT], [GOTm], y [GATL] were determined, based
on the premise of [ASL] ¼ 2.2E(cid:6)6 METRO [29], vArgase ¼ 6.6E(cid:6)6 M s(cid:6)1 [29], y [GOTc] ¼ 1E(cid:6)6 METRO
[28]. The kcat’s of glutaminase and glutamine synthase were calculated from the fluxes through the
enzymes in the perfused rat liver: 72 y 151 nmol min(cid:6)1 per gram [19], with the assumptions
[GS] ¼ 1E(cid:6)5 M and [Glnase] ¼ 1E(cid:6)4 METRO. The activity of glutaminase was approximated as
1.786mi(cid:6)5 M s(cid:6)1 based on reported conversion factors as follows: 0.8 g hepatocyte wet wt per gram
liver wet wt, 0.42 g dry wt per gram hepatocyte wet wt [6], 0.2 ml mitochondrial water per gram dry
wt of liver [1]. The activity in M s(cid:6)1 of glutamine synthase was calculated from the ratio of the
two enzymes’ activities described above. The Vmax’s of system N and system L were determined
from this premise. vAGS and vGTL were set at [AGS] ¼ 2E(cid:6)5 METRO [2] y [GTL] ¼ 1E(cid:6)7 METRO [28],
+-tp was assumed to be 5E(cid:6)5 M s(cid:6)1. The values of vGDH and vOAT were obtained as
and v NH4
follows:

vGDH ¼ vCPS þ vGS (cid:6) vGlunase (cid:6) vNHþ

4 -tp

vOAT ¼ vGOTm þ vGDH

ð4Þ

ð5Þ

Artificial Life Volume 14, Número 1

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
a
r
t
yo
/

a
r
t
i
C
mi
–
pag
d

F
/

1
4
1
3
1
6
6
2
4
6
6
a
r
t
yo
.

2
0
0
8
1
4
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

h. Ohno et al.

Construction of a Biological Tissue Model Based on a Single-Cell Model

These equations gave [GDH] y [OAT]. The glutamate transport between the cytoplasm and the
sinusoid (vGlu-tp) and the inflow of glutamate from other pathways in mitochondria (vGlu-spp) eran
modeled to meet the requirements as follows:

vGlu-tp ¼ vGS þ vGTL (cid:6) vGOTc þ vGATL

vGlu-spp ¼ vAGS (cid:6) vGlunase (cid:6) vGTL þ vGOTm þ vGDH (cid:6) vOAT (cid:6) vGATL

ð6Þ

ð7Þ

Además, the flux of ornithine from other pathways in mitochondria was set equal to vOAT (ver
Web supplements, Table S2).

To develop a hepatic lobule model, eight constructed zone models were put in a row and con-
nected one to the next through sinusoidal compartments (Cifra 3),
in which substances pass
through the sinusoids while the hepatocytes are isolated from each other. The first zone (el
influx compartment) and the eighth zone (the efflux compartment) were joined to compartments of
the upstream periportal tracts and the downstream central vein. Four substances — ammonia, glu-
tamine, glutamate, and urea — flow through the sinusoid and upstream/downstream vessels. Su
fluxes from the periportal influx compartment to the perivenous efflux compartment are represented
by a simple mass action model as the product of the rate constant and substance concentration (ver
Apéndice 1). No enzymatic reaction is placed in the vessels.

All rate equations and initial concentrations of metabolites were set to be identical among all
compartments, but some enzymes were given a slope to their content, representing the regulated
heterogeneous gene expressions. In order to evaluate the effects of gradients of the enzyme
expressions on metabolic state, six combinations of the gene expression conditions were examined
(Mesa 1). The first model, named the N model, had no gradient of the enzyme along the porto-central
axis. The second model, named the GCO model, in which steep gradients of carbamoyl phosphate
synthase, glutamine synthase, and ornithine aminotransferase were introduced, most faithfully
modeled the actual
lobular ammonia metabolism among the six models. The remaining four
models — the G model, GC model, O model, and GO model — partially incorporated the enzyme gradients
(ver tabla 1 for details). These significant enzyme slopes were incorporated using a mechanistic
modelo, which assessed the transcription rates of carbamoyl phosphate synthase and glutamine
synthase by the relative position in the hepatic lobule (see Appendix A1.3) [5]. en este estudio, el
relative expression levels were assumed to correspond to the transcription rates. The total contents of
the enzymes in each model were set equal. The expression status of ornithine aminotransferase was
presumed to be evaluable in the same manner as glutamine synthase, based on the reports of
coexpression of glutamine synthase and ornithine aminotransferase in the hepatic lobule [30, 31].
Además, 60 instances of the models were prepared for each model type by varying the parameters
of the flux balance of the glutamate transport system (four patterns): the glutamate flux from outside
pathways (three patterns) and the rate constant of sinusoidal substance flow (5 patrones), for a total of
4 (cid:8) 3 (cid:8) 5 ¼ 60 patrones (see Appendix A1.4).

3 Métodos

3.1 Numerical Integration
Once each chemical and transport reaction rate had been set, a numerical integration of the model
was conducted using E-CELL system version 1.1 [42]. The model was implemented by defining the
variable Reactor, which describes reaction processes, and the variable Rule, which provides organi-
zational information, substances, and stoichiometry. Simulations were performed using Sun Grid
Engine 5.3 en 40 clustered Xeon 2.0 GHz HPC-IAX, and employing the fourth-order Runge-Kutta
método. The step interval for integration was set to 0.01 s.

Artificial Life Volume 14, Número 1

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
a
r
t
yo
/

a
r
t
i
C
mi
–
pag
d

F
/

1
4
1
3
1
6
6
2
4
6
6
a
r
t
yo
.

2
0
0
8
1
4
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

h. Ohno et al.

Construction of a Biological Tissue Model Based on a Single-Cell Model

Cifra 3. Schematic of eight-cellular-compartment model with sinusoidal compartments. PP and PV represent the peri-
+), urea, glutamate (Glu), and glutamine (Gln) flow from
portal end and the perivenous end, respectivamente. Ammonia (NH4
the periportal inflow compartment to the perivenous outflow compartment, interacting with cellular compartments.

3.2 Análisis de los datos
To compare the metabolic aspects in the periportal zone and in the perivenous zone, the flux dis-
tributions were examined. To evaluate the effects of the enzyme slope along the lobule metabolic
estado, the following rates were calculated and used as the indices:

Rate of ammonia degradation: JNHþ

4;deg ¼ vCPS þ vGS

Rate of ammonia generation: JNHþ

4;gen ¼ vGlnase þ vGDH

Rate of ammonia detoxification: JNHþ

4;detox ¼ JNHþ

4;deg (cid:6) JNHþ

4;generación

Rate of ATP consumption: JATP;consum ¼ 2vCPS þ vASS

ð8Þ

ð9Þ

ð10Þ

ð11Þ

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
a
r
t
yo
/

a
r
t
i
C
mi
–
pag
d

F
/

1
4
1
3
1
6
6
2
4
6
6
a
r
t
yo
.

2
0
0
8
1
4
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Mesa 1. Types of model. Six models examined in this study had different combinations of enzyme gradients along the
porto-central axis. Letters G, C, and O included in the names of model types are the first letter of gradually expressed
enzymes: glutamine synthase (GS), carbamoyl phosphate synthase (CS), and ornithine aminotransferase (OAT ),
respectivamente. Enzyme gradients were incorporated into models in an all-or-none fashion. Symbol + o (cid:6) means whether
the enzyme gradient existed in the models. The letters G, C, and O also indicate the existence of the gradient of the
respective enzyme. The N model had no gradient of the enzyme.

Model type

norte

GRAMO

GCO

(cid:6)

Gradual expression of enzyme

CPS

OAT

(cid:6)

Artificial Life Volume 14, Número 1

h. Ohno et al.

Construction of a Biological Tissue Model Based on a Single-Cell Model

Energy efficiency g: ¼

JNHþ
4;detox
JATP;consum

Rate of bicarbonate consumption : JHCO(cid:6)

3 ;consum ¼ vCPS

ð12Þ

ð13Þ

+,detox and vNH4

RNH4
as the mean F SD of 60 models for each gradient pattern of the model.

+-tp are nearly equal under the assumption of steady state. Data were summarized

4 Resultados

4.1 Simulation of the Single-Zone Model
The zone model, which consists of a hepatocellular compartment and a sinusoidal compartment,
preserved a quasi steady state for longer than 100,000 s with the initial values mainly quoted from
the published literature based on experimental data (see Web supplement, Table S1). The results
support the appropriateness of the zone model, as described below.

4.2 Comparison of the Hepatic Lobule Models with Different Enzyme

Expressions Patterns

Each model with slopes of the various enzyme expressions exhibits lobule-wide metabolic aspects
very different from the N model with no such enzymatic slope. The simulated flux heterogeneities
among the porto-central axis are presented in Figures 4 y 5. In the GCO model, which is the
best-approximated model to actual lobular metabolism, the active pathways were quite different
between the periportal and the perivenous zones (Cifra 4). Urea production, urea exportation, y
creatine generation were pronouncedly predominant in the periportal zone (red arrows in Figure 4B,
Figure 5F a, b, j, k, yo, q, t), while glutamine formation and exportation were predominantly seen in
the perivenous zone (blue arrows in Figure 4B, Figure 5F c, d, mi, h, i, oh, r, s). Because mitochondrial
ornithine aminotransferase is mainly expressed in the perivenous zone, the concentration of gluta-
compañero, which is a reaction product of ornithine aminotransferase, was higher in the perivenous than in
the periportal zone. The glutamate concentration in mitochondria was increased from 6.97E(cid:6)3 a
8.70mi(cid:6)2 M along the porto-central axis. Como consecuencia, the velocity of glutamate dehydrogenase,
which catalyzes glutamate, was larger in the perivenous than in the periportal zone ( Figure 5F d).
Glutamate-aspartate translocase and mitochondrial GOT also exhibited higher activities in the
perivenous zone, while cytoplasmic GOT showed an opposite trend of flux between the periportal
and the perivenous zone ( Figura 4B, Figure 5F e, i, oh). Cytoplasmic GOT catalyzed transamination
between glutamate and oxaloacetate to produce aspartate, and the generated bulk of aspartate was
used as a substrate for argininosuccinate synthetase in the periportal zone ( Figura 4B, Figure 5F j). En
the N model with no enzyme gradient, most of the chemical reactions and transportation exhibited
larger fluxes in the periportal zone than in the perivenous zone ( Figure 5A). Due to the high affinity
for ammonia of glutamine synthetase, a saber, 1/10 of the Km of carbamoyl phosphate synthetase,
ammonia predominantly converted to glutamine in the periportal zone. The fluxes gently changed
from the periportal to the perivenous zone, while dramatic alterations were seen in the sixth and
seventh compartments in the GCO model, revealing that the perivenous hepatocytes played a lesser
role in metabolism in the N model ( Figure 5A, F). The G model and the GC model exhibited higher
activities of ureagenesis in the periportal zone and greater formation and export of glutamine in
the perivenous zone, just like the GCO model. Sin embargo, in contrast to the GCO model, más grande
fluxes of OAT, GDH, mitochondrial GOT, and GATL were observed in both models ( Figure 5B,C
C, d, mi, oh). In the O model, most of the reactions exhibited higher activity in the perivenous zone,
except for the predominant detoxification of ammonia by glutamine synthetase ( Figure 5D). Lobule-
wide metabolic aspects of the GO model resembled those of the GCO model except for the
urea cycle and glutamate transport ( Figure 5E). There were fewer contrasts in activities of the urea

Artificial Life Volume 14, Número 1

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
a
r
t
yo
/

a
r
t
i
C
mi
–
pag
d

F
/

1
4
1
3
1
6
6
2
4
6
6
a
r
t
yo
.

2
0
0
8
1
4
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

h. Ohno et al.

Construction of a Biological Tissue Model Based on a Single-Cell Model

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
a
r
t
yo
/

a
r
t
i
C
mi
–
pag
d

F
/

1
4
1
3
1
6
6
2
4
6
6
a
r
t
yo
.

2
0
0
8
1
4
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 4. Flux disparities between the two ends of the porto-central axis in N model (A) and GCO model (B). The width
of each arrow proportionally reflects the flux ratio between the two ends (the first and the eighth compartment). El
thickest line indicates the flux disparity to be fivefold or more. Red and blue arrows indicate fluxes predominant in the
periportal and the perivenous zone, respectivamente. Fluxes with a disparity of less than 1.5 are indicated by the black arrow.
The size of the arrows is proportional to the flux except for extremely high fluxes: the Glu-tp in A, ornithine amino-
transferase, mitochondrial GOT, and GATL in B. Pronounced urea production, urea export, and creatine generation
were seen in the periportal region, while pronounced glutamine formation and reactions which mediate glutamate were
seen in the perivenous. The figure shows a representative result among the 60 parameter conditions (see Appendix A1.4
for details).

Artificial Life Volume 14, Número 1

h. Ohno et al.

Construction of a Biological Tissue Model Based on a Single-Cell Model

Cifra 5. Flux heterogeneities along the porto-central axis. Relative fluxes of 20 representative processes (enzyme
reaction or transportation across a membrane) are indicated as color matrices. For each process, the depth of color is
proportional to the relative magnitude of its flux, and the maximum absolute flux is indicated by the deepest color. Verde
and red indicate positive and negative direction of the process, respectivamente. Colors within the same process are com-
parable, but inter-process comparison is inappropriate. The numbers on the horizontal axis (1 – 8) indicate the com-
partment number. Por lo tanto, the left side represents the periportal and the right side represents the perivenous zone.
Grupo A, N model; B, G model; C, GC model; D, O model; mi, GO model; F, GCO model. On the vertical axis: a, CPS; b,
OCT; C, OAT; d, GDH; mi, GOTm; F, Glnase; gramo, AGS; h, GS; i, GOTc; j, ASS; k, ASL; yo, Argase; metro, GAT; norte, GAMT; oh, GATL;
pag, GTL; q, OTL; r, SysL; s, SysN; t, Urea-tp. The figure shows a representative result among the 60 parameter conditions
(see Appendix A1.4 for details).

cycle and glutamate transport along the porto-central axis in the GO model than in the GCO model
( Figure 5E).

4.3 Evaluation of the Effects of Gene Expression Gradients along the

Porto-central Axis

The GCO model ranks highest among six models in the rate and energy efficiency of ammonia
detoxification. The mean rate of elimination of ammonia from the sinusoid was 11.8% greater in the
GCO model than in the control ( N model) ( Mesa 2). Although the rate of degradation of ammonia
in all eight compartments was 20.0% slower in the GCO model than in the control, the rate of
ammonia generation was also 53.8% slower than in the control model ( Mesa 2), showing that the
GCO model was able to remove ammonia more efficiently than the control. The mean rate of ATP
consumption in the GCO model was 9.5% less than in the control model ( Mesa 2). The O model
and GO model also exhibited less ATP consumption than the control. The energy efficiency g,
which means the number of consumed ATP molecules required for the elimination of one ammonia
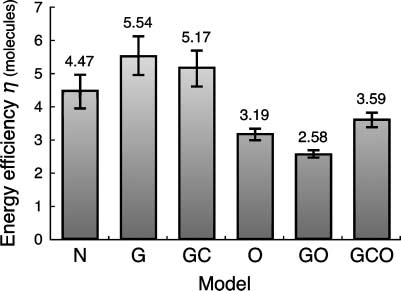
molecule, was smaller in the GCO model than in the control ( Cifra 5, 3.59 F 0.22 versus 4.47 F
0.49). The O model and the GO model also displayed smaller g, and the G model and the GC
model greater g, than the control ( Cifra 6).

Elimination of bicarbonate in the GCO model was comparable in rate to that in the control
( Mesa 2). The G and GC models exhibited greater elimination of bicarbonate, but the O and GO
models exhibited a lesser elimination of bicarbonate, than the control ( Mesa 2).

5 Discusión

en este estudio, a mathematical model in which rough histological structure and several forms of reg-
ulation of gene expression has been implemented, and it succeeded in representing the metabolic
heterogeneity of ammonia detoxification in the liver. Heterogeneous flux distributions bearing a
close resemblance to the actual hepatic lobule were observed along the porto-central axis in the

Artificial Life Volume 14, Número 1

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
a
r
t
yo
/

a
r
t
i
C
mi
–
pag
d

F
/

1
4
1
3
1
6
6
2
4
6
6
a
r
t
yo
.

2
0
0
8
1
4
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

h. Ohno et al.

Construction of a Biological Tissue Model Based on a Single-Cell Model

Mesa 2. The rates of metabolic processes of five models relative to the N model. The highest relative rate of ammonia
detoxification was seen in the GCO model. The O model had the lowest relative rate of ATP consumption and the
lowest relative rate of bicarbonate consumption.

Process

Model N

Ammonia degradation

Ammonia generation

Ammonia detoxification

1.00

Relative rate

GRAMO

0.95

1.00

0.90

1.01

0.99

1.03

0.79

0.48

1.09

0.76

0.46

1.04

GCO

0.80

0.46

1.12

ATP consumption

1.00

1.12

1.19

0.78

0.86

0.90

Bicarbonate consumption

1.00

1.26

1.34

0.77

0.94

0.99

GCO model, which is an approximation of the actual regulation of gene expression in the ammonia-
metabolism-related enzymes. The periportal hepatocytes play a role in urea production and creatine
generación, while the perivenous cells play a role in glutamine generation and glutamate metabolism
in this model ( Cifra 4). The model without any regulation of gene expression, the N model, también
displayed heterogeneous metabolism, but the extent of the heterogeneity was quite reduced com-
pared to the GCO model, indicating that two factors, the histological structure and gradual gene
expresión, are likely sufficient to simulate the zonal heterogeneity in liver ammonia detoxification,
while the histological structure alone was insufficient. The simulation results also suggest that the
gradients of expression of the three enzymes (CPS, GS, and OAT) along the porto-central axis im-
prove the energy efficiency of ammonia detoxification ( Mesa 2 y figura 6).

Flux distributions in the model with the gradients of CPS, GS, and OAT are close to the schemes
of heterogeneous ammonia metabolism in the lobule discussed in many reports [20, 31]. It has been
suggested that urea production and bicarbonate consumption in exchange for ammonia detoxification
by the urea cycle are more highly activated in periportal hepatocytes, and glutamine generation and
reactions that mediate glutamate (OAT, GDH) are more highly activated in perivenous (opposite-
lado) hepatocytes [20, 31]. Three enzymes, CPS, GS, and OAT, chiefly restrict and characterize the flux
distributions in each zone. The flux distributions between the periportal and perivenous zone have a
mutually exclusive relationship. Glutamine metabolism ( both of synthesis and consumption) era

Cifra 6. Energy efficiency in the six models with different gene expression patterns. Energy efficiencies g were calculated
from JNH4

+,detox and JATP,consum (see text for details). Data are means F SD.

Artificial Life Volume 14, Número 1

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
a
r
t
yo
/

a
r
t
i
C
mi
–
pag
d

F
/

1
4
1
3
1
6
6
2
4
6
6
a
r
t
yo
.

2
0
0
8
1
4
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

h. Ohno et al.

Construction of a Biological Tissue Model Based on a Single-Cell Model

hardly seen in the periportal zone, while urea production and creatine generation were not seen in the
perivenous zone. Cytoplasmic GOT showed opposite trends between the two zones. Ornithine
aminotransferase in the perivenous hepatocytes is speculated to lead to an accumulation of glutamate,
which is the substrate for glutamine synthetase, and to increase the elimination of ammonia [31].

Our model differs in some features from previous investigations. Glutamate dehydrogenase has
been suggested to have significantly increased activity in the perivenous zone [33]. In our model,
higher activities were also shown in the perivenous than in the periportal zone, but the direction of
the reaction was different from the suggestion in a previous report [4]. For glutamate dehydrogenase
in the perivenous zone, a reverse reaction to that suggested by other investigators was predominant
[4]. This might be attributable to the lack of the a-ketoglutarate transport system in our model. Si
that mechanism were implemented in our model and the influxes of a-ketoglutarate to the
perivenous mitochondria increased, the reaction direction might be the same as suggested by previ-
ous work. Phosphate-dependent glutaminase has been suggested to be highly activated in the peri-
portal zone [20, 45]. Sin embargo, the tendency towards emphasized activity of phosphate-dependent
glutaminase in the periportal hepatocytes was not recreated in our model.

Several factors are considered to be responsible for the result in our experiments. One factor is
the roughness of the mathematical model of phosphate-dependent glutaminase, such as the lack of a
pH effect despite the actual high sensitivity to pH [41]. Another factor is the absence of regulation of
phosphate-dependent glutaminase gene expression. It might be necessary to give a slope to gene
expression along the hepatic lobule, as we did with GS, OAT, and CPS. Although this model does
not yet have the requisite accuracy, it is the first realization of a model able to yield metabolic aspects
with both quantitative information at the micro, or kinetic, level and functional significance at the
macro, or tissue, level in the liver.

It is proposed that one major advantage of the functional separation in the hepatic lobule is that
the periportal urea synthesis flux is flexible with regard to the requirement of the acid-base condition
without the risk of hyperammonemia, because effective elimination of ammonia is carried out by
perivenous glutamine synthetase [13 –18, 20]. It is also proposed that ornithine aminotransferase,
which is co-localized with glutamine synthetase, would lead to more efficient removal of ammonia.
en este estudio, because the effect of pH is excluded, no indication is given of its relation to the major
advantage of the functional separation, which has been discussed by previous investigators. pero lo es
newly suggested that the functional separation that is formed by steep gradients of GS, OAT, y
CPS along the hepatic lobule contributes to effective ammonia elimination with efficient energy use.
Curiosamente, the glutamine synthetase and ornithine aminotransferase expression patterns are not
the same in other organs, such as the kidney, cerebro, and intestine [31]. This fact indicates cooperation
of the expression of the two enzymes evolved specifically in the hepatic lobule. The steep gradients
of the three enzymes along the porto-central axis are considered to have been evolved into effective
ammonia detoxification, which takes place exclusively in the liver. Although the improvement in the
energy efficiency shown by simulation is not robust, it is sufficient to confer an adaptive advantage,
since ammonia metabolism consumes a large quantity of ATP in the liver. Schneider and colleagues
have reported ureagenesis accounts for 15% of the total energy consumption of rat hepatocytes
incubated in a nutriment-enriched medium [38]. Por último, this simulation will have to be verified
with wet ( physiological) experimentos, but it is difficult to evaluate changes in the lobular energy
efficiency along with changes in the porto-central axial regulation of gene expression by wet experi-
ments at present. Technology is continually advancing, sin embargo, and the day should not be far off
when such confirmation will be within reach.

En resumen, we have shown that a novel systems biological approach for tissue modeling well
simulated the functional separation in the hepatic lobule, and the simulation results suggested con-
tribution of the gradual expressions of three enzyme (CPS, GS, and OAT ) along the porto-central axis
to effective ammonia detoxification with efficient energy use. This method of reconstructing the intra-
cellular chemical processes, based on module architectures such as the hepatic lobule, enables analysis of
certain metabolic aspects with both quantitative information at the kinetic level and functional signifi-
cance at the tissue level, and to evaluate the effect of enzyme gene expression gradients on metabolic

Artificial Life Volume 14, Número 1

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
a
r
t
yo
/

a
r
t
i
C
mi
–
pag
d

F
/

1
4
1
3
1
6
6
2
4
6
6
a
r
t
yo
.

2
0
0
8
1
4
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

h. Ohno et al.

Construction of a Biological Tissue Model Based on a Single-Cell Model

estado. We here present a novel model system constructed by merging the single-cell model, cual estafa-
sisted of intracellular biochemical reactions, together with a proper structure (the histological structure
of the hepatic lobule) and emergent new properties of a higher-level order (zonal heterogeneity in
ammonia metabolism). Using such a model, it is possible to study how nanoscopic and microscopic
biological entities influence mesoscopic and macroscopic biological phenomena. Such approaches hold
great promise for advancing our understanding of complicated multicellular tissues, organs, y el
organism in a fitness landscape. This is an extremely useful and exclusive feature of systems biology.

Expresiones de gratitud
This work was financially supported by a Grant-in-aid for the Leading Project for Biosimulation, a
Grant-in-aid for the 21st Century Center of Excellence (COE) Program: Understanding and Control
of Life’s Function via Systems Biology, and a Grant-in-aid for Young Scientists B from the Ministry
of Education, Cultura, Sports, Ciencia, and Technology of Japan; research funds from Yamagata
Prefectural Government and Tsuruoka City; and the Inamori Foundation. Pacific Edit reviewed the
manuscript prior to submission.

Referencias
1. Achs, METRO. J., anderson, j. h., & Garfinkel, D. (1971). Gluconeogenesis in rat liver cytosol. I. Computadora
analysis of experimental data. Computers and Biomedical Research, an International Journal, 4(1), 65 – 106.

2. Bachmann, C., & Colombo, j. PAG. (1981). Computer simulation of the urea cycle: Trials for an

appropriate model. Enzyme, 26(5), 259 – 264.

3. Bachmann, C., Krahenbuhl, S., & Colombo, j. PAG. (1982). Purification and properties of acetyl-CoA:L-glutamate

n-acetyltransferase from human liver. The Biochemical Journal, 205(1), 123 – 127.

4. Boon, l., Geerts, W.. J., Jonker, A., Lamers, W.. h., & Van Noorden, C. j. (1999). High protein diet induces
pericentral glutamate dehydrogenase and ornithine aminotransferase to provide sufficient glutamate for
pericentral detoxification of ammonia in rat liver lobules. Histochemistry and Cell Biology, 111(6), 445 – 452.

5. Christoffels, V. METRO., Sassi, h., Ruijter, j. METRO., Moorman, A. F., Grange, T., & Lamers, W.. h. (1999).
A mechanistic model for the development and maintenance of portocentral gradients in gene
expression in the liver. Hepatology, 29(4), 1180 – 1192.

6. Crawford, j. METRO., & Blum, j. j. (1983). Quantitative analysis of flux along the gluconeogenic, glycolytic
and pentose phosphate pathways under reducing conditions in hepatocytes isolated from fed rats.
The Biochemical Journal, 212(3), 585 – 598.

7. eliot, k. r., & Tipton, k. F. (1974). Kinetic studies of bovine liver carbamoyl phosphate synthetase.

The Biochemical Journal, 141(3), 807 – 816.

8. eliot, k. r., & Tipton, k. F. (1974). Product inhibition studies on bovine liver carbamoyl

phosphate synthetase. The Biochemical Journal, 141(3), 817 – 824.

9. Gebhardt, R. (1992). Metabolic zonation of the liver: Regulation and implications for liver function.

Pharmacology & Therapeutics, 53(3), 275 – 354.

10. Gebhardt, r., Gaunitz, F., & Mecke, D. (1994). Heterogeneous ( positional) expression of hepatic

glutamine synthetase: Características, regulation and implications for hepatocarcinogenesis. In G. Weber &
C. mi. Forrest Weber (Editores.), Advances in enzyme regulation: Proceedings of the Twenty-Seventh Symposium
on Regulation of Enzyme Activity and Synthesis in Normal and Neoplastic TI (páginas. 3427 – 3456). Nueva York:
Elsevier Science.

11. Gebhardt, r., & Mecke, D. (1983). Glutamate uptake by cultured rat hepatocytes is mediated by
hormonally inducible, sodium-dependent transport systems. FEBS Letters, 161(2), 275 – 278.

12. Gupta, S., Rajvanshi, PAG., Sokhi, R. PAG., Vaidya, S., Irani, A. NORTE., & Gorla, GRAMO. R. (1999). Position-specific

gene expression in the liver lobule is directed by the microenvironment and not by the previous cell
differentiation state. The Journal of Biological Chemistry, 274(4), 2157 – 2165.

13. Haussinger, D. (1989). Glutamine metabolism in the liver: Overview and current concepts. Metabolism:

Clinical and Experimental, 38(8 Suplemento. 1), 14 – 17.

14. Haussinger, D. (1990). Nitrogen metabolism in liver: Structural and functional organization and

physiological relevance. The Biochemical Journal, 267(2), 281 – 290.

Artificial Life Volume 14, Número 1

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
a
r
t
yo
/

a
r
t
i
C
mi
–
pag
d

F
/

1
4
1
3
1
6
6
2
4
6
6
a
r
t
yo
.

2
0
0
8
1
4
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

h. Ohno et al.

Construction of a Biological Tissue Model Based on a Single-Cell Model

15. Haussinger, D. (1990). Organization of hepatic nitrogen metabolism and its relation to acid-base

homeostasis. Klinische Wochenschrift, 68(22), 1096 – 1101.

16. Haussinger, D. (1992). Liver and systemic pH-regulation. Zeitschrift fu¨r Gastroenterologie, 30(2),

147 – 150.

17. Haussinger, D. (1997). Liver regulation of acid-base balance. Mineral and Electrolyte Metabolism, 23(3 – 6),

249 – 252.

18. Haussinger, D. (1998). Hepatic glutamine transport and metabolism. Advances in Enzymology and Related

Areas of Molecular Biology, 72, 43 – 86.

19. Haussinger, D., Gerok, w., & Sies, h. (1983). Regulation of flux through glutaminase and glutamine

synthetase in isolated perfused rat liver. Biochimica et Biophysica Acta, 755(2), 272 – 278.

20. Haussinger, D., Lamers, W.. h., & Moorman, A. F. (1992). Hepatocyte heterogeneity in the metabolism

of amino acids and ammonia. Enzyme, 46(1 – 3), 72 – 93.

21. ideker, T., Galitski, T., & Hood, l. (2001). A new approach to decoding life: Systems biology. Annual

Review of Genomics and Human Genetics, 2, 343 – 372.

22. Jungermann, k. (1986). Functional heterogeneity of periportal and perivenous hepatocytes. Enzyme,

35(3), 161 – 180.

23. Jungermann, k. (1995). Zonation of metabolism and gene expression in liver. Histochemistry and Cell

Biología, 103(2), 81 – 91.

24. Jungermann, K., & katz, norte. (1989). Functional specialization of different hepatocyte populations.

Physiological Reviews, 69(3), 708 – 764.

25. Jungermann, K., & Kietzmann, t. (1996). Zonation of parenchymal and nonparenchymal metabolism

in liver. Annual Review of Nutrition, 16, 179 – 203.

26. Kitano, h. (2002). Systems biology: A brief overview. Ciencia, 295(5560), 1662 – 1664.

27. Kohn, METRO. C. (1992). Propagation of information in metanet graph models. Journal of Theoretical Biology,

154(4), 505 – 517.

28. Kohn, METRO. C., Tohmaz, A. S., Giroux, k. J., Blumenthal, GRAMO. METRO., Feezor, METRO. D., & Millington, D. S.
(2002). Robustness of metanet graph models: Predicting control of urea production in humans.
Bio Systems, 65(1), 61 – 78.

29. Kuchel, PAG. w., Roberts, D. v., & Nichol, l. W.. (1977). The simulation of the urea cycle: Correlación
of effects due to inborn errors in the catalytic properties of the enzymes with clinical-biochemical
observaciones. The Australian Journal of Experimental Biology and Medical Science, 55(3), 309 – 326.

30. kuo, F. C., & Darnell, j. MI., Jr. (1991). Evidence that interaction of hepatocytes with the collecting
(hepatic) veins triggers position-specific transcription of the glutamine synthetase and ornithine
aminotransferase genes in the mouse liver. Molecular and Cellular Biology, 11(12), 6050 – 6058.

31. kuo, F. C., Hwu, W.. l., Valle, D., & Darnell, j. mi. (1991). Colocalization in pericentral hepatocytes
in adult mice and similarity in developmental expression pattern of ornithine aminotransferase and
glutamine synthetase mRNA. Actas de la Academia Nacional de Ciencias de los Estados Unidos de América,
88(21), 9468 – 9472.

32. Bajo, S. y., Salter, METRO., Knowles, R. GRAMO., Pogson, C. I., & Rennie, METRO. j. (1993). A quantitative analysis
of the control of glutamine catabolism in rat liver cells. Use of selective inhibitors. The Biochemical
Diario, 295(punto. 2), 617 – 624.

33. Maly, I. PAG., & Sasse, D. (1991). Microquantitative analysis of the intra-acinar profiles of glutamate

dehydrogenase in rat liver. The Journal of Histochemistry and Cytochemistry, 39(8), 1121 – 1124.

34. Maynard Smith, j. (1998). Evolutionary genetics, (2y ed.) Nueva York: prensa de la Universidad de Oxford.

35. McGivan, j. D., & Bradford, norte. METRO. (1983). Characteristics of the activation of glutaminase by ammonia

in sonicated rat liver mitochondria. Biochimica et Biophysica Acta, 759(3), 296 – 302.

36. Notenboom, R. GRAMO., de Boer, PAG. A., Moorman, A. F., & Lamers, W.. h. (1996). The establishment of
the hepatic architecture is a prerequisite for the development of a lobular pattern of gene expression.
Desarrollo, 122(1), 321 – 332.

37. Sasse, D., Spornitz, Ud.. METRO., & Maly, I. PAG. (1992). Liver architecture. Enzyme, 46(1 – 3), 8 – 32.

Artificial Life Volume 14, Número 1

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
a
r
t
yo
/

a
r
t
i
C
mi
–
pag
d

F
/

1
4
1
3
1
6
6
2
4
6
6
a
r
t
yo
.

2
0
0
8
1
4
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

h. Ohno et al.

Construction of a Biological Tissue Model Based on a Single-Cell Model

38. Schneider, w., Siems, w., & Grune, t. (1990). Balancing of energy-consuming processes of rat

hepatocytes. Cell Biochemistry and Function, 8(4), 227 – 232.

39. Segel, I. h. (1993). Enzyme kinetics: Behavior and analysis of rapid equilibrium and steady state enzyme systems.

Nueva York: wiley.

40. Seyama, S., Kuroda, y., & Katunuma, norte. (1972). Purification and comparison of glutamine synthetase

from rat and chick livers. Journal of Biochemistry, 72(4), 1017 – 1027.

41. Szweda, l. I., & Atkinson, D. mi. (1989). Response of rat liver glutaminase to pH. Mediation by

phosphate and ammonium ions. The Journal of Biological Chemistry, 264(26), 15357 – 15360.

42. Tomita, METRO., Hashimoto, K., Takahashi, K., Shimizu, t. S., Matsuzaki, y., Miyoshi, F., saito, K., Tanida, S.,
Yugi, K., Venter, j. C., & hutchison, C. A., III. (1999). E-CELL: Software environment for whole-cell
simulation. Bioinformatics, 15(1), 72 – 84.

43. Wagenaar, GRAMO. T., Chamuleau, R. A., de Haan, j. GRAMO., Maas, METRO. A., de Boer, PAG. A., Marx, F., Moorman,
A. F., Frederiks, W.. METRO., & Lamers, W.. h. (1993). Experimental evidence that the physiological position
of the liver within the circulation is not a major determinant of zonation of gene expression. Hepatology,
18(5), 1144 – 1153.

44. Wagenaar, GRAMO. T., Chamuleau, R. A., Maas, METRO. A., de Bruin, K., Korfage, h. A., & Lamers, W.. h. (1994).
The physiological position of the liver in the circulation is not a major determinant of its functional
capacity. Hepatology, 20(6), 1532 – 1540.

45. Watford, METRO. (1993). Hepatic glutaminase expression: Relationship to kidney-type glutaminase and to the

urea cycle. The FASEB Journal, 7(15), 1468 – 1474.

Apéndice 1: Details of Mathematical Model

A1.1 Mathematical Models of Chemical Reactions and Transports
See Web Supplement, Table S3, for parameter values.

A1.1.1 Carbamoyl Phosphate Synthetase (EC. 6.3.4.16)
The enzyme catalyzes

2ATP þ NH4

þ þ HCO3

(cid:6) ! 2AMP þ 2Pi þ CP

in mitochondria. The kinetic model was obtained from previous literature [7, 8]:

vCPS ¼

kcat;CPS½CPS(cid:11)
denominatorCPS

Artificial Life Volume 14, Número 1

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
a
r
t
yo
/

a
r
t
i
C
mi
–
pag
d

F
/

1
4
1
3
1
6
6
2
4
6
6
a
r
t
yo
.

2
0
0
8
1
4
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

h. Ohno et al.

Construction of a Biological Tissue Model Based on a Single-Cell Model

dónde

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
a
r
t
yo
/

a
r
t
i
C
mi
–
pag
d

F
/

1
4
1
3
1
6
6
2
4
6
6
a
r
t
yo
.

2
0
0
8
1
4
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Artificial Life Volume 14, Número 1

h. Ohno et al.

Construction of a Biological Tissue Model Based on a Single-Cell Model

A1.1.2 N-Acetyl Glutamate Synthetase (EC. 2.3.1.1)
The enzymes catalyze AcCoA + Glu ! CoA + NAG.
The reaction mechanism is a nonreversible rapid equilibrium random bi-bi mechanism [3]:

kcat;AGS½AGS(cid:11)½AcCoA(cid:11)½Glu(cid:11)

(cid:1)

1þ

KaArg;AGS
½Arg(cid:11)

(cid:2)

denominatorAGS

vAGS ¼

dónde

denominatorAGS ¼ K iAcCoA;AGS K mGlu;AGS 1 þ

(cid:3)

þ K mGlu;AGS 1 þ

(cid:3)

þ K mAcCoA;AGS 1 þ

½NAG(cid:11)
K iNAG;AGS
½CoA(cid:11)
K iCoA;AGS

(cid:4)

(cid:3)

1 þ

(cid:4)

½NAG(cid:11)
K iNAG;AGS

½CoA(cid:11)
K iCoA;AGS
(cid:4)

½AcCoA(cid:11)

(cid:4)

½Glu(cid:11) þ ½AcCoA(cid:11)½Glu(cid:11)

A1.1.3 Glutamine Synthetase (EC. 6.3.1.2)
The enzyme catalyzes ATP + Glu + NH4

+ ! AMP + Pi + Gln:

vGS ¼
vGS ¼

(cid:7)
(cid:7)

(cid:5)
þ
kcat;GS½GS(cid:11)d ½iscretionary(cid:8) Glu(cid:11)½ATP(cid:11) NHþ
kcat;GS½GS(cid:11)½Glu(cid:11)½ATP(cid:11) NH4
(cid:11)
½
4
(cid:2)
(cid:1)
(cid:1)
(cid:2)
(cid:6)
(cid:5)
(cid:8) KmNH þ
(cid:7)
(cid:8) KmATP;GS þ ½ATP(cid:11)
(cid:8) KmNHþ
(cid:7)
(cid:8) KmATP;GS þ ½ATP(cid:11)
(cid:5)
(cid:6)
4 ;GS þ NH þ
4 ;GS þ NHþ
4
4

(cid:6)

KmGlu;GS þ ½Glu(cid:11)
KmGlu;GS þ ½Glu(cid:11)

A1.1.4 Phosphate-Dependent Glutaminase (EC. 3.5.1.2)
+. It is activated by the product: ammonia [27]. Co-
The enzyme catalyzes Gln + Pi ! Glu + NH4
operativity of glutamine and Pi, which is an essential activator for phosphate-dependent glutaminase,
were modeled by the Hill equation [39]:

vGlnase ¼

½Gln(cid:11)nGln;Glnase
0:5

(cid:3)

1 þ

½Gln(cid:11)nGln;Glnase

kcat;Glnase½Glnase(cid:11)
Ka;Glnase
(cid:11)
½
NH þ
4
(cid:4)
þ ½Gln(cid:11)nGln;Glnase 1 þ

nPi;Glnase
½Pi(cid:11)
0:5
½Pi(cid:11)nPi;Glnase

(cid:3)

(cid:4)

nPi;Glnase
½Pi(cid:11)
0:5
½Pi(cid:11)nPi;Glnase

Artificial Life Volume 14, Número 1

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
a
r
t
yo
/

a
r
t
i
C
mi
–
pag
d

F
/

1
4
1
3
1
6
6
2
4
6
6
a
r
t
yo
.

2
0
0
8
1
4
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

h. Ohno et al.

Construction of a Biological Tissue Model Based on a Single-Cell Model

A1.1.5 Ornithine Carbamoyltransferase (EC. 2.1.3.3)
The enzyme catalyzes CP + Orn X Pi + Cit. The reaction mechanism is an ordered bi-bi sequential
mechanism [29]:

k1;OCTk3;OCTk5;OCTk7;OCT½CP(cid:11)½Orn(cid:11) (cid:6) k2;OCTk4;OCTk6;OCTk8;OCT½Cit(cid:11)½Pi(cid:11)

(cid:8)½OCT(cid:11)

denominatorOCT

(cid:7)

vOCT ¼

dónde

denominatorOCT ¼ k2;OCTk7;OCT k4;OCT þ k5;OCT

(cid:7)

(cid:7)
þ k2;OCTk8;OCT k4;OCT þ k5;OCT

(cid:8) þ k1;OCTk7;OCT k4;OCT þ k5;OCT
(cid:7)
(cid:8)½Pi(cid:11) þ k3;OCTk5;OCTk7;OCT½Orn(cid:11)

(cid:8)½CP(cid:11)

þ k2;OCTk4;OCTk6;OCT½Cit(cid:11) þ k1;OCTk3;OCT k5;OCT þ k7;OCT

(cid:7)

(cid:8)½CP(cid:11)½Orn(cid:11)

(cid:7)
þ k6;OCTk8;OCT k2;OCT þ k4;OCT

(cid:8)½Pi(cid:11)½Cit(cid:11) þ k1;OCTk4;OCTk6;OCT½CP(cid:11)½Cit(cid:11)

þ k1;OCTk3;OCTk6;OCT½CP(cid:11)½Orn(cid:11)½Cit(cid:11) þ k3;OCTk5;OCTk8;OCT½Orn(cid:11)½Pi(cid:11)

þ k3;OCTk6;OCTk8;OCT½Orn(cid:11)½Pi(cid:11)½Cit(cid:11)

A1.1.6 Argininosuccinate Synthetase (EC. 6.3.4.5)
The enzyme catalyzes ATP + Cit + Asp X AMP + Pi + ASA. The reaction mechanism is an or-
dered ter-ter mechanism [29]:

ðk1;ASSk3;ASSk5;ASSk7;ASSk9;ASSk11;ASS½Cit(cid:11)½Asp(cid:11)½ATP(cid:11)
(cid:6)k2;ASSk4;ASSk6;ASSk8;ASSk10;ASSk12;ASS½ASA(cid:11)½AMP(cid:11)½Pi(cid:11)Þ
denominatorASS

½ASS(cid:11)

vASS ¼

Artificial Life Volume 14, Número 1

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
a
r
t
yo
/

a
r
t
i
C
mi
–
pag
d

F
/

1
4
1
3
1
6
6
2
4
6
6
a
r
t
yo
.

2
0
0
8
1
4
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

h. Ohno et al.

Construction of a Biological Tissue Model Based on a Single-Cell Model

dónde

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
a
r
t
yo
/

a
r
t
i
C
mi
–
pag
d

F
/

1
4
1
3
1
6
6
2
4
6
6
a
r
t
yo
.

2
0
0
8
1
4
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Artificial Life Volume 14, Número 1

h. Ohno et al.

Construction of a Biological Tissue Model Based on a Single-Cell Model

A1.1.7 Argininosuccinate Lyase (EC. 4.3.2.1)
The enzyme catalyzes ASA X Fum + Arg. The reaction mechanism is an ordered uni-bi mechanism:

(cid:7)

vASL ¼

k1;ASLk3;ASLk5;ASL½ASA(cid:11) (cid:6) k2;ASLk4;ASLk6;ASL½Fum(cid:11)½Arg(cid:11)

k5;ASL k2;ASL þ k3;ASL
(cid:7)

þ k6;ASL k2;ASL þ k3;ASL

(cid:8) þ k1;ASL k3;ASL þ k5;ASL

(cid:7)

(cid:8)½ASA(cid:11) þ k2;ASLk4;ASL½Fum(cid:11)

(cid:8) þ k4;ASLk6;ASL½Fum(cid:11)½Arg(cid:11) þ k1;ASLk4;ASL½ASA(cid:11)½Fum(cid:11)

(cid:8)½ASL(cid:11)

A1.1.8 Arginase (EC. 3.5.3.1)
The enzyme catalyzes Arg ! urea + Orn. The reaction is an irreversible process and inhibited by ornithine:

vArgase ¼

(cid:7)

k4;Argase k2;Argase þ k3;Argase
(cid:7)

þ k1;Argase k3;Argase þ k4;Argase

(cid:8)½Arn(cid:11)

k1;Argasek3;Argasek4;Argase½Arn(cid:11)½Argase(cid:11)

(cid:8) þ k5;Argase k2;Argase þ k3;Argase

(cid:7)

(cid:8)½Orn(cid:11)

A1.1.9 MetaNet Model
OTL, GTL, GATL, OAT, GOTm, GOTc, GDH, GAT, and GAMT were modeled using MetaNet
[28]. The reaction stoichiometries were defined as follows:

OTL : Citm þ Ornc X Citc þ Ornm

GTL : Gluc X Glum

GATL : Gluc þ Aspm

X Glum þ Aspc

OAT: Orn þ AKG X Pyrroline-5-carboxylate þ Glu

GOTm : Glu þ OAA X Asp þ AKG

GOTc : Asp þ AKG X Glu þ OAA

GDH: Glu þ NADþ X AKG þ NH þ

4 þ NADH

GAT: Gly þ Arg X Orn þ GAA

GAMT:

SAM þ GAA ! Cre

Although MetaNet is not guaranteed to accurately reproduce enzyme kinetics, it was used in our
model with the expectation it would roughly estimate the rates of reactions. The velocities of the
reactions were calculated as follows:

B
Vmax;X 1 (cid:6) Vr; X
B
Vf;X
@

(cid:3)

j
jx

j
ix

(cid:4)nix; X

1 þ

(cid:3)

cix
KVix ;X

1 þ

(cid:3)

cjx
KVjx ;X

(cid:4)njx ;X

1 þ

vx ¼

C
C
A

(cid:4)

cjx
KVjx ;X
cix
KVix; X
(cid:3)
X

kVx

KVkx ;X
ckVx

(cid:4)nk Vx ;X

(cid:3)

hVx

chVx
KVhx x

(cid:4)nh Vx ;X

Artificial Life Volume 14, Número 1

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
a
r
t
yo
/

a
r
t
i
C
mi
–
pag
d

F
/

1
4
1
3
1
6
6
2
4
6
6
a
r
t
yo
.

2
0
0
8
1
4
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

h. Ohno et al.

Construction of a Biological Tissue Model Based on a Single-Cell Model

dónde

KVs; x ¼ Ks; X 1 þ

(cid:3)

Kkx;X
ckx

(cid:4)nkx; X

(cid:3)

chx
Kh; X ;X

(cid:4)nhx;X

Ks,x and ns,x are the binding constant and the cooperativity index (essentially a Hill exponent ) of sub-
postura (or effector) s of enzyme x (equilibrium constant for dissociation of the enzyme-ligand com-
complejo), respectivamente, and KVs,x is the former’s effective binding constant, which reflects the activities of
the competitive activators kx and the competitive inhibitors hx; cs is the concentration of substance s;
and kVx and h Vx are the noncompetitive activators and noncompetitive inhibitors of the reaction cata-
lyzed by enzyme x, respectivamente [27].

A1.1.10 System N
Glutamine is transported into the cytoplasm by a sodium-dependent transport mechanism. Este
process is inhibited by histidine [32]:

vSysN ¼ Vmax;SysN

(cid:3)

Naþ

½
(cid:11)mi
(cid:11)e þ KmNa;SysN

Naþ

(cid:4)

B
B
@

½Glu(cid:11)mi
(cid:1)
½Glu(cid:11)e þ KmGlu;SysN 1 þ ½His(cid:11)mi
KiHis;SysN
#
1

C
C
A

(cid:2)

(cid:3)

(cid:6)

Naþ

½
(cid:11)C
(cid:11)c þ KmNa;SysN

Naþ

(cid:4)

B
B
@

½Glu(cid:11)C
(cid:1)
½Glu(cid:11)c þ KmGlu;SysN 1 þ ½His(cid:11)C
KiHis;SysN

C
C
A

(cid:2)

A1.1.11 System L
Glutamine is transported into the cytoplasm by a sodium-independent transport mechanism. Este
process is inhibited by tryptophan [32].

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
a
r
t
yo
/

a
r
t
i
C
mi
–
pag
d

F
/

1
4
1
3
1
6
6
2
4
6
6
a
r
t
yo
.

2
0
0
8
1
4
1
3
pag
d

vSysL ¼ Vmax;SysL

B
B
@

½Glu(cid:11)mi
(cid:1)
½Glu(cid:11)e þ KmGlu;SysL 1 þ ½Trp(cid:11)mi
KiTrp;SysL

(cid:2) (cid:6)

½Glu(cid:11)C
(cid:1)
½Glu(cid:11)c þ KmGlu;SysL 1 þ ½Trp(cid:11)C
KiTrp;SysL

(cid:2)

C
C
A

A1.1.12 Ammonia Transport between Sinusoid and Cytoplasm
Ammonia transport between the sinusoid and cytoplasm was modeled based on the general mass
action law:

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

vNH þ

4 4-tp ¼ kNH þ

(cid:1)
(cid:5)
4 4-tp NH þ

(cid:6)

(cid:5)
C (cid:6) NH þ

(cid:6)
mi

(cid:2)

A1.1.13 Transportation of Glutamine, Arginine, and Ammonia between

Cytoplasm and Mitochondria

Transports of glutamine, arginine, and ammonia across the mitochondrial membrane were presumed
to rapidly attain equilibrium:

(cid:7)

Keq;x ½S(cid:11)C (cid:6) vx

(cid:7)
(cid:8) ¼ ½S(cid:11)m þ vx

(cid:8)

Artificial Life Volume 14, Número 1

h. Ohno et al.

Construction of a Biological Tissue Model Based on a Single-Cell Model

A1.1.14 Urea Transport to Sinusoid
Excretion of urea in the sinusoidal space was modeled based on the general mass action law:

(cid:7)
vUrea-tp ¼ kUrea-tp ½urea(cid:11)C (cid:6) ½urea(cid:11)mi

(cid:8)

A1.1.15 Glutamate Transport between Sinusoid and Cytoplasm
Glutamate transport between the sinusoid and cytoplasm was modeled as Michaelis-Menten reversible
kinetics:

vGlu-tp ¼ VmF;Glu-tp

(cid:3)

½Glu(cid:11)mi
½Glu(cid:11)e þ KmGlu;Glu-tp

(cid:4)

(cid:6) VmR;Glu-tp

(cid:3)

½Glu(cid:11)C
½Glu(cid:11)c þ KmGlu;Glu-tp

(cid:4)

A1.1.16 Glutamate Flux from the Outside Pathways
Glutamate flux from the outside pathways of the model was represented by the difference between
zero-order influx and efflux based on the general mass action law:

vGlu-spp ¼ JGlu-spp (cid:6) kGlu-spp½Glu(cid:11)C

A1.1.17 Degradation of Metabolites
Degradation of N-acetyl glutamate, Pi, and CoA was modeled based on the general mass action law
under the assumption of steady state:

vdeg;s ¼ kdeg;s½s(cid:11)

where s is a substance.

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
a
r
t
yo
/

a
r
t
i
C
mi
–
pag
d

F
/

1
4
1
3
1
6
6
2
4
6
6
a
r
t
yo
.

2
0
0
8
1
4
1
3
pag
d

A1.1.18 Ornithine Inflow from Other Reactions
To hold the steady state, ornithine inflow from other reactions was presumed to be equal to the flux
of ornithine aminotransferase, vOAT.

A1.2 Mathematical Model of Metabolite Flows in Sinusoid
Flows of ammonia, glutamine, glutamate, and urea from the nth sinusoidal compartment to the
n+1th compartment, ve,sn, were modeled based on the general mass action law:

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

re;sn ¼ ke½sn(cid:11)mi

where sn represents a substance in the nth compartment of the sinusoid.

A1.3 Mathematical Model of Gene Expression of Carbamoyl Phosphate

Synthetase, Glutamine Synthetase, and Ornithine Aminotransferase
in Hepatic Lobule

To describe the regulated gene expression of three enzymes — carbamoyl phosphate synthetase, glu-
tamine synthetase, and ornithine aminotransferase —along the porto-central axis, we adopted the

Artificial Life Volume 14, Número 1

h. Ohno et al.

Construction of a Biological Tissue Model Based on a Single-Cell Model

mechanistic model proposed by Christoffels et al. [5]. The model is based on simple receptor-ligand
kinetics, and the parameters are fitted by experimental values. [ Fx*] is the concentration of the active
transcription factor F of enzyme x, and assumed as follows [5]:

Carbamoyl phosphate synthetase: ½F (cid:12)

CPS(cid:11) ¼ 0:2 (cid:6) 0:01X

Glutamine synthetase and ornithine aminotransferase: ½F (cid:12)

GS(cid:11) ¼ ½F (cid:12)

OAT(cid:11) ¼ 0:1X

where X is the radius of the hepatic lobule: X ¼ 0 corresponds to the portal tracts, and X ¼ 10
corresponds to the central vein. De este modo, X was defined as follows in our model:

X ¼ 10 (cid:8)

norte
total number of sinusoidal compartments

where n is the number of a compartment among the eight compartments, n ¼ 1 corresponds to the
compartment adjacent to the portal tracts, and n ¼ 8 corresponds to the compartment adjacent to
the central vein. The total number of sinusoidal compartments is eight in our model.

RGX,x is the relative rate of transcription, assumed to correspond to the transcription rate in our
modelo. RGX,x is calculated using the fractional saturation YGX,X, the dissociation constant KGX,X, y
the Hill coefficient nGX,x as follows [5]:

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
a
r
t
yo
/

a
r
t
i
C
mi
–
pag
d

F
/

1
4
1
3
1
6
6
2
4
6
6
a
r
t
yo
.

2
0
0
8
1
4
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

YGX;x ¼

(cid:12)(cid:11)nGX;X

½Fx
(cid:12)(cid:11)nGX;x þK

½Fx

GX;X

nGX;X

RGX;x ¼ Rmax;GX;xYGX;X

Carbamoyl phosphate synthetase was fitted with high-affinity ( YGX,CPS,h) and low-affinity ( YGX,CPS,yo)
units as follow [5]:

(cid:8)
(cid:7)
RGX;CPS ¼ Rmax;GX;CPS YGX;CPS;h þ YGX;CPS;yo

A1.4 Varying the Uncertain Parameters
The rate constants for glutamate supply from other pathways (the glutamate transport system and
the sinusoidal flow model) were uncertain. Therefore we prepared 60 model instances for each type
by varying these rate constant values under a steady-state assumption.

Figures 4 y 5 presented the results under the conditions in Table 3 as a representative of the
60 model instances in each gene expression pattern; después 50,000 s from the start of simulation, con
the value 3E(cid:6)5 M s(cid:6)1 for the glutamate influx from pathways outside of the model, the ratio of
VmF,Glu-tp and VmR,Glu-tp were set to 4.15 in the glutamate transport system, and ke ¼ 1.0 en el
sinusoidal flow model.

Apéndice 2: Abbreviations

CPS, carbamoyl phosphate synthetase; GS, glutamine synthetase; OAT, ornithine aminotransferase;
AGS, N-acetyl glutamate synthetase; Glnase, phosphate-dependent glutaminase; OCT, ornithine car-
bamoyltransferase; ASS, argininosuccinate synthetase; ASL, argininosuccinate lyase; Argase, arginase;

Artificial Life Volume 14, Número 1

h. Ohno et al.

Construction of a Biological Tissue Model Based on a Single-Cell Model

Mesa 3 . Variation parameters.

Regulation of gene expression

1. Not incorporated (N model)

2. Incorporated GS, CPS, and OAT gradients (GCO model)

3. Incorporated only GS gradients (G model)

4. Incorporated GS and CPS gradients (GC model)

5. Incorporated OAT gradients (O model)

6. Incorporated GS and OAT gradients (GO model)

Glutamate transporter

1. VmF,Glu-tp: VmR,Glu-tp ¼ 4.15 (VmF,Glu-tp ¼ 1.0629E(cid:6)2 M s(cid:6)1, VmR,Glu-tp ¼ 2.5611E(cid:6)3 M s(cid:6)1)

2. VmF,Glu-tp: VmR,Glu-tp ¼ 4.5 (VmF,Glu-tp ¼ 1.2573E(cid:6)3 M s(cid:6)1, VmR,Glu-tp ¼ 2.7940E(cid:6)4 M s(cid:6)1)

3. VmF,Glu-tp: VmR,Glu-tp ¼ 5.0 (VmF,Glu-tp ¼ 6.1467E(cid:6)4 M s(cid:6)1, VmR,Glu-tp ¼ 1.2293E(cid:6)4 M s(cid:6)1)

4. VmF,Glu-tp: VmR,Glu-tp ¼ 7.0 (VmF,Glu-tp ¼ 2.6560E(cid:6)4 M s(cid:6)1, VmR,Glu-tp ¼ 3.7943E(cid:6)5 M s(cid:6)1)

Glutamate Flux from Outside Pathways

1. JGlu-spp ¼ 3E(cid:6)5 M s(cid:6)1, kGlu-spp ¼ 7.0866E(cid:6)2 s(cid:6)1

2. JGlu-spp ¼ 6E(cid:6)5 M s(cid:6)1, kGlu-spp ¼ 8.2539E(cid:6)2 s(cid:6)1

3. JGlu-spp ¼ 8E(cid:6)5 M s(cid:6)1, kGlu-spp ¼ 9.0321E(cid:6)2 s(cid:6)1

Substance Flow in Sinusoid

1. ke ¼ 0.5

2. ke ¼ 0.8

3. ke ¼ 1.0

4. ke ¼ 1.2

5. ke ¼ 1.6

Artificial Life Volume 14, Número 1

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
a
r
t
yo
/

a
r
t
i
C
mi
–
pag
d

F
/

1
4
1
3
1
6
6
2
4
6
6
a
r
t
yo
.

2
0
0
8
1
4
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

h. Ohno et al.

Construction of a Biological Tissue Model Based on a Single-Cell Model

GOT, glutamate:oxaloacetate; GDH, glutamate dehydrogenase; GAT, arginine:glycine amidinotrans-
ferase; GAMT, guanidinoacetate methyltransferase; OTL, ornithine-citrulline translocase; GTL, glu-
+-tp, ammonia transporter; Glu-tp,
tamate translocase; GATL, glutamate-aspartate translocase; NH44
glutamate transporter; Gln-tp, glutamine transporter in mitochondrial membrane; Urea-tp, urea trans-
porter. The entity abbreviation may be used with an index that represents the location of the entity.
The indices c, metro, and s indicate the cytoplasm, mitochondria, and sinusoid, respectivamente.