COLLEGE MAJOR CHOICE AND
NEIGHBORHOOD EFFECTS IN A
HISTORICALLY SEGREGATED SOCIETY:
EVIDENCE FROM SOUTH AFRICA
Biniam E. Bedasso
Collaborative Africa Budget
Reform Initiative
Centurion, 0062 South Africa
biniam.bedasso@cabri-sbo.org
Abstracto
This paper explores factors affecting the choice of investment in
specific human capital in the presence of significant inter-group
and spatial inequalities. I use four years of admissions application
data at an elite university in South Africa in conjunction with quar-
terly labor force data to trace the link between aptitude-adjusted
expected earnings, neighborhood effects, and the choice of college
major. The paper relies on the availability of a rich set of academic
and geographical information in the admissions database to make
causal inference. The results show that expected earnings have
a positive impact on major choice independently of high school
background when the ex ante distribution of earnings captures
the full range of between-major and within-major income differ-
entials. White applicants are more responsive to differentials in
expected earnings than black applicants. Neighborhood effects in-
fluence college major choice through near-peer role models and
relative achievement at the high school level.
https://doi.org/10.1162/edfp_a_00249
© 2019 Asociación para la política y las finanzas educativas
472
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
F
mi
d
tu
mi
d
pag
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
1
4
3
4
7
2
1
6
9
3
0
1
4
mi
d
pag
_
a
_
0
0
2
4
9
pag
d
.
F
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Biniam E. Bedasso
INTRODUCCIÓN
1 .
In an era of increasing specializations and rising wage differentials, not all diplomas are
created equal. There are a number of studies in the existing literature that show the link
between the distribution of college majors and income inequality (Grogger and Eide
1995; Arcidiacono 2004). Gender and racial income gaps are also partly explained by
the heterogeneity of human capital (Daymont and Andrisani 1984; Weinberger 1998).
As one goes up the education ladder, differences in income will be as much about the
type of training acquired as about the number of years spent in school. Por eso, bajo-
standing inequality, especially in the middle part of the income distribution, requires
having a good grasp of factors influencing the allocation of heterogeneous human cap-
ital. The impact of the allocation of specialized training is likely to be pronounced in
developing countries where it has more power to shape the composition of elites and
the nature of the middle class. The allocation of talent across various fields of specializa-
tion with differential impact on innovation and technological change will affect growth
in the long run (Murphy, Schleifer, and Vishny 1991). The effect of the allocation of spe-
cialized human capital could be far-reaching enough to influence institutional quality
to the extent that it shapes the preferences of elites (Bedasso 2015).
This paper examines the determinants of college major choice in South Africa in
the context of significant inter-group and spatial inequalities that have continued to
characterize South African society.1 By investigating factors influencing college major
choice, I seek to shed light on the role of heterogeneous human capital in the repro-
duction of inequality in South Africa. Específicamente, the paper attempts to answer two
preguntas: (1) How do various groups respond to differentials in major-specific expected
earnings against the backdrop of sizeable inequality in economic and sociopolitical en-
dowments? y (2) How do peer effects and relative achievement influence college
major choice at the levels of specific neighborhoods and high schools? I exploit the
extensive information contained in the admissions database of the University of Cape
Ciudad (UCT) entre 2010 y 2013, jointly with the Quarterly Labor Force Survey con-
ducted at a national level. The novelty of the dataset lies in the amount of information
it provides about the high school education and area of residence of college applicants.
Además, the status of UCT as the best ranked institution of higher education on the
African continent allows me to put the analysis in the context of elite formation in a
society that has been undergoing social and political transformation.2
In standard theoretical frameworks, college major choice is analyzed as part of a
lifecycle model of stochastic career choice (Altonji, Blom, and Meghir 2012). This ap-
proach helps establish a link between educational choices at earlier stages in life and
the choice of college major. Por lo tanto, to the extent that pre-college educational oppor-
tunities are determined by space, it is possible to draw a connection between spatial
inequality and major choice. There are a number of channels through which spatial
1. The educational inequalities of the Apartheid era continue to persist in South Africa, as manifested in disparities
in schooling outcomes between historically black and historically white schools (Van der Berg 2007). Regional
inequality is rife in the schooling system in South Africa. As of 2013, less than 44 percent of public schools in
one of the poorest provinces offer math in grades 10 a través de 12. The corresponding figure for the best served
province is 91 por ciento.
2. Two of the most widely cited university rankings—the Times Higher Education Ranking and the QS World
University Ranking—consistently rank the University of Cape Town as the best university in Africa.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
F
/
/
mi
d
tu
mi
d
pag
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
1
4
3
4
7
2
1
6
9
3
0
1
4
mi
d
pag
_
a
_
0
0
2
4
9
pag
d
.
/
F
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
473
College Major Choice
inequality may influence individual decisions in college. This includes the quality of
schools in a given geographical area, the influence of near-peer role models, and the ef-
fect of relative achievement in different schools. Esencialmente, individuals are constrained
by all or some of these background factors as they optimize expected lifetime earnings
from each major.
I estimate a random utility model of the determinants of choice between five fac-
ulties (or departments) at UCT with nesting structure elicited from the data. I exploit
the availability of two sets of national test scores with varying emphasis on measur-
ing overall ability and college adaptability to identify the effect of aptitude-adjusted ex-
pected earnings while controlling for academic ability directly. I use two specifications
of expected earnings based on alternative assumptions regarding the information set
applicants face about future income. The results show that aptitude-adjusted expected
earnings exert a positive impact on major choice. Sin embargo, the effect of expected earn-
ings is absorbed by the antecedent effect of high school curriculum choice when the
ex ante distribution of earnings is assumed to be egalitarian. On the contrary, cuando
the ex ante distribution of earnings accounts for merit-based differentials in income,
expected earnings continue to hold a positive effect on major choice independently of
high school curriculum. As far as racial disparities are concerned, white applicants are
shown to be, on average, 1.8 times more responsive to major-specific earnings differen-
tials than black applicants.
With regard to neighborhood effects, I exploit the variation in past admission trends
to UCT across 3,773 postcodes represented in the database to capture the influence of
near-peer role models. Correcting for possible clustering of unobserved preferences
along postcodes, a one standard deviation increase in the ratio of near-peers who were
admitted to a certain faculty during the last three years is shown to increase by around 9
percent the probability of choosing the same faculty. I also endeavor to explore whether
there is a bright side to spatial inequality. Based on the assumption that applicants who
belong to the high end of the grade distribution in a less competitive high school have
better self-esteem than academically similar students who have gone to more competi-
tive high schools, I test whether being a “big frog in a small pond” induces applicants to
choose high return majors. The results show that top ranking applicants from a bottom
quartile high school are consistently more likely to choose health and other sciences
over humanities than applicants with higher average grades who nevertheless belong
to a lower rung of the grade distribution in a top quartile high school.
This paper belongs in a long vein of literature on career choice under uncertainty
(see for example, Altonji 1993; Keane and Wolpin 1999; Arcidiacono 2004; Montmar-
quette, Cannings, and Mahseredjian 2002; Wiswall and Zafar 2015). For that matter,
much of the theoretical framework I formulate in the next section is based on these
documentos. Most studies have, either implicitly or explicitly, dealt with the impact of major
choice on income inequality. Sin embargo, there has been little focus on the implications of
overall inequality, let alone group and spatial inequality, for the pattern of major choice.
To be sure, there have been notable theoretical contributions linking segregation and
human capital investment to overall inequality (ver, Por ejemplo, Bénabou 1996). El
economics and sociology literatures are rich in empirical evidence on the impact of ge-
ographical segregation on educational outcomes (Braddock 1980; Card and Rothstein
2007; Goldsmith 2009). But there is still little evidence on the effect of neighborhood
474
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
F
mi
d
tu
mi
d
pag
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
1
4
3
4
7
2
1
6
9
3
0
1
4
mi
d
pag
_
a
_
0
0
2
4
9
pag
d
.
F
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Biniam E. Bedasso
characteristics on educational outcomes in the context of heterogeneous human cap-
ital. This paper contributes to the literature in three ways. Primero, it takes advantage of
extensive geographical variation in the data to analyze the determinants of college ma-
jor choice in perspective with spatial inequality. Segundo, it enriches the empirical mea-
surement of expected earnings by using alternative assumptions regarding the ex ante
distribution of future income. Tercero, it exploits big administrative data to estimate the
determinants of major choice in a developing country, which would otherwise have
been impossible due to the absence relevant survey data.3
The remainder of the paper is organized as follows. Sección 2 outlines the theoretical
framework and the empirical strategy I apply to answer the questions raised in this
paper. Sección 3 provides an overview of the data and summary statistics. Sección 4 es
devoted to presentation of results. Sección 5 concluye.
2 . T H E O R E T I C A L F R A M E WO R K A N D E M P I R I C A L S T R AT E G Y
The choice of college major is part of a dynamic lifecycle decision-making process.
In most cases, the sequence of choices starts as early as high school, where students
and their parents may have to choose the type of curriculum to be pursued. This will
then be followed by a series of choices on whether to go to college or join the labor
market, which college to attend, and what major to choose. The last stage of decision-
making often consists of the choice of occupation conditional on education. Because I
am dealing with the choice of college major at the point of admission, I will start with
specifying the value function of individual i who has already chosen to go to college and
picked out major j from a set of available alternatives j = 1, 2, . . . , j,
(cid:2)
v1i j = E1(u1i j | a, i ) + b
E1(v2i j | a)da,
(1)
where u1i j is the flow utility in period 1 (es decir., college) conditional on ability, a, and pref-
erence, i , both of which might not be directly observable. The second term in equation
1 comprises the terminal value of lifetime earnings expected in period 2 (es decir., trabajar)
conditional on ability. β is the discount rate. The utility received by the student while
attending college in major j is determined by the psychic and pecuniary costs of major
j, as well as individual preference for that particular major. This can be written as
u1i j = α1Ci j + α2Xi + ε1i j,
(2)
where Xi is a vector of individual, escuela, and neighborhood characteristics that may
influence the inclination of student i towards major j. ε1i j is the unobserved preference
of the individual. Ci j is a combination of psychic and pecuniary costs specific to the
individual. The individualized cost function is given by
Ci j = γ1Ai j(h) + γ2Zi j,
(3)
where Ai j(h) is the observed academic ability of the individual for major j that is as-
sumed to affect the psychic cost of major j through the intensity of effort required to
3. Most of the existing studies of college major choice are based on the National Longitudinal Surveys of Youth in
the United States.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
F
mi
d
tu
mi
d
pag
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
1
4
3
4
7
2
1
6
9
3
0
1
4
mi
d
pag
_
a
_
0
0
2
4
9
pag
d
/
F
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
475
College Major Choice
complete college. At the point of college admission, observed ability is a function of high
school preparation, h, y, por lo tanto, conditional on choices made earlier in life. Zi j is
the pecuniary cost of major j, which is assumed to be specific to individual i because
the relative cost of college varies across socioeconomic backgrounds. This is because
credit markets are imperfect. Substituting equation 3 in equation 2, the flow utility of
attending college in major j can be parameterized as follows,
u1i j = α1γ1Ai j(h) + α1γ2Zi j + α2Xi + ε1i j.
(4)
The measure of expected lifetime earnings—that is, the second term of the value
function in equation 1—depends on the type of information applicants have, ex ante,
about earnings differentials across and within college majors. Respectivamente, I formu-
late two discrete form specifications of expected earnings based on alternative assump-
tions regarding the information set applicants face. Primero, assuming that applicants have
generic information about the returns to major j, the expected earnings of individual i
in major j can be written as
E1(v2i j ) = pi j(a)eg
j
+ (1 − pi j(a))ed
j
,
(5)
j and ed
where pi j(a) is the probability of successfully completing college, which is assumed to
be a function of ability (a), and eg
j represent, respectivamente, median income after
graduating in major j and median income after dropping out of college. Because ap-
plicants are assumed to have generic information about earnings differentials, capacidad
affects expected earnings, ex ante, only through the probability of successfully com-
pleting college. In a way, this specification can be considered to be based on egalitarian
distribution of expected earnings.
Segundo, assuming that applicants have full information, ex ante, about where they
are likely to fall in the earnings distribution based on their ability, the expected earnings
of individual i with ability a in major j is given as
E1(v2i j ) = eg
j,a
.
(6)
In contrast to the egalitarian measure of expected earnings in equation 5, this spec-
ification can be considered to be predicated on meritocratic distribution of expected
earnings.
I can now combine equations 4 y 5 o 6 to arrive at a reduced form equation
that can be estimated empirically. This means the indirect utility for individual i from
majoring in j can be written as a linear function of observed academic ability, individual
and neighborhood characteristics, and expected earnings:
v1i j = α1γ1Ai(h) + α1γ2Zi j + α2Xi + μβ[E1(v2i j )] + ε1i j,
(7)
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
F
mi
d
tu
mi
d
pag
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
1
4
3
4
7
2
1
6
9
3
0
1
4
mi
d
pag
_
a
_
0
0
2
4
9
pag
d
/
.
F
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
where E1(v2i j ) = pi j(a)(eg
i j
− ed
i j ) + pi jed
i j or E1(v2i j ) = eg
j,a.
Generally, the choices made in high school, which are expected to influence ma-
jor choice through Ai j, are constrained by geographical space. In countries such as
South Africa that are characterized by significant spatial inequality, neighborhood char-
acteristics affect major choice both directly through shaping preferences and indirectly
through Ai j(h). Por eso, provided there are appropriate constructs to measure regional
476
Biniam E. Bedasso
distribution of resources and neighborhood characteristics, the model specified in
equation 7 can be estimated to explain the choice of college major in South Africa.
The parameters in equation 7 can be estimated using standard techniques as long
as certain assumptions are made regarding the distribution of unobservables. Primero, I
assume that ε1i j is independently distributed across individuals once relevant neighbor-
hood characteristics are controlled for. Segundo, I assume ε1i j is correlated across majors
sharing certain characteristics. Por ejemplo, the unobserved preference of a student for
a physics degree is likely to be correlated with the unobserved preference for a chem-
istry degree. The same might not hold between physics and history. Formalmente, suppose
there are N groups of academic streams across which the J majors are distributed. Este
means a student will have to choose an academic stream n = 1, . . . , N before deciding
on which specific major to pursue. This implies that the final choice set can be written
como sigue:
j ∈ {( j11, . . . , jJ11), ( j12, . . . , jJ22), . . . , ( j1N, . . . , jJN N )}.
This type of structure leads to nested logit probabilities with J alternatives and N
nests. Suppose the full set of explanatory variables can be split into explanatory variables
of nest choice, Wn, and explanatory variables of the choice of specific alternatives, Sn j.
Note that I have dropped the individual index i and the period index 1 por simplicidad.
This means equation 7 can be rewritten as
(cid:3)
v j = W
norte
(cid:3)
κn + S
n j
λ j + εn j.
(8)
Provided that εn j is drawn from a generalized extreme value distribution, the prob-
ability of choosing the jth alternative belonging to the nth nest is given by
Pr( j) = Pr( j | norte) Pr(norte)
=
(cid:3)
λ j/τn)
exp.(S(cid:3)
n j
exp.(S(cid:3)
n j
j∈Jn
λ j/τn)
(cid:4)
(cid:3)
exp.[W. (cid:3)
norte
n∈N exp[W. (cid:3)
norte
κn + τnIVn)]
κn + τnIVn)]
(cid:5)
,
(9)
(cid:3)
where IVn = ln(
nest.
Jn
j=1 exp(S(cid:3)
n j
λ j )) and τn measures the correlation of εn j within a given
The coefficients in equation 9, including the dissimilarity coefficient τn, can be es-
timated using the full information maximum likelihood method. I will return to the
issue of identification once I have presented the data in the next section.
3 . DATA
I use the admissions application database of the UCT to estimate the model of major
choice specified in the previous section. The data are available for the entire popula-
tion of applicants, which ranges between 13,897 y 16,077 applicants per year, para el
four years from 2010 a 2013. In addition to basic demographic information and aca-
demic record, as of 2013, UCT has started collecting data on family background and
high school characteristics from all applicants. Por lo tanto, I use the population of ap-
plicants in 2013 to estimate the model. Además, information from previous years is
utilized to identify neighborhood trends based on patterns of admission of applicants
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
F
mi
d
tu
mi
d
pag
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
1
4
3
4
7
2
1
6
9
3
0
1
4
mi
d
pag
_
a
_
0
0
2
4
9
pag
d
/
F
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
477
College Major Choice
from a given neighborhood over the four years. The application database is rich in geo-
graphical information as applicants could be traced to the level of residential postcode.
Además, the names of the high schools of the applicants are given in the dataset. Este
means I can exploit spatial variations across 3,773 postcodes and 1,577 high schools.
Much of the analysis is based on the entire population of applicants, regardless of
admission status. This is done in the interest of minimizing the selection bias that
may arise due to the university admission process, as well as the decision of applicants
whether or not to accept offers. Prospective students apply for majors in one or two of
UCT’s faculties as their first and second choices. Applications to individual faculties
are evaluated independently and admission is offered or denied by the respective fac-
ulty. Por lo tanto, the first choices of prospective students at the point of application are
supposed to reflect the revealed preferences of individuals before supply constraints
are imposed. Second choices, por el contrario, are less informative because applicants may
act strategically by listing a less popular major as a second choice in order to minimize
potential loss.4
Estimation of the model specified in the previous section requires data on expected
earnings. The combination of earnings and college major data are available for the third
and fourth quarters of the Quarterly Labor Force Survey in 2012. Idealmente, the expected
lifetime earnings of applicants in each field of study are estimated using a sample of cur-
rent workers of various age groups who share similar characteristics as the applicant.
Sin embargo, this approach can be problematic in the case of South Africa because the earn-
ings trajectories of mature workers in 2012 are likely to have been shaped by a distorted
system during apartheid. This dynamic is unlikely to hold in the postapartheid period.
Por lo tanto, I have restricted the age limit of the sample of workers that are used to cal-
culate expected earnings to thirty years.5 Another challenge in this case is that there are
not enough observations of college educated, under-thirty-years-olds in the Quarterly
Labor Force Survey data to estimate earnings on a full range of personal and group
características. Por lo tanto, I have chosen to use the earnings of the under-thirty-year-
olds sample for each major to approximate expected earnings of college applicants. El
fact that the earnings of current workers are based on realized choices of college ma-
jor might introduce selection bias in the sense that current workers are already sorted
by aptitude. This means the expected earnings of high-scoring applicants in less se-
lective majors could be biased downwards. The bias is upward in case of low-scoring
applicants in more selective majors. Sin embargo, I expect the effect of such biases to be
minimal since the earnings differential among majors is more likely to emanate from
systematic differences in the occupations in which they lead than from individual abil-
idad. I will return to the calculation of individualized aptitude-adjusted expected earnings
later in this section.
Mesa 1 presents a summary of variables that are used to estimate the model of major
choice. The categories of choice are organized in terms of official faculties at UCT. I have
combined the faculties of humanities and law to simplify the choice set into five facul-
corbatas: three in science and technology (health sciences, engineering, ciencia) and two in
I would like to thank one of the anonymous referees for pointing out this scenario.
4.
5. This choice makes more practical sense particularly if one assumes that college students are able to observe
more closely the incomes of those who are the in same generation as they are than that of older people.
478
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
F
mi
d
tu
mi
d
pag
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
1
4
3
4
7
2
1
6
9
3
0
1
4
mi
d
pag
_
a
_
0
0
2
4
9
pag
d
/
F
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Biniam E. Bedasso
Mesa 1. Summary Statistics of College Applications and Labor Market Data
Commerce
Ingeniería
3,359
0.22
2,600
0.12
Number of applicants
Ratio of admitted
Academic record
NSC Math
NSC English
NSC Life orientation
NBT Math
NBT Academic literacy
Number of high school science courses
Socioeconomic background
Ratio of public school
Ratio of private school
Ratio of first-generation college
Demographic variables
Male
Female
Negro
Blanco
Colored and Asian
Labor market variables
67.8
(17.2)
70.5
(9.9)
79.6
(9.3)
46.9
(17.3)
63.5
(12.7)
1.5
(1.1)
0.27
0.73
0.42
0.48
0.52
0.50
0.24
0.25
Salud
Ciencias
3,738
0.08
65.9
(17.5)
71.2
(10.2)
80.8
(8.9)
43.6
(16.8)
60.2
(13.9)
Ciencia
1,263
0.21
64.1
(17.1)
68.8
(9.8)
77.9
(9.2)
43.5
(16.4)
61.1
(14.1)
Humanities
y ley
3,257
0.20
59.5
(18.1)
66.6
(10.5)
75.1
(10.0)
36.0
(12.7)
60.9
(13.7)
69.0
(16.4)
68.5
(9.8)
78.3
(9.3)
48.2
(17.2)
60.2
(14.3)
2.4
(0.81)
2.3
(0.71)
2.3
(0.78)
1.1
(0.90)
0.33
0.67
0.47
0.70
0.30
0.55
0.22
0.21
0.31
0.69
0.48
0.31
0.69
0.53
0.17
0.28
0.31
0.69
0.51
0.47
0.53
0.51
0.26
0.22
0.27
0.73
0.47
0.34
0.66
0.48
0.25
0.25
Total
14,217
0.15
65.4
(17.7)
69.3
(10.3)
78.4
(9.6)
44.7
(17.0)
61.2
(13.8)
1.8
(1.0)
0.29
0.71
0.47
0.44
0.56
0.51
0.24
0.25
Undergraduate median earnings:
16,000
20,000
18,000
16,000
15,000
15,000
Under 30 years old (in rand)
Technical school median earnings:
10,200
11,000
10,000
10,000
9,000
10,500
Under 30 years old (in rand)
Expected earnings 1: Egalitarian
distribución (in rand)
Expected earnings 2: Meritocratic
distribución (in rand)
11,939
(738)
19,399
(13,831)
13,195
(1,978)
21,760
(13,311)
12,582
(1,364)
20,023
(12,015)
10,545
(1,375)
17,912
(12,269)
9,449
(555)
16,662
(11,746)
11,487
(1,879)
19,079
(12,791)
Notas: Standard deviation is given in parentheses in case of mean. NBT = National Benchmark Test; NSC = National Senior Certificate.
Ciencias Sociales (commerce, humanities and law). The admission rates show that health
sciences and engineering are by far the most selective faculties. Academic preparation
is measured by six variables displayed in the second panel of table 1. Primero, scores in
the three compulsory subjects of the National Senior Certificate (NSC) examination—
Inglés, matemáticas, and life orientation—are applied to measure basic academic
capacidad. Segundo, scores in the National Benchmark Test (NBT), which is used as an ad-
ditional requirement for admission into major universities in South Africa, is utilized
to measure the probability of success in college and in a professional environment.
The NBT is specifically designed to gauge the adaptability of students to college cur-
riculum. The test is given in three modules: academic literacy, quantitative literacy,
y matemáticas. Tercero, the number of science courses a student has taken in high
school is used as a proxy for the level of preparation in science and technology. The high
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
F
mi
d
tu
mi
d
pag
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
1
4
3
4
7
2
1
6
9
3
0
1
4
mi
d
pag
_
a
_
0
0
2
4
9
pag
d
F
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
479
College Major Choice
standard deviation, relative to the mean of the number of science courses, indicates that
high school graduates vary significantly in terms of their preparation in science.
Mesa 1 also presents variables that are used to measure socioeconomic background.
A majority of the applicants attended private high schools, signifying the middle-class
status of most applicants. In terms of the educational background of families, encima 47
percent of applicants would be the first ones in three generations to have earned a col-
lege degree. Demographic characteristics of applicants show that women constitute the
majority of applicants. Black applicants form 51 percent of the applicant pool. White ap-
plicants constitute 24 percent and Colored applicants (people of mixed ancestry, cual
has become a distinctive group through the lines drawn by the Apartheid regime) y
Indians make up 25 por ciento.
The bottom panel in table 1 presents summary of expected earnings for each faculty.
The first row contains the median monthly earnings of workers under thirty years of
age with a three- or four-year college degree in each field. The second row presents the
median income of workers in the same age group who have completed only a technical
school diploma in one of the five fields. The incomes of technical school graduates are
utilized to approximate the expected earnings of applicants in case they drop out of
college.
I use the two alternative specifications that are laid out in equations 5 y 6 a
calculate aptitude-adjusted expected earnings for every applicant. To compute the first
measure, I apply the formula in equation 5 to individualize the median income of each
major by adjusting it with the probability of each applicant’s success in college. I use
the NBT scores to predict the probability of success. It is to be expected that each faculty
has a specific requirement of skill sets determining success in that particular field. En
order to determine which NBT module to use as a weight to calculate expected earnings
in a given field, I run a probit regression of admission probability on the three types of
NBT scores for the years prior to 2013. This is done under the assumption that university
officials know the skill sets that are required to succeed in a given field and have already
incorporated that information in the admission process. Based on the results of the
probit regression (reportado en el Apéndice A), math scores are used to adjust expected
earnings in engineering, health sciences, and science, whereas academic literacy scores
are used to adjust expected earnings in commerce and humanities and law.
In computing the second measure, I simply calculate the decile distribution of
monthly income of each major and assign individuals to different deciles based on their
aptitude. I assume the distribution of income for a certain major is aligned with the dis-
tribution of aptitude for that particular major. Respectivamente, a person with a median NBT
score can expect to earn the median income, whereas a person with a 95th-percentile
NBT score can expect to fall in the top decile of the income distribution for that ma-
jor. This is a simplistic measure that is intended to emphasize the potential impact of
ability on labor market returns and inequality within the same major. As in the first
measure, math scores are used to determine aptitude for engineering, health sciences,
and science, whereas academic literacy scores are used in the cases of commerce and
humanities and law. The last two rows in table 1 present descriptive statistics for the
alternative measures of aptitude-adjusted expected earnings.
The next step concerns identification of the nesting structure that is supposed to
govern the choice process of applicants. Intuitivamente, one can assume that applicants
480
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
F
/
mi
d
tu
mi
d
pag
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
1
4
3
4
7
2
1
6
9
3
0
1
4
mi
d
pag
_
a
_
0
0
2
4
9
pag
d
F
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Biniam E. Bedasso
Mesa 2. Correlation Between First and Second Choice Faculties
Second Choice
First Choice
Commerce
Ingeniería
Health Sciences
Ciencia
Humanities and Law
Commerce
Ingeniería
Health sciences
Ciencia
Humanities and law
0.22
−0,04
−0.11
−0,03
−0,04
−0.09
0.32
−0,02
0.08
−0.23
−0.12
−0,06
0.27
0.03
−0.12
−0,08
0.10
0.21
−0.11
0.44
0.02
−0.22
−0.22
−0.05
−0.15
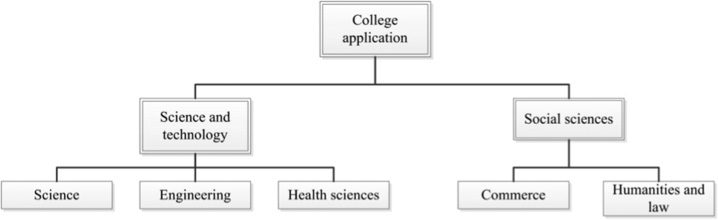
Cifra 1. Nesting structure
differentiate between the broad categories of science and technology on the one hand
and social sciences on the other hand before picking specific faculties and departments
within those categories. This assumption is corroborated by the clustering of skill sets
required for admission along the science and technology versus social sciences divide.
On top of all this, I am able to explicitly show the correlation of choices across facul-
ties because there are data on the first and second choices of most applicants. Mesa 2
shows that an overwhelming number of applicants choose two majors in the same fac-
ulty as first and second choices. When applicants decide to choose a second major in
another faculty, they mostly choose within the nests of social sciences and science and
tecnología. These results justify the assumption that unobserved preference for spe-
cific majors is correlated within nests. Cifra 1 displays the nesting structure that will
be used to implement the nested logit estimation in the next section.
En este punto, I can turn to the model specified in equation 8 to discuss the sources
of empirical identification. Note that the main coefficients of interest in the vectors
of parameters Wn and Sn j relate to the effects of expected earnings and neighborhood
características. The fact that expected earnings are measured by the quantile income
of contemporary workers can be used as an exclusion restriction to identify the effect
of expected earnings on the choices of college applicants. Sin embargo, the effect of quan-
tile income is conditional on the probability of success or aptitude, which is measured
by NBT results. The test scores of applicants in relevant modules are likely to influ-
ence major choice through channels other than the probability of success. Por lo tanto,
μβ in equation 6 may not be identified independently of pi j unless there is exogenous
variation in test results. The strategy I follow to identify μβ involves using the NSC
scores in math, Inglés, and life orientation to control for unobserved preference that
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
F
/
mi
d
tu
mi
d
pag
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
1
4
3
4
7
2
1
6
9
3
0
1
4
mi
d
pag
_
a
_
0
0
2
4
9
pag
d
/
F
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
481
College Major Choice
would otherwise be attributed to NBT results. Por ejemplo, a high score in NSC math
is sufficient to predict whether an applicant would enjoy attending college in engineer-
En g. Once that effect is controlled for, the residual effect of NBT, which is designed to
measure adaptability of prior knowledge to college curriculum, can be assumed to be
affecting major choice through expected future earnings.
The coefficients of neighborhood effects are identified because they are estimated
based on geographical variations. There is a valid concern that unobserved preference
for educational outcomes could be correlated with the choice of residence. En otra
palabras, parents choose decent neighborhoods and good schools in the interest of bet-
ter educational outcomes for their children. Sin embargo, it is unlikely that parents would
choose one neighborhood over the other because they want their children to study, decir,
engineering, in college. Even if they do, all they can consider, at high school level, es
curriculum and quality, which are directly controlled for through high school science
preparation and NSC grades for core subjects.
4 . RESULTADOS
Determinants of High School Curriculum Choice
Both theory and existing empirical evidence suggest that the choice of college major
is conditional on high school preparation. More accurately, the choice of high school
curriculum is often made in an anticipation of a certain college major and career path.
This means an important part of the decision is already made in high school. Cómo-
alguna vez, individuals make two more nontrivial decisions at the point of college application.
Primero, they can choose whether or not to switch the broad field they pursued in high
school based on the information they have discovered about their own aptitude dur-
ing high school. Segundo, whether or not they are switching fields, college applicants
need to choose majors that are more specific than high school curriculums. I begin the
presentation of results with the determinants of the choice of high school curriculum.
Mesa 3 presents the determinants of the number of high school science electives
students take. I consider both individual-level and municipality-level correlates of cur-
riculum choice. En columna 1, all the explanatory variables are basic demographic and
socioeconomic variables that are also included in the college major choice estimations
(to be presented later). Both black and white students are found to take fewer science
courses than Colored and Indians. The dummies for female and first-generation col-
lege are also negative, and public high schools are associated with more science courses.
The positive coefficient of public high school is probably because those students from
public high schools who apply to an elite university, such as UCT, self-select themselves
on their inclination for technical subjects.
Considering that geographical location may have an impact on school quality and
availability of some electives in such a historically segregated country as South Africa, I
account for municipality-level effects by introducing 240 municipality dummies in col-
umn 1. Después, in column 2, I examine what might be driving the municipality-
level effects by estimating the correlation between key socioeconomic and political
variables at the municipality level, and the municipality fixed-effects calculated based
on column 1. Finalmente, columna 3 controls for the municipality-level socioeconomic and
political variables directly in estimating the determinants of high school curriculum.
482
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
F
mi
d
tu
mi
d
pag
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
1
4
3
4
7
2
1
6
9
3
0
1
4
mi
d
pag
_
a
_
0
0
2
4
9
pag
d
/
.
F
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Biniam E. Bedasso
Mesa 3. Determinants of Science Curriculum in High School
Número de
Science Electives
Municipality
Fixed Effect
Número de
Science Electives
(1)
(2)
(3)
Dependent Variable
Individual-level correlates
Female dummy
Public school dummy
First-generation college dummy
Black dummy
White dummy
−0.215***
(0.008)
0.070***
(0.009)
−0.064***
(0.008)
−0.359***
(0.012)
−0.086***
(0.012)
Municipality-level correlates
Ratio of households above poverty line
Ratio of individuals with high school certificate
Percentage of ANC votes
Municipality fixed effect (240 municipality dummies)
R2
Number observations
Sí
0.08
11,644
−2.28***
(0.047)
1.21***
(0.032)
.792***
(0.011)
No
0.70
234
Notas: Standard errors are given in parentheses. ANC = African National Congress.
***Statistically significant at the 99% confidence level.
−0.219***
(0.008)
0.061***
(0.009)
−0.076***
(0.008)
−0.338***
(0.011)
−0.080***
(0.011)
−2.18***
(0.137)
1.14***
(0.100)
.788***
(0.035)
No
0.07
11,644
The results in columns 2 y 3 show that students applying from municipalities with
higher levels of secondary school attainment are more prepared in science subjects. A
the extent that high school completion is linked to availability of schooling resources,
this result suggests that students from municipalities with better schooling resources
come better prepared in science subjects. Sin embargo, once educational attainment is con-
trolled for, the coefficient of households above poverty line becomes strongly negative.
This indicates that students from poorer municipalities apply to UCT probably because
they are well prepared in high school science curriculum. Coupled with the positive
coefficients of the public school variable in column 1, this finding points to the likeli-
hood that students from poorer backgrounds self-select themselves to applying to UCT
based on their preparation in high school science subjects. This result may have impli-
cations for the possibility of using improvements in high school science education in
poorer areas as a means to reduce inequality through equitable access to elite higher
education.
The Effects of Expected Labor Market Returns
This section focuses on the role of expected labor market earnings in the choice of
college major. The choice between science and technology on the one hand and social
sciences on the other hand, which represents the first-level decision according to the
nesting structure in figure 1, is specified as a function of high school curriculum or, Alabama-
ternatively, municipality-level variables influencing high school curriculum choice. El
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
F
/
/
mi
d
tu
mi
d
pag
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
1
4
3
4
7
2
1
6
9
3
0
1
4
mi
d
pag
_
a
_
0
0
2
4
9
pag
d
/
F
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
483
College Major Choice
choice of specific faculties, which is modeled as a second-level decision, is a function
of major-specific expected earnings, family background, and demographic variables.
Mesa 4 presents the coefficient estimates of the random utility model of major
choice. Because the magnitude of the coefficients in table 4 is not directly interpretable,
average marginal effects of selected variables are presented in table 5 to provide an in-
tuitive interpretation of the estimates. columnas 1 y 2 show that expected earnings,
measured under alternative assumptions about ex ante distribution of earnings after
graduation, exert a positive effect on the probability of choosing a given major. En el
very least, the comparison between columns 1 y 2 demonstrates that the role of ex-
pected earnings is robust to alternative specifications with fundamentally different as-
sumptions about the impact of ability on income distribution.
The effect of expected earnings, as measured by the more egalitarian indicator, dis-
appears once high school curriculum is controlled for in column 4. A diferencia de, el
meritocratic measure of expected earnings, which captures more information about
post-college income differentials, continues to hold a strong effect on major choice
independently of high school curriculum, as shown in column 5. It may be that the
coefficient of the egalitarian measure is picking up the correlation between expected
earnings and unobserved preferences, which is removed once high school curriculum
is controlled for. The fact that this is not the case with the meritocratic measure sug-
gests that expected earnings need to capture long-term income differentials to predict
major choice net of unobserved preferences.
As columns 3 a 5 espectáculo, the number of science electives applicants took in high
school increases the probability of choosing a major in college in science and technol-
ogia. The choice of high school curriculum contains so much information about the
aptitude of individuals for alternative fields with varying levels of financial desirability
that it absorbs the explanatory power of major-specific median income. En otras palabras,
as far as median income can predict, applicants have already incorporated information
on potential earnings when they decided on high school curriculum a few years earlier.
Columna 7 in table 5 displays that a one standard deviation increase in the number of
high school science subjects raises the probability of choosing a major in science and
technology by 0.22, on average. In order to account for the indirect effects of geograph-
ical factors on major choice, I control for municipality-level variables that are shown
in the previous section to be correlated with the number of high school science elec-
tives applicants took. Respectivamente, columnas 6 y 7 show that applicants coming from
poorer municipalities tend to choose majors in science and technology over majors in
Ciencias Sociales. This result indicates that prospective students from poorer areas apply
to UCT mainly because they aspire to major in areas of science and technology.
The responsiveness of individuals to expected earnings might depend on the
amount and quality of information they have about a number of factors, including the
academic requirements of—and labor market returns to—different majors. As with
many other things in South Africa, the information young people have about college
and the labor market may be influenced significantly by their ethnic or racial back-
ground. In an attempt to disentangle the potential effect of race on shaping the respon-
siveness of applicants, the first two specifications in table 4 are repeated for the black
and white subpopulations in columns 8 a 11. The results show that both measures
of major-specific expected earnings have positive and statistically significant effects on
484
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
F
mi
d
tu
mi
d
pag
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
1
4
3
4
7
2
1
6
9
3
0
1
4
mi
d
pag
_
a
_
0
0
2
4
9
pag
d
F
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Biniam E. Bedasso
*
*
*
8
9
4
0
.
)
3
8
0
0
(
.
*
*
*
3
5
3
0
.
)
8
4
0
0
(
.
*
*
*
7
9
2
0
.
)
7
3
0
0
(
.
*
*
*
8
1
2
0
.
)
2
4
0
0
(
.
*
*
*
5
7
3
0
.
)
5
3
0
0
(
.
mi
t
i
h
W.
)
1
1
(
mi
t
i
h
W.
)
0
1
(
*
*
*
7
1
1
4
.
)
5
7
5
0
(
.
k
C
a
B
yo
)
9
(
k
C
a
B
yo
)
8
(
*
*
*
2
0
5
2
.
)
8
4
4
0
(
.
yo
yo
tu
F
)
7
(
yo
yo
tu
F
)
6
(
*
*
*
3
9
8
1
.
)
2
1
3
0
(
.
yo
yo
tu
F
)
5
(
yo
yo
tu
F
)
4
(
3
0
2
0
.
)
8
0
3
0
(
.
yo
yo
tu
F
)
3
(
yo
yo
tu
F
)
2
(
yo
yo
tu
F
)
1
(
*
*
*
9
6
6
2
.
)
6
8
2
0
(
.
*
*
*
3
4
2
1
.
)
2
3
0
0
(
.
*
*
*
2
5
2
1
.
)
2
3
0
0
(
.
*
*
*
9
2
4
1
.
)
9
2
0
0
(
.
)
s
mi
C
norte
mi
C
S
i
yo
i
a
C
oh
S
norte
oh
i
t
tu
b
i
r
t
s
i
d
norte
a
i
r
a
t
i
yo
a
gramo
mi
:
1
s
gramo
norte
norte
r
a
mi
i
d
mi
t
C
mi
pag
X
mi
norte
yo
norte
oh
i
t
a
tu
pag
oh
PAG
yo
norte
oh
i
t
tu
b
i
r
t
s
i
d
C
i
t
a
r
C
oh
t
i
r
mi
metro
:
2
s
gramo
norte
norte
r
a
mi
i
d
mi
t
C
mi
pag
X
mi
norte
yo
:
mi
C
norte
mi
r
mi
F
mi
R
(
yo
y
gramo
oh
oh
norte
h
C
mi
t
d
norte
a
mi
C
norte
mi
C
S
i
i
:
mi
C
oh
h
C
1
yo
mi
v
mi
l
s
mi
v
i
t
C
mi
mi
yo
mi
C
norte
mi
C
s
i
yo
oh
oh
h
C
s
h
gramo
h
i
F
oh
r
mi
b
metro
tu
norte
s
norte
r
tu
t
mi
R
t
mi
k
r
a
metro
norte
oh
norte
d
norte
a
t
mi
k
r
a
METRO
h
t
i
w
mi
C
oh
h
C
i
j
r
oh
a
METRO
F
oh
yo
mi
d
oh
METRO
y
t
i
yo
i
t
Ud.
metro
oh
d
norte
a
R
F
oh
s
mi
t
a
metro
i
t
s
mi
.
4
mi
yo
b
a
t
*
*
*
0
4
4
2
−
.
*
*
*
1
9
5
2
−
.
)
7
0
7
0
(
.
)
2
4
5
0
(
.
1
6
7
0
−
.
*
*
0
7
4
0
.
)
5
8
1
0
(
.
)
7
1
7
0
(
.
)
3
4
5
0
(
.
7
5
8
0
−
.
*
*
*
4
0
5
0
.
)
6
8
1
0
(
.
y
t
i
yo
i
i
a
pag
C
norte
tu
metro
norte
i
mi
t
a
C
fi
i
t
r
mi
C
yo
oh
oh
h
C
s
h
gramo
h
i
h
t
i
w
s
yo
a
tu
d
i
v
i
d
norte
i
F
oh
oh
i
t
a
R
y
t
i
yo
i
i
a
pag
C
norte
tu
metro
norte
i
mi
norte
i
yo
y
t
r
mi
v
oh
pag
mi
v
oh
b
a
yo
s
d
oh
h
mi
s
tu
oh
h
F
oh
oh
i
t
a
R
y
t
i
yo
i
i
a
pag
C
norte
tu
metro
norte
i
s
mi
t
oh
v
C
norte
A
F
oh
mi
gramo
a
t
norte
mi
C
r
mi
PAG
*
*
2
6
0
0
.
)
6
0
0
0
(
.
*
*
*
2
7
0
0
.
)
7
0
0
0
(
.
*
*
5
4
0
0
.
)
7
0
0
0
(
.
*
*
4
4
0
0
.
)
8
0
0
0
(
.
*
*
*
4
6
0
0
.
)
6
0
0
0
(
.
*
*
*
4
5
0
0
.
)
8
0
0
0
(
.
*
*
*
5
3
0
0
.
)
7
0
0
0
(
.
*
*
*
3
3
0
0
.
)
8
0
0
0
(
.
*
*
*
7
4
0
0
.
)
4
0
0
0
(
.
*
*
*
2
5
0
0
.
)
4
0
0
0
(
.
*
*
*
4
3
0
0
.
)
4
0
0
0
(
.
*
*
*
0
3
0
0
.
)
5
0
0
0
(
.
*
*
*
8
4
0
0
.
)
4
0
0
0
(
.
*
*
*
9
4
0
0
.
)
5
0
0
0
(
.
*
*
*
4
3
0
0
.
)
4
0
0
0
(
.
*
*
*
1
3
0
0
.
)
5
0
0
0
(
.
*
*
*
4
5
0
0
.
)
2
1
0
0
(
.
*
*
*
6
6
0
0
.
)
2
1
0
0
(
.
*
*
*
6
3
0
0
.
)
8
0
0
0
(
.
*
*
*
2
3
0
0
.
)
8
0
0
0
(
.
*
*
*
4
7
0
0
.
)
5
1
0
0
(
.
*
*
*
3
8
0
0
.
)
4
1
0
0
(
.
*
*
*
6
4
0
0
.
)
9
0
0
0
(
.
*
*
*
2
4
0
0
.
)
0
1
0
0
(
.
*
*
*
7
9
0
0
.
)
7
1
0
0
(
.
*
*
*
7
6
0
0
.
)
3
1
0
0
(
.
*
*
*
6
5
0
0
.
)
1
1
0
0
(
.
*
*
*
4
5
0
0
.
)
1
1
0
0
(
.
)
1
0
0
0
(
.
0
0
0
0
−
.
*
*
*
3
2
0
0
−
.
)
4
0
0
0
(
.
)
3
0
0
0
(
.
1
0
0
0
−
.
0
0
0
0
.
)
4
0
0
0
(
.
*
*
*
9
0
6
0
.
)
8
8
0
0
(
.
*
*
*
5
6
5
0
.
)
7
8
0
0
(
.
*
*
*
2
0
2
0
.
)
3
3
0
0
(
.
*
*
*
6
8
1
0
.
)
5
3
0
0
(
.
*
*
*
1
5
0
0
.
)
3
0
0
0
(
.
*
*
*
4
5
0
0
.
)
3
0
0
0
(
.
*
*
*
4
3
0
0
.
)
3
0
0
0
(
.
*
*
*
2
3
0
0
.
)
3
0
0
0
(
.
*
*
*
2
5
0
0
.
)
2
0
0
0
(
.
*
*
*
8
4
0
0
.
)
3
0
0
0
(
.
*
*
*
3
3
0
0
.
)
2
0
0
0
(
.
*
*
*
1
3
0
0
.
)
3
0
0
0
(
.
)
w
a
l
d
norte
a
s
mi
i
t
i
norte
a
metro
tu
h
:
mi
C
norte
mi
r
mi
F
mi
R
(
s
mi
i
t
yo
tu
C
a
F
i
C
fi
C
mi
pag
S
i
:
mi
C
oh
h
C
2
yo
mi
v
mi
l
mi
C
r
mi
metro
metro
oh
C
h
t
a
metro
C
S
norte
gramo
norte
i
r
mi
mi
norte
gramo
norte
mi
i
s
mi
C
norte
mi
C
s
i
h
t
yo
a
mi
h
mi
C
norte
mi
C
S
i
3
9
4
3
−
,
5
8
4
3
−
,
7
5
0
6
−
,
8
6
0
6
−
,
,
4
1
1
3
1
−
,
9
2
1
3
1
−
,
6
4
2
2
1
−
,
2
2
2
2
1
−
,
5
8
3
5
1
−
,
5
5
1
3
1
−
,
9
6
1
3
1
−
1
5
6
1
.
7
0
0
1
.
1
5
1
2
.
1
9
3
1
.
1
9
5
0
.
1
0
9
1
.
6
6
1
1
−
.
7
6
1
0
−
.
5
5
2
2
.
.
6
2
8
3
y
metro
metro
tu
d
yo
mi
a
metro
mi
F
,
y
metro
metro
tu
d
k
C
a
B
yo
,
y
metro
metro
tu
d
mi
gramo
mi
yo
yo
oh
C
norte
oh
i
t
a
r
mi
norte
mi
gramo
–
t
s
r
i
F
,
y
metro
metro
tu
d
yo
oh
oh
h
C
s
C
i
yo
b
tu
PAG
,
norte
oh
i
t
a
t
norte
mi
i
r
oh
mi
F
i
yo
C
S
norte
,
h
s
i
yo
gramo
norte
mi
C
S
norte
,
h
t
a
metro
C
S
norte
:
s
yo
oh
r
t
norte
oh
C
i
C
fi
C
mi
pag
s
–
mi
s
a
C
r
mi
h
t
oh
yo
y
gramo
oh
oh
norte
h
C
mi
t
d
norte
a
mi
C
norte
mi
C
s
i
s
mi
C
norte
mi
C
s
i
yo
i
a
C
oh
s
norte
norte
t
t
d
oh
oh
h
i
yo
mi
k
i
yo
–
gramo
oh
l
7
6
4
2
,
7
6
4
2
,
2
1
3
4
,
2
1
3
4
,
9
3
2
9
,
9
3
2
9
,
7
6
2
9
,
7
6
2
9
,
2
1
5
1
1
,
7
6
2
9
,
7
6
2
9
,
s
mi
s
a
C
F
oh
r
mi
b
metro
tu
norte
.
s
s
mi
r
gramo
norte
oh
C
yo
a
norte
oh
i
t
a
norte
norte
a
C
i
r
F
A
=
C
norte
A
.
mi
r
mi
h
d
mi
t
r
oh
pag
mi
r
t
oh
norte
mi
r
a
yo
mi
b
a
t
mi
h
t
norte
i
d
mi
t
s
i
yo
s
yo
oh
r
t
norte
oh
C
yo
a
norte
oh
i
t
i
d
d
a
norte
mi
v
mi
s
r
oh
F
i
s
t
norte
mi
C
fi
F
mi
oh
C
.
s
mi
s
mi
h
t
norte
mi
r
a
pag
norte
i
norte
mi
v
i
gramo
mi
r
a
s
r
oh
r
r
mi
d
r
a
d
norte
a
t
S
:
s
mi
t
oh
norte
.
yo
mi
v
mi
yo
mi
C
norte
mi
d
fi
norte
oh
C
%
9
9
mi
h
t
t
a
t
norte
a
C
fi
norte
gramo
i
s
i
y
yo
yo
a
C
i
t
s
i
t
a
t
s
*
*
*
;
yo
mi
v
mi
yo
mi
C
norte
mi
d
fi
norte
oh
C
%
5
9
mi
h
t
t
a
t
norte
a
C
fi
norte
gramo
i
s
i
y
yo
yo
a
C
i
t
s
i
t
a
t
S
*
*
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
F
/
/
mi
d
tu
mi
d
pag
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
1
4
3
4
7
2
1
6
9
3
0
1
4
mi
d
pag
_
a
_
0
0
2
4
9
pag
d
.
F
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
485
College Major Choice
Mesa 5. Average Marginal Effectsa
Expected Earnings 1:
Egalitarian Distribution
(Own Effect)
Expected Earnings 2:
Meritocratic Distribution
(Own Effect)
Number of High
School Science
Electivesf
(1)
(2)
(3)
(4)
(5)
(6)
(7)
Choice
Blackb
Whitec
White to
Black ratio
Blackd
Whitee
White to
Black Ratio
Science and technology
Commerce
Ingeniería
Health sciences
Ciencia
Humanities and law
0.504***
(0.090)
0.426***
(0.077)
0.561***
(0.101)
0.229***
(0.042)
0.141***
(0.026)
0.913***
(0.128)
0.617***
(0.089)
0.713***
(0.103)
0.470***
(0.069)
0.465***
(0.068)
1.81
1.45
1.27
2.05
3.29
0.071***
(0.009)
0.060***
(0.008)
0.079***
(0.011)
0.032
(0.004)
0.019***
(0.003)
0.110***
(0.018)
0.074***
(0.013)
0.086***
(0.015)
0.056***
(0.009)
0.056***
(0.009)
1.55
1.23
1.09
1.75
2.94
0.222***
(0.090)
Notas: aStandard deviations of the mean are given in parentheses. bCalculation based on column 8 in table 4. cCalculation based on
columna 10 in table 4. dCalculation based on column 9 in table 4. eCalculation based on column 11 in table 4. fCalculation based on
columna 3 in table 4.
***Statistically significant at the 99% confidence level.
the probability of choosing a given major in both subpopulations. More importantly,
columnas 1 a 6 in table 5 present the average marginal effects of a one standard de-
viation increase in the natural logarithm of expected earnings in a certain major on
the probability of choosing that major for the black and white subpopulations. Notablemente,
white applicants are more responsive to changes in expected earnings across all majors
and specifications of expected earnings. Sin embargo, the gap in responsiveness between
black and white applicants is the smallest for the more selective and financially reward-
ing majors, such as health sciences and engineering. En general, the meritocratic mea-
sure of expected earnings is shown to result in smaller gaps in responsiveness between
black and white applicants. En otras palabras, when we account for finer distinctions in
potential income after graduation, black applicants appear more responsive to expected
earnings than when we only take median income.
Spatial Inequality and Neighborhood Effects
I have begun to account for the effect of spatial inequality on major choice through
the use of municipality-level controls in the previous section. Sin embargo, spatial in-
equality in South Africa is much finer than differences at the municipality level. Este
section focuses on neighborhood effects down to the postcode and specific high school
niveles. Primero, I construct a measure of neighborhood-level admission trends for each of
el 3,773 postcodes. This variable measures the ratio of students admitted to UCT to
a given program from a single postcode out of the total number of students admitted
from the same geographical area in the same year. This is calculated using admissions
data between 2010 y 2012. I expect this variable to capture the influence of near-peer
role models in a given neighborhood on the career decisions of college applicants. El
notion of nearness in this context has both generational and spatial dimensions. El
486
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
F
/
mi
d
tu
mi
d
pag
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
1
4
3
4
7
2
1
6
9
3
0
1
4
mi
d
pag
_
a
_
0
0
2
4
9
pag
d
.
/
F
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Biniam E. Bedasso
Mesa 6. Average National Senior Certificate Scores in Student-School Quartiles
Quartiles of Students Within a School
1st
1st
2nd
3rd
4th
54.5
63.6
71.1
78.3b
Quartiles of Schools
2nd
59.5
68.4
75.3
82.9
3rd
62.2
70.9
77.8
85.5
4th
65.2
73.8
80.2a
87.1
Notas: aThis cell represents a group of applicants from a highly competitive high
escuela: Small Frog in a Big Pond. bThis cell represents a group of applicants from
a less competitive high school: Big Frog in a Small Pond.
neighborhood-level admission variable might be picking up a correlation between the
unobserved preferences of applicants in the same neighborhood. Por eso, in order to
isolate the temporal near-peer effect, I correct for clustered errors at the postcode level.
In addition to influencing current decisions through past role models, the neighbor-
hood effect might impact major choice by shaping the beliefs of individuals about their
own ability. This hypothesis draws on established arguments about the “frog-pond” ef-
fect in the sociology of education literature (davis 1966; Espenshade, Hale, and Chung
2005). The hypothesis predicts that a high-achieving student from a relatively less
competitive school, eso es, a big frog in a small pond (BFSP), tends to choose a more
demanding major in college than a relatively low-achieving student from a more com-
petitive school, eso es, a small frog in a big pond (SFBP). In order to assign frog–pond
identification to the population of applicants in the data, I create a pool of 1,557 alto
schools with at least five applicants to UCT between 2010 y 2013. Then I calculate a
three-subject average NSC score for each school based on average scores in math, En-
inglés, and life orientation. This makes it possible to allocate schools across a distribution
of average grades divided into four quartiles. The next step is creating school-level quar-
tiles of students using the same measurement as above. Mesa 6 displays the average
grades for the sixteen student–school quartile combinations. The tightness of the dis-
tribution indicates that applicants to UCT already self-select themselves on their high
school grades. I have identified one pair of BFSP and SFBP based on the criteria that
the “big frogs” belong to the top quartile in their school even if their grades on average
are lower than the “small frogs” in a more competitive school. The average score in the
SFBP cell in table 6 is statistically greater than the average grade in the BFSP cell. I
compare the effect of belonging to the BFSP cell as opposed to belonging to the SFBP
cell on major choice, controlling for all other cell categories.
Mesa 7 presents the estimated coefficients of the random utility model with neigh-
borhood and school effects described above. The results show that the impact of
neighborhood-level admission trend on the choice for the respective major is highly
significant under all specifications. The higher the number of students admitted to a
certain field in the previous three years, the more likely it is for current applicants to
choose the same field. The marginal effects obtained in table 8 show that the highest
impact of near-peer role models is manifested in the choice of health sciences. A one
standard deviation increase in the ratio of near-peers who were admitted to a health
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
F
/
mi
d
tu
mi
d
pag
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
1
4
3
4
7
2
1
6
9
3
0
1
4
mi
d
pag
_
a
_
0
0
2
4
9
pag
d
F
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
487
College Major Choice
Mesa 7. Estimates of Random Utility Model of Major Choice with Neighborhood and School Effects
Population
ln Expected earnings 1: Egalitarian distribution
ln Expected earnings 2: Meritocratic distribution
Ratio of near-peers admitted to the same faculty
Lleno
(1)
0.386
(0.374)
0.703***
(0.195)
Lleno
(2)
0.230***
(0.038)
0.724***
(0.172)
Lleno
(3)
0.798
(0.417)
Lleno
(4)
0.234***
(0.044)
Lleno
(5)
1.231***
(0.374)
0.435**
(0.220)
Lleno
(6)
0.233***
(0.043)
0.568***
(0.129)
Nivel 1 Choice: Science and Technology (Reference: Social Sciences)
Number of high school science electives
1.244***
(0.041)
1.235***
(0.041)
1.249***
(0.042)
1.243***
(0.042)
1.238***
(0.042)
1.237***
(0.042)
Nivel 2 Choice: Specific Faculties (Reference: Humanities and Law)
Dummy of Top-quartile NSC Score in a Bottom-quartile School (Reference: Dummy of 3rd Quartile NSC score in a Top-quartile School)
Commerce
Ingeniería
Health sciences
Ciencia
0.937**
(0.490)
0.987**
(0.487)
1.059**
(0.492)
1.056**
(0.492)
1.108**
(0.542)
0.972*
(0.538)
1.284**
(0.538)
1.243**
(0.548)
0.656
(0.439)
0.494
(0.413)
0.862*
(0.480)
0.813*
(0.477)
0.852**
(0.428)
0.553
(0.454)
1.078**
(0.450)
0.998**
(0.474)
Other Case-specific Controls: NSC math, NSC English, NSC life orientation, Public school dummy, First-generation college dummy,
Black dummy, Female dummy, 14 school-student quartile combinations
τn Science and technology
τn Social sciences
0.907
0.986
1.613
−12,243
9,267
1.847
−12,227
9,267
0.116
0.487
0.596
0.851
0.855
−10,894
8,334
1.032
−10,893
8,334
0.556
−10,884
8,334
0.727
−10,875
8,334
Log-likelihood
Number of cases
Notas: Standard errors are given in parentheses. Coefficients for 21 additional controls listed in the table are not reported here. NSC = National
Senior Certificate.
*Statistically significant at the 90% confidence level; **statistically significant at the 95% confidence level; ***statistically significant at the
99% confidence level.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
F
/
mi
d
tu
mi
d
pag
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
1
4
3
4
7
2
1
6
9
3
0
1
4
mi
d
pag
_
a
_
0
0
2
4
9
pag
d
F
/
.
Mesa 8. Average Marginal Effects of Ratio of Near-Peers
Admitted to the Same Facultya
Choice
Commerce
Ingeniería
Health sciences
Ciencia
Humanities and law
(1)b
0.104***
(0.037)
0.115***
(0.052)
0.147***
(0.041)
0.071***
(0.026)
0.040***
(0.032)
(2)C
0.104***
(0.037)
0.110***
(0.049)
0.143***
(0.040
0.067***
(0.025)
0.037***
(0.030)
Notas: aStandard deviations of the mean are given in paren-
tesis. bCalculation based on column 1 in table 7. cCalculation
based on column 2 in table 7.
***Statistically significant at the 99% confidence level.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
488
Biniam E. Bedasso
sciences faculty during the last three years increases the probability of choosing health
sciences by over 14 por ciento. On the contrary, the same increase in the case of humani-
ties and law results in no more than a 4 percent rise in the probability of choosing the
same field.
columnas 3 a 6 in table 7 include the frog–pond indicators generated based on table
6. The frog–pond effect is mainly about the self-evaluation of students in high school in
comparison with their schoolmates. Por lo tanto, the effect is more accurately measured
after controlling for choices in high school, such as high school curriculum. The results
show that there is an indication of a frog–pond effect in the choice of commerce, salud
sciences, and science under most specifications. For engineering, the effect is limited
to specifications excluding admission trends of near-peer role models. Estos resultados
are unlikely to be spurious because, out of twelve student–school quartile combinations
that are characterized by average NSC scores lower than the SFBP cell, the only category
that has a positive and significant effect on any choice is the BFSP cell. It might be
interesting to put these results in perspective with the effect of near-peer role models.
The path-dependent effect of neighborhood-level admission trends may suggest that
applicants from less competitive schools might end up choosing low return majors. El
frog–pond effect adds a twist to that story. Después de todo, the career destiny of some students
from less competitive and, presumably, underresourced schools might be improved by
the fact that they have maintained relatively high self-esteem coming out of high school.
5 . CONCLUSIÓN
This paper has set out to examine the determinants of college major choice against
the backdrop of inter-group and spatial inequalities. I have used the extensive set of
academic, geographical, and socioeconomic information contained in the admissions
application database of the University of Cape Town to estimate random utility models
of major choice. In line with the predictions of the lifecycle model of career choice,
the choice of high school curriculum is shown to be crucial for the choice of college
major. Sin embargo, expected earnings maintain a positive impact on major choice inde-
pendently of high school background when the ex ante distribution of earnings captures
the full range of between-major and within-major income differentials. At a neighbor-
hood level, the influence of near-peer role models on the choices of college applicants
is found to be large and significant.
The dynamics of major choice at a selective institution such as UCT is likely to
have significant implications in the long run for social and economic transformation.
Potential inefficiencies in the allocation of talent that might be caused by persistent in-
equalities will hamper innovation and mass flourishing à la Edmund Phelps (Phelps
2014). Although the gap between white and black students in response to potential
differentials in expected earnings remains, it is encouraging that the magnitude is sig-
nificantly smaller in the case of high-return majors, such as health sciences. Además,
good preparation in high school science electives seems to embolden applicants from
poorer and far-off municipalities to apply to UCT, hoping to major in science and tech-
nology fields. Considering the importance of high school curriculum and neighbor-
hood effects, policy measures that will improve the availability of science education at
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
F
/
/
mi
d
tu
mi
d
pag
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
1
4
3
4
7
2
1
6
9
3
0
1
4
mi
d
pag
_
a
_
0
0
2
4
9
pag
d
F
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
489
College Major Choice
the high school level or account for the effect of near-peer role models in college admis-
sions may go a long way in terms of moderating income inequality in South Africa.
EXPRESIONES DE GRATITUD
I would like to thank the Information and Communication Technology Services of the University
of Cape Town for allowing me access to the admissions database. I am grateful to Kende Kefale
for facilitating access to the database. I thank Max Price and two anonymous referees for com-
ments and suggestions. I thank Chris Rooney and Callee Davis for excellent research assistance.
Financial support for this research has been provided by Economic Research Southern Africa.
This paper was completed during my time at Princeton University.
REFERENCIAS
Altonji, Joseph G. 1993. The demand for and return to education when education outcomes are
uncertain. Journal of Labor Economics 11(1): 48–83.
Altonji, Joseph G., Erica Blom, and Costas Meghir. 2012. Heterogeneity in human capital in-
vestments: High school curriculum, college major, and careers. Annual Review of Economics 4(1):
185–223.
Arcidiacono, Peter. 2004. Ability sorting and the returns to college major. Journal of Econometrics
121(1–2): 343–375.
Bedasso, Biniam E. 2015. Educated bandits: Endogenous property rights and intra-elite distribu-
tion of human capital. Ciencias económicas & Política 27(3): 404–432.
Bénabou, roland. 1996. Equity and efficiency in human capital investment: The local connection.
Review of Economic Studies 63(2): 237–264.
Braddock II, Jomills Henry. 1980. The perpetuation of segregation across levels of education.
Sociology of Education 53(3): 178–186.
Card, David, and Jesse Rothstein. 2007. Racial segregation and the black-white test score gap.
Journal of Public Economics 91(11–12): 2158–2184.
davis, James A. 1966. The campus as a frog pond: An application of the theory of relative depri-
vation to career decisions of college men. American Journal of Sociology 72(1): 17–31.
Daymont, Thomas N., and Paul J. Andrisani. 1984. Job preferences, college major, and the gender
gap in earnings. Journal of Human Resources 19(3): 408–428.
Espenshade, Tomás J., Lauren E. Hale, and Chang Y. Chung. 2005. The frog pond revisited:
High school academic context, class rank, and elite college admission. Sociology of Education
78(4): 269–293.
Goldsmith, Pat Rubio. 2009. Schools or neighborhoods or both? Race and ethnic segregation
and educational attainment. Social Forces 87(4): 1913–1941.
Grogger, Jeff, and Eric Eide. 1995. Changes in college skills and the rise in the college wage
premium. Journal of Human Resources 30(2): 280–310.
Keane, Michael P., and Kenneth I. Wolpin. 1999. The career decisions of young men. Diario de
Political Economy 105(3): 473–522.
Montmarquette, Claude, Kathy Cannings, and Sophie Mahseredjian. 2002. How do young peo-
ple choose college majors? Revisión de la economía de la educación 21(6): 543–556.
490
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
F
/
/
mi
d
tu
mi
d
pag
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
1
4
3
4
7
2
1
6
9
3
0
1
4
mi
d
pag
_
a
_
0
0
2
4
9
pag
d
/
.
F
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Biniam E. Bedasso
Murphy, Kevin M., Andrei Shleifer, and Robert W. Vishny. 1991. The allocation talent: Implica-
tions for growth. Revista trimestral de economía 106(2): 503–530.
Phelps, Edmund. 2014. Mass flourishing: How grassroots innovation created jobs, challenge and
cambiar. Princeton, Nueva Jersey: Prensa de la Universidad de Princeton.
Van der Berg, Servaas. 2007. Apartheid’s enduring legacy: Inequalities in education. Diario de
African Economies 16(5): 849–880.
Weinberger, Catherine. 1998. Race and gender wage gaps in the market for recent college grad-
uates. Industrial Relations 37(1): 67–84.
Wiswall, Matthew, and Basit Zafar. 2015. Determinants of college major choice: Identification
using an information experiment. Review of Economic Studies 82(2): 791–824.
APÉNDICE A : P RO B I T R E G R E S S I O N R E S U LT S
Cuadro A.1. Probit Estimates of Admission Probability as a Function of National Benchmark Test Scores (Pooled Population
of Applicants from 2010 a 2012)
Commerce
Ingeniería
Health Sciences
Ciencia
Humanities and Law
Academic Literacy score
Quantitative Literacy score
Mathematics Score
Pseudo R2
Log likelihood
Number of observations
0.026***
(0.002)
0.004**
(.002)
0.024***
(0.002)
0.14
−3,516
6,452
0.010***
(0.002)
−0,001
(0.002)
0.040***
(0.001)
0.20
−2,174
5,050
0.017***
(0.003)
−0,003
(0.002)
0.020***
(0.002)
0.10
−1,732
5,970
0.002
(0.003)
0.004
(0.003)
0.028***
(0.002)
0.11
−1,161
2,144
0.023***
(0.003)
−0,001
(0.003)
0.013
(0.003)
0.08
−1,094
2,008
Notas: Standard errors are given in parentheses.
**Statistically significant at the 95% confidence level; ***statistically significant at the 99% confidence level.
A P P E N D I X B : DATA S O U R C E S
(1) Admission application data: The database of the Information and Communication
Technology Services of the University of Cape Town.
(2) Earnings Data: Quarterly labor force survey, Statistics South Africa.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
F
/
mi
d
tu
mi
d
pag
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
1
4
3
4
7
2
1
6
9
3
0
1
4
mi
d
pag
_
a
_
0
0
2
4
9
pag
d
/
.
F
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
491