CAP AND GAP: THE FISCAL EFFECTS OF

PROPERTY TAX LEVY LIMITS IN NEW YORK

Phuong Nguyen-Hoang

School of Planning and

Public Aﬀairs & Público

Policy Center

University of Iowa

Iowa City, IA 52242

phuong-nguyen@uiowa.edu

Pengju Zhang

School of Public Aﬀairs and

Administration

Rutgers University, Nueva York

Nueva York, Nueva Jersey 07102

pengju.zhang@rutgers.edu

Abstracto
This is the ﬁrst study to examine the ﬁscal eﬀects of the New York
property tax levy limit, using variation from the degree of ﬁscal
stringency across school districts and over time in its ﬁrst ﬁve
years of implementation. Based on a diﬀerence-in-diﬀerences es-
timator, coupled with an event study speciﬁcation, we ﬁnd that the
tax limit has imposed a real cap on many school districts; eso es,
at-limit districts’ total current expenditures per pupil are signif-
icantly lower than what they would have spent absent the limit.
For those aﬀected school districts, this expenditure gap does not
come from spending on teacher salaries or fringe beneﬁts but
rather from other instructional salaries/expenses, central admin-
istración, transportation, interfund transfers, and undistributed
spending. We also ﬁnd heterogeneity in the constraining eﬀects of
the tax limit across diﬀerent need-based groups of school districts.

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
mi
d
pag
a
r
t
i
C
mi
–
pag
d

F
/

1
7
1
1
1
9
7
7
6
2
4
mi
d
pag
_
a
_
0
0
3
2
7
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

https://doi.org/10.1162/edfp_a_00327

Cap and Gap: Tax Limits in New York

INTRODUCCIÓN

1 .
Under Chapter 97 of the Laws of 2011, the state of New York (Nueva York) established a property
tax levy limit (herein referred to as the tax limit) that aﬀects all local governments with
property taxing power, including school districts. Eﬀective in ﬁscal year 2013, the tax
limit basically restricts the annual growth of property tax levies to 2 percent or the rate
of inﬂation, whichever is less. The tax limit has been criticized for limiting NY school
districts’ ability to raise property taxes—their largest revenue source—for educational
services (Yinger 2019). Recent data from the NY State Education Department (NYSED)
seem to support this criticism. In ﬁscal years 2017 y 2018, 369 (55 por ciento) y 328
(49 por ciento) of the districts, respectivamente, proposed to raise taxes by every dollar they
could within the limit. A few districts (es decir., 36 districts in 2017) even proposed to over-
ride the tax limit. Despite criticisms, the NY State Senate and Assembly recently made
permanent the limit, which had been scheduled to expire in 2020 (NYSDTF 2020).

The tax limit in NY is one of the most recent examples of state-imposed tax and
expenditure limitations (TELs) that have been adopted in many states in the United
Estados (Downes and Figlio 2015; Lincoln Institute of Land Policy and George Washing-
ton Institute of Public Policy 2020).1 Applied public ﬁnance scholars have extensively
investigated the intended eﬃcacy and unintended consequences of TELs. The literature
demonstrates two contrasting perspectives: The “institutional irrelevance view” holds
that ﬁscal rules can be strategically circumvented by local governments in many ways,
whereas the “public choice view” suggests that ﬁscal rules represent important and
eﬀective constraints on the behavior of local political actors (Poterba 1996).

Empirical research on the ﬁscal impact of TELs on local general-purpose govern-
ments basically buttresses the “institutional irrelevance view” by pinning down mul-
tiple strategies that localities have used to escape the constraint of TELs (Mullins
and Joyce 1996; Shadbegian 1999; Skidmore 1999; Hoene 2004; Cheung 2008;
McCubbins and Moule 2010; Sol 2014; zhang 2018; Eliason and Lutz 2018; Zhang and
Hou 2020). Sin embargo, when it comes to school districts, studies on the ﬁscal impact of
TELs provide mixed ﬁndings. Based on seventeen empirical articles, a meta-regression
analysis ﬁnds that TELs have a complex eﬀect on education ﬁnancial resources, y
recent studies are more inclined to support the “public choice view” when compared
to studies conducted in the past (Ballal and Rubenstein 2009).

To provide new evidence on the eﬀect of TELs on school ﬁnance, this study focuses
on the most recent tax limit in NY and seeks to answer three closely related research
preguntas. Considering that not all TELs are ﬁscally constraining, the ﬁrst question
is whether the tax limit has a constraining eﬀect, or has put an eﬀective cap, on NY
school districts’ total current expenditures per pupil. The second research question is
whether the tax limit may have diﬀerential expenditure-stiﬂing eﬀects on diﬀerent dis-
trict groups. Tercero, this study asks which expenditure categories and subcategories bear
the brunt of this constraint; eso es, how districts under ﬁscal constraint make spending
cuts across diﬀerent functions.

1. En 2018, thirty-six states and Washington, DC imposed TELs on local governments’ property tax levy, though not
all of the TELs apply to school districts (Lincoln Institute of Land Policy and George Washington Institute of
Public Policy 2020).

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
mi
d
pag
a
r
t
i
C
mi
–
pag
d

F
/

1
7
1
1
1
9
7
7
6
2
4
mi
d
pag
_
a
_
0
0
3
2
7
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Phuong Nguyen-Hoang and Pengju Zhang

By deﬁnition, a property tax levy limit is ﬁscally constraining or binding when it
prevents a school district from reaching the level of total spending desired or preferred
by local voters (or determined by the local median voter). This deﬁnition suggests that
“at-limit” school districts—those that exhaust the limit—are most likely constrained
by the tax limit. We adopt a diﬀerence-in-diﬀerences (DID) estimation approach by ex-
ploiting unaﬀected or far-from-limit districts as comparison districts for at-limit school
districts. We also utilize an event study speciﬁcation to support causal links between
the tax limit and changes in school districts’ spending behaviors. Based on a data panel
de 666 school districts in NY between 2011 y 2017, we ﬁnd strong evidence to support
the public choice view that the tax limit has put an eﬀective cap or constraint on at-limit
school districts in the ﬁrst ﬁve years of implementation.

Our study makes three contributions to the literature. Primero, we investigate both
average and heterogeneous ﬁscal eﬀects of the tax limit, the latter of which has not been
adequately explored in the literature. Segundo, this is the ﬁrst study to take full advantage
of the ﬁnely disaggregated expenditure data from NY. Our estimations provide a holistic
picture of cutback strategies adopted by diﬀerent district types in response to the limit-
induced constraint. Tercero, this study evaluates the latest ongoing TEL measure, eso es,
the tax limit in NY and, por lo tanto, our ﬁndings can inform in a timely manner current
debates on its extension and potential changes in design.

The remainder of the paper proceeds as follows. The next section provides technical
details of the tax limit, followed by a review of the literature. We then present a simple
theoretical framework on the eﬀect of the tax limit, discuss empirical challenges, y
present our empirical strategies. The next section brieﬂy describes data and provides
a descriptive analysis, followed by a discussion of regression results. The last section
concludes with policy implications and suggestions for future research.

2 . B AC K G RO U N D
The property tax levy limit in NY imposes a percentage limit on total property tax levies
set by local governments, not on assessed property values or tax rates. Basically, local
governments may not adopt a budget funded by a property tax levy that exceeds the prior
year’s levy by more than 2 percent or the rate of inﬂation, whichever is less. The tax limit
on school districts does not apply to ﬁscally dependent large-city school districts (Nuevo
York City, Buﬀalo, Rochester, Siracusa, and Yonkers).

Property Tax Limit Formula
To calculate a school district’s tax limit, the formula starts with the district’s prior-
year property tax levy and then adds a prior-year reserve oﬀset, from which the re-
serve amount (including interest earned) needs to be deducted, como se muestra en la figura 1.
It is multiplied by a district-speciﬁc tax base growth factor determined by the NY State
Department of Taxation and Finance (NYSDTF). Prior-year payments in lieu of taxes
(PILOTs) receivable are then added to the resulting product, while the prior-year capital
tax levy and tort exclusions are subtracted, leading to an adjusted prior-year tax levy.

The adjusted prior-year tax levy is multiplied with the allowable levy growth factor,
which is the lesser of either 2 percent or the inﬂation rate. The levy growth factor was 2
por ciento en 2013 y 2014, but fell to 1.46 por ciento, 1.62 por ciento, e incluso 0.12 por ciento en

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
mi
d
pag
a
r
t
i
C
mi
–
pag
d

F
/

1
7
1
1
1
9
7
7
6
2
4
mi
d
pag
_
a
_
0
0
3
2
7
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cap and Gap: Tax Limits in New York

Nota: Information on this formula, district-specific annual tax base growth factor, and statewide annual allowable levy growth
is available at https://www.osc.state.ny.us/local-government/property-tax-cap/real-property-tax-cap-local-governments. PILOT =
payments in lieu of taxes.

Cifra 1. Property Tax Limit Formula

2015, 2016, y 2017, respectivamente. After subtracting PILOTs receivable in the coming
year and adding available carryover, a school district will subsequently obtain its tax levy
limit for the coming or current ﬁscal year.

Sin embargo, the tax levy limit can be higher because of three excludable property tax
levies—namely, levies for court orders or judgments exceeding 5 percent of the prior-
year tax levy, a levy for an increase of over 2 percentage points in the rate of state-
mandated contributions to district pension funds, and the current-year levy for capital
projects. Además, a school district can still legally override the tax levy limit with
exclusions when there is 60 percent voter approval.

Property Tax Levy Limit and School District Budgeting Process
To examine whether the tax limit is binding or not, one also needs to understand lo-
cal budgeting processes in NY. The school districts’ ﬁscal year begins on 1 Julio. Every
año, the NYSDTF calculates a tax base growth factor for each school district, and by 15
Febrero, notiﬁes those with a positive change in the factor. School districts can then
incorporate this growth factor, which is part of the tax limit formula, into the coming
year’s budget. Por 1 Marzo, school districts must report their proposed budget (incluido
levy) and data necessary to compute their property tax levy limit (as in ﬁgure 1) via the
Property Tax Report Card to the state comptroller, the commissioner of education, y
the NYSDTF. In this report card, the diﬀerence between the tax levy limit and the total
proposed tax levy is calculated. If the proposed levy is higher than the tax levy limit, el
budget, as explained above, must be approved by 60 percent or more of local voters to
override the limit (whereas regular budgets only need a 50 percent majority). In late
Abril, districts must transmit the report card to the NYSED and to local newspapers for
general circulation. Shortly after a public hearing, districts will mail budget notices to
eligible voters who cast their vote on the proposed budget sometime in May.2

A school district’s budget is not always successfully passed. The failure of budget
passage is not uncommon, especially before the enactment of the tax limit. In NY, if a
school district’s initial override budget is defeated, it has only one additional chance to
gain voter approval. In the second vote, the school board has three budget vote options:

2. A timeline of annual budget votes and school board elections since 2008 can be found on the Web site of NY

State School Boards Association at nyssba.org/news-media/school-budget-votes/.

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
mi
d
pag
a
r
t
i
C
mi
–
pag
d

F
/

1
7
1
1
1
9
7
7
6
2
4
mi
d
pag
_
a
_
0
0
3
2
7
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Phuong Nguyen-Hoang and Pengju Zhang

the original failed budget; a revised budget that is lower than the original but still higher
than the levy limit and therefore requires 60 percent approval; and ﬁnally, a revised
budget that is lower than or equal to the levy limit and needs only 50 percent voter
approval. Given that the school year commences on 1 July for school districts, budget
revote activities must be completed in June.

If a second budget vote is again defeated, the district must operate under a con-
tingency budget no greater than its prior-year levy. (Alternately, the district can adopt
the contingency budget right after the ﬁrst budget defeat.) Voting records show that
defeated budgets have dramatically decreased to less than 5 por ciento desde 2013, y
the number of cases adopting contingency budgets has become extremely rare—only
a single district adopted a contingency budget in two of the post-tax limit years.

3 . REVISIÓN DE LITERATURA
Because the tax limit under investigation is imposed by the state on local governments,
this review focuses on state-imposed TELs.3 The eﬀect of state-imposed TELs has been
extensively studied by public ﬁnance scholars (Rose 2010). An empirical consensus in
the literature is that state-imposed TELs have little eﬀect on the overall size of local
general-purpose government budgets (Mullins and Joyce 1996; Shadbegian 1999; Sol
2014; Eliason and Lutz 2018). Localities subjected to property tax limitations, both in
the United States and in some European countries, are found to tap into other un-
constrained revenue sources (other taxes and fees), establish special districts or home-
owners’ associations, and issue more nonguaranteed debt (Shadbegian 1999; Skidmore
1999; Hoene 2004; Cheung 2008; McCubbins and Moule 2010; Blom-Hansen, Houl-
berg, and Serritzlew 2014; zhang 2018; Kioko and Zhang 2019).

School districts diﬀer from other local, general-purpose governments, possibly lead-
ing to a diﬀerent impact of TELs on school districts’ ﬁscal behaviors. Primero, escuela
districts are not authorized to create special districts through enabling legislations. Sec-
ond, property taxes constitute the lion’s share of own-source revenue for most school
districts in the United States. Por lo tanto, when confronted with a constraining limit on
property taxes, they are less able to raise adequate, other own-source revenues to oﬀ-
set the shortfall, as conﬁrmed by the historical analysis in Downes and Killeen (2014).
También, the constraining eﬀects of TELs on school districts may become stronger over
tiempo (Dye, McGuire, and McMillen 2005). Ballal and Rubenstein (2009) argue that
studies with more recent data tend to consistently ﬁnd a negative association between
TELs and local spending on education, although empirical ﬁndings are more incon-
sistent across studies analyzing older data. Extant studies also explore whether state
governments may help ﬁll the gap when local revenues decline. Shadbegian (2003),
Blankenau and Skidmore (2004), and Shadbegian and Jones (2005) all ﬁnd that TELs
result in increased state aid, suggesting the reduction of local spending is, to some
extent, oﬀset by the growth of state ﬁscal transfers.

Two studies examine previous TELs in New York. Ebdon (1997) analyzes the impact
of constitutional property tax levy limits on small city school districts in NY and ﬁnds the
limit reduced spending in small city school districts by 2 percent from 1984 a 1986.

3. Kioko (2011) and Brooks, Halberstam, and Phillips (2016) provide reviews on state-level TELs and city-level self-

imposed TELs, respectivamente.

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
mi
d
pag
a
r
t
i
C
mi
–
pag
d

F
/

1
7
1
1
1
9
7
7
6
2
4
mi
d
pag
_
a
_
0
0
3
2
7
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cap and Gap: Tax Limits in New York

Nguyen-Hoang (2013) examines the eﬀects of the 1986 repeal of these constitutional
limits and ﬁnds that the repeal had no eﬀect on school operating expenditures in NY
durante 1980 a través de 1994. Sin embargo, the repealed constitutional tax levy limit diﬀers
from the tax limit in our study for two major reasons. Primero, a constitutional limit is
harder to change than a statutory one, like the tax limit. Segundo, el 2013 tax limit starts
with the prior-year levy, and the constitutional limit restricts school operating levies to
a maximum 2 percent of a ﬁve-year average of the full value of taxable property.

In addition to the eﬀects of TELs on school funding sources and total expenditures,
some studies also examine whether school districts respond to TELs by changing their
expenditure structure or reallocating educational inputs. Dye and McGuire (1997) ﬁnd
that the property tax cap enacted in 1991 in the Chicago metropolitan area decreased
operating expenditures but had no eﬀect on instructional expenditures in the short
run. Downes and Figlio (2015) suggest that the protection of instructional spending at
the expense of noninstructional spending found in Dye and McGuire (1997) is prob-
ably related to Tiebout’s (1956) theory of competition through which unaﬀected dis-
tricts could put competitive pressure on aﬀected districts. Dye, McGuire, and McMillen
(2005), sin embargo, ﬁnd that, in the long run, growth rates in both operating and instruc-
tional expenditures are slower in districts subject to the same Chicago tax cap. Figlio
(1998) also ﬁnds the reduction of school district resources caused by Measure 5 in Ore-
gon was borne more heavily by instruction than by administration. Además, Figlio’s
(1997) study on school-level data from forty-nine states ﬁnds schools subject to prop-
erty tax levy limitations did not reduce administrative costs but lowered instructional
services. As an explanation for the stronger expenditure eﬀects of TELs on instruction
than administration, Downes and Figlio (1999, 2015) argue that a larger cut in instruc-
tional spending is consistent with administrative rents (deﬁned as use of resources to
beneﬁt those in control of resources) and with TEL provisions’ lack of incentives for
administrators to improve eﬃciency. Considerándolo todo, the literature seems to reveal mixed
evidence that TELs reduce resources for instruction or administration.4 Also, none of
the existing studies explores whether or how ﬁscally constrained school districts, in re-
sponse to a TEL, cut subcategories of instructional expenditures and other spending cat-
egories beyond instruction and administration—a literature gap that our study seeks to
ﬁll.

The current study also supplements the education ﬁnance literature on how school
districts respond to the ﬁscal impacts of a major economic bust. The Great Recession,
which started in 2007, induced most states to cut education aid (Oliﬀ and Leachman
2011) and shrank their property tax base (Collins and Propheter 2013). Without a prop-
erty tax levy limit, school districts could raise property taxes (by levying higher tax rates
on their smaller tax base) to buﬀer the impact of decreased state aid (Chakrabarti, Liv-
ingston, and Roy 2014; evans, Schwab, and Wagner 2019). Sin embargo, had a property
tax levy limit similar to NY’s current limit been in place during the Great Recession

4. Another strand of relevant research examines the eﬀects of TELs on educational outcomes. Figlio (1997) ﬁnds
that TELs are associated with lower student performance, which is partly explained by the ﬁndings that tax limits
systematically reduce the quality of new teacher hires (Figlio and Rueben 2001), whereas Downes, Dye, y
McGuire (1998) ﬁnd only limited evidence that student performance declines in districts subject to TELs. De este modo,
the literature does not provide clear guidance on the relationship between TELs and student performance, either.
A recent literature review on this can be found in Downes and Figlio (2015).

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
mi
d
pag
a
r
t
i
C
mi
–
pag
d

F
/

1
7
1
1
1
9
7
7
6
2
4
mi
d
pag
_
a
_
0
0
3
2
7
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Phuong Nguyen-Hoang and Pengju Zhang

años, school districts’ ability to stabilize their budgets via raises in property taxes would
have been seriously undermined. A recent oﬃcial report sounded a grim warning of
the ongoing COVID-19 pandemic’s implications for NY schools. The state’s pandemic
response includes substantial cuts to state aid; coupled with school districts’ tax cap-
induced inability to shore up local revenue, the reduction in state aid could have dra-
matic eﬀects on NY school districts’ resources (Oﬃce of the New York State Comptroller
2020). This study’s ﬁndings give credence to that warning.

4 . T H E O R E T I C A L F R A M E WO R K
This section presents a conceptual framework for how the tax limit may exert ﬁscal con-
straint on school districts. Districts are constrained when the tax limit prevents them
from achieving the spending level desired, or determined, by the majority of local vot-
ers (or by the median voter). Tal como, constrained districts refer to the those who spend
less than what they would have spent absent the tax limit.

The ﬁrst cause for the possible constraining eﬀect of the tax limit is associated with
the important role that property taxes play in funding school districts’ operations. Como
with most school districts in the United States, NY school districts rely primarily on
two major revenue sources: property taxes and state aid. In the three-year period before
2013, the percentage share of state aid in total revenue sources experienced a slight
decline, de 37.9 por ciento en 2010 a 37.5 por ciento en 2012, whereas property taxes on
average accounted for an increasingly large share of all school district revenues (de
41.5 por ciento en 2010 a 44.2 por ciento en 2012). Given the important role of property taxes,
a limit on this revenue source may translate into ﬁscal constraint on some districts.

The constraint may be felt particularly strongly by districts that rely heavily on prop-
erty taxes. Statewide averages mask substantial variation in districts’ reliance on prop-
erty taxes. To present this variation clearly, we rely on the state oﬃcial classiﬁcation
of school districts based on the need/resource capacity (NRC) índice: low NRC, aver-
age NRC, urban–suburban high NRC, and rural high-NRC districts.5 Given that the
NRC index—a ratio of a school district’s standardized poverty percentage to its com-
bined wealth ratio—indicates the district’s ability to meet the needs of students through
local resources, these groups are, for ease of presentation, hereinafter referred to as low-
need, average-need, urban high-need, and rural high-need districts. Columna 2 de mesa 1
shows that 85 percent of low-need districts’ total revenue comes from property tax levy,
followed by average-need districts (55 por ciento). Logically, these two groups of districts
with higher reliance on property taxes are more likely to be constrained by the tax limit.
Por el contrario, rural high-need districts with relatively much lower reliance on property
taxes (31 por ciento) are less likely to be constrained.

Beyond the degree of reliance on property taxes, the ﬁscal impact of the tax limit
may be oﬀset by how much state aid and federal aid a district receives during the limit

5. A measure for need used in the NRC index is the share of eligible free or reduced-priced lunch students, y
capacity is measured partly by full property valuation. While table A.1 (available in a separate online appendix that
can be accessed on Education Finance and Policy’s Web site at https://doi.org/10.1162/edfp_a_00327) proporciona
more information on how each group is oﬃcially deﬁned, columnas 3 y 4 de mesa 1 show that low-need districts
have only 11 percent of economically disadvantaged students (con $3.8 million full property value per pupil), whereas urban high-need districts are relatively property-poor ($434,669 full property value per pupil), con
a much higher share of economically disadvantaged students (64 por ciento). Our data also show that districts
retained their NRC-based classiﬁcation during our sample period.

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
mi
d
pag
a
r
t
i
C
mi
–
pag
d

F
/

1
7
1
1
1
9
7
7
6
2
4
mi
d
pag
_
a
_
0
0
3
2
7
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cap and Gap: Tax Limits in New York

Mesa 1. Basic Information on Four District Groups

Average Total Current
Expenditure per
Pupil ($) Average Share of Property Tax Levy to Total Revenue (%) Average Share of Free or Reduced-Priced Lunch Students (%) Average Total Full District Valuation per Pupil ($)

District Groups

Low-need

Average-need

Urban high-need

Rural high-need

(1)

30,264

20,388

20,373

21,005

(2)

84.8

54.7

41.3

31.0

(3)

11.2

34.7

64.1

52.2

(4)

3,808,624

760,233

434,669

538,832

Nota: The averages come from our sample period between 2011 y 2017.

years.6 A district that has been hit hard by the limit may receive more intergovernmen-
tal aid, which oﬀsets the shortfall of property taxes. Because the amount of intergov-
ernmental aid that a district receives is usually outside its control, we allow aid to fully
play this oﬀsetting role by leaving out aid variables in our empirical models. De este modo, nosotros
compare the results from models with and without aid variables to diagnose the size of
the oﬀsetting eﬀects of intergovernmental aid, if any.

A district may attempt to escape limit-induced constraints by overriding the limit, como
mentioned before. Sin embargo, for two reasons, overriding the limit successfully is neither
easy nor tantamount to permission for the district to spend at the level desired absent
the limit. Primero, the required 60 percent voter approval for overriding is a more diﬃ-
cult hurdle to overcome than a 50 percent majority for regular budgets. Segundo, a levy
limit serves as a reference levy. According to the theory on reference-dependent pref-
erences (Ashworth and Heyndels 1999), when voters are more readily able to compare
the diﬀerence between a proposed levy and the levy limit, they are more likely to reject
the override. The combination of the supermajority threshold and reference-dependent
preference enhances the likelihood of failed budgets. The consequence of two consec-
utive failed proposed budgets is the adoption of a contingency budget (cual, de nuevo,
will be no greater than the prior-year levy). This consequence may induce the district
to be more conservative in its proposed overriding amount, which suggests, absent the
limit, this district could still have spent more than the overriding level.

Finalmente, one can expect that constrained districts do not cut spending equally across
all categories; some categories receive fewer resources or get cut whereas resources for
other categories remain intact. Expenses that school districts are legally and contrac-
tually bound to incur may be hard to reduce or cut. Examples of these expenses are
teacher salaries and beneﬁts, including retirement, that result from union agreements.
School districts are, sin embargo, more likely to spend less on expenditure items that are
non-core to their operations (p.ej., support staﬀ, paraprofessionals, undistributed funds,
interfund transfers) or less contractually binding (p.ej., school supplies, materiales). Nosotros
use the detailed expenditure data to provide by far the most nuanced picture of how
at-limit districts across district groups change their spending patterns in response to
the tax limit.

6. Other revenue sources for NY school districts include user charges, and sales and use taxes. But our data show

that school districts received less than 2 percent of total revenue from those two sources in 2013.

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
mi
d
pag
a
r
t
i
C
mi
–
pag
d

F
/

1
7
1
1
1
9
7
7
6
2
4
mi
d
pag
_
a
_
0
0
3
2
7
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Phuong Nguyen-Hoang and Pengju Zhang

5 . E M P I R I C A L C H A L L E N G E S A N D S T R AT E G I E S
A Measure of the Fiscal Stringency of Property Tax Limit
Multiple measures can be used to capture TELs. The most common approach is to
use a dichotomous indicator to identify the existence of a TEL law (p.ej., Shadbegian
1999). The indicator approach makes sense when the event of interest is simply the
occurrence of a TEL law with little consideration of heterogeneity in TEL law designs.
A second approach is to construct a continuous index of TEL degrees of stringency by
assigning weights to diﬀerent components in each TEL law (p.ej., Deller, Stallmann,
and Amiel 2012). This approach quantiﬁes TEL laws and allows for engaging more
advanced econometric tools in TEL analysis.

Our measure deviates from those two approaches for two reasons. Primero, both ap-
proaches are more appropriate for cross-state analyses. As the tax limit formula in NY
applies identically to all districts, adopting either of those two measures would lead
to zero cross-district variation for our study. Segundo, of our interest is not whether NY
adopts a limit, but rather whether the tax limit really exerts binding constraints on some
districts, and how the tax limit changes the spending behaviors of those constrained or
aﬀected districts. En otras palabras, we need a working measure of ﬁscal stringency for
the tax limit in NY.

Conceptually, a district’s limit-induced ﬁscal constraint can be measured by distance
to limit (DL), deﬁned as the percentage gap between the maximum property levy legally
allowed by the limit (or levy limit, LL) and the district’s proposed property tax levy (PL).
Eso es,

DL = (LL − PL)/LL.

(1)

By deﬁnition, DL in equation 1 is continuous, and a large positive DL indicates that
a district does not have to tap all available property tax levy allowed—an indication of
nonconstraint. Por el contrario, a district is more likely to be ﬁscally constrained when it
overrides the limit (DL < 0), exhausts the limit (DL = 0), or raises almost every property tax dollar it can under the limit (0 < DL (cid:2) ε, where ε is a very small positive number). All districts with DL (cid:2) ε are referred to in this study as at-limit districts.7 Note that DL is not a sound direct measure of ﬁscal constraint. A unit increase in DL does not necessarily indicate a unit decrease in the degree of constraint; that is, DL is not linearly correlated with the degree of constraint. Additionally, what really concerns us is not the limit-induced ﬁscal behaviors of the average-DL district, but of constrained districts. Thus, instead of using DL directly, we use DL to develop a dichotomous variable of being at limit, D. D is coded 1 for at-limit districts with DL (cid:2) ε, where ε is a numeric positive benchmark, and 0 otherwise. As indicated, ε must be very small. For instance, Bradbury, Mayer, and Case (2001) consider a school district to be at limit in a year when its proposed levy is within 0.1 percent of its levy limit in that year, that is, when ε is 0.1 percent. This small value of ε is consistent with our deﬁnition of an at-limit district and we therefore adopt this ε, 0.1 percent, as our preferred benchmark as well. 7. At-limit districts may be theoretically unconstrained when their maximum levy limits happen to equal exactly the amount needed to fund their desired spending levels. We suspect that, in practice, the probability at-limit districts are not constrained is very low. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . f / / e d u e d p a r t i c e - p d l f / / / / / 1 7 1 1 1 9 7 7 6 2 4 e d p _ a _ 0 0 3 2 7 p d . f f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 9 Cap and Gap: Tax Limits in New York Admittedly, this chosen value of ε may not be perfect. For instance, a district that is actually constrained by the tax limit could be classiﬁed as a control unit in our research design when its DL is just slightly larger than ε, leading to an attenuation of estimated tax limit eﬀects on at-limit districts. This attenuation suggests that our estimated eﬀects are conservative, and the true eﬀects could be even stronger when at-limit districts are perfectly identiﬁed. It may not be a good idea to choose a relatively larger ε. With a relatively larger ε, an at-limit district would have considerable untapped property taxes. This is logically self-contradictory because an at-limit district would not have much excessive revenue slack if they were really at limit or constrained. Regardless, we start with ε = 0.1 percent and increase ε to 1 percent and 2 percent to test the robustness of our measure. Empirical Models Difference-in-Differences Estimator To examine whether and how the tax limit aﬀects the ﬁscal behaviors of at-limit school districts in NY, we start with a DID framework and estimate a model of the following form: ln Eit = τt + μi + αDit + (cid:5)it, (2) where E stands for total current expenditures per pupil, i and t index school districts and years, and τ and μ are year- and school district–ﬁxed eﬀects, respectively.8 As dis- cussed earlier, D in equation 2 is coded as 1 for at-limit school districts with DL (cid:2) 0.1 percent—districts that are most likely constrained by the tax limit—and 0 otherwise. The coeﬃcient of this variable, α, indicates how much more or less spending (in per- centage terms) would, on average, have changed for at-limit school districts. A key identifying assumption underlying a DID estimator is that the pre-limit trend in total current expenditures per pupil of at-limit school districts parallels that of coun- terfactual school districts. Similar to Lafortune, Rothstein, and Schanzenbach (2018), school districts not at limit in a particular year serve as the counterfactual for at-limit school districts in that year. To test the common pre-trend assumption, we add the lin- ear pre-trend variable (P), as shown in equation 3, to capture diﬀerences in E between at-limit and counterfactual districts during the years before a district is ﬁrst at limit (in year t*). Of note, not all school districts are at limit immediately in 2013 when the tax limit comes into eﬀect. Therefore, the initial at-limit year, t*, varies from one district to another. P equals (t − t0) before t* (where t0 is the baseline year that immediately precedes t*, or t0 = t* − 1), and 0 otherwise. A small insigniﬁcant coeﬃcient of P, β, is expected, should the common pre-trend assumption hold. ln Eit = τt + μi + αDit + βPit + δTit + βWit + (cid:5)it. (3) According to the tax limit formula, a school district’s current levy will factor into the calculation of the proposed levy in the following year, suggesting a dynamic eﬀect of 8. The tax limit may aﬀect capital spending. However, capital investment tends to be lumpy (i.e., not spreading evenly across the years). Therefore, a valid investigation of a policy or intervention’s eﬀect on capital spending usually requires a long data panel and a diﬀerent methodological approach than that used to investigate current expenditures (Wang, Duncombe, and Yinger 2011). 10 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / f e d u e d p a r t i c e - p d l f / / / / / 1 7 1 1 1 9 7 7 6 2 4 e d p _ a _ 0 0 3 2 7 p d f . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Phuong Nguyen-Hoang and Pengju Zhang the tax limit during its post-initial (t > t*) período. To capture this post-initial eﬀect, nosotros
include the post-trend variable (t) in equation 3. Específicamente, T captures whether, encima
tiempo, the expenditure change associated with D stays constant (δ is insigniﬁcant), dis-
sipates (δ is signiﬁcantly positive), or increases (δ is signiﬁcantly negative). Por lo tanto,
T equals (t − t*) for at-limit districts when t > t*, y 0 de lo contrario. For school districts
that are never at limit, P and T are set to zeros during the entire sample period.9

Following the education cost-function literature (Duncombe and Yinger 2011), equa-
ción 3 also includes a series of control variables (W.), such as student characteristics (es decir.,
logged enrollment as well as the percentages of English Language Learner students,
special education students, economically disadvantaged students, and African Ameri-
can students), and factors inﬂuencing eﬃciency and demand for school expenditures
(es decir., logged median household income, logged median tax share, logged state and fed-
eral aid per pupil, the percentages of owner-occupied housing units, and population
aged 25 years and over with a four-year college education). The median tax share is de-
rived as the ratio of a district’s median housing value to its total taxable property value
per pupil.

We also estimate equation 3 separately with ε = 2 percent and ε = 1 por ciento. Como
discussed earlier, a larger ε is more likely to produce nonnegative and insigniﬁcant
eﬀects of the limit because more far-from-limit and plausibly unconstrained districts
are treated as at-limit constrained districts in those scenarios.

Event Study Specification
A major empirical challenge of equation 3 is that even with school district and year ﬁxed
efectos, as well as all controls in W, the key variable D is still potentially biased, as are
its derived variables P and T. The more a school district would like to spend, the more
likely it is to be at limit, leading to a reverse causation or a positive bias in the estimate
of α. Eso es, the negative coeﬃcient of D is likely to be attenuated toward zero. Uno
way to address this endogeneity is to use instrumental variables. Sin embargo, it is hard
to ﬁnd three or more instrumental variables that are time-varying (because of district
efectos fijos), exogenous of equation 3, and strongly correlated with D, PAG, and T.

Another way to diagnose and reduce the bias is to use nonparametric event-study
modelos. The use of event-study speciﬁcations is also warranted when there is variation
in treatment timing (Goodman-Bacon 2021), as in the current study. An event occurs in
a year when a district is at limit (DL ≤ 0.1 por ciento). We estimate models of the following
forma:

ln Eit = τt + μi +

5(cid:2)

k=−4

θkTk,él + βWit + (cid:5)él,

(4)

where τ , μ, and W are deﬁned as in equation 3; Tk equals 1 for at-limit districts when
t = t0 + k, where k represents the number of years before (k < 0) or after (k > 0) el
baseline year, t0. While year 5 is the farthest year after t0 in our dataset, −4 represents
four or more years before t0. También, t0 is excluded and serves as the reference year. Cuando

9. Year ﬁxed eﬀects obviate the need for a general trend variable (coded 1 para 2011, 2 para 2012, etcétera) for all school
districts. Including such a general trend variable would require a drop of a year dummy while the results stay
sin alterar.

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
mi
d
pag
a
r
t
i
C
mi
–
pag
d

F
/

1
7
1
1
1
9
7
7
6
2
4
mi
d
pag
_
a
_
0
0
3
2
7
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cap and Gap: Tax Limits in New York

k > 0, the coeﬃcient for a Tk, θk, indicates the eﬀect of an event in t0 on outcomes k
años después. Compared to parametric estimations, the θ coeﬃcients with k > 0 captura
dynamic eﬀects of the tax limit on at-limit districts. Similar to the DID design, an event-
study design requires, for a causal interpretation, a common pre-trend of treatment (en-
limit) and comparison (not-at-limit) districts. This assumption is statistically supported
when the series of lead indicators (θ−4 to θ−1) are not signiﬁcant.

There are two important issues related to equation 4. Primero, as explained earlier, un
at-limit school district may receive federal and state aid to meet their desired spending
nivel. Por lo tanto, in addition to the models with aid variables, our preferred speciﬁcation
is one without these variables so that intergovernmental aid is allowed to oﬀset property
tax shortfall. Segundo, as with the standard event-study design, equation 4 accounts only
for the ﬁrst event of being at limit. Sin embargo, a school district may experience subse-
quent events, in subsequent years, after the ﬁrst. There is no established econometric
method to account for multiple events. Following Lafortune, Rothstein, and Schanzen-
bach (2018), we replicate the data for school districts with multiple events; Por ejemplo,
a district with three at-limit events has three copies (or cohorts). We then stack all repli-
cated cohorts with no-event districts. Each cohort of the same multiple-event district
now has only one event in this stacked dataset. The coding method for Tk in equation
4 is the same as before, and μ now represents district-cohort ﬁxed eﬀects.

Additional Analyses
To explore the second research question, which concerns the diﬀerential eﬀects of
the tax limit, we estimate equation 4 using four NRC-based district groups: low-need,
average-need, and urban and rural high-need districts. Específicamente, we allow each
district group, gramo, to have a separate series of Tk for the ﬁve-year limit period (es decir.,
(cid:3)
θkgTkg), where Tkg captures the average within-g eﬀect of an event in t0 on
outcomes k years later.10 This ﬂexibility allows us to see how districts in four groups
respond diﬀerently to the limit. Finalmente, for the third research question on cutback
estrategias, we use equation 4 with Tkg for disaggregated expenditure categories and
subcategories as dependent variables.

5
k=1

4
g=1

(cid:3)

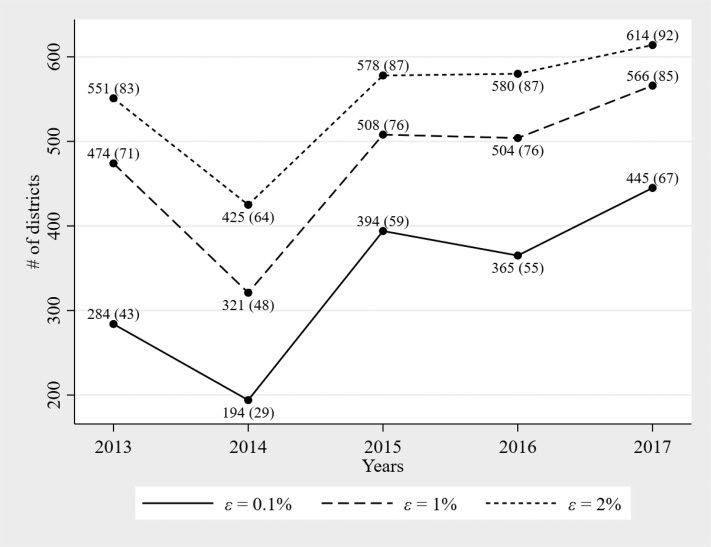
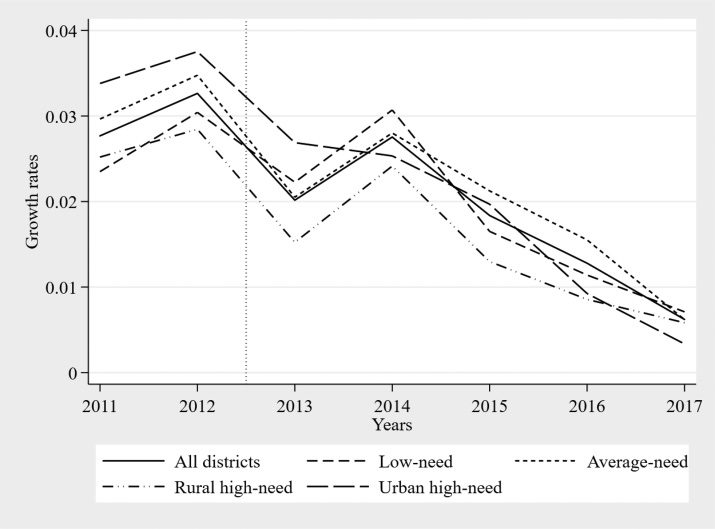
6 . DATA A N D D E S C R I P T I V E A N A LY S I S
Datos
The data panel consists of all school districts, except for Buﬀalo, Nueva York,
Rochester, Siracusa, and Yonkers.11 The sample period is between 2011 y 2017.12 Mayoría
of our data come from NYSED. We also take some data from the American Commu-
nity Surveys, a saber, median house value (to calculate tax share), median homeowner

10.As shown in table 3, the number of comparison districts that are never at limit is quite small (only six low-need and
θkTk,

nine urban high-need districts). Por lo tanto, all district groups have the same pre-trend variables, o
to maximize pre-trend variation.

(cid:3)−1

k=−4

11. These ﬁve large city school districts, called the “Big Five,” are not subject to the tax limit. Education budgets for
these ﬁscally dependent school districts are included in their respective municipal budgets. Además, each city,
including the Big Five cities, is subject to an individual constitutional tax limit; education in each city is funded
within that set limit (New York State Oﬃce of the State Comptroller 2018). Constitutional tax limits do not apply
to the independent school districts that comprise our sample.

12. We do not extend the data further back beyond 2011 to head oﬀ potential eﬀects of the Great Recession years on

school districts’ resources.

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
mi
d
pag
a
r
t
i
C
mi
–
pag
d

F
/

1
7
1
1
1
9
7
7
6
2
4
mi
d
pag
_
a
_
0
0
3
2
7
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Phuong Nguyen-Hoang and Pengju Zhang

Mesa 2. Summary Statistics

Variables

Key variables

Total current expenditures per pupil, $ D (= 1 if DL (cid:2) 0.1 y 0 de lo contrario) Control variables Enrollment Percent of free or reduced-price lunch students Percent of special education students Percent of ELL students Percent of black students Median homeowner income Tax share Mean SD Minimum Maximum Data Source 22,247 9,246 11,368 279,812 0.4 0.5 2,267 35.9 13.9 2.2 4.9 2,306 18.9 3.0 4.3 8.9 0 16 0 4.1 0 0 1 19,457 100 32.3 37.1 79.7 78,794 30,856 37,930 250,000 0.33 0.15 0.004 1 1, 3 1 1 1 1 1 2 1, 2, 3 2 2 1 1 Percent of adults with college education Percent of owner-occupied housing units 29.2 77.2 15.0 12.3 Intergovernmental aid Staid aid per pupil Federal aid per pupil 9,018 779 4,711 606 6.1 5.0 816 0 1.04 89.1 100 47,613 13,082 Notas: Hay 4,630 observaciones. This table summarizes fiscal, económico, and demographic information for 666 New York school districts between 2011 y 2017. SD = standard deviation; ELL = English language learner. income, and district-level information on percent of college-educated population and owner-occupied housing units. Mesa 2 provides summary statistics and sources of the variables used in our estimations. We follow the NYSED categorization of current ex- penditure categories and subcategories, and table 4 provides the deﬁnitions of all cate- gories and subcategories we use for our estimations. Descriptive Analysis New York state’s property tax limit law’s primary objective is to combat the growth of property tax revenue. In ﬁgure 2, we delineate the trends of the average annual growth rates of property tax levy by four district groups. Basically, all district groups exhibit a similar declining pattern in the growth rate of property tax levy. Of note, urban high- need districts had the highest levy growth rate before 2013, experienced the fastest de- clining trend, and had the lowest levy growth rate ﬁve years after the limit enactment. Cifra 3 presents the number of at-limit districts as a share of total districts by diﬀerent values of ε. When ε is set at 2 por ciento, 551 districts (o 83 percent of all) would be counted as at-limit districts in 2013, and this number increases to 614 (o 92 por ciento) en 2017. When using ε = 1 por ciento, the number of at-limit districts increases from 474 (o 71 por ciento) en 2013 a 566 (o 85 por ciento) en 2017. Finalmente, with ε = 0.1 por ciento (our preferred benchmark), at-limit districts number 284 (42 por ciento) en 2013 y 445 (67 por ciento) en 2017. Cifra 3 provides two takeaways. Primero, the annual number of at-limit districts in NY increases substantially with larger ε. Starting with ε = 0.1 por ciento, the number of at- limit districts in 2013 expands by 67 percent with ε = 1 percent and by 94 percent with ε = 2 por ciento. Segundo, all ε options illustrate the substantial temporal upward trend in the frequency of at-limit districts. This trend is consistent with ﬁndings in other states. l D o w n o a d e desde h t t p : / / directo . mi t . F / / e d u e d p a r t i c e – pdlf / / / / / 1 7 1 1 1 9 7 7 6 2 4 e d p _ a _ 0 0 3 2 7 pd . f f b y g u e s t t o n 0 7 septiembre 2 0 2 3 13 Cap and Gap: Tax Limits in New York Figure 2. The Average Annual Growth Rates of Total Property Tax Levy by District Groups l D o w n o a d e d f r o m h t t p : / / directo . mi t . / / partícula alimentada – pdlf / / / / / 1 7 1 1 1 9 7 7 6 2 4 e d p _ a _ 0 0 3 2 7 pdf . f por invitado 0 7 septiembre 2 0 2 3 Nota: The numbers in parentheses indicate the percentage shares of total school districts. Cifra 3. The Numbers and Shares of At-Limit School Districts Over Time by Different Values of ε 14 Phuong Nguyen-Hoang and Pengju Zhang Table 3. Distribution of School Districts by the Number of Times Being at Limit (with ε = 0.1%) and by Need Groups Number of Times at Limit Low-Need Average-Need Urban High-Need Rural High-Need All Districts 0 1 2 3 4 5 Total 6 (5) 12 (9) 30 (23) 21 (16) 45 (34) 19 (14) 133 29 (9) 59 (18) 66 (20) 90 (27) 55 (16) 37 (11) 336 9 (20) 8 (18) 7 (16) 11 (25) 5 (11) 4 (9) 44 33 (22) 35 (23) 33 (22) 26 (17) 19 (12) 7 (5) 153 77 (12) 114 (17) 136 (20) 148 (22) 124 (19) 67 (10) 666 Nota: The numbers in parentheses indicate at-limit districts as a percent of all districts within a group. Por ejemplo, Dye, McGuire, and McMillen (2005) ﬁnd the binding eﬀect of the tax limit in Illinois becomes stronger over time. Mesa 3 shows the distribution of at-limit districts by instances of being at limit and by type of need. Of all districts, 77 (12 por ciento) are never at limit and the number of these districts is suﬃciently large to serve as a comparison group. Being at limit three times during the ﬁve-year limit duration, as occurs for 148 districts, is the mode. Three in- stances of being at limit is also the mode for average-need and urban high-need groups. As many as 67 (10 por ciento) districts are at limit in all ﬁve years. Mesa 3 indicates sub- stantial within- and across-district variation for our estimations. Our data show that only 8.9 percent of all at-limit cases needed budget overrides (es decir., DL < 0). Finally, in over two thirds of no-override at-limit cases, the proposed limit exactly equals levy limit (DL = 0). The primary dependent variables are total current expenditures per pupil deﬁned as ([total district expenditures − debt service]/enrollment).13 Table 2 shows the mean cur- rent expenditure per pupil is $22,247 with a standard deviation of nearly $9,246. The last four columns of table 4 also show three spending patterns from the group-based shares of each expenditure category in their total current expenditures, and the group- based shares of each subcategory in their respective category. First, the two largest categories are instruction and beneﬁts, while the smallest expenditure categories are, in ascending order, interfund transfers, undistributed, administration, and transporta- tion. These categories represent only 0.5 percent to 5.6 percent of total current expen- ditures, far less than the second highest category of beneﬁts (23 percent to 25 percent). Of note, the share of administration in total current expenditures is lower than that of transportation. Second, one expenditure subcategory dominates across instruction, beneﬁts, and administration. Teacher salary constitutes the largest shares of districts’ instructional budget, 54 percent to 60 percent, followed by other instructional expenses (24 percent to 35 percent), and other instructional salaries (13.3 percent to 15.4 percent). Central ad- ministration and other fringes account for at least 76 percent of total administration and beneﬁts, respectively. Finally, there is some expenditure variation in both categories and subcategories across district groups. There is a six percentage point diﬀerence between 13. Once logged enrollment is controlled for on the right-hand side, the results with either logged expenditures or logged expenditures per pupil are the same. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / f e d u e d p a r t i c e - p d l f / / / / / 1 7 1 1 1 9 7 7 6 2 4 e d p _ a _ 0 0 3 2 7 p d f . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 15 Cap and Gap: Tax Limits in New York . ] 8 3 5 [ . ] 3 3 1 [ . ] 9 2 3 [ . ) 5 1 6 ( . ] 9 2 2 [ . ] 1 7 7 [ . ) 4 2 ( . ) 8 4 ( ) 2 2 ( . ) 5 0 ( . ] 1 2 [ ] 9 7 [ . ) 8 2 2 ( p u o r g t c i r t s i d h c a e . ] 9 1 5 [ . ] 5 3 1 [ . ] 6 4 3 [ . ) 3 5 5 ( . ] 8 7 1 [ . ] 2 2 8 [ ) 8 3 ( . ) 5 5 ( . . ) 1 3 ( . ) 4 1 ( . ] 5 7 1 [ . ] 5 2 8 [ . ) 7 4 2 ( d e e N - h g i H n a b r U d e e N - h g i H l a r u R d e e N - e g a r e v A d e e N - w o L s n o i t i n fi e D s e i r o g e t a c b u S . ] 2 7 5 [ . ] 0 4 1 [ . ] 3 0 6 [ . ] 4 5 1 [ i n e t r a g r e d n k e r p , s e s r u n , s r e k r o w l i a c o s l , s t s i g o o h c y s p , s r o e s n u o c l l o o h c s o t i d a p s e i r a a S l s e i r a a s l l a n o i t c u r t s n i r e h t O s r e h c a e t 2 1 — K o t i d a p s e i r a a S l y r a a s l r e h c a e T . ] 8 8 2 [ . ] 3 4 2 [ ) S E C O B ( s e c i v r e S l a n o i t a c u d E e v i t a r e p o o C f o s d r a o B , n o i s i v r e p u s d n a l t n e m p o e v e d m u u c i r r u C l s e s n e p x e f f a t s t r o p p u s r e h t o d n a , s d a i r e h c a e t , s l a n o i s s e f o r p a r a p , s n a i r a r b i l , s r e h c a e t , . g . e ( s e r u t i d n e p x e l a n o i t c u r t s n i l y r a a s n o n d n a , s n o i t i u t t c i r t s i d r e t n i , s e c i v r e s l a n o i t c u r t s n i l a n o i t c u r t s n i r e h t O . ) 4 6 5 ( . ] 4 0 2 [ ) 9 5 ( . ] 8 2 2 [ . ] 6 9 7 [ . ] 2 7 7 [ . ) 1 3 ( . ) 6 5 ( ) 4 2 ( . . ) 3 1 ( . ] 8 9 1 [ . ] 2 0 8 [ . ) 8 4 2 ( . ) 1 3 ( . ) 7 4 ( . ) 9 1 ( . ) 4 1 ( . ] 7 3 2 [ . ] 3 6 7 [ ) 3 2 ( c i l b u p , t n e m e g a n a m s d r o c e r s t n e g a l a c s fi r o f s e e f ; s e c i v r e s d n a , n o i t a m r o f n i , l e n n o s r e p , g n i s a h c r u p , s s e n i s u b f o s e c fi f o e h t ; r e c fi f o l o o h c s i f e h C n o i t a r t s i n m d a i l a r t n e C n o i t a r t s i n m d a i l a t o T , k r e c l t c i r t s i d f o s e c fi f o e h t ; s e c i v r e s l a g e l d n a g n i t i d u a ; g n i t e e m t c i r t s i d ; n o i t a c u d e f o d r a o B n o i t a c u d e f o d r a o B n o i t a r t s i n m d A i ) s e i t i v i t c a l r a u c i i r r u c , t n e m p u q e , s l a i r e t a m , s e i l p p u s n o i t c u r t s n i l a t o T r o t c e l l o c x a t d n a , r e r u s a e r t ) s e s n e p x e l a t i p a c i g n d u c x e ( l g n d i l i u b e g a r a g d n a s e s u b l o o h c s i g n d u c n l i s e c i v r e s n o i t a t r o p s n a r T l e b a l i a v a s e u d i n o i t a c o s s a l o o h c s , g n i s s e c o r p a t a d , g n i l i a m , g n i t n i r p , m o o r e r o t s l a r t n e C l e b a l i a v a s d n u f l a t i p a c d n a e c i v r e s d o o f l o o h c s o t r e f s n a r T l e b a l i a v a t o N t o N t o N s r e f s n a r t d n u f r e t n I n o i t a t r o p s n a r T d e t u b i r t s i d n U s t fi e n e b e e y o p m e l r e h t o , s e e y o p m e l r o f e g a r e v o c l a t n e d d n a l i a c d e M s e g n i r f r e h t O s t fi e n e b l a t o T m e t s y s t n e m e r i t e r r e h c a e t n i s l a u d i v i d n i r o f s t n e m y a P t n e m e r i t e r r e h c a e T s t fi e n e B s e i r o g e t a C n o i t c u r t s n I d n a s e i r o g e t a c e r u t i d n e p x e l l a r o f l a u m r o f t n e t s i s n o c a s e s u D E S Y N . p u o r g t c i r t s i d h c a e i n h t i w s e i r o g e t a c e r u t i d n e p x e n i s e i r o g e t a c b u s e r u t i d n e p x e f o s e r a h s t n e c r e p e h t e t a c d n i i s t e k c a r b n i s r e b m u n e h T . d o i r e p l e p m a s e h t g n i r u d l e b a t e h t n i d e t r o p e r t o n e r a ) e c i v r e s y t i n u m m o c d n a , e c n a n e t n a m d n a i n o i t a r e p o , y l e m a n ( s e i r o g e t a c e r u t i d n e p x e o w t m o r f s e r u t i d n e p x e t n e r r u c l a t o t f o t n e c r e p 7 n a h t s s e l , y n o m i s r a p r o F . d o i r e p l e p m a s e h t g n i r u d s e i r o g e t a c b u s l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / f e d u e d p a r t i c e - p d l f / / / / / 1 7 1 1 1 9 7 7 6 2 4 e d p _ a _ 0 0 3 2 7 p d . f f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 . m e h t n o t c e f f e y n a e v a h o t n w o h s t o n s i t i m i l x a t e h t e s u a c e b i n h t i w s e r u t i d n e p x e t n e r r u c l a t o t n i s e i r o g e t a c e r u t i d n e p x e f o s e r a h s t n e c r e p e h t e t a c d n i i s e s e h t n e r a p n i s r e b m u n e h T . ) 9 1 0 2 D E S Y N ( t n e m t r a p e D n o i t a c u d E e t a t S k r o Y w e N n o d e s a b e r a s n o i t i n fi e d e h T : s e t o N s e i r o g e t a c b u S d n a s e i r o g e t a C e r u t i d n e p x E f o s e r a h S d n a s n o i t i n fi e D . 4 e l b a T 16 Phuong Nguyen-Hoang and Pengju Zhang Table 5. Parametric Results ε = 2% ε = 1% ε = 0.1% Current Expenditure Current Expenditure Current Expenditure with Benefits Excluded Key variables (1) (2) (3) (4) (5) (6) D (= 1 if DL (cid:2) ε and 0 otherwise) Pre-trend (P) Post-trend (T) With aid 0.0029 (0.003) 0.0026 (0.005) 0.0033 (0.005) Yes −0.0017 (0.002) 0.0011 (0.003) 0.0010 (0.003) Yes −0.0026 (0.002) −0.0020 (0.002) −0.0041* (0.002) −0.0023 (0.002) −0.0018 (0.002) −0.0038* (0.002) −0.0053* (0.002) −0.0030 (0.002) −0.0070** (0.002) −0.0050* (0.002) −0.0028 (0.002) −0.0068** (0.002) Yes No Yes No Notes: There are 4,630 observations. The dependent variables are the logged total current expenditures per pupil in columns 1 to 4 and non-benefit current expenditures (total current expenditures − benefits defined in table 4) per pupil in columns 5 and 6. Estimates are obtained with year and district fixed effects as well as all control variables in table 2. Robust standard errors clustered at the school district level are reported in parentheses. *p < 0.05; **p < 0.01. the groups with the highest and lowest instructional shares of total current expendi- tures: urban high-need at 61.5 percent versus rural high-need at 55.3 percent. Another diﬀerence of similar size comes from the shares of teacher salary in instruction: 60.3 percent for low-need districts versus 53.8 percent for urban high-need districts. 7 . R E G R E S S I O N R E S U LT S Table 5 reports the DID regression results for the ﬁrst research question. The results in columns 1 through 3 are obtained with state and federal aid per pupil and with diﬀerent values on ε. Column 1 shows that when at-limit districts are deﬁned as those with ε = 2 percent, the coeﬃcient on D is positive but not statistically signiﬁcant. When ε = 1 percent, D is still not statistically signiﬁcant, but it becomes negative (column 2). Also, the post-trend variable, T, is not signiﬁcant with these values of ε. Columns 3 through 6 report results when our preferred value of ε is 0.1 percent, or a proposed levy within 0.1 percent of the limit is used to deﬁne at-limit districts. In columns 3 and 4, while the negative coeﬃcients of D remain insigniﬁcant, T becomes negative and signiﬁcant. Its coeﬃcient in column 3 indicates that an at-limit district spends 0.4 percent less each year in the wake of ﬁrst exhausting their limit than what they would have spent absent the tax limit. Districts may ﬁnd it hard to reduce spending on beneﬁts, the major contractually binding category. With non-beneﬁt current expenditures per pupil as the dependent variable, both D and T are signiﬁcant in columns 5 and 6. The coeﬃcients of D indicate that absent the limit, at-limit districts would have annually spent approximately 0.5 percent more on non-beneﬁt current categories. Columns 4 and 6 show that state and federal aid have a negligibly oﬀsetting eﬀect on the property tax shortfall among at- limit districts, evidenced by slightly smaller (in absolute value) coeﬃcients of D and T relative to those in columns 3 and 5, respectively. Finally, the insigniﬁcance of the pre-trend variable, P, provides statistical evidence that the common trend assumption holds for all six columns. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / f e d u e d p a r t i c e - p d l f / / / / / 1 7 1 1 1 9 7 7 6 2 4 e d p _ a _ 0 0 3 2 7 p d f . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 17 Cap and Gap: Tax Limits in New York Table 6. Nonparametric Results with the Event-Study Design ε = 0.1% ε = 1% Current Expenditure Current Expenditure Current Expenditure with Benefits Excluded Current Expenditure with Stacked Data Current Expenditure Key Variables Four or more years before t0 (T−4) Three years before t0 (T−3) Two years before t0 (T−2) One year before t0 (T−1) One year after t0 (T1) Two years after t0 (T2) Three years after t0 (T3) Four years after t0 (T4) Five years after t0 (T5) With aid Observations (1) 0.0082 (0.009) 0.0036 (0.006) 0.0006 (0.004) −0.0017 (0.002) −0.0066* (0.003) −0.0080* (0.004) −0.0122* (0.005) −0.0135* (0.007) −0.0245** (0.009) Yes 4,630 (2) 0.0068 (0.009) 0.0031 (0.006) 0.0001 (0.004) −0.0019 (0.002) −0.0062* (0.003) −0.0073 (0.004) −0.0112* (0.005) −0.0121 (0.007) −0.0234* (0.009) No 4,630 (3) 0.0096 (0.010) 0.0070 (0.007) 0.0031 (0.005) −0.0003 (0.003) −0.0096** (0.003) −0.0124** (0.005) −0.0198** (0.007) −0.0233** (0.008) −0.0376** (0.011) No 4,630 (4) 0.0090 (0.006) 0.0057 (0.005) 0.0033 (0.003) 0.0018 (0.002) −0.0042* (0.002) −0.0060 (0.003) −0.0089 (0.005) −0.0110 (0.006) −0.0174* (0.008) No 12,121 (5) −0.0098 (0.016) −0.0013 (0.012) −0.0044 (0.008) −0.0066 (0.004) −0.0041 (0.004) −0.0033 (0.007) −0.0003 (0.011) −0.0014 (0.014) −0.0010 (0.017) No 4,630 Notes: The dependent variable is the logged total current expenditures per pupil for all columns, except for column 3, where the dependent variable is non-benefit current expenditures per pupil. An event is defined as when a district’s property tax levy is at limit with ε = 0.1 percent. Estimates are obtained with year and district fixed effects as well as all other control variables in table 2. Robust standard errors clustered at the district-cohort level for column 4 and at the school district level for other columns are reported in parentheses. *p < 0.05; **p < 0.01. As discussed earlier, the DID regression results in table 5 are likely to be biased by endogeneity. Table 6 shows event-study results to address the endogeneity. With ε = 0.1 percent, similar to the results in table 5, columns 1 and 2 in table 6 report little dif- ference in the coeﬃcients estimated with or without intergovernmental aid. A major reason for such a minor diﬀerence could be the current state education aid formula en- acted in 2007 does not factor in potential ﬁscal eﬀects of a state-imposed TEL measure on school districts.14 Column 2 (without aid) shows that at-limit districts’ total current expenditures are reduced by 0.6 percent in the ﬁrst event year and the reduction in- creases in size over the next four years. By year 5, the tax cap results in a cumulative reduction of 2.3 percent in at-limit districts’ expenditures.15 Column 3, where the depen- dent variable is non-beneﬁt current expenditures per pupil, shows a similar declining trend but with larger reductions. Figure 4 visualizes the increasingly constraining ef- fects of the tax limit on total current expenditures and non-beneﬁt expenditures over the years. 14. In fact, during the period of 2013–17, the average annual change in state aid per pupil for at-limit districts in year t > t0 is $477, which is even lower than that for never-at-limit districts and at-limit districts in year t ≤ t0 ($496).
This diﬀerence is not statistically signiﬁcant, aunque.

15. We also test whether the tax cap has diﬀerential eﬀects on school districts that were at limit in all ﬁve years (2013–
17) and on those that were at limit less than ﬁve years. The coeﬃcients of T1 to T5 in this test are similar in size
and signiﬁcance both for these two at-limit district groups and to those in column 2 de mesa 6.

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
mi
d
pag
a
r
t
i
C
mi
–
pag
d

F
/

1
7
1
1
1
9
7
7
6
2
4
mi
d
pag
_
a
_
0
0
3
2
7
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

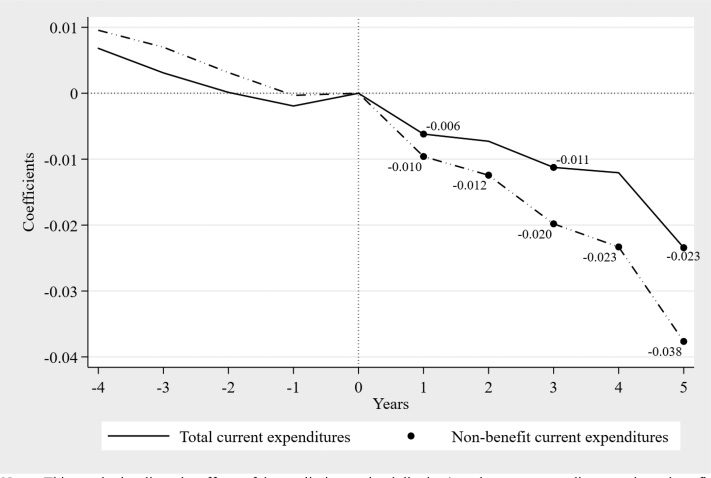
Phuong Nguyen-Hoang and Pengju Zhang

Notas: This graph visualizes the effects of the tax limit on school districts’ total current expenditures and non-benefit current expen-
ditures per pupil, reported in columns 2 y 3 de mesa 6. A black circle indicates a significance level of at least 5 por ciento.

Cifra 4. The Effects of the Tax Limit on Total Current Expenditures and Non-Benefit Current Expenditures

We conduct two additional robustness tests by using stacked data and ε = 1 por ciento.
The results prove to be robust to a certain degree when within-district multiple events
are taken into account with stacked data. Compared with column 2, the coeﬃcients of
T1 through T5 in column 5 de mesa 6 are slightly smaller in absolute value, and those
of T2 through T4 are signiﬁcant only at 10 por ciento (although not indicated by any aster-
isk). Given ε = 1 por ciento, none of the coeﬃcients is signiﬁcant (columna 5 de mesa 6),
providing evidence that the 1 percent distance to limit is so large as to include many
unconstrained districts. In all columns, the pre-trend variables (T−4 to T−1) are not sig-
niﬁcant, providing statistical evidence to support the common pre-trend assumption.
Mesa 7 reports empirical results for the second and third research questions. Columna-
umn 1 shows the diﬀerential eﬀects of the tax limit on the total current expenditures of
four district groups. Of the four groups, only rural high-need districts are not aﬀected
by the tax limit. This ﬁnding makes sense given these districts rely the least on property
tax levy (31 percent of their total revenue, as shown in column 2 de mesa 1). Por el contrario,
the tax limit has expenditure-stiﬂing eﬀects on the other three district groups. Absent
the tax limit, at-limit average-need districts’ annual total current expenditures would
have been from 1.1 por ciento a 2.3 percent higher in all ﬁve limit years. The tax limit,
sin embargo, reduces total current expenditures for at-limit low-need and urban high-need
districts in only three of the years. The left panel of ﬁgure 5 clearly depicts the declining
trends for the three limit-aﬀected district groups.

Columna 2 de mesa 7, which is visually represented in the right panel of ﬁgure 5,
shows the size and signiﬁcance of the eﬀects of the tax limit on non-beneﬁt current
expenditures are stronger for the three top-panel groups. In the ﬁrst two years, urban

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
mi
d
pag
a
r
t
i
C
mi
–
pag
d

F
/

1
7
1
1
1
9
7
7
6
2
4
mi
d
pag
_
a
_
0
0
3
2
7
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cap and Gap: Tax Limits in New York

r
mi
h
t
oh

s
mi
gramo
norte
i
r
F

)
0
1
(

*
*
9
1
0
0

*
*
6
2
0
0

*
*
9
2
0
0

*
*
6
3
0
0

*
*
6
4
0
0

1
0
0
0

3
0
0
0

2
1
0
0

*
3
2
0
0

1
2
0
0

5
1
0
0

1
1
0
0

2
1
0
0

*
9
3
0
0

*
5
4
0
0

2
0
0
0

6
0
0
0

7
1
0
0

0
3
0
0

5
2
0
0

*
*
9
0
0
0
−

*
2
1
0
0
−

3
1
0
0
−

3
0
0
0
−

0
3
6
4

d
norte
tu
F
r
mi
t
norte
I

s
r
mi
F
s
norte
a
r
t

)
9
(

9
3
8
0
−

0
2
0
1
−

*
*
7
5
1
2
−

*
*
4
6
2
2
−

*
*
8
2
7
2
−

7
8
2
0
−

*
8
2
0
1
−

5
6
9
0
−

6
6
8
0
−

3
2
2
1
−

*
2
4
3
1
−

3
6
6
1
−

9
2
3
0
−

4
2
3
0

9
8
2
0

4
9
0
0
−

8
5
0
0
−

4
4
7
0
−

2
6
3
0
−

8
0
6
1
−

5
8
0
0

4
5
5
0

1
9
5
0

8
6
0
1

4
2
6
4

d
mi
t
tu
b
i
r
t
s
i
d
norte
Ud.

.
t
r
oh
pag
s
norte
a
r
t

)
8
(

8
1
0
0
−

4
2
0
0
−

5
4
0
0
−

*
6
8
0
0
−

*
*
1
2
1
0
−

0
2
0
0
−

9
1
0
0
−

2
3
0
0
−

*
2
6
0
0
−

4
3
0
0
−

0
1
0
0

4
3
0
0

2
3
0
0
−

9
4
0
0
−

7
2
0
0

9
3
0
0

5
1
0
0

5
2
0
0

2
6
0
0

1
8
0
0

7
0
0
0

1
0
0
0

1
2
0
0

5
0
0
0

0
3
6
4

)
7
(

*
*
4
3
0
0
−

*
4
3
0
0
−

*
2
4
0
0
−

2
4
0
0
−

1
5
0
0
−

*
*
4
2
0
0
−

*
*
9
2
0
0
−

*
5
3
0
0
−

*
2
4
0
0
−

3
4
0
0
−

2
3
0
0
−

8
2
0
0
−

7
3
0
0

4
5
0
0

3
6
0
0

4
2
0
0

4
3
0
0

6
1
0
0

9
3
0
0

0
3
0
0

1
0
0
0
−

2
0
0
0
−

4
2
0
0
−

0
3
6
4

a
r
t
norte
mi
C

.
norte
metro
d
A

)
6
(

*
5
2
0
0
−

*
5
3
0
0
−

*
6
3
0
0
−

*
2
5
0
0
−

*
0
7
0
0
−

2
1
0
0
−

9
1
0
0
−

0
3
0
0
−

*
7
4
0
0
−

1
4
0
0
−

1
2
0
0
−

7
5
0
0
−

6
5
0
0
−

*
1
8
0
0
−

*
*
5
3
1
0
−

4
1
0
0

8
0
0
0

0
0
0
0
−

7
1
0
0
−

8
0
0
0
−

2
0
0
0

5
1
0
0

3
0
0
0

2
1
0
0

0
3
6
4

.
r
t
s
norte
I

r
mi
h
t
oh

s
mi
s
norte
mi
pag
X
mi

.
r
t
s
norte
I

r
mi
h
t
oh

y
r
a
a
S

)
5
(

)
4
(

9
0
0
0
−

*
2
2
0
0
−

*
7
3
0
0
−

*
4
4
0
0
−

3
4
0
0
−

2
0
0
0
−

4
0
0
0

6
0
0
0

7
0
0
0

5
0
0
0
−

1
3
0
0
−

4
1
0
0
−

4
0
0
0
−

9
1
0
0

0
0
0
0

*
*
9
2
0
0

*
5
3
0
0

4
3
0
0

8
4
0
0

8
0
0
0

4
0
0
0
−

8
0
0
0
−

6
0
0
0
−

0
2
0
0
−

0
3
6
4

5
0
0
0
−

4
1
0
0
−

2
2
0
0
−

4
3
0
0
−

*
0
5
0
0
−

*
*
7
2
0
0
−

*
*
0
3
0
0
−

*
*
2
4
0
0
−

*
*
5
4
0
0
−

*
3
5
0
0
−

*
7
2
0
0
−

0
2
0
0
−

6
1
0
0
−

3
2
0
0
−

6
0
0
0
−

1
0
0
0
−

0
1
0
0
−

6
1
0
0
−

4
3
0
0
−

2
2
0
0
−

2
0
0
0

6
0
0
0

3
0
0
0

0
3
6
4

r
mi
h
C
a
mi
t

y
r
a
a
S

)
3
(

6
0
0
0

7
0
0
0

6
0
0
0

9
0
0
0

0
0
0
0

3
0
0
0

2
0
0
0

0
0
0
0

1
0
0
0
−

*
6
1
0
0
−

0
2
0
0
−

7
1
0
0
−

9
1
0
0
−

1
2
0
0
−

0
0
0
0
−

1
0
0
0
−

2
0
0
0

3
0
0
0

2
0
0
0

2
0
0
0
−

8
0
0
0
−

6
0
0
0
−

5
0
0
0
−

0
3
6
4

.
norte
mi
b
–
norte
oh
norte

t
norte
mi
r
r
tu
C

a
t
oh
t

t
norte
mi
r
r
tu
C

y
mi
k

)
2
(

)
1
(

s
mi
yo
b
a
i
r
a
V

s
pag
tu
oh
r
GRAMO

t
C
i
r
t
s
i
D

*
0
1
0
0
−

*
*
6
1
0
0
−

*
*
2
3
0
0
−

*
*
3
3
0
0
−

*
*
2
5
0
0
−

*
*
5
1
0
0
−

*
*
6
1
0
0
−

*
*
2
2
0
0
−

*
*
9
2
0
0
−

*
*
6
3
0
0
−

*
*
0
3
0
0
−

*
4
2
0
0
−

3
2
0
0
−

4
0
0
0
−

6
0
0
0
−

*
*
7
1
0
0
−

*
8
1
0
0
−

*
*
3
3
0
0
−

*
*
1
1
0
0
−

*
1
1
0
0
−

*
3
1
0
0
−

*
7
1
0
0
−

*
3
2
0
0
−

*
*
1
2
0
0
−

*
1
2
0
0
−

7
1
0
0
−

1
1
0
0
−

*
*
6
4
0
0
−

*
8
2
0
0
−

9
0
0
0

3
0
0
0

2
0
0
0

2
1
0
0

2
1
0
0
−

0
0
0
0

4
0
0
0

9
0
0
0

2
1
0
0

0
3
6
4

7
0
0
0

3
0
0
0

5
0
0
0

6
1
0
0

3
0
0
0
−

2
0
0
0
−

1
0
0
0

4
0
0
0

8
0
0
0

0
3
6
4

1
t

2
t

3
t

4
t

5
t

1
t

2
t

3
t

4
t

5
t

1
t

2
t

3
t

4
t

5
t

1
t

2
t

3
t

4
t

5
t

1
−
t

2
−
t

3
−
t

4
−
t

d
mi
mi
norte
–
w
oh
l

d
mi
mi
norte
–
mi
gramo
a
r
mi
v
A

d
mi
mi
norte
–
h
gramo
h

norte
a
b
r
Ud.

d
mi
mi
norte
–
h
gramo
h

a
r
tu
R

s
mi
b
a
i
r
a
v

d
norte
mi
r
t
–
mi
r
PAG

mi
r
a

s
mi
t
a
metro

i
t
s
mi

:
s
mi
t
oh
norte

s
norte
oh
i
t
a
v
r
mi
s
b
oh

d
mi
r
mi
t
s
tu
C

s
r
oh
r
r
mi

d
r
a
d
norte
a
t
s

t
s
tu
b
oh
R

2
mi
b
a
t

norte

s
mi
b
a
i
r
a
v

oh
r
t
norte
oh
C

r
mi
h
t
oh

yo
yo

s
a

yo
yo

mi
w
s
a

s
t
C
mi
F
F
mi

d
mi
X
fi

t
C
i
r
t
s
i
d

d
norte
a

r
a
mi
y

h
t
i

t
tu
b
,
d
a

a
t
norte
mi
metro
norte
r
mi
v
oh
gramo
r
mi
t
norte

t
tu
oh
h
t
i

w
d
mi
norte
a
t
b
oh

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
mi
d
pag
a
r
t
i
C
mi
–
pag
d

F
/

1
7
1
1
1
9
7
7
6
2
4
mi
d
pag
_
a
_
0
0
3
2
7
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

.
s
mi
s
mi
h
t
norte
mi
r
a
pag

norte

d
mi
t
r
oh
pag
mi
r

mi
r
a

mi
v
mi

t
C
i
r
t
s
i
d

oh
oh
h
C
s

mi
h
t

t
a

1
0
0
< p * * ; . 5 0 0 < p * ) . % 1 0 = ε ( s t c i r t s i D t i m i L - t A f o s p u o r G t n e r e f f i D y b i s e g e t a r t S k c a b t u C . 7 e l b a T 20 Phuong Nguyen-Hoang and Pengju Zhang Notes: This graph visualizes the regression results of columns 1 and 2 in table 7. A black circle indicates a significance level of at least 5 percent. Figure 5. The Effects of the Tax Limit on Total Current and Non-Benefit Current Expenditures by At-Limit District Groups high-need at-limit districts are most ﬁscally constrained, with a 3 percent reduction. In year 5, the non-beneﬁt current expenditures are reduced by 5.2 percent, 3.6 percent, and 4.6 percent for at-limit low-need, average-need, and urban high-need districts, re- spectively. The results in column 2 suggest beneﬁts dilute the eﬀects of the tax limit on total current expenditures in column 1. Columns 3 through 5 report whether at-limit school districts cut any of the three in- structional subcategories (ﬁgure A.1 in the online appendix visualizes these columns). School districts mostly do not cut spending on teacher salary; only T1 for urban high- need districts is signiﬁcant.16 Teacher salary may enjoy union protection and NY is among the states with the strongest teacher union strength (Winkler, Scull, and Zee- handelaar 2012). At-limit average-need districts reduce other instructional salaries by 2.7 percent to 5.3 percent annually in ﬁve limit years, whereas at-limit low-need dis- tricts cut other instructional expenses in three limit years. We ﬁnd that at-limit districts in all four groups do not cut expenses incurred on their board of education and therefore for parsimony we do not present these results in table 7. However, three small expenditure (sub)categories, namely, central admin- istration, undistributed, and interfund transfers, experience some reduction, made by at-limit low-need districts and by at-limit average-need districts (columns 6 through 8 of table 8 and ﬁgure A.2 in the online appendix). Throughout the ﬁve limit years, at-limit low-need districts cut central administration annually by between 2.5 percent and 16.In an estimate with the logged number of full-time-equivalent (FTE) teachers as the dependent variable, we also ﬁnd similar results to teacher salary: Only T1 for urban high-need districts is signiﬁcant. Speciﬁcally, the tax limit induces urban high-need districts to reduce the number of FTE teachers by 1.6 percent in the ﬁrst limit year. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / f / e d u e d p a r t i c e - p d l f / / / / / 1 7 1 1 1 9 7 7 6 2 4 e d p _ a _ 0 0 3 2 7 p d . f f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 21 Cap and Gap: Tax Limits in New York 7 percent. They also cut transportation in years 1 through 3 and undistributed expenses in years 4 through 5. At-limit average-need districts reduced transportation in years 1 through 4, and central administration and undistributed funds only in year 4. At-limit urban high-need districts substantially cut spending on central administration in years 4 and 5, by 8.1 percent and 13.5 percent, respectively. Column 9 of table 7 also shows that at-limit low-need districts make substantial an- nual cuts in interfund transfers, between 216 percent to 273 percent in the last three years. At-limit average-need and urban high-need districts also cut this item substan- tially by 103 percent and 134 percent, respectively, in a limit year. Despite the substantial- ity of these cuts in terms of percentages, the actual dollar amount cut is relatively small because interfund transfers take a tiny share in total current expenditures (0.5 percent to 1.4 percent, table 4). Interfund transfers refer to transfers from a school district’s general fund to its food service fund and/or capital fund. A plausible reason for these decreases in interfund transfers is that, as indicated in ﬁgure 1, current-year property tax levy for capital spending is added to the calculation of the property tax limit. This addition may incentivize school districts to increase their capital tax levy while reducing cash ﬂows from general funds to capital funds. Finally, we ﬁnd at-limit districts in all groups do not cut teacher retirement (and we therefore do not present these results in table 7). As with teacher salary, teacher retirement beneﬁts are most likely protected by teacher union agreements. The last column of table 7 for other fringe beneﬁts shows a counterintuitive ﬁnding that all key limit variables, T1 through T5, are positive and many of them are even statistically signiﬁcant, especially for low-need districts. However, the coeﬃcients of two pre-trend variables, T−1 and T−2, for other fringes are statistically signiﬁcant; we therefore refrain from making a causal interpretation of this ﬁnding. 8 . C O N C L U S I O N S The literature on the ﬁscal impact of TELs on school districts has been substantial since the 1970s, but a consensus on whether and how TELs change districts’ ﬁscal behaviors has yet to be achieved. To shed additional light on the relationship between TELs and school ﬁnance, we analyze the property tax levy limit in NY, which is one of the most recent tax revolts in the United States. This study provides the most comprehensive pic- ture thus far of how constrained, or at-limit, school districts adopt cutback strategies diﬀerentially across need-based groups and across operational functions or categories. In this study, we perform descriptive analyses on the distribution of at-limit dis- tricts across district groups and their spending patterns across expenditure categories. Also, we conduct empirical estimations on the eﬀects of the tax limit on at-limit dis- tricts using a DID model supplemented with an event-study design—our preferred speciﬁcation. The New York tax limit is popularly referred to as the “tax cap.” Overall, we ﬁnd that, consistent with this popular name, the tax limit does put an eﬀective cap on school dis- tricts’ spending. At-limit school districts on average reduce total current expenditures, and the reductions or gaps increase in size over the years from 0.6 percent in year 1 to 2.3 percent in year 5. Proponents of the public choice view have identiﬁed TELs as a way to counter tax-maximizing governments (Brennan and Buchanan 1980), and our primary ﬁndings support this view of TELs’ eﬃcacy. 22 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / f / e d u e d p a r t i c e - p d l f / / / / / 1 7 1 1 1 9 7 7 6 2 4 e d p _ a _ 0 0 3 2 7 p d f . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Phuong Nguyen-Hoang and Pengju Zhang The tax limit’s constraining eﬀects vary across at-limit district groups. On the one hand, rural high-need districts do not show limit-induced constraint on all expenditure categories and subcategories. This makes sense to us because, of all district types, ru- ral high-need districts rely the least on property taxes in their annual budget. On the other hand, school districts with a heavier reliance on property tax revenue may ﬁnd it diﬃcult to escape from the ﬁscal pressure. Indeed, the tax limit does negatively aﬀect total current expenditures for at-limit districts in the other three district groups in our analysis. Variation manifests even among these three groups; at-limit average-need dis- tricts’ total current expenditures are constrained in all limit years, which is not the case for at-limit low-need and urban high-need districts. When all districts are considered together, a district’s given revenue structure seems to be quite relevant to whether it is heavily constrained by the tax limit. We also ﬁnd that at-limit school districts in the three aﬀected groups do not make equal or similar cuts across current functions. Consistent with Downes and Figlio’s (2015) explanation of union rents, the two largest union-protected items (teacher salary and beneﬁts), which account for 53 percent to 58 percent of total current expenditures, appear to remain unscathed across at-limit districts. We ﬁnd that reductions are made in other instructional salaries/expenses, central administration, transportation, inter- fund transfers, and undistributed categories, all of which—taken together—represent approximately one ﬁfth of the three aﬀected groups’ total current expenditures. Finally, contrary to earlier ﬁndings that increased state aid might compensate for declines in local own-source revenue (Shadbegian 2003), we ﬁnd that intergovernmental aid pro- vides little help in oﬀsetting expenditure gaps imposed by the tax limit. Although we cannot rule out that our estimates may be biased, a number of pieces of evidence lend credibility to a causal interpretation that the tax cap does create a ﬁscal gap between what at-limit school districts spend and what they would otherwise have spent. First, except for column 10 of table 7, all pre-trend variables are small and insignif- icant, thereby satisfying the common trend assumption. Second, the negative eﬀects of the tax limit consistently manifest themselves across diﬀerent DID and event-study speciﬁcations, including the use of stacked data and the exclusion of intergovernmental aid variables. Our focus on the tax limit in a single state warrants a caveat—our empirical ﬁnd- ings should not be externalized to other state-imposed TEL provisions with diﬀerent designs or rules. In addition, this study looks only at the tax limit’s ﬁscal eﬀects in its ﬁrst ﬁve years and leaves several issues unanswered. For example, how will school districts ﬁscally cope with this tax limit over the long term? Do the limit-induced expen- diture gaps found in this study lead to gaps in student performance? Does the property tax cap also have any constraining eﬀect on capital spending? Most importantly, while the ongoing COVID-19 pandemic’s full impact on the state economy remains to be seen, how will the tax limit compound the ﬁscal constraint on school districts’ local resources caused by the COVID-19 pandemic? All of these questions warrant future research. ACKNOWLEDGMENTS The authors are grateful for helpful comments from Robert Bifulco, Eric Brunner, Julien Lafor- tune, Michah Rothbart, Thomas Downes, and Stéphane Lavertu. The authors would also like to l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . f / / e d u e d p a r t i c e - p d l f / / / / / 1 7 1 1 1 9 7 7 6 2 4 e d p _ a _ 0 0 3 2 7 p d . f f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 23 Cap and Gap: Tax Limits in New York thank two anonymous reviewers and editors Nora Gordon and Randall Reback for constructive feedback. Any errors are solely our own. REFERENCES Ashworth, John, and Bruno Heyndels. 1999. Reference point eﬀects in local taxation: It all de- pends on how you look at it. Proceedings. Annual Conference on Taxation and Minutes of the Annual Meeting of the National Tax Association 92:335–341. Ballal, Sonali, and Ross Rubenstein. 2009. The eﬀect of tax and expenditure limitations on public education resources: A meta-regression analysis. Public Finance Review 37(6): 665–685. 10.1177/ 1091142109345265 Blankenau, William, and Mark Skidmore. 2004. School ﬁnance litigation, tax and expenditure limitations, and education spending. Contemporary Economic Policy 22(1): 127–143. 10.1093/cep/ byh010 Blom-Hansen, Jens, Kurt Houlberg, and Søren Serritzlew. 2014. Size, democracy, and the eco- nomic costs of running the political system. American Journal of Political Science 58(4): 790–803. 10.1111/ajps.12096 Bradbury, Katharine, Christopher Mayer, and Karl Case. 2001. Property tax limits, local ﬁscal behavior, and property values: Evidence from Massachusetts under Proposition 2½. Journal of Public Economics 80(2): 287–311. 10.1016/S0047-2727(00)00081-5 Brennan, Geoﬀrey, and James Buchanan. 1980. The power to tax: Analytic foundations of a ﬁscal constitution. New York: Cambridge University Press. Brooks, Leah, Yosh Halberstam, and Justin Phillips. 2016. Spending within limits: Evidence from municipal ﬁscal restraints. National Tax Journal 69(2): 315–352. 10.17310/ntj.2016.2.03 Chakrabarti, Rajashri, Max Livingston, and Joydeep Roy. 2014. Did cuts in state aid during the Great Recession lead to changes in local property taxes? Education Finance and Policy 9(4): 383– 416. 10.1162/EDFP_a_00141 Cheung, Ron. 2008. The eﬀect of property tax limitations on residential private governments: The case of Proposition 13. National Tax Journal 61(1): 35–56. 10.17310/ntj.2008.1.02 Collins, Catherine, and Geoﬀrey Propheter. 2013. The property tax base and the Great Recession. State Tax Notes 69(7): 445–448. Deller, Steven, Judith Stallmann, and Lindsay Amiel. 2012. The impact of state and local tax and expenditure limitations on state economic growth. Growth and Change 43(1): 56–84. 10.1111/ j.1468-2257.2011.00577.x Downes, Thomas, Richard Dye, and Therese McGuire. 1998. Do limits matter? Evidence on the eﬀects of tax limitations on student performance. Journal of Urban Economics 43(3): 401–417. 10.1006/juec.1997.2052 Downes, Thomas, and David Figlio. 1999. Do tax and expenditure limits provide a free lunch? Evidence on the link between limits and public sector service quality. National Tax Journal 52(1): 113–128. 10.1086/NTJ41789380 Downes, Thomas, and David Figlio. 2015. Tax and expenditure limits, school ﬁnance and school quality. In Handbook of research in education ﬁnance and policy, 2nd edition, edited by Helen Ladd and Margaret Goertz, pp. 341–353. New York: Routledge. 24 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / f e d u e d p a r t i c e - p d l f / / / / / 1 7 1 1 1 9 7 7 6 2 4 e d p _ a _ 0 0 3 2 7 p d f . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Phuong Nguyen-Hoang and Pengju Zhang Downes, Thomas, and Kieran Killeen. 2014. So slow to change: The limited growth of nontax revenues in public education ﬁnance, 1991–2010. Education Finance and Policy 9(4): 567–599. 10.1162/EDFP_a_00147 Duncombe, William, and John Yinger. 2011. Are education cost functions ready for prime time? An examination of their validity and reliability. Peabody Journal of Education 86(1): 28–57. 10.1080/ 0161956X.2011.539954 Dye, Richard, and Therese McGuire. 1997. The eﬀect of property tax limitation measures on local government ﬁscal behavior. Journal of Public Economics 66(3): 469–487. 10.1016/S0047-2727(97) 00047-9 Dye, Richard, Therese McGuire, and Daniel McMillen. 2005. Are property tax limitations more binding over time? National Tax Journal 58(2): 215–225. 10.17310/ntj.2005.2.03 Ebdon, Carol. 1997. The eﬀects of tax limits and budget referenda in New York State school districts. Doctoral dissertation, State University of New York, Albany, NY. Eliason, Paul, and Byron Lutz. 2018. Can ﬁscal rules constrain the size of government? An anal- ysis of the “crown jewel” of tax and expenditure limitations. Journal of Public Economics 166(C): 115–144. 10.1016/j.jpubeco.2018.07.008 Evans, William, Robert Schwab, and Kathryn Wagner. 2019. The Great Recession and public education. Education Finance and Policy 14(2): 298–326. 10.1162/edfp_a_00245 Figlio, David. 1997. Did the “tax revolt” reduce school performance? Journal of Public Economics 65(3): 245–269. 10.1016/S0047-2727(97)00015-7 Figlio, David. 1998. Short-term eﬀects of a 1990s-era property tax limit: Panel evidence on Ore- gon’s Measure. National Tax Journal 51(1): 55–70. 10.1086/NTJ41789311 Figlio, David, and Kim Rueben. 2001. Tax limits and the qualiﬁcations of new teachers. Journal of Public Economics 80(1): 49–71. 10.1016/S0047-2727(00)00116-X Goodman-Bacon, Andrew. 2021. Diﬀerence-in-diﬀerences with variation in treatment timing. Journal of Econometrics 225(2): 254–277. Hoene, Christopher. 2004. Fiscal structure and the post-Proposition 13 ﬁscal regime in Califor- nia’s cities. Public Budgeting & Finance 24(4): 51–72. Kioko, Sharon N. 2011. Structure of state-level tax and expenditure limits. Public Budgeting & Fi- nance 31(2): 43–78. Kioko, Sharon N., and Pengju Zhang. 2019. Impact of tax and expenditure limits on local govern- ment use of tax-supported debt. Public Finance Review 47(2): 409–432. 10.1177/1091142117723706 Lafortune, Julien, Jesse Rothstein, and Diane Schanzenbach. 2018. School ﬁnance reform and the distribution of student achievement. American Economic Journal: Applied Economics 10(2): 1–26. Lincoln Institute of Land Policy and George Washington Institute of Public Policy. 2020. Signif- icant features of the property tax. Available https://bit.ly/2E63Ju0. Accessed 2 August 2020. McCubbins, Mathew, and Ellen Moule. 2010. Making mountains of debt out of molehills: The pro-cyclical implications of tax and expenditure limitations. National Tax Journal 63(3): 603–621. 10.17310/ntj.2010.3.09 Mullins, Daniel, and Philip Joyce. 1996. Tax and expenditure limitations and state and local ﬁscal structure: An empirical assessment. Public Budgeting & Finance 16(1): 75–101. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / f e d u e d p a r t i c e - p d l f / / / / / 1 7 1 1 1 9 7 7 6 2 4 e d p _ a _ 0 0 3 2 7 p d . f f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 25 Cap and Gap: Tax Limits in New York New York State Department of Taxation and Finance (NYSDTF). 2020. 2019 property tax-related legislation. Available https://on.ny.gov/30Vk2m3. Accessed 2 August 2020. New York State Education Department (NYSED). 2019. A guide to the headings of the ﬁscal proﬁle. Available https://bit.ly/3hbUd6N. Accessed 2 August 2020. New York State Oﬃce of the State Comptroller. 2018. Understanding the Constitutional tax limit: Cities. Available https://bit.ly/34GhF91. Accessed 2 August 2020. Nguyen-Hoang, Phuong. 2013. Tax limit repeal and school spending. National Tax Journal 66(1): 117–148. 10.17310/ntj.2013.1.05 Oﬃce of the New York State Comptroller. 2020. Under pressure: Local government revenue chal- lenges during the COVID-19 pandemic. Albany, NY: Oﬃce of the New York State Comptroller. Oliﬀ, Phil, and Michael Leachman. 2011. New school year brings steep cuts in state funding for schools. Washington, DC: Center on Budget and Policy Priorities. Poterba, James. 1996. Do budget rules work? NBER Working Paper No. 5550. Rose, Shanna. 2010. Institutions and ﬁscal sustainability. National Tax Journal 63(4): 807–837. 10.17310/ntj.2010.4.11 Shadbegian, Ronald. 1999. The eﬀect of tax and expenditure limitations on the revenue structure of local government, 1962–1987. National Tax Journal 52(2): 221–238. 10.1086/NTJ41789391 Shadbegian, Ronald. 2003. Did the property tax revolt aﬀect local public education? Evidence from panel data. Public Finance Review 31(1): 91–121. 10.1177/1091142102239136 Shadbegian, Ronald, and Robert Jones. 2005. Did Proposition 2½ aﬀect local public education in Massachusetts? Evidence from panel data. Global Business and Economics Review 7(4): 363–380. 10.1504/GBER.2005.008296 Skidmore, Mark. 1999. Tax and expenditure limitations and the ﬁscal relationships between state and local governments. Public Choice 99(1): 77–102. 10.1023/A:1018311425276 Sun, Rui. 2014. Reevaluating the eﬀect of tax and expenditure limitations: An instrumental vari- able approach. Public Finance Review 42(1): 92–116. 10.1177/1091142112459210 Tiebout, Charles. 1956. A pure theory of local expenditures. Journal of Political Economy 64(5): 416–424. 10.1086/257839 Wang, Wen, William Duncombe, and John Yinger. 2011. School district responses to matching aid programs for capital facilities: A case study of New York’s building aid program. National Tax Journal 64(3): 759–794. 10.17310/ntj.2011.3.01 Winkler, Amber, Janie Scull, and Dara Zeehandelaar. 2012. How strong are U.S. teacher unions? A state-by-state comparison. Unpublished paper, Thomas B. Fordham Institute. Yinger, John. 2019. It’s elementary: The case against New York State’s tax cap. Available https:// bit.ly/320bRUE. Accessed 2 August 2020. Zhang, Pengju. 2018. The unintended impact of tax and expenditure limitations on the use of special districts: The politics of circumvention. Economics of Governance 19(1): 21–50. 10.1007/ s10101-017-0198-4 Zhang, Pengju, and Yilin Hou. 2020. The impact of tax and expenditure limitations on user fees and charges in local government ﬁnance: Evidence from New England. Publius: The Journal of Federalism 50(1): 81–108. 26 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / f e d u e d p a r t i c e - p d l f / / / / / 1 7 1 1 1 9 7 7 6 2 4 e d p _ a _ 0 0 3 2 7 p d f . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 CAP AND GAP: THE FISCAL EFFECTS OF image

Descargar PDF