Más allá del dominio hemisférico: Regiones del cerebro
Underlying the Joint Lateralization of Language
and Arithmetic to the Left Hemisphere
Philippe Pinel1,2,3 and Stanislas Dehaene1,2,3,4
Abstracto
& Language and arithmetic are both lateralized to the left
hemisphere in the majority of right-handed adults. Todavía, does
this similar lateralization reflect a single overall constraint of
brain organization, such an overall ‘‘dominance’’ of the left
linguistic and symbolic operations? Is it
hemisphere for all
related to the lateralization of specific cerebral subregions? O
is it merely coincidental? To shed light on this issue, nosotros
performed a ‘‘colateralization analysis’’ over 209 healthy sub-
jects: We investigated whether normal variations in the degree
of left hemispheric asymmetry in areas involved in sentence
listening and reading are mirrored in the asymmetry of areas
involved in mental arithmetic. Within the language network,
a region-of-interest analysis disclosed partially dissociated
patterns of lateralization, inconsistent with an overall ‘‘domi-
nance’’ model. Only two of these areas presented a lateraliza-
tion during sentence listening and reading which correlated
strongly with the lateralization of two regions active during
calculation. Específicamente, the profile of asymmetry in the pos-
terior superior temporal sulcus during sentence processing
covaried with the asymmetry of calculation-induced activation
in the intraparietal sulcus, and a similar colateralization linked
the middle frontal gyrus with the superior posterior parietal
lobule. Given recent neuroimaging results suggesting a late
emergence of hemispheric asymmetries for symbolic arithmetic
during childhood, we speculate that these colateralizations
might constitute developmental traces of how the acquisition
of linguistic symbols affects the cerebral organization of the
arithmetic network. &
INTRODUCCIÓN
Strong left hemispheric asymmetry is a striking character-
istic of the cerebral regions involved in language process-
En g, both at the functional and at the anatomical level,
noticeably around the peri-sylvian and temporal struc-
turas (Toga & Thompson, 2003; Geschwind & Levitsky,
1968). The left hemisphere also plays a key role in mental
aritmética, as revealed by both lesion patterns (acalculia
being strongly linked to left parietal lesions, as shown by
Jackson & Warrington, 1986) and by more recent fMRI
(Chochon, cohen, van de Moortele, & Dehaene, 1999).
Based on the observation of joint deficits in language and
calculation following unilateral brain lesions, the classical
neurological wisdom stipulates that the left hemisphere is
‘‘dominant’’ for both language and calculation. En esto
vein, Semenza et al. (2006) reported, in the special case of
right hemisphere aphasia, a co-occurrence of language
and arithmetic impairments.
The neuropsychological concept of ‘‘dominance,''
sin embargo, seems very coarse in the face of our recent
ability to finely dissect, with neuroimaging methods, el
specific areas involved in language and arithmetic tasks.
1INSERM, Gif-sur-Yvette, Francia, 2CEA, Gif-sur-Yvette, Francia,
3Universite´ Paris-Sud, Gif-sur-Yvette, Francia, 4Colle`ge de France,
París, Francia
Are all of these areas equally lateralized to the left hemi-
sphere, as would be predicted by a single overarching
‘‘dominance’’ factor? Or are there much more specific
patterns of colateralization between language and arith-
metic, restricted to a small subset of brain areas linking
the two domains? Finalmente, a third possibility is that al-
though both language and arithmetic relate to the left
hemisferio, these are two independent patterns that
just happen to coincide. Por ejemplo, the left hemi-
spheric lateralization for language could result from an
early asymmetry in structure and functions of the tem-
poral lobe (Tervaniemi & Hugdahl, 2003; Chi, Dooling,
& Gilles, 1977), whereas the parietal hemispheric spe-
cialization for quantities processing (the left parietal lobe
being more involved in exact calculation and the right
one more involved in judgment on analogical quantities;
Piazza, Mechelli, Precio, & Butterworth, 2006; Stanescu-
Cosson et al., 2000) may mirror an initial left hemispheric
advantage for processing stimuli as categories, mientras
the right hemisphere shows a preference for process-
ing analogical dimensions (Kosslyn et al., 1989; see also
Vauclair, Yamazaki, & Gu¨ntu¨rku¨n, 2006 for an extension
to animals studies).
In the present work, we aimed to further specify the
anatomical bases of the joint lateralization of language
and arithmetic to the left hemisphere, using as a source
D 2009 Instituto de Tecnología de Massachusetts
Revista de neurociencia cognitiva 22:1, páginas. 48–66
D
oh
w
norte
yo
oh
a
d
mi
d
yo
yo
/
/
/
/
j
F
/
t
t
i
t
.
:
/
/
F
r
oh
metro
D
h
oh
t
w
t
norte
pag
oh
:
a
/
d
/
mi
metro
d
i
F
t
r
oh
pag
metro
r
C
h
.
s
pag
i
yo
d
v
i
mi
r
mi
r
C
C
t
.
h
metro
a
i
r
mi
d
.
tu
C
oh
oh
metro
C
/
norte
j
a
oh
r
C
t
i
norte
C
/
mi
a
–
pag
r
d
t
i
2
C
2
yo
1
mi
–
4
pag
8
d
1
F
9
/
3
2
8
2
4
/
1
1
1
/
oh
4
C
8
norte
/
1
2
7
0
0
6
9
9
1
2
1
1
5
1
/
8
4
j
oh
pag
C
d
norte
.
b
2
y
0
gramo
0
tu
9
mi
.
s
t
2
oh
1
norte
1
8
0
4
8
.
S
pag
mi
d
pag
F
mi
metro
b
y
b
mi
gramo
r
tu
2
mi
0
2
s
3
t
/
j
t
.
F
/
.
.
oh
norte
1
8
METRO
a
y
2
0
2
1
of data the normal interindividual variability in functional
lateralization. Using a very large database of fMRI activa-
tion from 209 healthy subjects, we could study the inter-
correlations between the lateralization indices of many
brain regions active during either sentence listening, sen-
tence reading, or mental arithmetic tasks. As we shall see,
this ‘‘colateralization analysis’’ suggests that functional
lateralization is not a simple issue of one hemisphere
‘‘dominating’’ over the other, but a more subtle phe-
nomenon linking specific cortical areas.
Our interest in the lateralization of arithmetic stemmed
from a much broader debate, which concerns whether
mental arithmetic is shaped by the organization of the
language system (gordon, 2004; Pica, Lemer, Izard, &
Dehaene, 2004). Although arithmetical procedures are
mainly based on a language-like system with a dedicated
set of symbols and syntax, several published results un-
derline the relative independence of linguistic and ar-
ithmetical abilities. Mastery of arithmetical procedures,
por ejemplo, has been reported to be dissociable from lan-
guage impairment in many different neurological cases,
including aphasic patients (cohen, Dehaene, Chochon,
Lehe´ricy, & Naccache, 2000), patients affected by semantic
dementia (Cappelletti, Butterworth, & Kopelman, 2001),
or agrammatic patients (Varley, Klessinger, Romanowski,
& Siegal, 2005). This suggests that, at least for adult
subjects, the core system for number manipulation is largely
independent from the language network (Butterworth,
2005).
According to some theories, the extent to which cal-
culation relies on a linguistic coding of numbers may
depend on the arithmetic task. It is assumed in the
triple-code model (Dehaene & cohen, 1995), Residencia en
neurological dissociation reports, that quantity manipu-
lations rely on a nonverbal analogical representation of
numbers, used for instance to compare numbers or to
approximate simple operations, whereas the memoriza-
tion of exact arithmetical facts relies on a verbal memory
almacenar (Lefevre, 1996). To support this model, Dehaene,
Piazza, Pinel, y cohen (2003) published a meta-analysis
of numerical paradigms and reported two distinct sites
located in the fundus of the horizontal part of the in-
traparietal sulcus (hIPS) and in the angular gyrus (AG),
which may be the correlates of quantity manipulation
and of arithmetical fact storage, respectivamente. In agree-
ment with the model, activation during a mental calcu-
lation task shifts from the hIPS to the AG after arithmetic
training, as subjects rely less on active number manipu-
lation and more on fact retrieval ( Venkatraman, Siong,
che, & Ansari, 2006; Delazer et al., 2003). The core
system of ‘‘number sense,’’ located in the hIPS, would
thus be anatomically and functionally distinct from the
language areas, usually described as belonging to the
inferior frontal, peri-sylvian, and superior temporal re-
gions (Binder et al., 2000; Hickok & Poeppel, 2000).
Recientemente, sin embargo, it has become apparent that even
within the domain of simple nonsymbolic calculations
accessible to preverbal infants (Barth, La Mont, Lipton, &
Spelke, 2005; McCrink & Wynn, 2004), the acquisition of
number symbols and of a verbal counting routine ex-
tends arithmetic performance and leads to a radical
development of human arithmetical abilities. Compared
to uneducated adults who live in remote areas of the
Amazon and whose language has few number words,
Western children and adults represent numerical quan-
tities in a more precise manner (gordon, 2004; Pica et al.,
2004) and understand that numbers map onto space
in a linear rather than in logarithmic manner (Dehaene,
Izard, Spelke, & Pica, 2008; Siegler & Booth, 2004). Dur-
ing development, the integration of different codes for
number (verbal and Arabic symbols, preverbal quanti-
corbatas, and ordinal concepts) leads to massive changes in
children’s performance of simple numerical tasks such
as the ‘‘give a number’’ task, where one simply asks a
child ‘‘give me five objects’’ ( Wynn, 1992). En resumen,
current theories of numerical cognition propose that the
preverbal coding of numbers is profoundly changed and
refined by education with numerical symbols (Dehaene,
2007; Pica et al., 2004; carey, 1998). Although the ma-
ture systems for language and numbers appear largely
dissociated in the adult brain, these views predict that
they should be interdependent in the course of devel-
opment. Aquí, we investigated whether consistent func-
intercorrelations of these two systems across
tional
intersubject variability, in adulthood, may shed light on
that issue as traces of a linked development.
As a first and simple marker of cerebral organization,
we used an asymmetry index which evaluates, Dentro de un
given cortical area, the extent to which functional acti-
vation is stronger in one hemisphere relative to the
otro. Reasoning that developmental constraints would
be reflected in long-lasting correlations at the brain level
(Andresen & Marsolek, 2005), we examined, across very
different language comprehension and calculation tasks,
whether language-related areas colateralize with the
main areas related to mental arithmetic. Por supuesto, el
activation levels of the left and right hemispheres may
also be affected by a variety of other factors such as
subjects’ performance, estrategias, or attention that may
partially mask the predicted correlation. To mitigate this
problema, we used an unusually large-scale database of
209 subjects which contains individual functional mag-
netic resonance images and behavioral scores (Pinel
et al., 2007). Reliable networks for sentence compre-
hension and for simple calculation, both across the
visual and auditory modalities, were available for each
sujeto. Considering the large number of fMRI data, nosotros
hoped that our analysis would be sensitive to subtle
anatomo-functional links between the two sets of lan-
guage and calculation circuits.
We computed profiles of asymmetry (es decir., variations in
the degree of hemispheric lateralization over the group
of subjects) for each of the main areas activated during
the language comprehension and calculation tasks. Este
Pinel and Dehaene
49
D
oh
w
norte
yo
oh
a
d
mi
d
yo
yo
/
/
/
/
j
F
/
t
t
i
t
.
:
/
/
F
r
oh
metro
D
h
oh
t
w
t
norte
pag
oh
:
a
/
d
/
mi
metro
d
i
F
t
r
oh
pag
metro
r
C
h
.
s
pag
i
yo
d
v
i
mi
r
mi
r
C
C
t
.
h
metro
a
i
r
mi
d
.
tu
C
oh
oh
metro
C
/
norte
j
a
oh
r
C
t
i
norte
C
/
mi
a
–
pag
r
d
t
i
2
C
2
yo
1
mi
–
4
pag
8
d
1
F
9
/
3
2
8
2
4
/
1
1
1
/
oh
4
C
8
norte
/
1
2
7
0
0
6
9
9
1
2
1
1
5
1
/
8
4
j
oh
pag
C
d
norte
.
b
2
y
0
gramo
0
tu
9
mi
.
s
t
2
oh
1
norte
1
8
0
4
8
.
S
pag
mi
d
pag
F
mi
metro
b
y
b
mi
gramo
r
tu
2
mi
0
2
s
3
t
/
j
.
.
.
/
t
F
oh
norte
1
8
METRO
a
y
2
0
2
1
region-of-interest (ROI) approach allowed us to establish
a detailed region-based description of the lateralization
of the two networks. Using an intratask correlation anal-
ysis, we first examined whether a single ‘‘dominance’’
factor accounted for the data, or whether regional pat-
terns of asymmetry could be isolated within the activa-
tions evoked by our paradigms. In a second step, nosotros
analyzed the correlations of the lateralization profiles
across the language and arithmetic tasks, in order to
isolate the areas that presented a significant joint colat-
eralización. These pairs of areas were then specifically
explored in a voxel-based whole-brain analysis to deter-
mine more precisely which voxels exhibited, in one task,
an asymmetry that was well predicted by the asymmetry
profile of another region in the other task. Finalmente, to test
whether these joint colateralization patterns could be
related to a structural basis, we extracted, on an inde-
pendent sample of diffusion tensor images (DTI), el
white matter fiber tracks linking these areas.
MÉTODOS
Subjects and Protocol
We used fMRI data collected from 209 French healthy
adult volunteers (all were right-handed, 60% women/
40% hombres, edad media = 23.8 ± 4.4 años). The databasing
procedure and the experimental protocol are detailed
in Pinel et al., 2007; basically, we used a 5-minute-long
functional localizer to isolate in a reliable way individual
correlates of sentence reading, speech listening, y
mental calculation. Twenty short sentences and 20 sub-
traction problems were presented via visual or auditory
stimulation (half of the trials each) in a random-like
orden (a symbolic subtraction task was selected to en-
sure a strong activation of the various components of
the number processing system; see Chochon et al., 1999).
Twenty flashing checkerboards were also displayed and
served as control for the reading task.
Imaging Data Processing
Anatomical and fMRI data were acquired on a 3-Tesla
scanner (Brucker; TR = 2400 mseg, 34 slices of 4-mm
thickness covering the whole brain). Images were pre-
procesado (realignment, normalization to the Montreal
Neurological Institute [MNI] template, resampled voxel
size to 3 mm, 5 mm smoothing) with SPM2 (www.fil.ucl.
ac.uk) and analyzed according to the SPM general linear
modelo (hemodynamic response function plus its deriva-
tivo), resulting in five functional contrasts: visual sentence–
checkerboard for the reading task, sentence listening–rest
for speech listening task, visual calculation–visual sen-
tence for visual mental calculation, auditory calculation–
auditory sentence for auditory mental calculation, y
overall calculation–sentence for calculation task. Individ-
ual conjunction image were computed to isolate amodal
components of language comprehension (Boolean in-
tersection of the visual and the auditory language con-
trasts) and mental calculation (Boolean intersection of
the visual and the auditory calculation contrasts).
We also computed individual whole-brain images of
the degree of left/right asymmetry of activation for each
of these contrasts. To this aim, the standard SPM nor-
malization procedure was used to align each individual
flipped normalized anatomy (along the y axis) onto the
corresponding normalized anatomy image. This should
maximize alignment of homolog anatomical structures
in the two hemispheres despite macroscopic anatomical
asymmetry (petalia and torque effects). Entonces, the func-
tional contrast activation images were also realigned
using the same matrix, and activation from the right
hemisphere was subtracted voxel by voxel from the
corresponding left hemisphere activation.
Group Analysis
Random effect analyses (RFX) were performed with
SPM2 on the whole brain for group-level analyses ( pag <
.05 after family-wise error correction for multiple com-
parisons, 20 voxels cluster extent). An RFX was per-
formed onto the 209 individual contrasts images to show
task-related activation, and a left hemisphere RFX was
performed onto the 209 left–right asymmetry images to
test for any significant group-level asymmetry of the func-
tional circuits. In order to report asymmetry of activation
only, displays of asymmetry RFX maps were masked by
the corresponding RFX activation map. A two-sample
t-test analysis was performed on asymmetry images to
test for different pattern of lateralization between men
and women.
SPM-based regression analyses were also performed
on the individual asymmetry images to assess at the
whole-brain hemisphere level which voxels presented an
asymmetry of activation during the calculation task that
correlated with the laterality index (LI) of a given ROI in
reading task. To ensure that these regression analyses
were unaffected by subjects’ performance, which may
affect level of activation especially in left parietal cortex
(Menon et al., 2000), individual calculation score (avail-
able on a subset of 174 subjects) was added as a covari-
ate (defined as the number of correct two-digit additions
and subtractions solved in a limited time outside of the
scanner). To benefit from the entire set of fMRI data and
to maintain comparability with the ROI’s LI analysis
(described in the next paragraph), simple regressions
with LI are also reported. Finally, to ensure that the re-
ported colateralization were not due to a main effect of
sex, we performed a third regression analysis on asym-
metry images using both reading ROI’s LI and subjects’
sex as regressor.
Similar analyses were performed on the reading task
asymmetry images, using a predictor the LI from the cal-
culation task. We limited this SPM exploration to areas
50
Journal of Cognitive Neuroscience
Volume 22, Number 1
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
f
r
o
m
D
h
o
t
w
t
n
p
o
:
a
/
d
/
e
m
d
i
f
t
r
o
p
m
r
c
h
.
s
p
i
l
d
v
i
e
r
e
r
c
c
t
.
h
m
a
i
r
e
d
.
u
c
o
o
m
c
/
n
j
a
o
r
c
t
i
n
c
/
e
a
-
p
r
d
t
i
2
c
2
l
1
e
-
4
p
8
d
1
f
9
/
3
2
8
2
4
/
1
1
1
/
o
4
c
8
n
/
1
2
7
0
0
6
9
9
1
2
1
1
5
1
/
8
4
j
o
p
c
d
n
.
b
2
y
0
g
0
u
9
e
.
s
t
2
o
1
n
1
8
0
4
8
.
S
p
e
d
p
f
e
m
b
y
b
e
g
r
u
2
e
0
2
s
3
t
/
j
t
.
.
.
f
/
o
n
1
8
M
a
y
2
0
2
1
that presented a significant correlation across tasks in
the LI correlation analysis (see below).
Calculation of Laterality Index
The choice of an LI was constrained by the following
aims. First, the index must be robust in the face of inter-
individual variability in activation topography. In partic-
ular, it must take into account the fact that homologous
areas of the left and right hemispheres do not necessar-
ily occupy perfect mirror-image locations. Second, the LI
should be a normalized index, not influenced by overall
changes in amount of activation. Third, it must be un-
affected by the presence of deactivation in some subjects
and/or hemispheres which can create misinterpretation
in term of activation asymmetry (Seghier, 2008).
These issues were addressed as follows. For each func-
tional peak of interest, we selected two symmetrical
spheres (radius = 4 voxels, i.e., 12 mm, based on the
anatomical variability of individual peak reported for this
paradigm in Pinel et al., 2007) respectively in the left and
right hemispheres, centered on the peak coordinates of
the group-level analysis. For a given subject, within each
of these spheres, we then eliminated inactive or deacti-
vated voxels with a loose criterion that their t value
should be superior to 1. This procedure ensured that
the activation values entered in the LI formula were al-
ways positive, thus alleviating potential problems arising
from the presence of deactivation in some subjects and/
or areas. Within those active voxels, we then selected the
most activated voxels by keeping only up to 5% of the
original sphere volume. Finally, the LI was computed by
the classical formula LI = (R (cid:1) L)/(L + R) where L and R
are, respectively, the left and right average activations of
the selected voxels. The index ranged from (cid:1)1 (total left
lateralization) to +1 (total right lateralization), with 0 re-
flecting perfect symmetry of activation.
In this formula, activation for one hemisphere was
set to zero if no voxels passed the criterion of having a
t value > 1. En este caso, the LI always reached its max-
imum (plus or minus 1), regardless of the amount of
activation in the other hemisphere. This can add noise
to the analysis because even very small activations, cuando
passing threshold in one hemisphere and not the other,
are considered maximally asymmetrical. To mitigate this
problema, an LI defined from a total of less than 15 ac-
tivated voxels was excluded from analysis. Note that this
procedure rejected about 5% of subjects for most ROI,
and up to 15–30% for areas found active in only a sub-
group of subjects, such as the putamen, inferior parietal,
or cingulate. críticamente, the main reading–calculation cor-
relations reported here were calculated from 98% del
subjects for pSTS–hIPS and 85% for mFG–precuneus
pair.
To characterize the leftward lateralization of the lan-
guage comprehension cerebral network, we computed
the LI from seven local peaks of the RFX analysis for
reading lateralization, which were also part of the most
activated sites (6 maxima were present in both language
modalities). To explore the lateralization of the calcula-
tion network, we computed the LI from all nine local
peaks of the RFX analysis for areas active during cal-
culation. For each of these peaks, we performed a
two-sample t test on LI values with sex as independent
variable to test for a putative difference of lateralization
between male and female subjects.
We first investigated the colateralization patterns with-
in the seven language-related ROIs, both within and
across modalities of sentence presentation (visual and
auditory stimulation). We then calculated the matrix of
correlation corresponding to the 7 (cid:2) 9 combinations of
LI from reading and calculation tasks respectively. Nosotros
report matrices of p values testing the null hypothesis
of no correlation.
Fiber Tracking
To explore whether colateralization of brain areas may
be sustained by direct connections via anatomical fiber
bundles, we performed fiber tracking with the Brainvisa
software (Cointepas et al., 2003; http://brainvisa.info/) en
six subjects’ DTIs acquired in another protocol (Siemens
Trio 3-T whole-body scanner): TE/TR = 81 msec/14 sec,
0/700 s mm(cid:1)2 b1/b2 factor, 41 directions, FOV = 240,
1.9 (cid:2) 1.9 (cid:2) 2 mm voxel size, 60 slices.
Tracking was performed starting from five functionally
defined seed regions: middle frontal and posterior su-
perior temporal spheres (4 mm), centered on the peak
defined by the previously described reading task RFX,
and intraparietal, superior parietal and precuneus spheres
defined by the calculation task. Spheres were defined
in MNI space and then unnormalized to match the
individual diffusion-weighted images. To estimate how
these areas were linked, fiber trees were labeled accord-
ing to the pair of seed regions they crossed. Resulting
tracks were then converted into 3-D images, normalized
to MNI coordinates and added up for a group-level
descripción.
RESULTADOS
Language Lateralization
The overall networks activated during reading, speech
escuchando, and calculation reported in Figure 1 resembled
those classically reported in the literature (see Pinel
et al., 2007, for a detailed description of these networks).
Nearly all activated areas were strongly leftward lateral-
ized in these three cognitive tasks (Cifra 1, abajo
row). Two interesting and heretofore unreported ex-
ceptions were right postcentral cortex for reading and a
right middle temporal area for speech listening.
Based on those asymmetry images, the seven bilateral
ROIs which reflected both strong lateralization and
Pinel and Dehaene
51
D
oh
w
norte
yo
oh
a
d
mi
d
yo
yo
/
/
/
/
j
F
/
t
t
i
t
.
:
/
/
F
r
oh
metro
D
h
oh
t
w
t
norte
pag
oh
:
a
/
d
/
mi
metro
d
i
F
t
r
oh
pag
metro
r
C
h
.
s
pag
i
yo
d
v
i
mi
r
mi
r
C
C
t
.
h
metro
a
i
r
mi
d
.
tu
C
oh
oh
metro
C
/
norte
j
a
oh
r
C
t
i
norte
C
/
mi
a
–
pag
r
d
t
i
2
C
2
yo
1
mi
–
4
pag
8
d
1
F
9
/
3
2
8
2
4
/
1
1
1
/
oh
4
C
8
norte
/
1
2
7
0
0
6
9
9
1
2
1
1
5
1
/
8
4
j
oh
pag
C
d
norte
.
b
2
y
0
gramo
0
tu
9
mi
.
s
t
2
oh
1
norte
1
8
0
4
8
.
S
pag
mi
d
pag
F
mi
metro
b
y
b
mi
gramo
r
tu
2
mi
0
2
s
3
t
/
j
F
.
t
.
/
.
oh
norte
1
8
METRO
a
y
2
0
2
1
D
oh
w
norte
yo
oh
a
d
mi
d
yo
yo
/
/
/
/
j
t
t
F
/
i
t
.
:
/
/
F
r
oh
metro
D
h
oh
t
w
t
norte
pag
oh
:
a
/
d
/
mi
metro
d
i
F
t
r
oh
pag
metro
r
C
h
.
s
pag
i
yo
d
v
i
mi
r
mi
r
C
C
t
.
h
metro
a
i
r
mi
d
.
tu
C
oh
oh
metro
C
/
norte
j
a
oh
r
C
t
i
norte
C
/
mi
a
–
pag
r
d
t
i
2
C
2
yo
1
mi
–
4
pag
8
d
1
F
9
/
3
2
8
2
4
/
1
1
1
/
oh
4
C
8
norte
/
1
2
7
0
0
6
9
9
1
2
1
1
5
1
/
8
4
j
oh
pag
C
d
norte
.
b
2
y
0
gramo
0
tu
9
mi
.
s
t
2
oh
1
norte
1
8
0
4
8
.
S
pag
mi
d
pag
F
mi
metro
b
y
b
mi
gramo
r
tu
2
mi
0
2
s
3
t
/
j
.
.
F
/
.
t
oh
norte
1
8
METRO
a
y
2
0
2
1
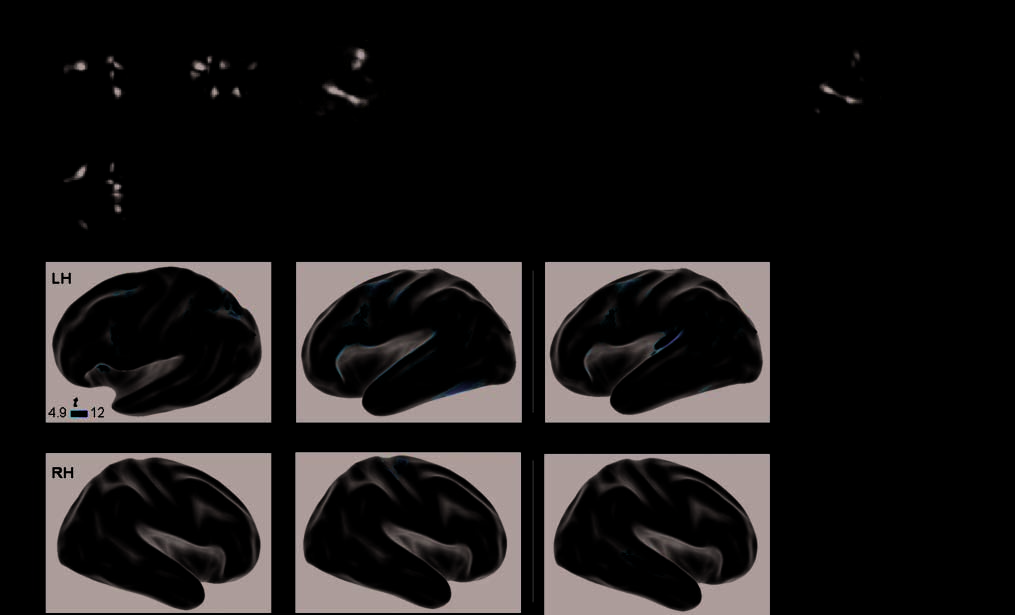
Cifra 1. Hemispheric asymmetries during language and calculation. The first row (glass brains) shows sagittal, axial, and coronal views of the
brain networks active during calculation, lectura, speech listening, and core language comprehension, respectivamente ( pcorr. < .05). Red numbers
indicate regions of interest of the calculation circuit for which a laterality index was computed: putamen (1), insula (2), middle frontal (3),
precentral (4), superior frontal (5), cingulate (6), hIPS (7), superior parietal lobule (8), and precuneus (9). Blue numbers indicate ROI of the
reading circuit: inferior frontal area (1), precentral area (2), middle frontal area (3), fusiform gyrus (4), pSTS (5), aSTS (6), and cingulate (7).
Note that all but one of these regions was also present in the core system of language comprehension. On the next two rows are displayed
series of left (LH) and right (RH) inflated hemisphere with projections of cortical sites of significant asymmetry, respectively, in favor of the left
or of the right hemisphere ( pcorr. < .05).
activation of the language cerebral organization were
centered on the following peaks: inferior frontal area
(close to Broca’s area; see Lindenberg, Fangerau, & Seitz,
2007, for a recent meta-analysis; MNI: x = (cid:1)43, y = 22,
z = (cid:1)2), precentral area (x = (cid:1)47, y = 6, z = 25), mid-
dle frontal gyrus (mFG, x = (cid:1)48, y = (cid:1)3, z = 53), fusi-
form gyrus (about 3 mm from the visual word form area;
Cohen & Dehaene, 2004; x = (cid:1)45, y = (cid:1)56, z = (cid:1)10),
posterior STS (pSTS; x = (cid:1)58, y = (cid:1)44, z = 8), anterior
STS (aSTS; x = (cid:1)57, y = (cid:1)3, z = (cid:1)9), and cingulate (x =
(cid:1)6, y = 3, z = 63). Only the fusiform gyrus activation
was specific to the visual modality.
No significant difference was observed between male
and female subjects in the voxel-based analysis (voxel
puncorr. < .001, pcorr. < .05 for cluster extent). The only
area associated with a sex effect with a p value < .1 in
the ROI analysis was the inferior frontal area ( p = .09
in reading and p = .01 in speech listening condition,
206 degrees of freedom) with a trend toward a larger
left lateralization for men (median LI = (cid:1)0.24 and (cid:1)0.11
for reading and speech listening, respectively) than for
women (median LI = (cid:1)0.16 and (cid:1)0.06).
Table 1 gives the correlation of the LIs across areas,
both within and across the language tasks. Looking first
at the diagonal values (bottom of Table 1), we see that
for all areas, the LIs were highly correlated across the
two modalities of linguistic input (visual or auditory),
suggesting that left lateralization in most areas arises
from amodal
levels of language processing. Even the
fusiform peak, which did not survive corrected thresh-
old for activation during the auditory trials, presented a
trend toward leftward asymmetry during speech listen-
ing that correlated with reading activation asymmetry in
this region (perhaps corresponding to a top–down acti-
vation of orthographic processing in the visual word form
area during speech listening; Cohen, Jobert, Le Bihan, &
Dehaene, 2004). This analysis also demonstrated that,
for each subject, the LI of each selected ROI was reli-
ably measured by our paradigm over two independent
language-related conditions.
In view of this high reproducibility of the LI within
each area, it is surprising that the LI across areas are
sometimes weakly correlated, suggesting that many re-
gions present relative independent pattern of hemispheric
52
Journal of Cognitive Neuroscience
Volume 22, Number 1
Table 1. Reproducibility and Colateralization of Asymmetries during Language Processing
LI Correlation within Each Language Task
Reading
Inferior Frontal
Precentral
Mid-frontal
Fusiform
Posterior STS
Anterior STS
Cingulate
Inferior Frontal
Precentral
Mid-frontal
Fusiform
Posterior STS
Anterior STS
Cingulate
g
n
i
d
a
e
R
g
n
i
n
e
t
s
i
l
h
c
e
e
p
S
Inferior Frontal
Precentral Mid-frontal
Fusiform Posterior STS
Anterior STS
Cingulate
–
–
–
–
–
–
–
.008
–
–
–
–
–
–
.077
.001
–
–
–
–
–
.185
.061
<10(cid:1)3
–
–
–
–
<10(cid:1)3
.005
<10(cid:1)3
<10(cid:1)3
–
–
–
Speech Listening
.001
.167
.033
.013
.002
–
–
<10(cid:1)3
<10(cid:1)3
.007
.783
<10(cid:1)3
.213
–
Inferior Frontal
Precentral Mid-frontal
Fusiform Posterior STS
Anterior STS
Cingulate
–
–
–
–
–
–
–
<10(cid:1)3
–
–
–
–
–
–
.004
<10(cid:1)3
–
–
–
–
–
.012
<10(cid:1)3
.006
.001
–
–
–
.002
.140
.021
.506
.628
–
–
.047
.003
<10(cid:1)3
.579
.046
.352
–
.393
.429
.951
–
–
–
–
Reading
LI Correlation across the Two Language Tasks
Inferior Frontal
Precentral Mid-frontal
Fusiform Posterior STS
Anterior STS
Cingulate
Inferior Frontal
<10(cid:1)3
g
n
i
n
e
t
s
i
l
h
c
e
e
p
S
Precentral
Mid-frontal
Fusiform
Posterior STS
Anterior STS
Cingulate
.027
.082
.381
.005
.016
.120
.019
<10(cid:1)3
.429
.585
.246
.103
.637
.472
.132
<10(cid:1)3
.178
.289
.503
.031
.041
.622
.352
.023
.031
.710
.796
.092
.307
.563
.050
<10(cid:1)3
.410
.476
.372
.101
.177
.695
.025
<10(cid:1)3
.664
.380
.012
.903
.666
.080
.737
<10(cid:1)3
The table shows the p values of the correlation between the lateralization indices (LI) of the seven main language-related ROIs during language
comprehension tasks. The upper part of the table reports the correlations within the same modality of language input (visual sentence reading and
auditory speech listening). Bold values indicate correlation values that are similarly significant ( p < .05) for the same pairs across modalities. The
bottom part reports the correlations across two independent trial types with visual and auditory language inputs. Bold values on the diagonal
highlight the level of LI reliability across modalities.
asymmetries, perhaps reflecting multiple determinants
of left hemispheric bias for language in the course of
development. For instance, although all of these regions
are highly asymmetrically activated, always in favor of
the left hemisphere, correlations between the LI of the
fusiform gyrus and of frontal areas are weak, as well as
those between aSTS and precentral gyrus, cingulate and
fusiform gyrus, cingulate and aSTS. It is remarkable that
this pattern of weak correlation was largely similar across
the two modalities of sentence presentation. Similarly,
Pinel and Dehaene
53
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
f
r
o
m
D
h
o
t
w
t
n
p
o
:
a
/
d
/
e
m
d
i
f
t
r
o
p
m
r
c
h
.
s
p
i
l
d
v
i
e
r
e
r
c
c
t
.
h
m
a
i
r
e
d
.
u
c
o
o
m
c
/
n
j
a
o
r
c
t
i
n
c
/
e
a
-
p
r
d
t
i
2
c
2
l
1
e
-
4
p
8
d
1
f
9
/
3
2
8
2
4
/
1
1
1
/
o
4
c
8
n
/
1
2
7
0
0
6
9
9
1
2
1
1
5
1
/
8
4
j
o
p
c
d
n
.
b
2
y
0
g
0
u
9
e
.
s
t
2
o
1
n
1
8
0
4
8
.
S
p
e
d
p
f
e
m
b
y
b
e
g
r
u
2
e
0
2
s
3
t
/
j
.
/
.
t
f
.
o
n
1
8
M
a
y
2
0
2
1
there were notable patterns of extremely high correla-
tion across areas, both for the reading and the speech
listening tasks. Such consistently high correlations were
found between the pSTS and both fusiform and frontal
areas; within the frontal lobe, between precentral and
both the mFG and the inferior frontal area; and finally,
between the aSTS and both the mFG and the inferior
frontal area. Only a few pairs of areas presented incon-
sistent level of LI correlation across modalities, notice-
ably the fusiform and mFG as well as the aSTS and pSTS,
probably due to the partially modality-specific involve-
ment of these areas, respectively, in orthographic and
phonological processing.
Arithmetic Lateralization
The nine ROIs from activation for the calculation task
were centered on the following maxima (Figure 1): puta-
men (x = (cid:1)18, y = 11, z = 4), insula (x = (cid:1)32, y = 20,
z = 6), mFG (x = (cid:1)44, y = 39, z = 15), precentral (x =
(cid:1)48, y = 8, z = 33), superior frontal gyrus (sFG close to
frontal eye fields; Simon et al., 2004; x = (cid:1)25, y = 2, z =
59), cingulate (x = 0, y = 14, z = 47; left and right parts
of the sphere were here considered), hIPS (virtually iden-
tical to the location reported from in the meta-analysis
of Dehaene et al., 2003; x = (cid:1)40, y = (cid:1)47, z = 47),
superior parietal lobule (sPL, close to the posterior sPL
from Dehaene et al., 2003; x = (cid:1)27, y = (cid:1)69, z = 44),
and precuneus (x = (cid:1)14, y = (cid:1)72, z = 54).
Because lateralization of calculation is less well char-
acterized than language lateralization, Figure 2 details
the RFX lateralization map of the calculation task with a
series of axial slices. All activated areas showed at least a
trend toward left lateralization, often reaching very high
degrees of significance: t(208) = 17.23 in cingular cortex
slightly posterior to the activation peak, t = 16.00 in pre-
central, t = 12.98 in the posterior parietal lobule close to
the sPL, t = 12.34 posterior to putamen peak, t = 11.90
about 3 voxels under the insula peak, t = 10.40 in the
sFG, t = 8.75 in the hIPS, and t = 8.19 in the middle
frontal area. Examination of the distributions of the LI
across subjects allowed for a more detailed and anatomy-
free analysis of the lateralization of these sites. A gradi-
ent emerged in the extent of lateralization for arithmetic,
with the highest value for the precentral area (median
LI = (cid:1)0.218); medium lateralization for sPL ((cid:1)0.148),
hIPS ((cid:1)0.125), cingulate ((cid:1)0.125), sFG ((cid:1)0.119), and
middle frontal ((cid:1)0.110); and low LI for the subcortical
system: putamen ((cid:1)0.028) and insula ((cid:1)0.012). The par-
tial discrepancy of the latter finding with the RFX
asymmetry map may be due to the fact that subcortical
peaks had approximately equal levels of BOLD activa-
tions in both hemispheres, but with a more extended
activation in the left hemisphere.
No significant differences were observed between male
and female subjects in the voxel-based analysis (voxel
puncorr. < .001, pcorr. < .05 for cluster extent). The only
areas associated to a sex effect with a p value < .1 in the
ROI analysis was the putamen area ( p = .04, 206 de-
grees of freedom), with a trend toward a larger, al-
though weak, left lateralization for men (median LI =
(cid:1)0.04) than for women (median LI = 0.01).
Colateralization of Language and Arithmetic:
ROI Analysis
To examine how arithmetic and language colateralized,
we first examined the full correlation matrix between
the asymmetry of activation in the above-selected ROI,
known to be asymmetrically activated during one or both
of these activities. As a proxy for language asymmetry,
we used the LI obtained during reading because (1) the
diagonal of Table 2 indicates a very highly correlation
with the LI obtained during language listening in all
regions; (2) in one region (left fusiform), reading yielded
stronger and more asymmetrical activation than lan-
guage listening (corresponding to the putative ortho-
graphic role of this region as the visual word form area).
Surprisingly, the correlation matrix between reading
and calculation LIs indicated that most of the language-
and calculation-related areas varied independently in
their degree of lateralization (Table 2). However, a few
pairs of areas presented a significant positive correlation
across tasks: The mFG LI during reading correlated with
the precuneus LI during calculation (r = .25); the pSTS
LI during reading correlated with the precentral area
(r = .28), sFG (r = .23), hIPS (r = .21), and precuneus
(r = .23) LI during calculation; and finally, the cingulate
LI during reading correlated with the sFG LI during
calculation (r = .22). When considering separately the
auditory and visual modalities for calculation trials, only
a subset of correlations survived across these two inde-
pendent sets of data. On the one hand, lateralization in
the pSTS during reading was reliably correlated with lat-
eralization in the hIPS during calculation. On the other
hand, mFG lateralization during reading correlated with
precuneus lateralization during calculation.
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
f
r
o
m
D
h
o
t
w
t
n
p
o
:
a
/
d
/
e
m
d
i
f
t
r
o
p
m
r
c
h
.
s
p
i
l
d
v
i
e
r
e
r
c
c
t
.
h
m
a
i
r
e
d
.
u
c
o
o
m
c
/
n
j
a
o
r
c
t
i
n
c
/
e
a
-
p
r
d
t
i
2
c
2
l
1
e
-
4
p
8
d
1
f
9
/
3
2
8
2
4
/
1
1
1
/
o
4
c
8
n
/
1
2
7
0
0
6
9
9
1
2
1
1
5
1
/
8
4
j
o
p
c
d
n
.
b
2
y
0
g
0
u
9
e
.
s
t
2
o
1
n
1
8
0
4
8
.
S
p
e
d
p
f
e
m
b
y
b
e
g
r
u
2
e
0
2
s
3
t
/
j
t
/
.
.
.
f
Colateralization of Language and Arithmetic:
Voxel-based Analyses
We first confirmed our results by a voxel-based regres-
sion approach, which consisted in examining how the LI
of a selected region predicted, at the whole-brain level,
the asymmetry in activation in another task.
o
n
1
8
M
a
y
2
0
2
1
Link 1: sFG and hIPS
Even when exploring the entire left hemisphere, only
the sFG and the hIPS exhibited profiles of asymmetry
during the calculation task that were significantly pre-
dicted by the lateralization index of the pSTS during
54
Journal of Cognitive Neuroscience
Volume 22, Number 1
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
f
r
o
m
D
h
o
t
w
t
n
p
o
:
a
/
d
/
e
m
d
i
f
t
r
o
p
m
r
c
h
.
s
p
i
l
d
v
i
e
r
e
r
c
c
t
.
h
m
a
i
r
e
d
.
u
c
o
o
m
c
/
n
j
a
o
r
c
t
i
n
c
/
e
a
-
p
r
d
t
i
2
c
2
l
1
e
-
4
p
8
d
1
f
9
/
3
2
8
2
4
/
1
1
1
/
o
4
c
8
n
/
1
2
7
0
0
6
9
9
1
2
1
1
5
1
/
8
4
j
o
p
c
d
n
.
b
2
y
0
g
0
u
9
e
.
s
t
2
o
1
n
1
8
0
4
8
.
S
p
e
d
p
f
e
m
b
y
b
e
g
r
u
2
e
0
2
s
3
t
/
j
t
.
.
/
.
f
o
n
1
8
M
a
y
2
0
2
1
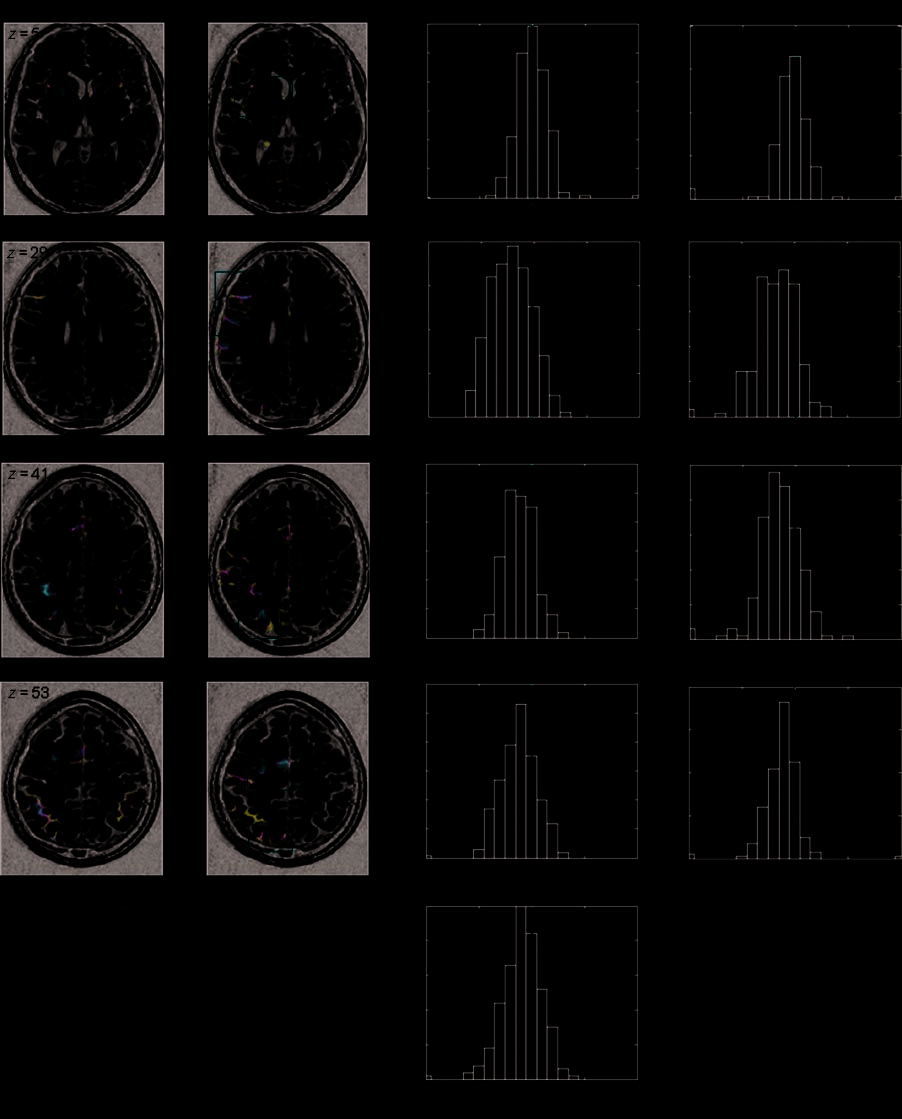
Figure 2. Quantifying functional asymmetries in the calculation network. Axial slices describe the entire pattern of activation and asymmetry
for the calculation task (neurological convention) from bottom to the top of the brain (RFX group analysis, pcorr. < .05). The histograms
at right show the distribution of LI across subjects for each of the nine selected ROIs. Red rectangles help locate these ROIs on the corresponding
slices. ppl = posterior parietal lobule; superior frontal = superior frontal cortex.
reading ( p < .05, corrected for multiple comparisons;
see Figure 3A, Table 3). Note that, in this analysis, the
subjects’ arithmetical performance was regressed out as a
covariate of noninterest, and thus, performance variabil-
ity did not contribute to this significant colateralization.
At a lower voxelwise threshold ( p < .01, uncorrected),
additional voxels were found in the precentral gyrus and
in the caudate nucleus (Table 3).
A number of control analyses were run to assess the
significance of these findings. First, a simple regression
Pinel and Dehaene
55
Table 2. Colateralization of Asymmetries during Calculation and Reading
Reading
Inferior Frontal
Precentral Mid-frontal
Fusiform Posterior STS
Anterior STS
Cingulate
l
n
o
i
t
a
u
c
l
a
C
l
n
o
i
t
a
u
c
l
a
c
o
e
d
i
V
l
n
o
i
t
a
u
c
l
a
c
o
i
d
u
A
Putamen
Insula
Mid-frontal
Precentral
Superior Frontal
Cingulate
hIPS
Superior Parietal
Precuneus
Putamen
Insula
Mid-frontal
Precentral
Superior Frontal
Cingulate
hIPS
Superior Parietal
Precuneus
Putamen
Insula
Mid-frontal
Precentral
Superior Frontal
Cingulate
hIPS
Superior parietal
Precuneus
.010*
.307
.077
.077
.101
.235
.288
.465
.146
.685
.226
.143
.566
.540
.860
.319
.953
.053
.551
.449
.349
.086
.100
.077
.184
.186
.265
.384
.203
.137
.464
.138
.830
.602
.222
.703
.391
.578
.170
.175
.943
.616
.644
.013
.433
.160
.443
.523
.942
.028
.167
.303
.899
.433
.653
.137
.838
.155
.080
.030
.026
.510
<10(cid:1)3**
.117
.445
.778
.064
.671
.025
.040
.756
.001**
.763
.332
.250
.198
.009*
.304
.107
.251
<10(cid:1)3**
.083
.456
.698
.736
.390
.069
.174
.784
.710
.151
.713
.763
.746
.913
.388
.510
.981
.930
.721
.407
.846
.466
.150
.053
.073
.971
.283
.394
.633
.050
.010*
.001**
.060
.002*
.035
.002*
.278
.725
.013
.133
.284
.007*
<10(cid:1)3**
.564
<10(cid:1)3**
.073
.896
.094
.020
.002*
.364
.005*
.067
.018
.678
.012
.993
.506
.166
.191
.248
.373
.100
.920
.002*
.480
.892
.766
.407
.783
.988
.038
.756
.297
.189
.283
.113
.040
.106
.433
.285
.015
.184
.922
.053
.004*
.018
.226
.486
.293
.016
.311
.311
.034
.231
.013
.146
.982
.069
.106
.463
.786
.158
.009*
.308
.284
.340
.815
The table shows the p values of the correlation between the lateralization indices (LI) of the reading and calculation ROIs. In each case, we report
the correlation of activation asymmetry on two independent sets of trials, the reading trials (horizontally) versus the calculation trial (vertically).
Significance is reported both for overall calculation trials (first part of the table), visually presented calculations only (second part) and auditory
presented calculations only (third part). Bold values highlight the two correlation patterns that were deemed reliable enough.
*p value < .01.
**p value < .001.
with the LI of the pSTS during reading, computed with-
out any behavioral regressor but applied to the whole
population images, gave comparable results. Three peaks
survived a corrected p value of .05 for cluster extent:
hIPS [(cid:1)36, (cid:1)48, 42; t(207) = 4.70, voxel pcorr. < .05],
sFG [(cid:1)18, 3, 66; t(207) = 5.10, voxel puncorr. < .001],
and precentral peak [(cid:1)51, 3, 27; t(207) = 4.30, voxel
puncorr. < .001]. Second, we checked whether the pos-
itive correlation found for calculation minus sentence
processing was, in fact, due to a negative correlation with
lateralization in the control task of visual sentence pro-
cessing. When analyzing the contrast of sentence reading
minus rest, no voxel of the superior frontal or parietal
sites presented any significant asymmetry predicted by
56
Journal of Cognitive Neuroscience
Volume 22, Number 1
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
f
r
o
m
D
h
o
t
w
t
n
p
o
:
a
/
d
/
e
m
d
i
f
t
r
o
p
m
r
c
h
.
s
p
i
l
d
v
i
e
r
e
r
c
c
t
.
h
m
a
i
r
e
d
.
u
c
o
o
m
c
/
n
j
a
o
r
c
t
i
n
c
/
e
a
-
p
r
d
t
i
2
c
2
l
1
e
-
4
p
8
d
1
f
9
/
3
2
8
2
4
/
1
1
1
/
o
4
c
8
n
/
1
2
7
0
0
6
9
9
1
2
1
1
5
1
/
8
4
j
o
p
c
d
n
.
b
2
y
0
g
0
u
9
e
.
s
t
2
o
1
n
1
8
0
4
8
.
S
p
e
d
p
f
e
m
b
y
b
e
g
r
u
2
e
0
2
s
3
t
/
j
f
.
.
.
t
/
o
n
1
8
M
a
y
2
0
2
1
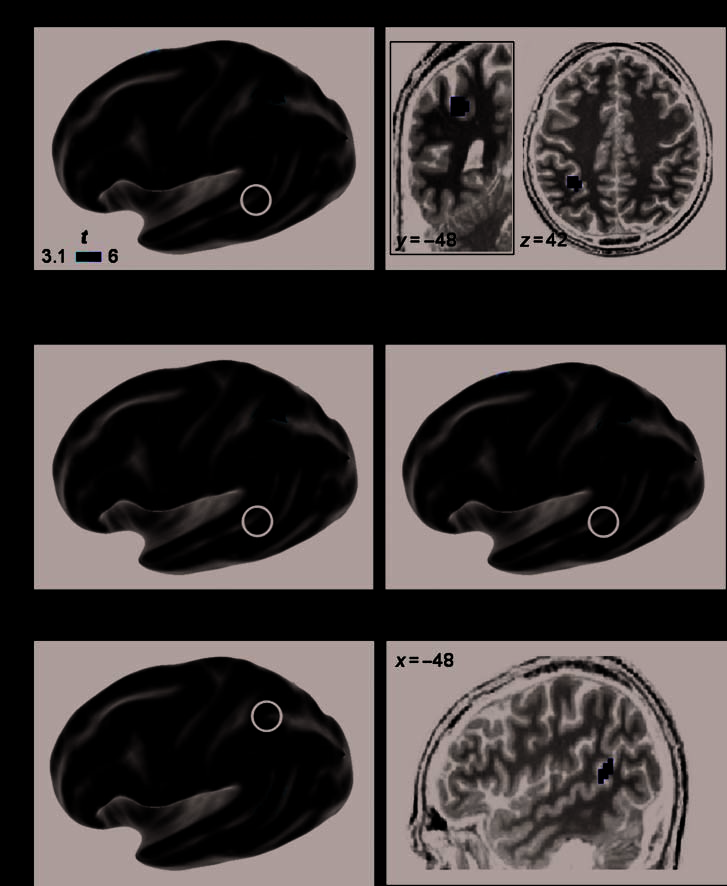
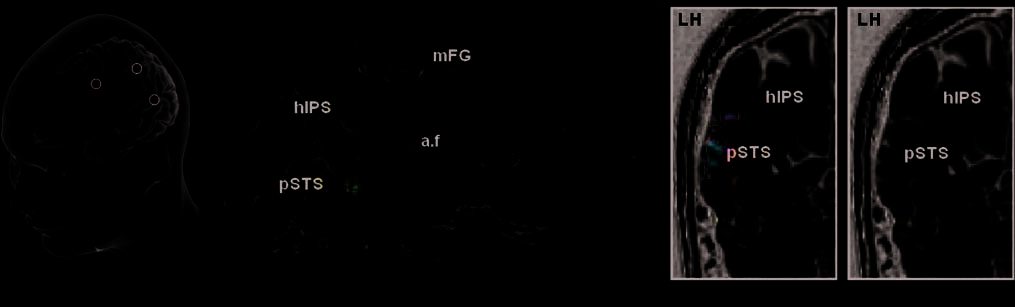
Figure 3. Colateralized
regions for reading and
calculation: pSTS and hIPS.
Whole-brain regression
analysis of the colateralization
between the reading temporal
area (pSTS) and the
calculation intraparietal area
(hIPS; p < .001, uncorrected
at the voxel level, p < .05,
corrected for the cluster
extent). (A) The first row
shows a 3-D rendering of
which voxels from the global
calculation–sentence contrast
showed an asymmetry that was
significantly predicted by the
LI of the pSTS region during
reading (this ‘‘source’’ region
is enclosed with a black circle).
The SPM statistical map was
projected onto an inflated left
hemisphere of the template
brain of the Caret software.
The observed intraparietal
cluster is detailed on coronal
and axial slices. On the second
row, similar analyses are
shown separately for the
auditory and visual calculation,
respectively. (B) 3-D rendering
of the converse analysis:
reading–checkerboard contrast
asymmetry predicted by the
LI of the hIPS during
calculation (black circle).
The observed temporal cluster
is detailed on the sagittal
view of one subject’s anatomy.
the pSTS LI, even at a low threshold at the voxel level
( p > .01, uncorrected). Además, when we directly
regressed the asymmetry of calculation versus rest to the
LI of the pSTS during reading, with calculation score as a
covariate (voxel puncorr. < .001, pcorr. < .05 for cluster ex-
tent), we still isolated the hIPS [(cid:1)36, (cid:1)48, 42; t(173) =
4.63], in addition to a broad sentence comprehension cir-
cuit that encompassed the pSTS [(cid:1)54, (cid:1)48, 15; t(173) =
5.63], the fusiform gyrus [(cid:1)42, (cid:1)63, (cid:1)12; t(173) = 5.16],
and an occipito-parietal area [(cid:1)36, (cid:1)48, 42; t(173) =
4.63]. Third, and most crucially, the hIPS was the only
area whose asymmetry during calculation was significantly
predicted by the LI of the pSTS during reading when we
did separate analyses on auditory and on visual calcula-
tion trials (Figure 3A, Table 3). Finally, the multiregres-
sion analysis with sex as a second regressor gave strictly
similar results with no sex effect at the selected threshold.
The converse regression analysis, starting with the LI
of the hIPS region during calculation and using it as a
regressor of the images of asymmetry during reading,
revealed a small set of voxels in the pSTS, close to the
maxima of asymmetry during the reading task (Figure 3B,
Table 3). Another significant cluster was found in the
anterior cingulum, but in a region not reported here as a
part of the reading network.
Link 2: mFG and Superior Parietal/Precuneus
Similar multiple regression analyses used the LI of the
mFG during reading as a predictor of calculation asym-
metry images, with behavioral calculation performance
as a covariate of noninterest. This SPM analysis isolated
two superior parietal/precuneus clusters (Figure 4A). The
regression was weaker and did not survive a corrected
p value at the voxel level, but approached significance at
the cluster level (Table 4). Here again, a simple regression
to the reading mFG LI, computed without any behavioral
regressor but applied to the whole population images,
Pinel and Dehaene
57
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
f
r
o
m
D
h
o
t
w
t
n
p
o
:
a
/
d
/
e
m
d
i
f
t
r
o
p
m
r
c
h
.
s
p
i
l
d
v
i
e
r
e
r
c
c
t
.
h
m
a
i
r
e
d
.
u
c
o
o
m
c
/
n
j
a
o
r
c
t
i
n
c
/
e
a
-
p
r
d
t
i
2
c
2
l
1
e
-
4
p
8
d
1
f
9
/
3
2
8
2
4
/
1
1
1
/
o
4
c
8
n
/
1
2
7
0
0
6
9
9
1
2
1
1
5
1
/
8
4
j
o
p
c
d
n
.
b
2
y
0
g
0
u
9
e
.
s
t
2
o
1
n
1
8
0
4
8
.
S
p
e
d
p
f
e
m
b
y
b
e
g
r
u
2
e
0
2
s
3
t
/
j
.
/
f
t
.
.
o
n
1
8
M
a
y
2
0
2
1
Table 3. Whole-brain Analysis of Colateralization with pSTS
Coordinates
Voxel
Brain Area
x
y
z
puncorr.
pFWE-corr.
t(173)
Calculation Asymmetry Regressed by the Reading pSTS LI
puncorr. < .001
Intraparietal sulcus
Superior frontal gyrus
puncorr. < .01
Precentral gyrus
Caudate nucleus
(cid:1)36
(cid:1)18
(cid:1)48
(cid:1)18
(cid:1)48
3
0
(cid:1)9
42
66
30
24
Video Calculation Asymmetry Regressed by the Reading pSTS LI
puncorr. < .001
Superior frontal gyrus
Intraparietal sulcus
puncorr. < .01
Precentral gyrus
(cid:1)15
(cid:1)36
(cid:1)48
3
(cid:1)48
0
66
42
30
Audio Calculation Asymmetry Regressed by the Reading pSTS LI
puncorr. < .001
Intraparietal sulcus
(cid:1)33
(cid:1)48
puncorr. < .01
Precentral gyrus
(cid:1)36
x
(cid:1)6
y
Reading Asymmetry Regressed by the Calculation hIPS LI
puncorr. < .001
Anterior cingulum
(cid:1)15
33
puncorr. < .01
Mid-temporal gyrus
(cid:1)48
(cid:1)54
42
63
z
6
15
Cluster
pcorr.
.001
.011
.019
.030
.020
.040
.049
.007
.002
<.001
<.001
<.001
<.001
<.001
<.001
.004*
.010*
.117
.974
.012*
.054*
<.001
.638
<.001
<.001
.070
.093
5.26
4.73
4.61
3.70
5.11
4.48
4.12
4.98
4.66
puncorr.
pFWE-corr.
t(208)
pcorr.
<.001
<.001
.075
.666
4.68
4.05
.006
.017
Brain areas where the leftward asymmetry during calculation was significantly predicted by the lateralization index of the pSTS during reading
(whole left hemisphere analysis). Regression was performed separately for the overall images of asymmetry during calculation (pooling over visual
and auditory trials), for visual calculation trials only, and for auditory calculation trials only. For an exhaustive description of the regression, we
reported for each case statistical mapping results with a voxel threshold of .001 and with a more liberal threshold of .01, keeping .05 as a corrected
threshold for cluster extent. The bottom part of the table reports the converse analysis, that is, areas with a leftward asymmetry during reading that
was significantly predicted by the lateralization index of the hIPS during calculation.
gave comparable results: sPL [(cid:1)24, (cid:1)66, 54; t(207) = 3.44,
voxel puncorr. < .001], precuneus [(cid:1)9, (cid:1)69, 54; t(207) =
3.42, voxel puncorr. < .001], and postcentral gyrus [(cid:1)27,
(cid:1)45, 51; t(207) = 3.67, voxel puncorr. < .001]. Finally, the
multiregression analysis with sex as a second regressor
gave strictly similar results with no sex effect at the se-
lected threshold in active areas.
The converse regression analysis, considering the LI
from the sPL during calculation as the regressor of the
reading asymmetry images, showed that only a cluster of
voxels in the mFG exhibited an asymmetry during the
reading task that was significantly predicted by this LI.
The region clearly encompassed the ROI selected for its
asymmetry during the reading task (Figure 3B, Table 3).
Relation between Colateralization and
Anatomical Connectivity
In this final analysis, we wondered whether the observed
patterns of colateralization between two areas related to
58
Journal of Cognitive Neuroscience
Volume 22, Number 1
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
f
r
o
m
D
h
o
t
w
t
n
p
o
:
a
/
d
/
e
m
d
i
f
t
r
o
p
m
r
c
h
.
s
p
i
l
d
v
i
e
r
e
r
c
c
t
.
h
m
a
i
r
e
d
.
u
c
o
o
m
c
/
n
j
a
o
r
c
t
i
n
c
/
e
a
-
p
r
d
t
i
2
c
2
l
1
e
-
4
p
8
d
1
f
9
/
3
2
8
2
4
/
1
1
1
/
o
4
c
8
n
/
1
2
7
0
0
6
9
9
1
2
1
1
5
1
/
8
4
j
o
p
c
d
n
.
b
2
y
0
g
0
u
9
e
.
s
t
2
o
1
n
1
8
0
4
8
.
S
p
e
d
p
f
e
m
b
y
b
e
g
r
u
2
e
0
2
s
3
t
/
j
f
t
.
/
.
.
o
n
1
8
M
a
y
2
0
2
1
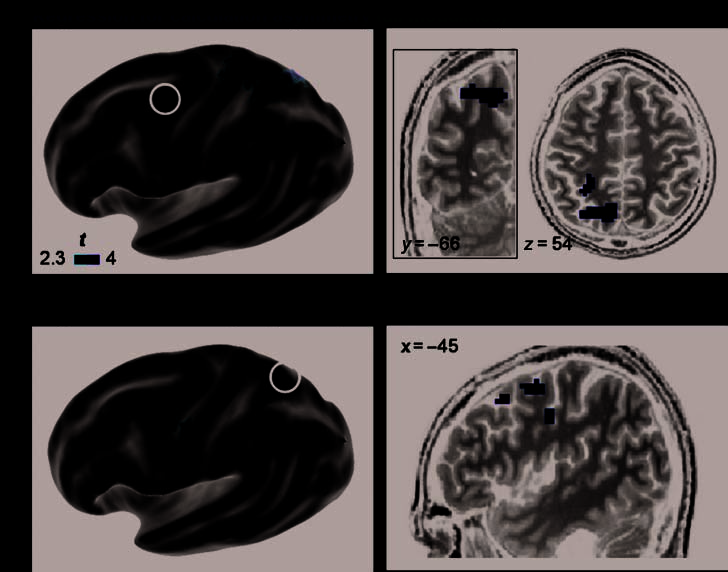
Figure 4. Colateralized
regions for reading and
calculation: mFG and
posterior parietal/precuneus.
Whole-brain regression
analysis of the colateralization
between the reading middle
frontal area (mFG) and the
calculation posterior parietal
lobe/precuneus ( p < .01,
uncorrected at the voxel level;
p < .05 correct for the cluster
extent). (A) 3-D rendering
of which voxels from the
calculation–sentence contrast
showed an asymmetry that
was significantly predicted by
the LI of the mFG during
reading (black circle). The
most posterior cluster is
detailed on coronal and
axial slices. (B) 3-D rendering
of the converse analysis:
reading–checkerboard contrast
asymmetry predicted by the
LI of the precuneus during
calculation (black circle). The
observed frontal clusters are
detailed on the sagittal view of
one subject’s anatomy.
the existence of actual anatomical connections between
them, such that if one area grew more asymmetrical in
the course of development, the other would also tend to
develop a growing asymmetry.
Fiber tracking from DTIs provided clear structural
support for our first finding of a strong pSTS–hIPS co-
lateralization: In all of the six subjects, projections were
found from the pSTS to inferior parietal cortex. As for
Cluster
pcorr.
.050
.080
Table 4. Whole-brain Analysis of Colateralization with the mFG
Coordinates
Voxel
Brain Area
x
y
z
puncorr.
pFWE-corr.
t(173)
Calculation Asymmetry Regressed by the Reading mFG LI
puncorr. < .01
Postcentral gyrus
Superior parietal gyrus
Precuneus
(cid:1)21
(cid:1)24
(cid:1)9
x
(cid:1)39
(cid:1)66
(cid:1)63
y
66
54
54
z
Reading Asymmetry Regressed by the Calculation Precuneus LI
<.001
<.001
<.001
.864
.999
1.0
3.90
3.46
3.46
puncorr.
pFWE-corr.
t(208)
pcorr.
puncorr. < .01
Mid-frontal gyrus
Mid-frontal gyrus
(cid:1)45
(cid:1)48
15
(cid:1)3
51
57
<.001
<.001
.275
.596
4.38
4.11
.030
Brain areas where the leftward asymmetry during calculation was significantly predicted by the lateralization index of the mFG during reading
(whole left hemisphere analysis). Regression was performed on the images of asymmetry during calculation, pooled over visual and auditory trials.
For an exhaustive description of the regression, we reported for each case statistical mapping results with a voxel threshold of .01 and .05 as a
corrected threshold for cluster extent (except for the superior parietal gyrus reported in ROI analysis). The bottom part of the table reports the
converse analysis, that is, areas with a reading leftward asymmetry during reading that was significantly predicted by the lateralization index of the
precuneus during calculation. Secondary peaks are reported in italic.
Pinel and Dehaene
59
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
f
r
o
m
D
h
o
t
w
t
n
p
o
:
a
/
d
/
e
m
d
i
f
t
r
o
p
m
r
c
h
.
s
p
i
l
d
v
i
e
r
e
r
c
c
t
.
h
m
a
i
r
e
d
.
u
c
o
o
m
c
/
n
j
a
o
r
c
t
i
n
c
/
e
a
-
p
r
d
t
i
2
c
2
l
1
e
-
4
p
8
d
1
f
9
/
3
2
8
2
4
/
1
1
1
/
o
4
c
8
n
/
1
2
7
0
0
6
9
9
1
2
1
1
5
1
/
8
4
j
o
p
c
d
n
.
b
2
y
0
g
0
u
9
e
.
s
t
2
o
1
n
1
8
0
4
8
.
S
p
e
d
p
f
e
m
b
y
b
e
g
r
u
2
e
0
2
s
3
t
/
j
/
f
.
.
t
.
o
n
1
8
M
a
y
2
0
2
1
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
f
r
o
m
D
h
o
t
w
t
n
p
o
:
a
/
d
/
e
m
d
i
f
t
r
o
p
m
r
c
h
.
s
p
i
l
d
v
i
e
r
e
r
c
c
t
.
h
m
a
i
r
e
d
.
u
c
o
o
m
c
/
n
j
a
o
r
c
t
i
n
c
/
e
a
-
p
r
d
t
i
2
c
2
l
1
e
-
4
p
8
d
1
f
9
/
3
2
8
2
4
/
1
1
1
/
o
4
c
8
n
/
1
2
7
0
0
6
9
9
1
2
1
1
5
1
/
8
4
j
o
p
c
d
n
.
b
2
y
0
g
0
u
9
e
.
s
t
2
o
1
n
1
8
0
4
8
.
S
p
e
d
p
f
e
m
b
y
b
e
g
r
u
2
e
0
2
s
3
t
/
j
f
.
.
/
.
t
o
n
1
8
M
a
y
2
0
2
1
Figure 5. Anatomical connections putatively supporting the observed colateralization patterns. (A) Location on a 3-D left hemisphere of the
three frontal, parietal, and temporal seed regions used for tracking. (B) Left hemisphere fibers of interest (from an internal view): long segment
of the arcuate fasciculus (a.f., in blue), posterior segment linking the pSTS and hIPS (red), superior segment linking the hIPS and mFG (green),
and projections connecting the mFG and pSTS (purple). (C) Coronal view of the projections to the left parietal region, respectively, from
seed regions in the pSTS (left) and the mFG (right). Color scale corresponds to the amount of overlap from five different individuals. The
pSTS clearly connects to the banks of the intraparietal sulcus, whereas the mFG projects more dorsally toward superior parietal cortex.
hIPS = horizontal segment of the intraparietal sulcus; mFG = middle frontal gyrus; pSTS = posterior superior temporal sulcus.
the second finding, as detailed in Figure 5A, white mat-
ter tracks also connected the mFG to the dorsal parietal
region (as well as, in some subjects, the mFG to the pSTS).
Although no direct connections were found from the mFG
to the sPL and the precuneus, dense local U-shaped fibers
were found linking the three parietal seed regions (intra-
parietal, superior parietal, and precuneus). Furthermore,
crucially, a close look at the organization of projections
to parietal cortex showed an anatomical segregation of
fibers originating from the pSTS and from the mFG, mir-
roring the parietal parcellation found by correlation with
the LI (Figure 5B). Projections from the pSTS were lo-
cated laterally in the inferior parietal lobule, often ex-
tending to the banks of the intraparietal sulcus, whereas
those from the mFG region projected more dorsally into
the sPL.
DISCUSSION
We studied the profile of functional brain asymmetries
for language and calculation over a large population of
200 subjects. Our goal was to study the colateralization
of these two functions across subjects, possibly reflect-
ing an influence of language organization onto the
cerebral architecture for calculation.
Purposely, our starting point was the definition of two
distinct and distributed networks; a vast language net-
work, defined by its activation to simple spoken or writ-
ten sentences and supported by frontal and peri-sylvian
areas, and a calculation network, defined by areas showing
more activity to verbally presented subtraction problems
(e.g., ‘‘compute 11 minus 3’’) than to other nonnumerical
sentences and supported by frontal, parietal, and subcor-
tical regions. Although both circuits showed significant
left hemispheric asymmetry, our results indicate that the
concept of a single hemispheric ‘‘dominance,’’ determin-
ing the lateralization of all regions of the language and cal-
culation networks, does not suffice to explain the patterns
of hemispheric asymmetries across individuals. In our data,
lateralization appears as a local regional phenomenon,
even within a given task. LIs are often uncorrelated across
distant areas, and therefore, probably have multiple de-
terminants. Indeed, interestingly, only two anatomically
restricted sets of areas showed a correlated asymmetry
across the language comprehension and the arithmetic
tasks: The lateralization profile of the pSTS during read-
ing correlated with the lateralization of the fundus of the
hIPS during calculation, and the lateralization of the mFG
during reading correlated with that of the sPL and the
precuneus during calculation. Although the asymmetry of
language areas only explained a relatively small propor-
tion of the variance in left/right parietal organization for
arithmetic, this amount was comparable to the correla-
tion observed within some areas of the language net-
work. Importantly, both findings were reproducible over
two separate sets of data (spoken and written arith-
metic problems), and both ROI-based and voxel-based
analysis.
These patterns of colateralization were further sup-
ported by the presence of anatomical connections, re-
spectively linking the pSTS with the hIPS, and the mFG
with the sPL, Notably, the pattern of white matter pro-
jections from the pSTS and mFG areas toward the parie-
tal lobe matched the pattern of colateralization between
parietal voxels and those two temporal and frontal sites.
Overall, these results underline an interesting subdivi-
sion of superior parietal cortex into two distinct regions
that could be subject to different influences in their de-
velopment and maturation.
60
Journal of Cognitive Neuroscience
Volume 22, Number 1
Colateralization of the Language-related pSTS and
the Core Numerical System
The global tasks used in the present study did not allow
us to precisely delineate the processing stages subtended
by the various brain areas reported here. However, a
striking aspect of our results is that language lateraliza-
tion in the pSTS is significantly related to those of the
frontal and parietal regions known to be crucial for the
representation and processing of numerical quantities.
The intraparietal site of colateralization reported here,
especially the fundus of the intraparietal sulcus, has
been systematically reported in various numerical tasks
(Venkatraman, Ansari, & Chee, 2005; Dehaene et al., 2003;
Delazer et al., 2003) and its neuronal coding properties
have been recently investigated in humans and non-
humans primates (Nieder, Diester, & Tudusciuc, 2006;
Piazza, Izard, Pinel, Le Bihan, & Dehaene, 2004). Contrary
to posterior parietal areas, which are shared with visuo-
spatial tasks, and to the AG, which is thought to relate to
the verbal coding of arithmetical facts, the intraparietal
location reported here is thought to house an amodal rep-
resentation of quantities (Piazza et al., 2006; Venkatraman
et al., 2005; Eger, Sterzer, Russ, Giraud, & Kleinschmidt,
2003; Pinel, Dehaene, Riviere, & Le Bihan, 2001). We
found the hIPS to be linked to the pSTS by a white matter
track that could correspond to the posterior segment of
the arcuate fasciculus, first described by Catani, Jones,
and Ffytche (2005) in their dissection of the human peri-
sylvian language network.
The second site of colateralization with the pSTS, lo-
cated in the precentral gyrus, although found at a lower
level of significance, has been repeatedly reported as
being coactivated with the hIPS in nearly all arithmetic
tasks requiring an active manipulation of numbers, by
opposition to mere priming or adaptation paradigms
(Pinel, Piazza, Le Bihan, & Dehaene, 2004; Delazer et al.,
2003; Stanescu et al., 2000). It is noteworthy that the
pSTS is quite remote from the precentral site (although
probably connected to it via the arcuate fasciculus; see
Schmahmann et al., 2007). Conversely, the precentral
site shows an asymmetry entirely independent of the
nearby sFG. Thus, covariations of asymmetry profiles, as
identified by the present ‘‘colateralization analysis,’’ may
reflect functionally significant connectivity rather than
spatial proximity.
It is interesting that the superior temporal language
area that colateralizes with the hIPS has been identified
as important for mapping linguistic inputs onto the
amodal representation of their meaning in adults. The
pSTS can be activated by either written and spoken words
or sentences (Beauchamp, Argall, Bodurka, Duy, & Martin,
2004), it appears essential for semantic-level processing
of words and pictures (Vandenbulcke, Peeters, Dupont,
Van Hecke, & Vandenberghe, 2007; Vandenberghe, Price,
Wise, Josephs, & Frackowiak, 1996), and it may form a
linking symbolic and
high-level
‘‘convergence zone’’
nonsymbolic information (Damasio & Damasio, 1994).
If so, the correlation between pSTS and hIPS asymmetry
may reflect the mapping of abstract representations of
number symbols (perhaps shared by Arabic numerals
and by spoken and written number words), putatively
coded in the left pSTS, to the corresponding numerical
quantities, putatively coded in the hIPS. According to
this scenario, although both left and right parietal lobes
appear to encode numerosity, the left parietal region
may be more susceptible to changes induced by the
acquisition of number symbols because of more direct
links with left hemispheric parietal and temporal areas
involved in word processing. Piazza, Pinel, Le Bihan, and
Dehaene (2007) first probed the convergence of sym-
bolic and nonsymbolic representations of numbers us-
ing a cross-notation paradigm of fMRI adaptation (Arabic
digits and sets of dots). They observed that the numeri-
cal information was transferred across those two nota-
tions in both the left and right hIPS, at a site only 6 mm
from the present parietal area whose asymmetry corre-
lates with the pSTS lateralization. Critically, Piazza et al.
(2007) found a hemispheric asymmetry, suggesting that
the coding of Arabic numerals was more precise in the
left hIPS than in the right hIPS. They suggested that
although both the left and right hIPS are involved in the
coding of numerical quantities, the quantity code in the
left hIPS is progressively refined through a direct inter-
action with number symbols coded in the left hemi-
sphere, such as words or Arabic numerals. Verguts and
Fias (2004) indeed showed in a neural network simula-
tion how the interaction of symbolic and nonsymbolic
codes for number could yield to such a refinement of
the precision of number coding. A developmental study
by Ansari and Dhital (2006) also observed that the left,
but not the right, IPS exhibited an increase in the size
of the numerical distance effect during a number com-
parison task—again compatible with the hypothesis that
the left IPS is the target of a particular development,
possibly including an increase in the precision of nu-
merical coding induced by the concomitant acquisition
of number symbols. Our study is compatible with this
assumption and tentatively suggests that the primary
source of this developmental change in the hIPS may be
its direct connection with a high-level representation of
numerical symbols in the pSTS.
Colateralization of the Language-related
mFG and the sPL
We now turn to our second finding, the colateralization
of the mFG during reading with a large extent of ac-
tivation in the sPL and the precuneus during calculation.
Although the sPL had been tentatively associated to
visuospatial mechanisms in the context of fronto-parietal
circuits (Astafiev et al., 2003; Simon et al., 2002), the mFG
implicated here is much more inferiorly positioned,
making this correlation of asymmetry more difficult to
Pinel and Dehaene
61
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
f
r
o
m
D
h
o
t
w
t
n
p
o
:
a
/
d
/
e
m
d
i
f
t
r
o
p
m
r
c
h
.
s
p
i
l
d
v
i
e
r
e
r
c
c
t
.
h
m
a
i
r
e
d
.
u
c
o
o
m
c
/
n
j
a
o
r
c
t
i
n
c
/
e
a
-
p
r
d
t
i
2
c
2
l
1
e
-
4
p
8
d
1
f
9
/
3
2
8
2
4
/
1
1
1
/
o
4
c
8
n
/
1
2
7
0
0
6
9
9
1
2
1
1
5
1
/
8
4
j
o
p
c
d
n
.
b
2
y
0
g
0
u
9
e
.
s
t
2
o
1
n
1
8
0
4
8
.
S
p
e
d
p
f
e
m
b
y
b
e
g
r
u
2
e
0
2
s
3
t
/
j
.
f
.
/
.
t
o
n
1
8
M
a
y
2
0
2
1
interpret. The mFG site that we observed, located dor-
sally to Broca’s region, has repeatedly been reported for
both speech listening and word reading tasks (Mechelli
et al., 2005; Binder et al., 2000), yet those studies did not
isolate which specific linguistic process is involved. This
site is also frequently activated during calculation tasks
(see details in Pinel et al., 2007). It may tentatively reflect
general working memory processes for storage and in-
tegration of information contained in a complex and
extended verbal stimulus. Interestingly, it is known that
although the frontal lobe supports working memory pro-
cesses independently of the nature of inputs (Owen
et al., 1998), additional posterior areas may be involved
according to the nature of the content. For instance,
Klingberg (2006) reported a developmental increase of
the white matter connections linking frontal and supe-
rior parietal areas involved in a visuospatial memory
task. Considering current theories that postulate shared
mechanisms for numerical and visuospatial processing
(Hubbard, Piazza, Pinel, & Dehaene, 2005), it may be pro-
posed that, in the case of our arithmetical operations (dis-
played in a sentence-like presentation), which consisted
of a simple canonical structure (first operand one, sign,
second operand), the relation between these quantities
would be jointly encoded syntactically in the mFG and
spatially in the sPL. This recruitment of spatial networks
would explain why numerical operations often elicit spa-
tial attentional and motor biases (for a review, see Hubbard
et al., 2005). Although speculative, this account fits with
reports of impaired arithmetic procedural skills with pre-
servation of number knowledge in the case of a frontal
lesion (Lucchelli & De Renzi, 1993), and may also par-
tially explain the spatial deficits reported in children with
mathematical disabilities (Geary, Hoard, Byrd-Craven, &
DeSoto, 2004; Noe¨l, Seron, & Trovarelli, 2004).
DTI analysis showed that the colateralized mFG and
sPL areas are connected by the anterior segment of the
arcuate fasciculus (Catani et al., 2005). Note that al-
though they showed similar profile of lateralization, no
fibers were found to link the mFG and the precuneus.
Because long-distance association fibers such as the
superior longitudinal fasciculus are known to connect
the frontal and posterior parietal lobes (Jellison et al.,
2004), it is likely that dense local parietal connections
may have artifactually limited the tracking algorithm to
the anterior hIPS portion. It is also plausible that a
cascade of local connections inside the parietal
lobe
propagates from the superior parietal lobe toward the
precuneus via U-shaped association fibers.
Implications for the Development of
Symbolic Arithmetic
It is tempting, although obviously speculative, to inter-
pret the present across tasks colateralizations within a
causal developmental framework. Although a detailed
lateralization analysis similar to the present one remains
to be done with fMRI data from children, studies of early
brain lesions and time windows for recovering linguistic
abilities suggest that the hemispheric organization for
language is already established within the first 5 years of
life (Bates & Roe, 2001). Indeed, recent neuroimaging
data indicate that a leftward lateralization of the tempo-
ral
lobe can be observed during speech listening in
infancy as early as 2 to 3 months after birth (Dehaene-
Lambertz, Dehaene, & Hertz-Pannier, 2004; Pen˜a et al.,
2003). A shift toward left hemispheric processing has been
reported during a lexical task around 14 to 20 months old
(Mills, Coffey-Corina, & Neville, 1997), and a strictly left-
lateralized set of fronto-inferotemporal activations has
been seen during an auditory semantic task in 5-year-olds
(Balsamo, Xu, & Gaillard, 2006).
Contrariwise, in 5-year-old children, the number pro-
cessing networks of the parietal lobe are equally activated
in both hemispheres, for both digits and dots manipu-
lation (Temple & Posner, 1998). With nonsymbolic pre-
sentations of numbers as sets of objects, activation during
number processing may even show a rightward laterali-
zation in 4-year-olds and even in infants (Izard, Dehaene-
Lambertz, & Dehaene, 2008; Cantlon et al., 2007).
One possible interpretation of these lateralization
patterns is that the pSTS lateralization for language
precedes and progressively biases the lateralization of
the hIPS for number. This implies that, although the
pSTS is not part of the mature arithmetic circuit in the
adult brain, proper functioning of the temporo-parietal
language system may be crucial for the normal develop-
ment and acquisition of mathematics. Such a develop-
mental model would seem to fit well with the scarce
developmental data available, to date, on how the num-
ber system evolves with age. Rivera, Reiss, Eckert, and
Menon (2005) observed that the fMRI correlates of
performance in a simple arithmetical task shifted from
the frontal lobe toward a more focused temporo-parietal
network as the age of the subjects varied from 8 to
19 years of age. The only two areas that increased in
activity with age were a left inferior/middle temporal
region and a left supramarginal/IPS region that both fall
close to those observed in the present study. This fMRI
result concurs with behavioral studies that indicate a
progressive automatization and strengthening of the link
between digit shapes and the corresponding quantities
from first- to fifth-grade children (Rubinsten, Henik,
Berger, & Shahar-Shalev, 2002). Indeed, in adults, this
interference effect of an irrelevant Arabic digit onto a
physical size comparison task has been related to intra-
parietal cortex (Pinel et al., 2004).
Based on this developmental scenario, it is then pos-
sible that the pivotal role of the left STS for symbol
processing decreases later in life in the special case of
number symbols, as number processing becomes highly
automatized. Such a decrease would fit with the clinical
dissociation between numerical and nonnumerical mean-
ing reported at the adult age: Zamarian, Karner, Benke,
62
Journal of Cognitive Neuroscience
Volume 22, Number 1
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
f
r
o
m
D
h
o
t
w
t
n
p
o
:
a
/
d
/
e
m
d
i
f
t
r
o
p
m
r
c
h
.
s
p
i
l
d
v
i
e
r
e
r
c
c
t
.
h
m
a
i
r
e
d
.
u
c
o
o
m
c
/
n
j
a
o
r
c
t
i
n
c
/
e
a
-
p
r
d
t
i
2
c
2
l
1
e
-
4
p
8
d
1
f
9
/
3
2
8
2
4
/
1
1
1
/
o
4
c
8
n
/
1
2
7
0
0
6
9
9
1
2
1
1
5
1
/
8
4
j
o
p
c
d
n
.
b
2
y
0
g
0
u
9
e
.
s
t
2
o
1
n
1
8
0
4
8
.
S
p
e
d
p
f
e
m
b
y
b
e
g
r
u
2
e
0
2
s
3
t
/
j
.
.
t
f
.
/
o
n
1
8
M
a
y
2
0
2
1
Donnemiller, and Delazer (2006) described a single-case
study of a patient with of severe atrophy of the tempo-
ral lobe, who presented great difficulties in understand-
ing or finding some words but performed at ceiling in
number tasks, notably with all numerical formats in
transcoding tasks.
Under the speculative hypothesis presented here,
lateralization of the left STS would serve as a seed that
constrains a subsequent cascade of secondary lateraliza-
tion in the associative parietal cortices to which it is
tightly interconnected (Andresen & Marsolek, 2005). It
should be remembered, however, that the present
correlational method is unable to assess the causality
of these events. Genuinely testing this developmental
model will therefore require an adaptation of the pres-
ent methods to future longitudinal developmental fMRI
data.
A Mosaic of Lateralizations
in all, our study questions the very concept of
All
hemispheric ‘‘dominance.’’ This concept,
indeed, has
been already challenged by occasional case studies that
reported interhemispheric dissociations between lan-
guage production and comprehension tasks (Dongwook
et al., 2008; Jansen et al., 2006). Here we showed that,
even within a given experimental situation such as
sentence comprehension, the strongly left-lateralized
speech processing network may be dissected into a com-
plex combination of distinct patterns of asymmetry. Sur-
prisingly, these patterns allow dissociating even closely
located areas. For instance, the profile of asymmetry of
the mFG is similar, during the reading task, to that of the
fusiform area, but is uncorrelated with that of inferior
frontal cortex. On the contrary, the latter region colater-
alizes strongly with remote sites in superior temporal
and cingulate cortex. Thus, our results suggest that func-
tional lateralization relates to a mosaic of partially inde-
pendent left/right shifts, and results from a complex sum
of regional events rather than a single overall ‘‘domi-
nance’’ factor. The observed networks of long-range
colateralizations may also reflect structural connections.
For instance, the independent patterns of colateraliza-
tion respectively associated with the pSTS and the aSTS
appear to reflect fiber pathways that link the middle and
posterior part of the superior temporal region to dif-
ferent areas of the frontal
lobe in the monkey brain
(Petrides & Pandya, 1988).
Our results refine the recent claim of Cai, Lavidor,
Brysbaert, Paulignan, and Nazir (2008) and Hunter,
Brysbaert, and Knecht (2007), who suggested that hemi-
spheric dominance for spoken language production in
the frontal lobe plays a causal role in the lateralization
of the posterior reading system. Cai et al. (2008) based
their claim on the observation of a colateralization of
event-related potentials associated with orthographic
processing (occipito-temporal N170) with those associ-
ated with verb generation (late frontal negativity), in a
population of right-handed or left-handed subjects se-
lected for their strong lateralization either to the left or
to the right hemisphere in the latter task. Likewise, in a
similar population, Hunter et al. (2007) found a shift in
the optimal viewing position for reading to the hemifield
contralateral the hemisphere that was found dominant
(in frontal areas) for a verbal fluency task. In our pop-
ulation of normal right-handers, during reading we also
found a strong colateralization of the fusiform activation
with the mFG. However, there was no such collaterali-
zation with nearby inferior frontal or precentral sites,
therefore indicating that lateralization must be consid-
ered at a finer scale than at the lobe level. Furthermore,
the fronto-fusiform correlation vanished during the au-
ditory speech listening task, whereas the pSTS–fusiform
correlation remained very high (indeed it was the only
one shared by the reading and speech listening tasks;
see Table 1). These data suggest that the lateralization of
orthographic processes in the fusiform may be driven
much more strongly by the temporal lobe than by the
frontal lobe.
The tight degree of colateralization of the pSTS with
essentially all other language-related areas, especially
during reading (Table 1), suggests that it represents a
central node in the asymmetry of these subnetworks.
This central role could be a direct consequence of the
structural asymmetry which is already detectable prena-
tally in the planum temporale (Chi et al., 1977) and
superior temporal sulcus (Dubois et al., 2008). An early
asymmetry in the processing of speech sounds may
create a subtle initial bias that contributes, during the
development, to the establishment of a leftward asym-
metry at other levels of the language system (Tervaniemi
& Hugdahl, 2003; Bates & Roe, 2001).
Among the other possible determinants of the mosaic
of asymmetry, our data suggest that sex is not a crucial
one. We only observed a weak trend to a greater
leftward asymmetry in the inferior frontal area for men
(especially during speech listening) in an ROI approach,
yet this was not replicated in the voxel-based analysis.
This result is in accordance with a series of large-scale
and meta-analysis studies (Sommer, Aleman, Bouma, &
Kahn, 2004; Pujol, Deus, Losilla, & Capdevila, 1999), that
found no significant sex differences for language laterali-
zation at the population level across tasks, challenging
widespread beliefs on men/women functional brain dif-
ferences (Kimura, 1999; Shaywitz et al., 1995). This ab-
sence of sex effect was extended here to the left/right
cortical organization of mental arithmetic. However,
the lateralization of other numerical skills, such as arith-
metical fact retrieval or approximate nonsymbolic cal-
culation, should be explored further before concluding
that men and women use strictly similar networks during
arithmetic.
Recent results showed that many genes are expressed
asymmetrically early on in fetal development (Sun,
Pinel and Dehaene
63
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
f
r
o
m
D
h
o
t
w
t
n
p
o
:
a
/
d
/
e
m
d
i
f
t
r
o
p
m
r
c
h
.
s
p
i
l
d
v
i
e
r
e
r
c
c
t
.
h
m
a
i
r
e
d
.
u
c
o
o
m
c
/
n
j
a
o
r
c
t
i
n
c
/
e
a
-
p
r
d
t
i
2
c
2
l
1
e
-
4
p
8
d
1
f
9
/
3
2
8
2
4
/
1
1
1
/
o
4
c
8
n
/
1
2
7
0
0
6
9
9
1
2
1
1
5
1
/
8
4
j
o
p
c
d
n
.
b
2
y
0
g
0
u
9
e
.
s
t
2
o
1
n
1
8
0
4
8
.
S
p
e
d
p
f
e
m
b
y
b
e
g
r
u
2
e
0
2
s
3
t
/
j
f
/
.
.
t
.
o
n
1
8
M
a
y
2
0
2
1
Collura, Ruvolo, & Walsh, 2006), and that different cor-
tical areas, noticeably peri-sylvian regions, may be char-
acterized by different patterns of genetic expression
(Abrahams et al., 2007) which, for some genes, seem
specific to humans. These data indicate that the later-
alization of the widespread human language networks
is probably under various local genetic influences, per-
haps through a cascade of successive influences on
sulcal shape and connectivity patterns (Leonard, Eckert,
& Kuldau, 2006). Indeed, the present fMRI analysis is
part of a larger databasing effort for which fMRI, but also
behavioral, connectivity and genetic data are also col-
lected from hundreds of subjects (see Pinel et al., 2007).
A next step will therefore be to clarify to what extent the
patterns of collateralization reported here result from
structural constraints, and at which level (fiber tracks,
sulci, neural microstructures, or functional biases) do
genetic factors induce local hemispheric preferences in
regional brain organization.
Acknowledgments
We thank all the investigators at Service Hospitalier Fre´de´ric
Joliot and the NeuroSpin center for sharing fMRI scanning time
and subjects with us, and particularly A. D. Devauchelle, J. B.
Poline, and B. Thirion for supporting this database project. We
also thank the NUMBRA Network student Alex Lopez Rolon for
his assistance in this project.
Reprint requests should be sent to Philippe Pinel, INSERM, U562,
Cognitive Neuroimaging Unit, CEA/Saclay/Neurospin, Bat. 145,
91191 Gif-sur-Yvette, France, or via e-mail: philippe.pinel@cea.fr.
REFERENCES
Abrahams, B. S., Tentler, D., Perederiy, J. V., Oldham, M. C.,
Coppola, G., & Geschwind, D. H. (2007). Genome-wide
analyses of human perisylvian cerebral cortical patterning.
Proceedings of the National Academy of Sciences, U.S.A.,
104, 17849–17854.
Andresen, D. R., & Marsolek, C. J. (2005). Does a causal
relation exist between the functional hemispheric
asymmetries of visual processing subsystems? Brain and
Cognition, 59, 135–144.
Ansari, D., & Dhital, B. (2006). Age-related changes in the
activation of the intraparietal sulcus during nonsymbolic
magnitude processing: An event-related functional magnetic
resonance imaging study. Journal of Cognitive
Neuroscience, 18, 1820–1828.
Astafiev, S. V., Shulman, G. L., Stanley, C. M., Snyder, A. Z.,
Van Essen, D. C., & Corbetta, M. (2003). Functional
organization of human intraparietal and frontal cortex for
attending, looking, and pointing. Journal of Neuroscience,
23, 4689–4699.
Balsamo, L. M., Xu, B., & Gaillard, W. D. (2006). Language
lateralization and the role of the fusiform gyrus in
semantic processing in young children. Neuroimage, 31,
1306–1314.
Barth, H., La Mont, K., Lipton, J., & Spelke, E. (2005). Abstract
number and arithmetic in preschool children. Proceedings
of the National Academy of Sciences, U.S.A., 102,
14116–14121.
Bates, E., & Roe, K. (2001). Language development in
children with unilateral brain injury. In C. Nelson &
M. Luciana (Eds.), Handbook of developmental cognitive
neuroscience (pp. 281–307). Cambridge, MA: MIT Press.
Beauchamp, M. S., Argall, B. D., Bodurka, J., Duy, J. H., &
Martin, A. (2004). Unraveling multisensory integration:
Patchy organization within human STS multisensory
cortex. Nature Neuroscience, 7, 1190–1192.
Binder, J. R., Frost, J. A., Hammeke, T. A., Bellgowan, P. S. F.,
Springer, J. A., Kaufman, J. N., et al. (2000). Human
temporal lobe activation by speech and nonspeech
sounds. Cerebral Cortex, 10, 512–528.
Butterworth, B. (2005). The development of arithmetical
abilities. Journal of Child Psychology and Psychiatry, 46,
3–18.
Cai, Q., Lavidor, M., Brysbaert, M., Paulignan, Y., & Nazir, T. A.
(2008). Cerebral lateralization of frontal lobe language
processes and lateralization of the posterior visual word
processing system. Journal of Cognitive Neuroscience, 20,
672–681.
Cantlon, J. F., Libertus, M. E., Pinel, P., Dehaene, S.,
Brannon, E. M., & Pelphrey, K. A. (2007). Symbolic &
non-symbolic number in the developing brain.
Poster presented at the Cognitive Neuroscience Society,
New York.
Cappelletti, M., Butterworth, B., & Kopelman, M. (2001).
Spared numerical abilities in a case of semantic dementia.
Neuropsychologia, 39, 1224–1239.
Carey, S. (1998). Knowledge of number: Its evolution and
ontogeny. Science, 282, 641–642.
Catani, M., Jones, D. K., & Ffytche, D. H. (2005). Perisylvian
language networks of the human brain. Annals of
Neurology, 57, 8–16.
Chi, J., Dooling, E., & Gilles, F. (1977). Left–right asymmetries
of the temporal speech areas of the human fetus. Archives
of Neurology, 34, 346–348.
Chochon, F., Cohen, L., van de Moortele, P. F., & Dehaene, S.
(1999). Differential contributions of the left and right
inferior parietal lobules to number processing. Journal of
Cognitive Neuroscience, 11, 617–630.
Cohen, L., & Dehaene, S. (2004). Specialization within the
ventral stream: The case for the visual word form area.
Neuroimage, 22, 466–476.
Cohen, L., Dehaene, S., Chochon, F., Lehe´ricy, S., &
Naccache, L. (2000). Language and calculation within
the parietal lobe: A combined cognitive, anatomical
and fMRI study. Neuropsychologia, 38, 1426–1440.
Cohen, L., Jobert, A., Le Bihan, D., & Dehaene, S. (2004).
Distinct unimodal and multimodal regions for word
processing in the left temporal cortex. Neuroimage, 23,
1256–1270.
Cointepas, Y., Poupon, C., Maroy, R., Riviere, D., Le Bihan, D.,
& Mangin, J. F. (2003). A freely available Anatomist/
BrainVISA package for analysis of diffusion MR data
[Proceedings of the 9th HBM Scientific Meeting, New York,
USA]. Neuroimage, 19, S810.
Damasio, A. R., & Damasio, H. (1994). Cortical systems for
retrieval of concrete knowledge: The convergence zone
framework. In C. Koch & J. L. Davis (Eds.), Large-scale
neuronal theories of the brain (pp. 61–74). Cambridge, MA:
MIT Press.
Dehaene, S. (2007). Symbols and quantities in parietal
cortex: Elements of a mathematical theory of number
representation and manipulation. In P. Haggard &
Y. Rossetti (Eds.), Attention & performance: XXII.
Sensori-motor foundations of higher cognition
(pp. 527–574). Cambridge, MA: Harvard University Press.
Dehaene, S., & Cohen, L. (1995). Towards an anatomical and
functional model of number processing. Mathematical
Cognition, 1, 83–120.
64
Journal of Cognitive Neuroscience
Volume 22, Number 1
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
f
r
o
m
D
h
o
t
w
t
n
p
o
:
a
/
d
/
e
m
d
i
f
t
r
o
p
m
r
c
h
.
s
p
i
l
d
v
i
e
r
e
r
c
c
t
.
h
m
a
i
r
e
d
.
u
c
o
o
m
c
/
n
j
a
o
r
c
t
i
n
c
/
e
a
-
p
r
d
t
i
2
c
2
l
1
e
-
4
p
8
d
1
f
9
/
3
2
8
2
4
/
1
1
1
/
o
4
c
8
n
/
1
2
7
0
0
6
9
9
1
2
1
1
5
1
/
8
4
j
o
p
c
d
n
.
b
2
y
0
g
0
u
9
e
.
s
t
2
o
1
n
1
8
0
4
8
.
S
p
e
d
p
f
e
m
b
y
b
e
g
r
u
2
e
0
2
s
3
t
/
j
f
.
/
.
t
.
o
n
1
8
M
a
y
2
0
2
1
Dehaene, S., Izard, V., Spelke, E., & Pica, P. (2008). Log or
linear? Distinct intuitions of the number scale in Western
and Amazonian indigene cultures. Science, 320, 1217–1220.
Dehaene, S., Piazza, M., Pinel, P., & Cohen, L. (2003). Three
parietal circuits for number processing. Cognitive
Neuropsychology, 20, 487–506.
Dehaene-Lambertz, G., Dehaene, D., & Hertz-Pannier, L.
(2004). Functional neuroimaging of speech perception in
infants. Science, 298, 2013–2015.
Delazer, M., Domahs, F., Bartha, L., Brenneis, C., Lochy, A.,
Trieb, T., et al. (2003). Learning complex arithmetic—An
fMRI study. Cognitive Brain Research, 18, 76–88.
Dongwook, L., Swanson, S. J., Sabsevitz, D. S., Hammeke, A.,
Winstanley, F. S., Possing, E. T., et al. (2008). Functional
MRI and Wada studies in patients with interhemispheric
dissociation of language functions. Epilepsy & Behavior, 13,
350–356.
Dubois, J., Benders, M., Cachia, A., Lazeyras, F., Ha-Vinh
Leuchter, R., Sizonenko, S. V., et al. (2008). Mapping the
early cortical folding process in the preterm newborn brain.
Cerebral Cortex, 18, 1444–1454.
Eger, E., Sterzer, P., Russ, M. O., Giraud, A. L., & Kleinschmidt, A.
(2003). A supramodal number representation in human
intraparietal cortex. Neuron, 37, 719–725.
Geary, D. C., Hoard, M. K., Byrd-Craven, J., & DeSoto, C. M.
(2004). Strategy choices in simple and complex addition:
Contributions of working memory and counting knowledge
for children with mathematical disability. Journal of
Experimental Child Psychology, 88, 121–151.
Geschwind, N., & Levitsky, W. (1968). Left–right asymmetry in
temporal speech region. Science, 161, 186–187.
Gordon, P. (2004). Numerical cognition without words:
Evidence from Amazonia. Science, 306, 496–499.
Hickok, G., & Poeppel, D. (2000). Towards a functional
neuroanatomy of speech perception. Trends in Cognitive
Sciences, 4, 131–138.
Hubbard, E. M., Piazza, M., Pinel, P., & Dehaene, S. (2005).
Interactions between number and space in parietal cortex.
Nature Reviews Neuroscience, 6, 435–448.
Hunter, Z. R., Brysbaert, M., & Knecht, S. (2007). Foveal word
reading requires interhemispheric communication. Journal
of Cognitive Neuroscience, 19, 1373–1387.
Izard, V., Dehaene-Lambertz, G., & Dehaene, S. (2008). Distinct
cerebral pathways for object identity and number in
human infants. PLoS Biology, 6, e11. doi:10.1371/journal.
pbio.0060011.
Lefevre, J. A. (1996). Selection of procedures in mental
addition: Reassessing the problem size effect in adults.
Journal of Experimental Psychology: Learning, Memory,
and Cognition, 22, 216–230.
Leonard, C. M., Eckert, M. A., & Kuldau, J. M. (2006). Exploiting
human anatomical variability as a link between genome
and cognome. Genes, Brain, and Behavior, 5, 64–77.
Lindenberg, R., Fangerau, H., & Seitz, R. J. (2007). ‘‘Broca’s
area’’ as a collective term? Brain and Language, 102, 22–29.
Lucchelli, F., & De Renzi, E. (1993). Primary dyscalculia after a
medial frontal lesion of the left hemisphere. Journal of
Neurology and Psychiatry, 56, 304–307.
McCrink, K., & Wynn, K. (2004). Large-number addition and
subtraction by 9-month-old infants. Psychological Science,
15, 776–781.
Mechelli, A., Crinion, J. T., Long, S., Friston, K. J., Lambon
Ralph, M. A., Patterson, K., et al. (2005). Dissociating reading
processes on the basis of neuronal interactions. Journal of
Cognitive Neuroscience, 17, 1–13.
Menon, V., Rivera, S. M., White, C. D., Eliez, G. H., Glover,
G. H., & Reiss, A. L. (2000). Functional optimization of
arithmetic processing in perfect performers. Cognitive
Brain Research, 9, 343–345.
Mills, D. L., Coffey-Corina, S., & Neville, H. J. (1997). Language
comprehension and cerebral specialization from 13 to
30 months. Developmental Neuropsychology, 13, 397–445.
Nieder, A., Diester, L., & Tudusciuc, O. (2006). Temporal
and spatial enumeration processes in the primate parietal
cortex. Science, 313, 1431–1435.
Noe¨l, M. P., Seron, X., & Trovarelli, F. (2004). Working memory
as a predictor of addition skills and addition strategies in
children. Current Psychology of Cognition, 22, 3–25.
Owen, O. M., Stern, C. E., Look, R. B., Tracey, I., Rosen, B. R., &
Petrides, M. (1998). Functional organization of spatial
and nonspatial working memory processing within the
human lateral frontal cortex. Proceedings of the National
Academy of Sciences, U.S.A., 95, 7721–7726.
Pen˜a, M., Maki, A., Kovacic´, D., Dehaene-Lambertz, G.,
Koizumi, H., Bouquet, F., et al. (2003). Sounds and silence:
An optical topography study of language recognition at
birth. Proceedings of the National Academy of Sciences,
U.S.A., 100, 11702–11705.
Petrides, M., & Pandya, D. N. (1988). Association fiber pathways
to the frontal cortex from the superior temporal region in
the rhesus monkey. Journal of Comparative Neurology,
273, 52–66.
Jackson, M., & Warrington, E. K. (1986). Arithmetic skills in
Piazza, M., Izard, V., Pinel, P., Le Bihan, D., & Dehaene, S.
patients with unilateral cerebral lesions. Cortex, 22, 611–620.
Jansen, A., Deppe, M., Schwindt, W., Mohammadi, S.,
Sehlmeyer, C., & Knecht, S. (2006). Interhemispheric
dissociation of language regions in a healthy subject. Archive
of Neurology, 63, 1344–1346.
Jellison, B. J., Field, A. S., Medow, J., Lazar, M., Salamat, M. S., &
Alexander, A. L. (2004). Diffusion tensor imaging of cerebral
white matter: A pictorial review of physics, fiber tract
anatomy, and tumor imaging patterns. American Journal
of Neuroradiology, 25, 356–369.
Kimura, D. (1999). Sex and cognition. Cambridge, MA:
MIT Press.
Klingberg, T. (2006). Development of a superior
frontal–intraparietal network for visuo-spatial working
memory. Neuropsychologia, 44, 2171–2177.
Kosslyn, S. M., Koenig, O., Barrett, A., Cave, C. B., Tang, J., &
Gabrieli, J. D. E. (1989). Evidence for two types of spatial
representations: Hemispheric specialization for categorical
and coordinate relations. Journal of Experimental
Psychology: Human Perception and Performance, 15,
723–735.
(2004). Tuning curves for approximate numerosity in the
human intraparietal sulcus. Neuron, 44, 547–555.
Piazza, M., Mechelli, A., Price, C. J., & Butterworth, B.
(2006). Exact and approximate judgements of visual and
auditory numerosity: An fMRI study. Brain Research,
1106, 177–188.
Piazza, M., Pinel, P., Le Bihan, D., & Dehaene, S. (2007). A
magnitude code common to numerosities and number
symbols in human intraparietal cortex. Neuron, 2, 293–305.
Pica, P., Lemer, C., Izard, V., & Dehaene, S. (2004). Exact and
approximate arithmetic in an Amazonian indigene group.
Science, 306, 499–503.
Pinel, P., Dehaene, S., Riviere, D., & Le Bihan, D. (2001).
Modulation of parietal activation by semantic distance in a
number comparison task. Neuroimage, 14, 1013–1026.
Pinel, P., Piazza, M., Le Bihan, D., & Dehaene, S. (2004).
Distributed and overlapping cerebral representations of
number, size, and luminance during comparative judgments.
Neuron, 41, 983–993.
Pinel, P., Thirion, B., Meriaux, S., Jobert, A., Serres, J., Le Bihan,
D., et al. (2007). Fast reproducible identification and
Pinel and Dehaene
65
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
f
r
o
m
D
h
o
t
w
t
n
p
o
:
a
/
d
/
e
m
d
i
f
t
r
o
p
m
r
c
h
.
s
p
i
l
d
v
i
e
r
e
r
c
c
t
.
h
m
a
i
r
e
d
.
u
c
o
o
m
c
/
n
j
a
o
r
c
t
i
n
c
/
e
a
-
p
r
d
t
i
2
c
2
l
1
e
-
4
p
8
d
1
f
9
/
3
2
8
2
4
/
1
1
1
/
o
4
c
8
n
/
1
2
7
0
0
6
9
9
1
2
1
1
5
1
/
8
4
j
o
p
c
d
n
.
b
2
y
0
g
0
u
9
e
.
s
t
2
o
1
n
1
8
0
4
8
.
S
p
e
d
p
f
e
m
b
y
b
e
g
r
u
2
e
0
2
s
3
t
/
j
/
f
.
.
.
t
o
n
1
8
M
a
y
2
0
2
1
large-scale databasing of individual functional cognitive
networks. BMC Neuroscience, 8, 91.
Pujol, J., Deus, J., Losilla, J. M., & Capdevila, A. (1999). Cerebral
lateralization of language in normal left-handed people
studied by functional MRI. Neurology, 52, 1038–1043.
Rivera, S. M., Reiss, A. L., Eckert, M. A., & Menon, V. (2005).
Developmental changes in mental arithmetic: Evidence for
increased functional specialization in the left inferior parietal
cortex. Cerebral Cortex, 15, 1779–1790.
Rubinsten, O., Henik, A., Berger, A., & Shahar-Shalev, S. (2002).
The development of internal representations of magnitude
and their association with Arabic numerals. Journal of
Experimental Child Psychology, 81, 74–92.
Schmahmann, D. D., Pandya, D. N., Wang, R., Dai, G.,
D’Arceuil, H. E., de Crespigny, A. J., et al. (2007). Association
fibre pathways of the brain: Parallel observations from
diffusion spectrum imaging and autoradiography. Brain,
130, 630–653.
Seghier, M. (2008). Laterality index in functional MRI:
Methodological issues. Magnetic Resonance Imaging, 26,
594–601.
Semenza, C., Delazer, M., Bertella, L., Grana`, A., Mori, I., Conti,
F. M., et al. (2006). Is math lateralised on the same side as
language? Right hemisphere aphasia and mathematical
abilities. Neuroscience Letters, 406, 285–288.
Shaywitz, B. A., Shaywitz, S. E., Pugh, K. R., Constable, R. T.,
Skudlarski, P., Fulbright, R. K., et al. (1995). Sex differences
in the functional organisation of the brain for language.
Nature, 373, 607–609.
Siegler, R. S., & Booth, J. L. (2004). Development of numerical
estimation in young children. Child Development, 75,
428–444.
Simon, O., Kherif, F., Flandin, G., Poline, J. B., Riviere, D.,
Mangin, J. F., et al. (2004). Automatized clustering and
functional geometry of human parietofrontal networks for
language, space, and number. Neuroimage, 23, 1192–1202.
Simon, O., Mangin, J. F., Cohen, L., Le Bihan, D., & Dehaene, S.
(2002). Topographical layout of hand, eye, calculation,
and language-related areas in the human parietal lobe.
Neuron, 33, 475–487.
calculation processes: Impact of number size on the cerebral
circuits for exact and approximate calculation. Brain, 123,
2240–2255.
Sun, T., Collura, R. V., Ruvolo, M., & Walsh, C. A. (2006).
Genomic and evolutionary analyses of asymmetrically
expressed genes in human fetal left and right cerebral
cortex. Cerebral Cortex, 16(Suppl. 1), i18–i25.
Temple, A., & Posner, E. (1998). Brain mechanisms of quantity
are similar in 5-year-old children and adults. Proceedings of
the National Academy of Sciences, U.S.A., 95, 7836–7841.
Tervaniemi, M., & Hugdahl, K. (2003). Lateralization of
auditory-cortex function. Brain Research Review, 43,
231–246.
Toga, A. W., & Thompson, P. M. (2003). Mapping brain
asymmetry. Nature Reviews Neuroscience, 4, 37–48.
Vandenberghe, R., Price, C., Wise, R., Josephs, O., &
Frackowiak, R. (1996). Functional anatomy of a common
semantic system for words and pictures. Nature, 383,
254–256.
Vandenbulcke, M., Peeters, R., Dupont, P., Van Hecke, P., &
Vandenberghe, R. (2007). Word reading and posterior
temporal dysfunction in amnesic mild cognitive impairment.
Cerebral Cortex, 17, 542–551.
Varley, R. A., Klessinger, N. J., Romanowski, C. A., & Siegal, M.
(2005). Agrammatic but numerate. Proceedings of the
National Academy of Sciences, U.S.A., 102, 3519–3524.
Vauclair, J., Yamazaki, Y., & Gu¨ntu¨rku¨n, O. (2006). The study of
hemispheric specialization for categorical and coordinate
spatial relations in animals. Neuropsychologia, 44,
1524–1534.
Venkatraman, V., Ansari, D., & Chee, M. W. (2005). Neural
correlates of symbolic and nonsymbolic arithmetic.
Neuropsychologia, 43, 744–753.
Venkatraman, V., Siong, S. C., Chee, M. W., & Ansari, D. (2006).
Effect of language switching on arithmetic: A bilingual fMRI
study. Journal of Cognitive Neuroscience, 18, 64–74.
Verguts, T., & Fias, W. (2004). Representation of number in
animals and humans: A neural model. Journal of Cognitive
Neuroscience, 16, 1493–1504.
Wynn, K. (1992). Addition and subtraction by human infants.
Sommer, I. E. C., Aleman, A., Bouma, A., & Kahn, R. S. (2004).
Nature, 358, 749–750.
Do women really have more bilateral language
representation than men? A meta-analysis of functional
imaging studies. Brain, 127, 1845–1852.
Stanescu-Cosson, R., Pinel, P., van de Moortele, P. F., Le Bihan,
D., Cohen, L., & Dehaene, S. (2000). Cerebral bases of
Zamarian, L., Karner, E., Benke, T., Donnemiller, E., &
Delazer, M. (2006). Knowing 7 (cid:2) 8, but not the meaning
of ‘‘elephant’’: Evidence for the dissociation between
numerical and non-numerical semantic knowledge.
Neuropsychologia, 44, 1708–1723.
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
f
r
o
m
D
h
o
t
w
t
n
p
o
:
a
/
d
/
e
m
d
i
f
t
r
o
p
m
r
c
h
.
s
p
i
l
d
v
i
e
r
e
r
c
c
t
.
h
m
a
i
r
e
d
.
u
c
o
o
m
c
/
n
j
a
o
r
c
t
i
n
c
/
e
a
-
p
r
d
t
i
2
c
2
l
1
e
-
4
p
8
d
1
f
9
/
3
2
8
2
4
/
1
1
1
/
o
4
c
8
n
/
1
2
7
0
0
6
9
9
1
2
1
1
5
1
/
8
4
j
o
p
c
d
n
.
b
2
y
0
g
0
u
9
e
.
s
t
2
o
1
n
1
8
0
4
8
.
S
p
e
d
p
f
e
m
b
y
b
e
g
r
u
2
e
0
2
s
3
t
/
j
.
f
t
.
.
/
o
n
1
8
M
a
y
2
0
2
1
66
Journal of Cognitive Neuroscience
Volume 22, Number 1