Artificial Metamorphosis:
Evolutionary Design of
Transforming, Soft-Bodied Robots
Michał Joachimczak*,**
Reiji Suzuki**
Takaya Arita**
Nagoya University
Palabras clave
Metamorphosis, artificial development,
soft robotics, body-brain coevolution,
automated design, evolutionary algorithm,
artificial life
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
Abstract We show how the concept of metamorphosis, together
with a biologically inspired model of multicellular development, poder
be used to evolve soft-bodied robots that are adapted to two very
different tasks, such as being able to move in an aquatic and in a
terrestrial environment. Each evolved solution defines two pairs of
morphologies and controllers, together with a process of transforming
one pair into the other. Animats develop from a single cell and grow
through cellular divisions and deaths until they reach an initial larval
form adapted to a first environment. To obtain the adult form adapted
to a second environment, the larva undergoes metamorphosis, durante
which new cells are added or removed and its controller is modified.
En tono rimbombante, our approach assumes nothing about what morphologies
or methods of locomotion are preferred. En cambio, it successfully
searches the vast space of possible designs and comes up with
complex, surprising, lifelike solutions that are reminiscent of
amphibian metamorphosis. We analyze obtained solutions and
investigate whether the morphological changes during metamorphosis
are indeed adaptive. We then compare the effectiveness of three different
types of selective pressures used to evolve metamorphic individuals.
Finalmente, we investigate potential advantages of using metamorphosis
to automatically produce soft-bodied designs by comparing the
performance of metamorphic individuals with their specialized
counterparts and designs that are robust to both environments.
/
/
/
2
2
3
2
7
1
1
6
6
6
3
0
1
a
r
t
yo
/
_
a
_
0
0
2
0
7
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
1 Introducción
Metamorphosis is a process during which an organism that has already finished its embryonic
growth undergoes a relatively fast and considerable modification of its body. It is usually accompa-
nied by a change of the environment the organism lives in. While the processes through which these
modifications occur are the very same as the ones through which multicellular development occurs,
metamorphosis is considered a distinct phenomenon due to the scope of the changes and the fact
that it effectively creates a complex life cycle with two or more phenotypes during the animalʼs
lifetime. Familiar and striking examples include amphibians (such as frogs) and insects (como
* Contact author.
** Department of Complex Systems Science, Graduate School of Information Science, Nagoya University, Furo-cho, Chikusa-ku, Nagoya
464-8601, Japón. Correo electrónico: mjoach@alife.cs.is.nagoya-u.ac.jp (M.J.); reiji@nagoya-u.jp (R.S.); arita@nagoya-u.jp (EJÉRCITO DE RESERVA.)
© 2016 Instituto de Tecnología de Massachusetts. Artificial Life 22: 271–298 (2016) doi:10.1162/ARTL_a_00207
Publicado bajo una atribución Creative Commons
3.0 no portado (CC POR 3.0) licencia.
METRO. Joachimczak et al. Artificial Metamorphosis: Evolutionary Design of Transforming, Soft-Bodied Robots
butterflies). Frogs begin their lives in an aquatic environment and develop first into a fishlike larval
stage (a tadpole). Matured tadpoles then undergo metamorphosis involving changes such as the loss
(reabsorption) of gills, tail, and lateral-line system and the gradual growth of jaw and limbs. El
modifications allow them to switch to a terrestrial habitat. A butterfly, por otro lado, develops
after hatching into a caterpillar, a soft-bodied, elongated larva that typically feeds on leaves, to later
transform into a winged imago1 that typically feeds on nectar.
Despite the additional developmental complexity created by metamorphosis, it is extremely com-
mon in the animal kingdom: Estimates suggest that just the metamorphosing insects amount to up
a 65% of all animal species [11], while 80–90% of insect species themselves undergo metamorpho-
hermana [14]. The enormous success of this reproductive strategy suggests that there is a strong evolu-
tionary advantage to having a complex life cycle. And while in the case of amphibians
metamorphosis can be explained by their aquatic evolutionary ancestry, in the case of insects, ambos
genetic and paleontological data suggest that early insects employed direct development (dónde
juvenile stages resemble the adult form). It has thus been suggested that it was the very emergence
of metamorphosis that sparked the extremely successful insect radiation [38, 28].
Por qué, sin embargo, is undergoing metamorphosis during oneʼs life cycle beneficial? The main expla-
nation of its evolutionary advantage is that it allows larvae and adults to occupy different ecological
niches. By relying on different food resources or occupying different habitats, larvae avoid the cost
of having to compete with adults of their own species [38]. And while there certainly must be a cost
of having two distinct phenotypes encoded in a single genome, the genetic and chemical machinery
required to assemble them is the same: What changes between the growth phases is the regulation
that controls which genes are active and what the rate of their transcription is [41]. De este modo, a pesar de
having two phenotypes requires more complex control of development than having one, each meta-
morphosis stage does not emerge independently, but results from an evolutionary process special-
izing preexisting developmental stages. While the exact molecular mechanisms of metamorphosis are
an active area of research, the emerging science of evo-devo has already provided us with a good
glimpse of how plastic animal forms are when evolution acts on parts of the genomes that control
desarrollo (ver, p.ej., [4]).
En este trabajo, we aim to investigate whether some of the benefits that metamorphosis provides to
evolving animal forms can also contribute to the domain of synthetic evolution of robotic morphol-
ojos. The very problem of evolving shape or, more typically, coevolving body and brain of an ani-
mat has been a staple of the artificial life field ever since Karl Simsʼ groundbreaking work in 1994
[34]. The classic approach is to evolve designs and evaluate each of them by measuring a robotʼs
(animatʼs) performance on a task it is evolved for, such as ability to move in a given environment.
Además, a phenotype is typically indirectly encoded in a genotype, through some abstraction of
desarrollo. Por último, sin embargo, a single genome encodes a single phenotype. What we thus de-
cided to investigate in this article is to what extent, by applying appropriate evolutionary pressures,
we can induce specialization of developmental stages. Por lo tanto, we investigate here a scenario in
which a single genome no longer encodes one phenotype but two, together with a method of trans-
forming one into another.
It is easy to see how such robotic designs could prove themselves extremely useful: Whenever
animats are required to operate in diverse environments during their lifetimes, they could switch
their form when transferring from one environment to another. Por ejemplo, a rescue robot
launched for a mission from sea could swim to shore, metamorphose into its terrestrial form,
and continue its mission on its newly grown legs. Por otro lado, from the point of view of
automatic design, the evolution of metamorphic solutions means obtaining two different designs
with a single evolutionary run. Such an approach would likely be of limited use if the designs were
to be entirely unrelated, as it would simply make the evolutionary search harder. Sin embargo, in prac-
tical scenarios this would rarely be the case, as any two robot designs will share many features. Y
as the science of evo-devo reveals [4], evolution creates its “endless forms most beautiful” by
1 Imago is the general name of the adult stage of insect development.
272
Artificial Life Volume 22, Número 3
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
2
2
3
2
7
1
1
6
6
6
3
0
1
a
r
t
yo
/
_
a
_
0
0
2
0
7
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
METRO. Joachimczak et al. Artificial Metamorphosis: Evolutionary Design of Transforming, Soft-Bodied Robots
actually reusing a limited number of body plans and only tweaking the genetic machinery that is
largely shared by both vertebrates and invertebrates. Por eso, if only we can make artificial evolution
replicate this phenomenon, evolving multiple phenotypes in a single evolutionary run through the
use of metamorphosis could be easier than attempting to evolve them separately. While this intro-
duces heavy constraints on what kinds of morphologies can be obtained through evolutionary
buscar, if the solutions are to share some of their structure, the constraints can work in favor of
evolutionary search.
The idea of taking inspiration in metamorphosis to improve evolutionary search is not new.
Bongard [1] has shown how a predefined morphological change during a legged robotʼs lifetime
(progressive extension of its legs) occurring during early evolutionary stages facilitated evolution
of higher-quality gaits. An evolutionary search of gaits for a long-legged robot is likely to be suscep-
tible to the bootstrapping problem [22], where initial generations will produce robots that fall.
Por eso, starting with a short-legged form that is not prone to falling effectively guides evolutionary
search towards the right regions of the search space where synchronized leg actuation emerges. Como
the author notes, the progressive change in morphology scaffolds behavior acquisition. While scaf-
folding techniques are well known as being helpful in guiding both biological and artificial learning
procesos [42, 1], our use of metamorphosis in this work has a very different motivation. Instead of
using a predefined metamorphosis process as a scaffolding for the search process, we are interested
in whether metamorphosis can evolve if appropriate evolutionary pressures are applied and whether
it allows obtaining two, self-transforming phenotypes in a single evolutionary run.
In another metamorphosis-related work, Corucci et al. [7] took metamorphosis as an inspiration
for a method of designing underwater robots. The authors explored a space of parametrized designs
(p.ej., having different length or stiffness of appendages) with novelty search [19] to find robots that
display possibly different behaviors while being close to each other in the morphological space. El
reasoning was that pairs of such designs make good candidates for being implemented as a robot
that changes some of its morphological properties on the fly, in order to induce new types of
comportamiento. While some of their motivation is shared with this work, a saber, the goal of producing
robots that change morphology depending on the problem, the approach of Corucci et al. is very
diferente. It assumes a fixed, parametrized morphology and does not deal with the metamorphosis
sí mismo: It is implicit, understood as having two related robotic morphologies that produce very dif-
ferent motion patterns.
An approach much closer to ours can be found in the work of Tufte [39], who used metamor-
phosis to evolve simple digital circuits implemented in a cellular automaton (California). The 2D CA would
grow a circuit starting from a single cell, and the growth rules were evolved so that a circuit would
maximize the number of flip-flops in the 1 state at the larval stage and make them perform as a coun-
ter in the adult stage. While Tufteʼs work seems to employ a similar setup, to our knowledge our work
is the first attempt at applying the idea of metamorphosis to evolve actual self-transforming
morphologies of robots.
As metamorphosis is an aspect of multicellular development, in our approach we employ artificial
embryogenesis to construct animat forms from hundreds of cells through the processes of cellular
division and death. In the next two sections we describe our developmental model. Then we show
how the concept of metamorphosis can enhance artificial development by allowing an evolutionary
algorithm to automatically produce solutions (aquí, soft robots) that can take two potentially very
different forms, each adapted to its target environment. En tono rimbombante, one form can transform into
otro, offering the exciting potential of automatically designing robots that could efficiently operate
in radically different environments and change their form on demand.
2 Growing Animats with Artificial Development
The field of artificial embryogeny, to which this work belongs, attempts to capture the seemingly
endless capability of nature to generate forms by attempting to replicate key properties of development
Artificial Life Volume 22, Número 3
273
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
2
2
3
2
7
1
1
6
6
6
3
0
1
a
r
t
yo
/
_
a
_
0
0
2
0
7
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
METRO. Joachimczak et al. Artificial Metamorphosis: Evolutionary Design of Transforming, Soft-Bodied Robots
in silico. This typically involves bio-inspired construction processes in which a structure (como una
robotʼs body) is progressively built from smaller elements. Depending on the chosen level of abstrac-
ción, this may involve elements such as rods [18], primitives and joints [34, 24], or artificial cells, as in
the case of the system employed by us and related ones [9, 10, 29, 2]. Self-assembly from higher-level
components such as blocks and joints has been repeatedly demonstrated to be an effective way to
generate interesting robotic designs. The reliance on high-level components makes it, sin embargo, solo
loosely reminiscent of biological development and its evolution. Por eso, in our line of work, we aim to
explore the potential and scalability of a much more biologically oriented fine-grained artificial devel-
opment, where morphologies are assembled from large numbers (hundreds, thousands) of cells, cada
making independent decisions about their fate and interacting through simulated physics. So far we
have demonstrated how this approach allows us to evolve a rich variety of complex soft-bodied
animats and were surprised to observe how higher-level structures, such as simple appendages,
emerge during evolution and function as legs or fins [15].
In the following sections, we describe the artificial embryogeny system that we employ. Its capa-
bility to evolve metamorphic individuals is a straightforward extension of the work we have introduced
en [15]. Generally, the design of the system came from the desire shared among many artificial life
approaches (and multi-agent systems in particular) of allowing complexity to emerge from a set of
simple rules. Sin embargo, finding simple sets of rules that allow complex phenomena to emerge is
not an easy task and is a very counterintuitive one. Después de todo, it is the very definition of emergence
that behavior of lower-level entities leads to a higher-level behavior that would be difficult to predict.
Por eso, the evolutionary approach has been long thought to be a promising method of discovering
simple rules that can lead to self-organization. Having this in mind, we designed our developmental
system to rely on possibly simple laws that govern the behavior of cells during development, mientras
providing a certain minimum level of richness of their interactions in the form of a simulated physical
ambiente. While using artificial development to simulate growth of multicellular structures neces-
sitates a level of unavoidable complexity, whenever we could, we attempted to keep our approach
simple by avoiding features that are not needed to obtain desired results.
As is common among developmental systems, the growth of a virtual embryo in our system
begins with a single cell and proceeds through subsequent cellular divisions and deaths (apoptosis).
The fate of each cell is determined by the same control mechanism, a simple abstraction of the gene
regulatory network (GRN) in the form of a feed-forward neural network. All cells are controlled by
the same network, yet will act differently, as the external signals that are fed to the inputs of the
network depend on their (potentially changing) position in the growing embryo, as well as signals
output by other cells. Por último, the purpose of artificial development is to produce nontrivial mor-
phologies that can then be used as templates for robots and evaluated for their performance in a
given task.
En particular, in our approach we focus on generating morphologies for robots that are soft-bodied.
Soft robotics is a very recent and rapidly developing branch of robotics focused on creating elastic
artefacts that can reshape themselves in order to generate gaits or navigate tight spaces (p.ej., en orden
to crawl through a small opening). Ideas for useful morphologies and methods of actuation are being
continually explored, both in simulations (ver, p.ej., [5, 13, 23, 25, 33, 40]) and in physical implementa-
ciones (p.ej., [3, 12, 32, 36, 37]). Given that this area of engineering is still underexplored, we believe that
an evolutionary approach, free from preconceived notions of a human designer, can provide us with
original and inspiring designs. As the fine-grained developmental approach we employ does not
assume the use of predefined building blocks and simply builds arbitrary morphologies from a mass
of cells, es, in principle, well aligned with the goal of automatic design of inventive soft robots.
In contrast with the version introduced in the original article [15], we have configured the system
in a way that would prioritize simplicity over biological plausibility. This meant, among other things,
allowing for only non-recurrent gene regulatory networks, sigmoidal-only gene activation functions,
and a simplified mechanism of actuation. We would like to note, sin embargo, that we were able to
obtain similar results with the original version of the model (recurrent GRNs); we simplified it
out of our desire to show a minimal system. As this also meant a reduced search space, we were
274
Artificial Life Volume 22, Número 3
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
2
2
3
2
7
1
1
6
6
6
3
0
1
a
r
t
yo
/
_
a
_
0
0
2
0
7
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
METRO. Joachimczak et al. Artificial Metamorphosis: Evolutionary Design of Transforming, Soft-Bodied Robots
able to obtain high-quality solutions more consistently. Finalmente, a minimal design of the developmen-
tal system in use suggests that obtained results can be expected to be replicable with other devel-
opmental systems. En efecto, we think that the results in this article are indicative of metamorphosis
being fairly easy to evolve in developmental systems in general.
The evolving networks that control cellular behavior during development are based on the
MultiNEAT library [6], an implementation of the NEAT evolutionary algorithm [35]. We used a signed
sigmoid as the default activation function, and kept most of the settings at their default values, con el
link to the library parameter file provided in [6].
2.1 Physics of Development
We assume that development takes place in a continuous 2D space, where cells are represented as
disks and undergo elastic collisions simulated with springs that connect them. A cellʼs physical state
is defined by its position, its velocity, and an orientation vector that determines the direction of
división. For the sake of simplicity, in the discussed experiments, all cells have uniform size and
mass. Springs connect only the nearest neighbors and are determined dynamically, as the embryo
grows, with the resting length set to the sum of two neighboring cellsʼ radii. Más precisamente, we use
Delaunay triangulation to determine the connectivity between cells and then remove links longer
than 150% of a cellʼs diameter. As this may result in a disjoint structure, a long spring is removed
only if some other path between the two nodes exists, thus preventing fragmentation of a grow-
ing embryo. To save some computational time, the neighborhood relation was recalculated every
10 steps of the physics simulation.
2.2 Morphogens
Morphogen gradients (both maternal and self-produced) have long been known to play a funda-
mental role in the developmental process and, En particular, in establishing the basic body plan
[4]. Además, given that the networks governing cell behavior in the presented experiments
are stateless, an environmental signal is necessary to allow cells to differentiate their behavior. Como
a simple mechanism that substitutes for the maternal gradients present during development, tenemos
provided the X and Y coordinates as inputs to every cell. Además, as a simple mechanism that
substitutes for the morphogens produced by cells, the control network has two morphogen outputs
and two associated morphogen inputs. For any given cell, the activation of the latter is set to be an
average of the corresponding morphogen outputs of its neighbors (see summary in Table 1).
2.3 Cell Division and Death
All cells are bound to divide with each subsequent update of the control network unless the output
interpreted as an inhibitor of division has activation value above 0. Además, the division is al-
lowed to occur if and only if the space in the direction of the division is not occupied already by
other cells. Although our elastic physics of development was designed to handle cells pushing others
away as the embryo grows, we have found that constraining divisions produces fitter and more in-
teresting animats (ver [15] for comparison and discussion).
The newly created cell is placed next to the original cell in the direction determined by the di-
vision angle output. The angle is determined at the moment of division and is relative to the mean
angle of the neighborsʼ orientation vectors (ver tabla 1). Unless the value of the division angle out-
put in cells is different from zero, all will simply divide in the same direction.
Apoptosis (cell death) occurs whenever the state of associated network output is found to be
above zero and leads to the cell being removed from the embryo.
We allowed for a maximum of 256 cells in the embryo. The limit was hard, eso es, cells would
stop dividing after the limit was reached. Only some of the individuals would, sin embargo, reach the
maximum. Además, in order to limit the occurrence of wasteful solutions in which cells con-
tinuously divide and die, we penalized individuals that had created more than 1024 cells during their
development by multiplying their fitness value by 0.1.
Artificial Life Volume 22, Número 3
275
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
2
2
3
2
7
1
1
6
6
6
3
0
1
a
r
t
yo
/
_
a
_
0
0
2
0
7
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
METRO. Joachimczak et al. Artificial Metamorphosis: Evolutionary Design of Transforming, Soft-Bodied Robots
Mesa 1. Summary of inputs and outputs of the control network. Each cell has a copy of the same network, but receives
different signals to its inputs.
Tipo
Input
Nombre
Descripción
Time
X position
Y position
Linearly scales from 0 a 1 until the final developmental step is reached.
Horizontal coordinate of physical position of the cell during development.
Vertical coordinate of physical position of the cell during development.
Neighborsʼ morphogen 1
Average value of morphogen output 1 of neighboring cells.
Neighborsʼ morphogen 2
Average value of morphogen output 2 of neighboring cells.
Bias
Fixed value 1.
Output
Inhibit division
Prevents divisions of the cell if above 0.
Relative division angle
Determines the angle at which the cell will divide and its future orientation
vector. Output value is multiplied by k and interpreted as a relative angle
from −k to k. The final division angle is relative to the mean angle of
neighboring cellsʼ orientation.
Die
If above 0, the cell is removed from the embryo.
Morphogen 1
The state of this output can be indirectly accessed by the cellʼs neighbors.
Morphogen 2
Same as above.
Oscillation period
The value of this output at the end of development is used to determine
the frequency of contractions of springs attached to the cell.
Oscillation phase shift
The value of this output at the end of development is scaled to the range
(−k, k) and determines the phase shift of contractions of springs attached
to this cell.
2.4 Soft-Bodied Locomotion
Although the animatʼs representation during development is similar to its representation during the
locomotion stage, the stages are separated. Both the growing embryo and the fully grown animat are
represented as a spring-mass system and simulated using the same physics engine, but their physical
properties and the rules that govern their reshaping are different: Development occurs without grav-
idad, in an environment with high spring damping coefficient (simulating a viscous fluid), and involves
continuous rearrangements of the body: Cells are created and removed and can change their neigh-
bors. During the locomotion stage, the morphology that emerged through development is assumed
to be final and is evaluated for its performance in the target environment (which may or may not
include gravity). Only elastic changes are allowed (see example in Figure 1).
The locomoting animat is represented as a spring-mass system with point masses located at the
final positions of the centers of the embryoʼs cells (Figure 1e), and springs forming a triangular
mesh. The springs that connect outer cells in the embryo define the final body shape, mientras que la
internal structure of the body is fully triangulated with Delaunay triangulation. This works as a
simple approximation of a body made from an elastic material. As this approach can and sometimes
276
Artificial Life Volume 22, Número 3
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
2
2
3
2
7
1
1
6
6
6
3
0
1
a
r
t
yo
/
_
a
_
0
0
2
0
7
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
METRO. Joachimczak et al. Artificial Metamorphosis: Evolutionary Design of Transforming, Soft-Bodied Robots
Cifra 1. An example of a developmental process leading to the creation of a (non-metamorphic ) animat. The last two
frames illustrate the transition from the representation used during the developmental stage to the locomotion stage.
Video for this figure can be accessed at https://goo.gl/PJbZTr.
will produce a morphology with a protrusion that is connected by a single spring to the main body,
such protrusions were removed during conversion of an embryo into the soft-body representation.
This prevented the emergence of degenerate morphologies with infinitely thin body regions. También,
animats consisting of less than eight cells were considered not interesting and assigned a zero fitness.
The assigned resting length of springs is based on the distances between cell centers at the end of
the developmental stage. Además, each triangular region has an equilibrium pressure S0 (rep-
resented by its surface area at the end of development), providing the animat with a hydrostatic
skeleton and preventing excessive compression or stretching of body regions, and we have
(cid:1)
Fp ¼ cp ⋅ L ⋅ S0
S
(cid:3)
− 1
(1)
where Fp is the pressure force acting outward along the normal of the edge that is considered, L is
the length of this edge, S and S0 represent the current and the original surface area of the triangle,
and cp is the global pressure coefficient.
Springs are governed by Hookeʼs law with damping. All springs share the same Hookeʼs constant
k. The force acting on a node is equal to
Fs ¼ −kx − c
dx
dt
(2)
where x is the difference between a springʼs length at time t and its resting length, while c is the
damping coefficient.
To avoid self-penetration of animat bodies, masses representing cells undergo elastic collisions
with springs. Actuation is achieved by modifying the resting lengths of the springs attached to a
given cell. This results in a body region contracting or expanding. The resting lengths are changed
according to a sinusoidal oscillation pattern associated with every cell. The period of oscillation and
the phase shift of every cell are determined by two corresponding outputs at the end of the
developmental stage (ver tabla 1). During locomotion, the length of each spring is modified ac-
cording to
(cid:4)
(cid:1)
(cid:3)
(cid:3)
(cid:1)
(cid:5)
L ¼ 1 þ A sin
þ f
1
þ A sin
þ f
2
⋅L 0
(3)
2kt
T1
2kt
T2
where t is the simulation time; A is the amplitude of the changes undergone by each of the two
cells (A = 0.15); T1, T2 are the evolved periods of oscillation of the two cells at the endpoints of
2 are their evolved phase shifts (scaled to (−k, k)).
the spring; yf
1, F
The ground-based environment was constructed by placing animats on top of a flat surface and
introducing gravity and friction between their nodes and the surface. To prevent sudden changes in
resting length for cells with nonzero phase shift at the start of the simulation, the amplitude of
Artificial Life Volume 22, Número 3
277
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
2
2
3
2
7
1
1
6
6
6
3
0
1
a
r
t
yo
/
_
a
_
0
0
2
0
7
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
METRO. Joachimczak et al. Artificial Metamorphosis: Evolutionary Design of Transforming, Soft-Bodied Robots
contractions was progressively increased during the first 200 steps of the locomotion stage. Más-
más, to prevent evolution from exploiting any initial motion that would come from relaxation of
the animat body at the beginning of evaluation when gravity is present, before actuation was enabled,
we waited for each animat to stabilize. This was implemented by making sure that the speeds of the
nodes were sustained below a threshold over a period of 800 time steps.
For the aquatic environment, gravity was disabled and fluid drag was introduced. We used the
fluid drag model used to simulate undulatory fish swimming by Sfakiotakis and Tsakiris [30], cual
assumes that the fluid is stationary and that the force acting on a single edge on the outline of the
body is the sum of the tangential and normal drag components for the motion of this edge against
the fluid:
FT ¼ −dT ⋅ L ⋅ sgn vTð
Þ ⋅ vTð
Þ2
FN ¼ −dN ⋅ L ⋅ sgn vNð
Þ ⋅ vNð
Þ2
(4)
(5)
where vT and vN are the normal and tangential motion components, and dT and dN are the drag
coefficients for the tangential and normal drag on a unit-length edge (dN = 100dT). Since the animat
structure is not rigid and the lengths of the springs change dynamically, the direction of motion of a
given edge is understood as the direction of motion of its center. The calculated force is then divided
by two and applied to the nodes associated with the edge. While this approach does not simulate
turbulent flow, it provides enough environmental complexity to allow for fin-driven, undulatory, y
jellyfish-like swimming patterns, observed in our earlier work [17].
2.5 Genetic Encoding and Genetic Algorithm
The neural network model and genetic representation are based on the MultiNEAT library [6], el
implementation of the NEAT evolutionary algorithm [35]. In the NEAT method, networks are rep-
resented in the genomes as a list of nodes and their types (aporte, producción, normal) and a list of con-
nections. The NEAT algorithm keeps track of the innovation history and uses it to perform
crossover between genomes. It also uses a fitness-sharing approach with the goal of preserving di-
versity and protecting new solutions before they have to compete with the rest of the population.
We used a population size of 300 and runs of 2000 generaciones. The initial population was created as
a fully connected feed-forward network with a hidden layer and random weights. During evolution,
mutations that created cycles in the network were rejected.
2.6 Metamorphosis
The evolution of metamorphic individuals is based on a simple modification of the underlying
developmental system. Rather than evaluate just once the morphology that has emerged during
development in a virtual environment, we evaluate it twice, at different stages of its development
(Cifra 2). Más precisamente, we allow each genome to control embryonic development for 600 tiempo
steps. Entonces, the performance of the emerged (larval) morphology is evaluated on the first task (p.ej.,
for its ability to swim). Próximo, the development is allowed to continue for another 600 time steps, y
la resultante (adult) morphology is evaluated one more time, on the second task (p.ej., for its capa-
bility to run in a terrestrial environment). En tono rimbombante, beyond defining the models of multicellular
growth and locomotion, there are no prior assumptions on what kinds of morphologies are desired,
their size, or their mode of locomotion. There is also no explicit assumption that morphological
change needs to occur if development is continued beyond the larval stage.
The discontinuity between developmental and locomotion stages that is inherent in our approach
means that after the performance of a larval morphology has been evaluated on its target task, el
system needs to resume development. We do that simply by continuing development from the point
before the larval morphology was converted into its representation as a soft-bodied animat.
278
Artificial Life Volume 22, Número 3
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
2
2
3
2
7
1
1
6
6
6
3
0
1
a
r
t
yo
/
_
a
_
0
0
2
0
7
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
METRO. Joachimczak et al. Artificial Metamorphosis: Evolutionary Design of Transforming, Soft-Bodied Robots
Cifra 2. A conceptual overview of a single genomeʼs evaluation used to evolve metamorphic individuals.
3 Evolutionary Experiments
To investigate the evolvability of metamorphic robots we considered a scenario in which soft-bodied
robots had to be adapted to aquatic locomotion at one stage of life and terrestrial at another. Este
allowed for two different scenarios. The first one assumes that a robot first grows from a single cell
into its aquatic larva. Entonces, after being evaluated for its performance in an aquatic environment, es
allowed to undergo metamorphosis that creates its terrestrial, adult form. The second scenario as-
sumes reversal of the stages, eso es, a terrestrial larva and an aquatic adult. The occurrence of the
first scenario in the natural world is well known, as it is a typical developmental strategy of a whole
class of vertebrates, namely the amphibians. Its occurrence is also well understood in evolutionary
terms as being the result of amphibiansʼ evolving from their aquatic ancestors. Natural examples of
the opposite scenario, terrestrial larvae metamorphosing into aquatic adults, seem to be less com-
mon, but can be found, Por ejemplo, among newts (the eastern newt has an aquatic larva, a terrestrial
juvenile, and an aquatic adult form) and among some beetles (family Dryopidae [31]). Qué es, cómo-
alguna vez, important from the point of view of artificial metamorphosis is that performing both of these
types of experiments allows us to gain insight into what kind of morphological constraints are
brought by the particular choice of developmental history.
As evolving robots optimize their performance for two different types of environments, the two
scenarios used in the experiments constitute a multi-objective optimization problem. A considerable
number of different approaches have been developed to simultaneously optimize for multiple ob-
jectives (ver, p.ej., [8]), typically employing the concept of Pareto dominance. To avoid having to
modify the single-objective-only genetic algorithm in the MultiNEAT library that we were using,
we first considered the simplest possible approach, namely scalarization, with a good result. Seeing
a potential for improvement, we extended it and compared it with two other simple modifications of
the search algorithm. We describe these three approaches below.
3.1 Simple Fitness Function
In the most basic approach, the fitness value of a single solution was scalarized using the geometric
mean of the distances achieved in the developmental stages:
pag
ffiffiffiffiffiffiffi
dl da
f ¼
(6)
where dl, da were the distances achieved by the larval and adult forms in their respective environ-
mentos. The use of geometric rather than arithmetic mean prevents the emergence of individuals that
overspecialize for one environment only and produce very little movement in the other.
Artificial Life Volume 22, Número 3
279
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
2
2
3
2
7
1
1
6
6
6
3
0
1
a
r
t
yo
/
_
a
_
0
0
2
0
7
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
METRO. Joachimczak et al. Artificial Metamorphosis: Evolutionary Design of Transforming, Soft-Bodied Robots
3.2 Progressive Fitness Function
The above (Ecuación 6) simple method of scalarization assumes that the performance of the larval
stage and that of the adult stage are of equal importance. This also means that viable solutions need
to achieve a nonzero distance for each of their developmental stages. Generating such individuals
randomly or by hand may not be difficult for tasks such as movement in aquatic and terrestrial
entornos; it may, sin embargo, be very difficult in more complex scenarios. Entonces, the lack of viable
individuals in the initial generation will make it impossible for the evolutionary algorithm to perform
selección, a situation known in the field of evolutionary search as the bootstrap problem (ver, p.ej.,
[22]). An example of such a more challenging task would be the necessity to produce a metamorphic
individual adapted to moving down a slope in its larval form and up the slope as an adult. Finding
random genomes that produce an adult form that moves up the slope even slightly is going to be
very difficult. Even if successful, the types of solutions that can be found randomly are likely to be
the types that lead evolutionary search to a low-quality local minimum (p.ej., pequeño, degenerate indi-
viduals). As a simple way of reducing the bootstrap problem, we took inspiration from the evolu-
tionary emergence of metamorphosis in amphibians. Individuals were first evolved to move in one
environment only. Próximo, the second developmental stage was evolved “on top” of an already found
solución, by extending the length of the developmental process and evaluating the adult form in a
new environment (but allowing the larval form to evolve as well). This creates a scenario in which, en
least initially, “ontogeny recapitulates phylogeny.”2
Más precisamente, for the first third of an evolutionary run we evolved individuals to develop only
para 600 time steps (es decir., the larval age) and move in the first environment. Entonces, we extended the
development time to 1200 time steps and began evaluating the performance of individuals at both of
their developmental stages. To avoid a potentially catastrophic reshuffling of individuals as soon as
the performance of an adult form becomes part of the fitness function, we have made the fitness of
the adult stage progressively increase in relevance until two-thirds of the evolutionary run length has
elapsed. Finalmente, over the remaining part of the evolutionary run, individuals would be evaluated as if
each phase had equal weight (using Equation 6). This approach allowed for a graceful and progres-
sive improvement of the adult-stage performance while introducing changes to the morphology and
controller of the larval stage. Formalmente, the scalarized, progressive fitness value fp was dependent on
the current generation g and the total length L of the evolutionary run as follows:
pag
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
Þ
Þ þ 1
d
dl w gð Þ da − 1
d
fp ¼
where w gð Þ ¼
8
>>>>>>>>>< >>>>>>>>>:
0
g − L
3
l
3
1
if g < L
3
≤ g < 2L
3
if
L
3
if g ≥ 2L
3
:
(7)
3.3 Novelty Search
The last approach we have evaluated as a method of evolving metamorphic agents was the novelty
search algorithm [19]. In brief, the novelty search algorithm is based on the radical idea that aban-
doning an objective, goal-focused fitness function altogether can lead to discovering solutions of
higher fitness. To do so, novelty search replaces the concept of objective fitness function with
the notion of novelty, a scalar quantity corresponding to how much a given phenotype differs from
phenotypes in the current population as well as from phenotypes that have been found to be novel
in previous generations. This modification causes the evolutionary search to pursue phenotypes that
2 Note, however, that Ernst Haeckelʼs theory of recapitulation to which we refer here has only historical significance.
280
Artificial Life Volume 22, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
3
2
7
1
1
6
6
6
3
0
1
a
r
t
l
/
_
a
_
0
0
2
0
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Joachimczak et al. Artificial Metamorphosis: Evolutionary Design of Transforming, Soft-Bodied Robots
are different from the already discovered ones instead of phenotypes that have higher fitness. While
methods that increase genetic diversity have long been demonstrated to be useful in evolutionary
algorithms (see, e.g., [21, 27]), novelty search differs from them in focusing solely on increasing
phenotypic, not genotypic, diversity. Novelty search had been suggested to improve evolvability
in problems that are deceptive in nature, that is, where greedily focusing the search on improving
the fitness will likely lead the population into local minima in the fitness landscape that are difficult
to escape from. It is suggested that the pressure to produce novel phenotypes will instead lead to the
discovery of more and more complex solutions, among them the evolutionary stepping stones that
open access to new regions of higher fitness in the solution space [19]. More precisely, Lehman and
Stanley [19] define the novelty of a phenotype x as proportional to how sparsely the phenotype
space surrounding x has been explored so far:
U xð Þ ¼ 1
k
Xk
i¼1
ð
d x; A
i
Þ
(8)
where A
i is the ith-nearest individual to x out of k according to the distance metric d.
The introduction of a novelty search algorithm into our system was limited to replacing the fit-
ness function computation with calculation of the novelty value, and introducing of a novelty archive
that stores past novel individuals and an algorithm for dynamic updating of the novelty threshold
value (the novelty value at which an individual is added to the archive). We chose to increase the
threshold by 10% if more than eight individuals were added to the archive one after another, and to
decrease it by 10% if no individuals were added within 50 generations.
We have opted to use one of the simplest possible approaches to measuring similarity between
phenotypes in our experiments: We characterized each individualʼs phenotype as a vector of size 4,
consisting of the final X and Y coordinates of the center of mass of larval and adult forms at the end
of their locomotion stages. We then used the Euclidean distance as the metric d, and k = 15.
4 Results
All of the approaches discussed above were found to be successful in evolving individuals that un-
dergo metamorphosis. More specifically, all of the 20 evolutionary runs performed for each ap-
proach would result in individuals with differing adult and larval forms that can move in their
respective environments. The difference between the three evolutionary approaches was found to
be mainly quantitative, with visually similar results, though with a different average quality of best
individuals obtained in multiple evolutionary runs. We will thus first discuss features of evolved
individuals and their metamorphosis, and will investigate quantitative differences between the sev-
eral approaches to generating them in a following section.
The fact that morphological change evolved between two developmental stages is not surprising in
itself. Unless individuals were specifically evolved to inhibit growth before the end of the first devel-
opmental stage (which can be done by introducing a penalty factor into the fitness function, as in
[15]), some growth is almost certain to occur if development is extended and the hard limit of cells
has not been reached. Thus, the type of metamorphosis that is of interest to us is not just any change
occurring between the two developmental stages, but a change that can be considered adaptive.
4.1 From Water to Land: Aquatic Larvae and Terrestrial Adults
Figure 3 presents morphologies and motion patterns of two examples of metamorphic soft robots
that are representative of high-fitness solutions. In both cases, a striking difference between the
larval and the adult stage can be observed, with clear adaptations to their respective environments
(likely best appreciated with the supplementary video materials; links are provided in figure cap-
tions). The aquatic larvae of both individuals have an elongated form. In the case of the individual
Artificial Life Volume 22, Number 3
281
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
3
2
7
1
1
6
6
6
3
0
1
a
r
t
l
/
_
a
_
0
0
2
0
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Joachimczak et al. Artificial Metamorphosis: Evolutionary Design of Transforming, Soft-Bodied Robots
Figure 3. Motion snapshots of two solutions ((a),(b)) evolved to move first in the aquatic environment and then in the
terrestrial environment (left column: larva; right column: adult ). Arrows indicate the direction of movement;
snapshots were selected to represent one motion cycle. Larval and adult stages are not to scale (larva is smaller ).
The individual in (a ) was obtained with the default fitness function; (b) comes from the novelty search experiment.
Colors represent whether the region of the body is currently expanded (red), contracted (blue), or at its resting size
(white). Videos for (a ) can be accessed at https://goo.gl/M9Ytym and https://goo.gl/M6K9gh; videos for (b) at https://
goo.gl/GAvNtb and https://goo.gl/UNw7lf.
in Figure 3a, the larva propels its body in a fishlike motion by bending it left and (mostly) right. The
actuation pattern has the form of waves of contraction and expansion that travel through the body
in the direction perpendicular to the direction of movement. The larva of the individual shown in
Figure 3b has a snakelike, streamlined shape and displays undulatory locomotion resembling that of,
for example, a nematode worm.
Perhaps the most interesting aspect of the evolved adult forms is that in both cases metamor-
phosis proceeds by restructuring the body in a way that involves growing two support appendages
that are essential to the terrestrial gait and thus serve as primitive legs. The gaits rely on elasticity of
the body and capability of the appendages to absorb and release elastic energy—once individuals get
to speed, they cycle between their front and back appendages, expanding them on contact with the
ground. The directions of motion of larval and adult stages (indicated by arrows in Figures 3 and 5)
seem not to be correlated. Since, however, virtual animats have no sensors and therefore no concept
of front or back, there is no direct reason for evolution to maintain the direction of movement
unchanged between the developmental stages.
Importantly, the solution type where the larval stage is streamlined and the adult form grows
appendages to support itself during terrestrial movement was commonly observed in the results
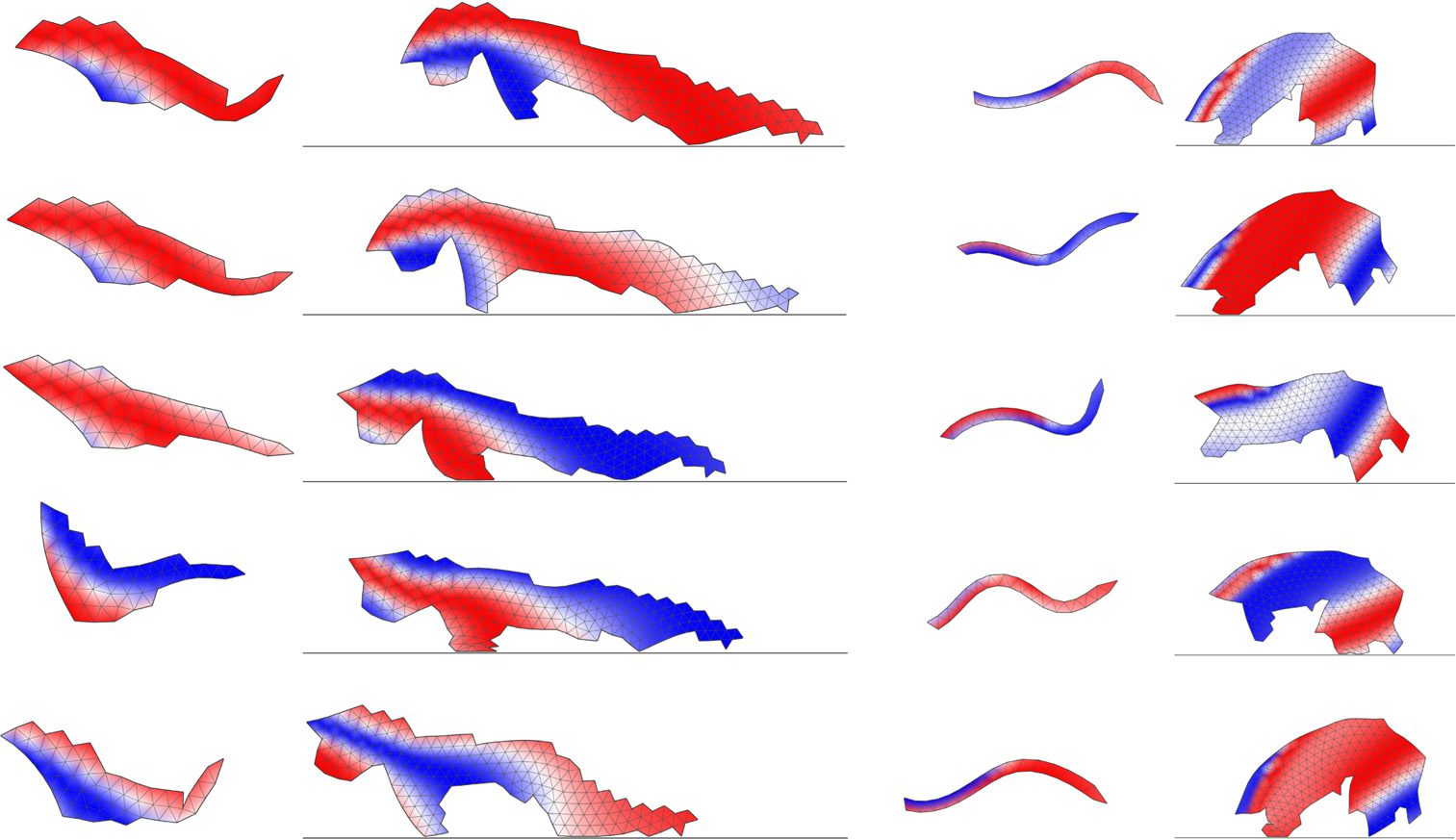
of many other evolutionary runs, of which eight additional examples are presented in Figure 5.
We find it remarkable that an attempt to evolve metamorphosis in silico produces solutions that
immediately bring amphibians to mind, with streamlined, tadpole-like larvae and adults that often
shed their tail and grow appendages to move in a terrestrial environment. Furthermore, we would
like to note that the propensity to assemble cells into higher-level structures that can function as
282
Artificial Life Volume 22, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
3
2
7
1
1
6
6
6
3
0
1
a
r
t
l
/
_
a
_
0
0
2
0
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Joachimczak et al. Artificial Metamorphosis: Evolutionary Design of Transforming, Soft-Bodied Robots
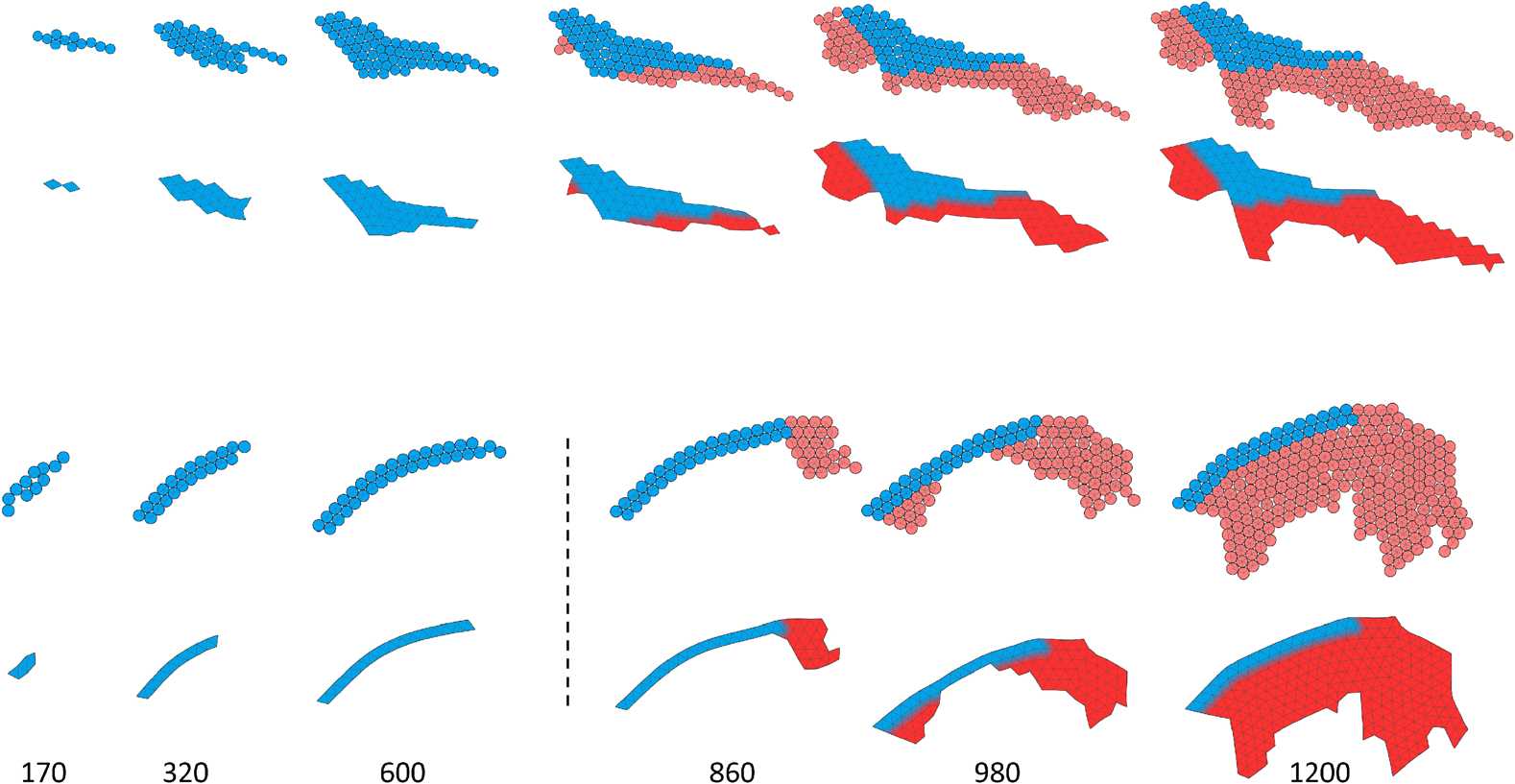
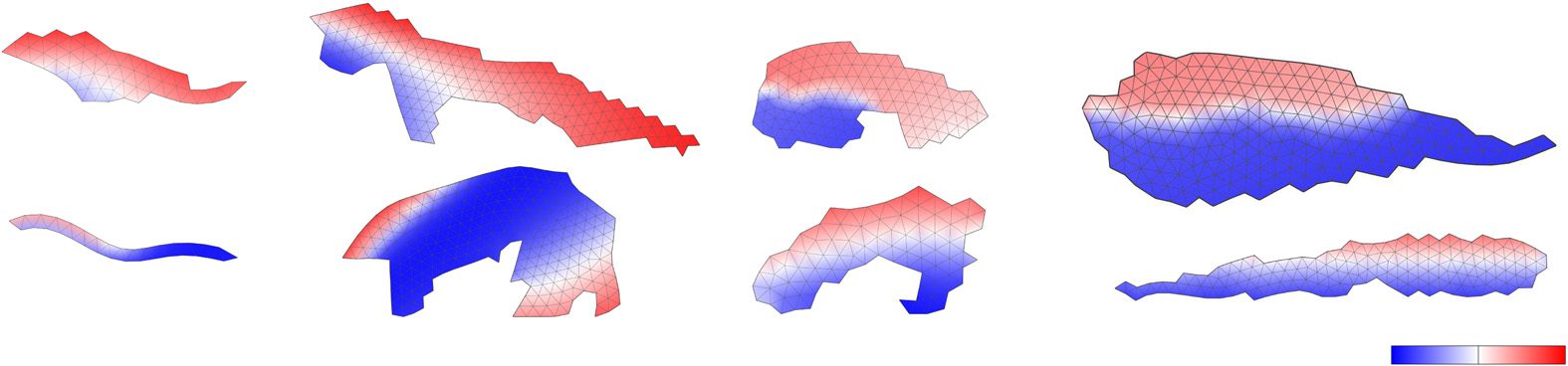
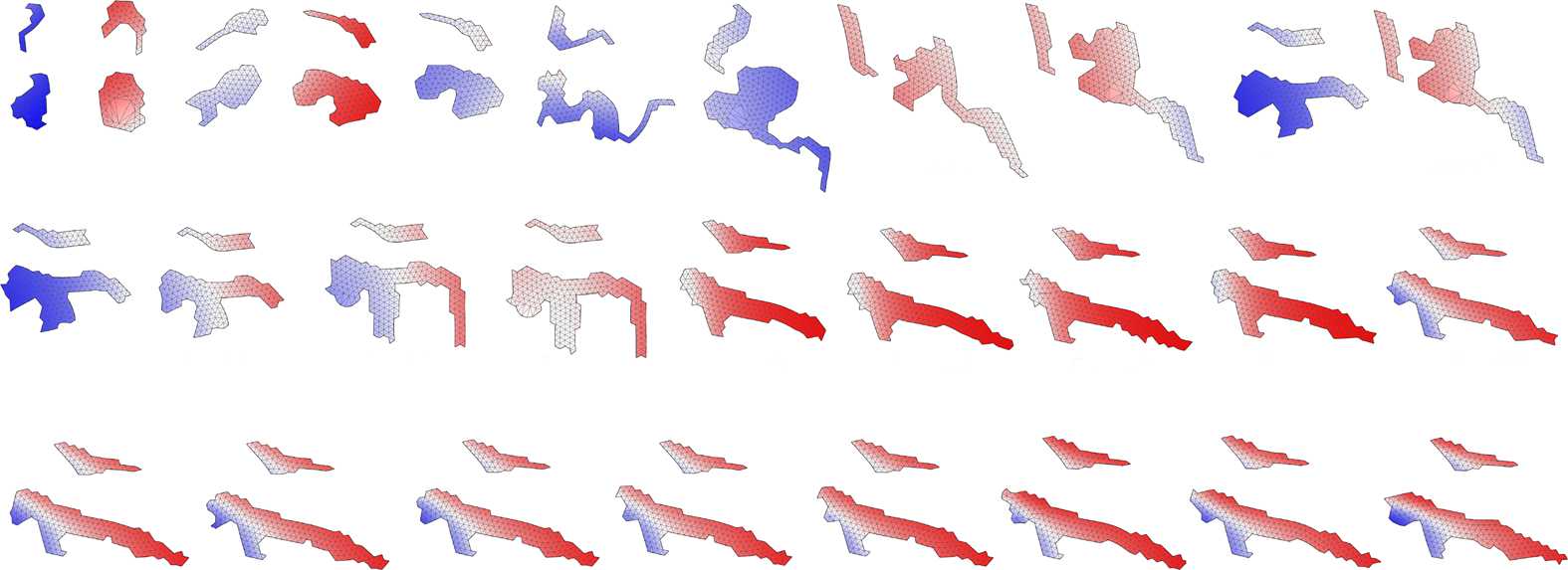
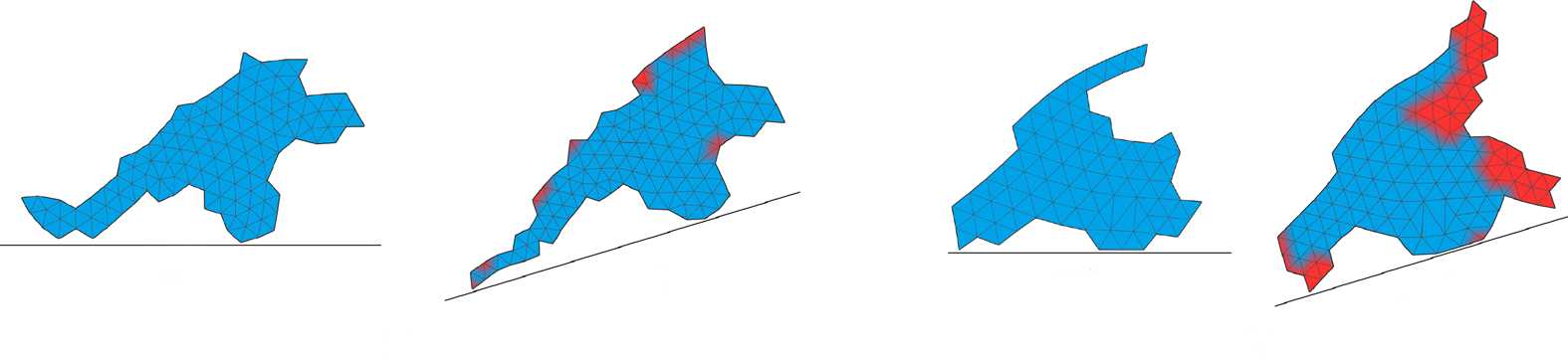
Figure 4. Developmental processes of the two individuals shown in Figure 3. The dashed line separates the larval stage
from the beginning of metamorphosis; labels indicate the development time. Upper rows show the multicellular
representation that is used during development; bottom rows show a preview of the soft-bodied representation.
Note that protrusions with a thickness of one cell are removed, and the soft-bodied representation is used only for
the evaluation of morphology, during locomotion stages. Blue color: cells that were created during the larval stage; red:
cells created during metamorphosis. Videos can be accessed at: https://goo.gl/P7m287 and https://goo.gl/6OOosd.
primitive legs or tails is nowhere explicitly encoded in the system. Their emergence is a testament to
the creative potential of artificial evolution.
To gain qualitative insight into how the two individuals depicted in Figure 3 grow from a single
cell and later undergo metamorphosis, we visualized developmental processes by coloring cells cre-
ated during larval development in blue and cells created during metamorphosis in red (Figure 4). In
these two cases, as well as in other inspected solutions (shown in Figure 5), metamorphosis proceeds
by adding cells to the larval stage, resulting in a structure that is considerably larger and has the larval
stage (or a part of it) embedded inside it. Apoptosis occurring during metamorphosis was not, how-
ever, uncommon and can be observed in the individuals seen in Figure 5 (e.g., the third from the
right) or later in Figure 6b.
That the adult stage was larger than the larval one was universally observed, and we think it is
most likely explained by developmental bias toward dividing cells by default unless inhibited by ac-
tivation of a corresponding gene. Thus, given that evolution typically chooses simple solutions, a
Figure 5. Animat zoo: additional examples of morphologies of metamorphic individuals with aquatic larval stage (upper
row) and corresponding terrestrial adult stage (below). Examples come from all of the three different types of
evolutionary search employed. Body parts grown during metamorphosis are colored red. Arrows indicate direction
of movement.
Artificial Life Volume 22, Number 3
283
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
3
2
7
1
1
6
6
6
3
0
1
a
r
t
l
/
_
a
_
0
0
2
0
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Joachimczak et al. Artificial Metamorphosis: Evolutionary Design of Transforming, Soft-Bodied Robots
Figure 6. Motion snapshots of two solutions ((a),(b)) evolved to move first in the terrestrial environment and then in the
aquatic environment (left column: larva; right column: adult). Arrows indicate direction of movement; snapshots were selected
to represent one motion cycle. Larval and adult stages are not to scale (larva is smaller ). The individual from (a) was obtained
with the novelty search function, and (b) with the progressive fitness function. Colors represent whether the region of the
body is currently expanded (red), contracted (blue), or at its resting size (white). Videos for (a) can be accessed at https://
goo.gl/elTiW3 and https://goo.gl/8WROSq; videos for (b) at https://goo.gl/yE5d6U and https://goo.gl/z8CMzG.
developmental controller is likely to lack self-termination of growth as long as the development is
terminated by an external clock.
4.2 From Land to Water: Terrestrial Larvae and Aquatic Adults
Looking at the metamorphosis of amphibians, we can observe how the aquatic larvae (tadpoles)
tend to display simpler morphologies, while terrestrial adults tend to have more complex shape,
having grown appendages that allow them to move on the ground. Even ignoring their evolution-
ary history, this could be, in principle, explained simply by the fact that appendages are useful for
moving in terrestrial habitats, while aquatic environments demand morphologies that have low drag
and hence must be more streamlined. Furthermore, it is also the very nature of the developmental
process that it constructs bodies by progressive complexification of an initially spherical embryo.
Thus, the above-discussed scenario, in which soft robots have to move in an aquatic environment
as larvae and a terrestrial one as adults, may be considered particularly well suited for evolving
metamorphic robots: It gives artificial metamorphosis the opportunity to exploit morphological
complexification that is inherent both in multicellular development and in the switch from aquatic
to terrestrial environment.
To find out to what extent the robotic designs obtained in the above experiments are a result of
evolution designing efficient morphologies and to what extent they are a fortunate result of com-
plexification inherent in growth, we performed experiments with environments for the developmen-
tal stages inverted: Larvae had to move on land and adult forms had to move in water. To provide a
fair comparison, all other parameters of the experiments remained unchanged.
284
Artificial Life Volume 22, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
3
2
7
1
1
6
6
6
3
0
1
a
r
t
l
/
_
a
_
0
0
2
0
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Joachimczak et al. Artificial Metamorphosis: Evolutionary Design of Transforming, Soft-Bodied Robots
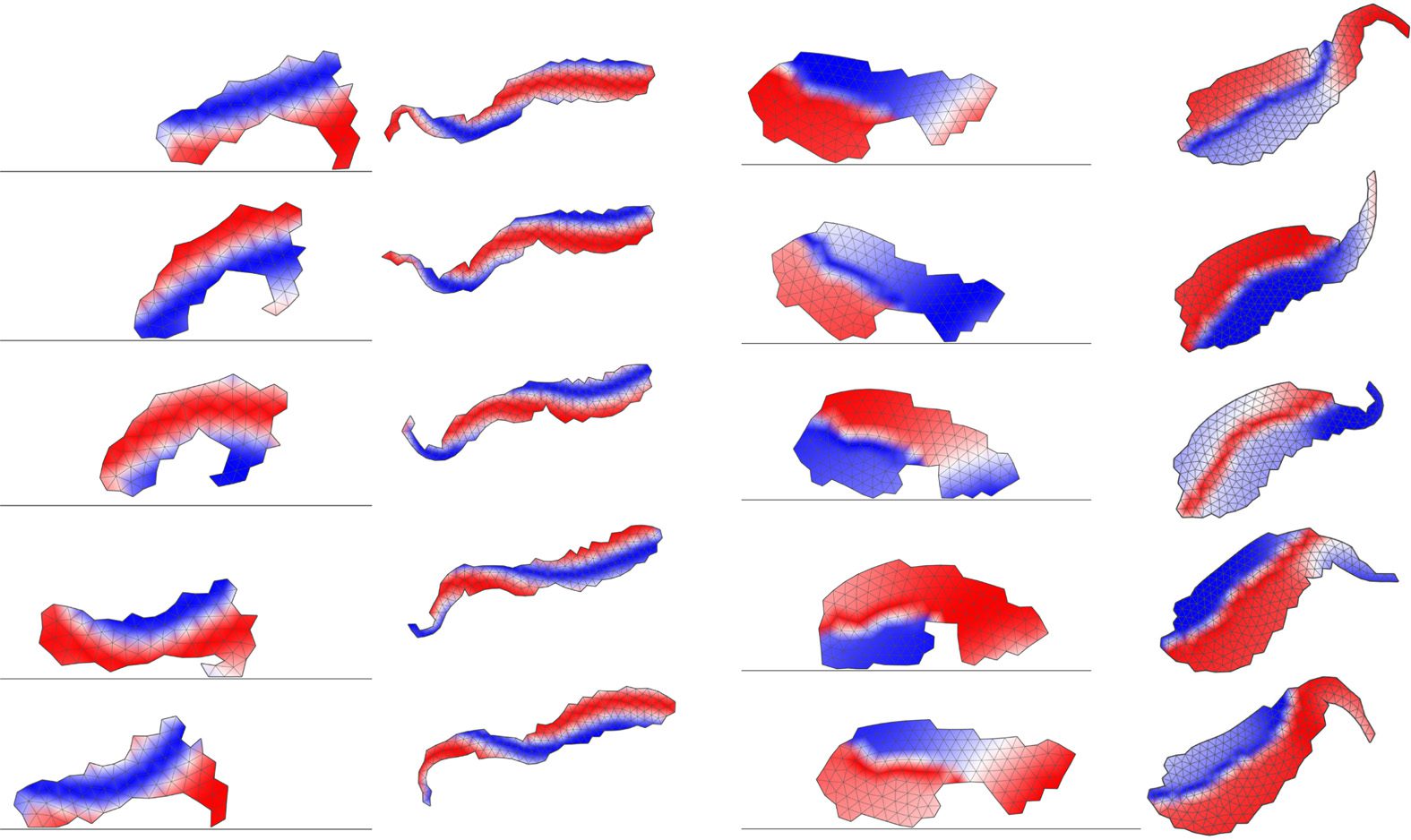
Figure 7. Animat zoo 2: further examples of metamorphic individuals evolved to first move in the terrestrial environment
and then in the aquatic. Examples come from all of the three types of evolutionary runs employed. Body parts grown
during metamorphosis are colored red. Arrows indicate direction of movement.
Again, evolutionary runs were successful in producing individuals that undergo clearly adaptive
metamorphosis, as seen in the selection of best individuals in Figure 7. Two examples of high-fitness
individuals and their motion strategies are shown in more detail in Figure 6. What can be immedi-
ately observed is that evolution has again come up with legged locomotion for the terrestrial envi-
ronment and fishlike morphologies for the aquatic one. Furthermore, the motion of the terrestrial
larvae is largely similar to the gaits of the terrestrial adults in earlier experiments, with the exception
that the legged individuals consist of smaller numbers of cells. Similarly, the adult forms propel
themselves with undulating movements, just as in the previous experiments. In the case of the adult
forms in Figure 6a they are the result of a wave of contractions of the body that moves through the
body in the direction perpendicular to the direction of movement (just like the larva in Figure 3a).
The adult form in Figure 6b, on the other hand, induces an undulating motion pattern by synchro-
nously contracting all cells on its right side while expanding the cells on the left side and vice versa,
with a division line separating the left and right sides of the body visible in the middle frame (t =
1854). The aquatic forms are largely symmetric along the direction of their motion, although hardly
perfect. Since our developmental system does not explicitly facilitate symmetrical growth (at least as
it was configured for the presented experiments), symmetric shapes emerge only as evolutionʼs
attempt to produce morphologies that swim consistently in one direction.
The fact that, in both discussed scenarios, artificial evolution converged to similar morphological
solutions, regardless of the order of developmental stages, suggests high evolutionary plasticity of
the employed approach. At the same time, the remaining differences, especially in the size of each
stage, show how developmental constraints alter the evolutionary trajectory: The walkers are now
smaller and grow into swimmers. Careful investigation of how the development proceeds (Figure 8)
and comparison with that of the water-to-land scenario (Figure 4) allow us to observe what happens
in detail: For both individuals, we can see how apoptosis removes some of the cells that formed
appendages while at the same time growing cells between them to reduce drag and elongating the
front and back of the creature.
4.3 Evolved Controllers
The movement of soft-bodied robots is a result of oscillating contractions, with each cell having
an independent period and phase shift determined at the end of the developmental process
(Equation 3). This simple method has been demonstrated to work well for a wide range of morphol-
ogies in experiments based on a similar approach in our earlier work [17]. The typical result of evo-
lutionary runs, also compatible with our previous observations, is that the period of oscillations
evolves to be uniform among the body and equal to the minimum allowed length. This is most likely
explained by the fact that, given the lack of energetic costs of actuation, higher frequency of contrac-
tions delivers more energy to the system, which can then be converted into kinetic energy of an ani-
mat and used to overcome drag and friction. Hence, selection highly favors individuals that have the
shortest allowed period of oscillation. Effective motion patterns are then produced by evolving a
varied phase shift of contractions along the body.
Qualitative analysis of how controllers change during metamorphosis of the four individuals
investigated earlier reveals that the oscillation patterns of cells are largely retained during metamor-
phosis (Figure 9), although small adjustments to it were common and larger changes were also
observed. As an example of an evident change, we marked the same cell (id 67) in the larval and
Artificial Life Volume 22, Number 3
285
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
3
2
7
1
1
6
6
6
3
0
1
a
r
t
l
/
_
a
_
0
0
2
0
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Joachimczak et al. Artificial Metamorphosis: Evolutionary Design of Transforming, Soft-Bodied Robots
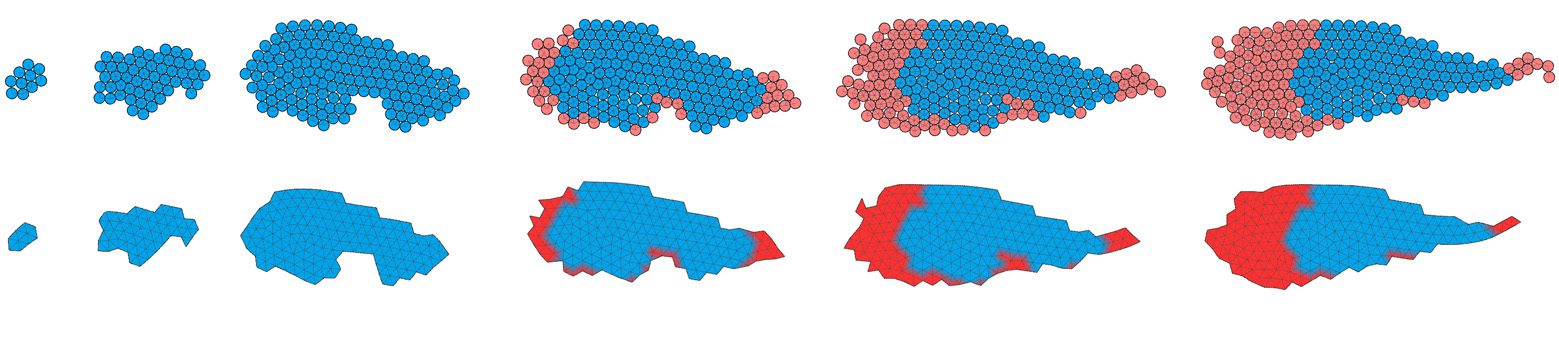
Figure 8. Developmental processes of the two individuals shown in Figure 6. The dashed line separates the larval stage
from the beginning of metamorphosis; labels indicate the development time. Upper rows show the multicellular
representation that is used during development; lower rows show a preview of the soft-bodied representation. Note
that protrusions with a thickness of one cell are removed, and the soft-bodied representation is used only for the
evaluation of morphology, during the locomotion stages. Blue: cells that were created during the larval stage; red: cells
created during metamorphosis. Videos can be accessed at https://goo.gl/nbg JYp and https://goo.gl/HfjmJ3.
adult stages of the top individual in Figure 9b. This shows that evolved metamorphosis does not rely
on morphological changes only, but fine-tunes the control mechanism as well.
4.4 Comparison of Evolutionary Search Methods
The best individuals obtained in the evolutionary experiments using the three different versions of
the search algorithm (Section 3) were qualitatively similar. Yet, quantitative analysis of each algorithmʼs
performance reveals that the success rate of producing high-quality individuals is very different for
each of them.
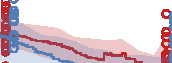
Compared to the basal, simple fitness function, the progressive fitness approach was observed to
produce on average higher quality of individuals (Figure 10), in both the cases of evolving aquatic
and terrestrial larvae first. A likely explanation is that the progressive fitness function relaxes the
requirement of both developmental phases having to produce moving individuals from the very
beginning. At the same time, metamorphosis is easier to evolve if modifications that occur in the
Figure 9. Controller comparison for the larval and adult stages of individuals shown in Figures 3 and 6. Colors represent
evolved phase shifts of cellular contractions and expansions.
286
Artificial Life Volume 22, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
3
2
7
1
1
6
6
6
3
0
1
a
r
t
l
/
_
a
_
0
0
2
0
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Joachimczak et al. Artificial Metamorphosis: Evolutionary Design of Transforming, Soft-Bodied Robots
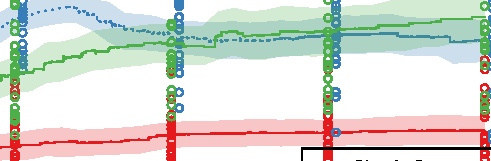
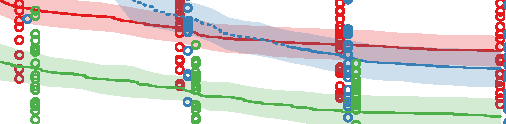
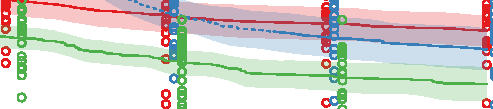
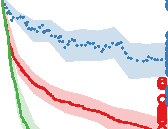
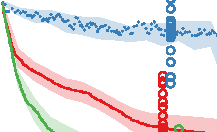
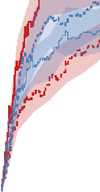
Figure 10. Comparison of the three different evolutionary search approaches to evolving metamorphic soft robots:
scalarized fitness. Lines represent the average fitness of the best individual in a population from 20 evolutionary runs; the
shaded area represents 95% bootstrapped confidence intervals. Fitness in the plot was calculated using the default fitness
function (Equation 6). Note that it was the same as the fitness function used by evolutionary search only in the simple
fitness method and after generation 1333 in the progressive fitness (Equation 7) method (solid blue line). Novelty search
did not rely on objective fitnesses at all.
larvae have a limited scope and reuse its underlying structure to create the adult. The progressive
approach supports metamorphosis by first solving an easier problem of finding a working larval
morphology and then starting to evolve metamorphosis while already having discovered a promising
region of search space: In this regard it can be considered a new type of scaffolding technique [1].
We expect that this method would perform especially well on problems in which bootstrapping
evolutionary search would be difficult.
The most surprising finding was, however, that the novelty search algorithm outperformed our
two objective fitness-based approaches by a large margin in both types of experiments (Figure 10).
Novelty search succeeded even despite the fact that (by definition) it does not explicitly optimize the
distances of each developmental stage and, instead, continuously searches for novel solutions. Fur-
thermore, our application of the novelty search algorithm should be considered very basic, as we did
not explore different phenotypic descriptors (e.g., based on overall motion patterns rather than the
final position of the center of mass only) or search for optimal parameters. We also did not attempt
to normalize final positions of individuals, and thus the novelty search may underperform by over-
exploiting one developmental stage. It has been suggested that novelty search excels in domains with
highly deceptive fitness landscapes [20]. Our earlier experiments employing the same developmental
model have also shown the advantage of using novelty search [16] on the gait evolution task. This
suggests high deceptiveness of the artificial development problem domain and overall usefulness of
novelty search for highly complex genotype-to-phenotype mappings.
Figure 11. Distance achieved by larvae and adults for best individuals in each type of experiment shown in Figure 10a. The
very low performance of the adult stage in progressive fitness experiments before generation 667 stems from the lack of
selection for their quality (see Equation 7).
Artificial Life Volume 22, Number 3
287
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
3
2
7
1
1
6
6
6
3
0
1
a
r
t
l
/
_
a
_
0
0
2
0
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Joachimczak et al. Artificial Metamorphosis: Evolutionary Design of Transforming, Soft-Bodied Robots
Figure 12. Distance achieved by larvae and adults for best individuals in each type of experiment shown in Figure 10b.
The very low performance of the adult stage in progressive fitness experiments before generation 667 stems from the
lack of selection for their quality (see Equation 7).
Finally, Figures 11 and 12 present how the performance of developmental stages improves over
evolutionary time when using each of the search algorithms. The larval stage evolved using the pro-
gressive fitness approach considerably outperforms the other two methods over the first third of the
evolutionary run, that is, while this is the only developmental stage that is under selection. This is
only, however, because the cost of balancing performance between the two developmental stages is
not incurred yet. Nonetheless, adding a second developmental stage on top of an already evolved
larva, even though it decreases its performance, does so only moderately (around 10–15% fitness
drop: Figures 11a and 12a, the blue line after 667 generations). This approach, on the other hand,
can be observed to bias the tradeoff in favor of the larval stage: The distance achieved by adults in
both types of experiments was lowest for the progressive fitness approach (Figures 11b and 12b).
The more detailed analysis also reveals that the novelty search approach did not universally outper-
form other approaches at the level of each developmental stage. The simple fitness approach pro-
duced on average better terrestrial adults, and so did the progressive fitness method for terrestrial
larvae. The record holders for the best obtained larvae and adults in each type of experiment belong,
however, to the novelty search.
4.5 Analysis of Evolutionary Runs
To understand how metamorphic individuals evolve over time, we have analyzed the most success-
ful set of evolutionary runs, namely, the ones using the novelty search algorithm. Figure 13 directly
compares the average fitnesses over time for two classes of experiments, namely, those with aquatic
larvae and terrestrial adults and those with terrestrial larvae and aquatic adults. Other than a poten-
tially small advantage of the first type of experiments (also observed for other search algorithms), the
Figure 13. Fitness of the best individual in the population over evolutionary time for the two types of experiments in
evolving metamorphic individuals using the novelty search algorithm. Lines show average fitnesses of 20 independent
evolutionary runs each; color stripes represent 95% bootstrapped confidence intervals for the averages. The plot is
based on the same data as used in Figure 10a and 10b.
288
Artificial Life Volume 22, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
3
2
7
1
1
6
6
6
3
0
1
a
r
t
l
/
_
a
_
0
0
2
0
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Joachimczak et al. Artificial Metamorphosis: Evolutionary Design of Transforming, Soft-Bodied Robots
Figure 14. Distances achieved by each developmental stage of the best individual in the population for both types of
experiments while using the novelty search algorithm. Lines show average distances from 20 independent evolutionary
runs of each experiment type; color stripes represent 95% bootstrapped confidence intervals for the averages. A
dashed line represents the larval stage performance; the solid line represents the adult stage.
difference in average result is small and not statistically significant for the data shown. By comparing
the performance in each developmental stage separately (Figure 14), we can see how the higher
average fitness of the water-to-land individuals comes from the longer average distances achieved
by their larvae than those achieved by aquatic adults in the land-to-water scenario, while the terres-
trial stages in both types of experiments achieved almost the same average distances. Importantly,
the variation between evolutionary runs is very large, indicating a very high effect of evolutionary
contingency on the quality of a final solution. Furthermore, it was universally observed for adult
forms to grow larger than larval forms (Figures 15 and 16).
There are, however, large differences between the two classes of experiments. More precisely,
Figure 15 shows how terrestrial larvae of the land-to-water scenario grow to be more than twice the
size of aquatic larvae in the alternative scenario. The growth happens very quickly on the evolution-
ary timeline (within the first 100 generations), suggesting very high selective pressure to do so. The
adults of this experiment also grew to be larger (Figure 15). Analysis of their process of metamor-
phosis further reveals that in the land-to-water scenario the changes that occur in the body are more
pronounced. The number of cells that undergo apoptosis is 2–3 times higher than in the water-to-
land scenario and averages to around 25% of the number of cells present in the larvae (Figure 17).
When it comes to a number of cells added during metamorphosis (Figure 18), the first 200 gener-
ations in both types of experiments show a steady increase of the parameter, likely indicating a
period in which the first functional metamorphic individuals emerge. Just as with apoptosis, larger
growth during metamorphosis occurred in the land-to-water scenario.
Why, however, would terrestrial larvae grow larger than aquatic larvae? We think this can be
explained by two effects. Firstly, the cells grow by default, unless the growth process is inhibited.
Figure 15. Number of cells in larvae over evolutionary time for the two types of experiments in evolving metamorphic
individuals using the novelty search algorithm. Lines show averages of 20 independent evolutionary runs each; color
stripes represent 95% bootstrapped confidence intervals for the averages.
Artificial Life Volume 22, Number 3
289
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
3
2
7
1
1
6
6
6
3
0
1
a
r
t
l
/
_
a
_
0
0
2
0
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Joachimczak et al. Artificial Metamorphosis: Evolutionary Design of Transforming, Soft-Bodied Robots
Figure 16. Number of cells in adults over evolutionary time for the two types of experiments in evolving metamorphic
individuals using the novelty search algorithm. Lines show averages of 20 independent evolutionary runs each; color
stripes represent 95% bootstrapped confidence intervals for the averages.
This has the side effect of biasing the second-stage morphologies towards being bigger: From the
control point of view, it is easier to grow cells than prevent growth, as the latter requires an explicit
control signal to do so. In the case of aquatic larvae it means that evolution produces highly elon-
gated, very slim shapes that later increase in size and produce appendages. The larvae, however,
remain relatively small, often displaying simple, snakelike morphology. This is not, however, possible
in the case of terrestrial larvae, which will move best only if they have appendages, and growing
these requires additional cells. Therefore, a second effect at play is that a minimal functional mor-
phology for terrestrial locomotion is of larger size and complexity than its aquatic counterpart. Dur-
ing the transformation, simpler aquatic larvae need only to grow appendages, whereas terrestrial
larvae have to somehow suppress the appendages to produce a streamlined shape. Suppression is
achieved most easily by growing additional cells that will fill the space between appendages, though
as mentioned previously, partial apoptosis of appendages would also occur (Figure 7). Finally, to see
what kinds of morphological changes the evolving animats undergo during their evolution, we have
selected the best individuals from each generation from the evolutionary run that produced the
individual in Figure 3a. Although the selected historical individuals shown in subsequent frames
(Figure 19) do not represent direct descendants, it is clear that throughout the later part of the evo-
lutionary history subsequent best individuals are closely related to each other. It can also be observed
how during the first 100 generations of the evolutionary run, morphological changes occurred very
frequently. At generation 125, the overall morphology of the best individual already resembles the
best final individual found in generation 1386 (although its fitness is only 5.07, compared to 11.15 for
Figure 17. Number of cells that undergo apoptosis during metamorphosis over evolutionary time for the two types of
experiments in evolving metamorphic individuals while using the novelty search algorithm. Lines show averages of 20
independent evolutionary runs each; color stripes represent 95% bootstrapped confidence intervals for the averages.
290
Artificial Life Volume 22, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
3
2
7
1
1
6
6
6
3
0
1
a
r
t
l
/
_
a
_
0
0
2
0
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Joachimczak et al. Artificial Metamorphosis: Evolutionary Design of Transforming, Soft-Bodied Robots
Figure 18. Number of cells that are added during metamorphosis over evolutionary time for the two types of experiments
in evolving metamorphic individuals while using the novelty search algorithm. Lines show averages of 20 independent
evolutionary runs each; color stripes represent 95% bootstrapped confidence intervals for the averages.
the latter ). The following generations bring multiple small changes to the morphology of the adult
form and almost no changes to the larval form. Both stages, however, undergo continuous modifi-
cations of their controllers, and it is these alterations that contribute the most to the improvements in
fitness. This pattern was also observed in other evolutionary runs: The final morphology would
emerge in the first few hundred generations, and the remainder of the run would be spent on small
tweaks to the bodies and optimization of controllers.
4.6 Comparison with Robust Robots
An alternative to creating a self-reconfiguring robotic design that can function in two different
environments would be either to create a single, robust solution that can function in both environ-
ments or to create two different designs, each specialized to its target environment. Each of these
approaches has its design compromises and advantages. In this and the following subsection we
attempt to find how the performance of evolved metamorphic individuals compares in the two
alternatives: a single, environmentally robust (here, amphibious) animat, and a pair of specialized
individuals evolved separately. A robust robot has its morphology and controller designed in a
way that allows it to function in any type of environment. If the environments are as different as
an aquatic and a terrestrial one, this imposes considerable tradeoffs on its design, and it is likely to
perform much worse in each environment than two specialized robots would. On the other hand, an
evolved metamorphic robot also faces tradeoffs coming from the fact that a single genome encodes
Figure 19. Evolution of a metamorphic individual: morphologies of larval (top) and adult stages (below) of the best individual
in a given generation for the evolutionary run that produced the individual shown in Figure 3a. Colors correspond to the
evolved phase shift of muscular contractions.
Artificial Life Volume 22, Number 3
291
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
3
2
7
1
1
6
6
6
3
0
1
a
r
t
l
/
_
a
_
0
0
2
0
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Joachimczak et al. Artificial Metamorphosis: Evolutionary Design of Transforming, Soft-Bodied Robots
two phenotypes, as well as the process of converting one into another. This makes evolutionary
design of a metamorphic robot much more challenging. Naturally, a physically implemented
shape-changing robot would be immensely useful owing to this unique property. What we thus
focus on and compare here is solely the evolvability of the metamorphic approach in the form pre-
sented in this article, understood as the quality of designs obtained at the end of evolutionary runs.
Confirming that the specialization observed in the experiments indeed outperforms evolved, robust
designs sets the baseline of the usefulness of metamorphosis as a technique of automated design.
We have evolved robotic designs using the same setting and algorithm as the metamorphic ones,
but with the goal of producing amphibious animats that can move both in aquatic and in terrestrial
environments. In this scenario, there was no metamorphosis, but adult forms were evaluated in both
environments. Hence, evolution had to strike a compromise between robotsʼ performance in each
of the environments.
A direct comparison poses challenges, however. In our experiments with metamorphosis, we
assumed that the growth of the larval stage takes 600 time steps, whereas the adult stage grows over
1200 time steps. As we have shown in the previous sections, allowing for a longer growth time leads
to the emergence of larger individuals. At the same time, larger individuals were observed to achieve
larger distances. Therefore, attempting to evolve robust individuals that grow for 1200 time steps
will lead to the emergence of larger swimming individuals than if the growth was allowed for only
600 time steps, giving them an unfair advantage over the smaller larvae of metamorphic individuals.
One way of ensuring a fairer comparison would thus be to employ some method of scaling the
achieved distance with body size. As this has challenges on its own (the choice of fair scaling func-
tion), in this experiment we instead decided to compare metamorphic individuals with two types of
robust individuals: animats that were allowed to grow for 600 time steps and animats that were
grown for 1200 time steps. We expected that robust individuals would thus have a size advantage
in the latter case. Having already observed the superior performance of the novelty search algorithm,
we evolved amphibious designs using novelty search as well.
Figure 20a shows the aggregate results of repeated evolutionary runs. The metamorphic individ-
uals clearly outperform robust individuals that were allowed to grow for 600 time steps. The par-
simonious explanation here is however that the longer development time of adults biased evolution
towards producing larger individuals, hence the larger distances achieved. The benefit of increased
development time becomes obvious when we look at the results achieved by the robust robots that
were allowed to grow for 1200 time steps: They clearly outperform those grown for a shorter time.
Although the average fitness of the robust individuals is not significantly different from that of meta-
morphic ones in the presented experiment, the variance of the data in the former case is much lower,
revealing that robust solutions are all of mediocre quality. On the other hand, despite novelty search
Figure 20. (a) Comparison of the performance of metamorphic individuals with amphibious designs. (b) Comparison
of the distances achieved by each developmental stage for the most favorable metamorphic scenario (aquatic larva
and terrestrial adult) and the most favorable amphibious scenario (development time of 1200 steps).
292
Artificial Life Volume 22, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
3
2
7
1
1
6
6
6
3
0
1
a
r
t
l
/
_
a
_
0
0
2
0
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Joachimczak et al. Artificial Metamorphosis: Evolutionary Design of Transforming, Soft-Bodied Robots
discovering some poor-quality metamorphic individuals, in both types of metamorphic experiments
the best individuals found were much better than the best ones from the robust experiments.
Figure 20b further compares the actual distances achieved in each type of environment in the
experiments that produced the best metamorphic individuals (viz., the ones with aquatic larvae and
terrestrial adults) and the best robust ones (viz., the ones grown for 1200 time steps). The two types
of experiments lead to comparable distances achieved in the terrestrial environment, and thus the
overall higher fitnesses of metamorphic individuals come from evolution being able to specialize the
aquatic stage and achieve longer distances when swimming.
The above results show that evolutionary search indeed finds metamorphic solutions that have
better performance than their robust alternatives. What may be surprising, however, is that robust
individuals grown for 1200 steps were able to reach performance almost at the level of metamorphic
individuals. We think it is largely a result of the configuration of our simulated system, in which it so
happens that a morphology and controller that can move in the simulated fluid can also exert enough
forces to move the same body on the ground. Changing physical constants related to body strength
would likely tip the balance much more in favor of metamorphic individuals.
4.7 Comparison with Specialized Robots
Each developmental stage of a metamorphic individual shares the same genetic machinery. Thus, it
should be expected that it introduces certain tradeoffs and limitations on the designs that could be
achieved using this approach—after all, the morphology of a larva not only has to be adapted to its
specific environment, but also needs to be malleable to the environment it has to move in during the
adult stage. The same applies to the genetic program that creates it: A single network has to be able
not only to control development in a way that leads to the emergence of the first morphology, but
also to control its metamorphosis. Specialized robots, each optimized independently for its target
environment, are free from these additional costs and thus should perform better in their respective
environments, much as a sports car will outperform an all-terrain vehicle on a highway. Indeed,
attempting to evolve individuals specialized for either aquatic or terrestrial environments would re-
sult in individuals that can move faster than corresponding life stages of metamorphic individuals.
We wondered, however, if scenarios exist in which the very necessity to come up with a malleable
design could make it easier to evolve a single metamorphic robot rather than to evolve two special-
ized ones independently. We hypothesized that one scenario in which this could happen would be if
evolving a design specialized for a particular problem de novo were difficult, but at the same time,
evolving a solution for a related problem could be much easier. In such a case, the need to perform
metamorphosis would guide an evolving population towards a region of search space that would
otherwise be difficult to discover.
To see if this could be the case, we investigated a scenario in which individuals were evolved for
two types of terrestrial gaits: Larvae had to move on a flat, horizontal surface, whereas adults had to
climb a sloped (17 degrees) surface and avoid sliding or rolling down. As both types of environ-
ments are terrestrial, it can be expected that morphologies for both would share the overall plan and
hence metamorphosis would need only relatively small adjustments to the body structure. At the
same time, an attempt to evolve specialized individuals to climb a slope is likely to experience the
bootstrapping problem, as finding initial solutions that can move uphill rather than roll or slide down
the slope may be difficult. To shorten the computation time, we reduced the maximum allowed
number of cells in the individuals to 128, which also allowed us to shorten the total development
time, from 1200 to 800 time steps (400 for the larval stage). Anticipating the bootstrapping problem,
we have used the progressive fitness approach (Section 3.2). Specialized individuals were evolved
using normal, NEAT search (the fitness was a single objective, viz., the distance achieved by a spe-
cialized robot). In each type of experiment, the fitness function rewarded only moving right.
We performed three types of evolutionary runs, each repeated 20 times using different random
seed values. The first involved evolving a metamorphic individual, and the remaining two were
individuals specialized for each of the environments. To make the comparison fair and avoid our
Artificial Life Volume 22, Number 3
293
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
3
2
7
1
1
6
6
6
3
0
1
a
r
t
l
/
_
a
_
0
0
2
0
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Joachimczak et al. Artificial Metamorphosis: Evolutionary Design of Transforming, Soft-Bodied Robots
Figure 21. Two examples of metamorphic individuals that move on a horizontal surface in their larval stage and climb a
slope in their adult form.
systemʼs bias towards producing smaller larvae and larger adults in the metamorphic scenario, we
allowed specialized individuals for the horizontal surface to develop for exactly the same number of
time steps as larvae of metamorphic individuals, namely, for 400 time steps.
The number of generations was the same in each type of experiment. Therefore, the amount of
computational time spent on obtaining a single metamorphic solution was not larger than that spent
for two separate individuals. In fact, it was smaller, as growing two specialized individuals would
mean 400 and 800 separate developmental steps, but only 800 in the case of a single metamorphic
individual.
The amount of observed change during metamorphosis in evolved animats was smaller than in
the case of aquatic and terrestrial individuals, though that should not be surprising: The two target
environments are closely related. We present two examples of metamorphic individuals obtained
with this method in Figure 21. Both individuals show only a minor morphological change. The in-
dividual in Figure 21a increases the surface of contact of its tail, while the one in Figure 21b shifts its
center of mass towards the front with additional cells and an appendage. The best individuals that we
observed would, however, only change their controllers, by adjusting the oscillation frequency of
their cells.
Figure 22 compares the average performance of individuals obtained using each evolutionary
search method, showing the performance of each stage of metamorphic individuals separately. As
can be seen in Figure 22a, after evolutionary pressure for slope climbing starts to increase after
generation 333, the performance of the larval stage of metamorphic individuals progressively de-
creases, being traded for the performance of the adult form. After 1000 generations, the individ-
uals specialized in moving on the horizontal surface achieve much longer distances than the
corresponding larvae of metamorphic solutions. The situation is reversed, however, if we look at
Figure 22. Performance of metamorphic individuals and specialized ones over evolutionary time: (a) larvae moving on a
horizontal surface, and specialized individuals evolved for the same environment; (b) adults climbing uphill, and
specialized individuals evolved for climbing. Lines show averages of 20 independent evolutionary runs each; color
stripes represent 95% bootstrapped confidence intervals for the averages.
294
Artificial Life Volume 22, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
3
2
7
1
1
6
6
6
3
0
1
a
r
t
l
/
_
a
_
0
0
2
0
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Joachimczak et al. Artificial Metamorphosis: Evolutionary Design of Transforming, Soft-Bodied Robots
the performance of metamorphic adults and animats specialized in climbing the slope. Here, for the
first 333 generations, the fitness of the metamorphic adults remains at 0, which means that before the
selection pressure was applied, all of these adults failed to move up the slope. Their improvement
over evolutionary time proceeds rapidly, and after 1000 generations they outperform specialized
solutions, though at the cost of lower performance on a flat surface. Additionally, if we considered
only the slope-climbing phenotypes and a matching number of evaluations in the virtual environment
for the two methods (i.e., metamorphic individuals evolved for 1000 generations and specialized ones
evolved for 2000 generations), the average performance of the specialized ones was still lower (mean
271 versus 340, although the difference between the final fitnesses was not statistically significant,
with large standard deviations of 204 and 319, respectively).
Ultimately, we think that the much faster improvement over evolutionary time of metamorphic
individuals can be best explained by the fact that the adult form does not have to be discovered
de novo, but instead emerges as a modification on top of the already functional larva. Naturally, other
methods exist to address the bootstrap problem that the specialized individuals faced. For example,
it is likely that increasing the angle of the slope progressively (or in stages) would help evolutionary
search. Furthermore, based on our preliminary runs, evolving metamorphic individuals is advanta-
geous only in a certain range of slope angles. This is to be expected: A very low angle will pose no
challenge when attempting to evolve a specialized hill climber, whereas for high angles, both
approaches will fail to find working solutions. Nonetheless, we see this experiment as a confirmation
that in certain scenarios, evolving metamorphic robots could allow us to discover useful solutions
faster than simply trying to evolve a set of specialized ones. In such cases, the necessity to evolve a
metamorphic design works as a scaffolding technique, helping the evolutionary search discover
stepping stones necessary to produce the desired solution.
5 Summary and Future Work
In this work, we have investigated how the concept of metamorphosis can enhance artificial devel-
opmental processes used to evolve designs of robotic morphologies and controllers. Metamorphosis
allowed us to evolve solutions in which a single genome encodes two related phenotypes, each
crafted for a different problem and/or environment, together with a method of self-restructuring
one phenotype into the other. We found that, given a biologically inspired model of development
(one that progressively constructs a body), this required simply employing a fitness function that
rewards each developmental stage for a different objective. We observed how evolution, searching
for morphologies de novo, without any prior assumptions about what they should be, was able to
discover designs that are well adapted to different tasks at each stage of development. Observed
rearrangements were highly reminiscent of amphibian metamorphosis in that we commonly ob-
served the growth of appendages for walking in terrestrial environments and tails for swimming,
as well as their removal after they were no longer needed. Reversing the order of environments
in which growing individuals were evaluated allowed us to confirm that observed morphological
changes were clearly a result of evolution shaping growing morphologies in a convergent way: legged
locomotion for a terrestrial environment and undulatory swimming for an aquatic one, regardless of
the order of evaluation. A further comparison with the evolution of a single amphibious solution
allowed us to find that metamorphic individuals indeed produced useful specialization, outperform-
ing environmentally robust solutions.
Finally, we were able to show that in scenarios where the two tasks in which each developmental
stage is evaluated are closely related, evolving a metamorphic, dual design can actually be faster than
evolving two specialized solutions independently. This means that even if we do not consider the
enormous advantages metamorphosis would bring to robots by allowing them to switch between
different environments, simply using metamorphosis as a method of evolving two designs at the
same time and disregarding the element of self-transformation can still be computationally advan-
tageous in some situations.
Artificial Life Volume 22, Number 3
295
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
3
2
7
1
1
6
6
6
3
0
1
a
r
t
l
/
_
a
_
0
0
2
0
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Joachimczak et al. Artificial Metamorphosis: Evolutionary Design of Transforming, Soft-Bodied Robots
The results presented in this work should be considered far from being a limit of what could be
achieved by exploiting the concept of metamorphosis. One of our design goals for the developmen-
tal system was to reduce constraints put on the evolutionary process, and we did so in order to
investigate what level of complexity of designs can be produced through evolutionary search alone
and how different they can be from what a human engineer might come up with. In our line of
research we are interested in finding ways of harnessing the creative potential of the evolutionary
process, with human bias removed, and we see in mimicking the way shape and form evolve in
nature a promising method to achieve that. We can however easily imagine methods that improve
the quality of obtainable designs by including more knowledge about problem domain in the search
algorithm and constraining the search space. For example, the use of multi-objective optimization is
likely to produce better results than the approach used in this article. Also, the way the development
is organized currently is such that mutations are likely to interfere with both developmental stages.
However, biological metamorphosis is well studied, and it is known that often a single hormonal
trigger induces metamorphosis. It does so by activating whole ensembles of physically closely lo-
cated genes associated with the new developmental stage. This was observed as early as in the 1950s
in developing Drosophila larvae and is visible owing to what is known as chromosomal puffing: an
enlargement of chromosomal regions that are undergoing transcription [26]. Hence, we expect
that using a mechanism that either fully or partially separates developmental stages on a genetic level
(e.g., by having genes explicitly assigned to each stage) is likely to enhance the evolvability of meta-
morphosis. We plan to investigate this in the future.
Finally, we believe that, given its relatively simple and generic design, the important result of this
article is that it shows how metamorphosis and fine-grained self-assembly, such as multicellular
development, are a natural combination, where the former enhances the latter. It is also easy to
see why: Metamorphosis and multicellular development are two sides of the same coin. We thus
hope that metamorphosis can find its use whenever artificial development is used as a method of
automated design.
Acknowledgments
This work was supported by the Japan Society for the Promotion of Science through the JSPS Fel-
lowship for Foreign Researchers and JSPS KAKENHI grant 26-04349. High-performance com-
puting resources were provided by the Interdisciplinary Center for Molecular and Mathematical
Modeling (University of Warsaw) and the Tri-City Academic Computer Center (TASK). The CGAL
library was used.
References
1. Bongard, J. (2011). Morphological change in machines accelerates the evolution of robust behavior.
Proceedings of the National Academy of Sciences, 108(4), 1234–1239.
2. Bongard, J. C., & Pfeifer, R. (2003). Evolving complete agents using artificial ontogeny. In F. Hara & R.
Pfeifer (Eds.), Morpho-functional Machines: The new species (pp. 237–258). Tokyo: Springer.
3. Calisti, M., Giorelli, M., Levy, G., Mazzolai, B., Hochner, B., Laschi, C., & Dario, P. (2011). An
octopus-bioinspired solution to movement and manipulation for soft robots. Bioinspiration & Biomimetics,
6(3), 036002+.
4. Carroll, S. (2005). Endless forms most beautiful: The new science of evo devo and the making of the animal kingdom.
New York: WW Norton & Company.
5. Cheney, N., MacCurdy, R., Clune, J., & Lipson, H. (2013). Unshackling evolution: Evolving soft
robots with multiple materials and a powerful generative encoding. In Proceedings of the 15th Annual
Conference on Genetic and Evolutionary Computation, GECCO ʼ13 (pp. 167–174). ACM.
6. Chervenski, P., & Ryan, S. (2014). MultiNEAT. http://multineat.com (configuration file: http://pastebin.
com/TTY3UKtt).
7. Corucci, F., Calisti, M., Hauser, H., & Laschi, C. (2015). Novelty-based evolutionary design of morphing
underwater robots. In Proceedings of the Genetic and Evolutionary Computation Conference, GECCO ʼ15
(pp. 145–152). ACM.
296
Artificial Life Volume 22, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
3
2
7
1
1
6
6
6
3
0
1
a
r
t
l
/
_
a
_
0
0
2
0
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Joachimczak et al. Artificial Metamorphosis: Evolutionary Design of Transforming, Soft-Bodied Robots
8. Deb, K. (2009). Multi-objective optimization using evolutionary algorithms (1st ed.). New York: Wiley.
9. Dellaert, F., & Beer, R. D. (1996). A developmental model for the evolution of complete autonomous
agents. In From animals to animats 4: Proceedings of the 4th International Conference on Simulation of Adaptive
Behavior (SAB 1996) (pp. 393–401). Cambridge, MA: MIT Press.
10. Eggenberger Hotz, P. (1997). Evolving morphologies of simulated 3D organisms based on differential
gene expression. In Proceedings of the 4th European Conference on Artificial Life (ECAL 1997) (pp. 205–213).
Cambridge, MA: MIT Press.
11. Groombridge, B. (Ed.) (1992). Global biodiversity: Status of the Earthʼs living resources: A report. London:
Chapman & Hall.
12. Hiller, J., & Lipson, H. (2012). Automatic design and manufacture of soft robots. IEEE Transactions
on Robotics, 28(2), 457–466.
13. Hiller, J. D., & Lipson, H. (2010). Evolving amorphous robots. In Artificial life XII: Proceedings of the 12th
International Conference on the Simulation and Synthesis of Living Systems (pp. 717–724). Cambridge, MA: MIT Press.
14. Jabr, F. (2012). How did insect metamorphosis evolve? Scientific American (online, 10 Aug.). http://www.
scientificamerican.com/article/insect-metamorphosis-evolution/.
15. Joachimczak, M., Suzuki, R., & Arita, T. (2014). Fine grained artificial development for body-controller
coevolution of soft-bodied animats. In Artificial life 14: Proceedings of the 14th International Conference
on the Synthesis and Simulation of Living Systems (pp. 239–246). Cambridge, MA: MIT Press.
16. Joachimczak, M., Suzuki, R., & Arita, T. (2015). Improving evolvability of morphologies and controllers
of developmental soft-bodied robots with novelty search. Frontiers in Robotics and AI, 2.
17. Joachimczak, M., & Wróbel, B. (2012). Co-evolution of morphology and control of soft-bodied
multicellular animats. In Proceedings of the 14th International Conference on Genetic and Evolutionary
Computation, GECCO ʼ12 (pp. 561–568). ACM.
18. Komosinski, M., & Rotaru-Varga, A. (2002). Comparison of different genotype encodings for simulated
three-dimensional agents. Artificial Life, 7(4), 395–418.
19. Lehman, J., & Stanley, K. O. (2011). Abandoning objectives: Evolution through the search for novelty
alone. Evolutionary Computation, 19(2), 189–223.
20. Lehman, J., Stanley, K. O., & Miikkulainen, R. (2013). Effective diversity maintenance in deceptive domains. In
Proceedings of the 15th Annual Conference on Genetic and Evolutionary Computation, GECCO ʼ13 (pp. 215–222). ACM.
21. Mahfoud, S. W. (1995). Niching methods for genetic algorithms. Ph.D. thesis, University of Illinois at
Urbana-Champaign.
22. Mouret, J., & Doncieux, S. (2009). Overcoming the bootstrap problem in evolutionary robotics using
behavioral diversity. In IEEE Congress on Evolutionary Computation, CEC ʼ09 (pp. 1161–1168). IEEE.
23. Orki, O., Ayali, A., Shai, O., & Ben-Hanan, U. (2012). Modeling of caterpillar crawl using novel tensegrity
structures. Bioinspiration & Biomimetics, 7(4), 046006+.
24. Pilat, M. L., Ito, T., Suzuki, R., & Arita, T. (2012). Evolution of virtual creature foraging in a physical
environment. In Artificial life XIII: Proceedings of the 13th International Conference on the Simulation and
Synthesis of Living Systems (pp. 423–430). Cambridge, MA: MIT Press.
25. Rieffel, J., Knox, D., Smith, S., & Trimmer, B. (2013). Growing and evolving soft robots. Artificial Life,
20(1), 143–162.
26. Russell, S., & Ashburner, M. (1996). Ecdysone-regulated chromosome puffing in Drosophila melanogaster.
In L. I. Gilbert, J. R. Tata, & B. G. Atkinson (Eds.), Metamorphosis: Postembryonic reprogramming of gene expression
in amphibian and insect cells. New York: Academic Press.
27. Sareni, B., & Krahenbuhl, L. (1998). Fitness sharing and niching methods revisited. IEEE Transactions
on Evolutionary Computation, 2(3), 97–106.
28. Savard, J., Tautz, D., Richards, S., Weinstock, G. M., Gibbs, R. A., Werren, J. H., Tettelin, H., & Lercher,
M. J. (2006). Phylogenomic analysis reveals bees and wasps (hymenoptera) at the base of the radiation
of holometabolous insects. Genome Research, 16(11), 1334–1338.
29. Schramm, L., & Sendhoff, B. (2011). An animatʼs cell doctrine. In ECAL 2011: Proceedings of the 11th
European Conference on the Synthesis and Simulation of Living Systems (pp. 739–746). Cambridge, MA: MIT Press.
Artificial Life Volume 22, Number 3
297
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
3
2
7
1
1
6
6
6
3
0
1
a
r
t
l
/
_
a
_
0
0
2
0
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Joachimczak et al. Artificial Metamorphosis: Evolutionary Design of Transforming, Soft-Bodied Robots
30. Sfakiotakis, M., & Tsakiris, D. (2006). Simuun: A simulation environment for undulatory locomotion.
International Journal of Modelling and Simulation, 26(4), 350–358.
31. Shepard, W. D. (2002). Dryopidae. In R. H. Arnett, Jr., M. C. Thomas, P. E. Skelley, & J. H. Frank (Eds.),
American beetles, Volume II: Polyphaga: Scarabaeoidea through Curculionoidea (1st ed.) (pp. 121–122). Boca Raton,
FL: CRC Press.
32. Shepherd, R. F., Ilievski, F., Choi, W., Morin, S. A., Stokes, A. A., Mazzeo, A. D., Chen, X., Wang, M.,
& Whitesides, G. M. (2011). Multigait soft robot. Proceedings of the National Academy of Sciences, 108(51),
20400–20403.
33. Shimizu, M., & Ishiguro, A. (2007). A self-reconfigurable robotic system that exhibits amoebic locomotion.
In 2007 IEEE/ICME International Conference on Complex Medical Engineering (pp. 101–106). IEEE.
34. Sims, K. (1994). Evolving virtual creatures. In Proceedings of the 21st Annual Conference on Computer Graphics
and Interactive Techniques, SIGGRAPH ʼ94 (pp. 15–22). ACM Press.
35. Stanley, K. O., & Miikkulainen, R. (2002). Evolving neural networks through augmenting topologies.
Evolutionary Computation, 10(2), 99–127.
36. Steltz, E., Mozeika, A., Rodenberg, N., Brown, E., & Jaeger, H. (2009). JSEL: Jamming skin enabled
locomotion. In 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2009)
(pp. 5672–5677). IEEE.
37. Sun, Y., Song, Y. S., & Paik, J. (2013). Characterization of silicone rubber based soft pneumatic actuators.
In 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (pp. 4446–4453). IEEE.
38. Truman, J. W., & Riddiford, L. M. (1999). The origins of insect metamorphosis. Nature, 401(6752),
447–452.
39. Tufte, G. (2011). Metamorphosis and artificial development: An abstract approach to functionality. In
Advances in artificial life. Darwin meets von Neumann: Proceedings of the 10th European Conference on Artificial
Life (ECAL 2009) (pp. 83–90). Berlin: Springer.
40. Umedachi, T., Takeda, K., Nakagaki, T., Kobayashi, R., & Ishiguro, A. (2010). Fully decentralized control
of a soft-bodied robot inspired by true slime mold. Biological Cybernetics, 102(3), 261–269.
41. Wolpert, L., & Tickle, C. (2011). Principles of development (4th rev. ed.). New York: Oxford University Press.
42. Wood, D., Bruner, J. S., & Ross, G. (1976). The role of tutoring in problem solving. Journal of Child
Psychology and Psychiatry, 17(2), 89–100.
298
Artificial Life Volume 22, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
3
2
7
1
1
6
6
6
3
0
1
a
r
t
l
/
_
a
_
0
0
2
0
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3