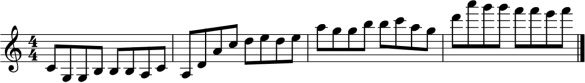Andrew R. Brown,∗ Toby Gifford,∗ - IA de Investigación especializada en el MIT

andres. Marrón,∗Toby Gifford,∗
and Robert Davidson†
∗Griffith University
140 Grey Street, South Brisbane, 4054, Australia
{andrew.r.brown, t.gifford}@griffith.edu.au
†The University of Queensland
St Lucia, Brisbane, 4072, Australia
r.davidson2@uq.edu.au

Techniques for Generative
Melodies Inspired by
Music Cognition

Abstracto: This article presents a series of algorithmic techniques for melody generation, inspired by models of music
cognition. The techniques are designed for interactive composition, and so privilege brevity, simplicity, and flexibility
over fidelity to the underlying models. The cognitive models canvassed span gestalt, preference rule, and statistical
learning perspectives; this is a diverse collection with a common thread—the centrality of “expectations” to music
cognition. We operationalize some recurrent themes across this collection as probabilistic descriptions of melodic
tendency, codifying them as stochastic melody-generation techniques. The techniques are combined into a concise
melody generator, with salient parameters exposed for ready manipulation in real time. These techniques may be
especially relevant to algorithmic composers, the live-coding community, and to music psychologists and theorists
interested in how computational interpretations of cognitive models “sound” in practice.

Gravity does not explain architecture, pero
architecture is subject to its law; likewise,
perceptual laws do not explain music, pero
music cannot escape their inﬂuence.

— Eugene Narmour (1990, pag. 4)

This article presents techniques for interactive
composition inspired by models of music cognition.
Many of the techniques presented here stem from
the practice of live coding—writing software that
generates music as a performance practice—and, en
particular, the challenge of real-time algorithmic
generation of melody.

Algorithmic composition has a long tradition
mostly focused on offline music generation, and live
coding is a decade-old and burgeoning digital per-
formance practice (McLean, Rohrhuber, and Collins
2014). Despite this, the generation of melodies in
real time is still relatively underdeveloped, con
many practitioners working in electroacoustic or
electronic dance music genres for which melody is
of peripheral interest.

Melodic construction has, sin embargo, been a central
touchstone for studies in music cognition, y ahí
has been particular focus on the principles of Gestalt
psychology—relating to the perception of holistic
structure and stable organization in the world. A
systematic application of Gestalt principles in music

Computer Music Journal, 39:1, páginas. 11–26, Primavera 2015
doi:10.1162/COMJ a 00282
C(cid:2) 2015 Instituto de Tecnología de Massachusetts.

theory was initiated by Leonard Meyer (1956) y
continued by Eugene Narmour (1992).

More recently, these ideas have been compared to
empirical data from computational music analysis
and modeled as probabilistic tendencies to which
people are sensitized through enculturation (Huron
2006; Temperley 2007). Tal como, these concepts
are amenable to computational implementation as
outlined in this article. Our motivation for this
work is to develop computer-assisted compositional
techniques for creative purposes and we are not
suggesting that the algorithms are either cogni-
tive or compositional models. En particular, we are
interested in achieving a parsimonious implementa-
tion that supports creative exploration, en vez de
providing a complete and accurate model of the
psychological process that inspired the algorithms.
The attention of many music cognition studies
is on symbolic music representations, En particular,
diatonic and metric music represented as a notated
puntaje. The techniques presented here inherit this
focus, and the examples use symbolic representa-
tion of music as “note” events. This article does not
discuss the direct application of these ideas to audio
signal processes—instead, we concentrate on prob-
abilistic modeling of melody, exemplified through
algorithmic music practices, for the application of
the techniques.

The choice of a common-practice musical context

for our research, which includes diatonic pitch
sets and metric rhythms, was made for several
razones. Primero, much of the music cognition research

Marrón, Gifford, and Davidson

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
/
C
oh
metro

j
/

a
r
t
i
C
mi
–
pag
d

F
/

3
9
1
1
1
1
8
5
6
0
4
9
/
C
oh
metro
_
a
_
0
0
2
8
2
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

that we are inspired by was conducted in these
contexts and its application beyond these is not
entirely certain. Segundo, the ability to judge the
success of the algorithmic techniques is made more
straightforward when comparing them to a well-
understood aesthetic framework. Finalmente, hay
many creative applications for diatonic and metrical
música, to which the techniques may be applied,
including most Western popular music.

Melody—a monophonic series of note events—is

an important musical element for many styles of
música, and consequently it is often an integral part
of the compositional process. Generated melodies
assist this process by providing material that may be
applied to a work in the form of musical riffs, bass
líneas, or themes, Por ejemplo.

Algorithmic music practices, especially live
codificación, benefit when techniques can be concisely
implemented and they are open to improvised mod-
ification (Brown and Sorensen 2009). In developing
these techniques inspired by music cognition, nosotros
have searched for succinct methods of expression
and sought to expose musically salient parameters
to facilitate control during live performance or
interactive composition. These practical consider-
ations have naturally acted as a filter on the types
and complexity of the psychological theories that
can be applied. En efecto, the individual techniques
we present are simplistic. In keeping with the
Gestalt perspective, sin embargo, we contend that their
use in combination amounts to more than their
sum. In implementing these techniques, tenemos
built on our previous work in algorithmic music
methods (Sorensen and Brown 2007) and utilized
libraries and design patterns from the Impromptu
programming environment (Sorensen 2005). el ex-
amples presented are coded in the language Scheme
with Impromptu extensions, although it should
be straightforward to translate them into other
computer music environments.

Fondo

The generative techniques presented in this article
take the form of probabilistic models from which

notes are generated stochastically. el uso de
probabilistic models has a long history in generative
música, both for sound synthesis (Xenakis 1992) y
for symbolic score generation (see Nierhaus 2009
for an overview). In score generation, probabilístico
models of music generation have included stochastic
grammars (Cope 2000), probabilistic music theory
(Cambouropoulos 1997), and purely statistical
modelos (Papadopoulos and Wiggins 1999).

Probabilistic models have also found their way
into perceptual theories of music. Adopting Meyer’s
(1956) theory of musical expectations, music cog-
nition researchers have articulated a “statistical
learning” account of musical expectations, y
formulated corresponding statistical descriptions of
música (Huron 2006, pag. 360). Such descriptions have
no, sin embargo, been widely utilized for generative
purposes. Some notable exceptions are Pearce and
Wiggins’s (2006) experiments in “analysis by syn-
tesis,” and the more recent work of Maxwell,
Pasquier, and Eigenfeldt (2011).

In this article, we implement functions for melody

generation loosely based on such probabilistic
models of expectation. Following Huron (2006),
Temperley (2007), y otros, we discuss these
techniques in relation to corresponding concepts
from Gestalt psychology, from which Meyer (1956)
and Narmour (1990) originally drew inspiration.

Proximity

Some of the better-known Gestalt principles are
those related to grouping. One of these is the law of
proximity, which states, “objects or stimuli that are
viewed as being close together will tend to be per-
ceived as a unit” (Corsini 1999). Although typically
discussed in terms of visual perception, the law of
proximity in its original formulation was proposed
to apply to both visual and auditory perception
(Wertheimer 1938). Numerous psychological studies
have established proximity as a general grouping
principle in music, via proximity in time (Deutsch
1999a), proximity in pitch (Bregman 1990), or prox-
imity or similarity along more abstract musical
dimensions (Deli `ege 1987).

Computer Music Journal

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
/
C
oh
metro

j
/

a
r
t
i
C
mi
–
pag
d

F
/

3
9
1
1
1
1
8
5
6
0
4
9
/
C
oh
metro
_
a
_
0
0
2
8
2
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 1. Gaussian
distribution used for
selecting the pitch,
dynamic, and duration
of a note.

Cifra 2. A random walk
function for iterative
melodic pitch selection.

Cifra 3. A random walk
exceeding reasonable
range bounds.

Cifra 1

Cifra 2

Cifra 3

These observations from music psychology are

Random Walk

consistent with rules expounded in traditional
composition texts advising that pitches in melodies
should often move by step, good voice leading
should minimize interval step size, etcétera (ver
Por ejemplo, Goetschius 1902).

For generative purposes, one of the areas where
proximity has an impact is in melodic sequences.
The code in Figure 1 uses a Gaussian distribution
for selecting the pitch, dynamic, and duration of a
nota. The use of a Gaussian distribution rather than,
Por ejemplo, a uniform distribution over a narrow
range, aligns with models from the literature (von
Hippel and Huron 2000; Temperley 2007), and seems
to us to produce pitch variation that sounds more
natural.

In Impromptu, the random-gaussian function
takes two arguments: mean and standard deviation.
The pitch is a MIDI pitch value in the range 0–127,
which we constrain within a diatonic pitch-class
colocar; the dynamic is a MIDI velocity, also in the
range 0–127; and the duration is in beats (1 beat =
1.0). This code will choose a random diatonic pitch
close to middle C (MIDI pitch 60) quantizing to a
C major (Ionian) pitch class set. Notes will have a
MIDI velocity near 100 and a duration of about 0.4
beats.

Pitch proximity, as a melodic tendency, can be
modeled by a random walk, a commonly used
process in generative music (Xenakis 1976; 1992,
pag. 289). A random walk is a sequence that moves
by randomly sized “steps.” That is, each element
is generated by adding a small step to the previous
element. We can use the Gaussian distribution to
construct a simple random walk melody as shown
in the code in Figure 2. The next pitch is randomly
selected in the last lines of the function.

Range Constraint

Although a random walk is an easy way to generate
material, the melody may meander beyond the
playable pitch range, as shown in Figure 3. El
beaming patterns in the early notated examples
are somewhat arbitrary. Later in the article metric
organization becomes explicit and time signatures
and barlines are introduced. Audio versions of the
musical examples accompanying this article are
available online at explodingart.com/cmj-melodies.
Equally problematic from the perspective of
music perception is that this undirected meandering

Marrón, Gifford, and Davidson

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
/
C
oh
metro

j
/

a
r
t
i
C
mi
–
pag
d

F
/

3
9
1
1
1
1
8
5
6
0
4
9
/
C
oh
metro
_
a
_
0
0
2
8
2
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 4. The elastic-g
function and a method to
constrain its output to a
diatonic context.

Cifra 5. Some output from
use of the elastic-g
function for pitch.

Cifra 4

Cifra 5

is at odds with computational musicology literature
claiming that “most melodies seem to favor the
center of their range” (von Hippel 2000, pag. 316).

A simple approach to range constraint is the
imposition of boundary limits by clipping. Hard
boundaries tend to trap values near the boundaries,
sin embargo, making for passages that sound unnatural.
A variation is to use “mirror” boundaries that
“bounce” the values away from the boundaries by
the extent of their overshoot (Xenakis 1992), cual
somewhat (but not entirely) mitigates boundary
hugging.

Alternativamente, in the spirit of research by von
Hippel and others we propose a range constraint
technique that operates by adding a tendency
toward the mean of the range. Rather than use of the
previous pitch as the point of departure for the next
step in the random walk, a mean value is selected
between the previous step and the middle of the
range.

This technique creates a kind of “elastic band”

fuerza (larson 2012) that increases with the dis-
tance away from the mean. Varying the strength
of this force—shown as the argument 8/10 en
Figure 4—allows the composer to control the pitch
range according to their stylistic preference. Code
implementing our elastic-g function is shown
En figura 4, with some example, iterated output
notated in Figure 5.

Goal-Oriented Behavior

The need for further structure in the melodies shown
so far is clear. The random walk process, even when

range-constrained, lacks larger-scale organization
and the “meandering” is, and sounds, directionless.
In music theory, the importance of “structural
tones” in a melody is widely discussed. Structural
tones, being important points in the harmonic and
melodic contexts, can provide points of climax,
variety, and resolution. In the field of musicology,
structural points in music have been characterized
as nodes in “time-span reductions” (Lerdahl and
Jackendoff 1983) or in “event hierarchies” (Bharucha
1984). Empirical research has found that structural
tones are important elements in musical improvisa-
ción (Large, Palmer, and Pollack 1995) and listening
(Bigand and Parncutt 1999).

Directed Random Walk

To provide the random walk melody with more
estructura, we constructed a technique that allows
target pitches to guide the melodic contour. We call
this a directed random walk.

The elastic-g function already has the desired
property of drawing the pitch toward a target; previ-
ously understood to be the middle of the range. A
obtain a directed random walk we combine the range
constraint tendency and the goal direction tendency
by calculating a moving target for the elastic-g
function that balances the two tendencies. So that
this is easy to use in dynamic creative contexts,
a new function that encapsulates this process is
creado, called directed-g. The code in Figure 6
shows the function and an example of using of it for
calculating a next pitch.

Computer Music Journal

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
/
C
oh
metro

j
/

a
r
t
i
C
mi
–
pag
d

F
/

3
9
1
1
1
1
8
5
6
0
4
9
/
C
oh
metro
_
a
_
0
0
2
8
2
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 6. The directed-g
function and its use in
selecting a pitch
constrained to a diatonic
contexto.

Hasta ahora, we have provided a process for moving
toward a single target. In order to provide a useful
guide to melodic contour, a series of pitch targets
is required, along with a way of progressing from
one to the next. A utility function, make-stepper,
was created to facilitate iteration through a list
of pitch values that will serve as structural tones.
When the target pitch is reached, the next target
pitch is selected. The code in Figure 7 implements
a directed random walk function that uses the
directed-g function and the make-stepper
utility.

The music in Figure 8 shows some typical output
from this directed Gaussian walk program. Notice
that each target (C5, G3, C6, and C4) is hit, eso
sometimes there is an overshoot of the target (either
before or after it is hit), and the time taken to hit
successive targets bears only a moderate correlation
to the pitch distance traveled.

Good Continuation

The Gestalt law of good continuation states that
there is an innate tendency to expect that a perceived
pattern or implied direction will continue. In music,
this might suggest that an upward series of pitches
can have a tendency to continue upwards, or that
an established 4/4 meter can be relied upon to
persist. Good continuation, entonces, is strongly aligned
with repetition, reuse, and development of musical
fragments.

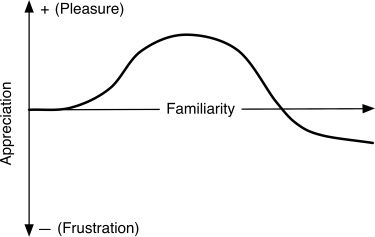
ance between interest and tedium changes with
repeated exposure was studied by the German psy-
chologist Wilhelm Wundt in the 1800s and resulted
in the Wundt curve, “a well-known arousal response
curve from studies of animals and humans to var-
ious forms of arousal” (Saunders and Gero 2001).
The curve, como se muestra en la figura 9, depicts change in
interest as the number of exposures (repetitions)
increase.

Meyer discusses this effect in the context of
música, by reference to the principle of saturation,
whereby “a figure which is repeated over and over
again arouses a strong expectation of change” (Meyer
1956, pag. 134).

Wundt’s theory suggests that recapitulation of
previous structure should be used in moderation to
maximize the benefits of familiarity and expecta-
ción, while avoiding being overly predictable and
uninteresting. In some musical circumstances, semejante
as in electronic dance music, repetition can become
stable and expectation of change is modified. en un
personal communication to the authors in 2013,
Narmour suggested that “once a certain point of
repetition is reached, the ongoing change recedes
to ground, like wallpaper, which is the nature of a
vamp (rather than ending in increasing frustration)."
En esta sección, we will look at techniques that help
provide more local structure and patterning, mientras
maintaining a degree of unpredictability.

Process

Wundt Curve

A factor that moderates tendencies of good con-
tinuation is the interest created by confounding
expectations: pleasant surprises. The way the bal-

According to Narmour, repeated notes (específicamente,
pitch repetition ignoring duration, which may
be different from note to note) and sequences
of small steps in the same direction are both
“subject to the bottom–up Gestalt laws of similarity,
proximity, and common direction” (Narmour 1990,

Marrón, Gifford, and Davidson

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
/
C
oh
metro

j
/

a
r
t
i
C
mi
–
pag
d

F
/

3
9
1
1
1
1
8
5
6
0
4
9
/
C
oh
metro
_
a
_
0
0
2
8
2
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 7. A melody
function iterates through a
list of pitch values that
serve as structural tones.

Cifra 8. Output from the
dir-g-walk program with
target pitches highlighted.

Cifra 9. The Wundt curve.

Cifra 7

Cifra 8

pag. 97). He suggests that when we hear repeated
intervals or pitches we infer a pattern, and anticipate
continuation of that pattern. Following Meyer, él
refers to a continuing pattern generally, incluido
repetition of “signed,” or directed, intervals, as a
registral process. Por ejemplo, a pitch step from C
to D would imply a step from D to E. In Narmour’s
theory, the process tendency only happens for
intervals smaller than five semitones. Por lo tanto,
in our implementation intervals smaller than five
semitones are candidates for repetition. Narmour’s
theory is more nuanced and proposes intervallic
proceso, where interval size is the expectation
regardless of direction.

Various theorists suggest, but for different
razones, that there is a tendency for a reversal
of direction after larger intervals. As indicated
previamente, we include procedures for ensuring
directional change that bear some similarity to
von Hipple’s (2000) notions of a regression to the
significar. We use a simplified notion of “process”
aquí, where directional momentum is maintained.
This can, en parte, be interpreted as a nod toward
the musical “forces” analogy proposed by Larson
(2012).

The code in Figure 10 shows our implementation

of an interval process tendency for use in our

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
/
C
oh
metro

j
/

a
r
t
i
C
mi
–
pag
d

F
/

3
9
1
1
1
1
8
5
6
0
4
9
/
C
oh
metro
_
a
_
0
0
2
8
2
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 9

melody generator, which will generate a repeat of
the previous interval when three conditions are
met. Primero, the interval should be less than a tritone.
Segundo, in keeping with the Wundt curve, el
number of consecutive processes (es decir., repeats) es
limited to four. Tercero, for variety, there is a small
(30 por ciento) chance that the intervallic process
will end on any given step. The percentage value
and maximum repeat value were chosen based on
experimentation and can be varied for aesthetic
efecto.

The process function created by make-process,

when called, returns either the next pitch in the
intervallic sequence or, if a nonsequence pitch needs

Computer Music Journal

Cifra 11. Use of the
repeat making function
make-process.

Cifra 10. This code
generates a function that
returns either the next
pitch in a sequence being
repeated or false when
repeat-halting conditions
are met.

Cifra 10

Cifra 11

to be selected, the value “false.” It can be embedded
into a melody generator as shown in Figure 11 con
the proc-g-walk function.

The effect of imposing some degree of interval
step process on the melody algorithm can be seen in
Cifra 12. There are more scalar and broken-chord
passages within the pitch contour. This reduces the
number of changes in direction and provides some
greater sense of intentionality at the note-by-note
nivel.

Segment Process

Hasta ahora, we have focused on the ways in which
pitch sequences are organized, based on features
that aid perceptual continuity. Many studies from
both music cognition and music theory have also
emphasized the way humans structure music into
larger chunks, or segments. Studies from both music

theory (Goetschius 1902) and music perception
(Narmour 1973; Huron 2006) have highlighted
the musical importance of structured reuse of
musical segments such as motifs, themes, y
variations. Reuse of materials makes the larger-scale
structuring quite evident, and studies have shown
that sequences structured in this way are easier to
understand and recall, and perhaps more readily
appreciated (Deutsch 1999b).

Por simplicidad, we focus on segment repetition
(possibly transposed), while continuing our strategy
of including stochastic variation to add novelty and
interés.

A utility function make-seg-repeat does much

of the hard work for repeating segments of the
melody. Like the make-process function, it takes
care of “remembering” recent note pitches, pero
in this case it stores the last n values, dónde
n is specified when the function is called. El
variability allows the composer to determine, en

Marrón, Gifford, and Davidson

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
/
C
oh
metro

j
/

a
r
t
i
C
mi
–
pag
d

F
/

3
9
1
1
1
1
8
5
6
0
4
9
/
C
oh
metro
_
a
_
0
0
2
8
2
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 12. A notated
sample of output from the
process-g-walk program.

Cifra 13. Output from the
seg-g-walk program.

Cifra 12

Cifra 13

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
/
C
oh
metro

j
/

a
r
t
i
C
mi
–
pag
d

F
/

3
9
1
1
1
1
8
5
6
0
4
9
/
C
oh
metro
_
a
_
0
0
2
8
2
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

run time, how large a segment should be to match
local considerations, such as metric context. El
second argument is bypass-amnt, which specifies
the degree to which the stored values should be
replaced with newly generated values.

There are options in the make-seg-repeat
function to allow for transposition of the segment.
The two options available are: (1) transpose-
range, the distance either side of the original
pitch the repetition may be transposed, measured
in semitones; y (2) pitch-class-set, the scale
that will be used for the transposition, which is most
likely to be the same as that used in other parts of the
generative process and will allow for approximately
diatonic transpositions. At the start of each repeated
secuencia, a random transposition amount within
the range is chosen. This function returns another
función, named seg-repeat, shown here, cual
is the function most directly used while composing
or performing:

(define seg-repeat (make-seg-repeat 4

0))

The use of the seg-repeat function is quite
straightforward. All pitches are passed through it
just before playback and the function either passes

these pitches on, or it replaces them with those from
a repeating segment it has stored. This approach is
achieved using the following code:

(colocar! pitch (seg-repeat pitch))

Output from the melody generation program
using seg-repeat is displayed in Figure 13. El
segment length is set to four, and the transpose
range value to two, which allows for sequences as
well as direct repetitions, and the bypass value is
set to 0.3, which introduces some variety into the
repetitions.

Rhythmic Pulse and Ratios

Up to this point we have neglected rhythm in
constructing melodies. We now apply the concept
of process to the sequential ordering of rhythmic
valores. Music is often pulse based, and durations
are generally simple multiples or divisors of this
pulse. In Western music theory, this is evident in the
relationships between commonly used durations.
In music psychology, the phenomenon of pulse
and of intervals of simple pulse ratios has been
demonstrated outside of any cultural music context

Computer Music Journal

Cifra 14. Code to generate
and play back a melody
that now includes
rhythmic variation
selected by the
next-g-beat function.

by various “tapping” tests (p.ej., Fraise 1984). Nosotros
are interested here in the selection, orden, y
distribution of durations for our melody case
estudiar.

Taking as a starting point the isochronous eighth-
note pattern we have used in examples until now, nosotros
can elaborate the rhythm by implementing simple
divisions and groupings of the eighth note. This has
a correspondence with dynamic attending theory
(Jones and Boltz 1989). Following the terminology
of this model, the eighth-note pulse serves as the
referent time period that “anchors” our temporal
atención. Subdivision and larger groupings of the
referent period are perceived as such.

Restricting attention to the ratio two, Por ejemplo,

rhythmic elaborations of the simple eighth-note
pulse are either subdivided into two sixteenth notes,
sticking with the eighth note, or extended to a
quarter note. To choose from this set of durations
we select randomly, with a Gaussian distribution
centered on the referent period (eighth note), y
quantize to this discrete set of choices.

To implement Gaussian selection of durations
from a set, we have developed some utility functions
using design patterns similar to those shown above
for pitch. Uno de estos, next-g-beat, will be used
directly. It accepts the previous duration value
and returns the next one. The function exposes
parameters that we feel are valuable to vary in real
tiempo. These include the referent time period (cual
might change infrequently), the duration list that
includes all the duration values from which to select
(typically an ordered set with the referent period in
the middle of the list), and the mean and standard

deviation values for the Gaussian distribution.
Varying the standard deviation is particularly useful
because as this value gets higher it makes it more
likely that outlying values (toward either ends of
the list) are selected. As with our early descriptions
of pitch organization, one perceptual effect that is
not taken into account in this implementation is
the ordering of rhythmic values, or groupings, nor
the musical significance of increasing or decreasing
information rates (note density).

We use the next-g-beat function as part of our
melody program, rhythmic-g-walk, which selects
note durations and ensures rhythmic groupings
based on the referent duration (one half beat, en esto
caso). In this code fragment, we have also added to
the play function some variation in onset timing
using the optional second argument. We also added
some variation in the performed duration of each
note—varying from 60 por ciento a 100 por ciento de
the interonset duration. The latest version of the
programa, which includes the rhythm generator, es
displayed in Figure 14. An example of output is
como se muestra en la figura 15.

As an experiment in the utility of the next-g-
beat function for variation at run time, the music
En figura 16 was generated by the same rhythmic-
g-walk program but with some changes: lo mismo
referent period, an addition to duration values to
include triplets, and a wider standard deviation for
more even use of the durations. Cifra 16 displays
output generated using the following settings:

(next-g-beat dur 1 (lista 1/3 1/4 1/2

1) 0 1.5)

Marrón, Gifford, and Davidson

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
/
C
oh
metro

j
/

a
r
t
i
C
mi
–
pag
d

F
/

3
9
1
1
1
1
8
5
6
0
4
9
/
C
oh
metro
_
a
_
0
0
2
8
2
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 15. Sample output
from the rhythmic-
g-walk program.

Cifra 16. Adding variety
that is more rhythmic by
varying beat selection
parámetros.

Cifra 17. Pulse strengths
en un 4/4 meter. (Adapted
from Lerdahl and
Jackendoff 1983.)

Cifra 15

Cifra 16

Metric Contextual Sensitivity

Musical meter is frequently described as a regular
pattern of strong and weak pulses (Cooper and
Meyer 1960; Lerdahl and Jackendoff 1983; Large
1994). Londres (2004, pag. 4) maintains that “meter is
a perceptually emergent property of musical sound,
eso es, of our engagement with the production
and perception of tones in time.” A number of
factors contribute to emphases of pulses (and hence
perception of meter) including accent, duración,
harmony, and timbre (Cooper and Meyer 1960,
pag. 7).

The manner in which musical features depend
on their position within the meter is an important
aspect of melodic structure (Narmour 1990; Lon-
don 2004). We refer to position of a beat within
the metrical pattern (such as downbeat, segundo
beat, etc.) as the metric context. En esta sección,
we discuss the importance of metric context, y
how we can use it to condition statistical distribu-
tions of dynamics, pitch, duración, and harmonic
progresión.

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
/
C
oh
metro

j
/

a
r
t
i
C
mi
–
pag
d

F
/

3
9
1
1
1
1
8
5
6
0
4
9
/
C
oh
metro
_
a
_
0
0
2
8
2
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 17

Metric Emphasis

The strength of various beat locations within the
meter is often shown as equivalent to the number
of metrical levels within which the beat belongs, como
como se muestra en la figura 17.

Metric emphasis differs from accent, cual es
a surface level property of the music. Accent may
be created by stress, by dynamics, by articulation
(Cooper and Meyer 1960, pag. 7), or more generally

Computer Music Journal

Cifra 18. Metric-g-walk
with metrically
conditioned pitch and
duración.

by a contrasted value of any salient musical param-
eter (Deli `ege 1987). Metric emphasis, in contrast,
is a purely perceptual phenomenon formed in re-
sponse to the patterning of accents. In order for
meter to emerge from patterning of accents, él
seems reasonable that the distribution of accents
should be conditioned in some way by the metric
contexto.

Some studies (Huron 2006; Temperley 2007)
have found that note onset probabilities correlate
with metric emphasis. Dynamics are also assumed
to correlate with metric emphasis (Cooper and
Meyer 1960; Clynes 1983), and harmonic changes
are most likely to occur on downbeats (Temperley
2007). Además, our own research indicates that
probability distributions for both duration and tonal
stability depend on metric emphasis.

In the following sections we implement a form
of metric contextual conditioning for these musical
parameters in our melody generator. In the interest
of brevity, we adopt a single simple mechanism
for approximating the contextual behavior of these
parámetros. The value for each parameter (dynamic,
pitch, duración, and harmony) is randomly selected
from a discrete list of possible values. These lists
are ordered by level of emphasis. Por ejemplo, el
possible values for pitch are drawn from the list
of diatonic scale degrees, ordered by tonal stability
based on the Krumhansl-Kessler key profiles: 1 5 3 4
6 2 7 (Krumhansl and Kessler 1982). In a given metric
context this list will be truncated, sin embargo, further
constraining the possible values. On the downbeat,
Por ejemplo, the list is truncated to triadic pitches
(es decir., 1 5 3) whereas on a metrically weak offbeat the
full list is available for random selection. Similarmente,
a list of available dynamics ordered from loud to
soft, and durations from long to short, are truncated
according to metric context. This technique is
implemented by the function shrink-list.

Metric Constraints

One application of the shrink-list function is for
pitch selection. The function is used as a modifier
for the pitch-class list, and the result is passed
to the pc:quantize function. The argument for
minimum length is set to three, so that the most
restrictive list (used on the downbeat) consists of the
first three pitches in the list—the triadic pitches.

(pc:quantize next-pitch (shrink-list

beat ’(0 7 4 5 9 2 11) 3))

To modify duration choices the shrink-list func-

tion is applied to the list of available durations
before selection. Recall that the second argument is
the reference time period (set here to 1 [es decir., a quarter
nota]) and that the duration list values have been
selected to be ratios of the reference time period
(p.ej., the argument 1/2 represents an eighth note).

(next-g-beat dur 1 (shrink-list beat

'(1 1/2 1/4 1/3) 2) 0 1)

The output shown in Figure 18 demonstrates that

with the metric constraints in place notes on the
downbeat are pitch limited to C, mi, and G and that
rhythmic groupings are based on the referent time
período; a quarter note.

Harmonic Progression

To implement a change in harmonic context,
substitutions to the active pitch class set can be
hecho. These changes are controlled by a simple
Markov process—a common approach to modeling
chord progression expectations that we based on
work by Huron (2006, pag. 251). A change of harmonic
context is triggered at the end of every four beats.

Marrón, Gifford, and Davidson

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
/
C
oh
metro

j
/

a
r
t
i
C
mi
–
pag
d

F
/

3
9
1
1
1
1
8
5
6
0
4
9
/
C
oh
metro
_
a
_
0
0
2
8
2
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 19. A melody with
shifts between C, D, y
B(cid:2) major.

Cifra 19 shows a sample of the output after
adding this change. For the purpose of visual clarity,
harmonic changes between C, D, y B(cid:2) major were
specified (even thought this is an unlikely harmonic
progresión) so that additional accidentals would
make the transitions more obvious in the notation.

Closure

Closure, or stability, is a fundamental notion in
Gestalt psychology, playing a complementary role
to good continuation, o proceso. The techniques
described earlier seek to engender continuation,
movimiento, momentum, instability, or otherwise imply
that the music is ongoing. Closure, conversely, es un
perception of completion, repose, or stability (Meyer
1956, pag. 139). Compositionally, we will use closure
to provide a sense of phrasing.

As a first step towards utilizing closure in
dynamic algorithmic music systems, we sought
to create a real-time measure of the “level of
closure” in a generated musical stream. Inspired
by Meyer’s theory, we consider numerous factors
as contributing to the overall sense of closure.
Completion of pattern—melodic, harmonic, y
rhythmic—are key components. Además, el
local dynamics of various musical parameters,
without reference to prior patterning, is attributed
with closural power (Meyer 1956, pag. 81).

Narmour (1990) has articulated an explicit theory

of parametric closure. His conditions of closure
include a number of simple properties of note-
to-note transitions: movement from a short to

long duration, weak to strong metric emphasis,
dissonance to consonance, large to small interval,
and change in registral direction.

We have previously implemented computational

analyses for tracking these conditions of closure
(Marrón, Gifford, and Davidson 2012), and applied
them to a corpus of folk songs, to find patterns of
congruence among the parameters and to assess their
relative contributions to melodic completion. Allá
we concluded that rhythmic, métrico, and tonal
conditions of closure contributed most strongly.

Phrase Endings

Meyer suggested that points of strong closure ar-
ticulate melodic structure, acting as the endpoints
of perceptual objects in the musical surface. Por
calculating a real-time measure of the total paramet-
ric closure in our generated melodies, we hope to
identify “opportune” moments for ending phrases,
or ending the melody. We have implemented closure
functions independently for metric, tonal, dynamic,
and durational closure. The total-closure func-
tion calculates the sum of these.

We have found that designing an algorithm to

find opportune points to stop playing is one of
the more problematic generative music tasks, y
this function seems to be reasonably effective,
though not entirely reliable. The notated examples
presented previously have used manually selected
end locations, but Figure 20 shows an entire melody
generated and halted by the melody program using
the closure measure.

Computer Music Journal

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
/
C
oh
metro

j
/

a
r
t
i
C
mi
–
pag
d

F
/

3
9
1
1
1
1
8
5
6
0
4
9
/
C
oh
metro
_
a
_
0
0
2
8
2
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 20. A melody
generated and concluded
algorithmically.

Cifra 21. A function that
integrates all the
techniques presented in
this article.

Cifra 20

Cifra 21

The code in Figure 21, closure-g-walk, no-
grates all the techniques presented in this article,
and produced the melody shown in Figure 20. El
size and complexity of the code are manageable
for creative purposes, although a complete work
would likely include more than melodic phrases.
The code is densely packed with variables that
enable run-time editing and manipulation. Como nosotros
have seen throughout this article the techniques
can be accumulated, and some could be omitted
as required. This ability for code structure to have
a developmental quality is particularly important
for performative practices—allowing a kernel of an
idea to be quickly articulated and then elaborated
con el tiempo. This kind of functionality can also assist

compositional processes and the fluid development
of melodic ideas.

As these techniques have been developed, ellos
have been tested in our musical practice. en par-
particular, they were used by the authors for the
performance of the original work Multiple Begin-
nings at the First International Live Code Festival
(Alemania) in April 2013; for the audio-visual in-
stallation Connections, selected for inclusion in
el [d]Generate exhibition of generative art at the
Gympie Art Gallery (Australia) in June 2013 (a
video excerpt of Connections is available online
at vimeo.com/67930857); and in the composition
of a work titled Entanglement, presented at the
2013 International Computer Music Conference

Marrón, Gifford, and Davidson

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
/
C
oh
metro

j
/

a
r
t
i
C
mi
–
pag
d

F
/

3
9
1
1
1
1
8
5
6
0
4
9
/
C
oh
metro
_
a
_
0
0
2
8
2
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 22. Results from the
listening trials including
the trend slope.

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
/
C
oh
metro

j
/

a
r
t
i
C
mi
–
pag
d

F
/

3
9
1
1
1
1
8
5
6
0
4
9
/
C
oh
metro
_
a
_
0
0
2
8
2
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

(a video of Entanglement is available online at
vimeo.com/82061102). As a further check on their
eficacia, they were subjected to some external
aesthetic evaluation.

Evaluation

In order to assess the effect of the incremental
developments in the melody algorithm, examples
of the generated output at each stage were recorded
and evaluated by experienced musicians.

Three melodies were sequentially generated
for each of ten stages of the developing melody
algoritmo. Audio examples of these 30 melodies
played by computer on a digital piano were presented
to participants in random order. These melodies
can be accessed online at explodingart.com/cmj-
melodies, where they have been categorized by
stage. Había 32 Participantes, all of whom were
experimentado, adult musicians. Los participantes fueron
asked to rank the melodies from poor to good on a
seven-point scale.

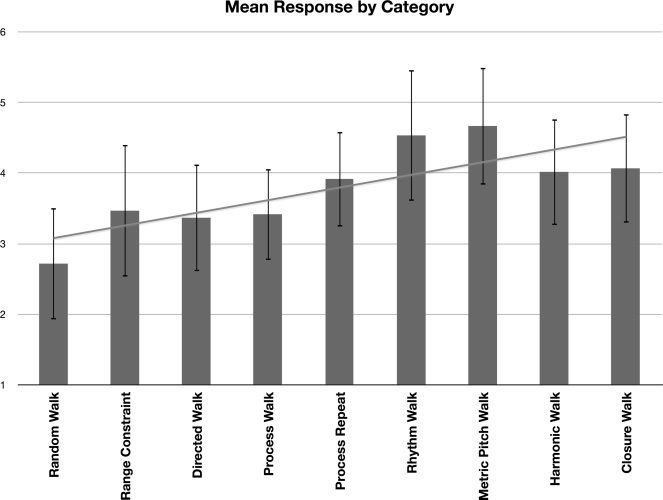
The mean scores for melodies at each stage are
shown diagrammatically in Figure 22. The stages

follow the developmental phases of the algorithm
outlined in this article. Although the data indicate
that there is, perhaps unsurprisingly, some variety
in the responses, there is a reasonably clear increase
in score as the melody algorithm becomes more
elaborate. There is a noticeable increase when
rhythmic variety is included, again not surprisingly.
We interpret these results as confirming our
own judgment that each stage of the algorithmic
development makes a perceivable contribution
to the melodic character. These results are only
indicative, sin embargo, given the modest sample of
melodies and number of participants involved.

Conclusión

This article has outlined a series of techniques for
generative music that have been inspired by theories
of music cognition, in particular on theories of
proximity, goal seeking, good continuation, contexto
sensitivity, and closure. They have been applied
to the generation of melodic contour, metrical
rhythms, and phrase endings. There has been some

Computer Music Journal

attention to harmonic movement but this could be
elaborated further in future research.

The techniques are focused on symbolic music-

making in a western tonal and metric setting.
They have been demonstrated in the context of an
algorithmic melody generator showing how they
integrate with one another, and have been evaluated
through listening trials that confirm a tendency for
improvement as the techniques accumulate.

The presented implementation is succinct, y un
balance has been sought between hiding complexity
and exposing parameters necessary for expressive
control. A number of the techniques have required
the writing of utility functions to support their
implementación. Where this has been necessary we
have tried to maintain the balance of brevity and
expressive control. Además, these techniques,
and their parsimonious implementation, tener
benefitted from our own research in modeling music
intelligence and seeking empirical evidence for
musicological theories in computational analysis of
musical works.

We hope that this article may provide some
insight into the richness of opportunity in applying
music cognition studies to generative techniques
and show how such techniques can be applied to
succinct compositional processes and live-coding
actuación.

Referencias

Bharucha, j. j. 1984. “Event Hierarchies, Tonal Hierarchies
and Assimilation: A Reply to Deutsch and Dowling.”
Revista de Psicología Experimental 113(3):421–425.
Bigand, MI., y r. Parncutt. 1999. “Perceiving Musical

Tension in Chord Sequences.” Psychological Research
62(4):237–254.

Bregman, A. S. 1990. Auditory Scene Analysis: El

Perceptual Organization of Sound. Cambridge, Mas-
sachusetts: CON prensa.

Marrón, A. r., t. Gifford, y r. Davidson. 2012. “Tracking
Levels of Closure in Melodies.” In Proceedings of the
International Conference on Music Perception and
Cognición, páginas. 149–152.

Marrón, A. r., y un. Sorensen. 2009. “Interacting with
Generative Music Through Live Coding.” Contempo-
rary Music Review 28(1):17–29.

Cambouropoulos, mi. 1997. “Musical Rhythm: A Formal
Model for Determining Local Boundaries, Accents,
and Meter in a Melodic Surface.” In M. Leman, ed.
Music, Gestalt, and Computing: Studies in Cognitive
and Systematic Musicology. Berlina: Saltador, páginas. 277–
293.

Clynes, METRO. 1983. “Expressive Microstructure in Music,

Linked to Living Qualities.” In J. Sundberg, ed. Estudios
of Music Performance. Stockholm: Royal Swedish
Academy of Music No. 39, páginas. 76–181. Disponible
online at www.speech.kth.se/music/publications/
kma/papers/kma39-ocr.pdf. Accessed November 2014.
Cooper, GRAMO., y yo. B. Meyer. 1960. The Rhythmic Structure
of Music. chicago, Illinois: Chicago University Press.
Cope, D. 2000. The Algorithmic Composer. Madison,

Wisconsin: A-R Editions.

Corsini, R. j. 1999. The Dictionary of Psychology. Nuevo

york: Prensa de Psicología.

Deli `ege, I. A. 1987. “Grouping Conditions in Listening
to Music: An Approach to Lerdahl and Jackendoff’s
Grouping Preference Rules.” Music Perception 4(4):325–
360.

Deutsch, D. 1999a. “Grouping Mechanisms in Music.” In
D. Deutsch, ed. The Psychology of Music. 2y ed.. san
diego: Prensa académica, páginas. 299–348.

Deutsch, D. 1999b. “The Processing of Pitch Combina-
tions.” In D. Deutsch, ed. The Psychology of Music.
2y ed.. San Diego: Prensa académica, páginas. 349–411.
Fraise, PAG. 1984. “Perception and Estimation of Time.”

Annual Review of Psychology 35:1–7.

Goetschius, PAG. 1902. Counterpoint Applied. Nueva York: GRAMO.

Schirmer.

von Hippel, PAG. 2000. “Redefining Pitch Proximity: Tessi-
tura and Mobility as Constraints on Melodic Intervals.”
Music Perception 17(3):313–327.

von Hippel, PAG. T., y D. Huron. 2000. “Why do Skips

Precede Reversals? The Effect of Tessitura on Melodic
Structure.” Music Perception 18(1):59–85.

Huron, D. 2006. Sweet Anticipation: Music and the

Psychology of Expectation. Cambridge, Massachusetts:
CON prensa.

jones, METRO. r., y M. Boltz. 1989. “Dynamic Attending and
Responses to Time.” Psychological Review 96(3):459–
491.

Krumhansl, C. l., and E. j. Kessler. 1982. “Tracing the

Dynamic Changes in Perceived Tonal Organization in a
Spatial Representation of Musical Keys.” Psychological
Revisar 89(4):334–268.

Large, mi. W.. 1994. “Dynamic Representation of Musical
Structure.” PhD dissertation, Ohio State University,
Department of Computer Science and Engineering.

Marrón, Gifford, and Davidson

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
/
C
oh
metro

j
/

a
r
t
i
C
mi
–
pag
d

F
/

3
9
1
1
1
1
8
5
6
0
4
9
/
C
oh
metro
_
a
_
0
0
2
8
2
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Large, mi. w., C. Palmer, y j. B. Pollack. 1995. “Reduced
Memory Representations for Music.” Cognitive Science
19(1):53–96.

larson, S. 2012. Musical Forces: Motion, Metaphor, y
Meaning in Music. Bloomington: Universidad de Indiana
Prensa.

Lerdahl, F., y r. Jackendoff. 1983. A Generative Theory
of Tonal Music. Cambridge, Massachusetts: CON prensa.
Londres, j. 2004. Hearing in Time: Psychological Aspects
of Musical Meter. Oxford: prensa de la Universidad de Oxford.
Maxwell, J., PAG. Pasquier, y un. Eigenfeldt. 2011. "El
Closure-Based Cueing Model: Cognitively-Inspired
Learning and Generation of Musical Sequences.” In
Proceedings of the Sound and Music Computing
Conferencia. Available online at www.smcnetwork.org/
system/files/smc2011 submission 189.pdf. Accedido
Octubre 2014.

McLean, A., j. Rohrhuber, y N. collins. 2014. “Editors’

Notes.” Computer Music Journal 38(1):4–5.

Meyer, l. B. 1956. Emotion and Meaning in Music.

chicago, Illinois: University of Chicago Press.

Narmour, mi. 1973. Beyond Schenkerism. chicago, Illinois:

University of Chicago Press.

Narmour, mi. 1990. The Analysis and Cognition of Basic
Melodic Structures. chicago, Illinois: Universidad de
Chicago Press.

Narmour, mi. 1992. The Analysis and Cognition of

Melodic Complexity: The Implication-Realization
Modelo. chicago, Illinois: University of Chicago Press.
Nierhaus, GRAMO. 2009. Algorithmic Composition: Paradigms
of Automated Music Generation. Viena: Saltador.

Papadopoulos, GRAMO., y G. Wiggins. 1999. “AI Methods
for Algorithmic Composition: Una encuesta, a Critical
View, and Future Prospects.” In Proceedings of the
AISB’99 Symposium on Musical Creativity, páginas. 110–
117. Available online at citeseerx.ist.psu.edu/viewdoc/
download?doi=10.1.1.3.8064&rep=rep1&type=pdf. C.A-
cessed November 2014.

Pearce, METRO., y G. Wiggins. 2006. “Expectation in
Melody: The Influence of Context and Learning.”
Music Perception 23(5):377–405.

Saunders, r., y j. S. Gero. 2001. “The Digital Clockwork
Muse: A Computational Model of Aesthetic Evolution.”
In Proceedings of Artiﬁcial Intelligence and the
Simulation of Behavior, volumen. 1, páginas. 12–21.

Sorensen, A. 2005. “Impromptu: An Interactive Program-
ming Environment for Composition and Performance.”
In Proceedings of the Australasian Computer Music
Conferencia, páginas. 149–153.

Sorensen, A., y un. R. Marrón. 2007. “aa-cell in Practice:
An Approach to Musical Live Coding.” In Proceedings
of the International Computer Music Conference,
páginas. 292–299.

Temperley, D. 2007. Music and Probability. Cambridge,

Massachusetts: CON prensa.

Wertheimer, METRO. 1938. “Laws of Organisation in Perceptual
Forms” [W.. Ellis, trans.]. In W. Ellis, ed. A Source Book
of Gestalt Psychology. Londres: Dover, páginas. 71–88.
Xenakis, I. 1976. “Foreword.” N’Shima [puntaje]. París: