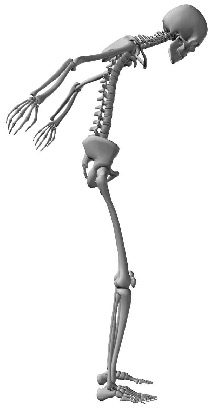
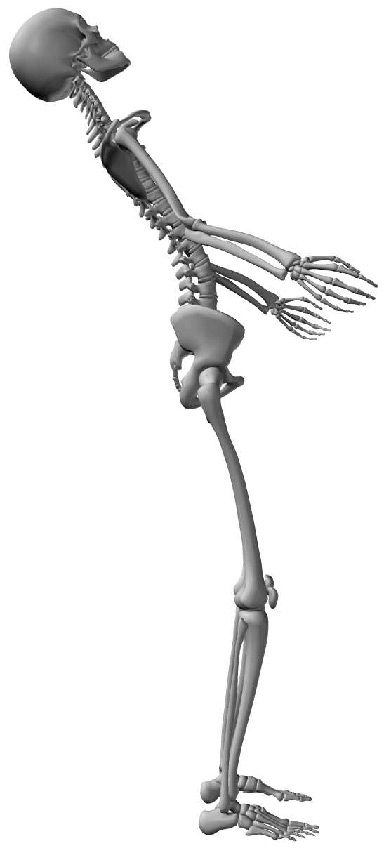
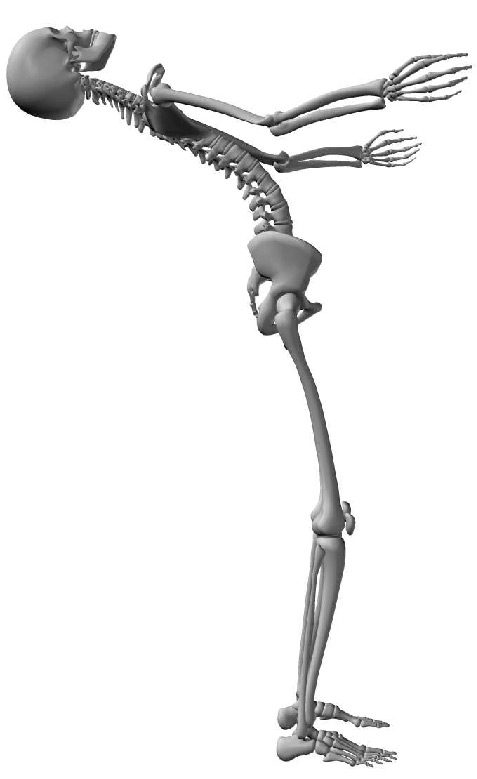
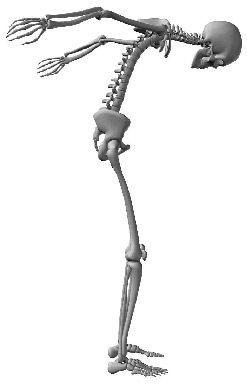
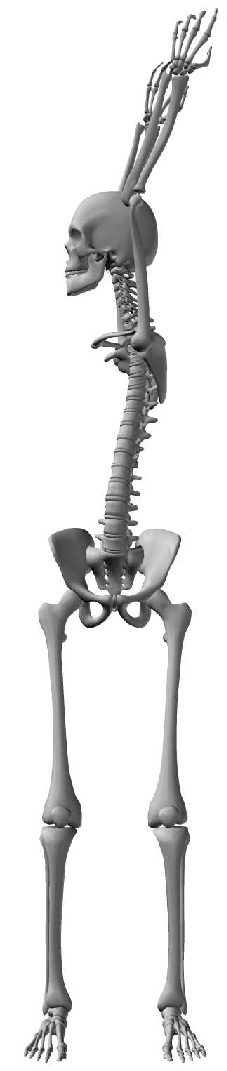
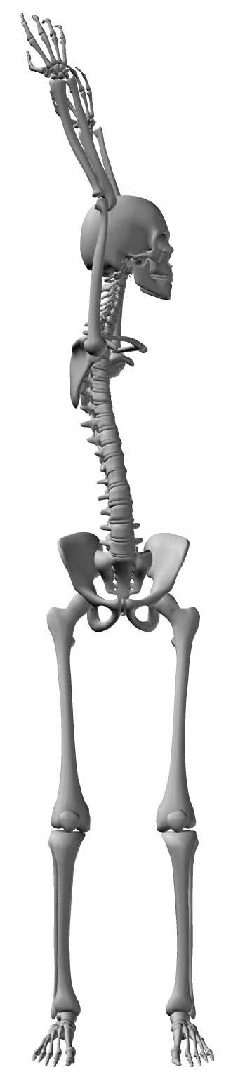
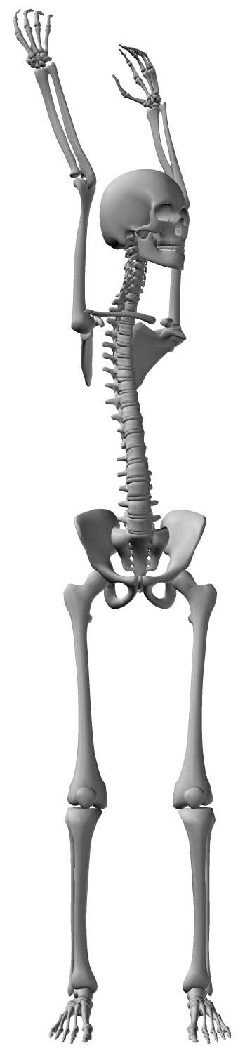
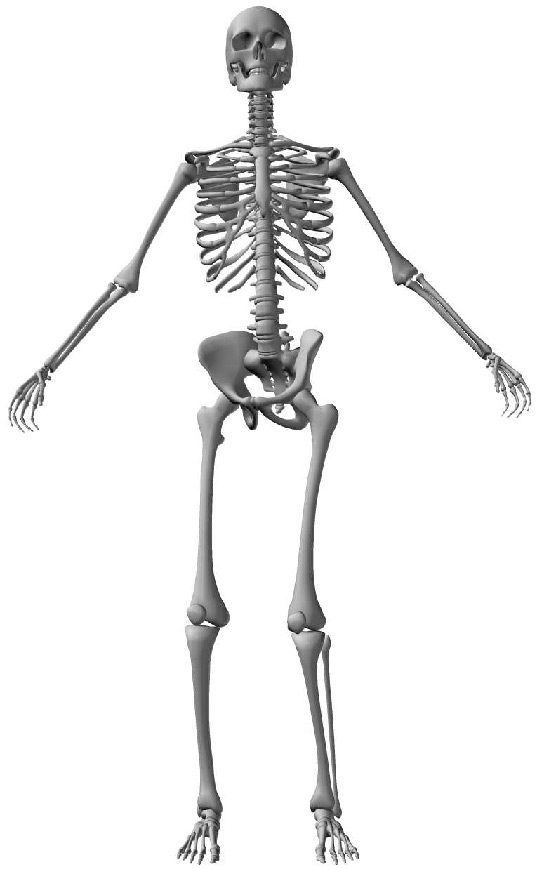
A Control System for a Flexible
Spine Belly-Dancing Humanoid
Abstract Recently, there has been a lot of interest in building
anthropomorphic robots. Research on humanoid robotics has
focused on the control of manipulators and walking machines.
The contributions of the torso towards ordinary movements
(such as walking, dancing, attracting mates, and maintaining
balance) have been neglected by almost all humanoid robotic
investigadores. We believe that the next generation of humanoid
robots will incorporate a flexible spine in the torso. To meet
the challenge of controlling this kind of high-degree-of-
freedom robot, a new control architecture is necessary. Inspired
by the rhythmic movements commonly exhibited in lamprey
locomotion as well as belly dancing, we designed a controller
for a simulated belly-dancing robot using the lamprey central
pattern generator. Experimental results show that the proposed
lamprey central pattern generator module could potentially
generate plausible output patterns, which could be used for all
the possible spine motions with minimized control parameters.
Por ejemplo, in the case of planar spine motions, only three
input parameters are required. Using our controller, the simulated
robot is able to perform complex torso movements commonly
seen in belly dancing as well. Our work suggests that the
proposed controller can potentially be a suitable controller
for a high-degree-of-freedom, flexible spine humanoid robot.
Además, it allows us to gain a better understanding of
belly dancing by synthesis.
Jimmy Or
Takanishi Laboratory
Humanoid Robotics Institute
Waseda University
#59-308, 3-4-1 Ookubo
Shinjuku-ku
Tokio, Japón 169-8555
jimmyor@kurenai.waseda.jp
Palabras clave
Next generation high-degree-of-freedom
flexible spine humanoid robot, belly
dancing, lamprey central pattern generator,
neural networks, robot controller, motor
primitives
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
1
2
1
6
3
1
6
6
2
2
5
5
1
0
6
4
5
4
6
0
6
7
7
5
1
8
6
4
6
4
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
1 Introducción
Recientemente, there has been much interest in anthropomorphic robots [5, 2, 15, 29, 31, 32, 24, 25].
Research on humanoid robots concentrates on three areas: control of manipulators, biped loco-
movimiento, and human-robot interaction.
Over the past 30 años, a lot of walking machines have been created, because only a small
percentage of the world is accessible by wheels. Although recently developed robots (como el
Sony SDR-4, Fujitsu HOAP-1, and Honda ASIMO) are able to walk and climb stairs, su
movements are not natural looking. A common feature of these robots is a rigid torso. Hasta ahora, el
interactions between body posture and leg movement during locomotion have been neglected by
almost all humanoid robotics researchers. In order to walk like a human, it is necessary for the robot
to have a flexible body trunk and hip.
Research on human-robot interaction is a relatively new field. Some researchers are using head
robots to communicate with humans [16, 4, 23]. Others are trying to find a simpler way to teach
norte 2006 Massachusetts Institute of Technolog y
Artificial Life 12: 63 – 87 (2006)
j. O
A Control System for a Flexible Spine Belly-Dancing Humanoid
robots complex motor skills by imitation learning [2, 3, 18, 22]. Although a few recently developed
head robots are capable of communicating with humans through speech and facial expressions, el
communication is not very natural, because body language is not involved. For this it would be
necessary to equip these robots with a pair of limbs and a flexible torso.
Similar to snakelike robots such as the ones proposed in [6, 30, 21] and the tendon driven robots
described in [24, 25], the next generation of humanoid robots will incorporate a flexible spine as
the torso.1 Given that such a robot will have a greater degree of freedom ( DOF) than existing
robots,
it is necessary to find a simple control strateg y to cope with the increased complexity.
Inspired by the rhythmic movements commonly seen in lamprey locomotion as well as belly dancing,
we designed a controller for a simulated belly-dancing robot based on the lamprey central pattern
generator (CPG).
According to Grillner [12], the lamprey belongs to the most primitive vertebrate group, el
cyclostomes. Its evolution diverged from the main vertebrate line about 450 million years ago. Él
is considered by biologists to be a prototype vertebrate because its brain stem2 and spinal cord have
all the basic vertebrate features, yet the neurons in each category are an order of magnitude fewer
than in other vertebrates [13]. The lamprey swimming circuitry has therefore been studied
extensively by neurobiologists who want to understand the principles underlying vertebrate (semejante
as human) locomotion [12]. We believe that some of the principles found in the motor control of
the lamprey can be applied to the design of a controller for a high-DOF humanoid robot. El
reason is that the lamprey has 100 segments, each of which has at least four muscles (to allow
yaw, pitch, and roll). By varying only the global and extra excitations from the brain stem, el
lamprey is able to change its body shape. Such simplicity is ideal in a controller for a high-DOF,
flexible spine humanoid robot. As a first step, we investigate the possibility of using a CPG-based
controller and a minimized number of input parameters to control a high-DOF, flexible spine
model humanoid.
Belly dancing was chosen as a motor task for the following reasons. Primero, belly dancers have very
flexible bodies. They can bend their arms, legs, and torso more smoothly than an average person.
Robots, por otro lado, have rigid torsos and tend to produce jerky movements. En segundo lugar, belly
dancers are able to maintain good balance, a quality that is very important for humanoid robots. If a
robot were as flexible as a belly dancer, it could perform tasks that no robot has done before. Para
instancia, it would generally be more agile, more able to work its way through tight spaces, y
perhaps able to climb steep inclines using hand- and footholds. It could also step over clutter and
walk naturally (or perhaps even jump) using sparse footholds. Other benefits would include walking
naturally, swimming efficiently, balancing, and playing golf. Belly dancing is also interesting from a
control point of view. The basic steps are rhythmic and often involve traveling waves along the torso
y brazos. Movements with these features can easily be generated by the lamprey CPG with no more
than three control parameters. They can also be extracted as motor primitives for a robot to learn
complex motor tasks through imitation learning. Finalmente, the study of traveling waves is important to
motor control because this kind of body undulation has been observed in other animals (como
anguilliform swimmers, salamanders, and cats) during locomotion.
1 In Mizuuchi et al. [24, 25], the authors presented two interesting flexible spine humanoid robots. But there are as yet no experimental
data to support their claims about the capabilities of these robots.
2 According to Grillner et al. [14], the lamprey brain stem consists of four different reticular nuclei. The most rostral nucleus is located
in the mesencephalon (MRN), and the rest of the nuclei are in the rhombencephalon: the anterior (ARRN), the middle (MRRN), y el
posterior (PRRN). Some of these reticulospinal neurons are active tonically, while others receive feedback from the spinal cord that
results in phasic modulation. The glutamatergic reticulospinal MRRN and PRRN neurons project to the spinal cord and are responsible
for the initiation of locomotion. These neurons can be activated from the rostral brain stem structures and other sensory stimuli. Al
activación, these reticulospinal cells in turn activate the AMPA /kainate- and NMDA-type glutamate receptors located on the spinal cells of
the locomotion CPGs to initiate locomotion. Note that the level of activity of the CPGs is controlled by the reticulospinal neurons. El
higher the level of activity in these neurons, the faster the animal moves. In our implementation, the brain stem itself is considered as a
neuron unit.
64
Artificial Life Volume 12, Número 1
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
1
2
1
6
3
1
6
6
2
2
5
5
1
0
6
4
5
4
6
0
6
7
7
5
1
8
6
4
6
4
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
j. O
A Control System for a Flexible Spine Belly-Dancing Humanoid
2 Fondo
2.1 Belly Dance
According to Ate´a [1],
‘‘Belly dance’’ consists of a movement vocabulary that sets it apart from any other dance form.
Its most distinguishing feature is its isolated movements of the abdomen. These abdominal
movements may be circular, rolling, angular, or vibrating, and are unique to this dance. Pero
belly dance is a form that involves every other part of the body too, isolating major muscle
groups and working them in isolation or in opposition to other parts of the body. Otro
distinguishing features are circular or wavelike moves of arms, manos, upper torso, and hips.
For over 2000 años, this dance form has been practiced for the relief of back pain, childbirth
preparation, physical education, entretenimiento, and ritual [1]. Although it is common to see male
belly dancers in the Middle East countries,
in other parts of the world belly dancing is mainly
performed by females. The main benefits of belly dancing is that it is good for the muscles used
during labor and delivery. The rhythmic movements are beneficial to pregnant women.
Some belly-dance moves, such as the camel, require independent control of muscle groups and
coordination between body segments. Typically, only advanced dancers are able to propagate a
traveling wave along their bodies with ease. Since we are interested in the control of flexible spine
humanoid robots, we focus on the torso movements in this article. For more details on belly
dancing, refer to [1, 27].
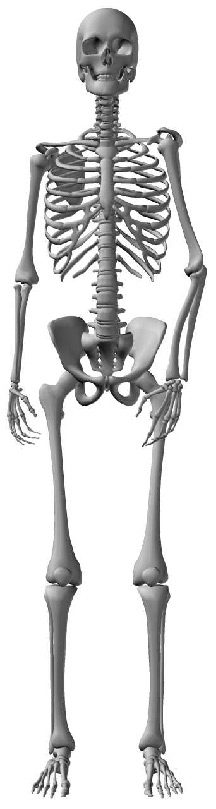
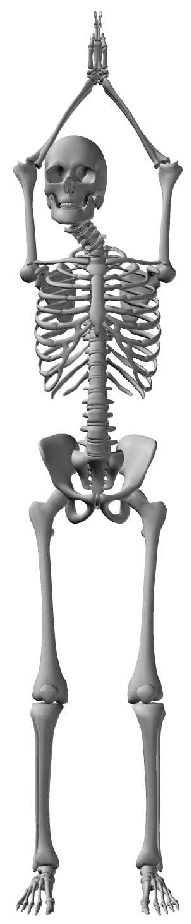
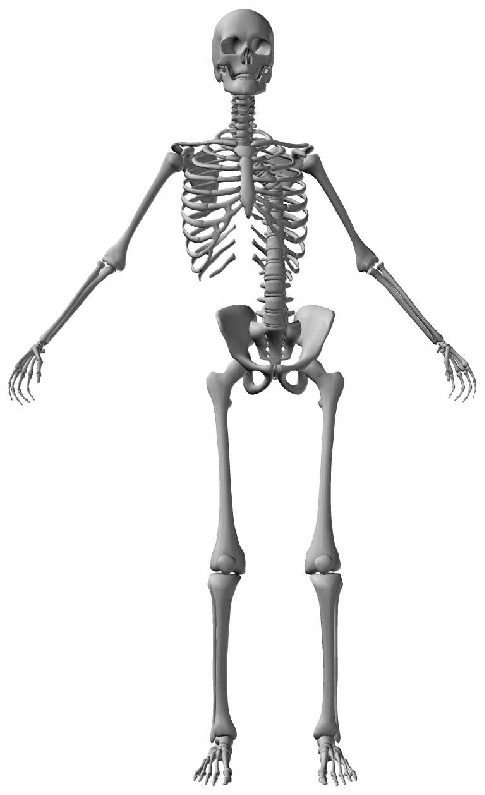
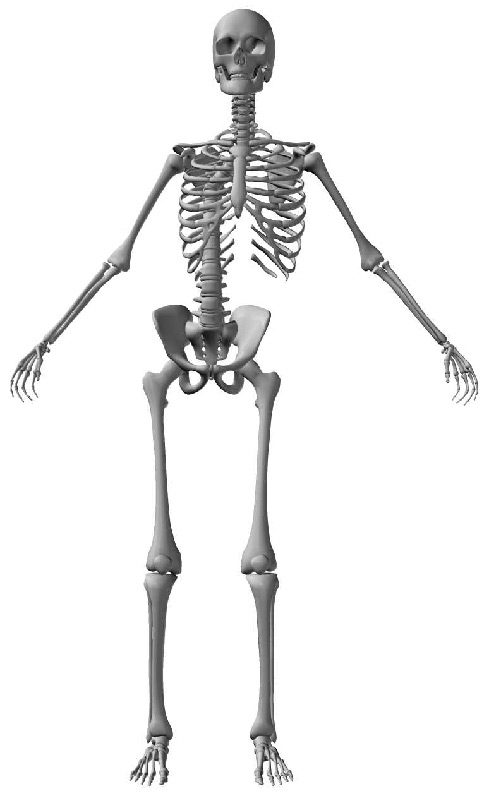
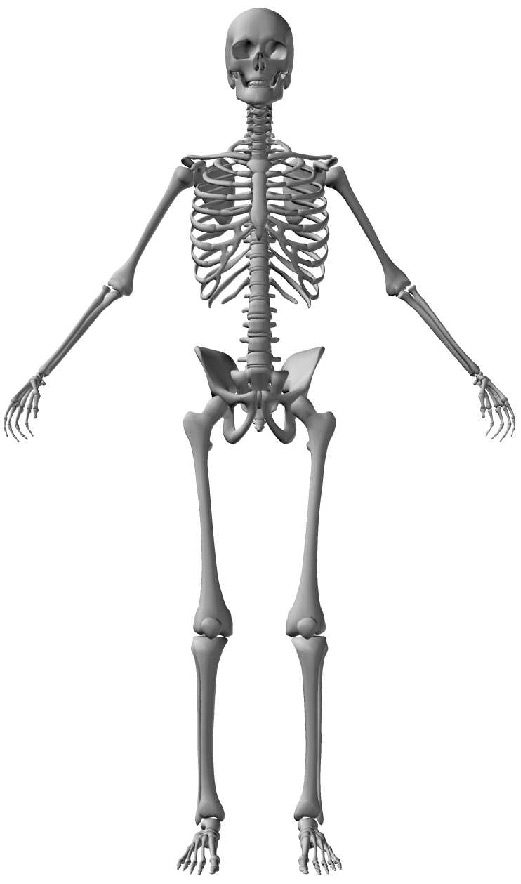
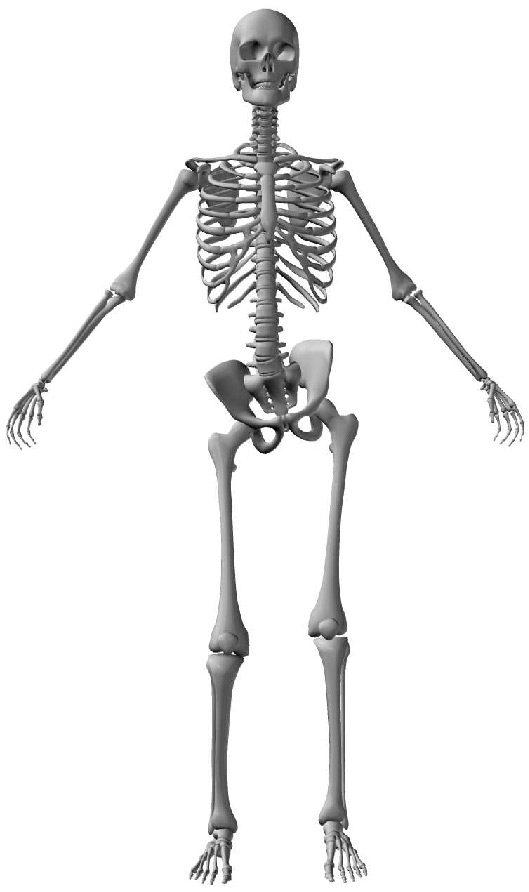
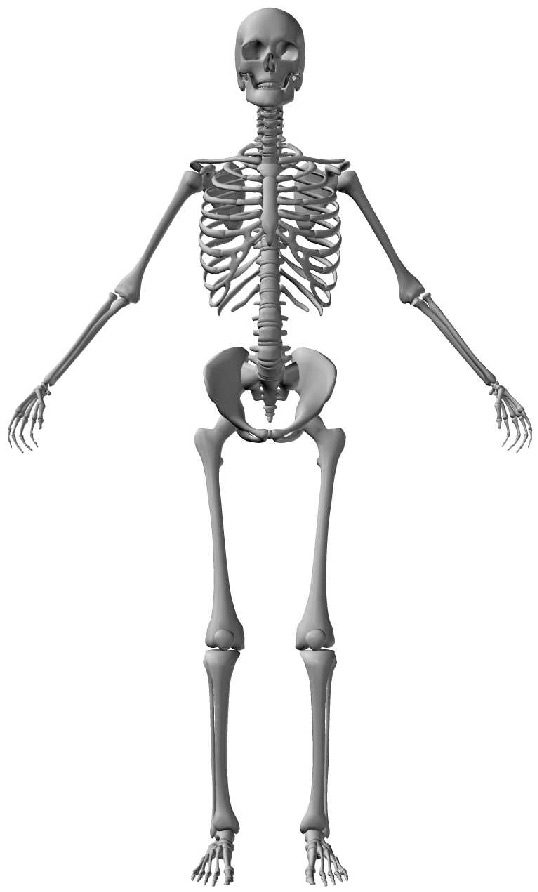
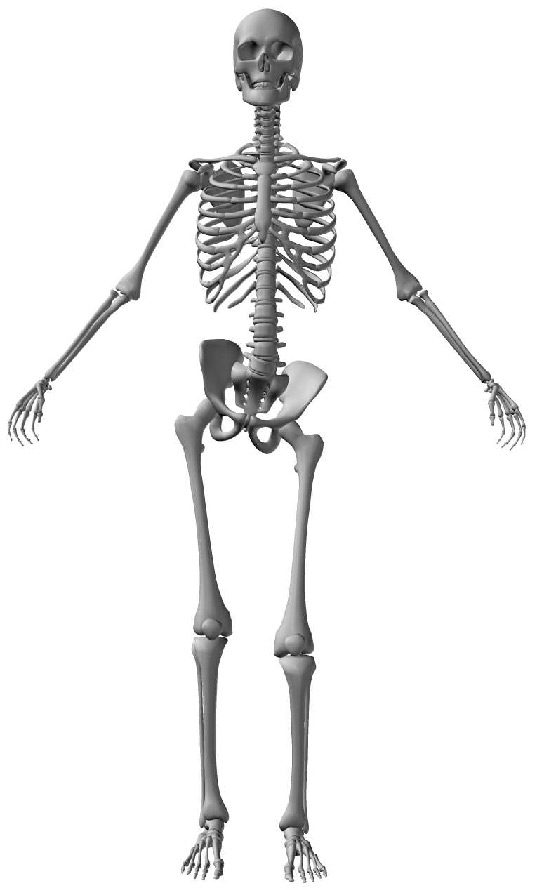
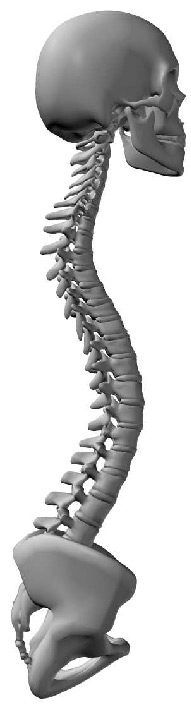
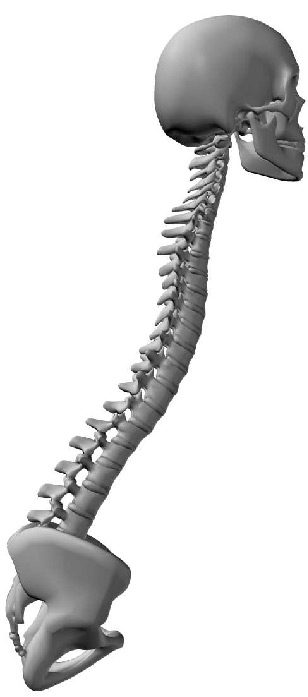
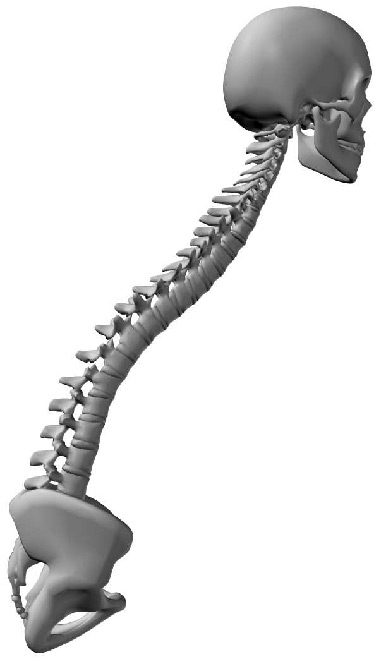
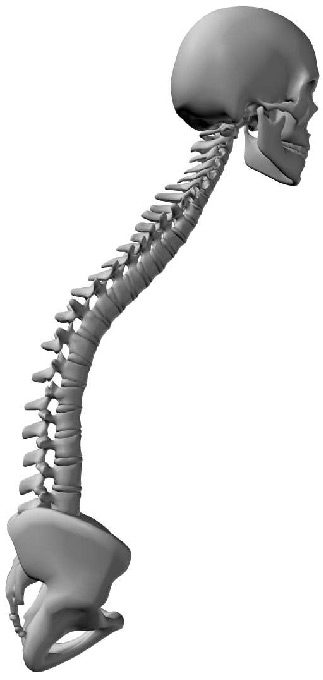
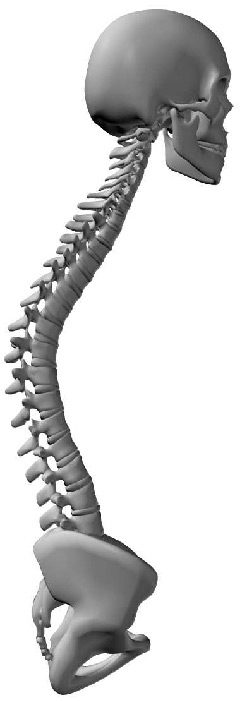
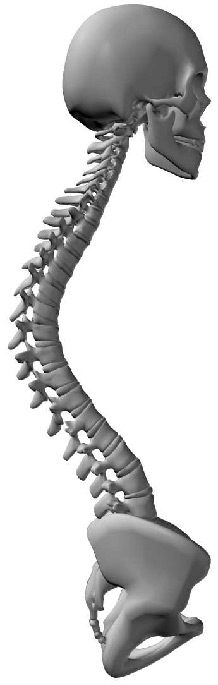
2.2 The Human Spine
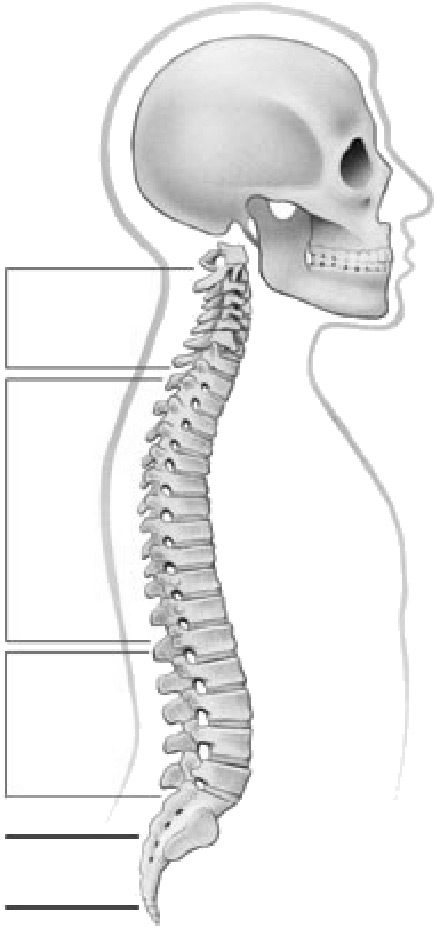
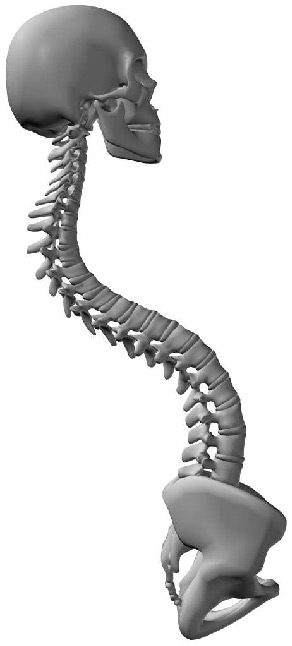
The human spine is an arched vertebral column. It consists of seven cervical vertebrae, twelve
thoracic vertebrae, five lumbar vertebrae, the coccyx, and the sacrum. Between each neighboring
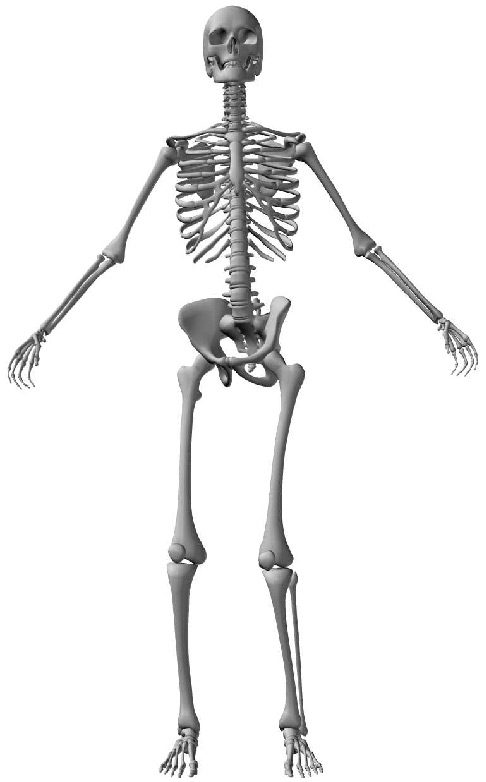
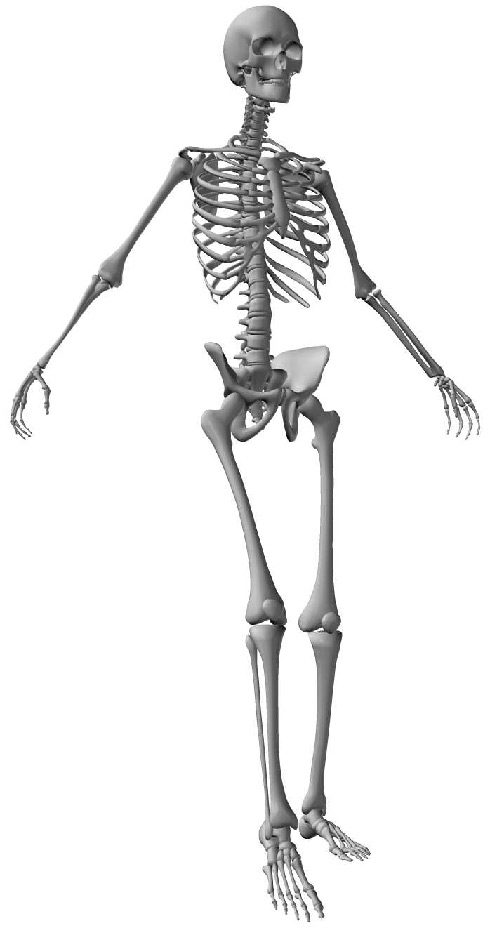
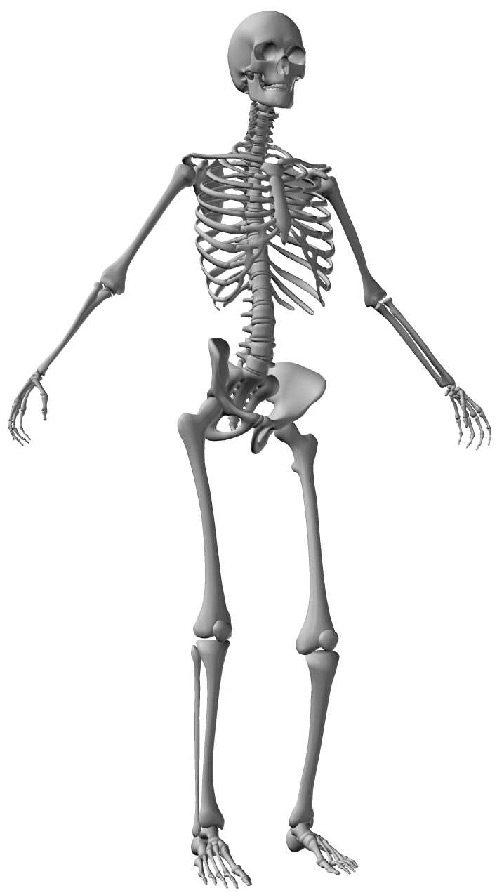
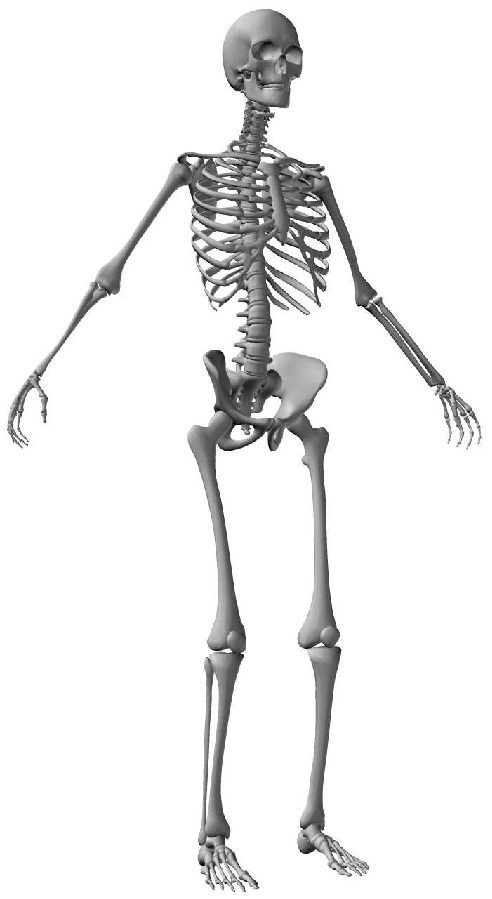
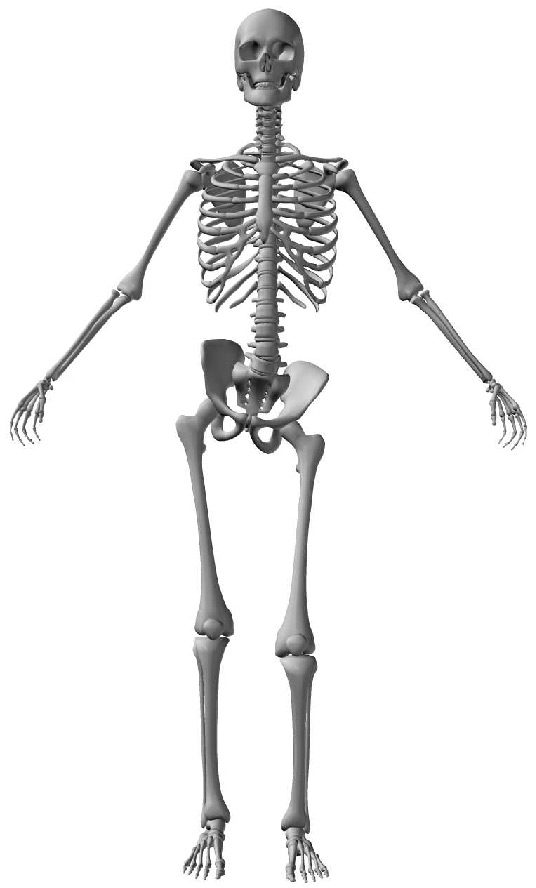
pair of vertebrae there is an intervertebral disk, which acts as a shock-absorbing cushion ( Cifra 1).
The actions that are possible in the three spinal regions (cervical, thoracic, and lumbar) sobre el
sagittal, frontal, and transverse planes3 depend on the different sizes, shapes, and articulations of the
bones [10]. According to kinesiologists such as Fitt, the possible actions achieved by the human
spine are:
1. Flexion and hyperextension on the sagittal plane.
2. Lateral flexion to either side of the body on the frontal plane.
3. Rotation to the left and right on the transverse plane. This is mainly achieved
in the thoracic region.
The main functions of the spine are to protect the spinal cord and to act as a support to the upper
body weight. Además, it provides both stability and mobility in our daily activities. The last two
functions are very important for flexible spine humanoid robots.
3 Neural Model of the Lamprey CPG
A connectionist model of the lamprey CPG has been handcrafted based on findings from
physiological experiments [9]. In this model the entire network consists of 100 interconnected
3 Sagittal plane: a vertical plane extending front to back that divides the body into right and left parts. Frontal plane: a vertical plane ex-
tending side to side that divides the body into front and back parts. Transverse plane: a horizontal plane extending side to side and front to
back that divides the body into upper and lower parts. Each kind of plane is perpendicular to the other two.
Artificial Life Volume 12, Número 1
65
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
1
2
1
6
3
1
6
6
2
2
5
5
1
0
6
4
5
4
6
0
6
7
7
5
1
8
6
4
6
4
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
j. O
A Control System for a Flexible Spine Belly-Dancing Humanoid
Cifra 1. The human spine. (Illustrated by Jim Shea. Modified with permission.)
copies of a segmental oscillator (Cifra 2). Within each segmental oscillator, there are eight neuron
units of four types, namely motoneurons (Minnesota), excitatory interneurons (EIN), contralateral
inhibitory interneurons (CIN), and lateral inhibitory interneurons (LIN). Each of these units rep-
resents a population of functionally similar neurons in the real lamprey. They all receive excitations
from the lamprey brain stem.
Since the details of the intersegmental connections of the real
lamprey CPG are not yet
conocido, Ekeberg [9] simplified the controller by giving each neuron symmetrical connections
extending in both rostral and caudal directions (except for the CIN neurons, which have longer
projections in the caudal direction). Given that the neurons at both ends of the CPG receive
fewer neural connections, synaptic weights are calibrated by dividing them by the number of
segments a neuron receives input from. The connection weights among the neurons are given in
Mesa 1.
Using the given neural couplings, we are able to control the intersegmental phase lag by varying
only the amount of extra excitation from the brain stem. Además, the frequency of segmental
oscilaciones (which affects the speed of locomotion) and intersegmental phase lag (which affects the
body shape) can be controlled almost independently (Sección 3.5).
3.1 Mathematical Model of Neurons
To model a neuron unit, we used a leaky integrator with a saturating transfer function. The output
tu (a [0, 1]) of the unit neuron is the mean firing frequency of the population it represents. Él
is calculated using the following set of formulas:
˙sþ ¼
1
sD
X
iaCþ
!
;
uiwi (cid:3) sþ
ð1Þ
66
Artificial Life Volume 12, Número 1
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
1
2
1
6
3
1
6
6
2
2
5
5
1
0
6
4
5
4
6
0
6
7
7
5
1
8
6
4
6
4
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
j. O
A Control System for a Flexible Spine Belly-Dancing Humanoid
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
1
2
1
6
3
1
6
6
2
2
5
5
1
0
6
4
5
4
6
0
6
7
7
5
1
8
6
4
6
4
pag
d
.
Cifra 2. Configuration of the lamprey CPG. The controller is composed of 100 interconnected segmental oscillators
(only five segments are shown here). Each segment consists of eight neurons of four types: motoneurons (Minnesota),
excitatory interneurons (EIN), lateral inhibitory interneurons (LIN), and contralateral inhibitory interneurons (CIN).
Connections with a fork ending represent excitatory connections, while those with a dot ending represent inhibitory
connections. Vertical lines indicate that there are intersegmental couplings among the neurons within the CPG. Due
to the complexity of the couplings, the actual intersegmental connections are not shown here. (Refer to Table 1 para
details.) Note that in our implementation, the brain stem itself is considered as a neuron unit. Each neuron within the
CPG receives the same amount of global excitation from this special neuron. Además, neurons near the head segments
receive extra excitation. In addition to input signals from the brainstem, the controller receives feedback from the
stretch sensitive edge EC cells. Note that these cells are not implemented in the current controller.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Artificial Life Volume 12, Número 1
67
j. O
A Control System for a Flexible Spine Belly-Dancing Humanoid
Mesa 1. Connection weight matrix for the lamprey CPG [9]. Excitatory and inhibitory connections are represented by
positive and negative weights respectively. Left and right neurons are indicated by l and r. BS stands for brain stem. El
extensions from a neuron to those in neighboring segments are given in brackets. The first number is the number of
extensions in the rostral direction; the second, in the caudal direction.
A:
EINl
De: EINl
CINl
0.4 [2, 2]
—
—
—
—
(cid:3)2.0 [1, 10]
(cid:3)2.0 [1, 10]
(cid:3)1.0 [1, 10]
(cid:3)2.0 [5, 5]
LINl
—
(cid:3)1.0 [5, 5]
—
—
—
—
—
—
EINr
CINr
LINr
—
—
—
—
0.4 [2, 2]
3.0 [2, 2]
13.0 [5, 5]
1.0 [5, 5]
(cid:3)2.0 [1, 10]
(cid:3)2.0 [1, 10]
(cid:3)1.0 [1, 10]
(cid:3)2.0 [5, 5]
—
—
—
—
—
—
—
—
—
(cid:3)1.0 [5, 5]
—
—
CINl
3.0 [2, 2]
LINl
13.0 [5, 5]
MNl
1.0 [5, 5]
EINr
CINr
LINr
MNr
—
—
—
—
!
;
uiwi (cid:3) s(cid:3)
˙s(cid:3) ¼
1
sD
X
iaC(cid:3)
˙# ¼
1
sA
ðu (cid:3) #Þ;
u ¼f 1 (cid:3) expfðQ (cid:3) sþÞGg (cid:3) s(cid:3) (cid:3) A# ðu > 0Þ;
ðu V 0Þ
0
BS
2.0
7.0
5.0
5.0
2.0
7.0
5.0
5.0
ð2Þ
ð3Þ
ð4Þ
where wi represents the calibrated synaptic weights, and C+ and C(cid:3) represent the groups of
presynaptic excitatory and inhibitory neurons, respectivamente. s+ and s(cid:3) are the delayed reactions to
excitatory and inhibitory inputs, and q represents the frequency adaptation4 observed in real neurons
[9]. Note that since the function of the brain stem is to excite the neurons in the CPG network, uno
of the ui inputs in Equation 1 is from the brain stem. De este modo, the more excitations from the brain stem
aporte, the more excited the neuron unit becomes and the higher the frequency of oscillation. A
simulate extra excitations, connection weights from the brain stem to the neurons in the first five
segments are amplified accordingly.
The parameters for each type of neuron are given in Table 2. The values of these parameters and
those for the connection weights are set up in such a way that the simulation results from the model
agree with physiological observations.
4 Frequency adaptation is a neural property. It means that the firing rate of a neuron is not constant for a constant input. Typically, allá
is a slight decrease in the firing rate over time.
68
Artificial Life Volume 12, Número 1
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
1
2
1
6
3
1
6
6
2
2
5
5
1
0
6
4
5
4
6
0
6
7
7
5
1
8
6
4
6
4
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
j. O
A Control System for a Flexible Spine Belly-Dancing Humanoid
Mesa 2. Neuron parameters. Q is the threshold, G the gain, HD the time constant of the dendritic sums, A the coefficient
of frequency adaptation, and HA the time constant of frequency adaptation.
Neuron type
EIN
CIN
LIN
Minnesota
q
(cid:3)0.2
0.5
8.0
0.1
GRAMO
1.8
1.0
0.5
0.3
HD (EM)
30
20
50
20
A
0.3
0.3
0.0
0.0
HA (EM)
400
200
—
—
To calculate the neural activity of the entire swimming controller, we integrate Equations 1 a 4
using a fourth-order Runge-Kutta (RK4) method with a fixed time step of 1 EM.
3.2 Behavior of a Segmental Oscillator
The behavior of a segmental oscillator can be described as follows (refer to the highlighted segment
En figura 2). The brain stem provides input signals to stimulate all the neurons. Only neurons that are
actively inhibited stay inactive.
Suppose that initially the neurons on the left are slightly more active. The EINl neuron excites
all the ipsilateral neurons, while the CINl neuron inhibits all the contralateral neurons. This pre-
vents simultaneous activity on both sides. Due to its higher threshold and time constant ( Mesa 2),
the LINl neuron becomes active later in the cycle to act as a burst suppressor to the CINl
neurona. This allows the neurons on the right to become active. The CINr neuron on the right in turn
inhibits all the neurons on the left. After a while, the activities of the neurons on the right are
terminated by the LINr neuron, and the entire cycle starts again. Using this mechanism, an alternating
pattern of muscular activity on the right and left sides of a single body segment can be generated.
3.3 Behavior of the Entire Lamprey CPG
The complete lamprey CPG functions as follows. Global excitation from the brain stem stimulates
all neurons in the CPG; sufficient stimulation results in oscillations in each individual segment at a
frequency that depends on the strength of this global excitation signal. Extra excitation is supplied
from the brain stem to the five most rostral segments of the CPG. The effect of this, interacting with
intersegmental coupling, is to induce a roughly equal relative phase lag between successive segments
in the CPG, with the result that caudally traveling waves of neural activity appear. The global
excitation controls the amplitude (mean firing frequency) of the motoneuron outputs as well as the
frequency of oscillation of the CPG. The extra excitation alters the intersegmental phase lag largely
independently of the global excitation.
3.4 Quantitative Analysis of a Segmental Oscillator
A quantitative analysis of our implementation of Ekeberg’s segmental oscillator model follows.
In order to determine how the segmental oscillator behaves under different excitations, probamos
our implementation of Ekeberg’s segmental oscillator with a brain stem excitation from 0.2 a 1.0 en
steps of 0.1. For each excitation value, a neural simulation is performed. At the end of each
simulation, the amplitude and frequency from the outputs of the left motoneurons are calculated.
The outputs from each neuron over time can optionally be stored in a data file for visualization
under MATLAB.
When the segmental oscillator with asymmetric initial conditions5 receives enough excitation from
the brain stem, an alternating pattern of neural activity is generated (ver figura 3).
5 s+ (0) = 1 and s(cid:3) (0) = 0 for all the left neurons, and s+ (0) = si (0) = 0 for all the right neurons.
Artificial Life Volume 12, Número 1
69
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
1
2
1
6
3
1
6
6
2
2
5
5
1
0
6
4
5
4
6
0
6
7
7
5
1
8
6
4
6
4
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
j. O
A Control System for a Flexible Spine Belly-Dancing Humanoid
Cifra 3. Output of neurons from a segmental oscillator with an excitation of 0.4.
Increasing the brain stem excitation from 0.2 a 1.0 increases the maximum amplitude as well as
the frequency of oscillation of the motoneuron outputs. The amplitude ranges from 0.38 a 0.81,
while the oscillation frequency ranges from 1.64 a 5.49 Hz (ver figura 4).
3.5 Quantitative Analysis of the Lamprey CPG
To determine how the entire CPG behaves under different excitation combinations, we tested our
implementation of Ekeberg’s model under global excitation ranges from 0.2 a 1.0 (in steps of 0.1)
and extra excitation ranges from 0% a 200% (in steps of 10%). Recall that global excitation is
the excitation that the brain stem applies to all the neurons in the CPG, and extra excitation is the
excitation applied only to the neurons located in the five segments closest to the head. The extra
excitation is a percentage of the global excitation. At each excitation combination, a neural simulation
is performed. The characteristics (such as amplitude, frequency, and phase lag) of the neural wave
that result from the outputs of the left motoneuron in the middle of the CPG, say segment 50, son
grabado. The results are shown in Figure 5.
The amplitude surface shows that as the global excitation increases, the amplitude of the
motoneuron outputs increase. The amplitude stays fairly constant when the extra excitation is
increased. Similar to what we observe for the amplitude surface, the frequency surface shows that as
the global excitation increases, the frequency of oscillation increases. Although there is a slight
increase in frequency with extra excitation, the frequency stays fairly constant. Por otro lado,
the phase lag surface indicates that the phase lag increases with extra excitation but stays fairly
constant with increase in global excitation. Note that the empty regions in all three surfaces
correspond to quantities that cannot be measured. We consider the outputs from the motoneurons
to be valid only when both the left and right signals oscillate and return to zero. The reason for this is
that the time instants when pulse onsets appear are required in order to calculate the frequency and
phase lag.
The frequency and phase lag surfaces show that the frequency of oscillation and the wavelength
of undulation can be changed almost independently. Por eso, just as in the real lamprey, the neural
70
Artificial Life Volume 12, Número 1
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
1
2
1
6
3
1
6
6
2
2
5
5
1
0
6
4
5
4
6
0
6
7
7
5
1
8
6
4
6
4
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
j. O
A Control System for a Flexible Spine Belly-Dancing Humanoid
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
1
2
1
6
3
1
6
6
2
2
5
5
1
0
6
4
5
4
6
0
6
7
7
5
1
8
6
4
6
4
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 4. Effect of excitation from the brain stem on the amplitude of motoneuron output (izquierda) and the frequency of
oscillation (bien) of the biological segmental oscillator.
Artificial Life Volume 12, Número 1
71
j. O
A Control System for a Flexible Spine Belly-Dancing Humanoid
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
1
2
1
6
3
1
6
6
2
2
5
5
1
0
6
4
5
4
6
0
6
7
7
5
1
8
6
4
6
4
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 5. Effect of the global and extra excitations on the amplitude of motoneuron output (arriba a la izquierda), the frequency of
oscillation (top right), and the phase lag (abajo) of the lamprey CPG.
model is capable of producing a range of oscillation frequencies while keeping the wavelength of
undulation constant.
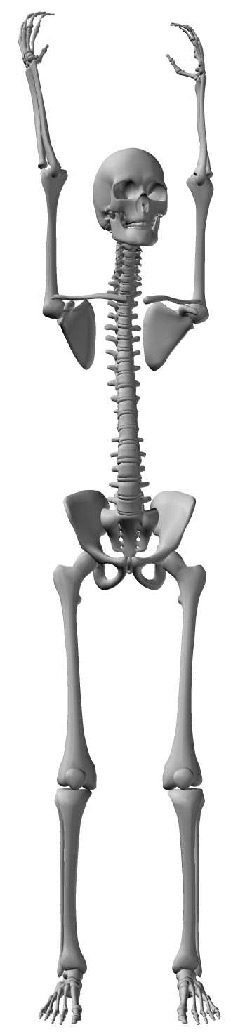
4 Mechanical Model of the Humanoid
We simulated a belly-dancing humanoid in Poser 5 (Curious Labs), using the 3D human skeleton
model developed by DAZ Productions. The reason for choosing this model is its similarity to a real
skeleton: each of the individual vertebrae has a 3-DOF joint, which allows rotations along the yaw,
pitch, and roll axes.6 To rotate a joint about a specific axis, one can use the dials in the parameters
palette or data from an external file. Another advantage of using the skeleton model is that it is easier
to show body movements without clothing.
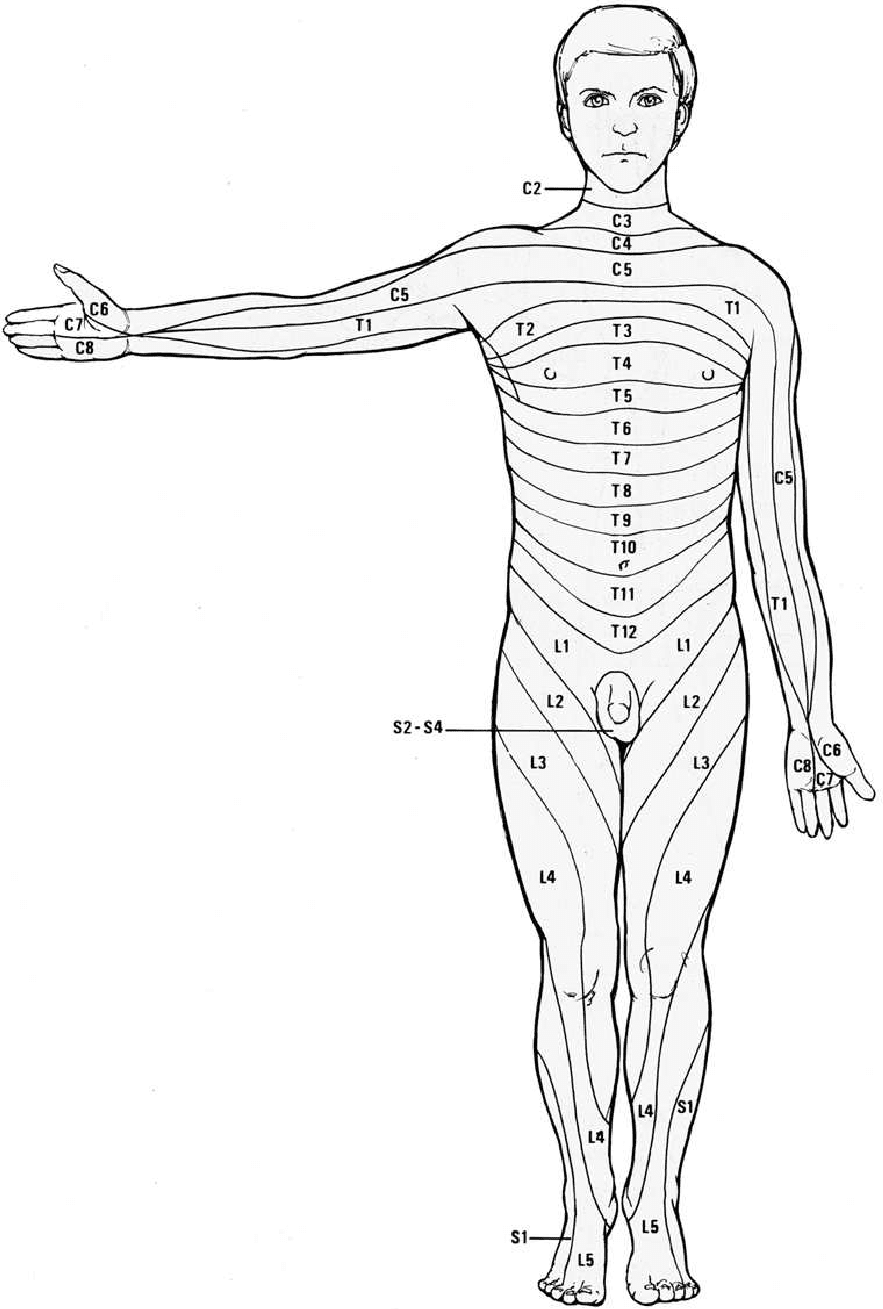
According to Kandel et al. [20],
Dermatomes7 are arranged in a highly ordered way on the body surface. It has been
possible to map the distribution along the body surface of the dermatomes for all of the
spinal segments by studying the sensibility and responsiveness that remain after injury
to dorsal roots . . . dermatomal maps provide an important diagnostic tool for localizing
levels of injury to the spinal cord and dorsal roots.
6 Note that the four basic spine motions and body undulations are planar motions. Once the plane of motions is specified, all the
vertebrae turn about the same axis and the other degrees of freedom are fixed.
7 A dermatome is a restricted peripheral region of the skin. It is innervated by a single dorsal root, which contains sensory neurons that
enter the spinal cord from the body.
72
Artificial Life Volume 12, Número 1
j. O
A Control System for a Flexible Spine Belly-Dancing Humanoid
Guided by the dermatomal maps (Cifra 6), we coupled the motoneuron outputs from the lamprey
CPG to the model spine ( Mesa 3).
Given that each motoneuron output is between 0 y 1 (Sección 3.1), the difference between
the left and right motoneuron outputs at each segment is amplified 20 veces. After this amplifica-
ción, the spinal movements become observable and realistic. Each calibrated value is then used as
the rotational angle (along a specific axis of rotation) for the corresponding vertebra. The effect of
global excitation from the brain stem on the maximum rotational angle is shown in Figure 7.
5 Posture Database
In a typical course on belly dancing, the students learn a set of basic body postures, which forms the
vocabulary of the dance. As the course progresses, more advanced dance movements can be
accomplished by sequencing and/or superposing the basic postures. These postures are analogous to
the motor primitives commonly described in literature on imitation learning [22, 19, 26].
As mentioned previously, the beauty of belly dancing is that the body motions are rhythmic
and well defined. Most of the seemingly complex dance moves emerge from a combination of
sliding, circulating, twisting, and wavelike moves of the torso and arms. Además, belly dancing
requires only a small movement envelope compared with other dances. These features allow us to
easily extract the trajectories of body segments without the use of expensive 3D motion capture
sistemas.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
1
2
1
6
3
1
6
6
2
2
5
5
1
0
6
4
5
4
6
0
6
7
7
5
1
8
6
4
6
4
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 6. The dermatomes of each spinal segment are located on particular regions of the body: C, cervical; t, thoracic; l,
lumbar; S, sacral [20].
Artificial Life Volume 12, Número 1
73
j. O
A Control System for a Flexible Spine Belly-Dancing Humanoid
Mesa 3. Mapping from the neural segments to the model spinal vertebrae: C, cervical; t, thoracic; l, lumbar. La razón
we do not use vertebrae C1 to C3 is that they function more as part of the head than of the neck. Refer to Figure 1 para
more details on the anatomy of the spine.
Spinal region
Cervical
Thoracic
Lumbar
Vertebra
Neural segment
C4
C5
C6
C7
T1
T2
T3
T4
T5
T6
T7
T8
T9
T10
T11
T12
L1
L2
L3
L4
L5
1
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
100
Through computer animations and immediate feedback from a professional dance teacher, we devel-
oped a database of belly dance movements. It contains a set of fundamental dance postures (Cifra 8).
By sequencing these basic building blocks, more complex dance movements can be reproduced.
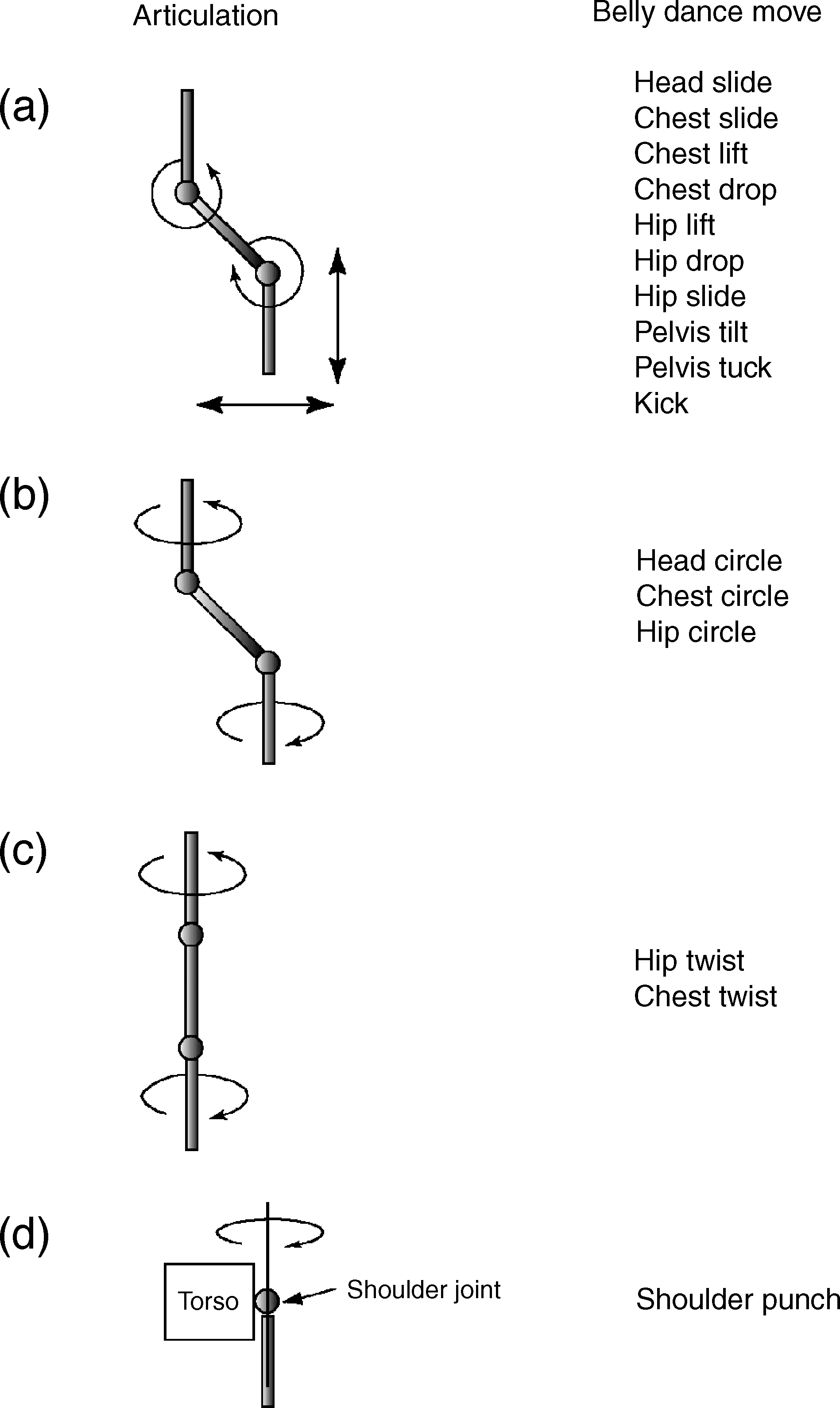
Our analysis shows that four types of articulations are involved in belly dancing ( Cifra 9). A set of
actuators which can produce the motions in (a) y ( b) can be used for the control of a real belly
dancing humanoid robot.
74
Artificial Life Volume 12, Número 1
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
1
2
1
6
3
1
6
6
2
2
5
5
1
0
6
4
5
4
6
0
6
7
7
5
1
8
6
4
6
4
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
j. O
A Control System for a Flexible Spine Belly-Dancing Humanoid
Cifra 7. Effect of global excitation on the maximum rotational angle at each vertebra.
Note that to simplify the control of a belly-dancing robot in both simulation and real hardware,
we tried to use the least number of body joints to imitate each posture. Curiosamente, Encontramos eso
except for some special postures (such as the kick and shoulder punch), the fundamental postures
can be approximated by opposite movements of two joints on the same plane (Mesa 4). This agrees
with the fact that except for the body segment required to display motions, the rest of the body
torso should remain still. This is another special feature of belly dancing, which we have taken advan-
tage of.
6 Control Architecture
After a careful analysis of belly dance movements, we found that the fundamental moves can be
broken down into three types of motions: rhythmic oscillations, circular motions, and alternate
contraction of muscles in two different body segments on the same plane. To mimic these
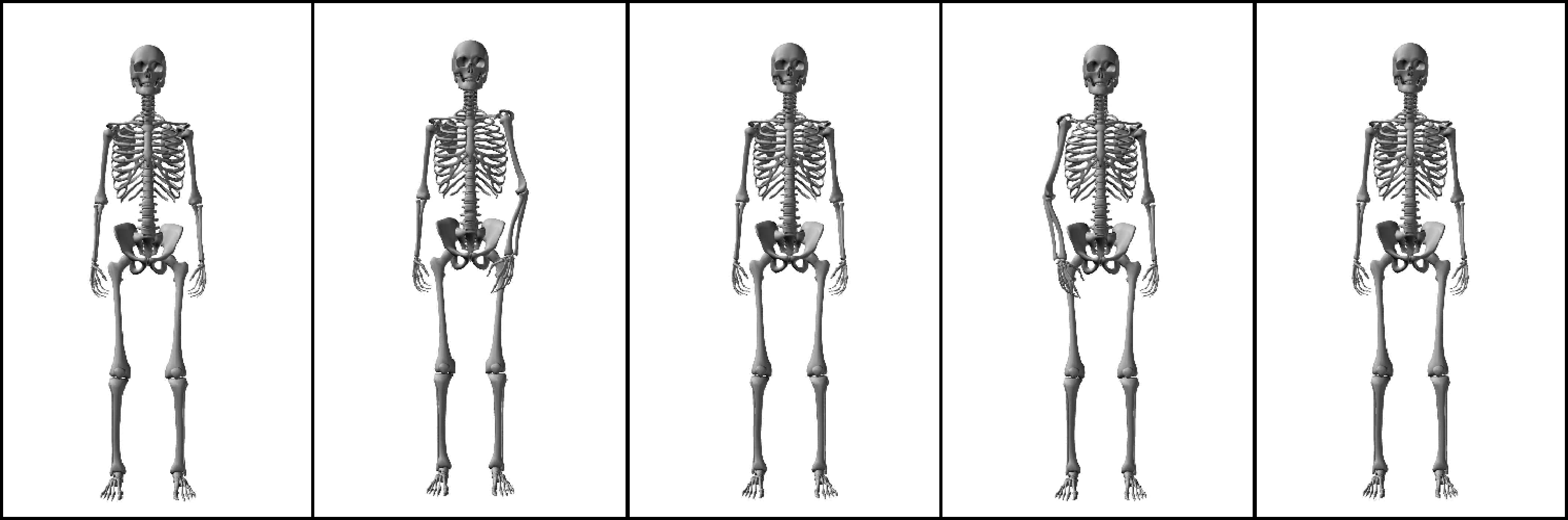
movimientos, our proposed behavioral controller consists of three modules ( Cifra 10).
The first module of our controller involves a simulated lamprey central pattern generator. Él
generates motions that involve rhythmic oscillations (such as bending the body back and forth) como
well as propagation of traveling waves along the body (as in the camel and snake arms). To generate
rhythmic spine motions using the lamprey CPG, we set the global and extra excitations from the
brain stem as well as the plane of motions. Since the four basic spine motions (flexion,
hyperextension, lateral flexion, and twisting) as well as body undulations are planar motions, todo
the 3-DOF joints along the spine rotate about the same axis, and the other DOF are fixed. De este modo, nosotros
only need one parameter to switch the connections between CPG outputs and motors. Como resultado, a
total of three input parameters are adequate to control these motions. After the neural simulation is
performed as described in [28], the outputs from the motor neurons are then saved into a data file
for the calculation of joint angles in MATLAB. Once the plane of motions is specified, the result is
used to control a simulated humanoid in Poser 5 through a script program written in PoserPython.
Artificial Life Volume 12, Número 1
75
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
1
2
1
6
3
1
6
6
2
2
5
5
1
0
6
4
5
4
6
0
6
7
7
5
1
8
6
4
6
4
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
j. O
A Control System for a Flexible Spine Belly-Dancing Humanoid
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
1
2
1
6
3
1
6
6
2
2
5
5
1
0
6
4
5
4
6
0
6
7
7
5
1
8
6
4
6
4
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 8. Fundamental dance postures commonly seen in belly dancing.
The second module of our behavioral controller is a posture database, which stores rotational
joint angles required for specific postures. By sequencing these postures, dance modules such as the
hip circle, vertical hip circle, hip release, hip shimmy, and shoulder shimmy can be made. Through a
combination of these modules, more advanced dance moves can be achieved.
Finalmente, in the third module, one needs to specify the amounts of rotation and the common plane
of motions of two chosen joints. It is then possible to step through the body joints in opposite
directions to generate circular motions.
76
Artificial Life Volume 12, Número 1
j. O
A Control System for a Flexible Spine Belly-Dancing Humanoid
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
1
2
1
6
3
1
6
6
2
2
5
5
1
0
6
4
5
4
6
0
6
7
7
5
1
8
6
4
6
4
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
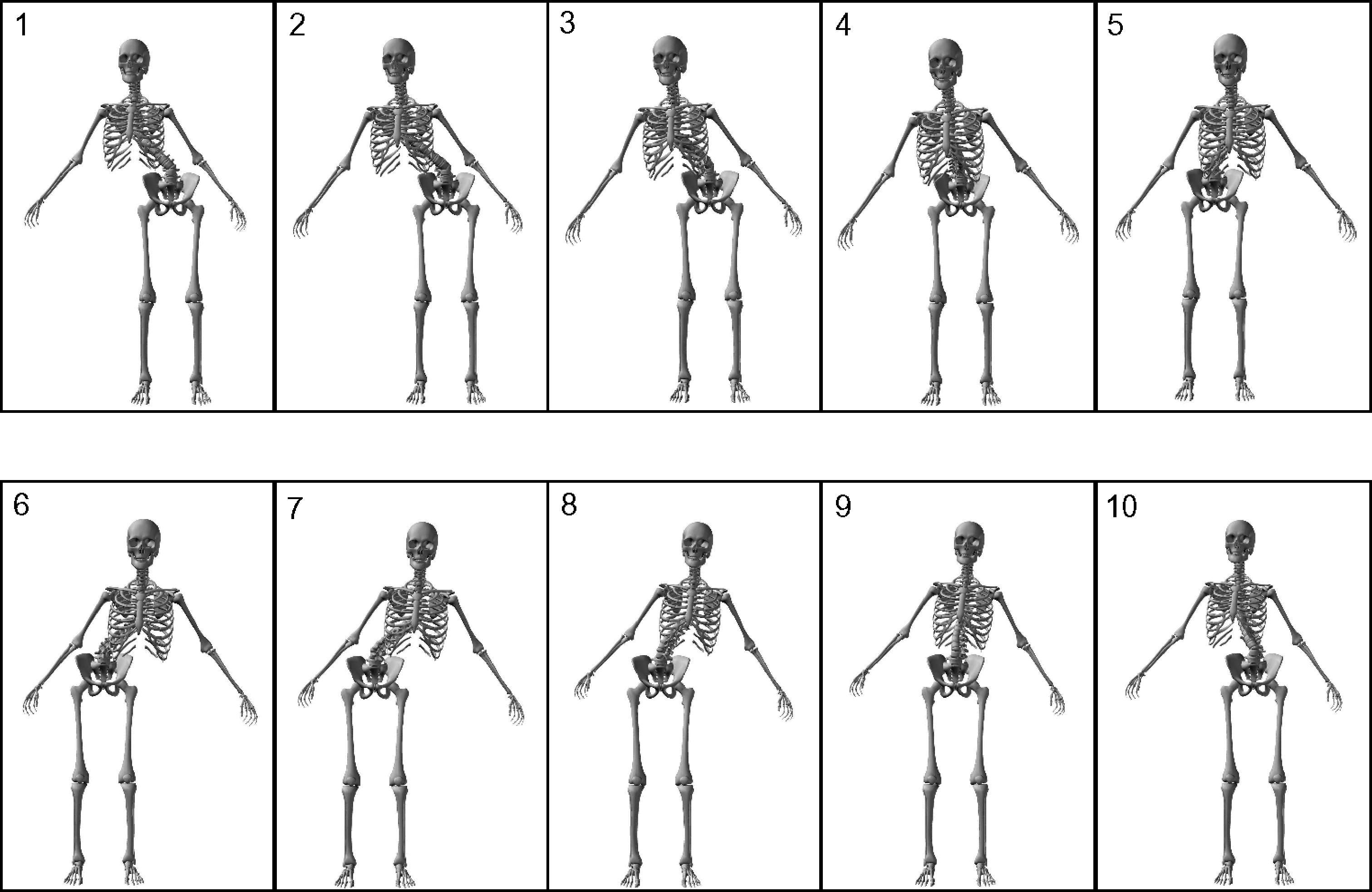
Cifra 9 . Functional classification of dance moves based on articulation (front view). Bars represent either the cervical,
thoracic, or lumbar parts of the spine. Circles represent rotation points, places around which functional rotation would
take place between the main spine segments.
7 Control of Basic Spine Motions
En esta sección, we investigate whether our controller is able to allow the model spine to perform all
four possible actions of the human spine as defined by kinesiologists (descrito en la Sección 2.2). Nota
that for these motions, only three control variables are used.
7.1 Flexion
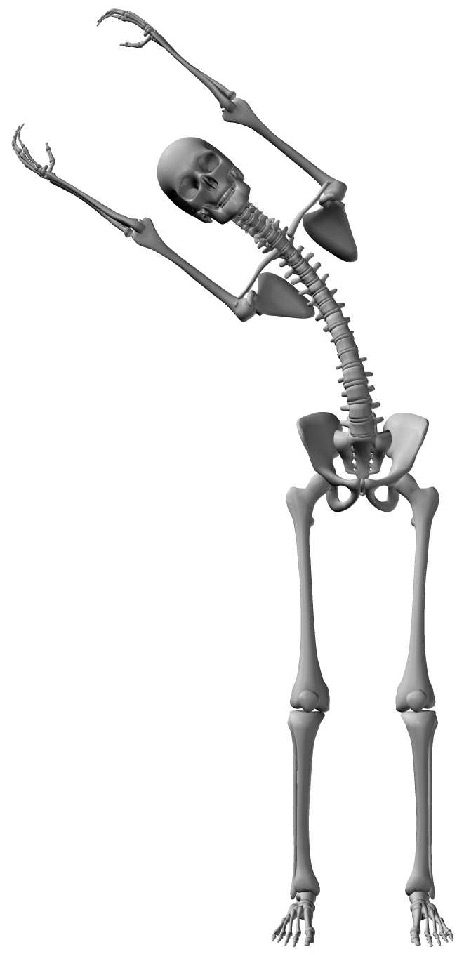
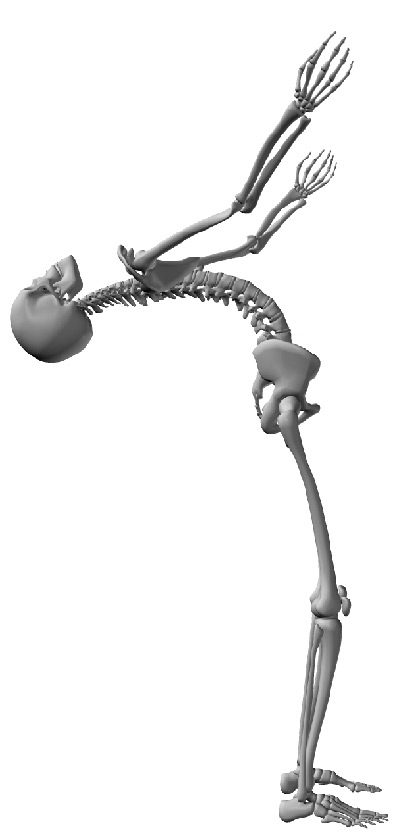
We simulated the lamprey CPG with global excitation 0.3 (out of 1.0) and no extra excitation.
Without extra excitation from the brain stem to the rostral segments, the entire 100-segment CPG
oscillates in phase, and a traveling wave is not generated. The effect of this is that, on specifying
sagittal as the plane of motions, the simulated body bends strongly first to the front and then to the
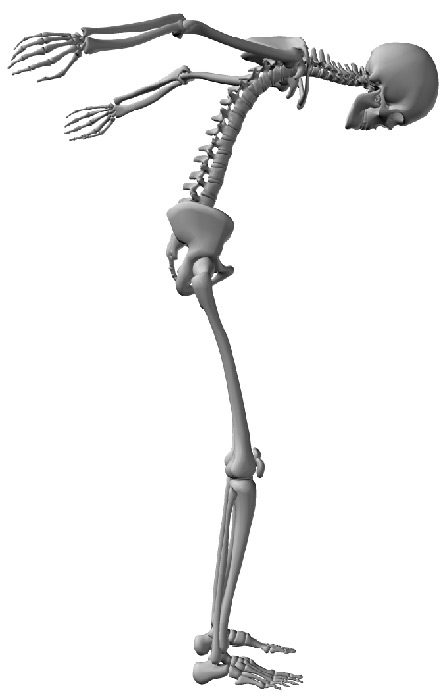
atrás. Body flexion is achieved (Cifra 11).
Artificial Life Volume 12, Número 1
77
j. O
A Control System for a Flexible Spine Belly-Dancing Humanoid
Mesa 4. Parameters for some of the sample dance postures. The notations xrot, yrot, and zrot represent respectively the
rotation along the x, y, and z axes. Note that for each posture, the rotation of one body joint is in the opposite direction
to that of its counterpart. Numbers are expressed in degrees.
Posture
Hip lift (izquierda )
Pelvis tilt
Pelvis tuck
C7
T2
T7
L4
Hip
(cid:3)15 (side to side)
15 (zrot)
(cid:3)25 (bend backward)
25 (xrot)
25 (bend forward) (cid:3)25 (xrot)
Chest lift
25 (lean forward) (cid:3)25 (lean backward)
Chest slide (izquierda )
(cid:3)40 (side to side)
40 (side to side)
Hip twist forward (izquierda )
25 (twist )
(cid:3)25 (yrot)
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
1
2
1
6
3
1
6
6
2
2
5
5
1
0
6
4
5
4
6
0
6
7
7
5
1
8
6
4
6
4
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 10 . Schematic diagram of the behavioral controller. For the spine experiments described in this article, el
transformation function F is the difference between the left and right motoneuron outputs amplified by a gain of 20. Por
sequencing the dance postures, more complicated dance movements can be accomplished.
78
Artificial Life Volume 12, Número 1
j. O
A Control System for a Flexible Spine Belly-Dancing Humanoid
7.2 Hyperextension
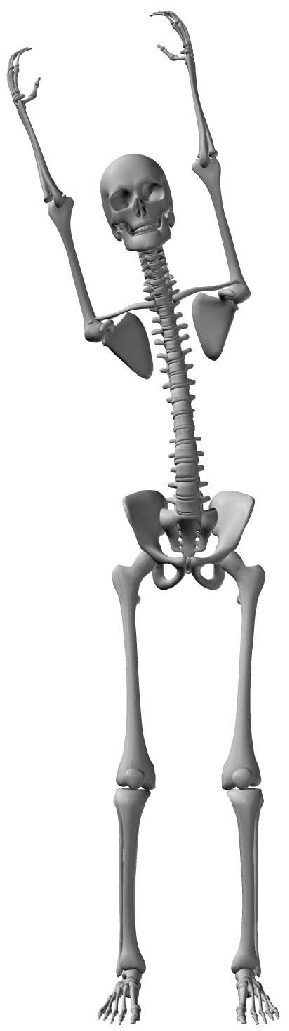
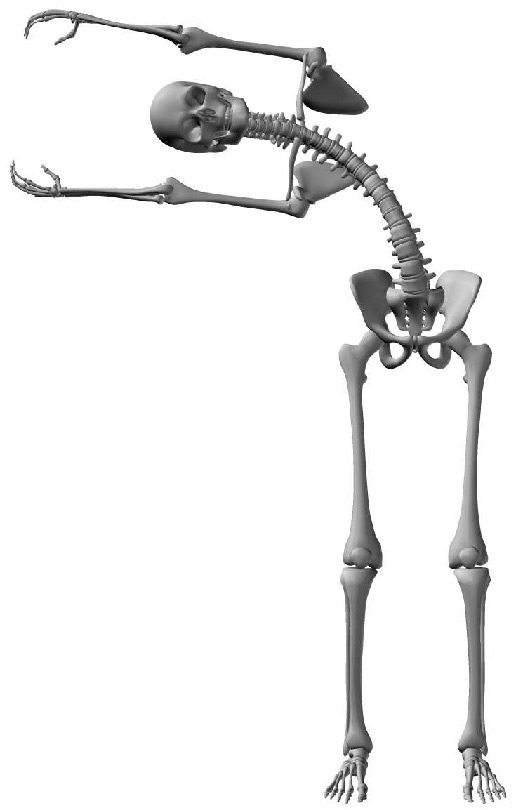
To cause the humanoid to bend more and at a higher frequency, we increased the strength of the
global excitation signal to 0.7. As in the previous experiment, there is no extra excitation from the
brain stem, and the plane of motions is sagittal. The stronger motoneuron outputs and higher
oscillation frequency allow the humanoid to bend more and at a faster rate than that in the previous
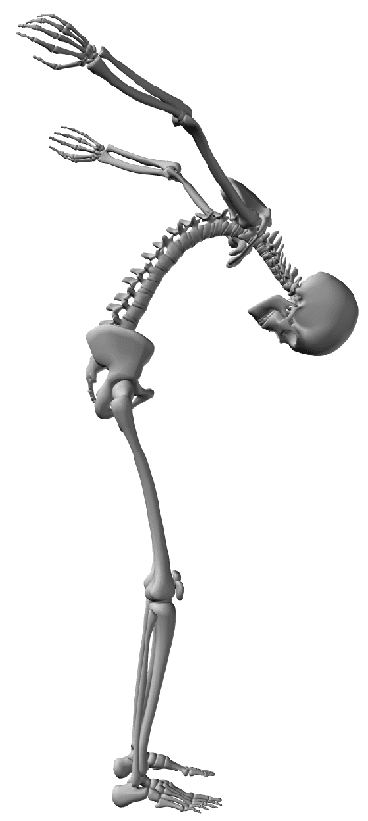
experimento. After this amplification, hyperextension results ( Cifra 12).
7.3 Lateral Flexion
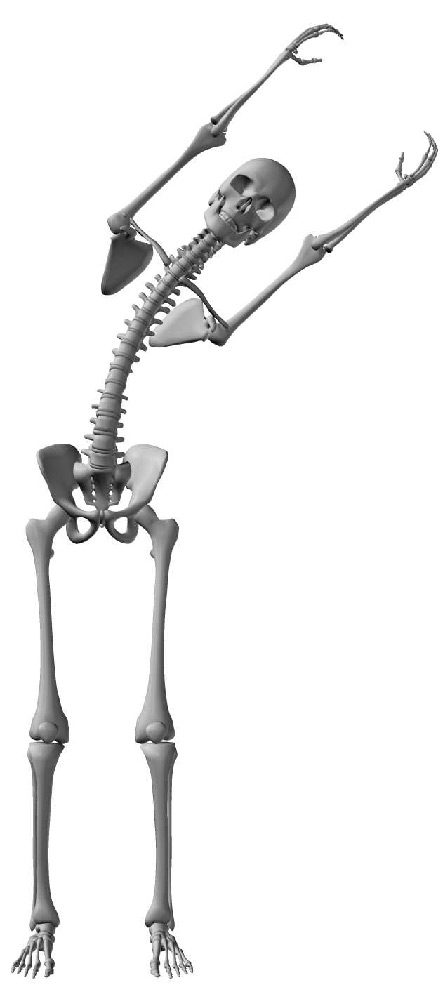
Rather than using the motoneuron outputs to control movements on the sagittal plane, we applied
the same neural wave obtained in the flexion experiment to control movements on the sides. Este
can be accomplished by setting the frontal plane as the plane of motion. The CPG outputs are
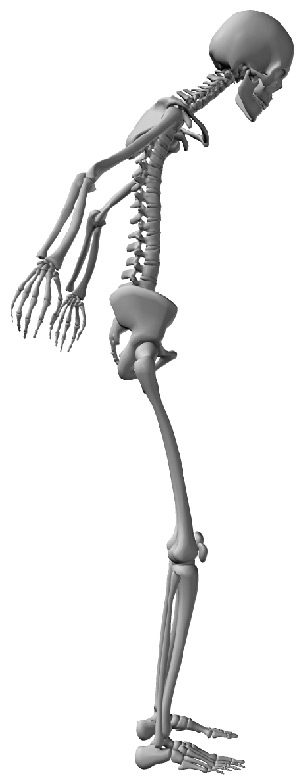
switched to control the bending on the frontal plane. Lateral flexion is made possible ( Cifra 13).
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
1
2
1
6
3
1
6
6
2
2
5
5
1
0
6
4
5
4
6
0
6
7
7
5
1
8
6
4
6
4
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 11. Neural wave generated by the lamprey CPG with global excitation 0.3 and no extra excitation. Solid lines
represent the outputs from the left motoneurons, and dashed lines the outputs from the right motoneurons (arriba). Usando
this neural wave, the humanoid is able to achieve body flexion (abajo).
Artificial Life Volume 12, Número 1
79
j. O
A Control System for a Flexible Spine Belly-Dancing Humanoid
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
1
2
1
6
3
1
6
6
2
2
5
5
1
0
6
4
5
4
6
0
6
7
7
5
1
8
6
4
6
4
pag
d
.
Cifra 12. Neural wave generated by the lamprey CPG with global excitation 0.7 and no extra excitation. Solid lines
represent the outputs from the left motoneurons, and dashed lines those from the right motoneurons (arriba). Using this
neural wave, the humanoid is able to achieve hyperextension (abajo).
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 13. The humanoid is showing lateral body flexion.
80
Artificial Life Volume 12, Número 1
j. O
A Control System for a Flexible Spine Belly-Dancing Humanoid
Cifra 14. The humanoid is twisting its body.
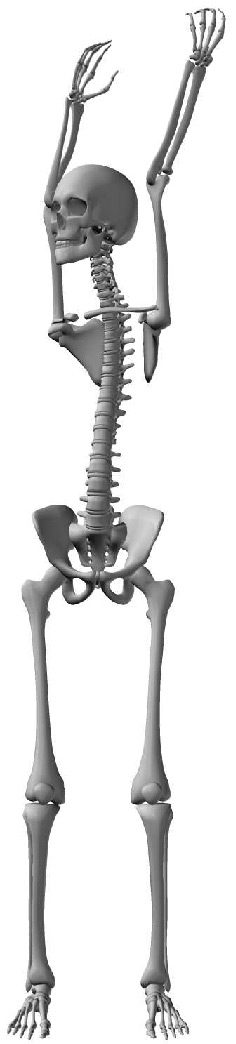
7.4 Twisting
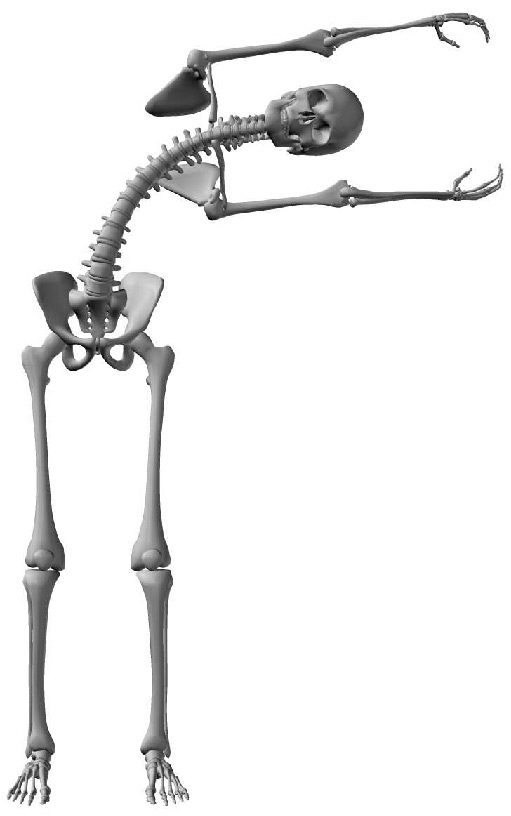
Finalmente, to twist the body (rotation on the transverse plane), we used the same motoneuron outputs
from the flexion experiment to control the rotational angles of the corresponding spinal vertebrae. En
este experimento, we chose the transverse plane as the plane of motion. The motoneuron outputs
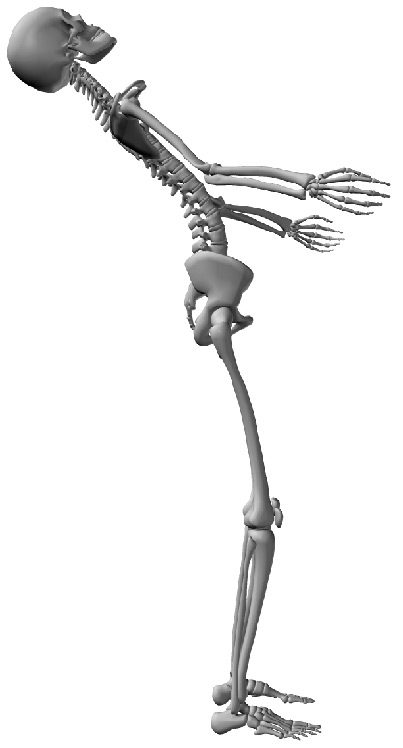
are used to control the rotations on this plane. Cifra 14 shows that the body of our humanoid is able
to twist.
8 Control of Complex Movements
In the previous section, we described how our model achieved basic actions of the human spine. En
this section we describe how to achieve more complex belly dance movements by combining the
basic postures described in Section 5. The movements we are interested in are the hip circle
(transverse plane), vertical hip circle (sagittal plane), hip shimmy (frontal plane), hip release (sagittal
plane), shoulder shimmy (sagittal plane), chest circle (sagittal plane), and camel (sagittal plane). Estos
are the fundamental composite movements one has to master in order to proceed to more advanced
niveles. Similar to the postures in the movement database, these dance modules are the foundations
for the most advanced dance moves. Since most of them are self-explanatory (Figures 15 a 19), nosotros
are describing only the chest circle and the camel here. For computer animations of the dance
modules described in this article, please visit our Web site, http://www.takanishi.mech.waseda.ac.jp/
jimmy/index.html.
8.1 Chest Circle
To imitate the dance move chest circle, we bend vertebrae T7 and L3 in opposite directions by 45 deg
to allow the upper torso and the lower body half to be parallel (see the first move in Figure 20). Entonces
we rotate the body joints in opposite directions on the transverse plane in steps of 36 deg. Este
allows the upper body torso to complete one circle in 10 steps. Note that for this dance move, No
CPG is required.
8.2 Camel (Undulation)
In this experiment we set the global and extra excitations from the brain stem to 0.3 y 120%
respectivamente. The extra excitation and intersegmental couplings cause a phase lag of 1% entre
successive segments along the CPG. Using the motoneuron outputs from the fifth to the sixth
second to control the joint angles at each frame, a traveling wave can be made to propagate along the
spine ( Cifra 21). This is analogous to the famous camel move.8 Note that if we use an appropriate
8 De término medio, it takes 5s to complete one cycle. To mimic the dance realistically, the playback rate is set to 5.4 frames/s.
Artificial Life Volume 12, Número 1
81
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
1
2
1
6
3
1
6
6
2
2
5
5
1
0
6
4
5
4
6
0
6
7
7
5
1
8
6
4
6
4
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
j. O
A Control System for a Flexible Spine Belly-Dancing Humanoid
Cifra 15. Hip circle. Dance sequence (from left to right): neutral, hip lift (bien), pelvis tilt, hip lift (izquierda), pelvis tuck, y
repeat.
set of neural segments to control the joints from the shoulders to the fingers, we can produce
sinusoidal motions along the arms and the hands. Movements such as the snake arms and hand
ripple can be mimicked.
9 Discusión
This article presents a novel control system for a simulated, flexible spine belly-dancing humanoid
robot. Using three control variables (global excitation, extra excitation, and plane of motions) para el
CPG model, we are able to reproduce the four basic spine movements defined by kinesiologists as
well as body undulations commonly seen in belly dancing. The CPG is particularly good at
controlling rhythmic motions.
By extending the lamprey CPG, Ijspeert [17 ] developed a walking controller for a simulated
salamander. He demonstrated that the lamprey swimming controller is robust and scalable. A pesar de
our CPG can be applied to generate rhythmic arm motions such as the snake arms and hand ripple,
it is likely that it can be combined with other limb controllers such as those developed by researchers
in imitation learning [3, 18, 22, 19] for the control of non-rhythmic arm movements in a real flexible
spine belly-dancing humanoid robot currently under development.
From the experiments, our control system seems to be flexible. It would be interesting to apply
the same controller to a different platform (such as a real robot with fewer spine segments) en orden
to demonstrate the adaptivity of the proposed control architecture.
When we reproduced the four basic motions of the human spine, we used the motoneuron
outputs from the lamprey CPG to control every other vertebra of the simulated spine. La razón
for this is that even at a global excitation of 0.3 (out of 1), the total amount of rotation from all 21
Cifra 16. Vertical hip circle. Dance sequence (from left to right): neutral, hip lift (bien), hip twist forward (bien), hip drop
(bien), hip twist backward (bien), and repeat.
82
Artificial Life Volume 12, Número 1
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
1
2
1
6
3
1
6
6
2
2
5
5
1
0
6
4
5
4
6
0
6
7
7
5
1
8
6
4
6
4
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
j. O
A Control System for a Flexible Spine Belly-Dancing Humanoid
Cifra 17. Hip shimmy. Dance sequence (from left to right): neutral, hip lift (izquierda), hip drop (izquierda), hip lift (bien), hip drop
(bien), and repeat. Note that hip drop is the same as neutral.
synchronized vertebrae becomes close to 200 deg. Given that the vertebrae are interconnected and
that it is less important to differentiate the action of adjacent joints in these movements, this CPG-
vertebrae mapping is acceptable to generate the motions for our model humanoid. For the control of
all spinal vertebrae using a wider range of control signals (the global and extra excitations), one can
reduce the amplification factor involved in the calculation of joint angles. Our controller also shows
flexibility in this aspect. Another benefit of controlling the spine motions using only every other
vertebra is that this mapping can potentially be applied to the control of a real mechanical spine using
one-third fewer motors. De este modo, power consumption can be reduced.
For the experiments on using the CPG outputs to reproduce the four basic and undulation spine
motions, we used one control variable to specify the plane of motion of all spinal vertebrae. Given
the fact that the four basic human spine motions are planar (eso es, all the joints rotate about the
same axis), there might be a mechanism that controls the switching of the plane of movements even
in real biological systems. This merits further investigation through collaboration with neuroscien-
tistas. Using a 3D motion capture system and comparative analysis of motions between the human
belly dancer and the simulated humanoid, our work has the potential to be extended toward the
biological plausibility of the proposed control scheme.
Actualmente, our CPG-to-vertebrae mapping scheme allows the switching of connections between
CPG outputs to motors about any of the three DOF axes. For nonuniform spine motions, the CPG
module can easily be modified to allow specifications of this variable for each individual vertebra.
Note that since some of the possible actions of the human spine are restricted by the articulation and
shape of the bony landmarks, 3-DOF motions at each joint are not necessary.
In this article, we have used the motoneuron outputs from 100 evenly divided neural segments
of a CPG network to control a skeleton model of 21 segments. The reason for this is that if we
Cifra 18. Hip release. Dance sequence (from left to right): neutral, hip lift (bien), hip drop (bien), hip lift (bien), hip drop
and kick (bien), and repeat.
Artificial Life Volume 12, Número 1
83
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
1
2
1
6
3
1
6
6
2
2
5
5
1
0
6
4
5
4
6
0
6
7
7
5
1
8
6
4
6
4
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
j. O
A Control System for a Flexible Spine Belly-Dancing Humanoid
Cifra 19. Shoulder shimmy. Dance sequence (from left to right): neutral, shoulder punch (izquierda), neutral, shoulder punch
(bien), neutral, and repeat.
used the motoneuron outputs from 21 consecutive neural segments to control the vertebrae, a small
intersegmental phase lag would not produce observable motions from the reduced body segments.
Además, since the intersegmental couplings were determined from physiological data (alguno
neurons have connections to neurons as far as 10 segments away), shortening the CPG network by
about one-fifth would change the behavior of the entire network. The special feature of relatively
independent control of frequency and phase lag, as well as the regular motor patterns, would be
affected.
Although the database component of our system seems to be a counterexample that shows the
limitation of the CPG, it was included for simplicity and the posing of static postures. La mayoría de
movements created by sequencing these postures can actually be generated using the CPG. Para
instancia, all the sliding motions can be accomplished by rhythmically rotating two joints in opposite
directions on the frontal plane.
Actualmente, our system does not have visual feedback or learning ability. It would be interesting to
investigate how humans learn complex and rhythmic dance movements through observation. Por
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
1
2
1
6
3
1
6
6
2
2
5
5
1
0
6
4
5
4
6
0
6
7
7
5
1
8
6
4
6
4
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 20. Chest circle.
84
Artificial Life Volume 12, Número 1
j. O
A Control System for a Flexible Spine Belly-Dancing Humanoid
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
1
2
1
6
3
1
6
6
2
2
5
5
1
0
6
4
5
4
6
0
6
7
7
5
1
8
6
4
6
4
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 21. Neural wave generated by the lamprey CPG with global excitation 0.3 and extra excitation 120% desde el
brain stem. Solid lines represent outputs from the left motoneurons while dashed lines represent the outputs from the
right motoneurons (arriba). Using this neural wave, the simulated humanoid is able to perform the move camel. For clarity,
limbs are removed. Note the traveling wave along the spine.
incorporating these research findings and a visual system, it would be possible to teach a humanoid
robot more complex motor behaviors by imitation learning.
Contrary to common belief, most of the movements in belly dancing are achieved through
motions from the spine and/or the pelvis. Only the belly roll requires solely movements from the
muscles. Due to limited resources, we used our controller to control a weightless skeleton figure in
3D animation without taking into consideration body dynamics or other physical constraints
(derived from the embodiment of the human skeleton model). To implement the controller in a real
Artificial Life Volume 12, Número 1
85
j. O
A Control System for a Flexible Spine Belly-Dancing Humanoid
humanoid robot, factors such as gravity, weight, balancing, collisions, inertia, and elasticity need to be
consideró. It would be interesting to model the human skeleton and abdominal muscles using a
realistic physical simulator such as the MathEngine.
Some of the frequencies of the neural waves appear to be fast for an untrained human (cerca de
3 Hz in Figure 11, and about 4.5 Hz in Figure 12); the motoneuron outputs from each neural
segment are actually used as a sequence of rotational commands to control the joint angles at each
time frame. Within a fixed time interval (6 s for the experiments described in this article), the neural
wave in Figure 11 corresponds to a slower motion than the one in Figure 12. Our approach can be
applied to specify the rotational angles of real motors at each time step.
Finalmente, although the behaviors of CPG networks such as rhythmic oscillations and propagation
of traveling waves have been reported in many articles [7, 11, 8], none has been applied to the
generation of spine motions of a simulated or real humanoid robot. A lo mejor de nuestro conocimiento,
our interdisciplinary approach is the first of its kind.
10 Conclusión
This article demonstrates that by applying the control principles observed in the prototype vertebrate
lamprey, it is possible to control the spine of a simulated humanoid robot. By varying the global and
extra excitations from the brain stem as well as the plane of movements, the proposed lamprey CPG
module could potentially generate plausible output patterns, which could be used for all the possible
motions of the human spine. Además, by incorporating the lamprey CPG and a posture
database into our control system, the simulated humanoid robot is able to mimic the fundamental
moves in belly dancing. Our work suggests that the proposed controller can potentially be applied to
the control of a high-degree-of-freedom, flexible spine humanoid robot.
Expresiones de gratitud
Many thanks for the useful comments of anonymous reviewers, Richard Stein, Lenhart Schubert, y
Martin Jagersand on the earlier versions of this manuscript. The author would like to thank Lorna
Gow and Alina Fischer for allowing him to attend belly dance lessons and performances. Special
thanks to the professional belly dance teacher Aldiah for helping to develop the posture database.
Referencias
1. Ate´a. (2000). What is belly dance and what should we really call it? http://www.magicalmotion.com/
bellydance3.htm.
2. Atkeson, C. GRAMO., Hale, j. GRAMO., Pollick, F., Riley, METRO., Kotosaka, S., Schaal, S., Shibata, T., Tevatia, GRAMO., Ude, A.,
Vijayakumar, S., & Loco, METRO. (2000). Using humanoid robots to study human behavior. IEEE Intelligent
Sistemas, 15(4), 46 – 56.
3. Billard, A., & Mataric´, METRO. j. (2001). Learning human arm movements by imitation: Evaluation of a
biologically inspired connectionist architecture. Robotics and Autonomous Systems, 941, 1 – 16.
4. Breazeal, C. (2002). Designing Sociable Robots. Cambridge, MAMÁ: CON prensa.
5. Arroyos, R. A., Breazeal, C., Marjanovic, METRO., Scassellati, B., & Williamson, METRO. (1999). The Cog
proyecto: Building a humanoid robot. In C. Nehaniv ( Ed.), Computation for metaphors, analog y, and agents
( páginas. 52 – 87 ). Nueva York: Saltador.
6. Chirikjian, GRAMO. (1995). A sidewinding locomotion gait for hyperredundant robots. Advanced Robotics,
9(3), 195 – 216.
7. Delcomyn, F. (1980). Neural basis for rhythmic behaviour in animals. Ciencia, 210, 492 – 498.
8. Delcomyn, F. (1998). Foundations of Neurobiolog y. Nueva York: W.. h. Hombre libre.
9. Ekeberg, O¨ . (1993). A combined neuronal and mechanical model of fish swimming. Cibernética biológica,
69, 363 – 374.
10. Fitt, S. S. (1988). Dance Kinesiolog y. Londres: Schirmer Books, a Division of Macmillan.
86
Artificial Life Volume 12, Número 1
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
1
2
1
6
3
1
6
6
2
2
5
5
1
0
6
4
5
4
6
0
6
7
7
5
1
8
6
4
6
4
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
j. O
A Control System for a Flexible Spine Belly-Dancing Humanoid
11. Grillner, S. (1981). Control of locomotion in bipeds, tetrapods, and fish. In V. B. Arroyos ( Ed.), Manual
of physiolog y. Sección 1. The nervous system II. Motor control (3tercera ed., páginas. 1179 – 1236). Bethesda, Maryland: Americano
Physiological Society.
12. Grillner, S. (1996). Neural networks for vertebrate locomotion. Scientific American, 274(6), 48 – 53.
13. Grillner, S., Walle´n, PAG., & Brodin, l. (1991). Neuronal network generating locomotor behavior in lamprey:
Circuitry, transmitters, membrane properties, and simulation. Revisión anual de neurociencia, 14, 169 – 199.
14. Grillner, S., Walle´n, PAG., & Viana di Prisco, GRAMO. (1991). The lamprey locomotor system — Basic locomotor
synerg y. En m. Shimamura, S. Grillner, & V. R. Edgerton ( Editores.), Neurobiological basis of human locomotion
( páginas. 77 – 92). Tokio: Japan Scientific Societies Press.
15. Hashimoto, S. (2000). Waseda University: Humanoid Robotics Institute. Tokio: Waseda University.
16. Iida, F., Tabata, METRO., & Hara, F. (1998). Generating personality character in a face robot through
interaction with human. In Proceedings of the 7th IEEE International Workshop on Robot and Human
Comunicación ( páginas. 481 – 486).
17. Ijspeert, A. j. (2001). A connectionist central pattern generator for the aquatic and terrestrial gaits of a
simulated salamander. Cibernética biológica, 84(5), 331 – 348.
18. Ijspeert, A. J., Nakanishi, J., & Schaal, S. (2002). Movement imitation with nonlinear dynamical systems
in humanoid robots. In Proceedings of the IEEE International Conference on Robotics and Automation ( ICRA2002)
( páginas. 1398 – 1403).
19. Jenkins, oh. C., & Mataric´, METRO. j. (2002). Deriving action and behavior primitives from human motion
datos. En Actas de la 2002 IEEE/RSJ International Conference on Intelligent Robots and Systems ( volumen. 3,
páginas. 2551 – 2556).
20. Kandel, mi. r., Schwatz, j. h., & Jessell, t. METRO. (Editores.) (1985). Principles of Neural Science (2y ed.). Nueva York: Elsevier.
21. Mamá, S. (2001). Analysis of creeping locomotion of a snake-like robot. Advanced Robotics, 15(2), 205 – 224.
22. Mataric´, METRO. (2002). Visuo-motor primitives as a basis for learning by imitation: Linking perception to
action and biolog y to robotics. In K. Dautenhahn & C. Nehaniv ( Editores.), Imitation in animals and artifacts
( páginas. 392 – 422). Cambridge, MAMÁ: CON prensa.
23. Miwa, h., Okuchi, T., Takanobu, h., & Takanishi, A. (2002). Development of a new human-like head
robot WE-4. En Actas de la 2002 IEEE/RSJ International Conference on Intelligent Robots and Systems
( volumen. 2, páginas. 2443 – 2448).
24. Mizuuchi, I., Inaba, METRO., & Inoue, h. (2001). A flexible spine human-form robot — Development
and control of the posture of the spine. En Actas de la 2001 IEEE/RSJ International Conference
on Intelligent Robots and Systems ( volumen. 3, páginas. 2099 – 2104).
25. Mizuuchi, I., Tajima, r., Yoshikai, T., Sato, D., Nagashima, K., Inaba, METRO., Kuniyoshi, y., & Inoue, h. (2002).
The design and control of the flexible spine of a fully tendon-driven humanoid ‘‘Kenta.’’ In Proceedings of the
2002 IEEE/RSJ International Conference on Intelligent Robots and Systems ( volumen. 3, páginas. 2527 – 2532).
26. Nakazawa, A., Nakaoka, S., Ikeuchi, K., & Yokoi, k. (2002). Imitating human dance motions
through motion structure analysis. En Actas de la 2002 IEEE/RSJ International Conference on Intelligent
Robots and Systems ( volumen. 3, páginas. 2539 – 2544).
27. Nugent, METRO. (2000). Bellydance movement vocabulary. http://www.venusbellydance.com/vocabulary.htm.
28. O, j. (2002). An investigation of artificially-evolved robust and efficient connectionist swimming controllers for a simulated
lamprey. Doctor. tesis, University of Edinburgh, Edimburgo.
29. Sakagami, y., Watanabe, r., Aoyama, C., Matsunaga, S., Higaki, NORTE., & Fujimura, k. (2002). The intelligent
ASIMO: System overview and integration. En Actas de la 2002 IEEE/RSJ International Conference on
Intelligent Robots and Systems ( volumen. 3, páginas. 2478 – 2483).
30. Sarrigeorgidis, k. (1999). The NTUA snake; Diseño, planar, kinematics, and motion planning. Diario de
Robotic Systems, 16(1), 37 – 72.
31. shan, J., & Nagashima, F. (2002). Neural locomotion controller design and implementation for
humanoid robot HOAP-1. In 20th Annual Conference of the Robotics Society of Japan (presentation 1C34).
Robotics Society of Japan.
32. Yamasaki, F., Endo, K., Asada, METRO., & Kitano, h. (2002). An energ y-efficient walking for a low-cost
humanoid robot PINO. AI Magazine, 23(1), 60 – 61.
Artificial Life Volume 12, Número 1
87
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
1
2
1
6
3
1
6
6
2
2
5
5
1
0
6
4
5
4
6
0
6
7
7
5
1
8
6
4
6
4
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
1
2
1
6
3
1
6
6
2
2
5
5
1
0
6
4
5
4
6
0
6
7
7
5
1
8
6
4
6
4
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3