ARTÍCULO DE INVESTIGACIÓN
Bayesian history of science: The case of Watson
and Crick and the structure of DNA
Henry Small
SciTech Strategies Inc., Berwyn, Pensilvania
un acceso abierto
diario
Palabras clave: Bayes’ theorem, confirmation, discovery, DNA, evidencia, Watson and Crick
Citación: Pequeño, h. (2023). Bayesian
history of science: The case of Watson
and Crick and the structure of DNA.
Estudios de ciencias cuantitativas, 4(1),
209–228. https://doi.org/10.1162/qss_a
_00233
DOI:
https://doi.org/10.1162/qss_a_00233
Revisión por pares:
https://www.webofscience.com/api
/gateway/wos/peer-review/10.1162
/qss_a_00233
Recibió: 8 Agosto 2022
Aceptado: 22 Noviembre 2022
Autor correspondiente:
Henry Small
hsmall@mapofscience.com
Editor de manejo:
Juego Waltman
Derechos de autor: © 2023 Henry Small.
Publicado bajo Creative Commons
Atribución 4.0 Internacional (CC POR 4.0)
licencia.
La prensa del MIT
ABSTRACTO
A naïve Bayes approach to theory confirmation is used to compute the posterior probabilities
for a series of four models of DNA considered by James Watson and Francis Crick in the
early 1950s using multiple forms of evidence considered relevant at the time. Conditional
probabilities for the evidence given each model are estimated from historical sources and
manually assigned using a scale of five probabilities ranging from strongly consistent to
strongly inconsistent. Alternative or competing theories are defined for each model based
on preceding models in the series. Prior probabilities are also set based on the posterior
probabilities of these earlier models. A dramatic increase in posterior probability is seen for the
final double helix model compared to earlier models in the series, which is interpreted as a
form of “Bayesian surprise” leading to the sense that a “discovery” was made. Implications for
theory choice in the history of science are discussed.
1.
INTRODUCCIÓN
Connecting empirical findings to theories is fundamental to science. Many of these connec-
tions are surprising and unexpected: Por ejemplo, that gravity can bend light as predicted by
general relativity, or that the speed of light can be deduced from electromagnetic theory as
James Maxwell did in the 19th century. Many such surprises are hidden inside scientific prob-
lems and are experienced only by scientists working on them. Por ejemplo, James Watson and
Francis Crick were surprised when they found a configuration of specific pairs of DNA bases
that were hydrogen bonded inside two sugar-phosphate backbones. The recent Nobel Prize
winner David Julius and his team were surprised when they discovered that they could clone a
pain receptor (Julius, 2021).
One way of understanding surprise is Bayesian analysis, when we have a low expectation
of success in solving a problem and then find a solution. Surprise can come about if our prior
probability is low, pero, on consideration of the evidence, our probability increases abruptly.
Alternativamente, a result that was considered well confirmed and thus had high probability is
undermined by new evidence, resulting in a sudden drop in its probability. In yet other
instancias, a new theory is found that accounts for the evidence dramatically better than the
existing theory, such as might occur in a scientific revolution.
In the Bayesian framework, our expectation about the validity of a theory is expressed as a
prior probability, and the impact of evidence on a theory leads to a posterior probability, el
probability of the theory given the evidence. This change is mediated by conditional proba-
bilities that express how well the old and new theories explain or do not explain the evidence.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
q
s
s
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
1
2
0
9
2
0
7
8
3
7
2
q
s
s
_
a
_
0
0
2
3
3
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Bayesian history of science
An equivalent formulation of the probability of a theory given the evidence is the joint prob-
capacidad, expressed as P(t & mi ), eso es, the probability that theory T and evidence E agree with
one another. When that happens, we can be surprised if our initial expectation of agreement
was low.
In this model, we can think of science as a gigantic jigsaw puzzle consisting of a mixture of
theoretical and empirical pieces that we are attempting to fit together. We would not expect
two pieces selected at random to fit together, although some pieces might come close. Este
puzzle must be hyperdimensional, like a complex network with some pieces linking to many
others but others linking to only a few (Precio, 1986, pag. 268). The problem with this jigsaw
puzzle model of science is that the pieces keep changing shape. A new or modified theory
becomes a new puzzle piece. The evidence pieces will change too when experimental accu-
racy increases or when new devices and experiments are devised that yield novel findings. Como
this puzzle dynamically changes, occasions arise when parts of the already assembled puzzle
may need to be radically rearranged, and perhaps totally dismantled and rebuilt, as in the case
of a scientific revolution.
Theories in the psychological sense used here are statements or generalizations claiming
to be universally true about which we have varying degrees of confidence. These can range
from Kepler’s first law that planets follow elliptical orbits to Bohr’s theory of the hydrogen
atom. But we also take theories to include hypotheses, presuppositions, and models, para
ejemplo, Guillemin and Schally’s model of thyrotropin releasing factor (TRF) as a peptide
(Latour & Woolgar, 1979), and Hershko and Ciechanover’s ubiquitin system for protein deg-
radation (Fry, 2022). If a theory agrees with empirical observations, we might say that it was
merely a fluke or coincidence, that somehow the theory was rigged to explain the experiment,
or we might conclude that the agreement was because this is the way the world works. In any
evento, it seems natural to say, as Bayesians do, that a theory has some probability of being true
depending on how well it fits the evidence, allowing for the possibility that other current or
future theories might fit the evidence as well or better.
Competition among theories is especially visible when there are a series of attempts to
model an entity or phenomenon, such as the atom in the early 20th century, high-temperature
superconductivity in the late 20th century (Hartman, 2008), or a specific substance, como
DNA in the 1950s, as will be discussed in this paper. In such a sequence of attempts, it seems
reasonable to use the probability of a previous model as the prior probability of the next
modelo. As the prior probability reflects our confidence in the correctness of some idea, si
we or others have made attempts to solve a problem, our level of confidence will increase
or decrease depending on previous successes or failures. A string of failures will make us less
confident that we are on the right track, but a string of near successes might encourage us to
keep trying.
2. THE BAYESIAN FRAMEWORK
In testing theories scientists rely on multiple forms of evidence. Each piece of evidence can be
taken one at a time using Bayes’ theorem or all the available evidence can be applied at the
mismo tiempo. In the latter case we need a formulation of Bayes’ theorem that accommodates
multiple kinds of evidence. A good candidate is the naïve Bayes model where, in network
terms, a theory is like the hub of a wheel with various forms of evidence radiating out like
spokes (Cifra 1).
This model requires us to assume that the various kinds of evidence are independent of
entre sí, or at least approximately so. Por ejemplo, hydrogen bonding does not guarantee
Estudios de ciencias cuantitativas
210
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
q
s
s
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
1
2
0
9
2
0
7
8
3
7
2
q
s
s
_
a
_
0
0
2
3
3
pag
d
/
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Bayesian history of science
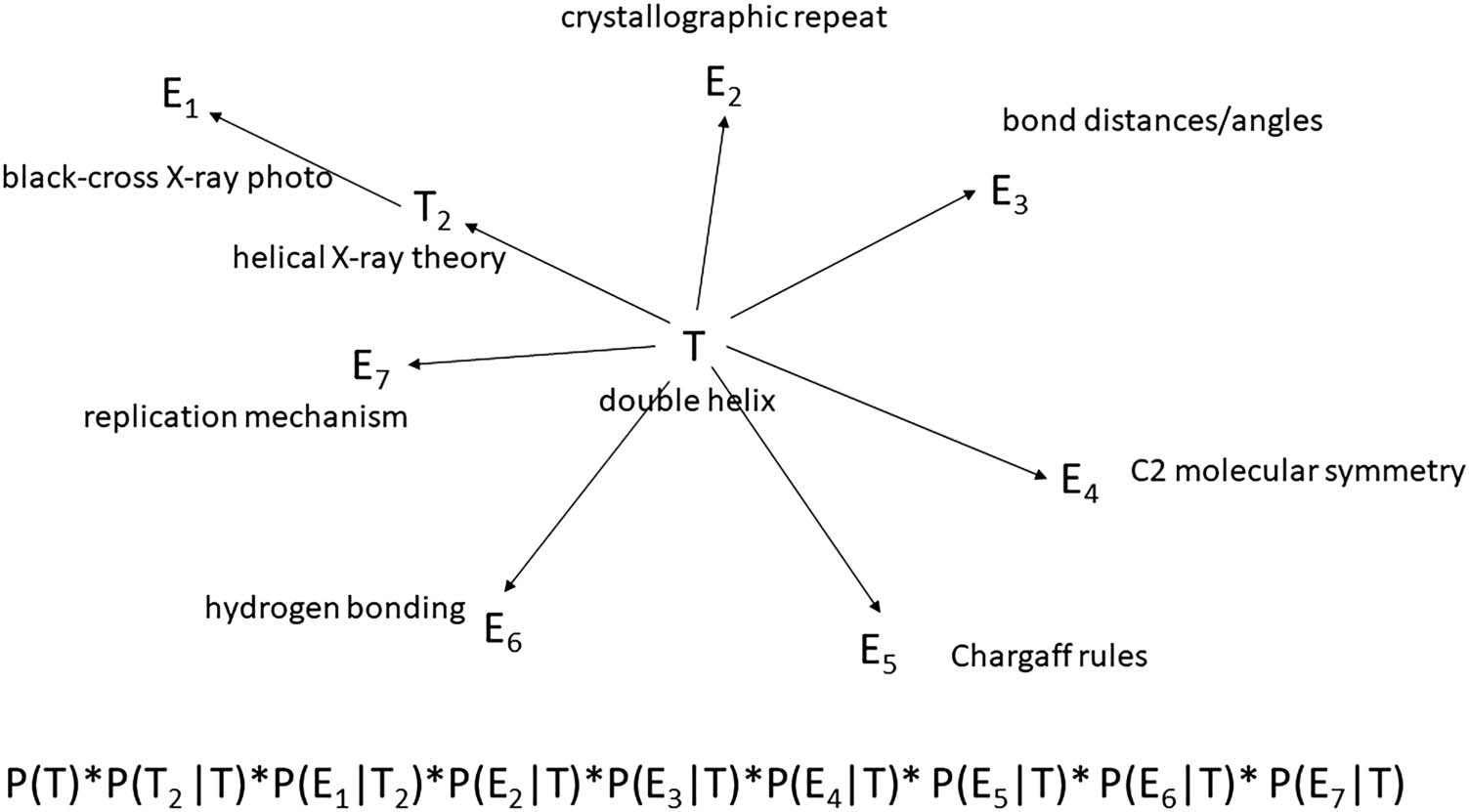
Cifra 1. Naïve Bayes network for evaluating Watson and Crick’s double helix model of DNA and
its algebraic equivalent as a product of the prior and conditional probabilities derived using the
chain rule. Each arrow corresponds to a conditional probability where the head of the arrow points
to what is supposedly predicted or explained, and the tail is what does the explaining. Note that a
two-step path leads from the DNA model to the “black cross” X-ray photo via a helical X-ray theory.
conformity to Chargaff rules or C2 symmetry. If such dependencies existed, arrows should con-
nect those evidence nodes. Fortunately, the naïve Bayes model has a closed form solution
which allows us to compute the posterior probability given the prior and conditional proba-
bilities for any number of evidence variables i:
q
d
q
Þ ¼
Þ
q
P Tð Þ
P T jEi; norte
i P EijTð
Þ þ P (cid:2)Tð
Þ
P Tð Þ
i P EijTð
Here the theory being evaluated is T and its negation is (cid:2)t. The evidence variables are E1, E2,
… EN where N is the number of forms of evidence being considered. Esencialmente, we assign
probabilities P (mi |t ) for each form of evidence i and multiply them together. This is done for
both the theory T under consideration and for the negation of the theory (cid:2)t, in which we
include any alternative or competing theories.
i P Eij(cid:2)t
d
(1)
Þ
The numerator can be interpreted as a joint probability of independent forms of evidence E1
to EN: PAG (t & E1 & E2 & E3 … & EN) =P (t ) * PAG (E1|t ) * PAG (E2|t ) * PAG (E3|t ) … * PAG (EN|t ). So, el
probability of the theory given all the forms of evidence is proportional to the product of the
prior probability of the theory and the probabilities of each form of evidence given the theory
under consideration. In the denominator of Eq. 1 the first term is the same as the numerator and
can be interpreted as the probability that the evidence fits with the theory. The second term is
the probability the evidence fits with the alternative theories P ((cid:2)t ) * PAG (E1|(cid:2)t ) * PAG (E2|(cid:2)t ) *
PAG (E3|(cid:2)t ) … * PAG(EN|(cid:2)t ). If these two terms are equal, then the probability the theory is correct
given all forms of evidence (the posterior) is equal to 0.5. De este modo, if there is no reason to favor
T over (cid:2)T we assign a probability of 0.5 to both. Another attractive feature of a 0.5 prior is
that it allows the widest range of confirming or disconfirming posterior probabilities.
Confirmation of the theory is indicated if the posterior probability is greater than the prior
probabilidad, PAG (t |E1,N) > P (t ) and disconfirmation if P (t |E1,N) < P (T ). If theory T is part of a series
of attempts to model some phenomena, then the posterior can be used as the prior for the next
attempt. Whether multiple forms of evidence are taken all at one time, as in Eq. 1, the result is
Quantitative Science Studies
211
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
1
2
0
9
2
0
7
8
3
7
2
q
s
s
_
a
_
0
0
2
3
3
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Bayesian history of science
the same as if each form of evidence had been evaluated separately, setting the prior of the
successor theory equal to the posterior of the predecessor theory.
The likelihood ratio (Howson & Urbach, 2006, 21), also called the Bayes factor (Morey,
Romeijn, & Rouder, 2016), is defined for Eq. 1 as the product of probabilities of all forms of
evidence given that the theory is true divided by the product of the probabilities given that the
theory is false:
Q
Q
iP EijTð
Þ
iP Eij(cid:2)T
ð
Þ
(2)
This ratio is greater than one for confirmation and less than one for disconfirmation. Thus,
confirmation does not depend on the value of the prior, only on the conditional probabilities.
This formula can be used to determine confirmation or disconfirmation but does not allow the
calculation of the posterior probability. To compute a posterior a prior must be specified.
Eq. 1 can be derived by enumerating all the terms in the probability function in Figure 1 for
the theory and evidence nodes, which must sum to 1 (Koller & Friedman, 2009, p. 292). To get
the posterior probability of the theory given the evidence being true, we omit the conditional
probability terms where the evidence nodes are set to “false” and divide by the “total proba-
bility,” that is, the sum of probabilities of T being true, and T not being true.
The question arises as to what happens if we consider more than one alternative theory?
Then we need to add additional terms to the denominator of Eq. 1. The general expressions is
ð
P T1jEi; n
Q
(cid:2) (cid:3) Q
Þ
Þ ¼ P T1ð
P
j P Tj
i P EijT1
Þ
ð
(cid:2)
i P EijTj
(cid:3)
(3)
where T1 is what we will call the target theory, or the theory being evaluated, and there are i
forms of evidence and j − 1 alternative theories. For example, if there are two alternative the-
ories, the index j goes from 1 for the target theory to 3. The denominator then consists of three
products of probabilities added together, one for the target theory and one for each of the
alternative theories.
3. ASSESSING PROBABILITIES
In applying the Bayesian framework to an actual historical case, we need a way of specifying
both the prior probability of the theory or model and the conditional probabilities that the
available evidence can be explained by the theory (Salmon, 1970, 1990). This applies to both
the theory being evaluated and any alternative or competing theories that are relevant in the
historical context. Thus, Bayesian analysis is always a comparative exercise.
Of course, we do not have direct access to an individual’s subjective probabilities. In con-
temporary science we could access the full text of scientific papers and aggregate statements
to give a collective assessment of probabilities (Small, 2022). However, for historical cases
focused on individual scientists, we need to rely on the statements of the scientists involved
or on the accounts of historians, and especially on statements regarding whether evidence
reflects favorably or unfavorably on a theory.
To implement a Bayesian approach, such evidence statements have been manually coded
to reflect the approximate strength of the scientists’ conviction that a theory is consistent or
inconsistent with the evidence. The scale was constructed with a limited number of discrete
values between 0 and 1 to simplify judgments and avoid unwarranted accuracy. Only five
degrees of strength are allowed, which are mapped to preset values of conditional probability
Quantitative Science Studies
212
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
1
2
0
9
2
0
7
8
3
7
2
q
s
s
_
a
_
0
0
2
3
3
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Bayesian history of science
Table 1. Coding scheme for conditional probabilities. P (E |T ) is the probability of the evidence
given the theory or model
P (E |T )
0.3
0.4
0.5
0.6
0.7
Description
strongly inconsistent
weakly inconsistent
neutral
weakly consistent
strongly consistent
(see Table 1). The probabilities assigned ranged from 0.7 for “strongly consistent” to 0.3 for
“strongly inconsistent,” with 0.5 signifying a neutral stance. A neutral probability means that
there is a 50/50 chance that the theory T is consistent with the evidence E in the expression
P (E |T ). The range of values in Table 1 is of course arbitrary and other scales could have been
used, which would have changed the absolute values of the posteriors computed but not their
relative values. For example, a five-point scale from 0.1 to 0.9 leads to more extreme values of
the posteriors for a series of models, which seemed at odds with the uncertainties expressed
by the historical participants. An “inconsistent” conditional P (E |T ) indicates that the theory
was unlikely to explain or predict the evidence, whereas a “consistent” probability means that
the theory was compatible to some degree with the evidence.
For example, regarding Watson and Crick’s first DNA model, a triple helix, Watson admit-
ted: “The awkward truth became apparent that the correct DNA model must contain at least
10 times more water than was found in our model.” (Watson, 1968, p. 94) Thus, the “water
content” was incorrect evidence and was coded 0.3 as “strongly inconsistent.” On the other
hand, the crystallographic data required that the model conform to a specific geometry: “Three
chains twisted about each other in a way that gave rise to a crystallographic repeat every 28
Angstroms along the helical axis” (Watson, 1968, p. 89). The crystallographic evidence was
coded as only “weakly consistent” because the triple helix model had to be designed to satisfy
this constraint.
Rather than trying to directly infer probabilities from the historical record, the approach is to
qualitatively assess the scientist’s opinion on how well or poorly the evidence fits with the
theory and then assign a probability from the prespecified scale. This approach can be con-
trasted with that of Dorling (1979), specifying approximate values for specific probabilities
based on general historical considerations but not the opinions of the scientists involved.
In addition to conditional probabilities, prior probabilities must be set. Here we can also
rely on the statements of scientists regarding their initial confidence in a theory. A special cir-
cumstance arises when the theory under consideration is the latest in a line of prior attempts.
For example, Kepler attempted to account for Tycho’s observations on Mars using a variety of
orbital shapes prior to his success with elliptical orbits. In such cases it is reasonable to assign
the prior for the most recent version of the theory to the posterior of the immediately preceding
unsuccessful theory. Failures should engender lower expectations for future success. This,
however, leaves the case of the first theory in the sequence without a prior. In the absence
of any written expression of confidence, or lack thereof, assigning a neutral 50/50 prior of
0.5 seems reasonable, and is the case, as noted above, when the theory and competing
theories are equally probable. There are numerous examples in the history of Bayesian
analyses where even odds have been used (McGrayne, 2011).
Quantitative Science Studies
213
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
1
2
0
9
2
0
7
8
3
7
2
q
s
s
_
a
_
0
0
2
3
3
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Bayesian history of science
4. THE CASE OF WATSON AND CRICK AND THE STRUCTURE OF DNA
We can now apply this framework to an historical example: the attempts to construct a molec-
ular model of DNA. Watson describes four models that were devised in the early 1950s:
1. A triple-helix model developed by Watson and Crick based on an analogy to Pauling’s
alpha helix for proteins;
2. A triple-helix model proposed independently by Pauling and Corey;
3. A double helix with like-to-like base pairing by Watson; and
4. A final double helix with adenine to thymine and guanine to cytosine base pairing by
Watson and Crick (Watson, 1968).
Different kinds of evidence were brought to bear on each model which either supported or
undermined the validity of each model. Only evidence brought to bear at the time the model
was evaluated is considered. Bayes’ theorem also requires us to evaluate the evidence for or
against the competing or alternative models if they exist.
As to the prior probability for the first model in the series, there may be a sense of what the
community of researchers regards as a prevailing or generally accepted view. For example,
when Avery, MacLeod, and McCarthy proposed that DNA was the “transforming substance,”
it was generally believed that proteins with their varying sequences of amino acids governed
heredity, not DNA (Judson, 1979, p. 30). In the case of DNA some researchers had entertained
the vague notion of a single linear chain of nucleotides (Watson, 1968, p. 52) but this idea was
not sufficiently defined to serve as a testable model.
4.1. Watson and Crick’s Triple Helix Model
Linus Pauling’s model for protein structure called the alpha helix (Pauling, Corey, & Branson,
1951) had shown that a long-chain polypeptide molecule could have a helical structure.
Despite not providing direct evidence for a helical structure for a long-chained nucleic acid
such as DNA, Pauling’s alpha helix made this possibility plausible. Watson stated: “Pauling’s
success with the polypeptide chain had naturally suggested to Francis [Crick] that the same
tricks might also work for DNA …. We could thus see no reason why we should not solve DNA
in the same way. All we had to do was to construct a set of molecular models and begin to
play—with luck, the structure would be a helix.” (Watson, 1968, pp. 48, 50). In addition to
being a powerful influence on Watson’s and Crick’s thinking, the alpha-helix idea served as a
justification for their model of DNA because, by analogy, this was the natural structure for a
long-chained molecule (Kuhn, 2000; Salmon, 1990; Thagard, 1992).
In their first attempt at a structure of DNA, Watson and Crick formulated a triple helix con-
sisting of three polynucleotide chains. They placed the intertwined sugar-phosphate backbones
on the inside and the bases (adenine, cytosine, guanine, and thymine) on the outside of the back-
bones (Watson, 1968, p. 79). Prior to their work on DNA, Crick, along with Cochran and Vand,
had developed a theory that predicted how a helical molecule would diffract X-rays, although at
that time no such X-ray pictures existed for DNA matching the predicted pattern (Cochran, Crick,
& Vand, 1952; Schindler, 2008). The X-ray evidence that did exist, from Rosalind Franklin at
King’s College, London, as well as earlier X-ray pictures by Astbury and Bell, suggested that
DNA had a regular crystal structure (Astbury, 1947). There was a crystallographic repeat at about
28 angstroms along the helical axis and the nucleotides were flat and 2.3 angstroms thick.
In November of 1951 Watson attended a colloquium at King’s College, London, organized
by Maurice Wilkins, where Rosalind Franklin presented X-ray diffraction results for DNA based
Quantitative Science Studies
214
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
1
2
0
9
2
0
7
8
3
7
2
q
s
s
_
a
_
0
0
2
3
3
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Bayesian history of science
on what would later be called the crystalline or “A-form” of DNA (Olby, 1974, pp. 349–350).
Wilkins supported a three-stranded polynucleotide configuration based on density consider-
ations, and Franklin, from her lecture notes, favored a spiral structure with a structural repeat
every 28 angstroms. On hearing about the colloquium from Watson, Crick concluded that
“only a small number of formal solutions were compatible both with the Cochran-Crick theory
and with Rosy’s [Rosalind Franklin’s] experimental data … and perhaps a week of fiddling with
the molecular models would be necessary to make us absolutely sure we had the right answer”
(Watson, 1968, p. 77).
They were already committed to the idea that DNA was a helix from Pauling’s alpha helix,
and the general idea that DNA contained a large number of nucleotides linked together line-
arly. The X-ray pictures showing a regular crystal implied that the sugar-phosphate backbones
were packed in a regular manner, although these ideas were too vague to constitute a concrete
model.
Following Wilkins’ suggestion, Watson and Crick then began playing with molecular
models involving three helical strands of sugar-phosphate polynucleotide chains coiled
around each other that would give rise to the observed crystallographic repeat (Watson,
1968, p. 89). This model was thus consistent, by design, with the X-ray evidence at that time.
Olby states that “At the time Watson and Crick were highly pleased with this 3-stranded helix …”
(Olby, 1974, p. 361).
However, three points of evidence were strongly inconsistent with the triple helix model.
First, there was a need for positive ions, so-called salt bridges, to hold the helical strands in
place, because the chains had a negative charge due to the ionization of the phosphate groups
on the backbones. However, there was no evidence that DNA contained positive ions such as
Mg++. Watson also acknowledged that some of the bond lengths between atoms were “too
close for comfort,” and finally that he had grossly underestimated the water content of the
DNA samples used for Franklin’s X-ray pictures, which would have affected the structure in
an indeterminate manner (Watson, 1968, pp. 80, 89).
The defects of the model were made clear in a meeting in Cambridge involving Watson and
Crick and the group from King’s College. After the meeting, news of the unsuccessful model
reached the head of the Cavendish Lab in Cambridge, Sir Lawrence Bragg, and Crick and
Watson were instructed to stop working on DNA. Crick later described this model as a “com-
plete waste of time” (Olby, 1974, p. 360) and Watson called it a “fiasco” (Crick, 1988; Watson,
1968, p. 201).
Table 2 summarizes the evidence Watson and Crick brought to bear on this initial triple
helix model and estimates of the conditional probabilities of the evidence they considered
relevant. Even though according to Olby they were initially pleased with their model, there
is no indication in the historical record that they were confident that it was correct. Thus, a
prior probability of 0.5, even odds, seems reasonable reflecting its equal chance of being cor-
rect or incorrect. Crick later commented that in retrospect he wished they had waited a week
before presenting it. There was no coherent alternative model to the triple helix.
The evidence derived from the existing X-ray diffraction pictures is coded as “weakly con-
sistent” because the model was specifically designed to account for that data. The analogy of
the DNA helical structure to Pauling’s alpha helix for proteins is also coded as “weakly con-
sistent” (see Table 1). The incorrect water content for the X-ray pictures, the inaccurate bond
lengths, and the absence of the positive ions to hold the three chains together are each coded
as “strongly inconsistent.” In summary, there were two weakly supporting points of evidence
and three in strong opposition. The resulting posterior probability, based on the naïve Bayes
Quantitative Science Studies
215
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
1
2
0
9
2
0
7
8
3
7
2
q
s
s
_
a
_
0
0
2
3
3
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Bayesian history of science
Table 2. Watson and Crick’s triple-helix model of DNA (no competing model). Evidence points
are numbered in the first column E 1 to E 5, for the target or alternative theory. The last row shows the
posterior probability, the percentage change between the prior and posterior, and the likelihood ratio
(LR) as defined in Eq. 2. The posterior is equal to 0.5 * 0.6 * 0.6 * 0.3 * 0.3 * 0.3/(0.5 * 0.6 * 0.6 * 0.3 *
0.3 * 0.3 + 0.5 * 0.5 * 0.5 * 0.5 * 0.5 * 0.5)
Probability
P (T )
P ((cid:2)T )
P (E 1|T )
P (E 1|(cid:2)T )
P (E 2|T )
P (E 2|(cid:2)T )
P (E 3|T )
P (E 3|(cid:2)T )
P (E 4|T )
P (E 4|(cid:2)T )
P (E 5|T )
P (E 5|(cid:2)T )
Estimate
0.5
0.5
0.6
0.5
0.6
0.5
0.3
0.5
0.3
0.5
0.3
0.5
Description
Evidence
neutral
neutral
prior of T
1 – prior
weakly consistent
analogy to alpha helix
neutral
hypothetical null model
weakly consistent
X-ray data (28 A repeat)
neutral
hypothetical null model
strongly inconsistent
water content too low
neutral
hypothetical null model
strongly inconsistent
bond lengths/angles wrong
neutral
hypothetical null model
strongly inconsistent
positive ions not found
neutral
hypothetical null model
P (T |E 1–E 5)
0.24
disconfirm
% change = −52.0, LR = 0.31
formulation, was 0.24, indicating disconfirmation compared to a prior of 0.5, a decrease in
probability of 52% with respect to the prior.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
1
2
0
9
2
0
7
8
3
7
2
q
s
s
_
a
_
0
0
2
3
3
p
d
/
.
Because the alternative model was assigned even odds for all forms of evidence, it serves as
a null or baseline model for comparison to the triple helix model. Other options for the alter-
native model were explored but led to similar results. For example, a single helical strand of
nucleotides was posited as a possible hypothetical model and evaluated on the same forms of
evidence. In this case the absence of positive ions to keep the strands together was “strongly
consistent” as only one strand was present, but the X-ray data called for a higher density of
strands and was “strongly inconsistent” with the single strand model. Bond lengths were set to
“weakly consistent” because having only one strand imposed fewer structural constraints. As
far as we know none of these judgments were shared by the participants and are purely hypo-
thetical. Nevertheless, the resulting posterior of 0.3 was only slightly higher than the compar-
ative baseline model of 0.24, but still disconfirming.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
4.2. Pauling’s Triple Helix Model of DNA
When Linus Pauling wrote up his triple helix model of DNA (Pauling & Corey, 1953), he was
unaware that Watson and Crick had made a similar attempt some months earlier, which was
unpublished. Pauling considered his a “promising structure” (Olby, 1974, pp. 381, 383),
although serious issues regarding interatomic distances arose in the days following the paper’s
submission for publication. As we did for Watson and Crick’s triple helix, we adopt a 50/50
prior probability.
Quantitative Science Studies
216
Bayesian history of science
Table 3.
Pauling’s view of his own model (no competing model)
Probability
P (T )
P ((cid:2)T )
P (E 1|T )
P (E 1|(cid:2)T )
P (E 2|T )
P (E 2|(cid:2)T )
P (E 3|T )
P (E 3|(cid:2)T )
Estimate
0.5
0.5
0.6
0.5
0.6
0.5
0.3
0.5
Description
Evidence
neutral
neutral
prior of T
1 − prior
weakly consistent
analogy to alpha helix
neutral
hypothetical null model
weakly consistent
X-ray data (Astbury)
neutral
hypothetical null model
strongly inconsistent
bond lengths/angles wrong
neutral
hypothetical null model
P (T |E 1–E 3)
0.46
disconfirm
% change = −8.0, LR = 0.86
We can evaluate Pauling’s model from either Pauling’s point of view or Watson and Crick’s.
Pauling was in the same position as Watson and Crick in that there was no competing model.
Pauling also appealed to his alpha helix for proteins to justify a helical structure for the long-
chained nucleic acid (Pauling et al., 1951). He constructed his model to be consistent with the
X-ray diffraction data available to him, namely the work of Astbury and Bell (Astbury, 1947),
including their density calculation, which suggested to Pauling that three-polynucleotide
chains were wrapped in a helical structure. The only troubling feature from Pauling’s point
of view was that the model involved “a tight squeeze for nearly all the atoms” (Olby, 1974,
p. 383). Scoring the poor fit with interatomic distances as “strongly inconsistent,” as we did for
Watson and Crick’s triple helix, gives a posterior probability of 0.46 versus the null model,
narrowly disconfirming Pauling’s model from his point of view. Again, we use 50/50 odds
for the hypothetical alternative model’s conditional probabilities, as we did for the Watson
and Crick triple helix (Table 3).
Seen from the Watson and Crick point of view, however, the situation is different. News of
Pauling’s model reached Cambridge via Pauling’s son Peter, then a student at Cambridge, who
gave the manuscript to Watson. After Watson’s initial surprise that the model was “suspiciously
like our aborted effort” of the previous year, he read the paper carefully and concluded that the
molecule could not be acidic because all the hydrogen atoms were bonded: “Everything I
knew about nucleic-acid chemistry indicated that phosphate groups never contained bound
hydrogen atoms” (Watson, 1968, p. 160). Watson did not investigate the question of bond
lengths in Pauling’s model but learned later in a letter from Pauling that they were having
problems with them (Olby, 1974, p. 409).
Because we are looking at Pauling’s model from Watson and Crick’s point of view, we use
their triple helix as the alternative model and its posterior probability of 0.24 as the prior for
Pauling’s model, thus expressing their diminished confidence in the model based on their prior
experience. Scoring the lack of acidity and the inaccurate bond lengths as “strongly inconsis-
tent” gives a disconfirming posterior probability of 0.16 (Table 4).
As the competing theory shared features with the Pauling model, such as helical structure
and consistency with X-ray data, these features are not advantages for the Pauling model
because they are scored with the same conditional probabilities as Watson and Crick’s triple
helix. Pauling’s difficulty with the interatomic distances also does not have an impact on the
Quantitative Science Studies
217
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
1
2
0
9
2
0
7
8
3
7
2
q
s
s
_
a
_
0
0
2
3
3
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Bayesian history of science
Table 4. Watson and Crick’s ( W/C) view of Pauling’s model (competing model is the W/C triple
helix)
Probability
P (T )
P ((cid:2)T )
P (E 1|T )
P (E 1|(cid:2)T )
P (E 2|T )
P (E 2|(cid:2)T )
P (E 3|T )
P (E 3|(cid:2)T )
P (E 4|T )
P (E 4|(cid:2)T )
Estimate
0.24
0.76
Description
Evidence
prior
prior of (cid:2)T
posterior of W/C triple helix
1 − P (T )
0.6
0.6
0.6
0.6
0.3
0.5
0.3
0.3
weakly consistent
analogy to alpha helix
weakly consistent
same as W/C triple helix
weakly consistent
X-ray data (Astbury)
weakly consistent
X-ray data (Franklin A-form)
strongly inconsistent
lack of acidity of DNA
neutral
not known for W/C triple helix
strongly inconsistent
bond lengths/angles wrong
strongly inconsistent
same as W/C triple helix
P (T |E 1–E 4)
0.16
disconfirm
% change= −33.3, LR = 0.6
posterior because the Watson and Crick triple helix suffered the same defect. Thus, disconfir-
mation is due solely to the lack of acidity of the model, the other features canceling each other
out. The lower absolute value of the posterior is in part due to the lower prior used.
4.3. Watson’s First Double Helix Model
The critical new piece of evidence in 1953 was the X-ray picture of the wet or B-form of
DNA taken by Rosalind Franklin in 1952, but not seen by Watson until January 1953. This
so-called cross-ways or black cross picture of DNA confirmed the helical nature of DNA via
the Cochran-Crick-Vand theory and also work by the King’s College physicist Alexander
Stokes. These theories showed how a helical molecule would diffract X-rays. Watson had
traveled to London to show the King’s College group the DNA structure paper by Pauling
and Corey. But when he saw the new X-ray picture by Franklin “… my mouth fell open
and my pulse began to race …. The black cross of reflections which dominated the picture
could arise only from a helical structure” (Watson, 1968, p. 167). The new pictures of the B
or wet form of DNA meant that there was a crystallographic repeat every 34 angstroms rather
than the 28 angstrom repeat seen in the A-form. Additional information was obtained from an
MRC report from the King’s College group that had been distributed in December 1952. The
MRC report revealed to Crick that DNA was a member of the C2 space group and had dyadic
symmetry, that “the molecule of DNA, rotated a half turn, came back to congruence with
itself” (Olby, 1974, p. 412).
On his way back to Cambridge Watson decided to try a two- rather than three-chain model.
Olby and Crick suggest that this was based on a density calculation of the more compact
A-form going to the more stretched out, and less dense, B-form, making a two-chain model
more feasible. Watson claims that it was from his conviction that “important biological objects
come in pairs” (Olby, 1974, p. 398). Whether this decision was motivated by evidence is not
clear.
Quantitative Science Studies
218
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
1
2
0
9
2
0
7
8
3
7
2
q
s
s
_
a
_
0
0
2
3
3
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Bayesian history of science
However, Watson had difficulty fitting two chains on the inside and bases on the outside, as
they had done with the three-chain model. Crick suggested he try putting the two chains on
the outside and try to fit the bases between them. Meanwhile, Watson had been reading about
titration of DNA and concluded that most of the bases were hydrogen bonded to other bases.
His first guess was that the bases were hydrogen bonded to bases of the same type (e.g., ade-
nine to adenine) and the available textbook diagrams of the bases seemed to confirm that the
bases could be hydrogen bonded like-to-like. This would make the sequence of bases on each
of the two chains identical and suggested to Watson a mechanism for gene replication where
one chain would serve as a template for the other, duplicating the sequences of bases (Watson,
1968, p. 186).
This idea was called into question when a crystallographer in their lab, Jerry Donohue,
asserted that the textbook diagrams were wrong and Watson had used the wrong tautomeric
forms for the bases—the enol rather than the keto form. However, adopting these alternative
forms disrupted the hydrogen bonding between the like bases and resulted in an even poorer
fit of bases between the two chains (Watson, 1968, p. 193). Crick added three more objections
to Watson’s like-with-like model. Crick ruled out the 34 angstrom repeat for the model on
X-ray diffraction grounds. In addition, the C2 symmetry deduced from the MRC report would
be violated (Olby, 1974, p. 411). Finally, the model did not provide an explanation of
Chargaff’s rules, regarding the ratio of bases in DNA, which Crick had taken more seriously
than Watson (Fry, 2016, p. 218). Chargaff had determined that the purine bases (adenine and
guanine) and pyrimidines bases (thymine and cytosine) occurred in DNA in a 1 to 1 ratio
(Chargaff, Zamenhof, & Green, 1950). These rules had not been relevant to their previous
model with bases unconstrained on the outside.
Table 5 shows the estimated conditional probabilities for the like-with-like model using the
Watson and Crick triple helix model as the competing theory. The rationale for using this
latter model as the competing one, rather than Pauling’s triple helix, is that it was more psy-
chologically relevant to use their own model as a basis of comparison, and Pauling’s model
was not acidic in Watson’s view. The new B-form X-ray pictures from King’s, in combination
with the Cochran-Crick-Vand theory, provided strong confirmation for the helical structure of
DNA. However, the triple-helix model was also helical and was thus supported by the new
B-form photos. The 34 angstrom crystallographic repeat derived from the X-ray picture, how-
ever, was inconsistent with the like-to-like model according to Crick and is thus scored as
“strongly inconsistent.” The triple helix model was based on the now incorrect 28 angstrom
repeat from the earlier A-form picture and thus is also “strongly inconsistent.” Likewise, the
interatomic distances were violated in the like-to-like model whether the keto or enol forms
for the bases were used, causing a buckling of the backbones, and hydrogen bonding was
disrupted because of the incorrect tautomeric forms. Hydrogen bonding had been ruled out
for the triple helix (Olby, 1974, p. 360) violating Watson’s new expectations. Bond lengths
were also violated in triple helix, and C2 symmetry was not fulfilled by either the like-with-
like model or the triple helix and hence both were “strongly inconsistent,” as were both
models for their failure to account for Chargaff’s rules. The only bright spot for the like-
with-like model was its potential explanation of gene replication, which is scored as “weakly
consistent” because it was only a conjecture. The triple helix model offered no such
explanation.
The posterior probability considering these seven forms of evidence was 0.32, which was,
however, an increase of 34% over the posterior of the Watson and Crick triple helix used as the
prior. This confirmation was due only to the prospect for a mechanism of gene replication
offered by the like-with-like model. The reason that the five sources of negative evidence
Quantitative Science Studies
219
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
1
2
0
9
2
0
7
8
3
7
2
q
s
s
_
a
_
0
0
2
3
3
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Bayesian history of science
Probability
P (T )
P ((cid:2)T )
P (E 1|T )
P (E 1|(cid:2)T )
P (E 2|T )
P (E 2|(cid:2)T )
P (E 3|T )
P (E 3|(cid:2)T )
P (E 4|T )
P (E 4|(cid:2)T )
P (E 5|T )
P (E 5|(cid:2)T )
P (E 6|T )
P (E 6|(cid:2)T )
P (E 7|T )
P (E 7|(cid:2)T )
Table 5. Watson’s like-with-like model ( Watson/Crick triple helix as competing model)
Estimate
0.24
0.76
Interpretation
prior of T
prior of (cid:2)T
posterior probability for W/C triple-helix
Evidence
1 − prior
0.7
0.7
0.3
0.3
0.3
0.3
0.3
0.3
0.3
0.3
0.3
0.3
0.6
0.4
strongly consistent
B-form X-ray picture predicted by the Cochran-Crick-Vand theory
strongly consistent
Triple helix also supported by the B-form X-ray
strongly inconsistent
34 Å crystallographic repeat for B-form not possible with
like-with-like model
strongly inconsistent
34 Å crystallographic repeat for W/C triple helix not possible
strongly inconsistent
Like-with-like bond lengths wrong
strongly inconsistent
Triple-helix bond lengths wrong
strongly inconsistent
Like-with-like C2 symmetry not present
strongly inconsistent
Triple-helix C2 symmetry not present
strongly inconsistent
Like-with-like Chargaff’s rules violated
strongly inconsistent
Triple-helix Chargaff’s rules violated
strongly inconsistent
Like-with-like hydrogen-bonding incorrect
strongly inconsistent
Triple-helix hydrogen-bonds not possible
weakly consistent
Like-with-like replication mechanism possible
weakly inconsistent
Triple-helix had no replication mechanism
P (T |E1–E 7)
0.32
confirm
% change = +33.3, LR = 1.5
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
1
2
0
9
2
0
7
8
3
7
2
q
s
s
_
a
_
0
0
2
3
3
p
d
/
.
did not lead to disconfirmation was that the alternative model, the Watson and Crick triple
helix, suffered from the same defects. Had the Pauling triple helix been used as the competing
model, the like-with-like model would still have been confirmed, but the absolute value of the
posterior would have been lower due to the lower posterior of the Pauling model.
The “black-cross” X-ray pictures gave no advantage to the like-with-like model, as the triple
helix was equally supported by it. Including as evidence the argument in favor of a double
helix advocated by Crick and Olby, that new density evidence favored a double helix, and
scoring it as 0.6 for the like-with-like model and 0.4 for the triple helix, would have given
the like-with-like model an improved posterior of 0.42. Hence, the like-with-like model could
have been seen as a step in the right direction.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
4.4. Watson and Crick’s Final Double Helix Model
Only a few days elapsed between Watson’s proposal of the like-with-like model and the
Watson and Crick final model with purine to pyrimidine hydrogen bonding, adenine to thymine
and guanine to cytosine. Although the evidence remained the same, the model changed in a
significant way. Watson’s failure to fit like bases together prompted him to make cardboard
cutouts of the bases in the enol configurations recommended by Donohue. “Shifting the bases
in and out of various pairing possibilities” Watson hit on the solution: “the adenine-thymine
Quantitative Science Studies
220
Bayesian history of science
pair held together by two hydrogen bonds was identical in shape to a guanine-cytosine pair …”
(Watson, 1968, p. 194).
All the pieces of evidence then seemed to fall into place. “I suspected that we now had the
answer to the riddle of why the number of purine residues exactly equaled the number of
pyrimidine residues …. Chargaff’s rules then suddenly stood out as a consequence of a
double-helical structure for DNA.” Furthermore, “This type of double helix suggested a repli-
cation scheme much more satisfactory than my briefly considered like-with-like pairing”
(Watson, 1968, p. 196). Shortly after this realization Crick “… spotted the fact that the two
glycosidic bonds ( joining the base and sugar on the backbone) of each base pair were syste-
matically related by a dyad axis perpendicular to the helical axis. Thus, both pairs could be
flipflopped …” (Watson, 1968, p. 197). Hence, the C2 symmetry criterion was also fulfilled.
Watson’s description of these realizations is close to what Koestler called a “Eureka moment”
(Koestler, 1964, p. 107). But Watson also knew that they would have to verify all the stereo-
chemical contacts. This did not deter Crick from announcing at lunch that they had discovered
the “secret of life” (Watson, 1968, p. 197).
In Table 6, Watson’s like-with-like model was used as the competing model, and its pos-
terior as the prior probability for the new double helix model. The reason for the strong con-
firmation of the final double helix was that it was consistent with five of the seven pieces of
evidence that the like-with-like model was inconsistent with: the 34 angstrom crystallographic
Probability
P (T )
P ((cid:2)T )
P (E 1|T )
P (E 1|(cid:2)T )
P (E 2|T )
P (E 2|(cid:2)T )
P (E 3|T )
P (E 3|(cid:2)T )
P (E 4|T )
P (E 4|(cid:2)T )
P (E 5|T )
P (E 5|(cid:2)T )
P (E 6|T )
P (E 6|(cid:2)T )
P (E 7|T )
P (E 7|(cid:2)T )
Table 6. Watson and Crick’s final double helix model (like-with-like as the alternative)
Estimate
0.32
0.68
Interpretation
prior of T
prior of not T
posterior of like-with-like model
Evidence
1 − prior
0.7
0.7
0.7
0.3
0.7
0.3
0.7
0.3
0.7
0.3
0.7
0.3
0.6
0.6
strongly consistent
X-ray picture of B-form supports helix via theory
strongly consistent
Like-with-like model is also a helix
strongly consistent
34 Å crystallographic repeat (B form X-ray picture)
strongly inconsistent
Like-with-like model did not give a 34 Å repeat
strongly consistent
bond lengths fit
strongly inconsistent
Like-with-like bond lengths did not fit
strongly consistent
C2 symmetry of structure
strongly inconsistent
Like-with-like model lacked C2 symmetry
strongly consistent
obeys Chargaff’s rules
strongly inconsistent
Like-with-like inconsistent with Chargaff rules
strongly consistent
hydrogen bonding of bases correct
strongly inconsistent
Like-with-like model has hydrogen bonding wrong
weakly consistent
mechanism for replication suggested
weakly consistent
Like-with-like also gave mechanism for replication
P (T |E 1–E 7)
0.97
Confirm
% change = +203.1, LR = 69.2
Quantitative Science Studies
221
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
1
2
0
9
2
0
7
8
3
7
2
q
s
s
_
a
_
0
0
2
3
3
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Bayesian history of science
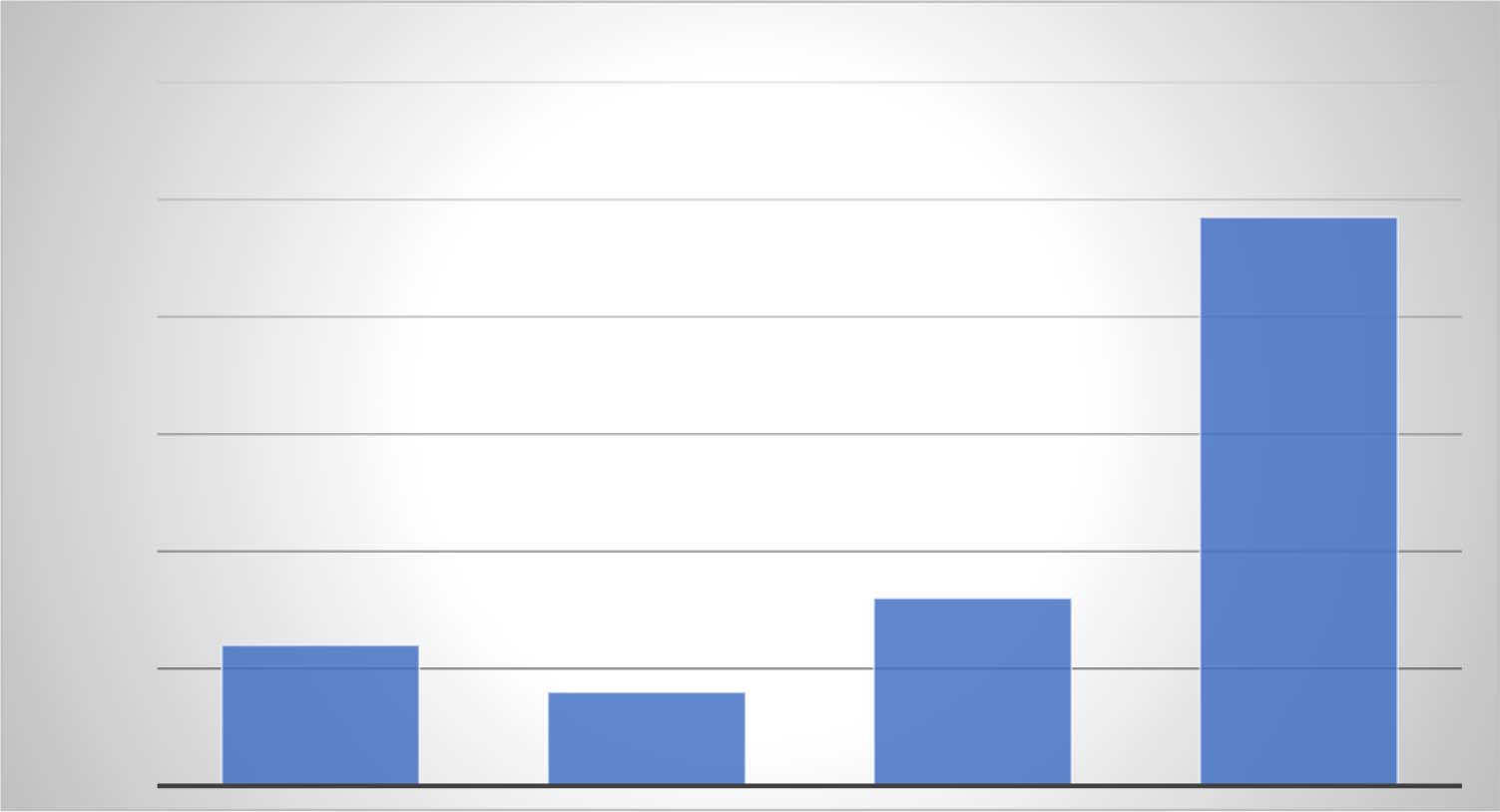
Figure 2. Posterior probabilities for four models of DNA ( W/C stand for Watson and Crick).
repeat for the B-form, bond distances and angles, C2 symmetry, Chargaff’s rules, and hydrogen
bonding. The posterior of 0.97 was a 203% increase over the prior probability, which was the
posterior of the like-with-like model. The dramatic increase in posterior probability can be
seen by plotting the posteriors for the four models as shown in Figure 2. If there is such a
phenomenon as “Bayesian surprise” this is certainly such a case. A similar and even more
dramatic trend from model to model is seen in the likelihood ratio (Eq. 3), which is not depen-
dent on the prior probability.
For many years after their discovery, Watson and Crick had to fend off various challenges to
their model, including rival models and skeptical colleagues, and made minor tweaks, such as
adding one more hydrogen bond to the base pairing (Crick, 1988). But the basic model
remained the same, the major change being the gradual accumulation of confirming evidence.
5. DISCUSSION
The concept of “Bayesian surprise” has been discussed in a number of papers from the fields of
cognitive science and neuroscience (Baldi & Itti, 2010; Gijsen, Grundei et al., 2021; Visalli,
Capizzi et al., 2021). These papers develop Bayesian models of “surprise” using experimental
results on human subjects responding to perceptual stimuli for studying attention, learning,
and belief updating often using electroencephalographic methods. Under the more general
rubric of the “Bayesian brain” (Friston, 2012), these studies assert that the brain generates pre-
dictions of future sensory input based on some internal model of the environment that is con-
tinuously updated as new sensory input arrives using Bayesian inference. In turn, the brain
attempts to minimize surprise or entropy by adjusting its internal model of reality. Whether
these neurological findings are applicable to surprising findings in science is beyond the scope
of this paper, but we can speculate that the types of scientific findings that we come to label as
“discoveries” are perhaps a byproduct of a dramatic increase in the probability of a theory.
Calling the double helix model of DNA a “discovery” allows us to update our prior expecta-
tions and adjust to a new normal so we can move on to the next question. Incoming evidence
and the model in our brain are clearly tightly interlocked in this process. A mismatch needs to
be resolved or minimized either by modifying our model or by disputing the evidence. A
match between model and evidence reduces entropy and uncertainty.
Quantitative Science Studies
222
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
1
2
0
9
2
0
7
8
3
7
2
q
s
s
_
a
_
0
0
2
3
3
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Bayesian history of science
On the evidence side we have allowed certain forms of “soft” evidence to play a role in
addition to harder evidence of an experimental or quantitative nature. For the early triple helix
models, for example, an analogy to Pauling’s successful helical model of proteins provided
weak evidence that a similar approach could be taken to nucleic acids. In his later writings,
Kuhn has pointed out the neglected role played by analogy in theory change (Kuhn, 2000,
p. 30). Thagard also used analogy to enhance the “coherence” of one theory over another
in his network activation scheme (Thagard, 1992).
In addition, evidence was considered “weakly consistent” if the model was purposefully
designed to accommodate the evidence, as in the case of the crystallographic repeat of the
triple helix. The rationale for considering this as evidence is that a physical model still needed
to be devised to meet that requirement, and the model could not be deduced directly from that
evidence. The prospect for a mechanism for gene replication offered by the last two models
was also considered as weak support. This is in line with Kuhn’s criterion of the “fruitfulness”
of a theory, because the models held promise of providing an explanation of gene replication
(Kuhn, 1977, p. 322; Salmon, 1990).
Some clear implications follow from the Bayesian formulas. First, confirmation or discon-
firmation is dependent only on the values of the conditional probabilities and not on the prior.
This is clear from the formula for the “likelihood ratio” (Eq. 2) which depends only on the
conditional probabilities of the target theory and competing theories. On the other hand,
the absolute value of the posterior depends on the value of the prior. But, similar to the pos-
terior, the likelihood ratio shows a sharp increase for the final double helix model (from 1.5 to
69.2). In fact, the likelihood ratio increased on a percentage basis 20 times faster than the
posterior going from the like-to-like to the final double helix model. The fact that both the
posterior and likelihood ratio show similar trends suggests that either method can be applied
to historical cases, although the likelihood ratio is more volatile.
One consequence of this is that it is not imperative to set the prior probability of a new
model equal to the posterior of a preceding model to get the same verdict on confirmation
or disconfirmation. This convention was adopted because, in a subjective interpretation of
probabilities, the prior should reflect the initial degree of confidence of participants on the
validity of the model, which depends in part on the success of previous models. Although this
convention will not affect whether the model is confirmed or disconfirmed, it will result in a
more meaningful trend of posterior probabilities.
For a theory that does not have a clearly defined predecessor, such as Watson and Crick’s
or Pauling’s triple helix, we have assigned a prior of 0.5, which would be the value of the
posterior if the theory and a hypothetical predecessor theory were equally probable. Condi-
tional probabilities for the hypothetical theory’s ability to account for the evidence are also set
at 0.5. This provides a null or baseline theory against which the new theory can be evaluated
and allows the initiation of the Bayesian process. We have also explored using a preliminary
hunch such as the single nucleotide chain as an alternative model. But, as this model is
undefined, and apparently not taken seriously by the participants, its fit with evidence remains
conjectural. Nevertheless, assuming some initial hypothetical comparison is performed, a
subsequent model can utilize the first model’s posterior as its prior as well as serve as the
alternative theory for comparison against subsequent theories, that is, become part of “not
T” ((cid:2)T ) in Eq. 1. If more than one predecessor theory exists, we can use the previous theory
with the highest posterior as the alternative theory, consistent with the perspective of the eval-
uators, in our case Watson and Crick. For example, Pauling’s model is not used as the alter-
native theory for the like-with-like model, but rather Watson and Crick’s triple helix. Another
Quantitative Science Studies
223
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
1
2
0
9
2
0
7
8
3
7
2
q
s
s
_
a
_
0
0
2
3
3
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Bayesian history of science
consideration that makes the initial prior for a sequence of models less important is called the
washing out or swamping of priors. This can occur if confirming (or nonconfirming) evidence
accumulates (Earman, 1992, p. 141). This is clearly the case for the final double helix model,
where confirming evidence became overwhelming.
The question arises of whether taking more than one alternative theory would affect the
results. For example, we might take both the like-with-like theory and Watson and Crick’s
triple helix as the alternative theories for the final double helix (see Eq. 3). This means that
we need to combine the various forms of evidence used for the three models and score each
model for each form updated to the time the double helix was proposed. This results in nine
forms of evidence to consider for each of the three models. To set the prior probabilities for the
alternative theories we use 0.32 for the double helix (the posterior of the like-with-like model)
and split the remainder (1 − 0.32 = 0.68) between the two alternatives, weighting them by their
posterior probabilities. The outcome of this exercise, however, results in increasing the poste-
rior for the double helix from 0.97 to 0.98. The reason for this increase appears to be that some
of the defects of the triple helix model remained valid (water content and absence of positive
ions) and some of its apparent advantages (the crystallographic repeat of the A-form) were
nullified by new evidence.
It is an open question whether it is legitimate to compare theories devised at different points
in time, as we have done above, using evidence valid either for the earlier or the later period.
In an extreme case discussed by Kuhn as “incommensurability,” he claimed that it is impos-
sible to compare Aristotle’s theory of motion with Newton’s because their terms of reference
were completely different (Kuhn, 2000, p. 16). Nevertheless, if a suitable mapping of the
theoretical and empirical terms (old to new theory, old to new evidence) can be achieved
there is no reason in principle that such a comparison could not be made using a Bayesian
approach (Earman, 1992, Ch. 8).
The prior probability plays a somewhat different role in the evaluation of theories than it
does in other statistical applications where quantitative rather than subjective priors are used.
In the case of quantitative priors, the prior represents a “base rate” for some event, such as the
incidence of a disease in a population (Kahneman, 2011, p. 166; Pearl & Mackenzie, 2018,
p. 106) where we are interested in our chance of having the disease given the results of a test.
In this case the “base rate” often plays a decisive role in the posterior probability, notably when
other forms of evidence are unavailable, and is often mistakenly overlooked by human
subjects. Technically, belief in the validity of a theory could also be measured for a population
of researchers and used as the prior. But in the case of individuals, such as Watson, Crick, or
Pauling, our only access to their levels of confidence is through contemporaneous writings or
reports. For example, we have shown that Pauling’s view of his own model and Watson’s view
of Pauling’s model would differ regarding the prior probability of the model as well as what
evidence was deemed relevant.
Another consequence of the Bayesian formulas and the fact that the posterior is a function
of the products of conditional probabilities is that the increase of the probability for one form of
evidence can be offset by a decrease in some other form of evidence, the multiplication of
probabilities being order independent. Similarly, if the target theory and the competing theory
are both equally consistent or inconsistent with some form of evidence, there will be no
change in the posterior. For example, if two successive models are consistent with the same
form of evidence and the earlier model is used as the competing model, then the target and
competing models can offset each other, resulting in no change in the posterior. This occurred,
for example, when the B-form X-ray pictures showed the black cross pattern predicted by
Quantitative Science Studies
224
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
1
2
0
9
2
0
7
8
3
7
2
q
s
s
_
a
_
0
0
2
3
3
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Bayesian history of science
theory as indicative of a helix. However, both the target and competing models were based on
helices and this was thus moot.
Not including some form of evidence can also lead to a different posterior. In the present
study two or more consistent accounts of events were used where possible to verify each form
of evidence. For example, Crick’s claim that the decision to try a double helix was based on
the lower density of the B-form of DNA was not consistent with Watson’s account of his reason
for taking up a double helix, namely, that biological objects should come in pairs. Because of
this inconsistency, the evidence was not considered. However, including either Watson’s or
Crick’s line of reasoning would have increased the posterior of the like-with-like model from
0.3 to 0.4, but would not have affected the final double helix model because both models
employed double helices.
One clear finding from this case study is that the number of forms of evidence increases
over time, from model to model, and in some cases the evidence changes as well. For
example, when the X-ray evidence changed from the A-form to the B-form pictures, the “crys-
tallographic repeat” changed from 28 angstroms to 34 angstroms. Consequently, one form of
evidence favoring the Watson and Crick triple helix became inconsistent. Because it was also
inconsistent with the like-with-like model (Watson, 1968, p. 193), it had no net effect on the
posterior.
Another “new” form of evidence for the two later models was the Chargaff rules, which
were not considered in the earlier triple helix models presumably because the bases were
on the outside of the backbone and were hence unconstrained. Also, Crick’s realization that
the X-ray evidence necessitated C2 symmetry of the bases was only a factor for the final two
models, as was hydrogen bonding, which was initially dismissed as not playing a role but later
became critical when the bases were placed on the inside of the backbones. This illustrates
how evidence only takes on meaning in the light of theory. Thus, finding new forms of evi-
dence is critical to the development of theory.
A more complex example of new data having relevance is when the X-ray diffraction pic-
ture of the B, or wet form, of DNA showed a “black cross” or “cross-ways” pattern. A theory of
how a helical molecule would diffract X-rays was developed by Cochran, Crick, and Vand
prior to the proposal of the various models for DNA considered by Watson and Crick.
Schindler argues that deductive reasoning from this theory “played a crucial part in the
discovery of the DNA structure” (Schindler, 2008, p. 627). In effect, the Cochran-Crick-Vand
theory allowed the X-ray picture to be deduced from a helical model. Figure 1 shows the
Cochran-Crick-Vand theory (T2) and the empirical finding of the “black cross” X-ray picture
(E1) as separate nodes allowing the helical X-ray theory to intervene between the helical
molecular model (T ) and the “cross-ways” X-ray picture (i.e., the DNA model causes the
helical X-ray theory to predict a “cross-ways” pattern, which is then observed). Ironically,
however, this new certainty regarding the helical nature of the DNA molecule did not improve
the posterior of the like-with-like model because the earlier competing model was also helical.
Thus, for new evidence to benefit a new theory it is necessary for the new evidence not to
benefit the older, competing theory.
Hartmann (2008), with reference to attempts to create a theory of high-temperature super-
conductivity, has discussed whether successive theories preserve the empirical successes of
their predecessors. This was generally the case with the four models of DNA, for example,
finding support for helical structures in different ways. Also, the replication mechanism con-
tinued from the like-with-like model to the final double helix. But there were steps backwards
as well. The crystallographic repeat failed for the like-with-like model but was restored in the
Quantitative Science Studies
225
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
1
2
0
9
2
0
7
8
3
7
2
q
s
s
_
a
_
0
0
2
3
3
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Bayesian history of science
final double helix. What was more striking than the continuity of empirical success was the
expansion of empirical criteria, as new evidence was found relevant.
6. CONCLUSIONS
The naïve Bayes formulation allows the comparison of a target theory with a competing theory
or theories across multiple forms of evidence. The resulting posterior probability for the target
theory can be compared to the prior probability, indicating whether the theory is confirmed or
disconfirmed. The weighting of evidence according to the scale in Table 1 reflects the idea that
some forms of evidence are better explained by a model than others. The conditional proba-
bilities express a participant’s confidence that a specific form of evidence follows from the
theory. In an historical case, these values must be inferred from the statements of the partici-
pants or from historical accounts. Whether other observers of these events would assign the
same weights to the evidence given the historical accounts, and whether they would agree on
the forms of evidence to be considered, remains to be seen and will require additional exper-
imentation. It should also be noted that some philosophers, such as Norton (2021), advocate a
non-Bayesian approach to induction grounded on physical “facts” and criticize Bayesians for
interpreting all belief as probabilistic. However, this case study shows the adequacy of the
Bayesian approach provided extreme values of probability are avoided (such as 0 or 1), which
is consistent with the contingent and uncertain nature of scientific work.
Kuhn argued that for scientists, replacing an old theory with a new one in a scientific rev-
olution is more like religious conversion than a matter of evidence. He maintained that it was
not possible for “… an individual to hold both theories in mind together and compare them
point by point with each other and with nature” (Kuhn, 1977, p. 338). This is precisely the
strategy we have advocated in this paper using a Bayesian framework.
We can only speculate whether the Bayesian approach is an alternative to Kuhn’s theory of
scientific revolutions (Earman, 1992; Kuhn, 1962; Weinert, 2014; Worrall, 2000). Like a
Kuhnian revolution, a Bayesian approach involves pitting a new theory against an older com-
peting theory, for example, the classic example of the Copernican versus the Ptolemaic system
(Weinert, 2010) or Lavoisier’s oxygen theory versus the phlogiston theory of combustion (Pyle,
2000). Using the evidence available at the time, including soft as well as hard forms, may
reveal that neither theory could claim a clear advantage, but that later developments in theory
and experiment finally decide the issue. To conclude, however, that the only option is to see
theory choice as a matter of “conversion” does not seem warranted (Norton, 2021).
In most work in the history of science, the approach is to show how a particular event or
outcome was the result of various social and intellectual influences. Bayesian history of
science, on the other hand, focuses on the lines of evidence relevant to the historical devel-
opment to see if the direction taken by an individual or group of scientists was consistent or
inconsistent with the evidence at hand. This turns the usual historical approach on its head.
Both are valid approaches, but an approach focusing on evidence as the leading factor is less
often taken. Indeed, sometimes influences can serve as evidence, as seen here in the case of
Pauling’s alpha helix.
Even in a Bayesian approach it is important to take point of view into consideration when
assessing whether a theory is confirmed or disconfirmed. This is illustrated by Pauling’s view of
his own triple helix model versus Watson’s view of that model. The evidence brought to
bear by different individuals can be different, as well as what competing theory is considered,
and the strength of evidence. Worrall has discussed some of the limitations of the subjective
Bayesian approach (Worrall, 2000).
Quantitative Science Studies
226
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
1
2
0
9
2
0
7
8
3
7
2
q
s
s
_
a
_
0
0
2
3
3
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Bayesian history of science
Another obvious difficulty with a Bayesian approach to scientific discovery and theory
choice is that it requires our brains to compute posterior probabilities. How this cognitive func-
tion is performed is a mystery. Perhaps such a mechanism has evolved to enhance our ability
to survive (Friston, 2012), for example, to differentiate friend from foe, and prey from predator.
Perhaps we are able somehow to simplify the multiple evidence inputs to just a few of the most
salient forms, such as Watson’s realization of the purine to pyrimidine base pairing, and then,
one by one, seeing how the other pieces of the puzzle fit together. Or as George Miller has
speculated: “We might argue that in the course of evolution those organisms were most
successful that were responsive to the widest range of stimulus energies in their environment”
(Miller, 1967, p. 29). The double helix exemplifies such a wide range.
Whether or not our brains can perform Bayes-like operations, it seems fruitful to apply this
methodology to other cases in the history and sociology of science, for example, to provide an
alternative view on how theories are transformed into “facts” (Latour & Woolgar, 1979), and
perhaps even to contemporary scientific or social debates that are yet to be resolved (e.g.,
Alzheimer’s disease). Despite not solving such problems, a Bayesian approach offers a system-
atic way of organizing the evidential pros and cons of competing views and a tentative verdict.
ACKNOWLEDGMENTS
I would like to thank the three anonymous reviewers for stimulating several revisions and addi-
tions, Hung Tseng for useful commentary, Friedel Weinert for recommending the book by John
Norton, and Ludo Waltman for help formatting equations.
COMPETING INTERESTS
The author has no competing interests.
FUNDING INFORMATION
No funding has been received for this research.
DATA AVAILABILITY
Data are available from the author.
REFERENCES
Astbury, W. T. (1947). X-ray studies of nucleic acids. Symposia of the
Society of Experimental Biology, 1, 66–76. PubMed: 20257017
Baldi, P., & Itti, L. (2010). Of bits and wows: A Bayesian theory of
surprise with applications to attention. Neural Networks, 23(5),
649–666. https://doi.org/10.1016/j.neunet.2009.12.007,
PubMed: 20080025
Chargaff, E., Zamenhof, S., & Green, C. (1950). Composition of
human desoxypentose nucleic acid. Nature, 165(4202), 756–757.
https://doi.org/10.1038/165756b0, PubMed: 15416834
Cochran, W., Crick, F., & Vand, V. (1952). The structure of syn-
thetic polypeptides. I. The transform of atoms on a helix. Acta
Crystallographica, 5, 581–586. https://doi.org/10.1107
/S0365110X52001635
Crick, F. (1988). This mad pursuit: A personal view of scientific dis-
covery. New York: Basic Books.
Dorling, J. (1979). Bayesian personalism, the methodology of scien-
tific research programmes, and Duhem’s problem. Studies in the
History and Philosophy of Science, 10(3), 177–187. https://doi
.org/10.1016/0039-3681(79)90006-2
Earman, J. (1992). Bayes or bust: A critical examination of Bayesian
confirmation theory. Cambridge, MA: MIT Press.
Friston, K. (2012). The history of the future of the Bayesian brain. Neu-
roImage, 62(2), 1230–1233. https://doi.org/10.1016/j.neuroimage
.2011.10.004, PubMed: 22023743
Fry, M. (2016). Discovery of the structure of DNA: The most famous
discovery of 20th century biology. In Landmark experiments in
molecular biology (pp. 143–247). Elsevier. https://doi.org/10
.1016/B978-0-12-802074-6.00005-9
Fry, M. (2022). Question-driven stepwise experimental discoveries
in biochemistry: Two case studies. History and Philosophy of the
Life Sciences, 44(2), 12. https://doi.org/10.1007/s40656-022
-00491-1, PubMed: 35320436
Gijsen, S., Grundei, M., Lange, R. T., Ostwald, D., & Blakenburg, F.
(2021). Neural surprise in somatosensory Bayesian learning.
PLOS Computational Biology, 17(2), e1008068. https://doi.org
/10.1371/journal.pcbi.1008068, PubMed: 33529181
Hartmann, S.
(2008). Modeling high-temperature superconduc-
tivity: Correspondence at bay? In L. Soler, H. Sankey, & P.
Quantitative Science Studies
227
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
1
2
0
9
2
0
7
8
3
7
2
q
s
s
_
a
_
0
0
2
3
3
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Bayesian history of science
Hoyningen-Huene (Eds.), Rethinking scientific change and
theory comparison: Stabilities, ruptures, incommensurabilities?
(pp. 109–129). https://doi.org/10.1007/978-1-4020-6279-7_8
Howson, C., & Urbach, P. (2006). Scientific reasoning: The Bayesian
approach (3rd Ed.). Chicago: Open Court Publishing Co.
Judson, H. F. (1979). The eight days of creation: The makers of the
revolution in biology. New York: Simon and Schuster.
Julius, D. (2021). From peppers to peppermints: Insights into
thermos-sensation and pain. Nobel Lecture. https://www
.nobelprize.org/prizes/medicine/2021/julius/lecture/
Kahneman, D. (2011). Thinking, fast and slow. New York: Farrar,
Straus and Giroux.
Koestler, A. (1964). The act of creation. London: Penguin.
Koller, D., & Friedman, N. (2009). Probabilistic graphical model:
Principles and techniques. Cambridge, MA: MIT Press.
Kuhn, T. S. (1962). The structure of scientific revolutions. Chicago:
University of Chicago Press.
Kuhn, T. S. (1977). Objectivity, value judgment and theory choice.
In The essential tension (pp. 320–339). Chicago: University of
Chicago Press.
Kuhn, T. S. (2000). What are scientific revolutions? In The road
since structure (pp. 13–32). Chicago: University of Chicago Press.
Latour, B., & Woolgar, S. (1979). Laboratory life: The social
construction of scientific facts. Beverly Hills: Sage Publications.
McGrayne, S. B. (2011). The theory that would not die. New
Haven: Yale University Press.
Sciences of the United States of America, 37(4), 205–211.
https://doi.org/10.1073/pnas.37.4.205, PubMed: 14816373
Pearl, J., & Mackenzie, D. (2018). The book of why. New York:
Basic Books.
Pyle, A. (2000). The rationality of the chemical revolution. In R.
Nola & H. Sankey (Eds.), After Popper, Kuhn and Feyerabend
(pp. 98–124). Kluwer Academic Publishers. https://doi.org/10
.1007/978-94-011-3935-9_3
Price, D. J. de Solla. (1986). Little science, big science … and
beyond. New York: Columbia University Press.
Salmon, W. C. (1970). Bayes’s theorem and the history of science. In
R. H. Stuewer (Ed.), Historical and philosophical perspectives of
science (Vol. V, pp. 68–86). Minneapolis: University of Minnesota
Press.
Salmon, W. C. (1990). Rationality and objectivity in science, or
Tom Kuhn meets Tom Bayes. University of Minnesota Press,
Minneapolis. Retrieved from the University of Minnesota Digital
Conservancy, https://hdl.handle.net/11299/185726
Schindler, S. (2008). Model, theory and evidence in the discovery
of the DNA structure. British Journal for the Philosophy of
Science, 59(4), 619–658. https://doi.org/10.1093/bjps/axn030
Small, H. (2022). The confirmation of scientific theories using
Bayesian causal networks and citation sentiments. Quantitative
Science Studies, 3(2), 393–419. https://doi.org/10.1162/qss_a
_00189
Thagard, P. (1992). Conceptual revolutions. Princeton, NJ: Princeton
Miller, G. A. (1967). The psychology of communication. New York:
University Press. https://doi.org/10.1515/9780691186672
Basic Books.
Morey, R. D., Romeijn, J. W., & Rouder, J. N. (2016). The philoso-
phy of Bayes factors and the quantification of statistical evidence.
Journal of Mathematical Psychology, 72, 6–18. https://doi.org/10
.1016/j.jmp.2015.11.001
Norton, J. D. (2021). The material theory of induction. University of
Calgary Press. https://prism.ucalgary.ca/ handle/1880/114133.
https://doi.org/10.2307/j.ctv25wxcb5
Olby, R. (1974). The path to the double helix. Seattle: University of
Washington Press.
Pauling, L., & Corey, R. B. (1953). A proposed structure for the
nucleic acids. Proceeding of the National Academy of Sciences
of the United States of America, 39(2), 84–97. https://doi.org/10
.1073/pnas.39.2.84, PubMed: 16578429
Pauling, L., Corey, R. B., & Branson, H. R. (1951). The structure of
proteins: Two hydrogen bonded helical configurations of the
polypeptide chain. Proceedings of the National Academy of
Visalli, A., Capizzi, M., Ambrosini, E., & Kopp, B. (2021). Electro-
encephalographic correlates of temporal Bayesian belief updat-
ing and surprise. Neuroimage, 231, 117867. https://doi.org/10
.1016/j.neuroimage.2021.117867, PubMed: 33592246
Watson, J. D. (1968). The double helix: A personal account of the
discovery of the structure of DNA. New York: Atheneum.
Weinert, F. (2010). The role of probability arguments in the history
of science. Studies in History and Philosophy of Sciences, Part A,
41(1), 95–104. https://doi.org/10.1016/j.shpsa.2009.12.003,
PubMed: 20527288
Weinert, F. (2014). Lines of descent: Kuhn and beyond. Founda-
tions of Science, 19(4), 331–352. https://doi.org/10.1007
/s10699-013-9342-y
Worrall, J. (2000). Kuhn, Bayes and theory-choice: How revolutionary
is Kuhn’s account of theoretical change? In R. Nola and H. Sankey
(Eds.), After Popper, Kuhn and Feyerabend (pp. 125–151). Kluwer
Academic Publishers. https://doi.org/10.1007/978-94-011-3935-9_4
Quantitative Science Studies
228
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
1
2
0
9
2
0
7
8
3
7
2
q
s
s
_
a
_
0
0
2
3
3
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3