La predicción de Dirac de
the Positron:
A Case Study for the
Current Realism Debate
Thomas Pashby
University of Pittsburgh
Much debate has ensued regarding the challenge to scientiªc realism provided
by consideration of certain problematic episodes of theory change in the history
of science. This paper contends that there is an interesting case which has been
overlooked in this debate, namely the prediction of the positron by Dirac from
his ‘hole’ theory, and its subsequent replacement by a theory which failed to
contain a central, and essential, theoretical posit: the ‘Dirac sea’ of negative
energy electrons. Accounting for this case with the ‘divide and conquer’ strat-
egy of contemporary scientiªc realism proves particularly troublesome, incluso para
the structural realist.
1. Introducción
Scientiªc realism is often described as the attitude that we should have to-
wards our most successful scientiªc theories, namely that they are, in an
appropriate sense, true. Eso es, they get things basically right about the
world. Actualmente, local relativistic quantum ªeld theories comprise a large
class of our best theories. We take them to provide the best description of
reality we have in circumstances where energies are large enough to re-
quire relativistic treatment but small enough such that gravitational ef-
fects can be neglected. To a high degree of accuracy, The Standard Model
(a renormalizable local Yang-Mills gauge theory with the internal symme-
try group SU(3) (cid:2) SU(2) (cid:2) Ud.(1)) provides a description of all the forces
This paper has beneªted from comments on previous drafts by Bryan Roberts, Alexander
Blum, Tony Duncan, and the editors of this volume. Tony Duncan in particular deserves
warm thanks for his generous help in matters of physics. Thanks to John Norton, Kyle
stanford, Don Howard, Katherine Brading, David Baker and Matt Gorski for useful con-
versations. Special thanks go to James Ladyman, without whom none of this would have
sido posible.
Perspectives on Science 2012, volumen. 20, No. 4
©2012 by The Massachusetts Institute of Technology
440
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
441
and phenomena encountered so far in terrestrial physics, save gravity. Uno
of the central characteristics of these theories is the ubiquity of antimatter:
each particle (or better, quantum matter ªeld) possesses a partner with,
apenas, the same mass and opposite charge.1
The existence of antimatter was predicted by Dirac in 1931 from for-
mal properties of the relativistic electron equation he had discovered in
1928, on the basis of arguments that were almost entirely theoretical.
Since the Dirac Equation was the ªrst successful application of the re-
quirement of relativistic invariance to quantum mechanics, prima facie it
seems Dirac’s successful prediction of antimatter embodies just the charac-
teristics that the realist ªnds most compelling: a uniªcation of two theo-
ries with disparate empirical support resulting in the prediction of en-
tirely novel phenomena. Sin embargo,
theory he based his
arguments upon was later supplanted, along with its essential posit: a
completely ªlled ‘sea’ of negative energy electrons.
the ‘hole’
The realism debate has been characterized as a pull between two com-
peting arguments: the No Miracles Argument (attributed to Putnam
1975), which argues from the success of scientiªc theories to their truth,
and the Pessimistic Meta-Induction (attributed to Laudan 1981), cual
points to instances where theories which the realist would have taken as
true have been replaced by theories failing to contain their central theoret-
ical posits. The task for the contemporary realist in making sense of the
historical record is, por lo tanto, to construct a philosophical account of sci-
ence that respects the realist intuition of the NMA, while avoiding falling
foul of the cases adduced in support of the PMI.
This paper contends that philosophers of science engaged in this proj-
ect have failed to consider a rich historical episode that deserves their at-
tention: Dirac’s prediction of antimatter, and the subsequent replacement
of hole theory by local relativistic quantum ªeld theory (the Quantum
ElectroDynamics of Feynman, Schwinger and Tomonaga). It is my conten-
tion that Dirac’s negative energy electron sea deserves a place in Laudan’s
famous ‘laundry list’ of discarded theoretical posits alongside caloric and
the ether, and is a case worthy of serious consideration by the current gen-
eration of scientiªc realists due to its close relation (genetically and theo-
retically) to our current best physical theories.
One reason which might explain why this example of theory replace-
ment has been overlooked is the lack of a suitable historical resource. Alabama-
though there are many which cover some of the requisite territory (Moyer
1. For a clear account of the “naïve” view of antimatter, and a mathematically sophisti-
cated replacement see Baker and Halvorson (2010). On this topic see also Wallace (2009).
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
442
Dirac’s Prediction of the Positron
1981a, 1981b; Pais 1986; Darrigol 1988; Kragh 1990; Molinero 1994;
Schweber 1994; Roque 1997; Mehra and Rechenberg 2001), the role of
hole theory in the transition from non-relativistic quantum mechanics to
the quantum electrodynamics of the post-war years has not yet been sub-
ject to a comprehensive study. The ªrst aim of this paper, por lo tanto, is to
present the historical details in a readily digestible form, which demon-
strates to the philosopher of science the relevance of this episode for the
scientiªc realism debate.
The second aim is to present a philosophically motivated account of the
challenge that the success of hole theory, closely followed by its replace-
mento, poses to scientiªc realism. One of the guiding assumptions is that
the historical and theoretical details matter. En otras palabras, it is not
enough to consider theories in the abstract, as set-theoretic constructions
or otherwise, since doing so would obscure or ignore distinctions and de-
velopments which are relevant to the questions scientiªc realism seeks to
address. Sin embargo, another reason why this episode might have been over-
looked is the continued controversy surrounding the interpretation of
relativistic quantum ªeld theory, and quantum mechanics is general. Inso-
far as it is possible, these general concerns will be bracketed in what fol-
lows, but it is assumed that it is incumbent on the realist to account for
the success of these theories in a way that also respects their historical
desarrollo.
The philosophical work in which Dirac’s prediction has featured most
prominently—namely as a case study for Hanson (1963) in his work on
the ‘logic of discovery’—could be taken to question whether Dirac’s pre-
diction of his anti-electron deserves to be considered as a prediction of the
positron soon to be observed by C. D. anderson. Although it will become
apparent that there is a degree of fortuity about the chain of reasoning
which led to Dirac’s prediction, I will maintain that there is no reason not
to accord to it the status of a genuine prediction of antimatter. Sin embargo,
as will become apparent, the details of the logic of discovery and its re-
placement by a different ‘logic of justiªcation’ are important for the sorts
of considerations that feature in asking the central question, a saber: es
scientiªc realism a plausible explanation of the empirical and predictive
success of the Dirac equation, and its hole theoretic interpretation?
The paper is organized as follows. En la sección 2, I present the relevant
history pertaining to Dirac’s prediction and the subsequent replacement of
hole theory by QED. Although much of the story is well known, Weyl’s
role in the prediction of antimatter is often underappreciated and proves
to be crucial in understanding Dirac’s chain of reasoning. En la sección 3, I
use this case to mount a Laudan-style challenge to the scientiªc realist.
I then proceed to assess the prospects for success of two well known re-
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
443
sponses of the contemporary scientiªc realist to this kind of argument.
Sección 4 discusses what I term restrictive realism, exempliªed by Psillos
(1999), while Section 5 considers how structural realism might fare in this
caso. I argue that each faces difªculties in accounting for the success of
hole theory, but it seems that structural realist has more room to maneu-
ver. The reader who wishes to skip the historical detail and go straight to
the philosophical discussion may proceed directly to Section 3, aided by
this schematic account of the history.
Chronology of Developments Leading to Dirac’s Prediction
1. Relativistic invariance of the wave equation (Klein 1926; gordon
1926).
2. Consistency with Dirac’s quantum mechanics (his transformation
theory of Dirac 1927b).
→ Linearity of the wave equation in time and momentum.
→ The Dirac Equation (Dirac 1928).
3. Klein paradox (Klein 1929).
4. Pauli Exclusion Principle (phenomenologically justiªed).
→ Filled negative energy states (the ‘Dirac sea’).
→ ‘Holes’ in the sea are positive energy particles (hole theory). El
holes behave as positively charged particles with positive energy.
→ Holes are protons. Pair production/annihilation. (Dirac 1930).
5. Completely ªlled vacuum state (Oppenheimer 1930).
6. Symmetrical masses in the presence of interactions (Weyl 1931).
→ Prediction of ‘anti-electron’ (Dirac 1931).
2. Historical Case Study: The ‘Hole’ Story
1. The Magic: The Dirac Equation
With the completion of his transformation theory (1927b), Dirac re-
garded the interpretation of quantum mechanics—both kinematically and
dynamically—as essentially ªxed. By extending and modifying classical
mecánica, he had established a systematic means for giving unambiguous
answers to all experimental questions that could be posed of an ensemble
of identical quantum systems (the probabilistic nature of the answers pro-
vided by the application of this recipe to a single system never really trou-
bled Dirac). With this work completed, he devoted his energies to the
task of ªnding a satisfactory relativistic treatment of the electron.2
Relativity was Dirac’s early passion, and he had been concerned with
2. This section draws on Dirac (1977), Kragh (1990), and Mehra and Rechenberg
(2001).
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
444
Dirac’s Prediction of the Positron
the relativistic treatment of problems in quantum theory since he ªrst be-
came a graduate student at St. John’s, Cambridge in 1925. This concern
led to his relativistic treatment of the Compton effect (1926, 1927a), en
which radiation is emitted by an electron in electromagnetic ªeld. A note
added in proof to the later paper indicates his awareness of Gordon’s
(1926) trabajar, which utilized the Klein-Gordon equation to calculate the
ªeld produced by a moving electron.
The Klein-Gordon equation was the result of a straightforward relativ-
istic generalization of the Schrödinger equation, obtained by applying the
quantum substitutions for the momentum and energy to the relativistic
mass-energy equation E2 (cid:3) p2c2 (cid:4) m2c4. De hecho, this equation had been
written down by Schrödinger himself as early as 1925, but was discarded
due to its failure to reproduce the correct hydrogen spectrum. El
Schrödinger equation for a free massive particle (in one dimension) is ob-
tained from the classical expression for the Hamiltonian as follows,
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
=
h
2
pag
2
metro
;
(cid:2)
→ =
pag
i
pag
(cid:3) ∂
∂
X
(cid:3)
i
∂
∂
t
ψ
(cid:2)
(X,t) H x t
( , )
ψ
=
= -
2
2
∂
(cid:3)
∂
2
m x
2
ψ
x t
( , )
.
El (gratis) Klein-Gordon equation results from taking the relativistic en-
ergy and performing the same substitutions of momentum and energy op-
erators for their classical counterparts. Since classically the Hamiltonian
represents the energy of the particle, this suggests that the operator on the
left hand side above is a suitable substitution for the energy E. So, in three
dimensions this time, tenemos,
2
pag
→ = − ∇ = −
(cid:3)
(cid:3)
2
2
(cid:2)
pag
⎛
⎜
⎝
2
∂
∂
X
2
+
2
∂
∂
y
2
+
2
∂
∂
z
2
⎞
(cid:2)
⎟ → =
E i
;
⎠
mi
(cid:3)
∂
∂ ;
t
E2 (cid:3) p2c2 (cid:4) m2c4 → (cid:3)
2
2
2
∂
∂
t
ψ
( , )
x t
=
(cid:3)
(
∇ −
2
2 2
C
2 4
m c
ψ
)
( , )
x t
.
While this wave equation retains the Lorentz invariance of the original ex-
presion, from the perspective of Dirac’s transformation theory it has a ma-
jor ºaw: whereas the Schrödinger equation is ªrst-order in the time deriv-
ative, the Klein-Gordon equation is second-order. This meant that the
interpretation of transformation theory that Dirac had developed could
not be applied in full generality to the Klein-Gordon equation since the
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
445
evolution of the system was no longer determined by the speciªcation of a
state at a single time.
Convinced of the validity of transformation theory, Dirac set about
ªnding a relativistic wave equation for the electron which would satisfy
this requirement while agreeing with the Klein-Gordon equation in an
appropriate way. Since the equation he sought would be ªrst-order in
tiempo, es decir. linear in the zeroth component of the 4-vector momentum p0, él
took relativistic symmetry to imply it must also be linear in the vector
momenta pr, r (cid:3) 1,2,3. This meant that a satisfactory equation would be a
linearized version of the Klein-Gordon equation, which would then result
from taking the (Minkowski) product of the linear equation with itself.
Speaking loosely, such an equation would be the square-root of the Klein-
Gordon equation. So, absorbing factors of c into p0, the wave equation he
sought is of the form,
(p0 (cid:4) α1p1 (cid:4) α2p2 (cid:4) α3p3 (cid:4) α4mc)ψ (cid:3) 0.
Although the four coefªcients (cid:5)(cid:6) were initially unknown, the require-
ment of consistency with the Klein-Gordon equation placed signiªcant
constraints upon them since all cross-terms involving more that one mo-
mentum pr must vanish, while squaring to unity. Eso es,
αμ
2 (cid:3) 1; αμαν (cid:4) αναμ (cid:3) 0, for μ ≠ ν.
The failure of commutativity displayed by these relations meant that the
coefªcients αμ couldn’t be ordinary numbers (c-numbers in Dirac’s lan-
guage). Sin embargo, Dirac noticed that the 2 (cid:2) 2 Pauli spin matrices had ex-
actly these properties, although they would only serve to linearize the
massless wave equation. The problem was solved when Dirac realized that
4 (cid:2) 4 matrices would afford a representation of the algebraic relations im-
posed by these conditions on the (cid:5)(cid:6). In doing so Dirac had found an equa-
tion of just the form he desired, which could be written in terms of a
Hamiltonian operator, and could be shown to retain the Lorentz invari-
ance of the Klein-Gordon equation. Eso es, the Dirac Equation (aquí
without an electromagnetic potential) which could be written as
i
(cid:3) ∂
∂
t
ψ
=
(cid:2)
h
d
ψ
;
(cid:2)
h
d
=
C(cid:2)
⋅∇ +
a
mc
2 .
4
Sin embargo, the interpretation in terms of transformation theory was not
entirely straightforward. Whereas the Schrödinger equation applies to a
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
446
Dirac’s Prediction of the Positron
single wave function, el 4 (cid:2) 4 matrices appearing in the Dirac Equation
meant that (cid:7) represented not a single wavefunction but a vector of 4 ola
funciones, (cid:7)norte(X,t). Two of these were enough to account for the known
properties of electrons with opposite spin—a triumph—but this left two
more solutions (also with opposite spin), and negative energy.
= ±
m c
−2 2
p c
This property is inherited from the classical expression for relativistic
2 4 , which provides both positive and negative so-
energy E
lutions for a given mass and momentum (and shared by the Klein-Gordon
equation). As Dirac (1928) notas, his linear wave equation had only man-
aged to solve the ªrst of the interpretative difªculties associated with the
Klein-Gordon equation: the problematic negative energy solutions re-
mained, only now there were two of them. It was convenient to ignore
these negative energy solutions for the initial purposes of calculation, pero
it soon became apparent that they could not be discounted.
Sin embargo, the success that Dirac’s breakthrough brought was remark-
capaz. At a stroke, Dirac had explained not only the spin of the electron,
but also derived its gyromagnetic ratio and (by considering the Dirac
equation with a central Coulomb potential) calculated the ªne structure of
the hydrogen atom spectrum, seemingly just from the requirements of Lo-
rentz invariance and conformity with quantum mechanics. These two re-
sults were not to be improved upon for 20 años.
2. The Sickness: Negative Energies and the Advent of Hole Theory
Whereas the free Dirac equation seemed to allow positive and negative en-
ergy solutions to be considered independently, including interactions into
the Hamiltonian led to transitions from positive to negative energy and
viceversa. In what became known as the ‘Klein paradox,’ Klein (1929)
demonstrated conclusively that the negative energy solutions could not be
ignored, and furthermore their presence led to behavior that initially
seemed pathological. In the situation he considered, an electron with en-
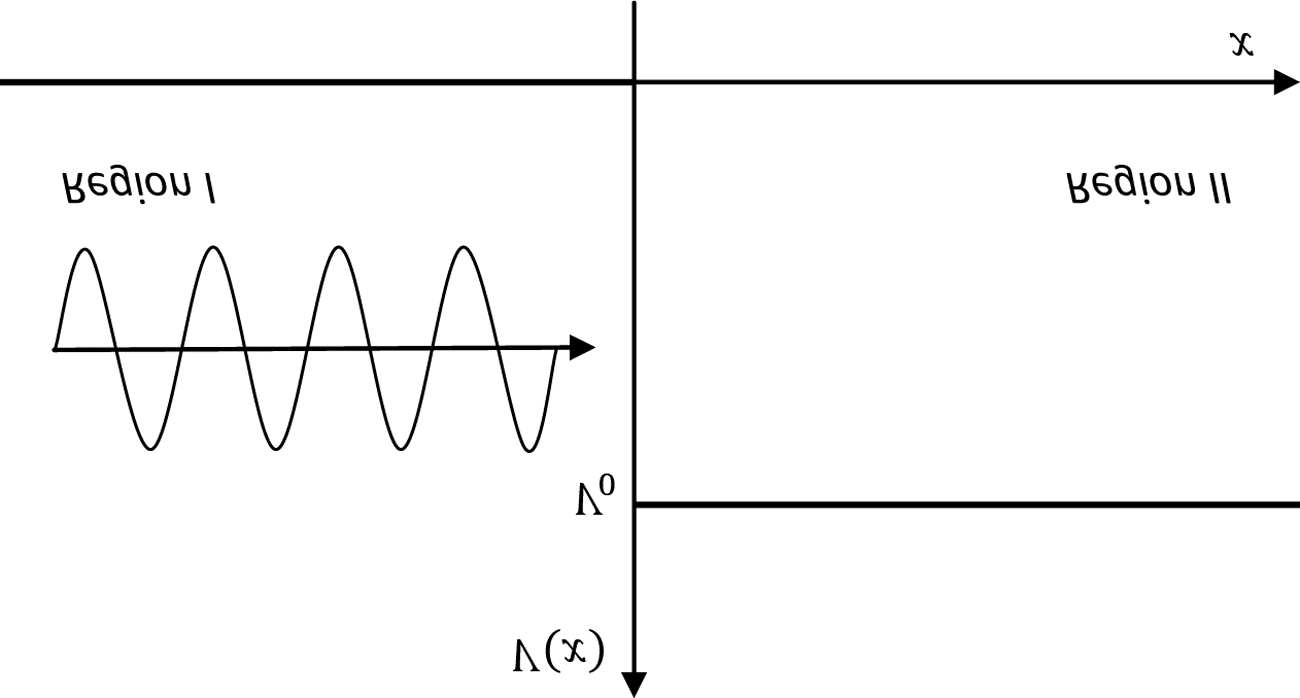
ergy E approaches a step potential from the left (ver figura 1). The elec-
tron is represented by an incident plane wave ψ (cid:3) mi(i(px
Et)), but as such ψ
cannot be restricted to a positive energy part alone. As Darwin (1928) had
observado, the system of linear equations encapsulated by the Dirac Equa-
tion introduced a dependency between the coefªcients of the positive and
negative energy solutions which entailed the inclusion of a small negative
energy term in a plane wave solution. Continuity requirements at the
boundary between Region I and II put conditions on the transmitted and
reºected waves so that the current density is properly normalized. Ahora,
Klein asked, what percentage of the wave is transmitted or reºected, ac-
cording to the Dirac Equation?
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
447
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
Cifra 1. The Klein Paradox (Setup). An electron approaches a step potential
from the left.
He found that if V0 (cid:8) mi (cid:4) mc2 then the transmitted wave decays expo-
nentially in Region II, with some proportion reºected back,—just as one
would expect if it obeyed the Schrodinger equation. Sin embargo, if V0 (cid:9) mi
(cid:4) mc2 then the transmitted wave is a plane wave in Region II which, nor-
malized to respect the continuity condition, is directed toward Region I, entonces
that the total reºected current appeared to be greater than the total inci-
dent current. This result seemed to be pure nonsense, and was deeply
troubling from the point of view of contemporary atomic theory which
(prior to the discovery of the neutron) explained the neutral charge of the
nucleus by the hypothesis of electronic nuclear conªnement.
Bohr wrote to Dirac in late 1929 posing this difªculty and expressed
his concerns that a wide scale conceptual revolution would be required to
resolve it. Dirac confronted the problem in his reply by proposing his
‘hole’ theory, which interprets the transmitted wave as the current of a pos-
itive particle moving right. His reasoning appeared as follows:3
• Electrons may transition to negative energy states by spontane-
ous emission of radiation. Sin embargo, bajo (negative) energy states
will be stable against further descent since to jump back up re-
quires incident high energy radiation.
• Since electrons are fermions they obey the Pauli exclusion princi-
ple so a state can be occupied by at most one electron. Suppose
3. See Moyer (1981a) for details of this exchange.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
448
Dirac’s Prediction of the Positron
eso (cerca de) all of the stable low (negative) energy states are oc-
cupied. This forces positive energy electrons to remain in posi-
tive energy states.
•
• The negative energy electrons will have uniform (inªnite) den-
sity so the net electromagnetic ªeld is zero. Only deviations
from uniformity will be observable.
‘Holes’ in the negative energy state distribution will act like
they have positive energy, but with opposite (positivo) charge.
These are protons, which are annihilated when an electron drops
into the corresponding negative energy state.
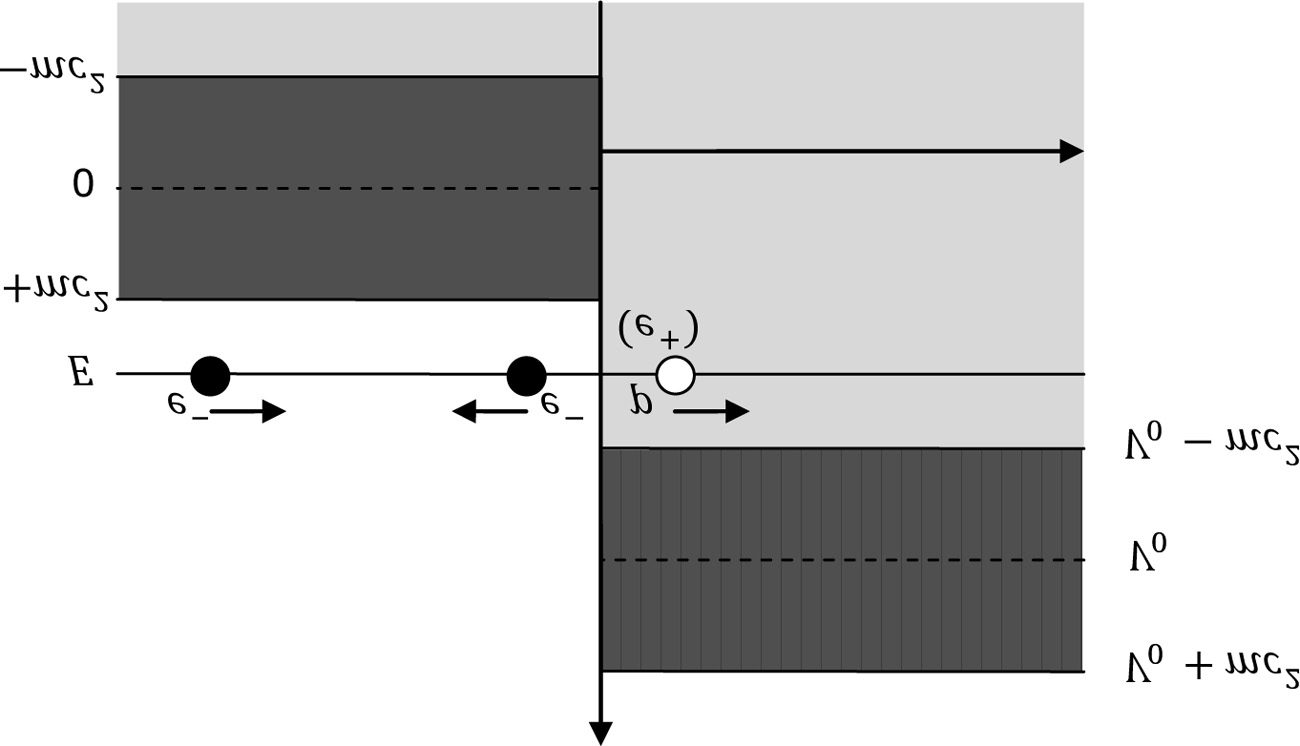
To explain how Dirac had resolved Klein’s paradox will require a fur-
ther diagram (ver figura 2). On the left in Region I, electrons may have
energies greater than (cid:4)mc2 (the rest mass) or less than (cid:10)mc2, and the elec-
tron current of a solution with energy (cid:4)E is directed right. Sin embargo,
since in this situation we have V0 (cid:9) mi (cid:4) mc2, this energy level corresponds
to a negative energy solution in Region II, where the potential V0 acts to
raise the energy of the “vacuum” state.4 In the hole theory interpretation,
the negative energy states are everywhere ªlled, but the states on the right
are above the “mass gap” and so, in Region I, are allowed positive energy
electron states. Thus the leftward directed current which seemed paradox-
ical due to the absence of electrons in Region II now had a ready explana-
ción: in Dirac’s hole theory there are plenty of electrons there to travel left,
En realidad, an uncountable inªnity of them. While the current directed left is
indeed an electron current, electrons moving to the left leave a ‘hole’ mov-
ing right, which is to be interpreted as a proton (later to become the anti-
electron). If an electron drops into such a hole, then both particles, cada
having positive energy, are annihilated. This ingenious solution explained
how negative energy solutions could be interpreted as particles with posi-
tive charge and positive energy, since a hole in an otherwise ªlled negative
energy electron sea corresponds to the absence of a negative energy particle.
The direct interpretation of negative energy solutions as protons had
been proposed by Weyl (1929), but only by adopting Dirac’s interpreta-
tion of protons as holes could they be included in the theory as particles
with physically reasonable properties.5 However, as Dirac was immedi-
ately aware, the mass discrepancy between the electron and proton (a fac-
tor of roughly 1800) was a signiªcant problem for his new theory, desde
the dynamics appeared to be entirely symmetric with respect to the nega-
tive and positive energy solutions. This meant that there could apparently
4. Scare quotes indicate the use of anachronistic language.
5. Por ejemplo, Dirac (1930) pointed out that on Weyl’s hypothesis a proton radiating
energy would accelerate, and would have to absorb energy to come to rest.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
449
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
Cifra 2. The Klein Paradox (Resolution). The electron current moving to the
left is now accompanied by a ‘hole’ moving to the right, which is interpreted as a
proton (later positron).
be no dynamically relevant difference between a situation in which the
vacuum state was ªlled by protons, with the holes being positive energy
electrons, and the situation in which the holes were protons, which made it
hard to see how they could not have the same mass.
In his letter to Bohr, he expressed his hope that this asymmetry might
emerge from taking into account interactions between the vacuum elec-
trons, but he had not managed to formulate the problem in a relativisti-
cally invariant way. Dirac (1930) gave a sketch of a formal argument in the
non-relativistic context, in which he claimed that the inªnite number of
electrons in the vacuum would serve to break the symmetry if the
Hamiltonian includes the energy due to pair-wise interactions. Since only
the term containing the sum over the vacuum electrons would contain an
inªnite sum, the situation could not fail to be asymmetric under an ex-
change of holes and electrons. This would serve to break the dynamical
symmetry and so might explain the observed difference in mass.
When Dirac later said that only “pure cowardice” prevented him from
immediately positing the existence of the anti-electron,6 he ignored the
plausibility of his expectation that the interaction of the holes with the
surrounding inªnity of vacuum electrons might serve to break the mass
symmetry. Sin embargo, as he freely admitted, this asymmetry must be dem-
6. This phrase appears in Dirac’s 1963 interview with Thomas Kuhn.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
450
Dirac’s Prediction of the Positron
onstrated to hold in the relativistic setting. Weyl took up this challenge
by considering the symmetry properties of a fully interacting relativistic
theory of the electron and proton, and demonstrated that the symmetry of
the masses remained unbroken.7
3. Interactions and Symmetries: The Role of Weyl
Although Weyl is often credited for providing Dirac with the crucial sym-
metry argument that convinced him that the holes could not be protons,
the signiªcance and sophistication of Weyl’s argument is perhaps not al-
ways fully appreciated.8 Weyl’s background in pure mathematics made
him ideally placed to provide a general framework in which he could ex-
plore the consequences of the nascent relativistic quantum treatment of
asunto. Key to this progress was his understanding of the geometrical
properties of the Dirac equation, which allowed him to express the equa-
tion in manifestly relativistic form and so generalize it beyond Dirac’s
(1928) single particle equation.
It had soon been realized (again by Darwin 1928) that Dirac’s electron
equation was not a tensor equation, and so its solutions were not the rela-
tivistic objects familiar to physicists at the time. These new relativistic
covariants were christened spinors (apparently by Ehrenfest) and were ini-
tially regarded with puzzlement by the physics community. Sin embargo,
Weyl’s geometrical knowledge provided him with the means to connect
spinors to the general Lorentz transformation since, as he was well aware,
spinors had in fact already been discovered by the French mathematician
Elie Cartan as a means to represent rotations in three-dimensional space
by a pair of complex numbers.
In the second edition of Gruppentheorie und Quantenmechanik (1931)
Weyl showed that while spinor representations of the restricted Lo-
rentz Group (of boosts and rotations) existir, representations of the full
Lorentz Group (including spatial and temporal reºections) required
bispinors (con 4 complex numbers) corresponding to the two pairs of so-
lutions to the Dirac Equation. The Dirac matrices could be understood as
forming a basis in this bispinor representation, analogous to the role of the
quaternions (known to physicists as the Pauli matrices) in the representa-
tion of rotations in three-dimensional space. This geometrical connection
must have been of great interest to Dirac given his fondness for projective
7. Pauli also claimed to have demonstrated a similar result, which Dirac was informed
of in a letter from Tamm in 1930. Sin embargo, it seems that Dirac considered Weyl’s demon-
stration to be superior since he was never to refer to Pauli’s proof. Lacking the details of
Pauli’s argument, it is hard to know whether or not they were equivalent.
8. See Darrigol (1986, pag. 243) for a notable exception.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
451
geometría, cual, as Weyl had explained in the ªrst edition (1928), también
provided a means to understand Lorentz transformations geometrically.9
With this understanding in place, Weyl was able to derive the Dirac
equation from an action principle written in manifestly relativistically
covariant form, which enabled him to easily investigate the symmetries of
the equations of motion. He went on to address the invariance properties
of the Dirac equation in two different contexts, ªrst without an electro-
magnetic-matter interaction (1932, páginas. 225–27), and then in fully inter-
acting form, called by Weyl “The Maxwell-Dirac Field Equations.” This
second treatment apparently provided the rigorous treatment that Dirac
required, but rather than conªrm his hypothesis that interactions would
explain the mass asymmetry of electrons and protons, Weyl instead dis-
played the insensitivity of hole theory to the exchange of electrons and
holes.
Weyl’s initial treatment of the (ªrst-quantized) Dirac Equation is es-
sentially as a classical theory, applied to a single electron under the
inºuence of an external classical ªeld (without back reaction). He made it
clear that a full quantum treatment of the interaction would require rela-
tivistic quantum ªeld theory, and thus second-quantization.10 That is,
rather than treating electrons as quantized point particles, Weyl was to
use Jordan’s formalism of matter ªelds, which had been extended to the
relativistic context by Heisenberg and Pauli.11 Having done so the crucial
argument which establishes the equality of masses of the electrons and
holes appears in the context of Weyl’s relativistic quantum ªeld theoretic
treatment of the electromagnetic ªeld, its interaction with matter, y el
matter ªeld.
Whereas the variables of the electromagnetic ªeld obey Canonical
Commutation Relations (CCR’s), the wave functions featuring in the mat-
ter part of the action obey canonical anti-commutation relations (CAR’s),
which serve to enforce the Pauli exclusion principle. Following Dirac’s
(1927C) approach to quantum electrodynamics, Weyl (1932, páginas. 256–60)
constructs creation and annihilation operators for the electromagnetic
9. The role of projective geometry in Dirac’s approach to relativistic quantum theory
and his derivation of the Dirac equation is the subject of Pashby (unpublished).
10. Second quantization refers to the procedure of describing a classical ªeld system by
ªeld conªguration variables and their conjugate momenta, and then applying the quanti-
zation procedure to promote these to quantum operators, rather than the position and mo-
mentum variables of individual particles, which became known as ªrst-quantization. De este modo
a second-quantized system is not “quantized twice,” but rather quantized according to a
procedure which was developed subsequently to the original.
11. See Darrigol (1986) for an admirably lucid account of the development of quantum
matter ªelds.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
452
Dirac’s Prediction of the Positron
ªeld and derives a dynamical equation which takes into account the inter-
action of an electron with the electromagnetic ªeld by emission and ab-
sorption of photons. Although Weyl doesn’t go on to carry it out in any
detail, he sketches the outlines of an analogous treatment of the Dirac
Equation with many of the features we recognize from the modern ac-
count.
There is, por supuesto, nothing to prevent us from quantizing the mat-
ter waves in a manner analogous to that applied to electro-magnetic
ondas. . . . [The energy] will then depend on the quantum num-
ber n(cid:6) which corresponds to the characteristic values (cid:6) which may
take only the values 0 y 1, and in addition on the numbers N(cid:11) de
photons. . . . The dynamical law allows only those quantum jumps
of the particles in which one n(cid:6) falls from 1 a 0 and another n(cid:6)(cid:12)
jumps from 0 a 1. (1932, pag. 262)
Although this is just a sketch of a fully interacting ªeld theoretic hole the-
ory, the continuity with the later quantum ªeld theory program and the
prescience Weyl shows is striking. En efecto, as Darrigol (1986, pag. 243) transmisión exterior-
serves, this section contains what must be the ªrst statement of the CPT
invariance of a relativistic quantum ªeld theory. The argument for the
mass equality of electrons and holes follows. First Weyl notes that:
[t]here is nothing to prevent us from replacing the numbers n(cid:10)(cid:6)
+ for positive (cid:6). El
for negative (cid:10)μ by n
− = −1
, keeping nμ
μ
theorem of conservation of charge is then Σ
S
−
+
norte
norte
μ
μ
(μ (cid:9) 0). (1932, pag. 263)
(cid:3) const.
norte
μ
−
Here we see the appearance of the idea that while charge is conserved, el
dynamics is indifferent to the number of positive and negatively charged
pairs of particles. This leads Weyl to a discussion of hole theory, y el
resulting interpretation of pair production and annihilation, about which
he says:
However attractive this idea may seem at ªrst, it is impossible to
hold without introducing other profound modiªcations to square
our theory with the observed facts. En efecto, according to it the mass
of a proton should be the same as the mass of an electron; further-
más, no matter how the action is chosen (so long as it is invariant
under interchange of right and left), this hypothesis leads to the
essential equivalence of positive and negative energy under all
circumstances—even on taking the interaction between matter
and radiation rigorously into account. (1932, pag. 263)
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
453
The ªrst thing to note is that Weyl takes the failure of hole theory to ex-
plain the divergent masses of the known particles to be evidence against
hole theory. A diferencia de, Dirac will retain his faith in the essential correct-
ness of his theory, and so turn this inference around to make his prediction
of antimatter. It is also clear that Weyl sees his argument as answering di-
rectly to Dirac’s hypothesis about the role of interaction in the mass asym-
metry, asserting that the details of the interaction are unimportant so long
as it preserves the symmetries of the action. It is remarkable how close
Weyl might have come to identifying instead the holes with the “positive
electrons” he had discussed earlier in the context of the ªrst-quantized
equation (1932, pag. 225). But he did not! It was left to Dirac to complete
the ªnal step of the argument.
4. Interpreting Holes: The Prediction of Antimatter
The manifest relativistic invariance of Weyl’s treatment of the interaction
of the electron with the electromagnetic ªeld had made it clear to Dirac
that holes could not be protons. While Weyl seems to have thought, como
bohr, that another conceptual revolution would be required to explain
the difference between “positive and negative electricity” (1932, pag. 264),
Dirac was instead led to straightforwardly identify holes with ‘anti-
electrons’—positively charged particles with positive energy and the same
mass as the electron. While this may seem today an almost trivial step to
have taken, the conceptual inertia generated under the sway of what
Kragh (1990) terms the “two particle paradigm” must have been enor-
mous. Para 30 años, there had been two forms of matter: electrons and
protons.
No experimental data compelled Dirac’s (1931) prediction of the exis-
tence of an entirely novel period. His prediction was made solely on the
basis of consideration of theoretical arguments, and the expectation that
since relativity and quantum mechanics were separately valid a theory
combining them must be also. Dirac’s prediction of the existence of anti-
matter on the basis of hole theory deserves quotation in full.12
A hole, if there was one, would be a new kind of particle, unknown
to experimental physics, having the same mass and opposite charge
to an electron. We may call such a particle an anti-electron. Nosotros
12. As Kragh (1990) notas, the prediction is not even the boldest made by Dirac in the
paper in which it appears! Dirac’s prediction occurs in the introduction of ‘Quantised sin-
gularities in the electromagnetic ªeld (1931),’ which predicts the existence of magnetic
monopoles. The prediction of the anti-electron (yet to be observed, remember) is offered in
support of the “method of theoretical advance” which leads Dirac towards that prediction
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
454
Dirac’s Prediction of the Positron
should not expect to ªnd any of them in nature, on account of their
rapid rate of recombination with electrons, but if they could be
produced experimentally in high vacuum they would be quite sta-
ble and amenable to observation. An encounter between two hard
(cid:13)-rays (of energy at least half a million volts) could lead to the cre-
ation simultaneously of an electron and anti-electron. . . . Presum-
ably the protons will have their own negative-energy states, todo
which normally are occupied, an unoccupied one appearing as an
anti-proton. (1932, páginas. 60–1)
So the prediction concerns quite speciªc conditions under which an ‘anti-
electron’ might be observed experimentally through the phenomenon of
pair production, and an explanation of why they have yet to be observed.
Note also that antimatter is expected by Dirac to be a quite general phe-
nomenon since by the same lights protons are predicted to have their own
anti-particles. A pesar de, as he later said, Dirac would have reason at the
time to know of the possibility of observing such particles as tracks in
bubble chamber cosmic-ray experiments (Dirac 1977, pag. 145), it would be
quite uncharitable to deny to this bold yet cautiously expressed statement
the status of a genuine prediction of the positron, soon to be observed by
anderson. The details of the development of Dirac’s reasoning given above
serve to demonstrate that was a bone ªde theoretical prediction of hole the-
ory, depending essentially on Dirac’s hypothesis of the ªlled ‘sea’ of nega-
tive energy electrons, and the subsequent interpretation of holes as anti-
electrons (positrons).
As it happened, just months later C. D. Anderson at Caltech ªrst report-
ing the observation of cloud chamber tracks which had the signature of a
positively charged electron, which were observed independently in Cam-
bridge by Blackett and Occhialini. Asombrosamente, even the Cambridge
experimentalists were initially unaware of Dirac’s prediction of anti-
electrons, and their explanation in terms of hole theory. While the identi-
ªcation of these particles with the anti-electrons of Dirac’s hole theory was
initially resisted, the prediction soon came to be seen as a vindication of hole
theory, which provided essential tools for understanding their behavior.
En 1933, when Dirac received his Nobel prize for “the discovery of new
productive forms of atomic theory,” hole theory stood triumphant: the ex-
istence of the ‘anti-electron’ had been posited and independently con-
ªrmed, and Blackett and Occhialini had begun to explore the properties of
this exotic new form of matter under controlled conditions in the labora-
(which despite being revived several times in the intervening years, has yet to be conªrmed
hoy).
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
455
conservador. Roque (1997) argues that it was conªrmation afforded to hole theory
by these latter developments which were essential to its acceptance. No
only did hole theory show positrons to be a consequence of Dirac’s relativ-
istic electron equation, but it also provided a theoretical and explanatory
framework for the prediction of qualitatively new processes, and gave
quantitative predictions which were in agreement with experiment.
While some physicists remained skeptical of Dirac’s hole theory despite
its apparent success, there were notable converts, including Blackett,
whose enthusiasm regarding the identiªcation of positrons with Dirac’s
anti-electron had initially been lukewarm at best. In late 1933 he ex-
pressed his faith in the theory thus: “That Dirac’s theory of the electron
predicts the existence of particles with just these properties, gives strong
reason to believe in the essential correctness of his theory” (in Roque
1997, pag. 110). This attitude was typical of the physics community at that
tiempo, and was a reasonable view to take given the prevalence of evidence in
favor of hole theory and the absence of a credible competitor.
5. Replacement: The Fate of Hole Theory
Despite his acceptance of Weyl’s argument for mass symmetry, Dirac
remained of the opinion that while the electromagnetic ªeld should be
subject to second-quantization, electrons should continue to be treated as
particles undergoing Schrödinger-style evolution. He continued to regard
the use of Jordan’s quantized matter ªelds as a formal device which could
lead to conceptual confusion, and proposed an alternative.13 In his ‘many-
time’ theory (Dirac 1932), which in the interests of relativistic invariance
assigned each particle its own time variable, particles and the ªelds
through which they interacted were kept separate. It was soon realized
(Dirac, Fock, and Podolosky 1933) that this was equivalent to the ªeld-
theoretic description, and with the beneªt of hindsight we can see that
Dirac’s attachment to the description of an electron as a quantized point
particle was misguided.14
The best indication of this at the time was provided by the papers of
Fock (1932), and Pauli and Weisskopf ([1934] 1994) who provided a re-
interpretation of the Klein-Gordon equation in ªeld theoretic terms with-
out the use of negative energies. Since this equation did not apply to spin-
half particles, Pauli’s exclusion principle couldn’t apply and so negative
13. Darrigol (1986, páginas. 199–200) attributes this to their differing presentations of
transformation theory: Jordan’s was axiomatic and abstract, while Dirac’s was closely tied
to the classical transformation theory.
14. Sin embargo, although soon abandoned by Dirac, these formal and conceptual tools
proved to be essential to the development of Tomonaga’s ‘super-many-time’ version of
QED.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
456
Dirac’s Prediction of the Positron
energy states could not have been “ªlled” by any number of particles. Como
Pauli and Weisskopf made clear (Pauli called it his “anti-Dirac paper”),
the existence of this interpretation of the Klein-Gordon equation made
Dirac’s original dissatisfaction with it unjustiªed, and made hole theory’s
essential use of the exclusion principle seem somewhat unprincipled.
In the Fock space treatment (Fock 1932) the Hilbert space of the ªeld
conªgurations is written as a direct sum of n-particle Hilbert spaces. En
this context creation and annihilation operators move between these sub-
spaces, and the number operators deªned from them return the number of
particles or antiparticles in a given state. The vacuum state was deªned as
the state that results from the application of annihilation operators to re-
move all particles (es decir., the state ‘with no particles in it’) and adding parti-
cles to this state by application of creation operators returns a state with
positive energy. The key feature of the new quantum ªeld theory was the
symmetrical treatment of particles and anti-particles by creation and anni-
hilation operators.15
In Pauli and Weisskopf’s second-quantized Klein-Gordon theory the
canonical commutation relations apply not to position and momentum
operators for particles, but ªeld operators and their conjugate momenta,
deªned by the usual recipe from the Lagrangian. Solving Hamilton’s equa-
tions allows one to write down an equation of motion for the operators that
is second-order in time (in the case of the Klein-Gordon equation), mientras
the dynamical evolution of the state of the system (still represented by a
ray in Hilbert space) is determined by a ªrst-order Schrodinger equation.
Thus Dirac’s initial dissatisfaction with the ªrst-quantized Klein-Gordon
equation no longer applied: Pauli and Weisskopf’s theory was entirely
consistent with Dirac’s transformation theory.
In this theory, there was no negative energy sea, no special role for the
Pauli exclusion principle, and a completely symmetrical treatment of mat-
ter and antimatter in which particle number is not necessarily conserved.
Although the merits of this approach seem obvious to us now, it is sig-
niªcant that Weisskopf continued to use the conceptual and theoretical
framework of hole theory and negative energies even when working with
the second-quantized Dirac equation.16 In retrospect, once Dirac had ac-
15. Introduced, ironically, by Dirac (1927C) to deal with photons. Sin embargo, his use of
the formalism had more in common with hole theory than Fock’s conception of the vac-
uum.
16. Weisskopf (1939) considered the theory that he had constructed with Pauli as a
competitor to Dirac’s rather than providing the means for a reconstruction of Dirac’s hole
theory. He continued to use the language of hole theory in his (1949) explanation of pair
production and vacuum polarization even though his theoretical treatment could have
been expressed without making use of negative energies.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
457
cepted Weyl’s argument that the interacting theory would be entirely
symmetric between particles and anti-particles, it amounted to a mere
choice of labeling to decide which were which in the theory and so the
failure of hole theory to respect this symmetry of the dynamics was an in-
dication that a more parsimonious description was possible.
De hecho, Fock (1933) and Furry and Oppenheimer (1934) had already
applied the formalism of creation and annihilation operators to the Dirac
equation with the aim of doing away with the postulation of negative en-
ergy electrons, apparently without knowledge of Pauli and Weisskopf’s
trabajar. They showed that in the second-quantized theory the Hamiltonian
operator could be constructed from annihilation and creation operators
with positive energy. Sin embargo, due to difªculties introducing interaction
without breaking gauge invariance, their presentation of the theory was
limited to the non-interacting case. This became an apparently insur-
mountable problem for their program during the 1930’s,17 and as a result
hole theory, in either ªrst- or second-quantized incarnation, remained es-
sentially the only game in town for understanding the electron and posi-
tron.
In various ways, the problem was solved after the Second World War by
Feynmann, Tomonaga and Schwinger, whose formulations of Quantum
ElectroDynamics were shown by Dyson to be essentially equivalent.18
Note that throughout this development there was little conceptual revo-
lution of the kind anticipated by Bohr in 1929: it turned out the formal-
ism required only an extension of the relativistic quantum electrodynam-
ics proposed by Heisenberg and Pauli in 1929, and was ultimately
consistent with Dirac’s transformation theory. Crucial to the acceptance of
the theory was the realization that the empirically relevant content of the
theory (given by the S-matrix) could be extracted without infection by the
divergences (arising from the electron self-interaction and vacuum polar-
ización) which had been thought to doom the program to failure.
3. The Challenge to the Scientiªc Realist
Laudan’s (1981) critique of realism on the basis of the historical record
marked the beginning of a “historical turn” in the realism debate. Reciente
defenses of scientiªc realism have sought to make sense of the historical
record in ways that favor a realist interpretation, introducing criteria
which allow the cursory dismissal of most of Laudan’s list of abandoned
theories while subjecting a few problematic cases to detailed analysis. Este
17. Mehra and Rechenberg (2001, cap. 4) provide a useful account of these develop-
mentos.
18. See Schweber (1994) for an account of this history.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
458
Dirac’s Prediction of the Positron
characteristic response of the contemporary realist to this predicament has
been dubbed the “divide and conquer” strategy. Sin embargo, they have failed
to address the historical episode I have detailed here, which ªts exactly the
logical form of Laudan’s argument against the realist’s use of success as an
indicator of the truth.
I claim that in Dirac’s hole theory we have a theory with strong realist
credentials which was subsequently replaced by a theory failing to contain
its central theoretical posit, the ‘Dirac sea’ of negative energy electrons.
The argument against the scientiªc realist arising from consideration of
this historical episode is therefore as follows:
1. Hole theory was an empirically successful and scientiªcally serious
theory that enjoyed considerable predictive and explanatory suc-
impuesto, including novel predictive success.
2. Por lo tanto, the scientiªc realist would have maintained that hole
theory was deserving of a realist attitude, including the existence of
the negative energy electron ‘sea.’
3. Sin embargo, hole theory was replaced by a successor in which its cen-
tral theoretical posit failed to appear.
4. Por lo tanto, even novel predictive success does not provide compel-
ling evidence for the adoption of a realist attitude towards our cur-
rent best theories.
The ªrst move of the divide and conquer strategy is to attempt to ex-
clude such problematic cases from the set of theories to which a realist
would have been committed. Leplin (1997) suggests that novel predictive
success is the gold standard against which empirical success is to be
judged, since this alone provides convincing evidence for the validity of
the abductive reasoning characteristic of science. He claims that no theo-
ries in Laudan’s list meet this criterion, including theories of the ether
(1997, pag. 146). Yet hole theory did enjoy remarkable novel predictive suc-
impuesto, comfortably meeting Leplin’s criteria of independence and unique-
ness (1997, pag. 77).
Still, the realist could argue that there was something about the theory
that gave it an essentially preliminary character. In support she might of-
fer the views of contemporary scientists such as Pauli who held the theory
to be deeply ºawed. While it is certainly the case that that there was wide-
spread skepticism in the relevant community in the period 1931–3, re-
marks of Pauli’s such as “I do not believe in your perception of ‘holes’,
even if the existence of the ‘anti-electron’ is proved!" (in Moyer 1981b)
should not be taken to characterize the attitude of the community as a
whole once the relevance of hole theory to the observed phenomena had
been established.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
459
Bohr had reportedly made remarks almost identical to that of Pauli’s,
pero, impressed by the continued empirical success of hole theory, his clos-
ing lecture of the 1934 Solvay conference spoke of “the marvelous con-
ªrmation of Dirac’s theory of the electron brought about by the discovery
of the positron” (in Roque 1997, pag. 108). As Roque emphasizes, hole the-
ory at this time was not just an abstract theoretical framework without ex-
perimental application. It had been put to good use deriving quantitative
predictions concerning experimental phenomena such as bremsstrahlung
and pair creation by a group of theorists including Peierls, Bethe, y
Oppenheimer.
Además, hole theory enjoyed considerably fecundity as a frame-
work from which to address the foundational problems that had been
opened up by the consideration of relativistic quantum electrodynamics,
most pressing of which were the seemingly unavoidable divergences that
arose in calculating electron self energy and vacuum polarization. The for-
mer of these was known to be a problem that arose in the classical ªeld
theory, but the latter was unique to the quantum realm. Hole theory pro-
vided the basis of the ªrst partial successes of renormalization techniques
(Dirac 1934; Weisskopf ([1936] 1994) and provided a vital explanatory
framework for understanding the properties of antimatter, even with the
use of second-quantized methods.
But what counts most strongly against excluding hole theory from the
set of theories to which the realist would have been committed is the ab-
sence of a credible competitor: the realist recommends belief in the best
theory available, provided that the theory has enjoyed the requisite suc-
impuesto. It would be unprincipled to deny that status to hole theory on the
basis of anachronistic considerations. In order to argue that the theory
doesn’t deserve to be included under the remit of the No Miracles Argu-
mento, the realist needs to supply a non-question begging criterion operat-
ing at the level of whole theories that clearly separates the successful but
false from the successful but true. In the absence of such a criterion which
works for Dirac’s hole theory, which not only enjoyed considerable success
but was formulated in a mature science in mathematical language, let us
assume that the realist takes hole theory to be a mature scientiªc theory.
Por lo tanto, its success counts for its truth, by application of the NMA.
Divide and Conquer?
Having failed to exclude hole theory from the list of theories to which she
would have been committed, the realist retreats to defend instead the
claim that, despite its replacement, the empirical and explanatory success
of hole theory would not have entailed an ontological commitment to any
problematic theoretical entities. The thought behind this strategy is the
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
460
Dirac’s Prediction of the Positron
following: the PMI relies on the failure of reference to theoretical entities
to be preserved through theory change, but theory change tends to be pro-
gressive, in that it results in a theory which not only retains and expands
upon the empirical successes of its predecessor, but also explains its suc-
impuesto. This thesis is often called preservative realism. It involves an identi-
ªcation of something that is a matter of historical contingency, a saber
facts about what is or is not retained in successive theories, with some-
thing that is the basis of the realist argument—the parts of theories that
“get things right.”
Whereas all parties (including the anti-realist) agree that there is prog-
ress at an empirical level, in order to support a realist conclusion it must
be argued that there is an accumulation of a suitable kind at the theoreti-
cal level. So the tendency of successive theories over time to preserve and
expand upon the empirical applications of their predecessors is consistent
with this thesis, but alone it is not sufªcient. Preservative realism requires
something stronger: it requires the retention through theory change of
theoretical content which sufªces to explain the success of the replaced the-
ory in light of its replacement. It should be clear, por lo tanto, that this claim
is very much hostage to the particularities of episodes of theory change.
The challenge for the preservative realist lies in providing a non-
question begging criterion that serves to delimit the parts of the theory
that were responsible for their success from those which were not, y entonces
can be safely discarded by the successor theory without doing damage to
the NMA. Here is an example of a criterion which will not do: the parts of
a theory that were responsible for its success are just those which are pre-
served through theory change. Clearly this begs the question since there is
no reason why what is preserved would be what was responsible for pre-
vious successes unless one presupposes preservative realism.19
Por supuesto, the preservative realist thinks that there is cumulative prog-
ress at the theoretical level, and so aims to provide just such a criterion. I
will distinguish between two brands, restrictive realism which retains a
mostly traditional account of the reference of theoretical terms (Psillos,
1999), and structural realism, which involves a novel semantics (yet to be
fully speciªed) (p.ej., Worrall 1989, 2007; French and Ladyman 2003;
Ladyman and Ross 2007). They each make signiªcant claims about the
nature of the historical record.
19. Note that the techniques of renormalization critical to dealing with these diver-
gences only received theoretical justiªcation with the later Wilsonian program, which pro-
vided a means to display the insensitivity of the dynamics of the theories (at energies rele-
vant for experimental particle physics) to contributions from smaller length scales.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
461
Restrictive Realism Evidential support accrues differentially to differ-
ent parts of the theory. Taking into account the differing empirical sup-
port of various components of a theory at the time it was replaced and the
attitudes of contemporary scientists, we can separate those parts which
were well-supported by the evidence and those which were not. se vuelve
out that only parts with little or no empirical support were replaced.
Structural Realism The success of a theory is explained by its ability to
capture the structure of the physical world. These structural (but physical)
relations are described by mathematically expressed theories in terms of
abstract structures and relations. Whereas there is little or no preservation
of ontology (in terms of objects and their properties) structure is preserved
through theory change.20 The question the remainder of this paper will
address is this: assuming hole theory to be a proper object of scientiªc re-
alism, does its eventual replacement offer conclusive evidence for or
against either of these expressions of preservative realism?
Against Restrictive Realism
The restrictive realist argues that we should only be committed to the
parts of the theory that were empirically supported at the time. In order to
avoid the challenge posed above she must argue that the theoretical con-
tent that was retained was responsible for the success of the theory, entonces
wouldn’t have committed her to the existence of the negative energy sea.
The problem in this case is making the cut in such a way that includes
more than mere empirical predictions, but avoids the negative energy sea.
Since she uses standard referential semantics, I claim the restrictive realist
is faced with a dilemma concerning the successful use of hole theory by
Dirac and other physicists in the 1930’s:
Either the empirical support for hole theory is conªned merely to quan-
titative predictions, in which case there is nothing to offer as an explana-
tion of the success of hole theory which differs from what an instrumental-
ist might say, or the successful use of the theory entails ontological
commitment to vacuum electrons.
In support of the second horn, note that the existence of the anti-
electron and the possibility of pair creation involve completely novel phe-
20. Structural realism may be further classiªed according to the stance taken on the on-
tological status of objects: Worrall’s epistemic structural realism maintains that all we can
know about objects are their structural relations, while French and Ladyman’s ontic struc-
tural realism maintains that there are no objects but only structural relations (or at least
that objects are not metaphysically primitive). This difference will be largely irrelevant for
what follows since either involves a commitment to the historical thesis above.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
462
Dirac’s Prediction of the Positron
nomena, which are only implied by the Dirac equation if the existence of
negative energy electrons is taken seriously. This is worth emphasizing.
The presence of negative energy solutions was not enough to predict anti-
asunto: each of the negative energy states had to be occupied by an elec-
tron for ‘anti-electrons’ (holes) to have physically reasonable properties,
and moreover properties which in detail turned out to be instantiated by
the positron. In the conceptual framework of hole theory, there could be
no antimatter without the Dirac sea. What is more, since the stability of
matter required that all the negative energy states be ªlled (pointed out
by Oppenheimer in 1930), the empirical adequacy of the Dirac equation
relied on the hole theory hypothesis.
Hence the defense offered by Psillos (1999, pag. 113) to explain away the
replacement of caloric will not work here. Although it is feasible that the
hypothesis that heat is a material substance failed to feature essentially in
the derivation of any thermodynamic law, the assumption that all the neg-
ative energy states of hole theory were ªlled by electrons was essential to
predict the existence of positrons, and to make physical sense of the Dirac
equation. In the case of the disappearing ether, the empirical support ac-
crued by electrodynamics was based on the uniªcation of theories of well-
known electric and magnetic phenomena, and led to the discovery of new
phenomena such as electromagnetic radiation. Compare also Psillos’ de-
scription of Maxwell’s methodology: “The new theory of electromagne-
tism was to be built up slowly, in response to the evidence available and
background knowledge of the physical world” (1999, pag. 136). En cambio,
Dirac’s methodology was driven by concerns of consistency with back-
ground theory, accompanied by occasional logical leaps made in response
to conceptual difªculties and new theoretical results. Since Dirac pro-
ceeded from the initial success of the Dirac equation to his prediction of
antimatter with little empirical input, the restrictive realist can’t use the
criterion of differing empirical support to partition off successful parts of
the theory.
Sin embargo, ultimately Psillos argues that the mechanical ether featured
essentially only in heuristic models which were regarded as such by the
scientists who made use of them. He claims that although Maxwellian
ªeld theory appeared to replace the mechanical ether with a new kind of
entity which allowed the propagation of electromagnetic phenomena
through free space (the ªeld), the role the ether had played as a mechanical
bearer of electromagnetic properties was merely heuristic. Could a similar
move account for the success of hole theory? This is certainly the most
promising avenue since as I already mentioned one could certainly argue
that hole theoretic models were regarded in the same skeptical light as
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
463
mechanical ether models by certain scientists. Sin embargo, the difference
here is that while mechanical ether models were (arguably) either demon-
strations of known phenomena or played a merely heuristic role in theory
construction, the hole theoretical account of pair production, decir, played
an ineliminable role in providing quantitative predictions and qualitative
understanding of genuinely novel phenomena.
This brings into play the ªrst horn of the dilemma: if hole theory was
not to be interpreted realistically, how does one explain its success in real-
ist terms? The difªculty for the realist here is again that the empirical suc-
cess enjoyed by hole theory involved novel predictive success. Por supuesto,
she may decide that she could do without this episode of novel predictive
success, but that move would be ill advised since then she would have bro-
ken the association of realism with genuine novel predictive success, sup-
posedly the most compelling evidence in its favor (Musgrave 1988). Hacer
so would be to throw out the baby with the bathwater.
Además, it was not just the ontology of hole theory that was dis-
carded: the explanations offered by hole theory became invalid in light of
its replacement. Por ejemplo, the explanation of pair production in terms
of transitions of electrons from negative to positive energy states was com-
pletely undermined. As explanatory success plays a key role for the scien-
tiªc realist in the conªrmation of a theory, the disappearance of an entire
explanatory framework should be just as worrying as the accompanying
ontological discontinuity. A last gasp attempt to retain something of the
traditional realist account of reference would be to claim that by “the
Dirac sea” scientists had meant “the vacuum state” all along, in analogy to
Hardin and Rosenberg’s claim that by “luminiferous ether” scientists had
meant “electromagnetic ªeld” (defended in Psillos 1999, cap. 12). Cómo-
alguna vez, it is unclear what set of causal properties would ground such a conti-
nuity of reference here.
En suma, having been ostensibly committed to hole theory in, decir, 1934,
there appears to be little that the restrictive realist could have hung on to
through the vicissitudes of theory change which would sufªce to explain
her initial commitment to hole theory while doing justice to her realist
credentials. Por otro lado, the structural realist has a way out of this
dilemma since she rejects the standard story of ontological commitment
entailed by the successful use of a theory. According to Worrall, episodes
of theory change exempliªed by Maxwell’s electrodynamics can be charac-
terized as “cumulative growth at a structural level combined with radical
replacement of the previous ontological ideas” (1989, pag. 160). The correct
level of theoretical commitment, says the structural realist, is at the level
of structure.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
464
Dirac’s Prediction of the Positron
4. The Case for Structural Preservation: Symmetries
In the progression towards Dirac’s prediction of antimatter, Weyl’s argu-
ment was crucial in convincing him of the inherent symmetry between
matter and antimatter. While it is tempting to attribute to Weyl (1931) a
prescient understanding of the second-quantized theories of electrons that
were to follow, the account he gives of his theory is only a rudimentary
sketch. Hence there is a puzzle here about Dirac’s unquestioning accep-
tance of Weyl’s argument. En primer lugar, Weyl had provided no proof that Dirac’s
theory was equivalent to his treatment, and the account he gave of this al-
ternative “theory” scarcely warrants the name. En segundo lugar, Dirac’s misgiv-
ings about the second-quantization of matter were well known, and soon
led him to propose his alternative ‘multi-time’ formalism. So why was
Dirac persuaded?
The answer lies in the generality of Weyl’s argument, which followed
from the symmetry properties of the relativistic action. The elegance and
power of Weyl’s group theoretic approach must have been quite clear to
Dirac, and it would have been immediately apparent that this afforded an
invaluable geometrical understanding of the Dirac equation in terms of
relativistic covariants: spinors. Since the CPT invariance of the action fol-
lowed directly from its construction from certain kinds of Lorentz co-
variant quantities (scalars, tensors, and spinors), it followed that any the-
ory constructed within these constraints would have this symmetry.
Por eso, irrespective of the precise details, any theory representing electro-
magnetism, asunto, and their interaction must inherit the symmetrical
description of matter and antimatter. Dirac’s conviction that this was a
general property of such theories is evinced by his prediction that protons
would have to have anti-particles too, despite a complete lack of any plau-
sible theory of protons at the time.
Thus rather than following from the detailed description of matter ac-
cording to a precisely expressed theory, Dirac’s prediction of antimatter re-
lied upon the formal characterization of symmetry properties that such a
theory must possess. This is just the sort of continuity that the structural
realist claims explains the success of the replaced theories in terms of their
replacements. De hecho, the foundational role of group theory in modern
quantum ªeld theory can be traced directly back to Weyl’s work on uni-
tary representations, which led eventually to proofs that any Lorentz in-
variant local quantum ªeld theory must be CPT invariant, and Wigner’s
characterization of the allowed matter ªelds according to the irreducible
unitary representations of the Poincaré Group.
Clearly then, there is an important historical structural continuity here.
But just what level of structural continuity is sufªcient to explain the suc-
cess of a replaced theory in terms of its replacement? Are these symmetry
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
465
properties alone enough to provide an explanation of the success of hole
theory in realist terms? One could protest that symmetries are properly
understood as properties of the phenomena. Certainly this would be
closer to Weyl’s philosophy of transcendental idealism, where the objec-
tivity of our description of nature arises from a common phenomenology
(see Ryckman 2003).
The structural realist takes a more ontological view of symmetries as
(de alguna manera) structural properties of the world, but should admit that that
there is more to a theory “getting things right” than just capturing the
correct symmetries. Writing in another context, here is Steven French:
the lesson [of metaphysical underdetermination] para el
structuralist is that this essential structure must be expanded be-
yond the group-theoretical ‘object’ structure to include the dynami-
California. Following Bain . . . we can informally represent this essential
structure in the following terms: [espacio de estados, dinámica, symme-
intentos]. The structural realist will insist this is what we should be re-
alists about. (Francés 2011, pag. 220)
So it seems that we are justiªed in demanding the preservation of more
than just these general dynamical symmetries. Turning ªrst to the conti-
nuity of state space, note that in Fock space the state of the system is rep-
resented by a one-dimensional ray in an inªnite-dimensional separable
Hilbert space, and any two such Hilbert spaces are isomorphic. Similarmente,
there is continuity in terms of the representation of the evolution of the
state of the system by a family of unitary operators parameterized by t,
generated by the Hamiltonian operator.
But the suspicion arises that the display of shared structure is perhaps
too opportunistic: modern physical theories are expressed in rich mathe-
matical language and so it is not at all surprising to ªnd some common
estructuras. Is the fact that many successful theories happen to be expressed
within the setting of an inªnite-dimensional separable Hilbert space mi-
raculous on an instrumentalist account of science? Me parece que
this kind of fact receives a perfectly satisfactory explanation in terms of
the utility of generalized function spaces. The question to ask whether or
not the structural continuities displayed by the structural realist are
sufªcient to warrant a realist interpretation of the historical record.21
21. Bain and Norton (2001) argue that the most suitable display of continuity in the
history of the electron is at the level of the Lagrangian. While I agree that this provides a
useful heuristic for understanding of the way in which theories of the electron are related,
it is blind to the structural discontinuities articulated here (which I take to be problematic
for the structural realist).
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
466
Dirac’s Prediction of the Positron
5. The Case Against Structural Preservation: The Dirac Equation
At ªrst sight, the Dirac Equation seems to be a most plausible candidate
for structural preservation since a casual comparison of Dirac (1928) y
the modern equation of a spin-half quantum ªeld found in a standard
quantum ªeld theory textbook reveals a striking similarity of form. Com-
pare the ªrst quantized Dirac Equation of Section 2.1 with Peskin and
Schroeder (1995, pag. 52), where the Hamiltonian appears as,
(cid:2)
h
D
=
∫ 3 (cid:2)
d x
(cid:2) ( )(
−
i
X
†
a
⋅∇ +
) (cid:2) ( )
b
(cid:2)
X
metro
.
Sin embargo, in the replacement of the ªrst-quantized Dirac equation by its
second-quantized ªeld theoretic analog a signiªcant structural change has
occurred that is disguised by the formal similarity of the equations.
Namely, for Dirac the equation concerned the evolution of a four-compo-
nent wave function (living in Hilbert space) which described the probabil-
ity distribution associated with a deªnite number of electrons, whereas for
the modern physicist the Dirac equation applies to ªeld operators (cid:2) ( )(cid:2) X ,
which are expressed as sums of creation and annihilation operators.
dicho eso, there are important structural continuities here introduced
by the construction of Fock space from the single particle Hilbert space.
Apenas, Fock space is just an (inªnite) direct sum of n-particle Hilbert
spaces each formed by taking the (anti-symmetrized) n-fold tensor prod-
uct of the space of solutions to the single particle Dirac equation. Este
leads to a natural extension from operators deªned on the single particle
space to operators on the Fock space.22 However, note that while a com-
plete speciªcation of ªeld operators determines an operator-valued distri-
bution over space-time points, it does not serve to determine a unique
state of the system. The ªeld theoretic Dirac equation determines the evo-
lution of the ªeld operators, not the system state.
A more acute discontinuity arises from the failure of particle number to
be conserved (en general) in the second-quantized case. For the ªrst-
quantized Dirac equation charge conservation amounts to the statement
that the number of electrons is conserved by the dynamics. We can see this
requirement as leading to hole theory: if electrons cannot be created or de-
stroyed they must be waiting in the vacuum, waiting to become manifest.
Sin embargo, in the second-quantized ªeld theory conservation of particle
number is the exception rather that the rule since the dynamics is not
conªned to any one n-particle subspace (unless the ªeld is free). Como
Saunders (1991, páginas. 93–103) demonstrates, this fact leads to considerable
22. See Bratelli and Robinson (1997, pag. 8), Saunders (1991), and Baez, Segal and Zhou
(1992, páginas. 163–65) for accounts of this procedure.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
467
difªculties in setting up a correspondence between the ªrst- y segundo-
quantized dynamics.
I contend that these structural differences correspond to accompany-
ing shifts in metaphysical or ontological assumptions. A central assump-
tion of Dirac’s hole theory is the use of spatial wave functions (cid:7)(X), cual
can be thought of as complex valued ªelds encoding the probability for
ªnding the particle within a particular spatial region. Despite the quan-
tum description employed, which provides a deªnite probability ampli-
tude for position rather than a deªnite value of position, Dirac (1928)
made clear that an electron is a point particle in this picture. Since a parti-
cle with negative energy is described by exactly the same spatial proper-
corbatas, a negative energy solution is just as “particle-like” as a positive en-
ergy solution.
When Dirac (1930) ªlls these negative energy solutions with electrons,
each one of them corresponds to a particle with deªnite spatial properties.
In the ªrst-quantized expression of hole theory, charge conservation
amounts to the statement that the number of electrons is conserved (inso-
far as it makes sense for inªnity to be the conserved value). So while posi-
trons (corresponding to the absence of an electron) are in a sense created
from the vacuum, the number of electrons remains unchanged. Sin embargo,
in the second-quantized theory particle number is not conserved by the dy-
namics, only charge is.
dicho eso, there may be an easy way out for the structural realist here
since she may plausibly deny that hole theory ever received a coherent
ªrst-quantized expression, es decir., it could be argued that there is no hole the-
ory without second quantization, on the basis that the ªrst-quantized
Dirac Equation only has the structural resources to describe ªnitely many
electrons, whereas hole theory had to involve inªnitely many. In so doing
the structural realist neatly sidesteps any problems relating to the struc-
tural discontinuities I described above, but it remains for her to explain
away the apparently discontinuous change resulting from the later reinter-
pretation of antimatter in terms of presence rather than absence.23
6. The Structure of Vacuum
One reason to think the change in vacuum might involve another struc-
tural discontinuity is the change that occurred in the spectrum of the
Hamiltonian operator, which represents the energies that a system de-
23. A potential problem this move brings is the need to then account for the success of
the ªrst-quantized Dirac equation in accounting for situations involving interactions. Este
must be addressed on a case by case basis but I suspect that to do so is unproblematic. Para
ejemplo, note that the Bethe-Salpeter equation recovers in ªeld-theoretic form Dirac’s ini-
tial treatment of the hydrogen atom as a Coulomb potential (Bethe and Salpeter 1951).
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
468
Dirac’s Prediction of the Positron
scribed by the theory may take: in hole theory it is unbounded, whereas in
modern quantum ªeld theories it is bounded from below, reºecting the re-
quirement that energies must be positive. Writing out the Hamiltonian
in terms of creation and annihilation operators, tenemos,
(
a
)
pag ,
)
(k,
a
(k,
(k,
(k,
(cid:2)
h
pag
pag
pag
=
+
b
b
(
)
)
)
†
†
∫ 3k k)
d E
D
where a†(k,(cid:14)) creates an electron with momentum k and spin (cid:14), b†(k,(cid:14))
creates a positron with momentum k and spin (cid:14), while their respective
conjugates act to destroy them. But why does this expression result in posi-
tive energies? The answer lies in the freedom of choice provided by the Ca-
nonical Anti-commutation Relations (CAR’s): since b† and b appear sym-
metrically in the relation {b†(k,(cid:14)),b(k,(cid:14))} (cid:3) 1 it is essentially a matter of
convention as to whether b† is chosen to be the operator that lowers the en-
ergy or raises it.
Let’s see how this works. One way of deªning creation and annihilation
operators would be to have pairs of operators ((cid:2) , (cid:2) )
†a a+
+ which create and de-
stroy positive energy electrons, and a pair ((cid:2) , (cid:2) )
− which create and destroy
negative energy electrons. In order to get a workable theory, we deªne the
vacuum as the state where every possible negative energy electron state is
ªlled but every positive energy electron state is empty, eso es |1,1,1, …;
0,0,0, ….(cid:15). Then in order to create a positive energy positron, we use â(cid:4) a
destroy a negative energy state, creating a positive energy hole. This is the
hole theory interpretation.
†a a−
†
≡
≡
(cid:2) , (cid:2)
†
a b
−
To obtain the modern vacuum interpretation, we exploit the sym-
− = 1 to deªne opera-
metry of the anti-commutation relation {(cid:2) , (cid:2) }
tores (cid:2)
− so that (cid:2) †b
(cid:2)
raises the energy and creates a positive
a
b
energy positron, which is then destroyed by the corresponding (cid:2)b. Accord-
ingly, the vacuum is deªned as the state |0,0,0, …; 0,0,0, ….(cid:15) and so the
theory no longer allows negative energy particles.24 This is maneuver is
known within the standard account of quantum ªeld theory as a Bogo-
liubov transformation.
†a a−
So the structural realist who maintains that only second-quantized hole
theory was worthy of a realist attitude could argue that this equivalence
allows us to see the structural continuity of the completely ªlled negative
energy vacuum state with the “empty” vacuum that replaced it. Unfortu-
nately, Baez, Segal and Zhou (1992, 166) demonstrate that the inter-
24. Note that in so doing we replace the (cid:2) (cid:2)†a a− −‘s appearing in the Hamiltonian operator
(cid:2) (cid:2)†b b+ + ‘s, conveniently forgetting about the inªnite constant that results from the CAR
1. Saunders (2002) discusses in depth the resulting reinterpretation
(cid:2) (cid:2)
†
a a
− −
+
=
por
(cid:2)
†
equality a a
− −
of vacuum energy.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
469
change of creation and annihilation operators described above is not unit-
arily implementable, which implies that there is a signiªcant structural
discontinuity corresponding to the replacement of the hole theoretic vac-
uum state since they cannot be accommodated within a single separable
Hilbert space.
Por otro lado, this may be no reason for the structural realist to
despair, since it turns out that even the Klein-Gordon vacuum state ad-
mits continuously many unitarily inequivalent Hilbert space representa-
ciones. This arises since, although in quantum mechanics (involving ªnite-
ly many canonical variables) the Stone-von Neumann theorem guarantees
the unitary equivalence of irreducible representations of the CCR’s, el
CCR’s of quantum ªeld theory involve inªnitely many variables, so allow-
ing for irreducible representations that are unitarily inequivalent. Este
hecho, por lo tanto, could be taken to indicate that unitary equivalence is a
poor criterion for physical equivalence in the setting of quantum ªeld
theory anyway.25 If the structural realist chose instead to invest only the
algebraic structure of the CAR’s with physical signiªcance then she
could point to the fact that there is a unique CAR C*-algebra (hasta
*-isomorphism), of which there may be many unitarily inequivalent
Hilbert space representations.26
Sin embargo, it will not do to invest only the algebraic structure with phys-
ical signiªcance since in certain contexts the difference between unitarily
inequivalent representations of an algebra of observables does seem to have
physical signiªcance, for example in explaining spontaneous symmetry
breaking in quantum statistical mechanics (Ruetsche, 2003). Francés
(próximo) suggests that, although each case requires consideration on
its own merits, the algebraic structure can be understood by the structural
realist as encoding physical possibilities at a suitably abstract level, mo-
dalities which may or may not be realized in our world.
On this understanding, although the hole theoretic vacuum and the
“empty” vacuum disagree about the structure of the actual world, they can
be seen as incompatible realizations of the way the world could have been
according to the abstract algebraic description of the theory. Sin embargo,
given the centrality of the spectral condition in formulations of quantum
ªeld theory today (which amounts to the assumption that energy must be
25. See Reutsche (2011) for a comprehensive (and comprehensible) introduction to
these issues.
26. See Theorem 5.2.5 of Bratelli and Robinson (15, 1997), which demonstrates that
any two C*-algebras generated by bounded operators obeying the CAR’s (on a separable
Hilbert space) are related by a unique *-isomorphism. Además, in this setting a Bogo-
luibov transformation is represented by a unique *-automorphism on the algebra of ob-
servables.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
470
Dirac’s Prediction of the Positron
positivo), there is also a clear sense in which hole theory is not a possible
world of contemporary quantum ªeld theory.
The point I wish to make is this: theory replacement involves structural
discontinuity as well as structural preservation, and since these disconti-
nuities may reºect the problematic ontological or metaphysical shifts that
the structural realist had hoped to avoid, she had better account for them
también. So rather than pointing to structural preservation to explain the suc-
cess of discarded theories in terms of their replacements, I would ask the
structural realist for an account of the historical record that addresses in-
stead structural discontinuities that arise. In taking account of cases such as
the replacement of hole theory, the danger is that the common thread of
shared structure becomes so thin as to fail to support an expressly realist
interpretation of the success of the replaced theory.
7. Conclusión
The purpose of this paper was to suggest a particular episode in the his-
tory of modern physics as being particularly pertinent for the contempo-
rary scientiªc realism debate. The history I have tried to uncover reveals a
surprising interpenetration of theoretical methods and an undeniable
logic to the chain of reasoning that led to Dirac’s prediction of antimatter.
The disappearance from the succeeding theories of the central posit of his
hole theory interpretation—the Dirac sea—is therefore all the more inter-
esting. It is hoped that the present discussion has served to make accessi-
ble the details of this episode to philosophers of science, while also demon-
strating the relevance of the details of these events for the preservative
realist, who has already sought to sophisticate her account in response to
challenges posed by the history of physics.
The main conclusion of this case study is a negative one: the position I
termed restrictive realism, exempliªed by Psillos (1999), either fails to ac-
commodate the disappearance of the Dirac sea, or fails to account for the
empirical and predictive successes of hole theory. Por lo tanto, the argument
of Laudan (1981) against the necessary connection of the reference of cen-
tral theoretical terms with empirical success and (en este caso) novel pre-
dictive success goes through despite the potential accommodation of other
cases of theory change by the restrictive realist.
The realist might be inclined to say, “Well, so much the worse for novel
predictive success!” But, aside from the inherent problem of reducing the
force of one of realisms key motivations, I have argued that hole theory
also enjoyed considerable empirical and explanatory success. Perhaps there
is some other criterion that could be provided for the acceptance of a the-
ory which would exclude this case, or perhaps we should adopt a more
cautious, yet hopeful, picture where it is only the ultimate, “fundamental”
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
471
theory which is deserving of a realist attitude, and our commitment to
present theories is to be cashed out in relation to this future theory. Pero
these would be quite different positions to the one considered here.
It seems that the structural realist fares considerable better in accom-
modating the peculiarities of this case of theory change, which indicates
that the accumulation of theoretical content is best understood in terms of
continuity between the mathematical frameworks in which the theories
are expressed rather than the commitments entailed by their current de-
gree of empirical support. En particular, the perspective on the Dirac equa-
tion offered by Weyl’s group theoretic understanding of Lorentz transfor-
mations proved not only to be vital to Dirac’s prediction of antimatter, pero
also to the future development of the Standard Model. It would be hard to
deny that this deserves recognition as a compelling instance of structural
preservación.
Sin embargo, despite this striking continuity of dynamical symmetries, el
structural realist faces problems accounting for the shift from the ªrst-
quantized Dirac equation to second-quantized hole theory, and thereby to
the modern notion of an “empty” vacuum. I have suggested that she
might avoid concerns relating to the ªrst of these shifts by arguing that
only the second-quantized theory was deserving of a realist attitude. Cómo-
alguna vez, there remains the problem of accounting for the disappearance of the
Dirac sea, since this difference is ontology is reºected in a structural dis-
tinction that can be understood as reºecting the asymmetry between mat-
ter and antimatter displayed by the hole theoretic vacuum state.
Perhaps this is the lesson to be drawn for structural realism: theory
change also involves discontinuity at the structural level. Thus even re-
stricting her theoretical commitments to structural components does not
sufªce to insulate the structural realist from problems of theoretical
cambiar. What makes the case considered here particularly interesting is
that it demonstrates how shifts in the metaphysical commitments of a
theory may also be displayed in terms of changes in theoretical structure.
It remains to be argued that a structuralist understanding of theory
change sufªces to support a compellingly realist interpretation of scien-
tiªc progress.27
27. French and Ladyman (2011, pag. 32) have recently claimed that only “a case where
the structure of a theory that had enjoyed novel predictive success was completely aban-
doned” would provide a legitimate challenge to structural realism. Sin embargo, in so doing
they forget the positive role that the historical record is supposed to play in establishing
the plausibility of realism in the ªrst place via the NMA. En otras palabras, structural real-
ism is the best explanation of the success of science only to the extent that its competitors
are not.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
472
Dirac’s Prediction of the Positron
Referencias
Bain, Jonathan and John Norton. 2001. “What Should Philosophers of
Science Learn from the History of the Electron?” Pp. 451–65 in The
Birth of Microphysics. Edited by J. z. Buchwald and A. Warwick. Leva-
puente, Masa.: CON prensa.
Baez, John C., Irving E. Segal, and Zhengfang Zhou. 1992. Introduction to
Algebraic and Constructive Quantum Field Theory. Princeton, NUEVA JERSEY.: Príncipe-
ton University Press.
Panadero, David J. and Hans Halvorson. 2010. “Antimatter.” The British
Journal for the Philosophy of Science 61:93–121.
Bethe, Hans A. and Edwin E. Salpeter. 1951. “A Relativistic Equation for
Bound-State Problems.” Physical Review 84:1232–42.
Brattelli, Ola and Derek W. robinson. 1997. Operator Algebras and Quan-
tum Statistical Mechanics. volumen. 2. Nueva York: Editorial Springer.
Darrigol, Oliver. 1986. “The Origin of Quantized Matter Waves.” Histori-
cal Studies in the Physical and Biological Sciences 16:197–253.
Darwin, Charles G. 1928. “The Wave Equations of the Electron.” Proceed-
ings of the Royal Society of London A 118:654–680.
Dirac, Paul A. METRO. 1926. “Relativity Quantum Mechanics with an Appli-
cation to Compton Scattering.” Proceedings of the Royal Society of London
A 111:405–23.
Dirac, Paul A. METRO. 1927a. “The Compton Effect in Wave Mechanics.”
Mathematical Proceedings of the Cambridge Philosophical Society 23:500–07.
Dirac, Paul A. METRO. 1927b. “The Physical Interpretation of the Quantum
Dynamics.” Proceedings of the Royal Society of London A 113:621–41.
Dirac, Paul A. METRO. 1927C. “The Quantum Theory of the Emission and Ab-
sorption of Radiation.” Proceedings of the Royal Society of London A
114:243–65.
Dirac, Paul A. METRO. 1928. “The Quantum Theory of the Electron.” Proceed-
ings of the Royal Society of London A 117:610–24.
Dirac, Paul A. METRO. 1930. “A Theory of Protons and Electrons.” Proceedings
of the Royal Society of London A 126:360–65.
Dirac, Paul A. METRO. 1931. “Quantised Singularities in the Electromagnetic
Field.” Proceedings of the Royal Society of London A 133:60–72.
Dirac, Paul A. METRO. 1932. “Relativistic Quantum Mechanics.” Proceedings of
the Royal Society of London A 136:453–64.
Dirac, Paul A. METRO. 1934. “Discussion of the Inªnite Distribution of Elec-
trons in the Theory of the Positron.” Mathematical Proceedings of the
Cambridge Philosophical Society 30:150–63.
Dirac, Paul A. METRO. 1977. “Recollections of an Exciting Era.” Pp. 109–46
in History of Twentieth Century Physics. Edited by C. Weiner. Nueva York:
Prensa académica.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
473
Dirac, Paul A. METRO., Fock, Vladimir and Boris Podolsky. 1932 “On Quan-
tum Electrodynamics.” Physikalische Zeitschrift der Sowjetunion 2:468–
79.
Fock, Vladimir. 1932. “Konªgurationsraum and zweite Quantelung.”
Zeitschrift Physik 75:622–47.
Fock, Vladimir. 1933. “Zur Theorie der Positronen.” Akademiia Nauk.
Documentos: 267–71.
Francés, Steven. 2011. “Metaphysical Underdetermination: Why Worry?"
Synthese 180:205–21.
Francés, Steven. (próximo) “Unitary Inequivalence as a Problem for
Structural Realism.” History and Philosophy of Modern Physics
Francés, Steven and James Ladyman. 2003. “Remodelling Structural Real-
ismo: Quantum Physics and the Metaphysics of Structure.” Synthese
136:31–56.
Francés, Steven and James Ladyman. 2011. “In Defense of Ontic Structural
Realism.” Pp. 25–42 in Scientiªc Structuralism. Edited by Alisa Boku-
lich and Peter Bokulich. Nueva York: Saltador.
Furry, Wendell H. y j. Robert Oppenheimer. 1934. “On the Theory of
the Electron and Positive.” Physical Review 45:245–62.
gordon, walter. 1926. “Der Comptoneffekt nach der Schrodingerschen
Theorie.” Zeitschrift Physik 40:117–32.
Hanson, Norwood R. 1963. The Concept of the Positron: A Philosophical
Análisis. Cambridge: Prensa de la Universidad de Cambridge.
Klein, Oskar. 1929. “Die Reºexion von Elektronen an einem Potential-
sprung nach der relativistischen Dynamik von Dirac.” Zeitschrift Physik
53:157–65.
Kragh, Helge. 1990. Dirac: A Scientiªc Biography. Cambridge: Cambridge
Prensa universitaria.
Ladyman, James and Don Ross. 2007. Every Thing Must Go: Metaphysics
Naturalized. Oxford: Clarendon Press.
Laudan, Larry. 1981. “A Confutation of Convergent Realism.” Philosophy
de Ciencia 48:19–49.
Leplin, Jarrett. 1997. A Novel Defense of Scientiªc Realism. Nueva York: Ox-
prensa de la Universidad de Ford.
Mehra, Jagdish and Helmut Rechenberg. 2001. The Historical Development
of Quantum Theory. volumen. 6. Nueva York: Saltador.
Moyer, Donald F. 1981a. “Evaluations of Dirac’s electron, 1928–1932.”
American Journal of Physics 49:1055–62.
Moyer, Donald F. 1981b. “Vindications of Dirac’s electron, 1932–1934.”
American Journal of Physics 49:1120–25.
Molinero, Arthur I. 1994. Early Quantum Electrodynamics: A Source Book. Leva-
puente: Prensa de la Universidad de Cambridge.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
474
Dirac’s Prediction of the Positron
Musgrave, alan. 1988. “The Ultimate Argument for Scientiªc Realism.”
Pp. 229–52 in Relativism and Realism in Sciences. Edited by R. Nola.
Dordrecht: Kluwer Academic Press.
Oppenheimer, j. Roberto. 1930. “On the Theory of Electrons and Protons.”
Physical Review 5:562–63.
Pais, Abrahán. 1986. Inward Bound: Of Matter and Forces In The Physical
Mundo. Oxford: prensa de la Universidad de Oxford.
Pashby, tomás. (unpublished) “Projective Geometry and the Origins of
the Dirac Equation.”
Pauli, Wolfgang and Victor Weisskopf. (1934) 1994. “Quantization of the
Scalar Relativistic Wave Equation.” Pp. 188–205 in Early Quantum
Electrodynamics: A Source Book. Edited by Arthur I. Molinero. Translated by
Walter Grant. Cambridge: Prensa de la Universidad de Cambridge.
Peskin, Michael E. and Daniel V. Schroeder. 1995. An Introduction to Quan-
tum Field Theory. Reading, Masa.: Addison-Wesley.
Psillos, Stathis. 1999. Scientiªc Realism: How Science Tracks Truth. Londres:
Routledge.
Putnam, Hilary. 1975. Philosophical Papers Vol. 2: Mente, Language and Re-
ality. Cambridge: Prensa de la Universidad de Cambridge.
Roque, Xavier. 1997. “The Manufacture of the Positron.” Studies in History
and Philosophy of Science B 28:73–129.
Ruetsche, laura. 2003.
“A Matter of Degree: Putting Unitary
Inequivalence to Work.” Philosophy of Science 70:1329–42.
Ruetsche, laura. 2011. Interpreting Quantum Theories: The Art of the Possible.
Oxford: prensa de la Universidad de Oxford.
Ryckman, Thomas A. 2003. “The Philosophical Roots of the Gauge Prin-
ciple: Weyl and Transcendental Phenomenological Idealism.” Pp. 61–
88 in Symmetries in Physics: Philosophical Reºections. Edited by Katherine
Brading and Elena Castellani Oxford: prensa de la Universidad de Oxford.
Saunders, Simón. 1991. “The Negative Energy Sea.” Pp. 65–110 in The
Philosophy of Vacuum. Edited by Simon Saunders and Harvey Brown.
Oxford: prensa de la Universidad de Oxford.
Saunders, Simón. 2002. “Is the Zero-Point Energy Real?” In Ontological
Aspects of Quantum Field Theory. Edited by M. Kuhlmann, h. Lyre, y
A. Wayne. Singapur: World Scientiªc.
Schweber, Silvan S. 1994. QED and the Men who Made It: Dyson, Feynman,
Schwinger, and Tomonaga. Princeton: Prensa de la Universidad de Princeton.
Wallace, David. 2009. “QFT, Antimatter, and Symmetry.” Studies in His-
tory and Philosophy of Science B 40:209–22.
Weisskopf, Victor.
(1936) 1994. “The Self-Energy of the Electron.”
Pp. 157–68 in Early Quantum Electrodynamics: A Source Book. Edited by
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
475
Arthur I. Molinero. Translated by Walter Grant. Cambridge: Cambridge
Prensa universitaria.
Weisskopf, Victor. 1939 “On the Self-Energy and the Electromagnetic
Field of the Electron,” Physical Review 56:72–85.
Weisskopf, Victor. 1949. “Recent Developments in the Theory of the
Electron,” Reviews of Modern Physics 21:305-15.
Weyl, Hermann. 1928. Gruppentheorie und Quantenmechanik. (First edition).
Leipzig: Hirzel.
Weyl, Hermann. 1931. Gruppentheorie und Quantenmechanik. (Second re-
vised edition). Leipzig: Hirzel.
Weyl, Hermann. 1932. The Theory of Groups and Quantum Mechanics. (Sec-
ond revised edition) Translated by H. PAG. Robertson. Mineola: Dover.
Worrall, John. 1989. “Structural Realism: The Best of Both Worlds?"
Dialectica 43:99–124.
Worrall, John. 2007. “Miracles and Models: Why Reports of the Death of
Structural Realism May Be Exaggerated.” Royal Institute of Philosophy
Supplements 82:125–54.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
0
4
4
4
0
1
7
8
9
7
8
0
pag
oh
s
C
_
a
_
0
0
0
8
1
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3