INVESTIGACIÓN
Trade-offs among cost, integración, y
segregation in the human connectome
Junji Ma1, Xitian Chen1, Yue Gu1, Liangfang Li1, Cam-CAN2, Ying Lin1, and Zhengjia Dai1,3
1Department of Psychology, Sun Yat-sen University, Guangzhou, Porcelana
2Cambridge Centre for Ageing and Neuroscience (Cam-CAN), University of Cambridge and
MRC Cognition and Brain Sciences Unit, Cambridge, Reino Unido
3Guangdong Provincial Key Laboratory of Brain Function and Disease, Zhongshan School of Medicine,
Sun Yat-sen University, Guangzhou, Porcelana
Palabras clave: Cost-efficiency trade-off, Segregation, Modularity, Diffusion MRI, Human brain network
un acceso abierto
diario
ABSTRACTO
The human brain structural network is thought to be shaped by the optimal trade-off between
cost and efficiency. Sin embargo, most studies on this problem have focused on only the trade-off
between cost and global efficiency (es decir., integración) and have overlooked the efficiency
of segregated processing (es decir., segregation), which is essential for specialized information
Procesando. Direct evidence on how trade-offs among cost, integración, and segregation shape
the human brain network remains lacking. Aquí, adopting local efficiency and modularity
as segregation factors, we used a multiobjective evolutionary algorithm to investigate this
problema. We defined three trade-off models, which represented trade-offs between cost
and integration (Dual-factor model), and trade-offs among cost, integración, and segregation
(local efficiency or modularity; Tri-factor model), respectivamente. Among these, synthetic
networks with optimal trade-off among cost, integración, and modularity (Tri-factor model [q])
showed the best performance. They had a high recovery rate of structural connections and
optimal performance in most network features, especially in segregated processing capacity
and network robustness. Morphospace of this trade-off model could further capture the
variation of individual behavioral/demographic characteristics in a domain-specific manner.
En general, our results highlight the importance of modularity in the formation of the human
brain structural network and provide new insights into the original cost-efficiency trade-off
hypothesis.
RESUMEN DEL AUTOR
The human brain structural network is hypothesized to be organized under an optimal trade-
off between cost and efficiency. Sin embargo, the efficiency of segregated processing in this trade-
off is overlooked. Adopting multiobjective evolutionary algorithm, we revealed that synthetic
networks with optimal trade-off among cost, eficiencia global, and modularity (Tri-factor model
[q]) could capture empirical brain network structure very well. Synthetic networks of Tri-factor
modelo (q) had a high recovery rate of structural connections and optimal performance in
network features, especially in segregated processing capacity and network robustness. El
morphospace of this model could further capture the variation of individual behavioral/demographic
características. These results highlight the indispensable role of modularity in shaping the
human brain structural network and provide new insights into the original cost-efficiency
trade-off hypothesis.
Citación: Mamá, J., Chen, X., Gu, y., li, l.,
Cam-CAN, lin, y., & dai, z. (2023).
Trade-offs among cost, integración, y
segregation in the human connectome.
Neurociencia en red, 7(2), 604–631.
https://doi.org/10.1162/netn_a_00291
DOI:
https://doi.org/10.1162/netn_a_00291
Supporting Information:
https://doi.org/10.1162/netn_a_00291;
https://osf.io/ebtks/?view_only
=7f4a89f06c464da7b32253c7f3bd0f3d
Recibió: 12 Julio 2022
Aceptado: 2 Noviembre 2022
Conflicto de intereses: Los autores tienen
declaró que no hay intereses en competencia
existir.
Autor correspondiente:
Zhengjia Dai
daizhengj@mail.sysu.edu.cn
Editor de manejo:
Petra Vertes
Derechos de autor: © 2022
Instituto de Tecnología de Massachusetts
Publicado bajo Creative Commons
Atribución 4.0 Internacional
(CC POR 4.0) licencia
La prensa del MIT
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
2
6
0
4
2
1
2
0
2
8
9
norte
mi
norte
_
a
_
0
0
2
9
1
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Trade-off models underlying the human connectome
Human connectome:
Structural human brain network with
brain regions as nodes and white
matter connections as edges.
Cost-efficiency trade-off:
An optimal trade-off between wiring
cost and communication efficiency
in the human brain network.
Integration:
Global neural communication
among all regions of the brain
network.
Segregation:
Local and specialized neural
processing within clusters of
regiones del cerebro.
INTRODUCCIÓN
At the macroscale, the human connectome, characterized as a complex network with brain
regions as nodes and white matter axonal pathways as connections, is the anatomical substrate
of information communication and ultimately supports brain functions and cognition
(bullmore & despreciar, 2009, 2012; despreciar, Tononi, & kötter, 2005). Identifying the principles
that guide the wiring pattern of the human connectome promotes our understanding of human
brain organization and how the organization evolves to support human brain functions.
Recientemente, incorporating neuroimaging data, researchers found diverse factors that are related
to the wiring of the human connectome, such as geometrical factors (p.ej., Euclidean distance;
Klyachko & stevens, 2003; Markov et al., 2013; Roberts et al., 2016) and topological factors
(p.ej., matching index; Betzel et al., 2016). Although diverse network constraints were
propuesto, it remains an open question what fundamental and general principle underlies
the various constraints on brain network configuration (stiso & bassett, 2018).
A review article proposed the hypothesis that the general principle of the human connec-
tome wiring is the optimal trade-off between minimizing wiring cost and maximizing commu-
nication efficiency (bullmore & despreciar, 2012). Wiring cost refers to the material cost that is
needed in construction and maintenance of anatomical brain connections (Ahn, jeong, &
kim, 2006; Mitchison, 1991), which is directly related to the length and density of connections
in the brain network. With limited material resources, cost minimization places a strong con-
straint on brain network structure and leads to the emergence of several network features (p.ej.,
distance-dependent connection pattern; Klyachko & stevens, 2003; Markov et al., 2013;
Samu, Seth, & Nowotny, 2014). Sin embargo, only cost minimization is insufficient to explain
the whole wiring pattern of the human connectome (Kaiser & Hilgetag, 2006). The existence
of long-distance connections, hubs, and some other topological characteristics (p.ej., pequeño-
worldness; bassett & bullmore, 2006, 2017; Liao, Vasilakos, & Él, 2017; van den heuvel &
despreciar, 2013), which violates the cost minimization principle, has suggested the additional
need to facilitate communication in the human brain network. Por lo tanto, the human connec-
tome was supposed to be constructed under the pressure of a cost-efficiency trade-off
(bullmore & despreciar, 2012). The influence of this trade-off was recently confirmed in the net-
work of human (Ma et al., 2021) and C. elegans/macaque brains (Y. Chen et al., 2013, 2017).
Notablemente, the above studies mainly focused on the trade-off between cost and global efficiency,
which is the overall efficiency of information transfer among all pairs of brain regions in the
network (Avena-Koenigsberger et al., 2014; Fornito et al., 2011). Sin embargo, effective commu-
nication of human brain requires not only efficient global information integration, but also the
capacity for segregated information processing (despreciar, 2013).
Segregation refers to specialized information processing that occurs within region clusters
(p.ej., modules or the neighbors of the node). The capacity of segregated information process-
ing not only enables flexible and rapid reconfiguration of the brain network in response to
different task demands, but also benefits network robustness (Peluca, 2017; despreciar & Betzel,
2016). In the human macroscopic connectome, segregation can be described in two different
maneras: the efficiency of local cluster and modularity (cohen & D'Esposito, 2016; despreciar, 2013).
The efficiency of local cluster (es decir., local efficiency and clustering coefficient) measures the
density of connections among neighboring brain regions, reflecting the efficiency of information
transfer within regional subnetworks (Achard & bullmore, 2007; latora & marchiori, 2001).
Modularity characterizes network structure with dense intra-module connections and sparse
inter-module connections (Meunier, Lambiotte, & bullmore, 2010; Meunier et al., 2009). Este
arrangement of the human connectome allows efficient and mutually independent segregated
processing within modules (Meunier et al., 2010). Además, the modular structure could give
Neurociencia en red
605
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
2
6
0
4
2
1
2
0
2
8
9
norte
mi
norte
_
a
_
0
0
2
9
1
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Trade-off models underlying the human connectome
Multiobjective evolutionary
algoritmo:
One type of search algorithm that
could simultaneously optimize
multiple objectives by imitating
natural evolutionary processes.
Non-dominated relationship:
Two solutions are non-dominated
over each other if neither of them can
have an advantage over the other
one on all the optimization
objectives of the given multiobjective
problema.
Non-dominated solution:
A solution is non-dominated if it is
feasible and cannot be improved on
any optimization objective without
worsening the other objectives.
Pareto front:
A front composed of non-dominated
solutions to a multiobjective problem
in the morphospace.
rise to richer distribution of information in the brain network and promote functional complex-
idad (Gallos, Makse, & Sigman, 2012; Kaiser, Hilgetag, & kötter, 2010). En suma, both segregation
measures capture unique segregated properties that could not be simply explained by the trade-
off between cost and global efficiency (Ma et al., 2021). Por lo tanto, the cost-efficiency trade-off
principle needs to be further extended by including segregation capacity. Sin embargo, so far,
direct evidence remains lacking for how segregation capacity participates in the cost-efficiency
trade-off and how the trade-off among these factors (es decir., costo, global integration, and segrega-
ción) shapes the human connectome.
To address this issue, primero, we modeled the wiring process driven by the trade-off among the
factors of cost, integración, and segregation as multiobjective optimization problems, con el
segregation factor expressed as local efficiency and modularity, respectivamente. For comparison,
we also modeled the wiring process driven solely by the trade-off between cost and integration
in the same way. Segundo, we implemented a multiobjective evolutionary algorithm (MOEA;
Zhou y cols., 2011) to solve the above problems. MOEA is one type of search algorithm for
multiobjective optimization problems that consider two or more conflicting objectives. Más
específicamente, MOEA imitates the natural evolutionary procedure of organisms to find a set of
mutually non-dominated (equally good from the perspective of multiple objectives) soluciones
that can approach the Pareto front (composed of solutions with optimal but different trade-offs
among objectives) of a multiobjective optimization problem (Tušar & Filipič, 2015; Zhou y cols.,
2011). Herein, MOEA was not for simulating the actual evolutionary processes of brain net-
obras, but served as a phenomenological model that can generate synthetic networks yielding
an optimal trade-off among constraints (p.ej., costo, integración, and segregation). This approach
has inherent advantages in solving multiobjective problems: (a) It has a good global searching
ability that allows efficient exploration in high-dimensional solution space. (b) It can generate
a set of solutions (es decir., synthetic networks in this study) that evenly approximate the entire
Pareto front of the problem, which facilitates exploration of equivalently optimal but diverse
trade-offs. Tercero, we compared the generated synthetic networks with empirical human brain
networks in topological characteristics. We then determined the best trade-off model that
could recover the most organization of empirical brain networks. Finalmente, considering the tight
relationship between brain network organization and human behavioral/demographic charac-
teristics (Cao et al., 2014; Heitger et al., 2012; Ingalhalikar et al., 2014; Parque & Friston, 2013),
we further examined whether the best trade-off model could also capture basic individual
behavioral/demographic characteristics (es decir., edad, género, and fluid intelligence) through their
variation of the brain network.
MATERIALES Y MÉTODOS
Participantes
en este estudio, to obtain empirical networks and corresponding demographic and behavioral
puntuaciones, we used two independent datasets. The first dataset included 93 healthy college stu-
abolladuras (edad media = 18.95 ± 1.08 years old; 29 machos) collected from the South China Normal
Universidad (SCNU dataset). All participants in this dataset did not have a history of neurological
or psychiatric disorders, sensorimotor or cognitive impairment, or other anatomical injuries of
the brain, and have provided informed consent before scanning. This study was approved by
the Institutional Review Board in the Department of Psychology of Sun Yat-sen University. El
second dataset was an openly available adult life span dataset collected from Cambridge
Centre for Ageing and Neuroscience (Cam-CAN dataset; Shafto et al., 2014; Taylor et al.,
2017). A sample of 589 Participantes (edad media = 54.01 ± 18.46 years old; 285 machos) eran
acquired from this dataset. Participants were all healthy adults with normal or corrected-to-
Neurociencia en red
606
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
2
6
0
4
2
1
2
0
2
8
9
norte
mi
norte
_
a
_
0
0
2
9
1
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Trade-off models underlying the human connectome
normal vision and hearing, scored 25 or higher on the Mini–Mental State Exam (MMSE), y
had no history of drug or alcohol abuse, or of neurological disorders. All participants underwent
a diverse set of neuropsychological tests, conducted cognitive tasks, and had MRI scans.
Informed consent was obtained from all participants and the study was approved by the
Cambridgeshire 2 Research Ethics Committee, Reino Unido. Notablemente, the SCNU dataset
was used in the main analyses for exploring the optimal trade-off models (for details see Defini-
tions of Trade-Off Models section). The Cam-CAN dataset was used for validating our main
findings as an independent sample and examining behavioral relevance of the trade-off model.
MRI Data Acquisition
For the SCNU dataset, all participants were scanned on a Siemens 3.0 Tesla MRI scanner
(Siemens, Erlangen, Alemania) at South China Normal University (Guangzhou, Porcelana). Head-
phones and foam pads were used to avoid interference of scanner noise and reduce head
motion of participants during the scan. Participants were required to keep their eyes closed,
stay awake without thinking about anything, and keep their heads fixed during the data acqui-
posición. Structural T1-weighted images were collected using magnetization prepared by rapid
gradient echo sequence: repetition time (TR) = 1,900 EM, tiempo de eco (EL) = 2.52 EM, flip angle =
9°, field of view (FOV) = 256 × 256 mm2, inversion time = 900 EM, matrix = 256 × 256, slices =
176, slice thickness = 1 mm, and voxel size = 1 × 1 × 1 mm3. The diffusion MRI (resonancia magnética nuclear) datos
were collected using a single-shot spin echo / echo planar sequence with the following param-
eters: TR = 10,000 EM, TE = 90 EM, matrix = 128 × 128, FOV = 256 × 256 mm2, flip angle = 90°,
and slice thickness = 2 mm without gap. The diffusion sensitizing gradients were applied along
64 noncollinear directions (b = 1,000 s/mm2), together with one acquisition without diffusion
weighting (b = 0 s/mm2). Resting-state functional MRI data were also acquired, but the data were
not used in this study.
For the Cam-CAN dataset, all participants were scanned on a 3T Siemens TIM Trio System
at the MRC Cognition Brain and Sciences Unit, Cambridge, Reino Unido. Structural
T1-weighted images were collected using magnetization prepared by rapid gradient echo
secuencia: repetition time (TR) = 2,250 EM, tiempo de eco (EL) = 2.99 EM, ángulo de giro = 9°, campo
of view (FOV) = 256 × 240 mm2, inversion time = 900 EM, slices = 192, slice thickness =
1 mm, and voxel size = 1 × 1 × 1 mm3. The dMRI images were acquired with a twice-
refocused spin echo sequence: TR = 9,100 EM, TE = 104 EM, matrix = 128 × 128, FOV =
192 × 192 mm2, slice = 66, and voxel size = 2 × 2 × 2 mm3.
Image Preprocessing and Anatomical Brain Network Construction
Preprocessing and network construction procedures were identically applied on imaging data
of two datasets. Específicamente, all the dMRI images were preprocessed using the standard pre-
processing procedure of the PANDA toolbox (Cui et al., 2013). The preprocessing procedure
included brain mask estimation, skull-stripping, eddy current, head motion correction, y
diffusion tensor metrics calculation (es decir., voxel-wise tensor matrix and fractional anisotropy
[FA]). Además, the T1-weighted images were aligned to the AC-PC line and then seg-
mented using SPM8 software to obtain the white matter ( W.M.) binary mask (with WM prob-
ability threshold > 0) in the T1 native space. Finalmente, the WM mask was transformed into the
native diffusion space of each participant for subsequent WM tractography with the inverse
transformation matrix, which was estimated in coregistration of the FA image to T1.
Then we defined nodes and edges of the human macroscopic connectome. For nodes, we used
the Automated Anatomical Labeling (AAL) atlas (Tzourio-Mazoyer et al., 2002) to define 90 nodos
Neurociencia en red
607
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
2
6
0
4
2
1
2
0
2
8
9
norte
mi
norte
_
a
_
0
0
2
9
1
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Trade-off models underlying the human connectome
covering the whole brain. Específicamente, an inverse warping transformation from the standard MNI
space to the native diffusion space can be obtained based on coregistering the individual FA image
to T1-weighted image and then nonlinearly registering to the ICBM152 template. The AAL was
then inversely warped back to individual native diffusion space by applying this inverse transfor-
mation to define the network nodes. For edges, we used deterministic tractography to construct the
network. All possible streamlines were reconstructed by seeding from the voxel within the WM
mask. A streamline was started from a seed, which was distributed at the center of each voxel with
an FA value greater than 0.2. The streamline was terminated when it reached a voxel with a turning
angle greater than 45° or an FA value less than 0.2, or out of the WM mask. The edge of each pair
of nodes was defined as one when existing at least one streamline with two endpoints located in
the corresponding node areas of the AAL atlas (Collin et al., 2014; Fukushima et al., 2018; van den
Colina & despreciar, 2011; Zalesky et al., 2016). Por lo tanto, we constructed a 90 × 90 binary struc-
tural network for each participant. We then constructed a group-level structural brain network by
retaining edges that existed in more than 50% of the participants’ structural brain networks
(Fukushima et al., 2018; Roberts et al., 2017; Zalesky et al., 2016). This group threshold is sug-
gested to have a good balance between controlling false positive and false negative rates of the
constructed connections (de Reus & van den heuvel, 2013).
Definitions of Trade-Off Models
To systematically examine how different trade-off models shape the human connectome, nosotros
needed to construct synthetic networks under specific trade-off models and then compare them
with empirical brain networks (Cifra 1). Three models were defined to simulate the wiring
process driven by optimizing the trade-offs among the above factors. En particular, since wiring
cost is related to both the number and the length of connections (Ahn et al., 2006; Mitchison,
1991), the cost factor here was formulated as the sum of Euclidian distances between centroids
of connected regions (Y. Chen et al., 2013, 2017; Ma et al., 2021), rather than measures that
simply consider connection numbers (p.ej., degree); the integration factor was formulated as the
eficiencia global (Eg) of the network; and the segregation factor was formulated either as the
local efficiency (Eloc) of network or as the modularity (q) of the network. The network-level
local efficiency was computed as the average of nodal local efficiency of all nodes. For detailed
mathematical definitions of the above measures, refer to the Supporting Information. Based on
the three factors, each trade-off model defined two optimization objectives to capture the com-
peting relationship between wiring cost and communication efficiency. The cost objective Fc
was defined directly based on the cost factor and was set the same in all the models, mientras que la
efficiency objective Fe was defined differently to express sole concern on network integration or
hybrid concern on network integration and segregation in different forms. To unify the optimi-
zation direction with the cost objective (es decir., minimization), the definitions of Fe were all formu-
lated in a way that smaller values indicated better efficiency. In detail, the definitions of Fe in the
three models are summarized below.
(cid:129) Dual-factor model: cost and integration
Fe ¼ 1 − Eg
(cid:129) Tri-factor model (Eloc): costo, integración, and segregation (local efficiency)
Fe ¼ wEloc 1 − Eg
d
Þ þ 1 − wEloc
d
d
Þ 1 − Eloc
Þ
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
2
6
0
4
2
1
2
0
2
8
9
norte
mi
norte
_
a
_
0
0
2
9
1
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
(cid:129) Tri-factor model (q): costo, integración, and segregation (modularity)
d
Fe ¼ wQ 1 − Eg
(cid:1)
Þ þ 1 − wQ
(cid:3)
1 − Qð
Þ
Neurociencia en red
608
Trade-off models underlying the human connectome
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
2
6
0
4
2
1
2
0
2
8
9
norte
mi
norte
_
a
_
0
0
2
9
1
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
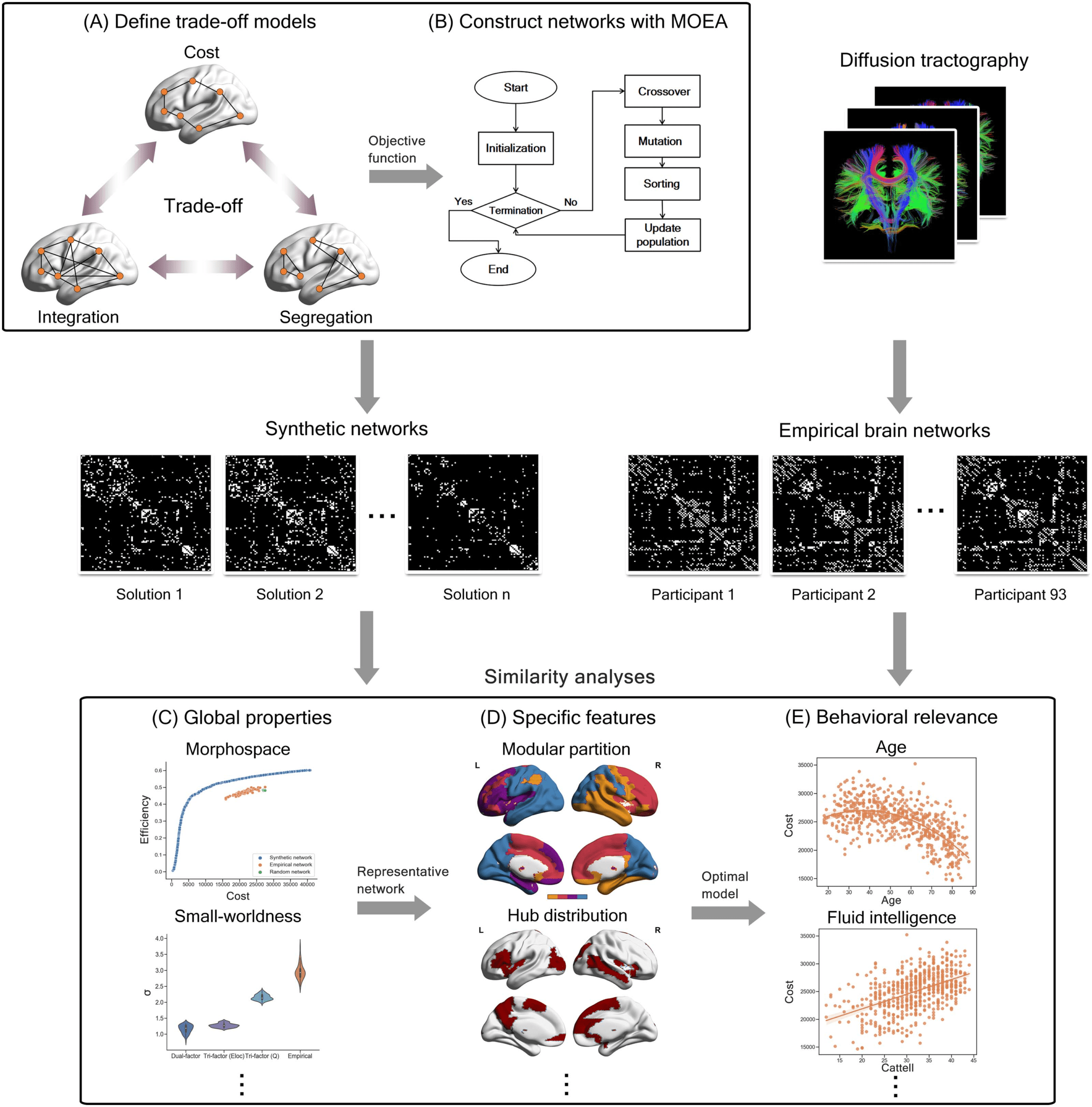
Cifra 1. Schematic diagram of study design. (A) Model the trade-off principles (p.ej., trade-off among cost, integración, and segregation) como
multiobjective problems. (B) Implement MOEA (multiobjective evolutionary algorithm) pipeline and construct synthetic networks under
corresponding optimal trade-offs. (C) Analyze the similarity between synthetic networks and empirical brain networks in the aspect of global
propiedades (p.ej., morphospace and small-worldness). (D) Analyze the similarity between synthetic networks and empirical brain networks in
the aspect of more specific features (p.ej., modular partition and hub distribution). (mi) Investigate the behavioral relevance of optimal trade-off
model obtained from previous steps.
Neurociencia en red
609
Trade-off models underlying the human connectome
Morphospace:
The objective space of a
multiobjective problem, with each
dimension defined as an objective of
the corresponding problem.
In the above definitions, wEloc and wQ were both weights in the range of (0, 1) for specifying
the relevant importance imposed on network segregation capacity when it was simultaneously
optimized with integration capacity. Parameter sensitivity investigations showed that the two
Tri-factor models performed the best in recovering the empirical brain connectome when
wEloc = 0.9 and wQ = 0.8 (Supporting Information Figure S1). These settings were thus
adopted in subsequent analyses. Notablemente, the Dual-factor model used in the current study
was highly consistent with the one proposed in our previous work (Ma et al., 2021), excepto
for the trivial difference in the mathematical formulation of Fe (the former and the current
formulations achieved a correlation of 0.983 [pag < 0.001] on the SCNU sample). The use of
current formulation was for consistent comparisons across the trade-off models.
Moreover, we further defined an efficiency index, computed as 1 − Fe, for each model. The
higher value of this index suggests better communication efficiency of the network. Taking this
index and the Fc objective as axes, we could construct a morphospace for each model, respec-
tively. Location of networks in the morphospace reflects their performance in objective func-
tions and their relative trade-off between objectives under the corresponding trade-off models,
which allows comprehensive comparisons between networks.
Construction of Synthetic Networks Using a Multiobjective Evolutionary Algorithm
Based on the above three models that represented different trade-offs underpinning the human
connectome organization, we tried to generate synthetic networks that achieved the optimal
trade-offs between the objectives of each model, respectively. Here, we applied the non-
dominated sorting genetic algorithm (NSGA-II; Deb et al., 2002; https://www.egr.msu.edu
/~kdeb/codes.shtml), a popular multiobjective evolutionary algorithm (MOEA), to construct
synthetic networks. Following the procedure in our previous study (Ma et al., 2021), the imple-
mentation of the NSGA-II algorithms (Deb et al., 2002) was described as follows:
Step 1: Population initialization. The algorithm started with initialization of a population of
synthetic networks, which were binary vectors representing upper triangle of 90 × 90 adjacent
matrices (i.e., candidate solutions to trade-off models). Individual (i.e., synthetic network) in
the population was initialized by randomly assigning a value (one or zero) to each entry,
which indicates whether each node pair was connected. The probability of assigning one to
entries is 0.1. According to the problem dimension (i.e., the number of decision variables to be
optimized), the population size was set to 200.
Step 2: Reproduction of the population. Imitating the reproduction in natural evolutionary
process, MOEAs design crossover operators to preserve high-quality genes (i.e., values of
decision variables) for subsequent generations. Specifically, the operator randomly chose a por-
tion of edge entries and swapped between synthetic networks to generate offspring networks.
Two hundred offspring networks, forming an offspring population, were generated at the cur-
rent step.
Step 3: Mutation of the population. Like mutation of chromosomes in nature, mutation in
MOEAs is a low-probability but indispensable step, which can introduce diversity into the
population and thereby enhance global search ability in the solution space. Here, the mutation
operator randomly flipped the edge entries (i.e., 1 to 0 or vice versa) in the network with a low
probability (probability = 0.1). The 200 mutated networks were then added to the offspring
population.
Step 4: Selection of the population. To select elites for the next generation, the selection
operator applied the fast non-dominated sorting approach (Deb et al., 2002) to rank the
Network Neuroscience
610
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
0
4
2
1
2
0
2
8
9
n
e
n
_
a
_
0
0
2
9
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Trade-off models underlying the human connectome
candidate networks according to their fitness (i.e., mutual dominance relationship of objec-
tive values) and local diversity (i.e., crowding distance between solutions in the objective
space). For the individuals in the union of the current population and its offspring popula-
tion, only the 200 that survived the selection process would enter the population of the next
generation.
Step 5: Termination check. The algorithm terminated when one of the following conditions
was satisfied: the population stopped evolving (i.e., < 5% of individuals were changed or the
difference of mean objective values < 0.1%) for 20 consecutive generations, or the number of
generations reach 2,000. Otherwise, the algorithm returned to Step 2 and started a new
generation based on the updated population of the networks derived from Step 4. Evaluation
of objective functions was performed right after new synthetic networks were generated at
each step.
Considering that MOEA is a probabilistic algorithm and its results can vary across different
runs, we ran the algorithm 30 independent times. The resulting solutions (i.e., synthetic net-
works) from all the runs were then sorted by the fast non-dominated sorting approach (Deb
et al., 2002) to select the set of solutions that approximated the Pareto front (Tušar & Filipič,
2015; Zhou et al., 2011) of the problem (i.e., the best trade-offs of each model) for subsequent
analyses. It should be noted that our MOEA approach is a theory-driven method. Instead of
generating a brain-like network, MOEA only generates networks that optimize trade-off among
specific objectives (e.g., cost-efficiency trade-off; Bullmore & Sporns, 2012). This optimization
process did not require guiding information from empirical brain networks. Hence, including
more constraints does not necessarily make the resulting synthetic networks more similar to
the empirical ones.
Recovery Rate of Synthetic Networks
Using the above NSGA-II algorithm, for each of the three models, a population of synthetic
networks that approximated the optimal trade-off between the cost and efficiency objectives
was generated. To explore the trade-off models underlying the human brain, we first compared
their capacity in recovering connections of the group-level empirical brain structural networks.
This capacity was evaluated by the recovery rate R, which measures the ratio of overlapping
entries between the adjacency matrices of synthetic and empirical networks (Y. Chen et al.,
2013, 2017; Costa, Kaiser, & Hilgetag, 2007; Ma et al., 2021). That is,
p
ffiffiffiffiffiffiffiffiffiffi
R0R1
;
R ¼
where R0 and R1 are the recovery rates regarding 0 and 1 entries in the adjacency matrices
(diagonal entries omitted), respectively. To examine how connections between regions with
different Euclidian distance were recovered under the trade-off models, we also calculated
the recovery rates within different distance groups (i.e., 0–20 mm, 20–40 mm, 40–60 mm,
60–80 mm, 80–100 mm, and 100–120 mm).
Besides the recovery rate of trade-off models, we also computed the recovery rate from
random networks to empirical networks as benchmarks for comparison. Specifically, we
constructed topological random networks (Maslov & Sneppen, 2002) that connections were
randomly rewired while preserving the numbers of nodes and edges, and the degree distribu-
tion of the empirical brain network. One hundred random networks of the random model
were generated and their recovery rates were computed, respectively.
Network Neuroscience
611
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
0
4
2
1
2
0
2
8
9
n
e
n
_
a
_
0
0
2
9
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Trade-off models underlying the human connectome
Topological Characteristics of the Synthetic Networks
Further, we would like to examine how well the synthetic networks of different models capture
the topological features of empirical brain networks. Here, we computed network-level
topological measures that were previously suggested to be important features of the human
connectome (Bullmore & Sporns, 2009; Rubinov & Sporns, 2010) and related to cost and effi-
ciency (i.e., integration and segregation; Liao et al., 2017; Sporns & Betzel, 2016; Samu et al.,
2014). The selected metrics include the small-world metrics (i.e., clustering coefficient [Cp],
characteristic path length [Lp], normalized clustering coefficient [γ], normalized characteristic
path length [λ], and small-worldness [(σ]), efficiency metrics (i.e., global efficiency [Eg] and
local efficiency [Eloc]), and modularity metrics (i.e., modularity [Q] and the number of mod-
ules [Mn]). These metrics describe the network integrated and segregated processing capacity
from different angles. Lower characteristic path length and normalized characteristic path
length and higher global efficiency of network all reflect higher global processing capacity.
Higher scores in clustering coefficient, normalized clustering coefficient, local efficiency,
and modularity are associated with better segregated processing capacity. Small-worldness
reflects a balance between network integration and segregation. Among these metrics, global
efficiency was trained in all the trade-off models, local efficiency was trained in the Tri-factor
model (Eloc), and modularity was trained in the Tri-factor model (Q). The rest of the measures
were not directly trained in any trade-off models. Detailed equations and definitions of the
topological measures are presented in the Supporting Information. Calculation of the above
topological metrics was performed using the Graph Theoretical Network Analysis Toolbox
(GRETNA; J. Wang et al., 2015) and Brain Connectivity Toolbox (BCT; Rubinov & Sporns,
2010). Notably, to avoid the potential effect of cost on these metrics, only the synthetic net-
works whose cost objective values were distributed in the cost range of the empirical networks
at the individual level were selected for comparison.
To measure the overall ability of trade-off models to recover the nine topological charac-
teristics above, we developed a distance-based cost function, termed topological dissimilarity.
Specifically, first, we normalized each topological metric across all networks, including syn-
thetic networks of the three models and empirical brain networks, with z-score normalization.
Then we computed the centroid of empirical brain networks by averaging each normalized
metric score across empirical brain networks. For each synthetic network, the topological
dissimilarity was defined as the Euclidean distance between normalized metric scores of the
synthetic network and normalized metric scores of the empirical centroid.
Specific Features of the Representative Synthetic Network
Besides the above network-level features, some other properties at a more specific level (e.g.,
nodal degree centrality) were also crucial for the network function (e.g., integration) of the
human brain (Aerts et al., 2016; Sporns, 2013; van den Heuvel & Sporns, 2013). To investigate
how these specific features emerge under the pressure of different trade-offs, we extracted one
representative network from the approximated Pareto sets of the three trade-off models,
respectively, and examined their relationship with the group-level empirical brain network.
The representative network of each trade-off model was defined as the synthetic network that
had the highest recovery rate within the cost range of the SCNU sample, which ensured the
extracted representative network would be comparable with the group-level empirical
network. The similarity between representative networks and the group-level empirical brain
network was examined in three aspects: modular structure, nodal degree centrality, and
robustness of network. The modular structure of networks was compared by their similarity
in modular partition obtained from the Louvain community detection algorithm (Blondel
Network Neuroscience
612
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
0
4
2
1
2
0
2
8
9
n
e
n
_
a
_
0
0
2
9
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Trade-off models underlying the human connectome
et al., 2008). The degree centrality was compared through the correlation of nodal degree
centrality and the overlap of hub distribution between synthetic networks and empirical brain
network. As for robustness, we examined the degree of network degeneration under compu-
tational attacks (i.e., random attack and targeted attack; Crossley et al., 2014; Kaiser, Martin,
Andras, & Young, 2007) in terms of global and local efficiency. Notably, all the above specific
metrics were not trained in any trade-off models.
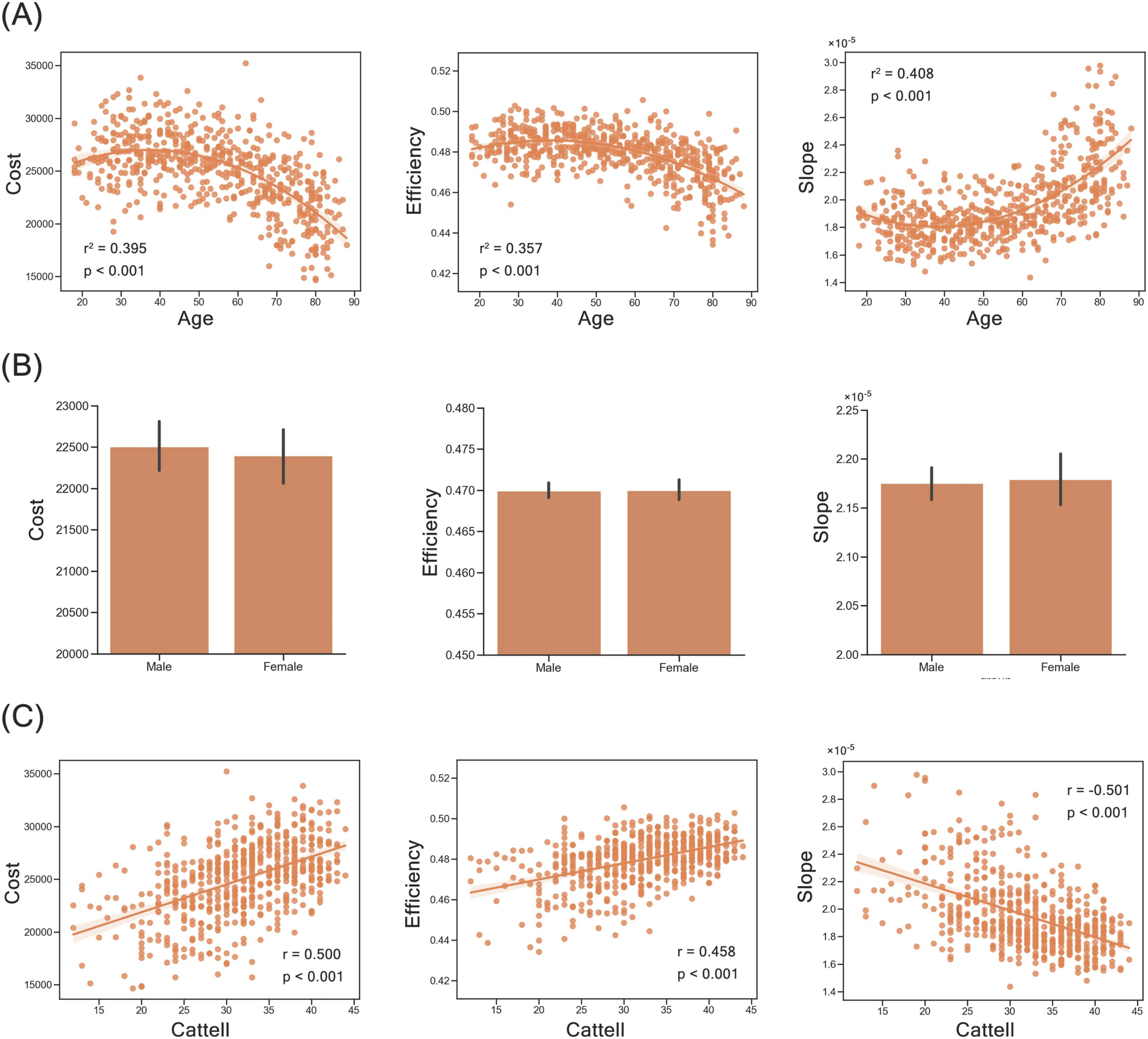
Behavioral Relevance of the Optimal Trade-Off Model
After the above analyses, we could infer the optimal trade-off model that best reproduced fea-
tures of empirical human brain networks. Considering the tight relationship between the brain
connectome and individual characteristics, we were interested in whether the optimal trade-off
model could also capture the basic demographic and behavioral characteristics of individuals.
Analyses of the current section were performed on the Cam-CAN sample, as it has a relatively
large sample size and considerable individual variance in demographic/behavioral scores
(Shafto et al., 2014; Taylor et al., 2017). Through computing the objective values (i.e.,
Fc and 1 − Fe) of networks, we mapped the structural networks of Cam-CAN participants
to the morphospace of the optimal trade-off model. Three indices were derived to characterize
the spatial location of each participant to reflect features of his/her structural brain network.
The three indices were the two axis values (i.e., Fc and 1 − Fe) and the slope of the vector
representing individual network (i.e., [1 − Fe]/Fc), which indicates the relative trade-off
between the wiring cost and the communication efficiency. The relationship between these
indices and demographic/behavioral data of participants were then investigated. For demo-
graphic data, we examined the relationship between age and the three indices, which was
examined through regression analysis, and the gender difference in each index (age con-
trolled). For behavioral data, we extracted the total score of the Cattell test (Cattell, 1963),
which measures the fluid intelligence of participants. Of the 589 participants in the Cam-
CAN sample, 575 participants have finished the Cattell test. Pearson correlation analyses were
performed between the morphospace indices and behavioral scores on the corresponding
subsample of participants.
To examine the significance of results in above analyses, we performed permutation tests.
First, we shuffle the demographic or behavioral values across participants. Then we computed
the correlation value (e.g., Pearson correlation coefficients) between shuffled valued and mor-
phospace indices, or the sexual difference based on shuffled gender groups. These operations
were then repeated 10,000 times to obtain a null distribution of corresponding analysis. The
ratio of values in the null distribution that is higher than actual correlation or difference value
will be defined as the significance of corresponding results.
RESULTS
Synthetic Networks and Morphospace of Trade-Off Models
Using the proposed MOEA, three final sets of synthetic networks achieving optimal trade-off of
the corresponding models were generated (Dual-factor: 347 networks [connection number:
337.133 ± 250.497; density: 0.084 ± 0.063]; Tri-factor [Eloc]: 312 networks [connection num-
ber: 227.398 ± 149.187; density: 0.057 ± 0.037]; Tri-factor [Q]: 281 networks [connection
number: 252.645 ± 153.270; density: 0.063 ± 0.038]). These networks (blue points in
Figure 2A–C) constituted the approximated Pareto fronts that represented a diverse and opti-
mal trade-off in their own morphospace, where efficiency of networks was computed based on
the definition in the corresponding trade-off model. Compared with the synthetic networks, the
Network Neuroscience
613
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
0
4
2
1
2
0
2
8
9
n
e
n
_
a
_
0
0
2
9
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Trade-off models underlying the human connectome
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
0
4
2
1
2
0
2
8
9
n
e
n
_
a
_
0
0
2
9
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
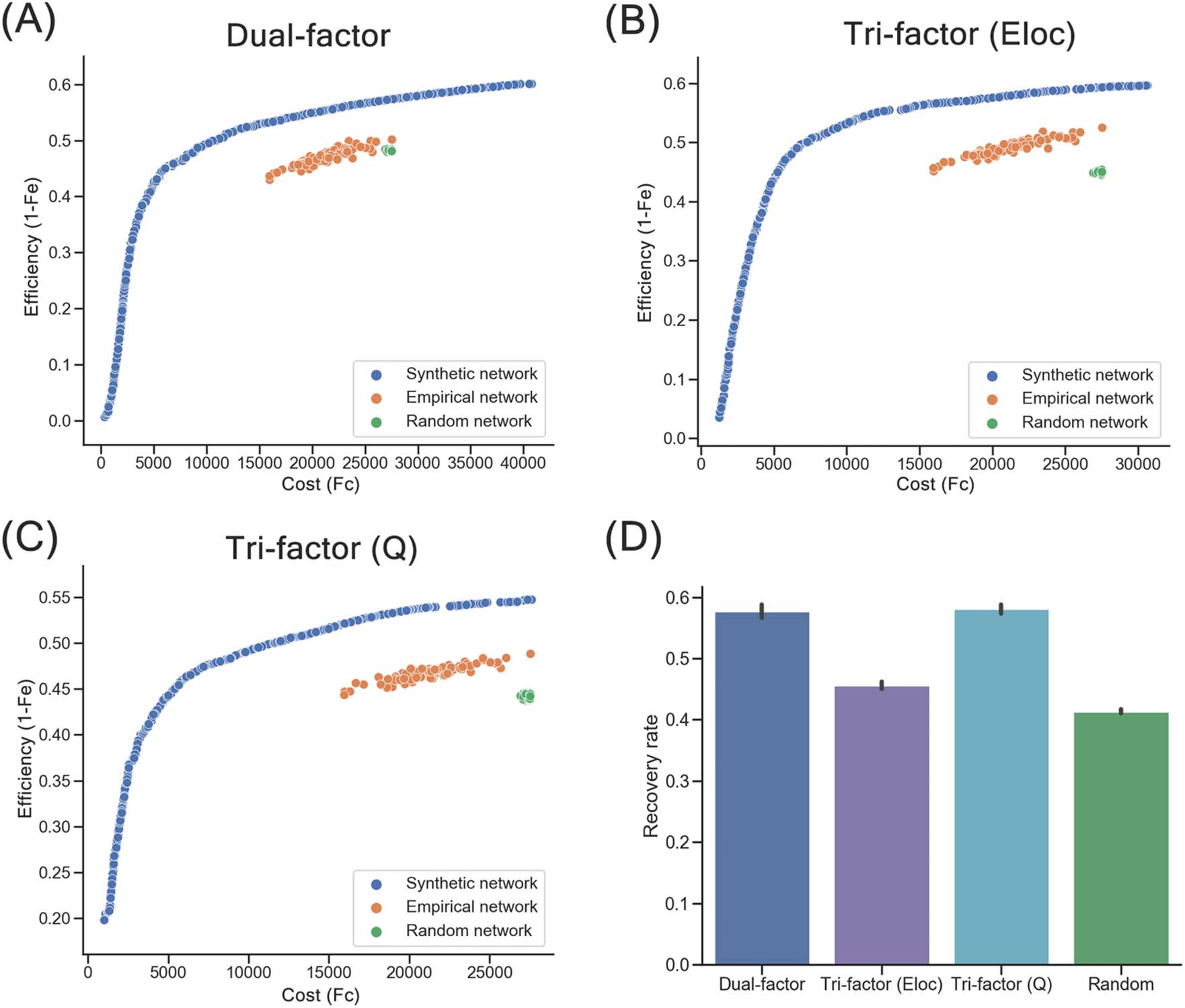
Synthetic networks of trade-off models. (A) Distribution of synthetic networks (blue points), empirical brain networks (orange
Figure 2.
points), and random networks (green points) in morphospace of the Dual-factor model. (B) Distribution of networks in morphospace of the
Tri-factor model (Eloc). (C) Distribution of networks in morphospace of the Tri-factor model (Q). Notably, the values of the Fe objective were
transformed by 1 − Fe (i.e., efficiency index). (D) Recovery rates of synthetic networks and random networks. Recovery rates were significantly
different between network groups (ps < 0.001), except for comparison between Dual-factor model and Tri-factor model (Q) (p = 0.608).
93 individual empirical brain networks (connection number: 477.688 ± 33.875; density:
0.119 ± 0.009; orange points) were distributed along a similar direction as the optimal fronts
(i.e., fronts composed of synthetic networks) within a narrower range, that is, as the networks’
efficiency gets higher their cost also increases to a similar degree, suggesting a similar trade-off
in the synthetic and empirical network groups. However, these individual empirical brain net-
works were all dominated by the synthetic networks and mainly distributed at the top right
area of the morphospace, which means empirical brain networks prioritize efficiency more
in the trade-offs but less optimal trade-offs compared with the synthetic networks of the three
models. Random networks (green points) were also distributed at the suboptimal area of the
space, all dominated by empirical brain networks. To reveal how synthetic networks of differ-
ent models related to each other in the morphospace, we further evaluated the synthetic net-
works using the efficiency objective functions of the three trade-off models and then mapped
the results onto the corresponding morphospace. We observed that for each model, the gen-
erated synthetic networks dominated those from the other two models in the morphospace of
the model, especially within the cost range of empirical brain networks (Supporting
Network Neuroscience
614
Trade-off models underlying the human connectome
Information Figure S5), suggesting the unique optimality of the synthetic networks under their
own models.
In terms of the recovery rate that quantitatively measures how well the connections of
group-level empirical brain networks were recovered, significant differences were found
among synthetic network groups and random networks (one-way analysis of variance
[ANOVA]: F = 605.140, p < 0.001). All three trade-off models showed significantly higher
recovery rates than random networks (R = 0.414 ± 0.016; two-sample t test: ts ≥ 13.547,
ps < 0.001; Figure 2D). Among these trade-off models, the Tri-factor model (Q) (R = 0.581 ±
0.030) and Dual-factor model (R = 0.577 ± 0.049) had the highest recovery rates, which were
significantly higher than the Tri-factor model (Eloc) (R = 0.456 ± 0.024; two-sample t test: ts ≥
18.377, ps < 0.001). No significant difference was observed between the Tri-factor model (Q)
and the Dual-factor model (two-sample t test: t = 0.514, p = 0.608). Note that to avoid the
potential effect of cost, the recovery rate analysis and the global topological analyses below
focused on only synthetic networks whose cost values fell in the range of individual empir-
ical brain networks (Fe range: 15,958–27,544), resulting in 77 networks of the Dual-factor
model (connection number: 465.013 ± 57.365; density: 0.116 ± 0.018), 65 networks of
the Tri-factor model (Eloc) (connection number: 437.013 ± 57.796; density: 0.109 ±
0.014), and 70 networks of the Tri-factor model (Q) (connection number: 460.532 ±
55.125; density: 0.115 ± 0.014).
Global Properties Under Trade-Off Models
Synthetic networks derived from the three different trade-off models also capture network-
level topological features of empirical brain networks to varying degrees. For the small-
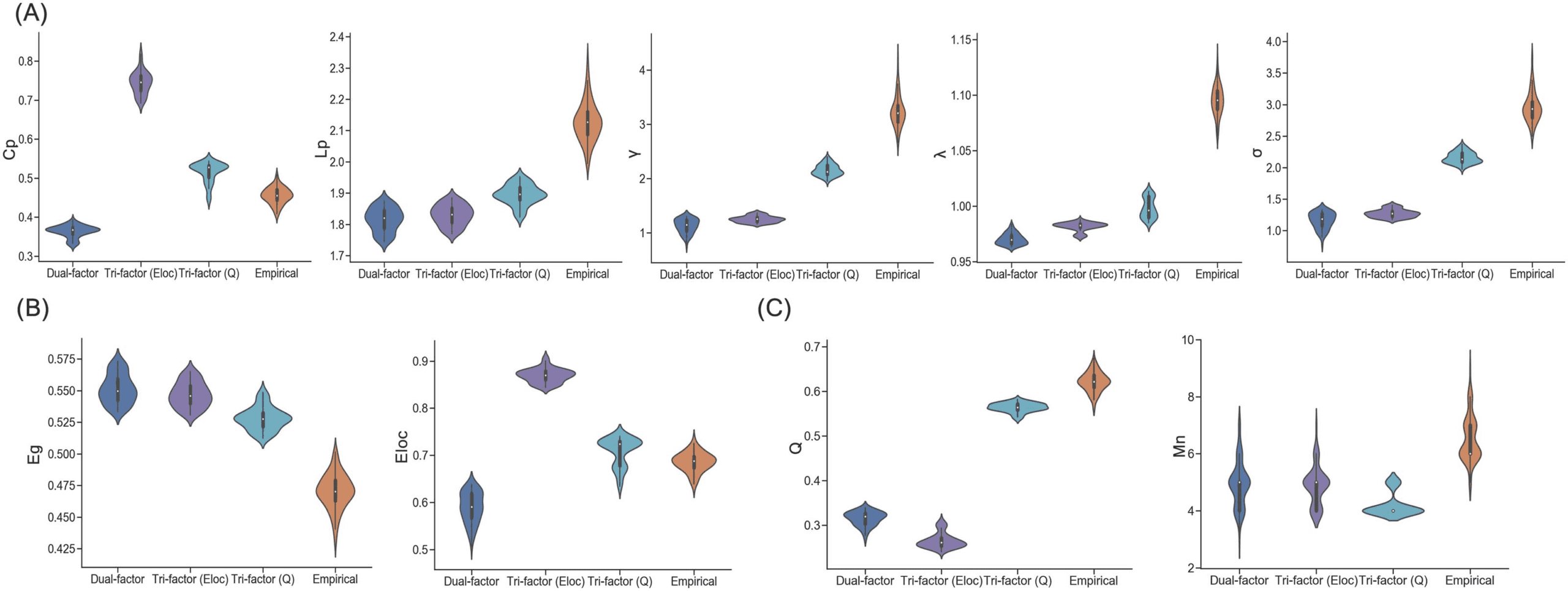
world-related metrics (Figure 3A), similar to empirical brain networks, synthetic networks
of all models showed a small-world structure (mean σ > 1; one-sample t test: ts ≥ 10.863,
ps < 0.001). However, significant differences of small-world metrics were also observed
among network groups (one-way ANOVA: Fs ≥ 881.836, ps < 0.001). The Tri-factor model
(Q) achieved the best performance in small-worldness among the trade-off models (two-
sample t test: ts ≥ 53.324, ps < 0.001), but relatively lower than individual empirical brain
networks (two-sample t test: t = −26.710, p < 0.001). More specifically, compared with the
Dual-factor model proposed in our previous study (Ma et al., 2021), the Tri-factor model (Q)
provided significant improvement in (normalized) clustering coefficient (two-sample t test:
ts ≥ 44.180, ps < 0.001) with the price of longer (normalized) characteristic path length
(two-sample t test: ts ≥ 13.710, ps < 0.001). The Tri-factor model (Eloc) also brought a small
improvement on the small-world metrics (i.e., [normalized] clustering coefficient and small-
worldness), but not as much as the Tri-factor model (Q) did (two-sample t test: ts ≥ 6.367,
ps < 0.001).
For efficiency metrics (Figure 3B), similar patterns of group difference were also observed
(one-way ANOVA: Fs ≥ 903.750, ps < 0.001). Compared with the Dual-factor model, synthetic
networks of the Tri-factor model (Q) sacrificed performance in global efficiency (two-sample
t test: t = −13.533, p < 0.001) for an obvious improvement in local efficiency (two-sample
t test: t = 23.215, p < 0.001). Both efficiency metrics were significantly higher in the Tri-factor
model (Q) than individual empirical brain networks (two-sample t test: ts > 5.860, pag < 0.001).
The Tri-factor model (Eloc) showed a similar pattern as the Tri-factor model (Q).
For modularity metrics (Figure 3C), these network groups again exhibited significant differ-
ences with each other (one-way ANOVA: Fs ≥ 168.520, ps < 0.001). Across the trade-off
models, synthetic networks of the Tri-factor model (Q) had the highest modularity (two-sample
Network Neuroscience
615
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
0
4
2
1
2
0
2
8
9
n
e
n
_
a
_
0
0
2
9
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Trade-off models underlying the human connectome
Figure 3. Network-level topological characteristics of networks. (A) Clustering coefficient (Cp), characteristic path length (Lp), normalized
clustering coefficient (γ), normalized characteristic path length (λ), and small-worldness (σ) of synthetic networks and empirical brain networks.
All the small-world metrics were significantly different between groups (ps < 0.05). (B) Global efficiency (Eg) and local efficiency (El) of
synthetic networks and empirical brain networks. All the small-world metrics were significantly different between groups (ps < 0.05). (C)
Modularity (Q) and module number (Mn) of synthetic networks and empirical brain networks. Modular metrics were significantly different
between network groups (ps < 0.001), except for comparison between module number of Dual-factor model and Tri-factor model (Eloc) (p =
0.718). Note, the synthetic networks are the networks whose cost values are distributed in the range of the SCNU dataset.
t test: ts ≥ 111.375, ps < 0.001), but relatively lower than individual empirical brain networks
(two-sample t test: t = −20.289, p < 0.001). Moreover, the modular number of the Tri-factor
model (Q) was lower than other networks (two-sample t test: ts ≤ −6.870, ps < 0.001).
Detailed descriptive data of the above topological metrics are presented in Table 1. Besides
the synthetic networks and empirical brain networks, we also computed topological metrics
on 100 topological random networks (Maslov & Sneppen, 2002) as the benchmark.
To access the ability of trade-off models to capture the above topological properties, we
further computed a cost function (i.e., topological dissimilarity) for each model. Results
demonstrate that the Tri-factor model (Q) had the statistically lowest topological dissimilarity
among the three models (two-sample t test: ts ≤ −51.609, ps < 0.001; Supporting Information
Figure S4A). Overall, the Tri-factor model (Q) revealed relatively better performance in cap-
turing both integrated (e.g., global efficiency) and segregated (e.g., modularity) topological
properties of empirical brain networks, regardless of whether these properties were trained.
Representative Synthetic Network and Pattern of Distance-Dependent Connections
As mentioned in the Materials and Methods section, to further examine more specific features
of networks, we extracted a representative synthetic network from each trade-off model.
Figure 4A presents the adjacency matrices and the brain maps of the three representative
synthetic networks and the group-level empirical brain network (connection number: 388;
density: 0.097). From visual inspection, the representative networks of the Dual-factor model
(connection number: 591; density: 0.148) and the Tri-factor model (Q) (connection number:
576; density: 0.144) were more similar to the group-level empirical brain network. The
representative network of the Tri-factor model (Eloc) (connection number: 429; density:
0.107) was relatively sparser, with connections mainly concentrating on a small group of
Network Neuroscience
616
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
0
4
2
1
2
0
2
8
9
n
e
n
_
a
_
0
0
2
9
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
T
r
a
d
e
-
o
f
f
m
o
d
e
l
s
u
n
d
e
r
l
y
i
n
g
t
h
e
h
u
m
a
n
c
o
n
n
e
c
t
o
m
e
Table 1. Network-level graph metrics. Cp, clustering coefficient; Lp, characteristic shortest path length; γ, normalized clustering coefficient; λ, normalized characteristic
shortest path length; σ, small-worldness; Eg, global efficiency; Eloc, local efficiency; Q, modularity; Mn, module number; Value, mean ± SD of the metric score; t, t scores of
two-sample t test between metric scores of corresponding network group and random networks. Since computation of γ, λ, and σ have been normalized with random
networks, we do not provide t scores for these metrics. *** p < 0.001, n.s. p > 0.05.
Dual-factor
Tri-factor (Eloc)
Tri-factor (q)
Empirical
Graph metrics
Cp
Value
0.364 ± 0.015
t
135.632***
Value
0.745 ± 0.029
t
200.035***
Value
0.516 ± 0.026
t
144.645***
Value
0.455 ± 0.021
t
148.507***
Lp
γ
λ
pag
Eg
Eloc
q
Mn
1.815 ± 0.038
−67.557***
1.830 ± 0.033
−73.119***
1.895 ± 0.032
−54.702***
2.128 ± 0.063
8.364***
1.127 ± 0.130
0.970 ± 0.005
1.161 ± 0.130
–
–
–
1.250 ± 0.059
0.982 ± 0.004
1.274 ± 0.064
–
–
–
2.155 ± 0.106
0.998 ± 0.009
2.158 ± 0.091
–
–
–
3.241 ± 0.287
1.095 ± 0.014
2.957 ± 0.237
–
–
–
0.551 ± 0.012
59.312***
0.547 ± 0.010
65.020***
0.528 ± 0.009
50.142***
0.470 ± 0.014
−8.379***
0.590 ± 0.032
115.799***
0.869 ± 0.015
280.944***
0.709 ± 0.030
154.996***
0.686 ± 0.021
196.516***
0.315 ± 0.016
14.946***
0.265 ± 0.017
−10.748***
0.564 ± 0.010
188.129***
0.621 ± 0.022
141.171***
4.922 ± 0.791
−13.799***
4.877 ± 0.673
−14.277***
4.200 ± 0.403
−23.080***
6.516 ± 0.789
−0.560n.s.
t
norte
mi
w
oh
r
k
norte
mi
tu
r
oh
s
C
mi
norte
C
mi
i
6
1
7
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
2
6
0
4
2
1
2
0
2
8
9
norte
mi
norte
_
a
_
0
0
2
9
1
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Trade-off models underlying the human connectome
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
2
6
0
4
2
1
2
0
2
8
9
norte
mi
norte
_
a
_
0
0
2
9
1
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 4. Representative synthetic network. (A) Adjacency matrices (upper panel) and brain maps (lower panel) of the representative syn-
thetic networks and the group-level empirical brain network. The white color in the adjacency matrices indicates the existence of edges. (B)
The recovery rate of edges with different distances.
regiones (es decir., global hubs). Consistent with visual inspection, the overall recovery rates of the
representative synthetic network from the Dual-factor model (R = 0.636) and the Tri-factor
modelo (q) (R = 0.632) were relatively high compared with the Tri-factor model (Eloc) (R = 0.503).
We then divided the connections in each representative synthetic network into six bins
according to the Euclidean distance between region pairs (es decir., 0–20 mm, 20–40 mm, 40–
60 mm, 60–80 mm, 80–100 mm, and 100–120 mm) and found that recovery of connections
was not uniform. Recovery rates of all three models shared a pattern that short-distance con-
nections (Euclidian distance < 40 mm) were better recovered (0.467 < Rs < 0.817) than
middle- or long-distance connections (Euclidian distance ≥ 40 mm, Rs < 0.516) in the syn-
thetic networks (Figure 4B). To quantify the ability of recovering middle- or long-distance con-
nections, we computed the area under curve (AUC) of the bars at middle- or long-distance bins
(i.e., Euclidian distance ≥ 40 mm; Figure 4B). Compared with the Dual-factor model (AUC =
13.421) and the Tri-factor model (Eloc) (AUC = 8.856), the representative network of the
Tri-factor model (Q) could recover relatively more middle- or long-distance connections. In
general, these findings suggested that local connections are preferable in all trade-off models
and the Tri-factor model (Q) was able to capture more middle- or long-distance connections
than others.
Network Neuroscience
618
Trade-off models underlying the human connectome
Modular Structure of Synthetic Networks Under Trade-Off Models
The above findings of global modularity metrics suggested the existence of modular structure
in both synthetic networks and individual empirical brain networks. To further examine sim-
ilarity among their modular structure, we considered the modular partition of the representa-
tive synthetic networks and the group-level empirical brain network (Figure 5A). Consistent
with the above patterns of global properties, the modularity score was higher in the group-
level empirical brain network (modularity score = 0.528) and the synthetic network of
the Tri-factor model (Q) (modularity score = 0.538), but lower in the synthetic networks
of the Dual-factor model (modularity score = 0.321) and the Tri-factor model (El) (modularity
score = 0.287), suggesting that the former two networks possessed stronger modular structure.
In addition, the modular partition of the Tri-factor model (Q) was relatively more similar to that
of the group-level empirical brain network (Kappa index = 0.413) than that of the Dual-factor
model (Kappa index = 0.370) and the Tri-factor model (El) (Kappa index = 0.312). Therefore,
the synthetic network of the Tri-factor model (Q) not only exhibited a stronger modular struc-
ture but also reproduced a more similar modular structure as the group-level empirical brain
network.
Nodal Degree Centrality and Spatial Distribution of Hub Regions
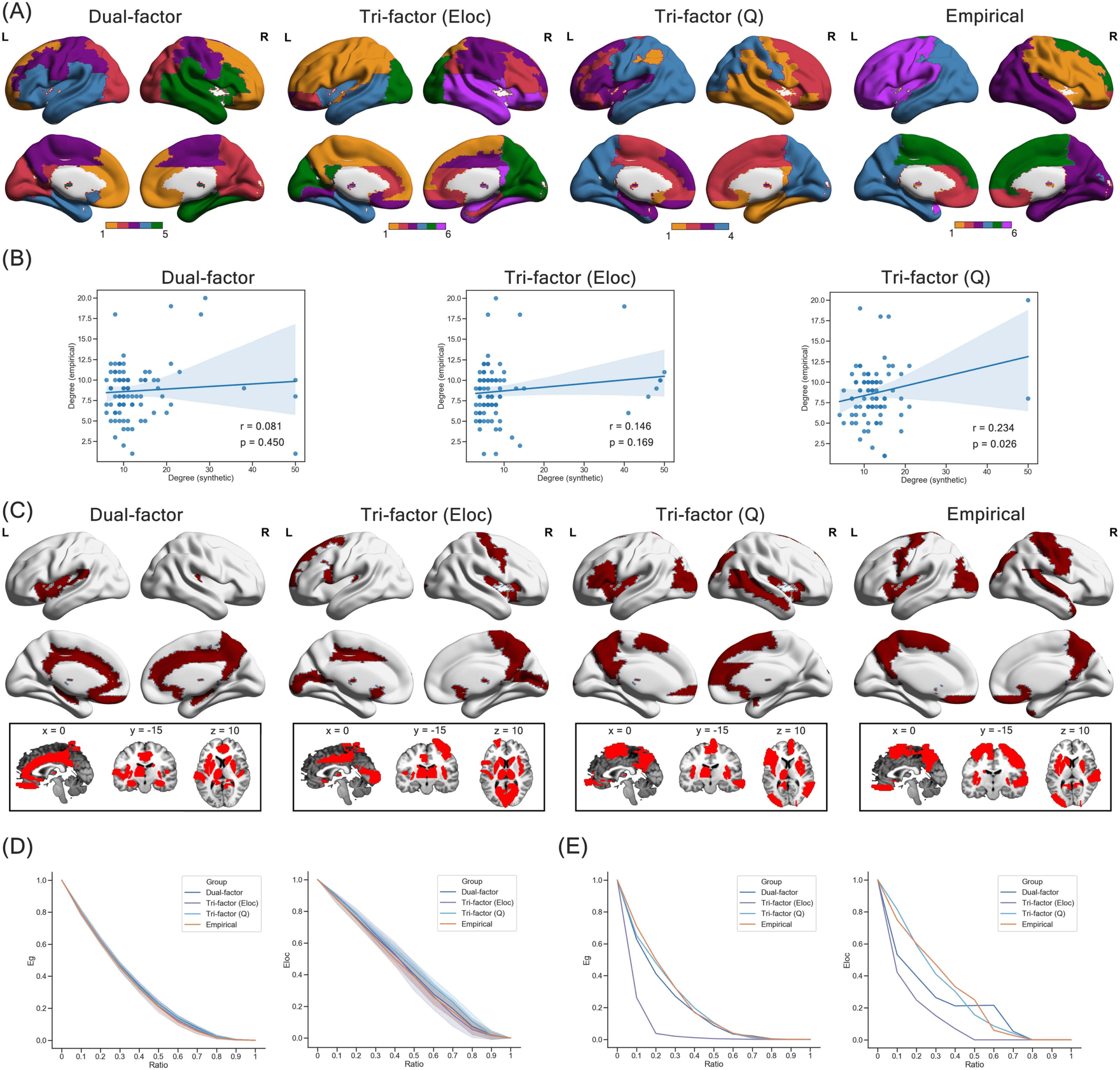
The second type of specific features we investigated was the nodal degree centrality (Figure 5B).
Correlation results revealed that the nodal degree centrality of both the Dual-factor model (r =
0.081, p = 0.450) and the Tri-factor model (El) (r = 0.146, p = 0.169) was not significantly
correlated with that in the group-level empirical brain network. Only in the Tri-factor model
(Q) did we find a significant positive correlation (r = 0.234, p = 0.026). Then we identified hub
regions in each network by selecting regions with the top 20% degree centrality. The spatial
pattern of hub regions is shown in Figure 5C. We could observe that hub regions of the dual-
factor model mainly concentrated at the subcortical area of the brain (e.g., thalamus), whilet
hub regions of the two Tri-factor models distributed more dispersedly around the whole brain.
To quantify the similarity of the hub distribution, we evaluated the number of overlapping hub
regions between synthetic and group-level empirical brain networks. We found that the Tri-
factor model (Q) (seven overlapping hubs; e.g., left insula, left precuneus) had more overlap-
ping hub regions than the Dual-factor model (six overlapping hubs) and the Tri-factor model
(Eloc) (five overlapping hubs). Together, our results suggested that the connection pattern of
the Tri-factor model (Q) could partially capture the relative importance of brain regions in
the group-level empirical brain network, which could not be achieved by the other trade-off
models.
Robustness of Synthetic Networks Under Trade-Off Models
Another important property we investigated was the robustness of network. Under random
attacks (Figure 5D), we found that the robustness was different among synthetic networks
and the group-level empirical brain network at most steps (one-way ANOVA: Fs > 4.048,
ps < 0.008), except for the steps of removing 10% (for preserved global efficiency) and
90% of nodes (for preserved local efficiency). The preserved network functions (i.e., global
efficiency and local efficiency) of the synthetic networks at most steps were slightly better than
the group-level empirical brain network. Specifically, the Dual-factor model showed better pre-
served global efficiency at steps from 0.2 to 0.9 (two-sample t test: ts > 3.722, ps < 0.001), and
better preserved local efficiency at steps of 0.3 to 0.4 and 0.6 to 0.7 (two-sample t test: ts >
2.333, ps < 0.021). The Tri-factor model (Eloc) had better preserved global efficiency at steps
of 0.2 and 0.6 to 0.8 (two-sample t test: ts > 2.630, ps < 0.010), and better preserved local
Network Neuroscience
619
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
0
4
2
1
2
0
2
8
9
n
e
n
_
a
_
0
0
2
9
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Trade-off models underlying the human connectome
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
0
4
2
1
2
0
2
8
9
n
e
n
_
a
_
0
0
2
9
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 5. Network features of representative synthetic network. (A) Modular partition of synthetic networks and empirical brain network. (B)
Scatterplot of degree centrality between synthetic networks and empirical brain network. (C) Spatial distribution of hub regions (red areas) in
the synthetic network and empirical brain network. (D) Degeneration of global efficiency (Eg) and local efficiency (El) under random attacks
on the synthetic and empirical brain networks. “Ratio” indicates the ratio of deleted nodes in the current step, and the shadow of lines
indicates the range of 1 standard deviation. (E) Degeneration of global efficiency (Eg) and local efficiency (El) under targeted attacks on
the synthetic and empirical brain network. “Ratio” indicates the ratio of deleted nodes in the current step.
Network Neuroscience
620
Trade-off models underlying the human connectome
efficiency at steps from 0.1 to 0.4 (two-sample t test: ts > 3.727, ps < 0.001). The Tri-factor
model (Q) showed better preserved global efficiency at steps from 0.2 to 0.9 (two-sample
t test: ts > 3.722, ps < 0.007), and better preserved local efficiency at steps from 0.1 to 0.8
(two-sample t test: ts > 2.333, ps < 0.001).
Under targeted attacks (Figure 5E), synthetic networks of the Dual-factor model (AUC of
global efficiency = 0.213; AUC of local efficiency = 0.239) and the Tri-factor model (Eloc)
(AUC of global efficiency = 0.084; AUC of local efficiency = 0.139) suffered more severe
degeneration than the group-level empirical brain network (AUC of global efficiency =
0.236; AUC of local efficiency = 0.299), suggesting that networks of these two trade-off models
were more vulnerable to attack on high-degree regions. Comparatively, the synthetic network
of the Tri-factor model (Q) (AUC of global efficiency = 0.231; AUC of local efficiency = 0.291)
was as resilient as the group-level empirical brain network. Hence, the representative synthetic
network of the Tri-factor model (Q) could achieve similar robustness as the empirical brain
network under both types of attacks. Combining the findings of the above sections, we could
find that although a subtle difference remained when compared with the empirical ones, the
Tri-factor model (Q) was the optimal trade-off model that underlaid the organization of the
human brain network.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
0
4
2
1
2
0
2
8
9
n
e
n
_
a
_
0
0
2
9
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Behavioral Relevance of Trade-Off Models
In addition to the recovery of the empirical brain structure, the optimal trade-off model, that is, the
Tri-factor model (Q), could further capture individual human functions through individual var-
iation of individual brain networks in the morphospace (Supporting Information Figure S2C).
For demographic characteristics (i.e., age and gender), we observed that wiring cost (r2 =
0.395, p < 0.001) and efficiency index (r2 = 0.357, p < 0.001) of individual human brain net-
works showed inverted U-shaped trajectories with age, where wiring cost and communication
efficiency of the human brain simultaneously increased before approximately 40 years old and
decreased at older ages. Conversely, their slopes in morphospace (r2 = 0.408, p < 0.001) had a
U-shaped trajectory with age (Figure 6A), indicating that the trade-off between cost and com-
munication efficiency tended to promote communication efficiency before approximately
40 years and gradually deviated to minimizing cost at older ages. From the perspective of mor-
phospace position (Supporting Information Figure S2C), it may suggest that individuals
gradually move to the top right area as they age before middle age (around 40 years old),
and then move back to the bottom left as they get older after middle age. As for gender dif-
ference, after controlling for the effect of age, we observed that the wiring cost ( p = 0.007) and
efficiency index ( p = 0.008) were higher in the brain structural networks of male participants
than in those of female participants (Figure 6B). The values of the slope metric (p = 0.032)
were lower in the brain structural networks of male participants than in those of female par-
ticipants (Figure 6B).
Besides the demographic characteristics, morphospace indices of the Tri-factor model (Q)
could also capture individual behavioral performance (i.e., Cattell test). As shown in
Figure 6C, wiring cost (r = 0.500, p < 0.001) and communication capacity (r = 0.458, p <
0.001) of individual human brain networks were positively correlated with the total scores of
the Cattell test. Slopes of individual human brain networks were negatively correlated with
the total scores of the Cattell test (r = −0.501, p < 0.001). Hence, individuals with efficient
and costly brain networks had better fluid intelligence. Since the cost index is related to
connection numbers, it may also mean that adding more connections in the human brain
would be more beneficial. Moreover, we also found a negative correlation between age and
Network Neuroscience
621
Trade-off models underlying the human connectome
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
0
4
2
1
2
0
2
8
9
n
e
n
_
a
_
0
0
2
9
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 6. Behavioral results of the Tri-factor model (Q). (A) Scatterplot between age and morphospace indices (i.e., cost, efficiency, and slope).
(B) Gender difference of morphospace indices (i.e., cost, efficiency, and slope). (C) Scatterplot between Cattell scores and morphospace indices
(i.e., cost, efficiency, and slope). Slope is computed as efficiency/cost.
Cattell scores (r = −0.660, p < 0.001; Supporting Information Figure S6). Combined with the
above results, it may further suggest that cognitive decline (i.e., fluid intelligence here) in
the aging progress is related to a simultaneous decrease of cost and efficiency in the struc-
tural human brain network. Besides the Tri-factor model (Q), we also analyzed the behav-
ioral relevance of other trade-off models and found similar results (Supporting Information
Table S2), which may be due to the identical cost index and slight difference in efficiency
index in all models.
Network Neuroscience
622
Trade-off models underlying the human connectome
Validation Results
To examine the reliability of trade-off models in recovering human brain networks, the main
analyses of recovery rate and global topological properties were also repeated in the indepen-
dent Cam-CAN sample. Similarly, empirical brain networks were dominated by the synthetic
networks from all the trade-off models (Supporting Information Figure S2A–C). The Tri-factor
model (Q) (R = 0.605 ± 0.014) showed a better recovery rate of connections than the Tri-factor
model (Eloc) (R = 0.491 ± 0.060) and random networks (R = 0.400 ± 0.020) (two-sample t test:
ts > 16.244, ps < 0.001), and a similar recovery rate as the Dual-factor model (R = 0.593 ±
0.058; two-sample t test: t = 1.881, p = 0.062; Supporting Information Figure S2D). Although
the recovery rate is similar, the Tri-factor model (Q) outperformed the Dual-factor model in
topological metrics of segregation capacity (e.g., clustering coefficient and modularity; two-
sample t test: ts > 7.635, ps < 0.001) and small-worldness (two-sample t test: t = 52.538,
p < 0.001; Supporting Information Figure S3 and Table S1). Topological dissimilarity analysis
also revealed that the Tri-factor model (Q) had the lowest topological dissimilarity among the
three models (two-sample t test: ts ≤ −33.666, ps < 0.001; Supporting Information Figure S4B).
As in the main results, these findings consistently revealed the predominant performance of the
Tri-factor model (Q) in recovering network structure of the empirical human brain and sup-
ported its optimality among the three trade-off models.
DISCUSSION
In this study, we explored the optimal trade-off model that underlies organization of the human
brain network using an MOEA approach and further examined its behavioral relevance. By
modeling the trade-offs among fundamental factors (i.e., cost, integration, and segregation)
as multiobjective optimization problems, we were able to generate synthetic networks under
the optimal trade-off of corresponding models. These synthetic networks exhibited consider-
able performance in capturing the connectome topology of the empirical human brain net-
work, including the overall connection pattern, network-level topological characteristics,
and specific and nodal topological features. Through comparison among trade-off models,
we found that the Tri-factor model (Q) had the best performance in segregated processing
capacity, network robustness, nodal degree centrality, and recovery of middle- or long-
distance connections, suggesting it as the optimal trade-off model of the human connectome.
Finally, based on the morphospace of this optimal model, we further revealed that individual
variation in the morphospace could not only capture performance in behavioral scores, but
also reflect different correlation patterns in different behavioral domains.
Trade-Off Among Cost, Segregation, and Integration
The human connectome wiring was widely hypothesized as the result of a trade-off between
two competing factors: cost and efficiency (Bullmore & Sporns, 2012; Stiso & Bassett, 2018).
Previous studies that examined this general principle mainly focus on the trade-off between
cost and global efficiency (Y. Chen et al., 2013, 2017; Fornito et al., 2011; Ma et al., 2021),
which neglected the effect of segregation (Sporns, 2013). In the current study, we further
extended the cost-efficiency principle to consider the optimal trade-off among cost, integra-
tion, and segregation. Synthetic networks under an optimal trade-off among these factors
showed high similarity with empirical brain networks in the edge pattern but fully dominated
empirical brain networks in the morphospace. The implication of this suboptimality is twofold.
First, it may suggest the existence of a trade-off, though a suboptimal trade-off among cost,
integration, and segregation in the human brain network. This implication aligns with the
Network Neuroscience
623
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
0
4
2
1
2
0
2
8
9
n
e
n
_
a
_
0
0
2
9
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Trade-off models underlying the human connectome
previous notion that the connection placement of the human connectome may be at a subop-
timal or near-optimal stage (Gollo et al., 2018). Second, the suboptimality implies that current
trade-off models could not adequately capture all the features of the human brain network.
Developmental constraints (Akarca et al., 2021; Nicosia, Vértes, Schafer, Latora, & Bullmore,
2013; Oldham et al., 2022) and other more specific constraints (e.g., cytoarchitectonic and
genetic constraints; Arnatkeviciute et al., 2021) may be needed to complement the current
framework.
Besides edge pattern, these synthetic networks were also able to reproduce several impor-
tant features of the empirical human brain network that could not be explained by the original
cost-efficiency model (Ma et al., 2021), including recovery of the segregated processing
capacity (e.g., local efficiency and modularity), nodal degree centrality, and network robust-
ness. The emergence of segregated properties was previously considered to be the result of
cost minimization (Y. Chen et al., 2013, 2017; Sporns & Betzel, 2016), such as the sparse
inter-module connections in modular structure. However, the segregated structure of the
human brain network is also organized to achieve other important functions, including flexible
and rapid specialized processing, and network robustness (Wig, 2017; Sporns & Betzel, 2016).
Results of both the previous cost-efficiency model (Ma et al., 2021) and the current Dual-factor
model also revealed that simply optimizing the trade-off between cost and global efficiency is
inadequate to capture the segregation of the empirical brain networks. Rather, these models
generated a more centralized network structure, where spatially central global hub regions
owned dense connections to nearly all other regions. This structure could achieve efficient
network communication with low cost, and did provide a good trade-off between cost and
global efficiency. The trade-off models could capture the segregated properties of the empirical
brain network only when segregated factors (e.g., modularity) were included as network con-
straints, suggesting the indispensable role of segregation in the wiring of the human brain net-
work. Similar to our notion, previous research on small-worldness (Bassett & Bullmore, 2006,
2017; Liao et al., 2017), which describes high clustering and short average path length of net-
works, also suggested that the human connectome organization facilitated both integration
and segregation of the brain (Deco et al., 2015). Besides small-worldness, many of the reca-
pitulated network properties were previously attributed to other more specific constraints
(Betzel et al., 2016; Markov et al., 2013; Roberts et al., 2016), such as the distance-dependent
connection pattern (geometrical constraint) and nodal degree centrality (topological con-
straint). Hence, the trade-off among cost, integration, and segregation can be considered to
be a more fundamental principle summarizing the effect of the above constraints. Current
work based on the well-designed MOEA approach provided direct evidence on how this fun-
damental principle causally influences the brain’s network structure.
Modularity as an Optimal Additional Factor of Trade-Off Models
Our study explored the effect of segregation in trade-off models from two aspects: local effi-
ciency and modularity. Although both depict segregated capacity of the network (Cohen &
D’Esposito, 2016), the trade-off model of modularity (i.e., Tri-factor model [Q]) obviously out-
performed the model of local efficiency in most network features, such as overall recovery rate
and robustness. This might be due to the adaptive properties of modular structure. First, mod-
ular structure of the brain network can not only support specialized neural processing, but also
help conserve wiring cost (Y. Chen et al., 2013, 2017; Clune, Mouret, & Lipson, 2013). The
spatially compact modules and their predominantly short within-module connections result in
low global wiring cost of the network (Samu et al., 2014). Comparatively, local efficiency
focuses on only the efficiency of local information transmission regardless of the global wiring
Network Neuroscience
624
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
0
4
2
1
2
0
2
8
9
n
e
n
_
a
_
0
0
2
9
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Trade-off models underlying the human connectome
cost (Latora & Marchiori, 2001). The cost conservation nature of modularity makes it a more
suitable additional factor in the trade-off model. Second, the modular structure increases
global robustness of network. On one hand, the dense within-modular connections and sparse
between-modular connections of modular structure could confine the propagation of local
perturbations within modules, which prevent or delay global distortion of the network (Sporns
& Betzel, 2016; van den Heuvel & Sporns, 2019). On the other hand, as observed in our
results, the pressure of modularity shifted the network from a single-core system to a multi-
core system, where the spatial pattern of hubs became more distributed under the Tri-factor
(Q) model. Accordingly, the robustness under targeted attack on high-degree regions was
improved in the synthetic network. Together, the modular structure confers adaptive advan-
tages to the network that were embedded in the evolution of the human brain rather than just
segregation capacity. Moreover, it is worth noting that although local efficiency and modular-
ity are two common segregation metrics, there are some other metrics with whichi to measure
segregation of the network (e.g., system segregation, assortativity coefficient, and odds ratio;
Bojanowski & Corten, 2014; Chan et al., 2014; Cohen & D’Esposito, 2016). Future work can
incorporate more segregation metrics to further explore how the trade-off among cost, integra-
tion, and segregation shapes the human connectome.
Degree Centrality and Long-Distance Connections of the Human Brain Network
Apart from segregation and robustness, the trade-off model of modularity also showed
improved performance in recovering nodal degree centrality and long-distance connections.
Both features are crucial to communication in brain networks. Degree centrality characterizes
the numbers of direct connections owned by brain regions, reflecting their relative importance
in network communication (van den Heuvel & Sporns, 2013; Zuo et al., 2012). The spatial
distribution of degree centrality was considered to be a configuration of minimal wiring cost
(Gollo et al., 2018). However, we could only find significant correlation in the Tri-factor model
(Q), but not in other models that also accounted for the effect of minimizing cost, suggesting
that nodal degree centrality is jointly determined by cost, integration, and modularity, rather
than by cost alone. Moreover, despite the significant similarity, there remained a large variance
of degree centrality that could not be explained by the Tri-factor model (Q). The spatial dis-
tribution of degree centrality might rely on not only the principle of fundamental factors (e.g.,
wiring cost and modularity), but also more specific nodal characteristics (e.g., cytoarchitec-
tonic and genetic constraints). For example, recent work using a transcriptomic atlas data
found a tight relationship between regional transcriptional activity and degree centrality of
the structural (Arnatkeviciute et al., 2021) or functional (Zhu et al., 2021) human brain net-
work. In future work, a model encompassing the trade-off principle and specific nodal infor-
mation may better capture the spatial distribution of nodal degree.
Long-distance connections were costly components of the brain network that occupied a
large amount of wiring cost. In return, they performed important roles in supporting direct
communication between remote regions (Bassett & Bullmore, 2017; van den Heuvel & Sporns,
2011) and functional diversity of the network (Betzel & Bassett, 2018). In line with these sug-
gestions, our model incorporating the trade-off among cost, integration, and modularity was
able to reproduce a considerable portion of long-distance connections. However, compared
with short-distance connections, the recovery rate of long-distance connections was relatively
low. What are the roles of these remaining long-distance connections? One possible explana-
tion is that these uncovered long-distance connections might serve as alternative nonoptimal
pathways that support direct communication between areas when needed by specific task
demands (Pappas et al., 2020). Under specific conditions (e.g., demanding cognitive tasks),
Network Neuroscience
625
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
0
4
2
1
2
0
2
8
9
n
e
n
_
a
_
0
0
2
9
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Trade-off models underlying the human connectome
brain network communication could reroute and take place on other suboptimal, potentially
“expensive,” pathways (Avena-Koenigsberger et al., 2017).
Shared and Fundamental Morphospace Underlies Human Functions
Based on the optimal trade-off model of the human brain network (i.e., the Tri-factor model
[Q]), we proposed a morphospace that captured diverse demographic/behavioral characteris-
tics of participants. In the past decade, mounting studies using network-based analyses have
found a tight relationship between brain network topological characteristics and human
behavior (Cohen & D’Esposito, 2016; Heitger et al., 2012; Park & Friston, 2013) or demo-
graphic characteristics (Cao et al., 2014; Ingalhalikar et al., 2014). Our morphospace, which
represented a continuum of all possible human brain network configurations, was able to
bridge the above brain-behavior relationship. On one hand, morphospace indices of individ-
ual brain networks had considerable correlation with both demographic characteristics and
behavioral performance, showing a high sensitivity and generalizability in capturing different
normal human functions. Findings of these correlations were also consistent with previous
related results, such as U-shaped or inverted U-shaped trajectories of topological features
(e.g., inter-/intra-module connectivity) along the life span (Cao et al., 2014; Luo et al.,
2020; Zuo et al., 2017) and positive correlation between network properties (e.g., global effi-
ciency) and intelligence (Fischer et al., 2014; Li et al., 2009). Our morphospace synthesized all
these relationships from a more general and fundamental perspective. On the other hand, indi-
vidual characteristics from different domains showed different correlation patterns with the
three morphospace indices (e.g., inverted U-shaped trajectories with age, and negative linear
correlation with Cattell scores), suggesting a specificity of the trade-off morphospace. Hence,
variation in the morphospace could not only capture common variance of individual charac-
teristics, but also reflect unique information of different characteristics. With the above advan-
tages, the Tri-factor model (Q) could serve as a fundamental and shared morphospace that
underlies various human functions of participants. Although the current study focused on
healthy adults, the present morphospace might be also be able to capture diagnostic and
symptom-specific abnormality of individuals through aberrant reconfiguration of the brain net-
work structure along the morphospace dimensions (van den Heuvel & Sporns, 2019). This
notion aligns with recent initiatives on neurobiological dimension-based diagnostic
approaches (Insel et al., 2010; Kebets et al., 2021). Future work with participants from diverse
diagnostic categories could adopt the present morphospace to verify this hypothesis.
Computational Models in Recapitulating the Organization of the Human Connectome
We note that our MOEA approach is similar to several existing computational models that try
to recapitulate the organization of the empirical brain network. For instance, the generative
model (Akarca et al., 2021; Betzel et al., 2016; Vértes et al., 2012; Zhang et al., 2021) gener-
ates synthetic networks with the probability determined by nodal geometric and topological
features, which can clarify contribution of these features and reveal potential factors driving
the formation of connections. Another related method is the random network model (Gollo
et al., 2018; Roberts et al., 2016; Samu et al., 2014), which randomizes network connections
while preserving certain network properties (e.g., geometry) and examines similarity with the
empirical brain network. Although similar, the MOEA approach has two unique features. First,
the MOEA model is more theory-driven. Synthetic networks are constructed based on the cost-
efficiency trade-off principle (Bullmore & Sporns, 2012) but not on explicit guiding information
of empirical brain networks (e.g., empirical local topology as in the generative model), which
allows direct examination of the effect of a specific trade-off model and further reveals the
Network Neuroscience
626
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
0
4
2
1
2
0
2
8
9
n
e
n
_
a
_
0
0
2
9
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Trade-off models underlying the human connectome
fundamental force (e.g., evolutionary force of cost and efficiency) underlying brain develop-
ment. Second, the MOEA approach is able to simultaneously optimize multiple competing
factors. This advantage makes MOEA a suitable approach for solving trade-off problems,
not only cost-efficiency trade-off problems, but also other problems (e.g., the trade-off between
within- and between-modular connection density in modular partition; Gu et al., 2022; Lin
et al., 2018).
Additional Considerations
Despite the novel findings, some limitations should be taken into consideration. First, our
study only investigated the trade-off between cost and efficiency of structural networks.
The efficiency of functional networks, which might be more directly related to communica-
tion efficiency of the human brain (Laughlin & Sejnowski, 2003), was not considered.
Whether efficiency of functional networks is another driving factor of the formation of the
human connectome remains an open question. Future work incorporating multimodal neu-
roimaging data (e.g., PET and fMRI) and functional network prediction models (e.g., commu-
nication models and biophysical models; Avena-Koenigsberger, Misic, & Sporns, 2018; Deco
et al., 2014; Demirtaş et al., 2019; Suárez et al., 2020) might be able to more accurately infer
how synthetic networks under trade-off models support human brain functions. Second, to
approximate the neural wiring cost, we computed the sum of the Euclidean distance between
connected brain areas. Since network connections constructed in the simulation process
might not correspond to actual connections in the empirical human brain network, which
makes it hard to evaluate the actual fiber length, Euclidean distance is a suitable proxy of
connection length (Y. Chen et al., 2013; Ma et al., 2021). However, Euclidean distance
between brain regions, especially interhemispheric region pairs, does not strictly follow the
exact fiber length, which might introduce bias in cost evaluation. Moreover, besides connec-
tion length, properties like fiber number and connection diameter also play a central role in
wiring cost (Bullmore & Sporns, 2012). Directly quantifying these properties in MOEA simu-
lation is often difficult. Therefore, in future work, a computational model that could more
precisely estimate connection cost is needed. Third, our examination of trade-off models
was mainly based on diffusion MRI data of the empirical human brain and did not link to
other empirical neurobiological phenomena. In the future, combining multimodal imaging
data and linking the neurobiological measures (e.g., T1/T2 ratio; Oldham et al., 2022) with
synthetic networks could provide converging evidence of the trade-off principle in the human
connectome. Fourth, with the consideration of reliability and high computational load of the
MOEA approach, we used the classical and reliable AAL atlas for node definition in the cur-
rent study. However, this nodal parcellation is relatively sparse and a different choice of nodal
parcellation may induce a different topological outcome (Zalesky et al., 2010). A parcellation
with higher resolution would be needed to further validate our findings in future studies.
ETHICS STATEMENT
This study was approved by the Institutional Review Board in the Department of Psychology of
Sun Yat-sen University, and all participants provided informed consent before the experiment.
DATA AND CODE AVAILABILITY
The newly acquired SCNU dataset for the present study is available at an open platform
(https://osf.io/ebtks/?view_only=7f4a89f06c464da7b32253c7f3bd0f3d; Zhengjia, 2022). Data
of the Cam-CAN dataset are collected from a published database of the Cambridge Centre for
Network Neuroscience
627
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
0
4
2
1
2
0
2
8
9
n
e
n
_
a
_
0
0
2
9
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Trade-off models underlying the human connectome
Ageing and Neuroscience. The raw data of the Cam-CAN dataset are available at https://
camcan-archive.mrc-cbu.cam.ac.uk/dataaccess/. The toolboxes and third-party code we used
are all stated and cited appropriately, and relevant links of code are also provided in the Mate-
rials and Methods section. Pseudocode of our implemented NSGA-II algorithm can be found
in Algorithm S1 in the Supporting Information.
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00291.
AUTHOR CONTRIBUTIONS
Junji Ma: Formal analysis; Methodology; Validation; Visualization; Writing – original draft;
Writing – review & editing. Xitian Chen: Formal analysis; Visualization; Writing – review &
editing. Yue Gu: Methodology; Validation; Writing – review & editing. Liangfang Li: Method-
ology; Validation; Writing – review & editing. Ying Lin: Conceptualization; Methodology;
Supervision; Writing – review & editing. Zhengjia Dai: Conceptualization; Funding acquisi-
tion; Methodology; Supervision; Writing – review & editing.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
FUNDING INFORMATION
Zhengjia Dai, STI2030-Major Projects of China, Award ID: 2022ZD0213300. Ying Lin, National
Natural Science Foundation of China (NSFC), Award ID: 61772569. Zhengjia Dai, Guangdong
Basic and Applied Basic Research Foundation (https://dx.doi.org/10.13039/501100021171),
Award ID: 2022A1515012005. Zhengjia Dai, Guangdong Basic and Applied Basic Research
Foundation (https://dx.doi.org/10.13039/501100021171), Award ID: 2019A1515012148.
Zhengjia Dai, Open Research Fund of the State Key Laboratory of Cognitive Neuroscience
and Learning, Award ID: CNLYB2001. Zhengjia Dai, Fundamental Research Funds for the Central
Universities (https://dx.doi.org/10.13039/501100012226), Award ID: 19wkzd20.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
0
4
2
1
2
0
2
8
9
n
e
n
_
a
_
0
0
2
9
1
p
d
.
t
REFERENCES
Achard, S., & Bullmore, E. (2007). Efficiency and cost of economical
brain functional networks. PLOS Computational Biology, 3(2), e17.
https://doi.org/10.1371/journal.pcbi.0030017, PubMed: 17274684
Aerts, H., Fias, W., Caeyenberghs, K., & Marinazzo, D. (2016).
Brain networks under attack: Robustness properties and the
impact of lesions. Brain, 139(12), 3063–3083. https://doi.org/10
.1093/brain/aww194, PubMed: 27497487
Ahn, Y.-Y., Jeong, H., & Kim, B. J. (2006). Wiring cost in the orga-
nization of a biological neuronal network. Physica A: Statistical
Mechanics and Its Applications, 367, 531–537. https://doi.org/10
.1016/j.physa.2005.12.013
Akarca, D., Vértes, P. E., Bullmore, E. T., & Astle, D. E. (2021). A gen-
erative network model of neurodevelopmental diversity in struc-
tural brain organization. Nature Communications, 12(1), 4216.
https://doi.org/10.1038/s41467-021-24430-z, PubMed: 34244490
Arnatkeviciute, A., Fulcher, B. D., Oldham, S., Tiego, J., Paquola, C.,
Gerring, Z., … Fornito, A. (2021). Genetic influences on hub
connectivity of the human connectome. Nature Communications,
12(1), 4237. https://doi.org/10.1038/s41467-021-24306-2,
PubMed: 34244483
Avena-Koenigsberger, A., Goñi, J., Betzel, R. F., van den Heuvel,
M. P., Griffa, A., Hagmann, P., … Sporns, O. (2014). Using Pareto
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
optimality to explore the topology and dynamics of the human
connectome. Philosophical Transactions of the Royal Society B:
Biological Sciences, 369(1653), 20130530. https://doi.org/10
.1098/rstb.2013.0530, PubMed: 25180308
Avena-Koenigsberger, A., Misic, B., Hawkins, R. X. D., Griffa, A.,
Hagmann, P., Goni, J., & Sporns, O. (2017). Path ensembles and a
tradeoff between communication efficiency and resilience in the
human connectome. Brain Structure and Function, 222(1), 603–618.
https://doi.org/10.1007/s00429-016-1238-5, PubMed: 27334341
Avena-Koenigsberger, A., Misic, B., & Sporns, O. (2018). Commu-
nication dynamics in complex brain networks. Nature Reviews
Neuroscience, 19(1), 17–33. https://doi.org/10.1038/nrn.2017
.149, PubMed: 29238085
Bassett, D. S., & Bullmore, E. T. (2006). Small-world brain networks.
Neuroscientist, 12(6), 512–523. https://doi.org/10.1177
/1073858406293182, PubMed: 17079517
Bassett, D. S., & Bullmore, E. T. (2017). Small-world brain networks
revisited. Neuroscientist, 23(5), 499–516. https://doi.org/10.1177
/1073858416667720, PubMed: 27655008
Betzel, R. F., Avena-Koenigsberger, A., Goni, J., He, Y., de Reus,
M. A., Griffa, A., … Sporns, O. (2016). Generative models of
the human connectome. NeuroImage, 124, 1054–1064. https://
Network Neuroscience
628
Trade-off models underlying the human connectome
doi.org/10.1016/j.neuroimage.2015.09.041 , PubMed:
26427642
Betzel, R. F., & Bassett, D. S. (2018). Specificity and robustness of
long-distance connections in weighted, interareal connectomes.
Proceedings of the National Academy of Sciences, 115(21),
E4880–E4889. https://doi.org/10.1073/pnas.1720186115,
PubMed: 29739890
Blondel, V. D., Guillaume, J.-L., Lambiotte, R., & Lefebvre, E.
(2008). Fast unfolding of communities in large networks. Journal
of Statistical Mechanics: Theory and Experiment, 2008, P10008.
https://doi.org/10.1088/1742-5468/2008/10/P10008
Bojanowski, M., & Corten, R. (2014). Measuring segregation in
social networks. Social Networks, 39, 14–32. https://doi.org/10
.1016/j.socnet.2014.04.001
Bullmore, E. T., & Sporns, O. (2009). Complex brain networks:
Graph theoretical analysis of structural and functional systems.
Nature Reviews Neuroscience, 10(3), 186–198. https://doi.org
/10.1038/nrn2575, PubMed: 19190637
Bullmore, E. T., & Sporns, O. (2012). The economy of brain network
organization. Nature Reviews Neuroscience, 13(5), 336–349.
https://doi.org/10.1038/nrn3214, PubMed: 22498897
Cao, M., Wang, J. H., Dai, Z. J., Cao, X. Y., Jiang, L. L., Fan, F. M., …
He, Y. (2014). Topological organization of the human brain func-
tional connectome across the lifespan. Developmental Cognitive
Neuroscience, 7, 76–93. https://doi.org/10.1016/j.dcn.2013.11
.004, PubMed: 24333927
Cattell, R. B. (1963). Theory of fluid and crystallized intelligence: A
critical experiment. Journal of Educational Psychology, 54(1),
1–22. https://doi.org/10.1037/h0046743
Chan, M. Y., Park, D. C., Savalia, N. K., Petersen, S. E., & Wig, G. S.
(2014). Decreased segregation of brain systems across the
healthy adult lifespan. Proceedings of the National Academy of
Sciences, 111(46), E4997–E5006. https://doi.org/10.1073/pnas
.1415122111, PubMed: 25368199
Chen, Y., Wang, S., Hilgetag, C. C., & Zhou, C. (2013). Trade-off
between multiple constraints enables simultaneous formation
of modules and hubs in neural systems. PLOS Computational
Biology, 9(3), e1002937. https://doi.org/10.1371/journal.pcbi
.1002937, PubMed: 23505352
Chen, Y., Wang, S., Hilgetag, C. C., & Zhou, C. (2017). Features of
spatial and functional segregation and integration of the primate
connectome revealed by trade-off between wiring cost and effi-
ciency. PLOS Computational Biology, 13(9), e1005776. https://
doi.org/10.1371/journal.pcbi.1005776, PubMed: 28961235
Clune, J., Mouret, J.-B., & Lipson, H. (2013). The evolutionary ori-
gins of modularity. Proceedings of the Royal Society B: Biological
Sciences, 280(1755), 20122863. https://doi.org/10.1098/rspb
.2012.2863, PubMed: 23363632
Cohen, J. R., & D’Esposito, M. (2016). The segregation and integra-
tion of distinct brain networks and their relationship to cogni-
tion. Journal of Neuroscience, 36(48), 12083–12094. https://
doi.org/10.1523/ JNEUROSCI.2965-15.2016, PubMed:
27903719
Collin, G., Sporns, O., Mandl, R. C., & van den Heuvel, M. P.
(2014). Structural and functional aspects relating to cost and
benefit of rich club organization in the human cerebral cortex.
Cerebral Cortex, 24(9), 2258–2267. https://doi.org/10.1093
/cercor/bht064, PubMed: 23551922
Costa, L. F., Kaiser, M., & Hilgetag, C. C. (2007). Predicting the
connectivity of primate cortical networks from topological and
spatial node properties. BMC Systems Biology, 1(1), 16. https://
doi.org/10.1186/1752-0509-1-16, PubMed: 17408506
Crossley, N. A., Mechelli, A., Scott, J., Carletti, F., Fox, P. T.,
McGuire, P., & Bullmore, E. T. (2014). The hubs of the human
connectome are generally implicated in the anatomy of brain
disorders. Brain, 137(8), 2382–2395. https://doi.org/10.1093
/brain/awu132, PubMed: 25057133
Cui, Z., Zhong, S., Xu, P., He, Y., & Gong, G. (2013). PANDA: A
pipeline toolbox for analyzing brain diffusion images. Frontiers
in Human Neuroscience, 7, 42. https://doi.org/10.3389/fnhum
.2013.00042, PubMed: 23439846
Deb, K., Pratap, A., Agarwal, S., & Meyarivan, T. (2002). A fast and
elitist multiobjective genetic algorithm: NSGA-II. IEEE Transac-
tions on Evolutionary Computation, 6(2), 182–197. https://doi
.org/10.1109/4235.996017
Deco, G., Ponce-Alvarez, A., Hagmann, P., Romani, G. L., Mantini,
D., & Corbetta, M. (2014). How local excitation–inhibition ratio
impacts the whole brain dynamics. Journal of Neuroscience,
34(23), 7886–7898. https://doi.org/10.1523/JNEUROSCI.5068
-13.2014, PubMed: 24899711
Deco, G., Tononi, G., Boly, M., & Kringelbach, M. L. (2015).
Rethinking segregation and integration: Contributions of
whole-brain modelling. Nature Reviews Neuroscience, 16(7),
430–439. https://doi.org/10.1038/nrn3963, PubMed: 26081790
Demirtaş, M., Burt, J. B., Helmer, M., Ji, J. L., Adkinson, B. D.,
Glasser, M. F., … Murray, J. D. (2019). Hierarchical heterogeneity
across human cortex shapes large-scale neural dynamics.
Neuron, 101(6), 1181–1194. https://doi.org/10.1016/j.neuron
.2019.01.017, PubMed: 30744986
de Reus, M. A., & van den Heuvel, M. P. (2013). Estimating false
positives and negatives in brain networks. NeuroImage, 70,
402–409. https://doi.org/10.1016/j.neuroimage.2012.12.066,
PubMed: 23296185
Fischer, F. U., Wolf, D., Scheurich, A., & Fellgiebel, A. (2014).
Association of structural global brain network properties with
intelligence in normal aging. PLOS ONE, 9(1), e86258. https://
doi.org/10.1371/journal.pone.0086258, PubMed: 24465994
Fornito, A., Zalesky, A., Bassett, D. S., Meunier, D., Ellison-Wright,
I., Yücel, M., … Nertney, D. (2011). Genetic influences on
cost-efficient organization of human cortical functional net-
works. Journal of Neuroscience, 31(9), 3261–3270. https://doi
.org/10.1523/JNEUROSCI.4858-10.2011, PubMed: 21368038
Fukushima, M., Betzel, R. F., He, Y., van den Heuvel, M. P., Zuo,
X. N., & Sporns, O. (2018). Structure–function relationships dur-
ing segregated and integrated network states of human brain
functional connectivity. Brain Structure and Function, 223(3),
1091–1106. https://doi.org/10.1007/s00429-017-1539-3,
PubMed: 29090337
Gallos, L. K., Makse, H. A., & Sigman, M. (2012). A small world of
weak ties provides optimal global integration of self-similar mod-
ules in functional brain networks. Proceedings of the National
Academy of Sciences, 109(8), 2825–2830. https://doi.org/10
.1073/pnas.1106612109, PubMed: 22308319
Gollo, L. L., Roberts, J. A., Cropley, V. L., Di Biase, M. A., Pantelis,
C., Zalesky, A., & Breakspear, M. (2018). Fragility and volatility
of structural hubs in the human connectome. Nature
Network Neuroscience
629
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
0
4
2
1
2
0
2
8
9
n
e
n
_
a
_
0
0
2
9
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Trade-off models underlying the human connectome
Neuroscience, 21(8), 1107–1116. https://doi.org/10.1038/s41593
-018-0188-z, PubMed: 30038275
Gu, Y., Li, L., Zhang, Y., Ma, J., Yang, C., Xiao, Y., … Dai, Z. (2022).
The overlapping modular organization of human brain functional
networks across the adult lifespan. NeuroImage, 253, 119125.
https://doi.org/10.1016/j.neuroimage.2022.119125, PubMed:
35331872
Heitger, M. H., Ronsse, R., Dhollander, T., Dupont, P., Caeyenberghs,
K., & Swinnen, S. P. (2012). Motor learning-induced changes in
functional brain connectivity as revealed by means of graph-
theoretical network analysis. NeuroImage, 61(3), 633–650. https://
doi.org/10.1016/j.neuroimage.2012.03.067, PubMed: 22503778
Ingalhalikar, M., Smith, A., Parker, D., Satterthwaite, T. D., Elliott,
M. A., Ruparel, K., … Verma, R. (2014). Sex differences in the
structural connectome of the human brain. Proceedings of the
National Academy of Sciences, 111(2), 823–828. https://doi.org
/10.1073/pnas.1316909110, PubMed: 24297904
Insel, T., Cuthbert, B., Garvey, M., Heinssen, R., Pine, D. S., Quinn,
K., … Wang, P. (2010). Research domain criteria (RDoC): Toward
a new classification framework for research on mental disorders.
American Journal of Psychiatry, 167(7), 748–751. https://doi.org
/10.1176/appi.ajp.2010.09091379, PubMed: 20595427
Kaiser, M., & Hilgetag, C. C. (2006). Nonoptimal component place-
ment, but short processing paths, due to long-distance projec-
tions in neural systems. PLOS Computational Biology, 2(7), e95.
https://doi.org/10.1371/journal.pcbi.0020095, PubMed:
16848638
Kaiser, M., Hilgetag, C. C., & Kötter, R. (2010). Hierarchy and
dynamics of neural networks. Frontiers in Neuroinformatics, 4,
112. https://doi.org/10.3389/fninf.2010.00112, PubMed:
20844605
Kaiser, M., Martin, R., Andras, P., & Young, M. P. (2007). Simulation
of robustness against lesions of cortical networks. European Jour-
nal of Neuroscience, 25(10), 3185–3192. https://doi.org/10.1111
/j.1460-9568.2007.05574.x, PubMed: 17561832
Kebets, V., Favre, P., Houenou, J., Polosan, M., Perroud, N., Aubry,
J.-M., … Piguet, C. (2021). Fronto-limbic neural variability as a
transdiagnostic correlate of emotion dysregulation. Translational
Psychiatry, 11(1), 545. https://doi.org/10.1038/s41398-021
-01666-3, PubMed: 34675186
Klyachko, V. A., & Stevens, C. F. (2003). Connectivity optimization
and the positioning of cortical areas. Proceedings of the National
Academy of Sciences, 100(13), 7937–7941. https://doi.org/10
.1073/pnas.0932745100, PubMed: 12796510
Latora, V., & Marchiori, M. (2001). Efficient behavior of small-world
networks. Physical Review Letters, 87(19), 198701. https://doi
.org/10.1103/PhysRevLett.87.198701, PubMed: 11690461
Laughlin, S. B., & Sejnowski, T. J. (2003). Communication in neu-
ronal networks. Science, 301(5641), 1870–1874. https://doi.org
/10.1126/science.1089662, PubMed: 14512617
Li, Y., Liu, Y., Li, J., Qin, W., Li, K., Yu, C., & Jiang, T. (2009). Brain
anatomical network and intelligence. PLOS Computational Biology,
5(5), e1000395. https://doi.org/10.1371/journal.pcbi.1000395,
PubMed: 19492086
Liao, X., Vasilakos, A. V., & He, Y. (2017). Small-world human brain
networks: Perspectives and challenges. Neuroscience and Biobe-
havioral Reviews, 77, 286–300. https://doi.org/10.1016/j
.neubiorev.2017.03.018, PubMed: 28389343
Lin, Y., Ma, J., Gu, Y., Yang, S., Li, L. M. W., & Dai, Z. (2018). Intrin-
sic overlapping modular organization of human brain functional
networks revealed by a multiobjective evolutionary algorithm.
NeuroImage, 181, 430–445. https://doi.org/10.1016/j
.neuroimage.2018.07.019, PubMed: 30005918
Luo, N., Sui, J., Abrol, A., Lin, D., Chen, J., Vergara, V. M., … Xu, Y.
(2020). Age-related structural and functional variations in 5,967
individuals across the adult lifespan. Human Brain Mapping,
41(7), 1725–1737. https://doi.org/10.1002/ hbm.24905,
PubMed: 31876339
Ma, J., Zhang, J., Lin, Y., & Dai, Z. (2021). Cost-efficiency trade-offs
of the human brain network revealed by a multiobjective evolu-
tionary algorithm. NeuroImage, 236, 118040. https://doi.org/10
.1016/j.neuroimage.2021.118040, PubMed: 33852939
Markov, N. T., Ercsey-Ravasz, M., Lamy, C., Gomes, A. R. R.,
Magrou, L., Misery, P., … Toroczkai, Z. (2013). The role of
long-range connections on the specificity of the macaque inter-
areal cortical network. Proceedings of the National Academy of
Sciences, 110(13), 5187–5192. https://doi.org/10.1073/pnas
.1218972110, PubMed: 23479610
Maslov, S., & Sneppen, K. (2002). Specificity and stability in topol-
ogy of protein networks. Science, 296(5569), 910–913. https://
doi.org/10.1126/science.1065103, PubMed: 11988575
Meunier, D., Lambiotte, R., & Bullmore, E. T. (2010). Modular and
hierarchically modular organization of brain networks. Frontiers
in Neuroscience, 4, 200. https://doi.org/10.3389/fnins.2010
.00200, PubMed: 21151783
Meunier, D., Lambiotte, R., Fornito, A., Ersche, K. D., & Bullmore,
E. T. (2009). Hierarchical modularity in human brain functional
networks. Frontiers in Neuroinformatics, 3, 37. https://doi.org/10
.3389/neuro.11.037.2009, PubMed: 19949480
Mitchison, G. (1991). Neuronal branching patterns and the econ-
omy of cortical wiring. Proceedings of the Royal Society B: Bio-
logical Sciences, 245(1313), 151–158. https://doi.org/10.1098
/rspb.1991.0102, PubMed: 1682939
Nicosia, V., Vértes, P. E., Schafer, W. R., Latora, V., & Bullmore, E. T.
(2013). Phase transition in the economically modeled growth of
a cellular nervous system. Proceedings of the National Academy
of Sciences, 110(19), 7880–7885. https://doi.org/10.1073/pnas
.1300753110, PubMed: 23610428
Oldham, S., Fulcher, B. D., Aquino, K., Arnatkevičiūtė, A., Paquola,
C., Shishegar, R., & Fornito, A. (2022). Modeling spatial, devel-
opmental, physiological, and topological constraints on human
brain connectivity. Science Advances, 8(22), eabm6127. https://
doi.org/10.1126/sciadv.abm6127, PubMed: 35658036
Pappas, I., Craig, M. M., Menon, D. K., & Stamatakis, E. A. (2020).
Structural optimality and neurogenetic expression mediate func-
tional dynamics in the human brain. Human Brain Mapping,
41(8), 2229–2243. https://doi.org/10.1002/ hbm.24942,
PubMed: 32027077
Park, H.-J., & Friston, K. (2013). Structural and functional brain net-
works: From connections to cognition. Science, 342(6158),
1238411. https://doi.org/10.1126/science.1238411, PubMed:
24179229
Roberts, J. A., Perry, A., Lord, A. R., Roberts, G., Mitchell, P. B., Smith,
R. E., … Breakspear, M. (2016). The contribution of geometry to the
human connectome. NeuroImage, 124, 379–393. https://doi.org
/10.1016/j.neuroimage.2015.09.009, PubMed: 26364864
Network Neuroscience
630
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
0
4
2
1
2
0
2
8
9
n
e
n
_
a
_
0
0
2
9
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Trade-off models underlying the human connectome
Roberts, J. A., Perry, A., Roberts, G., Mitchell, P. B., & Breakspear,
M. (2017). Consistency-based thresholding of the human con-
nectome. NeuroImage, 145, 118–129. https://doi.org/10.1016/j
.neuroimage.2016.09.053, PubMed: 27666386
Rubinov, M., & Sporns, O. (2010). Complex network measures of
brain connectivity: Uses and interpretations. NeuroImage, 52(3),
1059–1069. https://doi.org/10.1016/j.neuroimage.2009.10.003,
PubMed: 19819337
Samu, D., Seth, A. K., & Nowotny, T. (2014). Influence of wiring
cost on the large-scale architecture of human cortical connectiv-
ity. PLOS Computational Biology, 10(4), e1003557. https://doi
.org/10.1371/journal.pcbi.1003557, PubMed: 24699277
Shafto, M. A., Tyler, L. K., Dixon, M., Taylor, J. R., Rowe, J. B.,
Cusack, R., … Matthews, F. E. (2014). The Cambridge Centre
for Ageing and Neuroscience (Cam-CAN) study protocol: A
cross-sectional, lifespan, multidisciplinary examination of
healthy cognitive ageing. BMC Neurology, 14(1), 204. https://
doi.org/10.1186/s12883-014-0204-1, PubMed: 25412575
Sporns, O. (2013). Network attributes for segregation and integra-
tion in the human brain. Current Opinion in Neurobiology, 23(2),
162–171. https://doi.org/10.1016/j.conb.2012.11.015, PubMed:
23294553
Sporns, O., & Betzel, R. F. (2016). Modular brain networks. Annual
Review of Psychology, 67, 613–640. https://doi.org/10.1146
/annurev-psych-122414-033634, PubMed: 26393868
Sporns, O., Tononi, G., & Kötter, R. (2005). The human connec-
tome: A structural description of the human brain. PLOS Compu-
tational Biology, 1(4), e42. https://doi.org/10.1371/journal.pcbi
.0010042, PubMed: 16201007
Stiso, J., & Bassett, D. S. (2018). Spatial embedding imposes con-
straints on neuronal network architectures. Trends in Cognitive
Sciences, 22(12), 1127–1142. https://doi.org/10.1016/j.tics.2018
.09.007, PubMed: 30449318
Suárez, L. E., Markello, R. D., Betzel, R. F., & Misic, B. (2020). Link-
ing structure and function in macroscale brain networks. Trends
in Cognitive Sciences, 24(4), 302–315. https://doi.org/10.1016/j
.tics.2020.01.008, PubMed: 32160567
Taylor, J. R., Williams, N., Cusack, R., Auer, T., Shafto, M. A., Dixon,
M., … Henson, R. N. (2017). The Cambridge Centre for Ageing and
Neuroscience (Cam-CAN) data repository: Structural and func-
tional MRI, MEG, and cognitive data from a cross-sectional adult
lifespan sample. NeuroImage, 144, 262–269. https://doi.org/10
.1016/j.neuroimage.2015.09.018, PubMed: 26375206
Tušar, T., & Filipič, B. (2015). Visualization of Pareto front approx-
imations in evolutionary multiobjective optimization: A critical
review and the prosection method. IEEE Transactions on Evolu-
tionary Computation, 19(2), 225–245. https://doi.org/10.1109
/TEVC.2014.2313407
Tzourio-Mazoyer, N., Landeau, B., Papathanassiou, D., Crivello, F.,
Etard, O., Delcroix, N., … Joliot, M. (2002). Automated anatomical
labeling of activations in SPM using a macroscopic anatomical
parcellation of the MNI MRI single-subject brain. NeuroImage,
15(1), 273–289. https://doi.org/10.1006/nimg.2001.0978,
PubMed: 11771995
van den Heuvel, M. P., & Sporns, O. (2011). Rich-club organization
of the human connectome. Journal of Neuroscience, 31(44),
15775–15786. https://doi.org/10.1523/ JNEUROSCI.3539-11
.2011, PubMed: 22049421
van den Heuvel, M. P., & Sporns, O. (2013). Network hubs in the
human brain. Trends in Cognitive Sciences, 17(12), 683–696.
https://doi.org/10.1016/j.tics.2013.09.012, PubMed: 24231140
van den Heuvel, M. P., & Sporns, O. (2019). A cross-disorder con-
nectome landscape of brain dysconnectivity. Nature Reviews
Neuroscience, 20(7), 435–446. https://doi.org/10.1038/s41583
-019-0177-6, PubMed: 31127193
Vértes, P. E., Alexander-Bloch, A. F., Gogtay, N., Giedd, J. N.,
Rapoport, J. L., & Bullmore, E. T. (2012). Simple models of
human brain functional networks. Proceedings of the National
Academy of Sciences, 109(15), 5868–5873. https://doi.org/10
.1073/pnas.1111738109, PubMed: 22467830
Wang, J., Wang, X., Xia, M., Liao, X., Evans, A., & He, Y. (2015).
GRETNA: A graph theoretical network analysis toolbox for imag-
ing connectomics. Frontiers in Human Neuroscience, 9, 386.
https://doi.org/10.3389/fnhum.2015.00386, PubMed: 26175682
Wig, G. S. (2017). Segregated systems of human brain networks.
Trends in Cognitive Sciences, 21(12), 981–996. https://doi.org
/10.1016/j.tics.2017.09.006, PubMed: 29100737
Zalesky, A., Fornito, A., Cocchi, L., Gollo, L. L., van den Heuvel, M. P.,
& Breakspear, M. (2016). Connectome sensitivity or specificity:
Which is more important? NeuroImage, 142, 407–420. https://doi
.org/10.1016/j.neuroimage.2016.06.035, PubMed: 27364472
Zalesky, A., Fornito, A., Harding, I. H., Cocchi, L., Yücel, M.,
Pantelis, C., & Bullmore, E. T. (2010). Whole-brain anatomical
networks: Does the choice of nodes matter? NeuroImage, 50(3),
970–983. https://doi.org/10.1016/j.neuroimage.2009.12.027,
PubMed: 20035887
Zhang, X., Braun, U., Harneit, A., Zang, Z., Geiger, L. S., Betzel,
R. F., … Tost, H. (2021). Generative network models of altered
structural brain connectivity in schizophrenia. NeuroImage,
225, 117510. https://doi.org/10.1016/j.neuroimage.2020
.117510, PubMed: 33160087
Zhengjia, D. (2022). Trade-offs among cost, integration, and segre-
gation in the human connectome, OSF. https://osf.io/ebtks/?view
_only=7f4a89f06c464da7b32253c7f3bd0f3d
Zhou, A., Qu, B.-Y., Li, H., Zhao, S.-Z., Suganthan, P. N., & Zhang,
Q. (2011). Multiobjective evolutionary algorithms: A survey of
the state of the art. Swarm and Evolutionary Computation, 1(1),
32–49. https://doi.org/10.1016/j.swevo.2011.03.001
Zhu, D., Yuan, T., Gao, J., Xu, Q., Xue, K., Zhu, W., … Yu, C. (2021).
Correlation between cortical gene expression and resting-state
functional network centrality in healthy young adults. Human
Brain Mapping, 42(7), 2236–2249. https://doi.org/10.1002/hbm
.25362, PubMed: 33570215
Zuo, X.-N., Ehmke, R., Mennes, M., Imperati, D., Castellanos,
F. X., Sporns, O., & Milham, M. P. (2012). Network centrality
in the human functional connectome. Cerebral Cortex, 22(8),
1862–1875. https://doi.org/10.1093/cercor/ bhr269, PubMed:
21968567
Zuo, X.-N., He, Y., Betzel, R. F., Colcombe, S., Sporns, O., & Milham,
M. P. (2017). Human connectomics across the life span. Trends in
Cognitive Sciences, 21(1), 32–45. https://doi.org/10.1016/j.tics
.2016.10.005, PubMed: 27865786
Network Neuroscience
631
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
0
4
2
1
2
0
2
8
9
n
e
n
_
a
_
0
0
2
9
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3