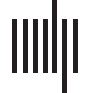MÉTODOS

From correlation to communication:
Disentangling hidden factors from
functional connectivity changes

Yuhua Yu1

, Caterina Gratton1,2,3, and Derek M. Smith1,4

1Department of Psychology, Northwestern University, Evanston, IL, EE.UU
2Department of Neurology, Northwestern University, Evanston, IL, EE.UU
3Department of Psychology, Universidad Estatal de Florida, Tallahassee, Florida, EE.UU
4Department of Neurology, Division of Cognitive Neurology/ Neuropsychology,
The Johns Hopkins University School of Medicine, baltimore, Maryland, EE.UU

un acceso abierto

diario

Palabras clave: Conectividad funcional, Neural correlations, Neural coupling, BOLD variance

ABSTRACTO

While correlations in the BOLD fMRI signal are widely used to capture functional connectivity
(FC) and its changes across contexts, its interpretation is often ambiguous. The entanglement of
multiple factors including local coupling of two neighbors and nonlocal inputs from the rest
of the network (affecting one or both regions) limits the scope of the conclusions that can
be drawn from correlation measures alone. Here we present a method of estimating the
contribution of nonlocal network input to FC changes across different contexts. To disentangle
the effect of task-induced coupling change from the network input change, we propose a new
métrico, “communication change,” utilizing BOLD signal correlation and variance. With a
combination of simulation and empirical analysis, we demonstrate that (1) input from the rest
of the network accounts for a moderate but significant amount of task-induced FC change and
(2) the proposed “communication change” is a promising candidate for tracking the local
coupling in task context-induced change. Además, when compared to FC change across
three different tasks, communication change can better discriminate specific task types. Taken
together, this novel index of local coupling may have many applications in improving our
understanding of local and widespread interactions across large-scale functional networks.

INTRODUCCIÓN

The brain is a dynamic system that integrates information in order to fulfill its functions. Este
system is characterized by both short- and long-range connections between regions that are
organized into large-scale brain networks (Fox et al., 2005; Power et al., 2011; Yeo et al.,
2011). The coupling in activity between different brain regions is referred to as functional
conectividad (FC). FC is typically measured by indices of statistical dependence, such as cor-
relation coefficients, coherencia, or transfer entropy (Baccalá & Sameshima, 2001; Patel et al.,
2006; Vicente et al., 2011). In human functional magnetic resonance imaging (resonancia magnética funcional), el
Pearson correlation derived from blood oxygen level–dependent (BOLD) time series is the
dominant means of quantifying FC and drawing inferences on neural coupling (Biswal
et al., 1995; David et al., 2004; Fiecas et al., 2013; Mahadevan et al., 2021).

Citación: Yu, y., graton, C., & Herrero,
D. METRO. (2023). From correlation to
comunicación: Disentangling hidden
factors from functional connectivity
cambios. Neurociencia en red, 7(2),
411–430. https://doi.org/10.1162/netn_a
_00290

DOI:
https://doi.org/10.1162/netn_a_00290

Supporting Information:
https://doi.org/10.1162/netn_a_00290

Recibió: 18 Marzo 2022
Aceptado: 2 Noviembre 2022

Conflicto de intereses: Los autores tienen
declaró que no hay intereses en competencia
existir.

Autor correspondiente:
Yuhua Yu
yyu@u.northwestern.edu

Editor de manejo:
Richard Betzel

Derechos de autor: © 2022
Instituto de Tecnología de Massachusetts
Publicado bajo Creative Commons
Atribución 4.0 Internacional
(CC POR 4.0) licencia

La prensa del MIT

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

/

/

t

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

7
2
4
1
1
2
1
1
8
4
5
5
norte
mi
norte
_
a
_
0
0
2
9
0
pag
d

t

.

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

From correlation to communication

Local coupling:
The causal interaction between two
neural regions that can be modulated
by influences such as the synaptic
strength or entrained oscillation.

Shared input:
Neural signals that simultaneously
affect two coupled network regions.

Unshared input:
Neural signals that are idiosyncratic
to one of the coupled network
regiones.

While functional connectivity patterns are largely stable over time within an individual
(Gordon et al., 2017; Gratton et al., 2018; Laumann et al., 2015), there is evidence that task
context induces subtle changes in FC (Arbabshirani et al., 2013; Cole y col., 2014; González-
Castillo & Bandettini, 2018; Gratton et al., 2016, 2018; Kriene et al., 2014; Wu et al., 2021).
Changes in FC between rest and task can help us understand how functional networks support
human cognition (Allen et al., 2014; Chang & guantero, 2010; Kietzmann et al., 2019), but its
interpretation remains controversial (Hutchison et al., 2013; Laumann & Snyder, 2021). Alguno
authors have raised concerns about interpreting change in correlation as change in neural cou-
pling (Behseta et al., 2009; Friston, 2011; Laumann et al., 2017). Por ejemplo, Duff et al.
(2018) suggested that many changes in BOLD correlation can be attributable to “additive sig-
nal change,” where a separate signal is added to one or both neighboring nodes. Additive
signal changes include changes in noise levels or the amplitude of a common signal driving
correlation between two nodes. By making an inference from the relationship between
changes in variances and covariances, the authors distinguished additive signal changes from
changes involving more complex combination of increases and decreases in the strength of
existing signal components. A conjunction analysis incorporating variances and covariances
was also proposed by Cole et al. (2016) to investigate the shared and unshared signals in
BOLD data.

In the current project, we distinguish two types of factors driving the change in BOLD FC
(Cifra 1). The first type involves a change in the local coupling between two nodes. Local
coupling can be altered by increased synaptic strength (p.ej., Yao et al., 2007; Zucker &
Regehr, 2002) in the cortical circuit. Local coupling can also be instantiated when the oscil-
lation in a neuronal group is entrained by the oscillation from another group (Fries, 2005).
Local coupling is closely related to the causal influence1 (Friston, 2011) between two regions,
regardless of anatomical distance.

The second type of factor involves input from the rest of the network that modulates the FC
of an edge even in the absence of causal interaction between two neighbors. We differentiate
two subtypes here. The first subtype, shared input, is comprised of neural signals that simul-
taneously affect both neighbors. Por ejemplo, increases in the correlation between visual
regions during visual stimulation could be explained by shared activity induced by the same
stimulus. There is also considerable evidence showing that the ascending arousal system plays
a role in modulating functional network topography globally (Guedj et al., 2017; Shafiei et al.,
2019; Brillar, 2019; Brillo y col., 2016, 2018; Turchi et al., 2018). Projections from critical neu-
romodulatory sources like the dorsal raphe, locus coeruleus, ventral tegmental area, pedun-
culopontine nucleus, and the cholinergic basal forebrain are widespread, thus making these
regions potential sources of shared input (Aston-Jones & cohen, 2005; Mena-Segovia &
Bolam, 2017; Morales & Margolis, 2017; Selden et al., 1998; Brillar, 2019). The second sub-
tipo, unshared input, involves neural signals that are idiosyncratic to each node of a pair. Para
ejemplo, signals from different modalities (p.ej., visual and auditory) can project to separate,
but coupled regions in the higher order cortex (Sepulcre et al., 2012). Unshared input can also
include local neural noises (Daunizeau et al., 2012) or measurement errors. Regardless of the
mechanism, the two subtypes of input are exogenous to the causal interaction between two
neighbors, and we collectively refer to them as (nonlocal) network input.

While neither network input, nor local coupling can be observed directly with fMRI, nosotros
aim to estimate their contributions to task-induced FC change by incorporating information
regarding the temporal variance of the BOLD signal. Específicamente, we focus on the FC changes

1 A pesar de, in the present work, we do not attempt to address the directionality in the local coupling.

Neurociencia en red

412

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

/

t

/

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

7
2
4
1
1
2
1
1
8
4
5
5
norte
mi
norte
_
a
_
0
0
2
9
0
pag
d

t

.

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

From correlation to communication

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

/

t

/

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

7
2
4
1
1
2
1
1
8
4
5
5
norte
mi
norte
_
a
_
0
0
2
9
0
pag
d

t

.

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 1. A schematic representation. Different factors can drive functional connectivity across contexts. When the BOLD correlation
between two regions increases, it can stem from stronger coupling between the two regions (direct synaptic input, etc.), higher shared input
from the rest of the network, or decreased unshared input that is idiosyncratic to one of the regions.

Communication change:
The part of task-induced functional
connectivity change that cannot be
attributed to the change of shared
and unshared input.

Partial correlation:
The correlation between a pair of
time series after the portion of their
variance explained by all other
observed time series is removed.

under “task state” that occur over a block (multiple minute period). Like correlation, BOLD
signal variance can change over contexts. Por ejemplo, resting-state BOLD data has been
reported to have a higher variance than task BOLD data (Ito et al., 2020). Sin embargo, for a pair
of neighbors, the shared and unshared input variance can have opposing effects. Shared sig-
nals are expected to increase the correlation between the pair while unshared signals to atten-
uate the correlation. We aim to quantify this relationship in both simulation and real data by
estimating the network input variance from BOLD signals.

Our simulation not only highlights the multiple factors modulating FC but also provides
insight on a new measure, communication change, that may be used to track local coupling
more closely than FC. Communication change utilizes a learned relationship between FC and
input variances during a baseline (or resting state) to mitigate the impact of input fluctuation on
task-induced FC change. Sin embargo, unlike correlation or partial correlation (see below) eso
can be used as a “standalone” metric for functional connectivity, communication change is
a method to disentangle factors underlying FC changes across task contexts.2

Previous work has used partial correlation (Marrelec et al., 2006) to disentangle the impact
of local coupling from the mutual dependencies on other brain regions. Partial correlation cal-
culates the correlation between a pair of time series after the portion of their variance
explained by all other observed time series is removed. De este modo, partial correlation can capture
a similar concept as communication change, but with a different modeling and computational
acercarse. To evaluate how partial correlation is affected by the changes in local coupling and
network input, we analyzed it in the same simulation framework.

2 In the following text, we may omit the word change when we refer to communication change for

convenience.

Neurociencia en red

413

From correlation to communication

When examining empirical data, we found that network input account for a significant but
moderate amount of task-induced FC change. To estimate FC and input variances during task
actuación, we used BOLD signal residuals after removing evoked task effects following the
“background connectivity” approach (Al-Aidroos et al., 2012; Fair et al., 2007). Depending on
the task context, communication change sometimes suggests local coupling changes in the
opposite direction as FC change would indicate. To gain insights into the informational con-
tent of communication change, we investigated whether it can reliably discriminate task type.

RESULTADOS

FC Is Sensitive to Both Local Coupling and Network Input, While Communication Tracks Local Coupling

More Closely
We simulated two interacting neural regions with a two-dimensional Wilson–Cowan dynamic
modelo (wilson & Cowan, 1972.) to illustrate that (1) FC change is sensitive to local coupling as
well as to network input and (2) the impact of network input is dampened in the communi-
cation change measure where the contribution from the rest of the network, proxied by shared
and unshared input variance (see section Communication Change in Methods), is removed
from FC changes. BOLD signals were computed from simulated neural activity via the
Balloon–Windkessel model (Friston et al., 2003). FC and communication changes were
derived from the simulated BOLD series. Throughout, we refer to the temporal correlation
between nodes in this model as “FC,” in equivalence to BOLD correlation.3

With all parameters (including the local coupling weight and shared/unshared neural signal
variances) fixed, we computed baseline FC, baseline input variance for each node, and regres-
sion coefficients of FC with respect to the input variance. These values will be used to compute
communication change in the following scenarios: (1) after varying local coupling strength, (2)
after varying shared neural signal variance, y (3) after varying unshared neural signal
variance.

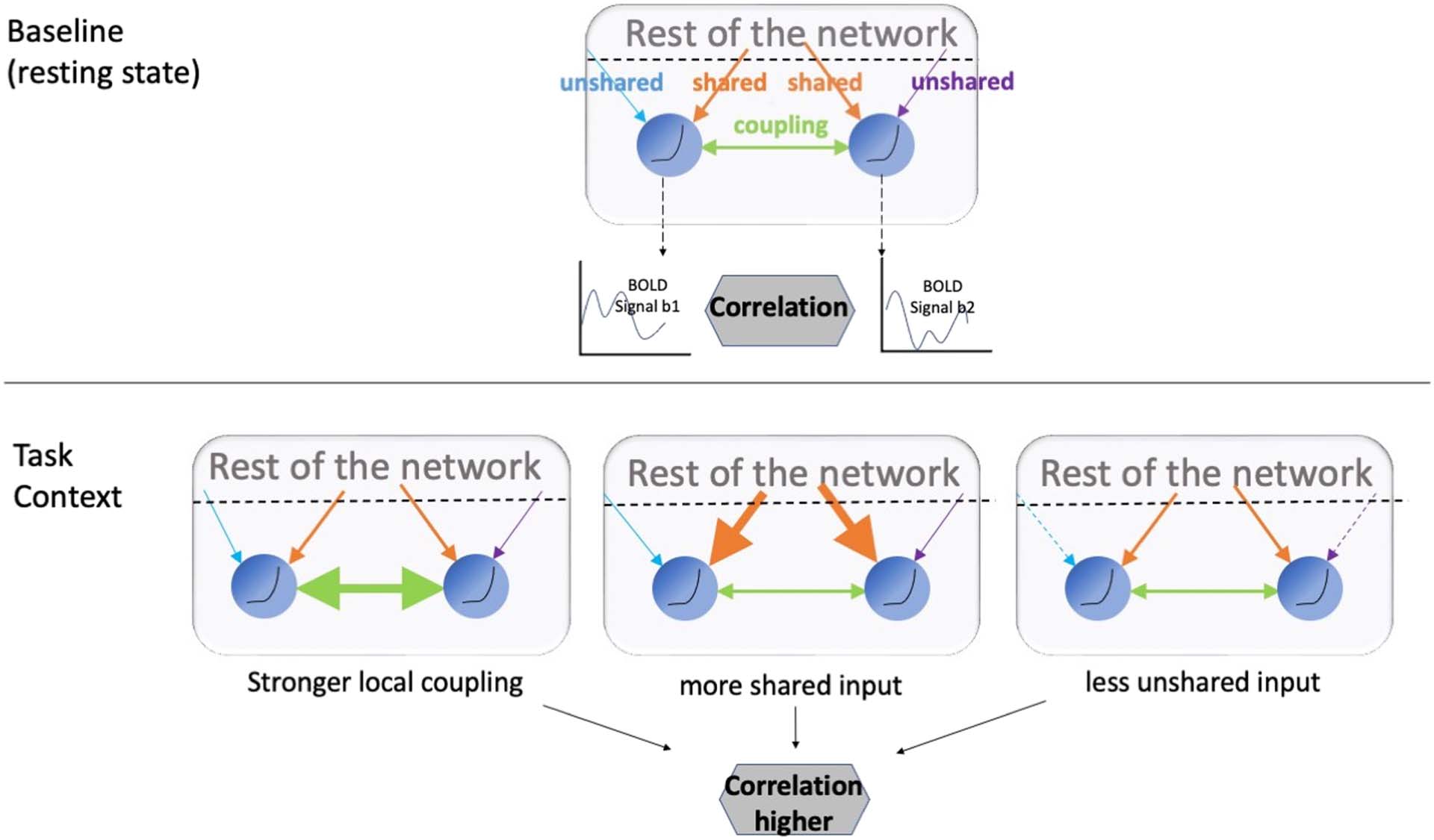
As expected, simulated FC is sensitive to both changes in local coupling and changes in
input signal variance, confounding the interpretation of FC measures. Both stronger local cou-
pling (Figura 2A) and amplified shared signal (Figura 2B) lead to higher FC, while amplified
unshared signals (Figura 2C) lowered the FC. En comparación, communication change shows a
dampened relationship to shared and unshared signal variance while remaining sensitive to
the local coupling (Figure 2A–C). Por ejemplo, with the current simulation setup, both FC and
communication were equally sensitive to local coupling. Sin embargo, FC was 5 times more sen-
sitive to shared signal (the slope in Figure 2B) y 2.5 times more sensitive to unshared signal
(the slope in Figure 2C) relative to communication.

Given that partial correlation is often used to account for the mutual dependence on other
regiones del cerebro, we computed partial correlation in the same three scenarios (see Methods). Nosotros
asked: Does partial correlation have less dependence on input signal variance than FC? En el
current simulation framework, partial correlation had similar sensitivity as FC with respect to
changes in local coupling and input signals (Figura 2D-F). Por lo tanto, it cannot discriminate
among those factors.

This analysis suggests that communication, compared to correlation and partial correlation,
more closely tracks changes in local coupling relative to changes in input variance. Commu-
nication diminishes the impact of network input by using the statistical relationship between

3 A pesar de, as discussed in the Introduction, correlation is only one of many possible ways to estimate func-

conectividad nacional.

Neurociencia en red

414

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

t

/

/

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

7
2
4
1
1
2
1
1
8
4
5
5
norte
mi
norte
_
a
_
0
0
2
9
0
pag
d

.

t

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

From correlation to communication

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

/

/

t

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

7
2
4
1
1
2
1
1
8
4
5
5
norte
mi
norte
_
a
_
0
0
2
9
0
pag
d

t

.

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 2. The sensitivity of FC, comunicación. and partial correlation with respect to model parameters. (A) Both FC and communication
increase with the coupling strength ( W.). (B) FC (but not communication) increases sharply with increases in shared signal variance. (C) FC
decreases with unshared signal variance while the effect is dampened for communication. (D-F) FC and partial correlation in the same sim-
ulated scenarios display similar behavior to one another.

FC and variance in a baseline state. Notablemente, this is an imperfect proxy because input signals
are unobservable in real data. Por lo tanto, communication is not guaranteed to have zero sen-
sitivity to shared and unshared input variances, but their impact is considerably dampened as
observed from the simulation. This property allows us to infer the change in local coupling
from real data when neither the coupling nor input signals are directly observable.

FC Is Related to Shared and Unshared Input Variance in Real fMRI Data

To compare communication and FC in empirical data, we used Midnight Scan Club (MSC)
conjunto de datos (Gordon et al., 2017), a precision fMRI dataset with 10 sessions of fMRI rest and task
data from nine participants. See Methods for BOLD data acquisition, preprocessing, FC, y
variance calculation for resting-state and task data. We computed BOLD FC, shared input var-
iance, and unshared input variance for each of the 10 resting-state scans. We fit a linear model
for each edge with the FC as the dependent variable and shared/unshared input variance as
independent variables. As expected, FC increased with shared input variance and decreased
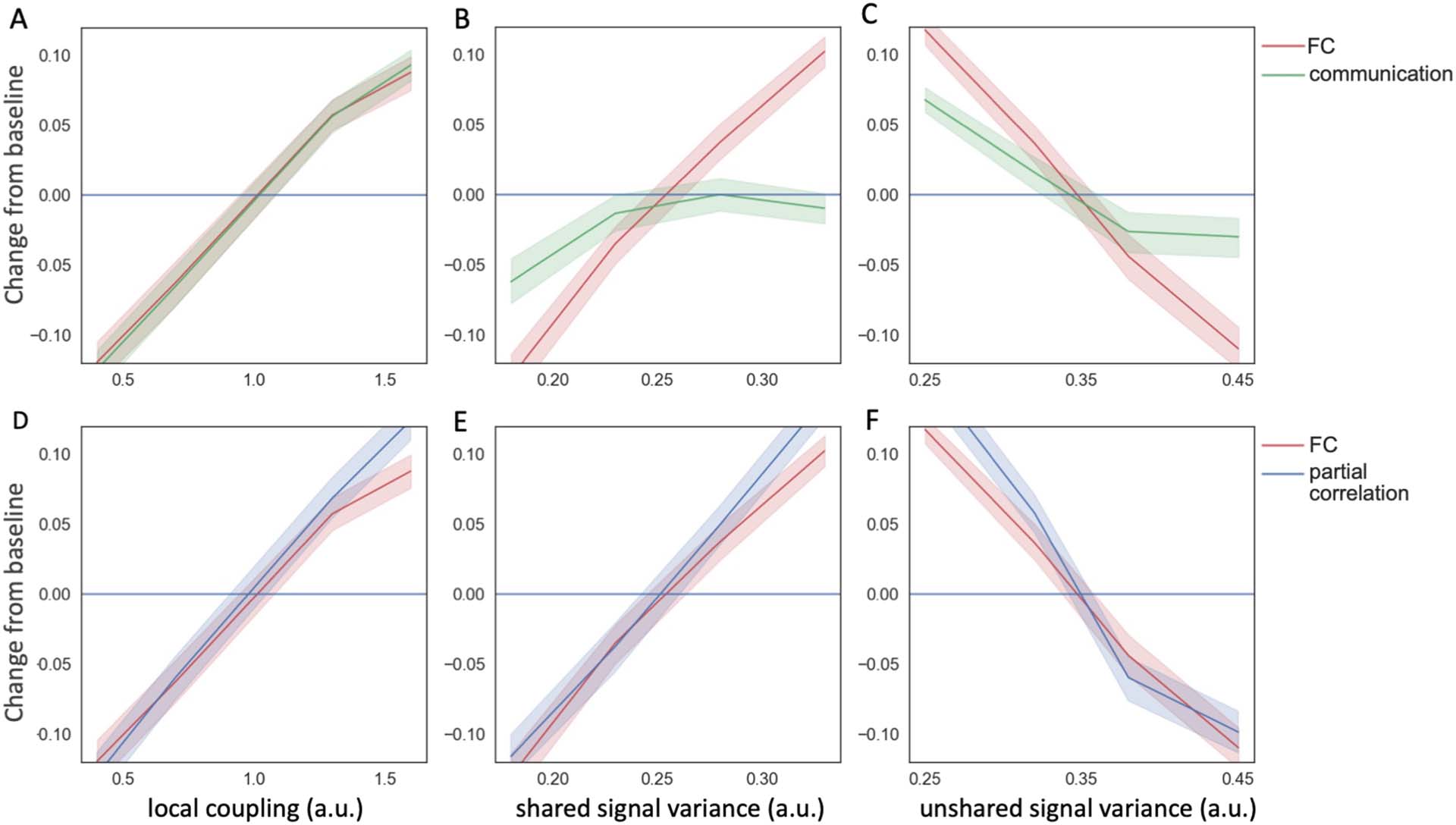
with unshared input variance in the MSC data. Cifra 3 shows the distribution of the regression
coefficients of all participants. Network input fluctuations jointly explained 24.7 ± 0.1% (adj.
R2) of the FC variability across resting-state sessions. Results from individual participants all
show a similar pattern and are included in Supporting Information Figure S1, indicating robust-
ness of the results.

De este modo, the empirical relationship between FC and network input is consistent with what we
observed in the simulation: FC increases with the shared input variance and decreases with
unshared variance idiosyncratic to one of the nodes. We next use the regression coefficients

Neurociencia en red

415

From correlation to communication

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

/

/

t

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

7
2
4
1
1
2
1
1
8
4
5
5
norte
mi
norte
_
a
_
0
0
2
9
0
pag
d

t

.

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 3. Distribution of regression coefficients of FC against the unshared and unshared input
variance in the Midnight Scan Club. The regression is run for each edge across resting-state scans
for each participant. Error bars show a standard error across edges. Data from all participants and
edges are plotted here. Results for individual participants are shown in Supporting Information
Figure S1.

learned from resting state to estimate the contribution of input variance in FC during task-
induced contexts.

Task-Induced FC Changes Are Related to Changes in Network Inputs

Próximo, we asked whether task-induced FC change can be predicted by network inputs, esti-
mated from variance changes. We computed the predicted FC changes during task perfor-
mance from the observed input variance change under (Ecuación 1). There was a significant
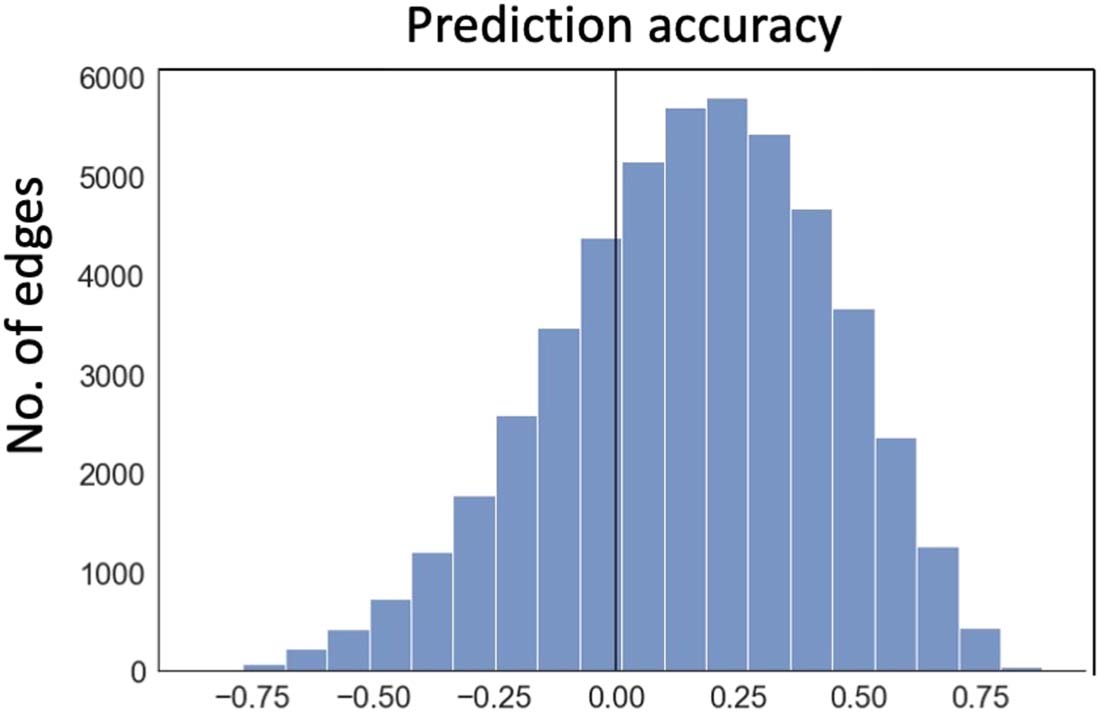
correlation between the predicted and actual FC changes across tasks for the majority of the
bordes (ver figura 4 for the aggregated group distribution of the correlations, mean is 0.152 ±
0.001; individual participants are shown in Figure S2). This indicates that input fluctuation
explains a small but significant proportion of task-evoked FC changes. The prediction error,
eso es, communication change in our definition, is the part of the FC change not explained by
input fluctuation.

predicted ΔFC ¼ β0 * Δshared input variance þ β1 * Δunshared input variance1

þ β2 * Δunshared input variance2

(1)

where β’s are computed from resting-state data (Cifra 3) and input variance changes are mea-
sured from the comparison in variances between task and rest.

Communication Change Differs From FC Change and Shows Improved Sensitivity to Task Information

Since the previous simulations suggest that communication tracks local coupling while damp-
ening the impact of input fluctuation, we next directly compare FC and communication mea-
sures in real data. We compared the task-induced changes in each measure, grouping edges

Neurociencia en red

416

From correlation to communication

Cifra 4. Ability of changes in input variance to predict FC changes during tasks in real fMRI data
from the Midnight Scan Club. For each edge, accuracy was measured using the correlation coeffi-
cients between actual FC changes and those predicted by task-induced input variance changes
across 30 task conditions (10 sessions for categorization tasks, 10 for motor task, y 10 for mixed
tarea). Data plotted here is based on the group average; individual participant relationships are
shown in Figure S2.

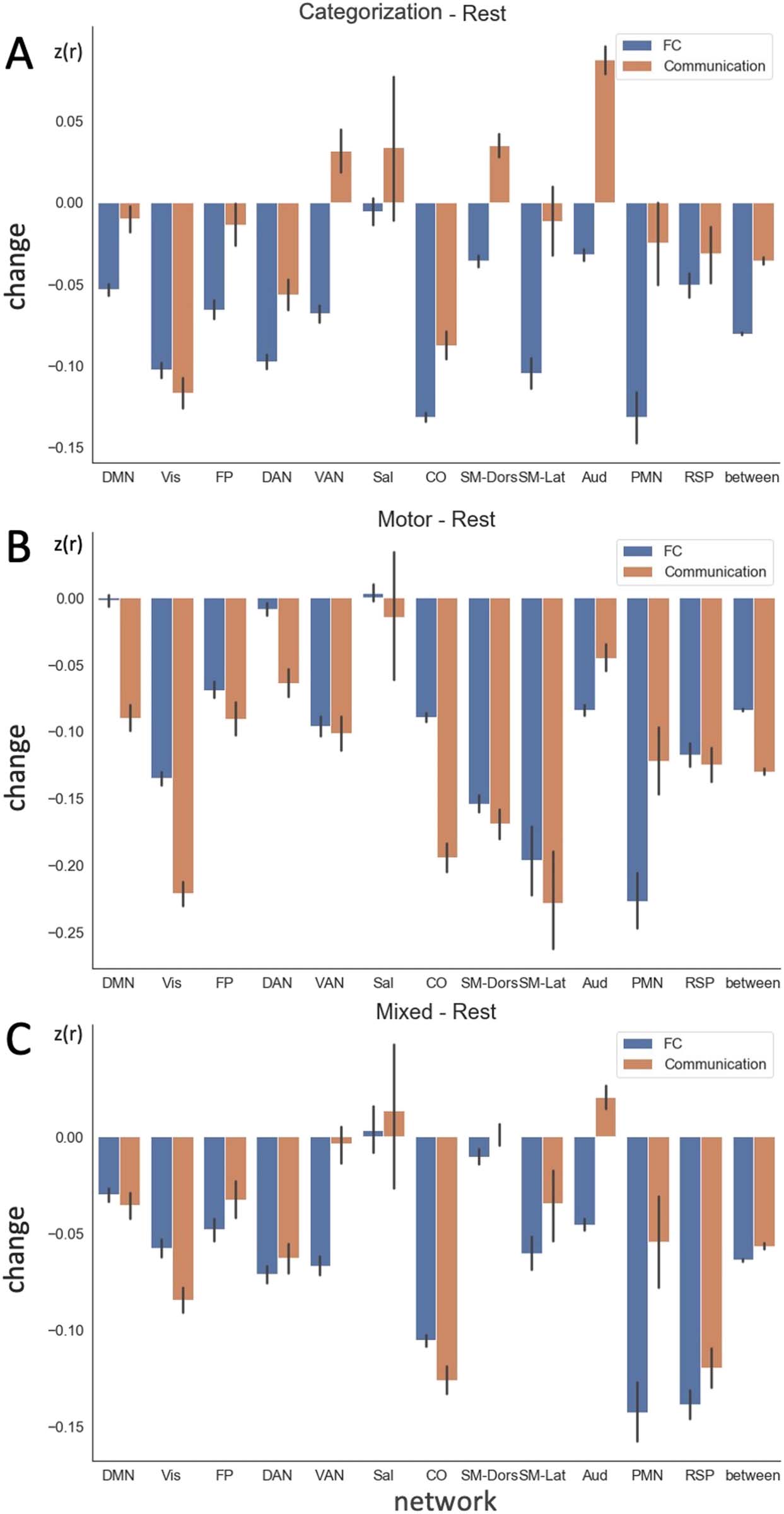
according to a widely used large-scale network designation (Gordon et al., 2016). comunal-
cation and FC changes during tasks differed in many networks and these differences were
modulated by the task type (Cifra 5). Sometimes communication was higher magnitude than
FC, and other times it was lower; on occasion it even showed relationships in the reverse
direction. Por ejemplo, when participants performed the categorization task4 (Figure 5A),
FC decreased on average within the ventral attention network, while communication (calcu-
lated from FC after removing the contribution from input variance, see Methods, Ecuación 2)
increased. This highlights the danger of interpreting an FC decrease directly as reduced inter-
regional interaction.

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

/

/

t

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

7
2
4
1
1
2
1
1
8
4
5
5
norte
mi
norte
_
a
_
0
0
2
9
0
pag
d

t

.

Intraclass correlation coefficient:
The percentage of variance
accounted for by the group
difference out of the overall
population variance.

To probe the informational content in the communication measure, we ask to what extent it
can discriminate among tasks with distinct task demands. Para tal fin, we computed the intra-
class correlation coefficient (CPI; see Methods) between task types for each edge across all
scan sessions (4 task types including the resting state with 10 sessions each). ICC measures
the percentage of variance accounted for by task types among all changes observed for the
same edge (Bartko, 1976; McGraw & Wong, 1996). If communication change contains task
información, ICC5 is expected to be closer to 1 (rather than to 0).

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

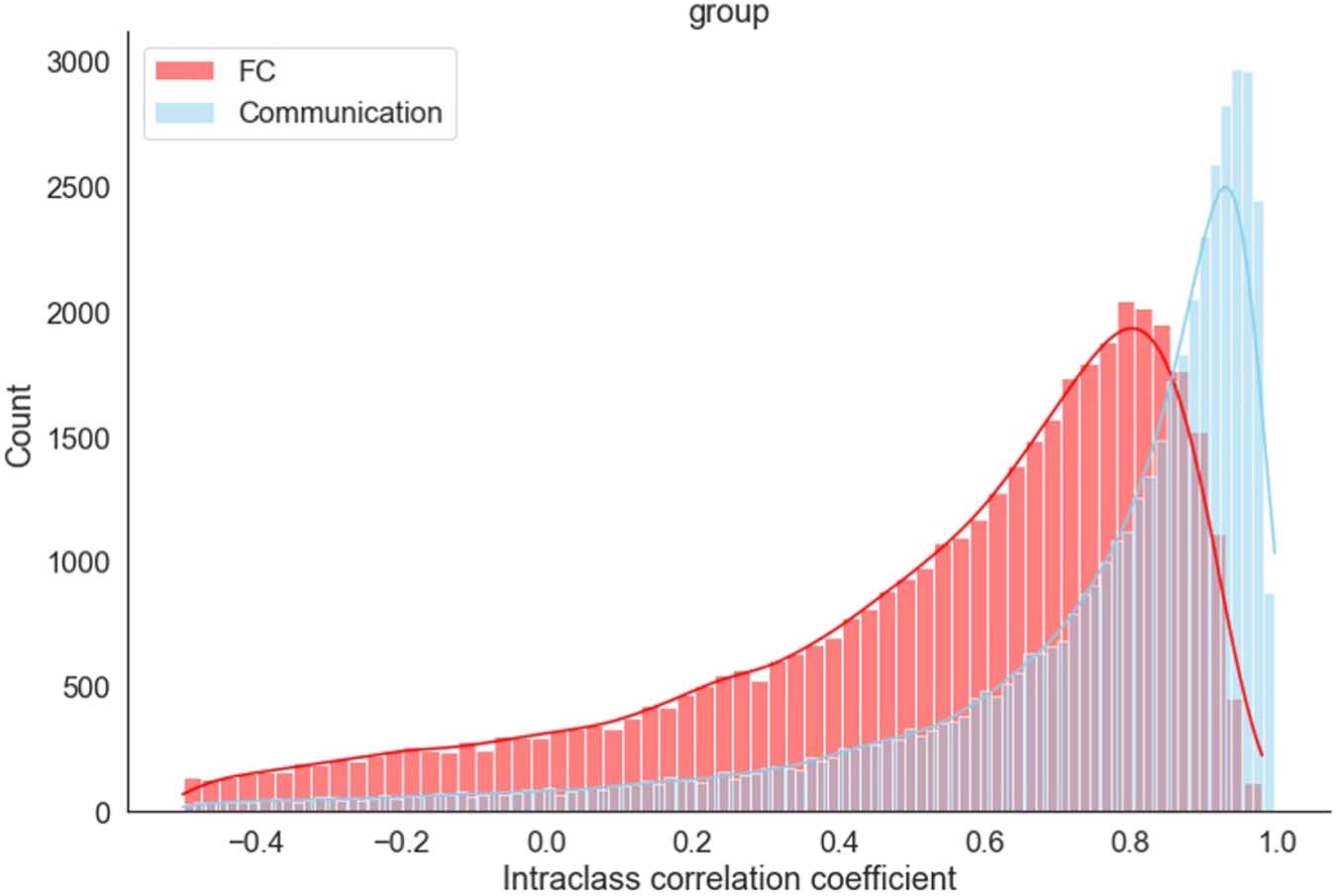
Across all edges and all participants, the average communication ICC = 0.699 ± 0.001,
con 71% of the edges showing a a p value less than 0.05 (F test), indicating that most edges
contain reliable information about task type (Cifra 6). For comparison, we computed the ICC
for FC changes using the same methodology. Similar to communication, FC changes reliably
represent task information (ICC = 0.462 ± 0.001; Cifra 6). Sin embargo, the ICC based on the

4 This task was called “memory task” in previous publications using the MSC dataset. We label it as “catego-

rization” here to better reflect the nature of the task; see Methods.

5 Although ICC is theoretically bounded by 0 y 1, in practice it is possible to obtain negative, unbounded
values due to sampling issues (Bartko, 1976). Por ejemplo, when the sample size is small, el estimado
within-group variance may exceed the variance of the whole population. It is often recommended that neg-
ative values be cut off. Although the threshold can affect the ICC statistics, our conclusion does not change
whether or not we apply the cutoffs.

Neurociencia en red

417

From correlation to communication

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

t

/

/

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

7
2
4
1
1
2
1
1
8
4
5
5
norte
mi
norte
_
a
_
0
0
2
9
0
pag
d

t

.

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 5. Group averaged, task-induced changes in FC and communication for all edges grouped by network affiliation during (A) catego-
rization task, (B) motor task, y (C) mixed task (dot coherence and semantic) relative to rest in the MSC. Error bar indicates the standard error
across edges. Data from individual participants are shown in Figure S3. DMN = default mode; Vis = Visual; FP = fronto-parietal; DAN = dorsal
atención; VAN = ventral attention; Sal = salience; CO = cinguloopercular; SM-Dors = dorsal somatomotor; SM-Lat = lateral somatomotor;
Aud = auditory; PMN = parietal memory; RSP = retrosplenial; between = between-network connectivity.

Neurociencia en red

418

From correlation to communication

Cifra 6. Distribution of intraclass correlation coefficients (CPI), across all edges and participants,
for discriminating among task conditions. The ICC between task types was computed for each edge
across 40 scans (10 each for rest, categorization, mezclado, and motor). Data from individual partic-
ipants are shown in Figure S4.

communication measure is significantly higher than the ICC of FC (z = 140, pag < .00001), sug- gesting that communication change increases the discrimination of task type. The same pattern was observed consistently for all participants (Figure S4). The difference between FC and communication in terms of task discrimination is not solely driven by the distinction between the resting state and any task state. ICC among the three task states exhibits a similar pattern (although the difference is narrower, z = 77, p < .00001; see Figure S5) indi- cating that communication change contains more task-specific information relative to FC. In summary, communication changes during tasks exhibit significant differences from FC in various networks of the brain. Importantly, communication contains more informational con- tent to discriminate specific task types, compared to FC. DISCUSSION While BOLD correlation is widely used to capture both static functional connectivity and its changes across contexts, the interpretation of this measure is often ambiguous. The entangle- ment of multiple latent factors including local coupling of two neighbors and network inputs from the rest of the network limits the scope of the conclusions that can be drawn from cor- relation measures alone. Here, we developed a method to compute the shared and unshared input variance to an edge and quantify their impact on task-induced FC changes. We further proposed a metric, termed “communication change,” that dampens the impact of input signals and thereby provides a promising candidate for more closely tracking local coupling changes. We first analyzed local and network impact on FC by conducting a simulation based on a well-established model of neural dynamics (Wilson & Cowan, 1972). The model suggests that FC can be driven by multiple factors. Increased local coupling as well as increased variance of shared inputs result in higher FC, while increases in the variance of unshared (idiosyncratic) input has the opposite effect. Although the conclusion seems intuitive, explicit modeling of the Network Neuroscience 419 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 7 2 4 1 1 2 1 1 8 4 5 5 n e n _ a _ 0 0 2 9 0 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 From correlation to communication three latent factors leads to a novel metric, communication, that dampens the impact of both shared and unshared inputs using only observable, statistical relationships. Our simulation shows that communication change is more likely to track local coupling. Interestingly, partial correlation, a metric often used to disentangle the impact of local cou- pling from the mutual dependencies on other brain regions (Marrelec et al., 2006; Smith, 2012), shows similar sensitivity as FC change in the current simulation framework. Partial cor- relation removes the contemporaneous signal dependence by using a linear residualization. However, as the BOLD signal exhibits temporal nonlinearity, the transformation from neural activity to BOLD signal (via Ballon–Windkessel model) is state and path dependent (Buxton et al., 2004; Friston et al., 2000). It is possible, therefore, that the correlation between residua- lized signals is still affected by the network input through their “history.” We are not aware of other simulative studies illustrating the (lack of ) efficacy of partial correlation, except for Cole et al. (2016), where the authors also reported that partial correlation retains limitations of the FC measure. In comparison, to compute communication change, we first aggregated inputs from the rest of the network into three terms, shared variance and two unshared variances idiosyncratic to each node. Communication then removes the input contribution via a “learned” statistical relationship between FC and variance at baseline (here operationalized as the average resting-state signal). Therefore, the method makes few assumptions about the underlying structure of the input signals. With empirical data, we computed the sensitivity of FC with respect to shared and unshared input during resting-state scans. As expected, FC in real BOLD data increased with the vari- ance of shared input and decreased with unshared input. We then analyzed task-induced FC changes using the coefficients learned from the resting state. Input fluctuation explained a sig- nificant, but moderate, amount of FC changes during task performance. After removing the input related contributions, the remaining FC change, that is, communication change, often had the opposite sign of the original FC change in various tasks and brain networks. This high- lights the ambiguity of interpreting task-induced FC change by itself. If the correlation of an edge increases, for example, it can be driven by an increase in shared input from the rest of the network, a decrease in an idiosyncratic input affecting only one of the nodes, an enhanced neural coupling between the nodes, or any combination of the above factors. Although we cannot directly observe how communication differentiates mechanisms behind FC changes in empirical data, evidence suggests that it shows better discrimination across the task types relative to the standard FC measure. Both simulation and empirical anal- ysis suggest that communication may be an improved measure (from FC) for tracking changes in causal interactions between regions across task contexts. Such changes can occur at the synaptic level due to short-term plasticity (Krystal et al., 2003; Yao et al., 2007; Zucker & Regehr, 2002), such as an elevated dopamine tone in the same cortical circuit (Vijayraghavan et al., 2007) and via increased coherence or phase locking (Fries, 2005). While FC is strongly related to shared and unshared network inputs, communication shows a diminished relationship to these latent signals. Shared input can arise from signals with wide- spread influence stemming from subcortical projections (Raut et al., 2021; Shine, 2019), while unshared (idiosyncratic) input can come from, for example, unique inputs from different modalities (visual or somatosensory) that only project to selected regions. The communication metric dampens the impact of network input changes using a statistical relationship and remains agnostic to the underlying biophysiological mechanism. This allows contextual fac- tors to guide the interpretation of the difference between FC and communication across a vari- ety of states. Network Neuroscience 420 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 7 2 4 1 1 2 1 1 8 4 5 5 n e n _ a _ 0 0 2 9 0 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 From correlation to communication Using BOLD Variance to Augment the Interpretation of FC Other researchers have also explored the idea of incorporating variance (or covariance) to disambiguate the interpretation of FC (Duff et al., 2018; Cole et al., 2016). For example, Duff et al. (2018) combined correlation and variance to classify FC changes into cases attributable to “additive signal change” (a type of “shared or unshared input”) and changes arising from modifying existing signals. While the current analysis echoes the importance of augmenting FC with variance/covariance, we propose a framework to quantitatively decompose FC changes into contributions from different underlying mechanisms. Communication shows higher intraclass correlation across tasks compared to FC, suggest- ing that the proposed measure better discriminates task types. This suggests that local coupling is modulated by specific task demands, while overall signal variance contains less task-specific information. Previous work has shown a simultaneous task-induced reduction in FC and var- iance (Ito et al., 2020). It is possible that task performance, relative to the resting state, reduces synchronized, spontaneous activity that affects a large region of the brain and leads to an FC reduction in a pattern that is similar across task types. By extracting the “excess” FC change after accounting for the variance-related effects, we can gain more insight into how specific task demand modulates the brain network. Furthermore, the current framework provides a way to decompose exogenous network inputs into shared and unshared variance. One powerful approach may be to use several of these metrics in combination. For example, an increase in communication implies stronger local coupling. If a decrease in FC is simultaneously observed, we can ask whether the discrepancy is due to a reduction of shared signal or an increase of idiosyncratic inputs by examining changes in shared and unshared variance simultaneously. Therefore, examining communication together with FC may allow researchers to draw inferences regarding how a particular region adjusts its interactions with its neighbors across a range of different contexts, providing an improved handle on whether local or shared inputs are at work in any given scenario. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 7 2 4 1 1 2 1 1 8 4 5 5 n e n _ a _ 0 0 2 9 0 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Limitations and Future Directions One pitfall of our approach is that the interpretation of our simulation results is dependent on the validity of our computational model. The communication change metric was inspired by a simplified neural dynamic simulation. Although Wilson–Cowan dynamics have been widely used and have had a major impact on computational neuroscience, it is a simplification of the underlying biological process (Chow & Karimipanah, 2020). Many extensions and generaliza- tions have been proposed since its initial introduction in 1972. To highlight the basic interac- tion between several statistical measures of interest, we adopted the simplest form of the model in a two interacting nodes setup. By doing this, we imposed the assumption that any effect from the rest of the system could be represented by Gaussian signals. Furthermore, we fixed the mean of the input signals and focus on the impact of their variance/amplitude. Because the neural dynamics involve sigmoid activation functions, the shift in the average level of the input signal would have a nonlinear impact on the resulting fMRI BOLD signals (Ito et al., 2020). Future work will explore how the average activity level interacts with the relationship between FC and input variances discussed in this article. When it comes to empirical data, a key premise of our analysis is based on evidence that fMRI signals are indirectly related to underlying neural population activity. Such a view is widely supported in the literature (Logothetis et al., 2001; Ma et al., 2016), but certain MRI artifacts can ambiguate the results (Friston et al., 1996). We employed multiple artifact Network Neuroscience 421 From correlation to communication mitigation measures (scrubbing, motion regression, global signal regression, white matter sig- nal regression, and ventricle signal regression) to minimize the impact of artifactual factors. Moreover, the BOLD signal analyses utilized nine highly sampled subjects from the MSC dataset (Gordon et al., 2016). This is a small sample, but there is evidence that results from MSC data extend to other independent datasets (Gordon et al., 2018). Importantly, the single subject results presented here are consistently observed in all individuals, demonstrating a cer- tain degree of robustness. However, communication change should be examined in other datasets in future work, especially with task conditions that impose varying degrees of cogni- tive demand and a larger number of subjects. There are unanswered questions that are beyond the scope of the current investigation that pertains to communication change. Task-induced communication increases in some regions (e.g., visual network, dorsal attention network), and the magnitude of the changes seems to be modulated by the type of task. In addition, the spatial pattern of communication exhibits sig- nificant individual differences (Figure S3), consistent with findings from previous work (Gratton et al., 2018; Porter et al., 2023). An intriguing question for future research is how differential communication is related to task performance. Finally, task discrimination is only one possible venue to explore the informational content in communication and its advantage over FC. Research directly modifying potentially wide- spread signals such as arousal (shared input), signals that might be expected to be more local such as selective stimulus-response features (unshared input), or manipulation at the local syn- aptic level (coupling) may help to validate the interpretation of communication change. Conclusions FC, computed as a correlation between paired BOLD signals, is not only determined by local coupling between pairs of regions but also by inputs from the rest of the network, among other factors. Utilizing the statistical relationship between FC and input variance, we developed a method to extract a component (communication change) from FC change with a dampened influence of network input. Examining changes in communication, along with FC, allows us to draw inferences regarding how the interaction between a particular region with its neighbors changes across different contexts. MATERIALS AND METHODS We used a combination of numerical simulations and empirical analysis to examine the effects of local interactions and input fluctuations on BOLD correlation and variance. These results led us to develop a new measure, communication change, that more closely tracks the change in coupling between two neural regions compared to the standard FC measure (BOLD correlation) across task contexts. Below, we first describe our modeling approach, then the derivation of the communication metric, and finally we include a description of a dataset and analyses used to empirically examine differences in communication change and correlation. Compute Communication Change in Both Simulated and Real Data We developed a novel metric to better capture the interregional coupling shift in task-induced FC change, which we termed communication change. To compute the communication change of an edge, we first need to estimate the shared and unshared network input variance. Shared/unshared input variance is computed from the variance of the BOLD signals from common and idiosyncratic neighbors. Specifically, assume node1 and node2 are the nodes of Network Neuroscience 422 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 7 2 4 1 1 2 1 1 8 4 5 5 n e n _ a _ 0 0 2 9 0 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 From correlation to communication the edge under consideration. Ns is the set of neighboring nodes that connect to both node1 and node2. N1 is the set of nodes that only connect to node1, and N2 is the set of nodes that only connect to node2. That is, Ns, N1, and N2 are mutually exclusive. Shared input variance is the total variance of the BOLD signals from Ns, computed by the trace of the covariance matrix. We residualized all the signals in N1 against all signals in Ns. Unshared input variance1 is the total variance of the residualized signals in N1. Likewise, unshared input variance2 is the total variance of the residualized signals in N2 against Ns. Communication change is computed with the following equation: ΔComm ¼ ΔFC − β0 * Δshared input variance − β1 * Δunshared input variance1 − β2 * Δunshared input variance2 (2) Where all the changes are based on comparisons of task-rest, or for the simulation, a scenario with parameter shock—baseline. The coefficients β0, β1, β2 are then computed from resting state (or the baseline simulation scenario) using linear regression: FC ¼ β0 * shared input variance þ β1 * unshared input variance1 þ β2 * unshared input variance2 þ constant þ noise (3) l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . All edges and neighbors in empirical data (including rest and task) are defined by 5% spar- sity based on the average resting-state correlation. We reevaluate the key findings using 10% sparsity and reached similar conclusions (Figure S6). Numerical Simulation of BOLD Signals From Two Interacting Neural Regions We examined the effects of local coupling and network inputs on BOLD correlation with a numerical simulation. A two-dimensional (two node) Wilson–Cowan type (Wilson & Cowan, 1972) dynamic was used to describe the activity of two interacting neural regions: τ dx1 tð Þ dt τ dx2 tð Þ dt ¼ −x1 tð Þ þ f w11x1 tð Þ þ w12x2 tð Þ þ s tð Þ þ I1 tð Þ ð Þ ; ¼ −x2 tð Þ þ f w21x1 tð Þ þ w22x2 tð Þ þ s tð Þ þ I2 tð Þ ð Þ where xi(t) represents the excitatory level of a neural group. (cid:1) (cid:3) The matrix W ¼ w11 w12 w21 w22 describes the information exchange within and between regions. In particular, the off-diagonal terms, w21, w12, determine the strength of interregion coupling. For the baseline scenario, the matrix was set to W ¼ : The diagonal entries (cid:1) (cid:3) 2 1 1 2 t / / e d u n e n a r t i c e - p d l f / / / / / 7 2 4 1 1 2 1 1 8 4 5 5 n e n _ a _ 0 0 2 9 0 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 were fixed throughout the simulation. The parameter values (and those in the following) are adapted from Ito et al. (2020) and adjusted to obtain a realistic baseline correlation. Shared input s(t) is a Gaussian signal with shared signal variance Vsh, which was set to Vsh = 0.25 in the baseline scenario. Vsh indexes the magnitude of the common exogenous input from the rest of the brain network to both regions. I1(t), I2(t) are two independent Gaussian signals representing idiosyncratic signals with unshared signal variance parameter Vun, which was set to 0.35 in the baseline. Vun indexes the magnitude of the idiosyncratic input to one of the neighbors. f is the sigmoid input-output activation defined as f (x) = 1/(1 + e^(−k * x)), where k is fixed at 0.5 throughout the simulation. Network Neuroscience 423 From correlation to communication Neural activities simulated from the above equations were transformed to BOLD signals using the Balloon–Windkessel model (Friston et al., 2003). The transformation assumes normalized deoxyhemoglobin content, normalized blood inflow, resting oxygen extraction fraction, and normalized blood volume. State equations and parameters were taken from pre- vious work (Friston et al., 2003). Correlation (FC), partial correlation, and communication change were then computed on the simulated BOLD signals as specified below. Each simu- lation (1 run) generated a pair of BOLD time series with 2,000 steps each. For the baseline simulation, we ran the scenario with fixed parameters 500 times (500 runs). We obtained the average FC, average shared/unshared input variance, and the regression coef- ficients as in Equation 3. The baseline simulation mimics the resting state as in real data. Next, we computed the sensitivity of correlation, communication, and partial correlation with respect to the input signal variance and local coupling parameters. To this end, we carried out the same simulation as above, but now independently varied the shared signal variance Vsh, unshared signal variance Vun, and the coupling parameter w12 (and symmetrically w21). We used inputs for Vsh ranging from 0.15 to 0.35, Vun ranging from 0.25 to 0.45, and w12 from 0.4 to 1.6 (centered around baseline 1). The range was chosen such that the parameters had comparable impact on FC. For each scenario, the model is run 500 times to obtain the mean and standard deviation of all quantities of interest. Correlation (FC) was then computed between a pair of simulated BOLD timeseries. Communication change was computed as described above. All the variances required in the formula were computed from the simulated BOLD signals. To simulate the input BOLD signals, we applied the Balloon–Windkessel model to transform the shared signal s(t) and the idiosyncratic signals I1(t ), I2(t ). Partial correlation was computed as the correlation between a pair of residualized series, after removing the common variance from the rest of the network. In the current simulation framework, inputs from the rest of the network are represented by the shared/unshared signals. Therefore, we residualized the BOLD signals derived from x1(t), x1(t), against the input BOLD signals derived from I1(t), I2(t), and s(t), and computed the correlation between the residualized signals. MSC Dataset In the second portion of our investigation, we examined the relationship between FC, vari- ance, and communication in an empirical dataset. We used the Midnight Scan Club (MSC), a precision fMRI dataset (Gordon et al., 2017) that contains large quantities of both task and resting-state data was selected, as large amounts of data are required to achieve highly reliable FC measures (Gordon et al., 2017; Laumann et al., 2015). The dataset includes data from 10 participants who each participated in 10 separate fMRI sessions. During each session, each participant completed three different tasks (a motor task, a categorization task, and a mixed dot coherence/verbal discrimination task) and rest. This dataset is described in detail else- where (see Gordon et al., 2017), but we will review parameters relevant to this study below. In addition, a dataset of 120 healthy adults ( WashU-120) was used as a reference set for the network definition and the calculation of graph theoretic metrics (Power et al., 2011; Power et al., 2013). This dataset has been described in detail in Power et al. (2013). Task design. Each resting-state session was 30 min, during which participants were asked to lie still while fixating on a white cross presented against a black background. Each motor task session included two runs (7.8 min total) of a blocked motor task adapted from the Human Network Neuroscience 424 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 7 2 4 1 1 2 1 1 8 4 5 5 n e n _ a _ 0 0 2 9 0 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 From correlation to communication Connectome Project (Barch et al., 2013). In each block (15.4 s in duration), participants were cued to move either their left or right hand, left or right foot, or tongue. Each run included two blocks of each type of movement, as well as three fixation blocks (15.4 s). Each mixed task session included two runs (14.2 min total) that each included four blocks, two of the semantic tasks and two of the coherence tasks. Both tasks had a mixed block/event-related design, mod- eled after the tasks in Dubis et al. (2016). During the semantic task, 30 individual trials were presented, consisting of words presented for 0.5 s with jittered 1.7–8.3 s intervals. Participants were asked to respond whether the words were nouns or verbs (50% nouns and 50% verbs were included). Forty-four second fixation periods separated blocks. During the coherence task (also 30 trials), individual trials consisted of arrays of Glass patterns (Glass, 1969) that were varied in how concentrically they were arranged (50% or 0% coherence to a concentric arrangement, displayed with equal frequency). Participants were asked to respond whether dots were arranged concentrically or randomly. Each categorization task session included three runs of an event-related categorization task with implicit repetitions, with a separate run per stimulus type (face, scenes, and words). Within each run, participants viewed 24 images, repeated three times and made binary decisions. MRI acquisition parameters. High-resolution T1-weighted (224 slices, 0.8 mm3 isotropic reso- lution, TE = 3.74 ms, TR = 2,400 ms, TI = 1,000 ms, flip angle = 8 degrees), T2-weighted (224 slices, 0.8 mm3 isotropic resolution, TE = 479 ms, TR = 3,200 ms) both with 0.8 isotropic resolution, and resting-state BOLD data were collected on a Siemens 3T Magnetom Tim Trio with a 12-channel head coil (Gordon et al., 2017). Functional scans were collected with a gradient-echo EPI sequence, isotropic 4-mm3 voxels, TE of 27 ms, and TR of 2,200 ms (Gordon et al., 2017). The MSC dataset is considered a deep (precision) dataset with 5 hours of resting-state data per subject in 30-min blocks over 10 separate sessions (Gordon et al., 2017). General preprocessing. The T1-weighted images were processed via automatic segmentation of the gray matter, white matter, and ventricles in Freesurfer 5.3 (Fischl et al., 2002). The default recon-all command in Freesurfer was then applied to produce the anatomical surface for each subject (Dale et al., 1999). These surfaces were manually edited to improve the qual- ity of the registration and the surfaces were registered to the fs_LR_32k surface space via the procedure outlined in Glasser et al. (2013). Functional data preprocessing began with field inhomogeneity distortion correction using the mean field map, which was applied to all ses- sions. Slice timing correction was implemented using sinc interpolation to account for tempo- ral misalignment in slice acquisition time. This step was followed by motion correction that was conducted within and across BOLD runs (aligned to the first frame of the first run) through a rigid body transformation. Then whole-brain intensity values across each BOLD run were normalized to achieve a mode value of 1,000 (Miezin et al., 2000). Functional BOLD data was first registered to a T2-weighted image and then to the T1. An affine transformation was employed for registration. The T1-weighted image was aligned to a template atlas (Lancaster et al., 1995) conforming to Talairach stereotactic atlas space (Talairach & Tournoux, 1988) using an affine transformation. All computed transformations and resampling to 3-mm isotropic voxels were simultaneously applied at the end of these steps. Functional connectivity preprocessing. Steps were taken to attenuate the impact of artifacts on BOLD time series. The effect of nuisance signals was mitigated through regression of average signal from the white matter, ventricles, whole brain (global signal), motion parameters, and derivatives and expansion terms of the motion parameters (Friston, 1998; Power et al., 2014). Removal of frames with FD > 0.2 mm, in addition to sequences containing less than five con-
tiguous low-motion frames, the first 30-s of each run, and runs with < 50 low-motion frames Network Neuroscience 425 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 7 2 4 1 1 2 1 1 8 4 5 5 n e n _ a _ 0 0 2 9 0 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 From correlation to communication was performed as an additional safeguard against the impact of motion (Power et al., 2014). A special filtering procedure was applied to two MSC subjects (MSC03 and MSC10) with respi- ratory contamination in their motion parameters. This procedure involved applying a low-pass filtered at 0.1 Hz to reduce the effects of respiratory artifacts on motion estimates stemming from the short-TR multiband acquisition, all before censoring high-motion frames (Fair et al., 2020; Gratton et al., 2018; Laumann et al., 2017). Then a filtered FD threshold of 0.1 mm was applied to censor frames. In all cases, flagged head motion frames were removed and the time points were replaced with interpolated data using a power-spectral matched approach (Power et al., 2014), and this was followed by the application of a bandpass filter (0.009–0.08 Hz). Previous research has shown that ~30 min of low-motion data is necessary to achieve high reliability of FC (Gordon et al., 2017). We therefore removed a participant (MSC08) that exhib- ited high degree of motion (Gordon et al., 2017). The excluded participant also reported a high level of drowsiness (Gordon et al., 2017; Laumann et al., 2017; Tagliazucchi & Laufs, 2014). The processed BOLD data were mapped to each individual’s native midthickness surface via the ribbon-constrained sampling procedure (Marcus et al., 2013) Then, the mapped data were registered to the fsaverage surface in one step using the deformation map generated from the ribbon-constrained sampling procedure described in Glasser et al. (2013). This was followed by spatial smoothing conducted via a geodesic Gaussian smoothing kernel to the surface registered data (FWHM = 6 mm, sigma = 2.55) (Gordon et al., 2016; Marcus et al., 2011). Next, temporally interpolated frames were removed (prior to functional connectivity analysis). Regions and networks. We examined a previously published set of 333 brain parcels associated with 12 networks somatomotor dorsal, somatomotor lateral, visual, auditory, cinguloopercular, fronto-parietal, dorsal attention, ventral attention, salience, default, parietal memory, and retro- splenial (Gordon et al., 2016). In the case of the task scans, task related activation was captured Task functional connectivity. with a general linear model (GLM) using in-house software written in IDL (Research Systems, Inc.), as described in Gratton et al. (2018), using a finite impulse response approach for trial- level regressors (Ollinger et al., 2001). Functional connectivity was then measured for the task scans following the “background connectivity” method (Al-Aidroos et al., 2012; Fair et al., 2007) with the residuals from the GLM analysis being used for BOLD time series correlations. The residuals were subjected to the aforementioned connectivity processing pipeline prior to functional connectivity calculation. There are multiple methods to measure task FC, that here we focus on background connectivity because of its simplicity and ability to track task changes at the resolution we are interested in, and that it is well suited for comparison with a resting baseline. Intraclass correlation coefficients to quantify task discrimination. We used the Python package Pingouin (Vallat, 2018) to evaluate how much variability in FC and communication across scans is attributable to task type. Specifically, we used the function intraclass_corr, where the “targets” are the task types (rest, mixed, categorization, motor), raters are the session index (1–10). We used “ICC1k” output indicating that the target (task type) is rated by different raters (the session) and the raters are selected at random. This is equivalent to the one-way ANOVA fixed effects model (Shrout & Fleiss, 1979). ACKNOWLEDGMENTS Derek M. Smith would like to thank The Therapeutic Cognitive Neuroscience Fund. Network Neuroscience 426 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 7 2 4 1 1 2 1 1 8 4 5 5 n e n _ a _ 0 0 2 9 0 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 From correlation to communication SUPPORTING INFORMATION Supporting information for this article is available at https://doi.org/10.1162/netn_a_00290. Midnight Scan Club data is publicly available (https://openneuro.org/datasets/ds000224). Code related to the analysis in this paper is located at https://github.com/ DijunQuant /communication_public/. AUTHOR CONTRIBUTIONS Yuhua Yu: Conceptualization; Formal analysis; Investigation; Methodology; Visualization; Writing – original draft; Writing – review & editing. Caterina Gratton: Funding acquisition; Supervision; Writing – review & editing. Derek M. Smith: Conceptualization; Data curation; Funding acquisition; Methodology; Writing – original draft; Writing – review & editing. FUNDING INFORMATION Derek M. Smith, National Institutes of Health (https://dx.doi.org/10.13039/100000002), Award ID: T32NS047987. Caterina Gratton, National Science Foundation (https://dx.doi.org/10 .13039/100000001), Award ID: CAREER2048066. Caterina Gratton, National Institutes of Health (https://dx.doi.org/10.13039/100000002), Award ID: R01MH118370. REFERENCES Al-Aidroos, N., Said, C. P., & Turk-Browne, N. B. (2012). Top-down attention switches coupling between low-level and high-level areas of human visual cortex. Proceedings of the National Academy of Sciences of the United States of America, 109(36), 14675–14680. https://doi.org/10.1073/pnas.1202095109, PubMed: 22908274 Allen, E. A., Damaraju, E., Plis, S. M., Erhardt, E. B., Eichele, T., & Calhoun, V. D. (2014). Tracking whole-brain connectivity dynamics in the resting state. Cerebral Cortex, 24(3), 663–676. https://doi.org/10.1093/cercor/bhs352, PubMed: 23146964 Arbabshirani, M. R., Havlicek, M., Kiehl, K. A., Pearlson, G. D., & Calhoun, V. D. (2013). Functional network connectivity during rest and task conditions: A comparative study. Human Brain Mapping, 34(11), 2959–2971. https://doi.org/10.1002/ hbm .22118, PubMed: 22736522 Aston-Jones, G., & Cohen, J. D. (2005). An integrative theory of locus coeruleus-norepinephrine function: Adaptive gain and optimal performance. Annual Review of Neuroscience, 28, 403–450. https://doi.org/10.1146/annurev.neuro.28.061604 .135709, PubMed: 16022602 Baccalá, L. A., & Sameshima, K. (2001). Partial directed coherence: A new concept in neural structure determination. Biological Cybernetics, 84(6), 463–474. https://doi.org/10.1007 /PL00007990, PubMed: 11417058 Barch, D. M., Burgess, G. C., Harms, M. P., Petersen, S. E., Schlaggar, B. L., Corbetta, M., Glasser, M. F., Curtiss, S., Dixit, S., Feldt, C., Nolan, D., Bryant, E., Hartley, T., Footer, O., Bjork, J. M., Poldrack, R., Smith, S., Johansen-Berg, H., Snyder, A. Z., & Van Essen, D. C. (2013). Function in the human connectome: Task-fMRI and individual differences in behavior. NeuroImage, 80, 169–189. https://doi.org/10.1016/j.neuroimage.2013.05 .033, PubMed: 23684877 Bartko, J. J. (1976). On various intraclass correlation reliability coef- ficients. Psychological Bulletin, 83(5), 762–765. https://doi.org /10.1037/0033-2909.83.5.762 Behseta, S., Berdyyeva, T., Olson, C. R., & Kass, R. E. (2009). Bayes- ian correction for attenuation of correlation in multi-trial spike count data. Journal of Neurophsiology, 101(4), 2186–2193. https://doi.org/10.1152/jn.90727.2008, PubMed: 19129297 Biswal, B., Zerrin Yetkin, F., Haughton, V. M., & Hyde, J. S. (1995). Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magnetic Resonance in Medicine, 34(4), 537–541. https://doi.org/10.1002/mrm.1910340409, PubMed: 8524021 Buxton, R. B., Uludağ, K., Dubowitz, D. J., & Liu, T. T. (2004). Modeling the hemodynamic response to brain activation. Neuro- Image, 23(Suppl. 1), S220–S233. https://doi.org/10.1016/j .neuroimage.2004.07.013, PubMed: 15501093 Chang, C., & Glover, G. (2010). Time-frequency dynamics of resting-state brain connectivity measured with fMRI. Neuro- Image, 50(1), 81–98. https://doi.org/10.1016/j.neuroimage.2009 .12.011, PubMed: 20006716 Chow, C. C., & Karimipanah, Y. (2020). Before and beyond the Wilson–Cowan equations. Journal of Neurophsiology, 123(5), 1645–1656. https://doi.org/10.1152/jn.00404.2019, PubMed: 32186441 Cole, M. W., Bassett, D. S., Power, J. D., Braver, T. S., & Petersen, S. E. (2014). Intrinsic and task-evoked network architectures of the human brain. Neuron, 83(1), 238–251. https://doi.org/10 .1016/j.neuron.2014.05.014, PubMed: 24991964 Cole, M. W., Yang, G. J., Murray, J. D., Repovš, G., & Anticevic, A. (2016). Functional connectivity change as shared signal dynam- ics. Journal of Neuroscience Methods, 259, 22–39. https://doi.org /10.1016/j.jneumeth.2015.11.011, PubMed: 26642966 Network Neuroscience 427 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 7 2 4 1 1 2 1 1 8 4 5 5 n e n _ a _ 0 0 2 9 0 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 From correlation to communication Dale, A. M., Fischl, B., & Sereno, M. I. (1999). Cortical surface-based analysis: I. Segmentation and surface reconstruc- tion. NeuroImage, 9(2), 179–194. https://doi.org/10.1006/nimg .1998.0395, PubMed: 9931268 Daunizeau, J., Stephan, K. E., & Friston, K. J. (2012). Stochastic dynamic causal modelling of fMRI data: Should we care about neural noise? NeuroImage, 62(1), 464–481. https://doi.org/10 .1016/j.neuroimage.2012.04.061, PubMed: 22579726 David, O., Cosmelli, D., & Friston, K. J. (2004). Evaluation of differ- ent measures of functional connectivity using a neural mass model. NeuroImage, 21(2), 659–673. https://doi.org/10.1016/j .neuroimage.2003.10.006, PubMed: 14980568 Dubis, J. W., Siegel, J. S., Neta, M., Visscher, K. M., & Petersen, S. E. (2016). Tasks driven by perceptual information do not recruit sustained bold activity in cingulo-opercular regions. Cerebral Cortex, 26(1), 192–201. https://doi.org/10.1093/cercor/bhu187, PubMed: 25150283 Duff, E. P., Makin, T., Cottaar, M., Smith, S. M., & Woolrich, M. W. (2018). Disambiguating brain functional connectivity. Neuro- Image, 173, 540–550. https://doi.org/10.1016/j.neuroimage .2018.01.053, PubMed: 29476911 Fair, D. A., Miranda-Dominguez, O., Snyder, A. Z., Perrone, A., Earl, E. A., Van, A. N., Koller, J. M., Feczko, E., Tisdall, M. D., van der Kouwe, A., Klein, R. L., Mirro, A. E., Hampton, J. M., Adeyemo, B., Laumann, T. O., Gratton, C., Greene, D. J., Schlaggar, B. L., Hagler, D. J., … Dosenbach, N. U. F. (2020). Correction of respiratory artifacts in MRI head motion estimates. NeuroImage, 208, 116400. https://doi.org/10.1016/j.neuroimage .2019.116400, PubMed: 31778819 Fair, D. A., Schlaggar, B. L., Cohen, A. L., Miezin, F. M., Dosenbach, N. U. F., Wenger, K. K., Fox, M. D., Snyder, A. Z., Raichle, M. E., & Petersen, S. E. (2007). A method for using blocked and event-related fMRI data to study “resting state” functional connectivity. NeuroImage, 35(1), 396–405. https:// doi.org/10.1016/j.neuroimage.2006.11.051, PubMed: 17239622 Fiecas, M., Ombao, H., van Lunen, D., Baumgartner, R., Coimbra, A., & Feng, D. (2013). Quantifying temporal correlations: A test-retest evaluation of functional connectivity in resting-state fMRI. NeuroImage, 65, 231–241. https://doi.org/10.1016/j .neuroimage.2012.09.052, PubMed: 23032492 Fischl, B., Salat, D. H., Busa, E., Albert, M., Dieterich, M., Haselgrove, C., van der Kouwe, A., Killiany, R., Kennedy, D., Klaveness, S., Montillo, A., Makris, N., Rosen, B., & Dale, A. M. (2002). Whole brain segmentation: Automated labeling of neuroanatomical structures in the human brain. Neuron, 33(3), 341–355. https:// doi.org/10.1016/S0896-6273(02)00569-X, PubMed: 11832223 Fox, M. D., Snyder, A. Z., Vincent, J. L., Corbetta, M., Van Essen, D. C., & Raichle, M. E. (2005). The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proceedings of the National Academy of Sciences, 102(27), 9673–9678. https://doi.org/10.1073/pnas.0504136102, PubMed: 15976020 Fries, P. (2005). A mechanism for cognitive dynamics: Neuronal communication through neuronal coherence. Trends in Cogni- tive Sciences, 9(10), 474–480. https://doi.org/10.1016/j.tics .2005.08.011, PubMed: 16150631 Friston, K. J. (1998). Modes or models: A critique on independent component analysis for fMRI. Trends in Cognitive Sciences, 2(10), 373–375. https://doi.org/10.1016/S1364-6613(98)01227-3, PubMed: 21227247 Friston, K. J. (2011). Functional and effective connectivity: A review. Brain Connectivity, 1(1), 13–36. https://doi.org/10.1089 /brain.2011.0008, PubMed: 22432952 Friston, K. J., Harrison, L., & Penny, W. (2003). Dynamic causal modelling. NeuroImage, 19(4), 1273–1302. https://doi.org/10 .1016/S1053-8119(03)00202-7, PubMed: 12948688 Friston, K. J., Mechelli, A., Turner, R., & Price, C. J. (2000). Nonlin- ear responses in fMRI: The Balloon model, Volterra kernels, and other hemodynamics. NeuroImage, 12(4), 466–477. https://doi .org/10.1006/nimg.2000.0630, PubMed: 10988040 Friston, K. J., Williams, S., Howard, R., Frackowiak, R. S. J., & Turner, R. (1996). Movement-related effects in fMRI time-series. Magnetic Resonance in Medicine, 35(3), 346–355. https://doi.org /10.1002/mrm.1910350312, PubMed: 8699946 Glass, L. (1969). Moiré effect from random dots. Nature, 223(5206), 578–580. https://doi.org/10.1038/223578a0, PubMed: 5799528 Glasser, M. F., Sotiropoulos, S. N., Wilson, J. A., Coalson, T. S., Fischl, B., Andersson, J. L., Xu, J., Jbabdi, S., Webster, M., Polimeni, J. R., Van Essen, D. C., & Jenkinson, M. (2013). The minimal preprocessing pipelines for the Human Connectome Project. NeuroImage, 80, 105–124. https://doi.org/10.1016/j .neuroimage.2013.04.127, PubMed: 23668970 Gonzalez-Castillo, J., & Bandettini, P. A. (2018). Task-based dynamic functional connectivity: Recent findings and open ques- tions. NeuroImage, 180(Pt B), 526–533. https://doi.org/10.1016/j .neuroimage.2017.08.006, PubMed: 28780401 Gordon, E. M., Laumann, T. O., Adeyemo, B., Huckins, J. F., Kelley, W. M., & Petersen, S. E. (2016). Generation and evaluation of a cortical area parcellation from resting-state correlations. Cerebral Cortex, 26(1), 288–303. https://doi.org/10.1093/cercor/bhu239, PubMed: 25316338 Gordon, E. M., Laumann, T. O., Gilmore, A. W., Newbold, D. J., Greene, D. J., Berg, J. J., Ortega, M., Hoyt-Drazen, C., Gratton, C., Sun, H., Hampton, J. M., Coalson, R. S., Nguyen, A. L., McDermott, K. B., Shimony, J. S., Snyder, A. Z., Schlaggar, B. L., Petersen, S. E., Nelson, S. M., & Dosenbach, N. U. F. (2017). Precision functional mapping of individual human brains. Neuron, 95(4), 791–807. https://doi.org/10.1016/j.neuron.2017.07.011, PubMed: 28757305 Gordon, E. M., Lynch, C. J., Gratton, C., Laumann, T. O., Gilmore, A. W., Greene, D. J., Ortega, M., Nguyen, A. L., Schlaggar, B. L., Petersen, S. E., Dosenbach, N. U. F., & Nelson, S. M. (2018). Three distinct sets of connector hubs integrate human brain function. Cell Reports, 24(7), 1687–1695. https://doi.org/10 .1016/j.celrep.2018.07.050, PubMed: 30110625 Gratton, C., Laumann, T. O., Gordon, E. M., Adeyemo, B., & Petersen, S. E. (2016). Evidence for two independent factors that modify brain networks to meet task goals. Cell Reports, 17(5), 1276–1288. https://doi.org/10.1016/j.celrep.2016.10.002, PubMed: 27783943 Gratton, C., Laumann, T. O., Nielsen, A. N., Greene, D. J., Gordon, E. M., Gilmore, A. W., Nelson, S. M., Coalson, R. S., Snyder, A. Z., Schlaggar, B. L., Dosenbach, N. U. F., & Petersen, S. E. (2018). Functional brain networks are dominated by stable group and individual factors, not cognitive or daily variation. Neuron, 98(2), 439–452. https://doi.org/10.1016/j.neuron.2018.03.035, PubMed: 29673485 Network Neuroscience 428 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 7 2 4 1 1 2 1 1 8 4 5 5 n e n _ a _ 0 0 2 9 0 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 From correlation to communication Guedj, C., Monfardini, E., Reynaud, A. J., Farnè, A., Meunier, M., & Hadj-Bouziane, F. (2017). Boosting norepinephrine transmission triggers flexible reconfiguration of brain networks at rest. Cerebral Cortex, 27(10), 4691–4700. https://doi.org/10.1093/cercor /bhw262, PubMed: 27600848 Hutchison, R. M., Womelsdorf, T., Allen, E. A., Bandettini, P. A., Calhoun, V. D., Corbetta, M., Della Penna, S., Duyn, J. H., Glover, G. H., Gonzalez-Castillo, J., Handwerker, D. A., Keilholz, S., Kiviniemi, V., Leopold, D. A., de Pasquale, F., Sporns, O., Walter, M., & Chang, C. (2013). Dynamic functional connectivity: Promise, issues, and interpretations. NeuroImage, 80, 360–378. https://doi.org/10.1016/j.neuroimage.2013.05 .079, PubMed: 23707587 Ito, T., Brincat, S. L., Siegel, M., Mill, R. D., He, B. J., Miller, E. K., Rotstein, H. G., & Cole, M. W. (2020). Task-evoked activity quenches neural correlations and variability across cortical areas. PLoS Computational Biology, 16(8), e1007983. https:// doi.org/10.1371/journal.pcbi.1007983, PubMed: 32745096 Kietzmann, T. C., McClure, P., & Kriegeskorte, N. (2019). Deep neural networks in computational neuroscience. In Oxford research encyclopedia of neuroscience (pp. 1–28). Oxford University Press. https://doi.org/10.1093/acrefore/9780190264086.013.46 Krienen, F. M., Yeo, B. T. T., & Buckner, R. L. (2014). Reconfigurable task-dependent functional coupling modes cluster around a core functional architecture. Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences, 369(1653), 20130526. https://doi.org/10.1098/rstb.2013.0526, PubMed: 25180304 Krystal, J. H., D’Souza, D. C., Mathalon, D., Perry, E., Belger, A., & Hoffman, R. (2003). NMDA receptor antagonist effects, cortical glutamatergic function, and schizophrenia: Toward a paradigm shift in medication development. Psychopharmacology, 169(3–4), 215–233. https://doi.org/10.1007/s00213-003-1582-z, PubMed: 12955285 Lancaster, J. L., Glass, T. G., Lankipalli, B. R., Downs, H., Mayberg, H., & Fox, P. T. (1995). A modality-independent approach to spa- tial normalization of tomographic images of the human brain. Human Brain Mapping, 3(3), 209–223. https://doi.org/10.1002 /hbm.460030305 Laumann, T. O., Gordon, E. M., Adeyemo, B., Snyder, A. Z., Joo, S. J., Chen, M. Y., Gilmore, A. W., McDermott, K. B., Nelson, S. M., Dosenbach, N. U. F., Schlaggar, B. L., Mumford, J. A., Poldrack, R. A., & Petersen, S. E. (2015). Functional system and areal organization of a highly sampled individual human brain. Neuron, 87(3), 657–670. https://doi.org/10.1016/j.neuron .2015.06.037, PubMed: 26212711 Laumann, T. O., & Snyder, A. Z. (2021). Brain activity is not only for thinking. Current Opinion in Behavioral Sciences, 40, 130–136. https://doi.org/10.1016/j.cobeha.2021.04.002 Laumann, T. O., Snyder, A. Z., Mitra, A., Gordon, E. M., Gratton, C., Adeyemo, B., Gilmore, A. W., Nelson, S. M., Berg, J. J., Greene, D. J., McCarthy, J. E., Tagliazucchi, E., Laufs, H., Schlaggar, B. L., Dosenbach, N. U. F., & Petersen, S. E. (2017). On the stability of BOLD fMRI correlations. Cerebral Cortex, 27(10), 4719–4732. https://doi.org/10.1093/cercor/ bhw265, PubMed: 27591147 Logothetis, N. K., Pauls, J., Augath, M., Trinath, T., & Oeltermann, A. (2001). Neurophysiological investigation of the basis of the fMRI signal. Nature, 412(6843), 150–157. https://doi.org/10 .1038/35084005, PubMed: 11449264 Ma, Y., Shaik, M. A., Kozberg, M. G., Kim, S. H., Portes, J. P., Timerman, D., & Hillman, E. M. C. (2016). Resting-state hemo- dynamics are spatiotemporally coupled to synchronized and symmetric neural activity in excitatory neurons. Proceedings of the National Academy of Sciences, 113(52), E8463–E8471. https://doi.org/10.1073/pnas.1525369113, PubMed: 27974609 Mahadevan, A. S., Tooley, U. A., Bertolero, M. A., Mackey, A. P., & Bassett, D. S. (2021). Evaluating the sensitivity of functional con- nectivity measures to motion artifact in resting-state fMRI data. N e u ro I m a g e , 2 4 1 , 11 8 4 0 8 . h t t p s : / / d o i . o r g / 1 0 . 1 0 1 6 / j .neuroimage.2021.118408, PubMed: 34284108 Marcus, D. S., Harms, M. P., Snyder, A. Z., Jenkinson, M., Wilson, J. A., Glasser, M. F., Barch, D. M., Archie, K. A., Burgess, G. C., Ramaratnam, M., Hodge, M., Horton, W., Herrick, R., Olsen, T., McKay, M., House, M., Hileman, M., Reid, E., Harwell, J., … Van Essen, D. C. (2013). Human Connectome Project informatics: Quality control, database services, and data visualization. Neu- roImage, 80, 202–219. https://doi.org/10.1016/j.neuroimage .2013.05.077, PubMed: 23707591 Marcus, D. S., Harwell, J., Olsen, T., Hodge, M., Glasser, M. F., Prior, F., Jenkinson, M., Laumann, T., Curtiss, S. W., & Van Essen, D. C. (2011). Informatics and data mining tools and strategies for the Human Connectome Project. Frontiers in Neuroinformatics, 5, 4. https://doi.org/10.3389/fninf.2011.00004, PubMed: 21743807 Marrelec, G., Krainik, A., Duffau, H., Pélégrini-Issac, M., Lehéricy, S., Doyon, J., & Benali, H. (2006). Partial correlation for func- tional brain interactivity investigation in functional MRI. Neuro- Image, 32(1), 228–237. https://doi.org/10.1016/j.neuroimage .2005.12.057, PubMed: 16777436 McGraw, K. O., & Wong, S. P. (1996). Forming inferences about some intraclass correlation coefficients. Psychological Methods, 1(1), 30–46. https://doi.org/10.1037/1082-989X.1.1.30 Mena-Segovia, J., & Bolam, J. P. (2017). Rethinking the pedunculo- pontine nucleus: From cellular organization to function. Neuron, 94(1), 7–18. https://doi.org/10.1016/j.neuron.2017.02.027, PubMed: 28384477 Miezin, F. M., Maccotta, L., Ollinger, J. M., Petersen, S. E., & Buckner, R. L. (2000). Characterizing the hemodynamic response: Effects of presentation rate, sampling procedure, and the possibility of ordering brain activity based on relative timing. NeuroImage, 11(6), 735–759. https://doi.org/10.1006/nimg.2000 .0568, PubMed: 10860799 Morales, M., & Margolis, E. B. (2017). Ventral tegmental area: Cellular heterogeneity, connectivity and behaviour. Nature Reviews Neuroscience, 18(2), 73–85. https://doi.org/10.1038 /nrn.2016.165, PubMed: 28053327 Ollinger, J. M., Corbetta, M., & Shulman, G. L. (2001). Separating processes within a trial in event-related functional MRI: II. Analysis. NeuroImage, 13(1), 218–229. https://doi.org/10.1006 /nimg.2000.0711, PubMed: 11133324 Patel, R. S., Bowman, F. D. B., & Rilling, J. K. (2006). A Bayesian approach to determining connectivity of the human brain. Human Brain Mapping, 27(3), 267–276. https://doi.org/10.1002 /hbm.20182, PubMed: 16092131 Porter, A., Nielsen, A., Dorn, M., Dworetsky, A., Edmonds, D., & Gratton, C. (2023). Masked features of task states found in Network Neuroscience 429 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 7 2 4 1 1 2 1 1 8 4 5 5 n e n _ a _ 0 0 2 9 0 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 From correlation to communication individual brain networks. Cerebral Cortex, 33(6), 2879–2900. https://doi.org/10.1093/cercor/bhac247, PubMed: 35802477 Power, J. D., Cohen, A. L., Nelson, S. M., Wig, G. S., Barnes, K. A., Church, J. A., Vogel, A. C., Laumann, T. O., Miezin, F. M., Schlaggar, B. L., & Petersen, S. E. (2011). Functional network organization of the human brain. Neuron, 72(4), 665–678. https://doi.org/10 .1016/j.neuron.2011.09.006, PubMed: 22099467 Power, J. D., Mitra, A., Laumann, T. O., Snyder, A. Z., Schlaggar, B. L., & Petersen, S. E. (2014). Methods to detect, characterize, and remove motion artifact in resting state fMRI. NeuroImage, 84, 320–341. https://doi.org/10.1016/j.neuroimage.2013.08 .048, PubMed: 23994314 Power, J. D., Schlaggar, B. L., Lessov-Schlaggar, C. N., & Petersen, S. E. (2013). Evidence for hubs in human functional brain net- works. Neuron, 79(4), 798–813. https://doi.org/10.1016/j .neuron.2013.07.035, PubMed: 23972601 Raut, R. V., Snyder, A. Z., Mitra, A., Yellin, D., Fujii, N., Malach, R., & Raichle, M. E. (2021). Global waves synchronize the brain's functional systems with fluctuating arousal. Science Advances, 7(30), eabf2709. https://doi.org/10.1126/sciadv.abf2709, PubMed: 34290088 Selden, N. R., Gitelman, D. R., Salamon-Murayama, N., Parrish, T. B., & Mesulam, M. M. (1998). Trajectories of cholinergic path- ways within the cerebral hemispheres of the human brain. Brain, 121(12), 2249–2257. https://doi.org/10.1093/ brain/121.12 .2249, PubMed: 9874478 Sepulcre, J., Sabuncu, M. R., Yeo, T. B., Liu, H., & Johnson, K. A. (2012). Stepwise connectivity of the modal cortex reveals the multimodal organization of the human brain. Journal of Neuro- science, 32(31), 10649–10661. https://doi.org/10.1523 /JNEUROSCI.0759-12.2012, PubMed: 22855814 Shafiei, G., Zeighami, Y., Clark, C. A., Coull, J. T., Nagano-Saito, A., Leyton, M., Dagher, A., & Mišić, B. (2019). Dopamine signaling modulates the stability and integration of intrinsic brain net- works. Cerebral Cortex, 29(1), 397–409. https://doi.org/10.1093 /cercor/bhy264, PubMed: 30357316 Shine, J. M. (2019). Neuromodulatory influences on integration and segregation in the brain. Trends in Cognitive Sciences, 23(7), 572–583. https://doi.org/10.1016/j.tics.2019.04.002, PubMed: 31076192 Shine, J. M., Bissett, P. G., Bell, P. T., Koyejo, O., Balsters, J. H., Gorgolewski, K. J., Moodie, C. A., & Poldrack, R. A. (2016). The dynamics of functional brain networks: Integrated network states during cognitive task performance. Neuron, 92(2), 544–554. https://doi.org/10.1016/j.neuron.2016.09.018, PubMed: 27693256 Shine, J. M., van den Brink, R. L., Hernaus, D., Nieuwenhuis, S., & Poldrack, R. A. (2018). Catecholaminergic manipulation alters dynamic network topology across cognitive states. Network Neu- roscience, 2(3), 381–396. https://doi.org/10.1162/netn_a_00042, PubMed: 30294705 Shrout, P. E., & Fleiss, J. L. (1979). Intraclass correlations: Uses in assessing rater reliability. Psychological Bulletin, 86(2), 420–428. https://doi.org/10.1037/0033-2909.86.2.420, PubMed: 18839484 Smith, S. M. (2012). The future of fMRI connectivity. NeuroImage, 62(2), 1257–1266. https://doi.org/10.1016/j.neuroimage.2012 .01.022, PubMed: 22248579 Tagliazucchi, E., & Laufs, H. (2014). Decoding wakefulness levels from typical fMRI resting-state data reveals reliable drifts between wakefulness and sleep. Neuron, 82(3), 695–708. https://doi.org /10.1016/j.neuron.2014.03.020, PubMed: 24811386 Talairach, J., & Tournoux, P. (1988). Co-planar stereotaxic atlas of the human brain. New York: Thieme Medical Publishers. Turchi, J., Chang, C., Ye, F. Q., Russ, B. E., Yu, D. K., Cortes, C. R., Monosov, I. E., Duyn, J. H., & Leopold, D. A. (2018). The basal forebrain regulates global resting-state fMRI fluctuations. Neuron, 97(4), 940–952. https://doi.org/10.1016/j.neuron.2018.01.032, PubMed: 29398365 Vallat, R. (2018). Pingouin: Statistics in Python. Journal of Open Source Software, 3(31), 1026. https://doi.org/10.21105/joss .01026 Vicente, R., Wibral, M., Lindner, M., & Pipa, G. (2011). Transfer entropy-a model-free measure of effective connectivity for the neurosciences. Journal of Computational Neuroscience, 30(1), 45–67. https://doi.org/10.1007/s10827-010-0262-3, PubMed: 20706781 Vijayraghavan, S., Wang, M., Birnbaum, S. G., Williams, G. V., & Arnsten, A. F. T. (2007). Inverted-U dopamine D1 receptor actions on prefrontal neurons engaged in working memory. Nature Neuroscience, 10(3), 376–384. https://doi.org/10.1038 /nn1846, PubMed: 17277774 Wilson, H. R., & Cowan, J. D. (1972). Excitatory and inhibitory interactions in localized populations of model neurons. Biophys- ical Journal, 12(1), 1–24. https://doi.org/10.1016/S0006-3495(72) 86068-5, PubMed: 4332108 Wu, L., Caprihan, A., & Calhoun, V. (2021). Tracking spatial dynamics of functional connectivity during a task. NeuroImage, 239, 118310. https://doi.org/10.1016/j.neuroimage.2021 .118310, PubMed: 34175424 Yao, H., Shi, L., Han, F., Gao, H., & Dan, Y. (2007). Rapid learning in cortical coding of visual scenes. Nature Neuroscience, 10(6), 772–778. https://doi.org/10.1038/nn1895, PubMed: 17468750 Yeo, B. T. T., Krienen, F. M., Sepulcre, J., Sabuncu, M. R., Lashkari, D., Hollinshead, M., Roffman, J. L., Smoller, J. W., Zöllei, L., Polimeni, J. R., Fischl, B., Liu, H., & Buckner, R. L. (2011). The organization of the human cerebral cortex estimated by intrinsic functional connectivity. Journal of Neurophysiology, 106(3), 1125–1165. https://doi.org/10.1152/jn.00338.2011, PubMed: 21653723 Zucker, R. S., & Regehr, W. G. (2002). Short-term synaptic plasticity. Annual Review of Physiology, 64, 355–405. https://doi.org/10 .1146/annurev.physiol.64.092501.114547, PubMed: 11826273 Network Neuroscience 430 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 7 2 4 1 1 2 1 1 8 4 5 5 n e n _ a _ 0 0 2 9 0 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3

Descargar PDF