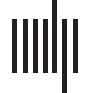INVESTIGACIÓN

La percolación puede explicar la eficiencia, robustez,
y economía del cerebro

Yang Tian1,2

y Pei Sun1

1Departamento de Psicología y Laboratorio Tsinghua de Cerebro e Inteligencia, Universidad de Tsinghua, Beijing, Porcelana
2Laboratorio de Computación Avanzada y Almacenamiento, Instituto Central de Investigaciones, 2012 Laboratorios,
Huawei Technologies Co.. Limitado., Beijing, Porcelana

Palabras clave: Filtración, Conectividad cerebral, Equilibrio excitación-inhibición, Transmisión de información
eficiencia, Gran flexibilidad, Economía cerebral

un acceso abierto

diario

ABSTRACTO

El cerebro está formado por miles de millones de neuronas conectadas por sinapsis ultradensas., demostración
notable eficiencia, flexibilidad robusta, y economía en el procesamiento de la información. Es generalmente
Se cree que estas propiedades ventajosas tienen su origen en la conectividad cerebral.; sin embargo, directo
La evidencia permanece ausente debido a limitaciones técnicas o vacancia teórica.. Esta investigación
explora los orígenes de estas propiedades en el conectoma cerebral más grande hasta el momento de la mosca de la fruta. Nosotros
revelan que la formación de conectividad funcional en el cerebro puede explicarse por una filtración
proceso controlado por excitación-inhibición sináptica (E/I) balance. Al aumentar el E/I
equilibrar gradualmente, Descubrimos el surgimiento de estas propiedades como subproductos de la percolación.
transición cuando el saldo E/I llega a 3:7. A medida que el saldo E/I sigue aumentando, un optimo
saldo E/I 1:1 se presenta para garantizar estas tres propiedades simultáneamente, consistente con
predicciones experimentales in vitro previas. Una vez que el saldo E/I supere 3:2, un intrínseco
limitación de estas propiedades determinada por estática (anatómico) La conectividad cerebral puede ser
observado. Nuestro trabajo demuestra que la filtración, una caracterización universal de la crítica
fenómenos y transiciones de fase, puede servir como una ventana para comprender
aparición de diversas propiedades cerebrales.

RESUMEN DEL AUTOR

Esta investigación presenta un marco novedoso para estudiar la conectividad funcional en el sistema más grande hasta el momento.
conectoma cerebral de la mosca de la fruta, revelando que la excitación-inhibición sináptica (E/I) balance
caracteriza la formación de conectividad cerebral dinámica como un proceso de filtración. Varios
propiedades notables de las funciones cerebrales, como la eficiencia de transmisión de información, robusto
flexibilidad, y economía, emergen como subproductos de la transición de percolación. Estas ventajas
se puede garantizar simultáneamente un equilibrio E/I óptimo 1:1, consistente con estudios in vitro previos.
predicciones experimentales. Nuestro trabajo demuestra la percolación como una forma potencial de entender
El surgimiento de características de la función cerebral a través de la conectividad..

INTRODUCCIÓN

Para sobrevivir a través de la evolución., nuestro cerebro debería ser lo suficientemente eficiente para procesar
información, resistente a daños accidentales (p.ej., lesiones), y económico en el uso de energía. Encima
las ultimas decadas, Esta inferencia evolutiva ha sido corroborada por numerosas neurociencias.

Citación: tian, y., & Sol, PAG. (2022).
La percolación puede explicar la eficiencia,
robustez, y economía del cerebro.
Neurociencia en red, 6(3), 765–790.
https://doi.org/10.1162/netn_a_00246

DOI:
https://doi.org/10.1162/netn_a_00246

Recibió: 3 Octubre 2021
Aceptado: 11 Marzo 2022

Conflicto de intereses: Los autores tienen
declaró que no hay intereses en competencia
existir.

Autores correspondientes:
Yang Tian
tiany20@mails.tsinghua.edu.cn
Pei Sol
peisun@tsinghua.edu.cn

Editor de manejo:
Álex Amueblado

Derechos de autor: © 2022
Instituto de Tecnología de Massachusetts
Publicado bajo Creative Commons
Atribución 4.0 Internacional
(CC POR 4.0) licencia

La prensa del MIT

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

/

/

t

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

6
3
7
6
5
2
0
3
5
9
8
5
norte
mi
norte
_
a
_
0
0
2
4
6
pag
d

.

t

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

La percolación explica la eficiencia, robustez, y economía del cerebro

estudios. Se ha descubierto que el cerebro apoya la transmisión de información altamente eficiente
entre neuronas, circuitos, y cortezas, permitiendo recopilar y distribuir rápidamente
externo
información (Amico et al., 2021; Avena-Koenigsberger, Varios, & despreciar, 2018;
graham, Avena-Koenigsberger, & Varios, 2020; Músculo, despreciar, & McIntosh, 2014). tal información-
eficiencia de transmisión de información, manifestado como el bajo costo de tiempo de las comunicaciones entre
Neuronas o alta capacidad de transmisión de información., is demonstrated to vary across different
topological attributes of brain connectivity (Avena-Koenigsberger et al., 2018). Mientras tanto, el
brain is revealed to feature robust flexibility, a kind of capacity to tolerate the large-scale
destruction of neurons or synaptic connections (p.ej., by lesions) (Aerts, Fias, Caeyenberghs,
& Marinazzo, 2016; Joyce, Hayasaka, & Laurienti, 2013; Kaiser, Martín, Andras, & Joven,
2007) while maintaining robust brain functions (Achard, Salvador, Whitcher, Suckling, &
bullmore, 2006; Aerts et al., 2016; Alstott, romper la lanza, Hagmann, Cammoun, & despreciar, 2009;
Avena-Koenigsberger et al., 2017; Crossley et al., 2014; Joyce et al., 2013; Kaiser & Hilgetag,
2004; Kaiser et al., 2007). Although it inevitably requires a vast energy supply and occupies
large space in the animal body due to the ultra-large neuron amounts, the brain is discovered
to be economic in network wiring (low costs for embedding brain network into physics space)
and network running (efficient in energy using) (bullmore & despreciar, 2012; Friston, 2010; Hahn
et al., 2015; Karbowski, 2007; Kiebel & Friston, 2011; Laughlin, van Steveninck, & anderson,
1998; despreciar, 2011; Strelnikov, 2010). Estas propiedades económicas se sugieren como las funciones
del tamaño de la red cerebral, topología, y propiedades sinápticas (bullmore & despreciar, 2012).

Hasta ahora, Aún no está claro de dónde se originan estas notables propiedades del cerebro.. El
Las estrechas relaciones entre estas propiedades y la red cerebral conducen naturalmente a una emergencia.-
hipótesis del gentismo que sostiene que estas propiedades pueden originarse a partir de características específicas de
conectividad cerebral. En las últimas décadas, Se han encontrado abundantes corolarios de esta hipótesis.
verificado desde diferentes perspectivas. Por ejemplo, Los caminos más cortos en la conectividad cerebral son
inferido como principal sustrato de comunicación en el cerebro según las propiedades de
eficiencia de transmisión de información (Avena-Koenigsberger et al., 2018). Aunque tener un
el camino promedio corto es costoso, La conectividad cerebral real todavía posee una longitud de ruta casi mínima
(Betzel et al., 2016; bullmore & despreciar, 2012; Kaiser & Hilgetag, 2006; Rubinov, ypma, watson,
& bullmore, 2015) en interacciones funcionales (Goñi et al., 2014; Hermundstad et al., 2013) a
apoyar la transmisión eficiente de información. Además, La conectividad cerebral se infiere como libre de escala.
según la robustez de las redes sin escala (Alberto, jeong, & Barrabás, 2000) e implícito
como un mundo pequeño por la longitud de camino casi mínima (bullmore & despreciar, 2012). Mientras que los mamíferos
Los cerebros con conectividad sin escala son robustos contra lesiones aleatorias., son significativamente vulnerables-
nerable a ataques dirigidos a centros (Kaiser & Hilgetag, 2004; Kaiser et al., 2007). Sin embargo, una vez el
La topología de conectividad se acerca a una red de mundo pequeño manteniendo la propiedad libre de escala.
(p.ej., El cerebro humano macroscópico) (Achard et al., 2006; Alstott et al., 2009; Crossley et al.,
2014; Joyce et al., 2013), el cerebro se vuelve más resistente a los ataques dirigidos al centro que un
Red comparable sin escala y se mantiene igualmente robusta ante ataques aleatorios.. Además de estos
corolarios mencionados, Se pueden encontrar muchos otros corolarios verificados., demostrando que
El patrón de conectividad cerebral da forma crítica a las funciones cerebrales..

Sin embargo, Estos corolarios por sí solos no son suficientes para una demostración completa de la
hipótesis del emergentismo. Sigue faltando evidencia clave que la respalde porque técnicamente es
No es factible capturar y controlar la aparición de estas propiedades in vitro o vivo., al menos
en el futuro cercano. Un desafío surge de la escasez de tecnología para grabar multimodo
(incluyendo conectividad estática y funcional), de grano fino, y conexión de alto rendimiento-
datos del tomo (despreciar, Tononi, & kötter, 2005). Otro desafío es la falta de experimentación.
Métodos para modificar la conectividad para controlar la aparición de estas propiedades.. A pesar de

Conectividad funcional:
La conectividad formada por dinámicas.
interacciones entre neuronas.

Neurociencia en red

766

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

t

/

/

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

6
3
7
6
5
2
0
3
5
9
8
5
norte
mi
norte
_
a
_
0
0
2
4
6
pag
d

.

t

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

La percolación explica la eficiencia, robustez, y economía del cerebro

Conectividad estática:
La conectividad anatómica del
cerebro, independientemente de la dinámica
interacciones entre neuronas.

Transición de fase:
El proceso físico de transición.
entre estados del sistema definidos por
algunos parámetros de control.

Transición de percolación:
La transición entre el sistema
estados de conectividad (p.ej., de ser
fragmentado hasta filtrarse).

El estudio teórico puede ser una opción alternativa., Los modelos clásicos actuales en neurociencia son
ya sea impulsado por experimentos y propuesto para análisis ex post facto o impulsado por simulación y
Diseñado para imitar fenómenos en lugar de explicar mecanismos.. Estos modelos son inap-
aplicable para un análisis libre de suposiciones cuando no hay ningún experimento de referencia. El
La ausencia de verificación directa debido a estos desafíos hace que la validez de la hipótesis sea
cuestionable.

Aquí discutimos la posibilidad de una demostración factible y físicamente fundamental de
la hipótesis del emergentismo. Estas propiedades ventajosas de las funciones cerebrales son todas relevantes.
a los beneficios o costos de formar una conectividad funcional específica (interacciones entre neuronas)
sobre la conectividad estática (estructura anatómica). Por lo tanto, la aparición de estas propiedades
será detectable si podemos formalizar la evolución de los patrones de conectividad funcional en estática
conectividad. En el presente estudio, Usamos un conectoma cerebral de grano fino y de alto rendimiento.
de la mosca de la fruta, Drosophila melanogaster (Puchero de barro, 2020; Schlegel et al., 2021; Xu et al., 2020) a
obtener información precisa de conectividad estática. En cuanto a la conectividad funcional, en cerebros reales, él
está sujeto tanto a la conectividad estática como a la excitación-inhibición (E/I) propiedades de las sinapsis; en
nuestro estudio, se analiza bajo un marco integrado: comenzamos con una dinámica neuronal masiva-
cálculo ics (Gerstner, Kistler, Beneficio, & paninski, 2014) en todo el cerebro (∼1,2 × 109
veces), permitiéndonos medir la probabilidad de coactivación de cualquier par de neuronas conectadas
y conectividad estática abstracta como un gráfico dirigido por peso. Entonces, formalizamos la formación de
conectividad funcional en la conectividad estática, aplicando su relación de equivalencia con la
percolación en gráficos dirigidos al azar, una caracterización universal de los fenómenos críticos
y transiciones de fase (Dorogovtsev, Mendes, & Samukhin, 2001; Le et al., 2021). la motivacion-
La función subyacente a este marco es regular la evolución de la conectividad funcional con un
factor biológico específico y verificar si estas propiedades pueden establecerse como consecuencia-
consecuencias de estas manipulaciones. Limitado por problemas tecnológicos., el factor biológico, el preciso
información E/I sináptica que requiere el cálculo de la dinámica neuronal, no se puede grabar en el
microscopio de electrones (EM) imágenes de un cerebro de insecto todavía (Xu et al., 2020). Sin embargo, el E/I
balance (es decir., la relación entre sinapsis excitadoras e inhibidoras) puede actuar como un parámetro de control-
eter para aleatorizar la propiedad E/I de cada sinapsis, ofreciendo la oportunidad de verificar si el cerebro
Las propiedades funcionales surgen después de transiciones de percolación específicas..

RESULTADOS

Formación de conectividad funcional como percolación

Propiedades de topología de la conectividad estática.. Comencemos con la conectividad estática o anatómica de
el cerebro de la mosca de la fruta. Los datos se adquieren del conectoma cerebral de código abierto publicado recientemente por
Proyecto FlyEM (Xu et al., 2020). En el presente estudio, Las neuronas y las sinapsis se consideran únicamente.
cuando los cuerpos celulares están colocados con precisión (asignado con una coordinación de resolución espacial de 10 nm-
nate). El conjunto de datos seleccionado, incluido 23,008 neuronas, 4,967,364 conexiones sinápticas (sináptico
hendiduras), y 635,761 pares de relaciones direccionalmente adyacentes (dos neuronas están direccionalmente adja-
ciento si una conexión sináptica sale de una neurona y conduce a otra), nos apoya para
analizar la conectividad estática en la región del cerebro o escala macroscópica (Figura 1A-B) y la celda
o escala microscópica (Figura 1C-D). Consulte los Materiales y métodos para la adquisición de datos..

La conectividad estática macroscópica se analiza en términos de las proyecciones de entrada potenciales.
o proyecciones de salida potenciales que una región del cerebro puede recibir o emitir a otro cerebro
región. Estas proyecciones se tratan como potenciales porque la conectividad estática puede no ser
equivalente al funcional. en el análisis, Contamos estos dos tipos de proyecciones.
entre regiones del cerebro, base en la cual las proyecciones de insumos potenciales totales (TPPI, el

Neurociencia en red

767

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

t

/

/

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

6
3
7
6
5
2
0
3
5
9
8
5
norte
mi
norte
_
a
_
0
0
2
4
6
pag
d

.

t

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

La percolación explica la eficiencia, robustez, y economía del cerebro

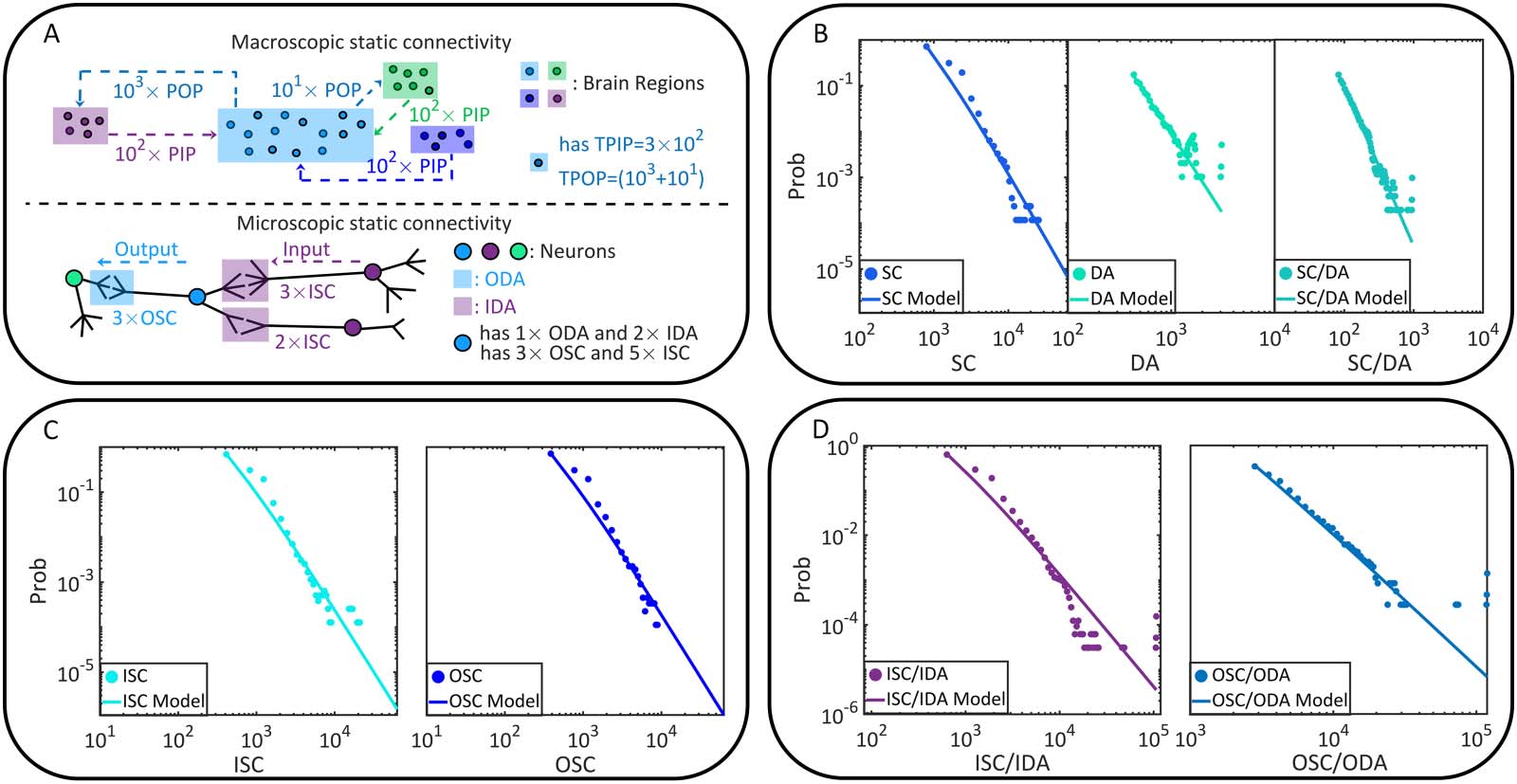
Cifra 1. La topología cerebral estática de la mosca de la fruta., Drosophila melanogaster. (A) La conectividad estática macroscópica, donde potencial
Las proyecciones de entrada/salida se cuentan entre dos regiones del cerebro cualesquiera.. Tenga en cuenta que las regiones del cerebro están ordenadas por sus nombres.. El mapa de calor y
Los histogramas se muestran en formato de grano grueso para una mejor visión.. El mapa de calor se puede interpretar como una matriz adyacente., donde el número de
Las posibles proyecciones de entrada/salida de una región del cerebro se pueden ver en la columna correspondiente. (o fila). (B) Variables de estática macroscópica.
La conectividad se ilustra gráficamente en este caso.. Las distribuciones de probabilidad de TPIP y TPOP se muestran con sus correspondientes estimaciones.-
modelos de ley de potencia acoplada. (C) La conectividad estática microscópica, donde cada nodo representa un cuerpo celular y cada borde dirigido representa
en. Las neuronas se colorean según el número de conexiones sinápticas involucradas.. (D) Las variables de la conectividad estática microscópica son
ilustrado gráficamente. Las distribuciones de probabilidad de IDA y ODA se presentan con modelos de ley de potencia estimados..

grado macroscópico) recibido por cada región y las proyecciones de producción potencial total
(TPOP, el grado exterior macroscópico) procedentes de cada región se pueden medir (Figura 1A).
Consulte los Materiales y métodos y la Figura 1B para obtener descripciones de las variables..

En la Figura 1B y Tabla 1, Analizamos las distribuciones de ley de potencia de TPIP y TPOP con un
enfoque de estimación de máxima verosimilitud (R. Obras & cláusula, 2014; Y. Obras & cláusula,
2014), lo que sugiere que la conectividad estática macroscópica es plausiblemente libre de escala (ley de potencia
exponente α 2 (2, 3) se estima con bondad ideal). Se pueden obtener más detalles del análisis de la ley de potencia.
verse en Materiales y Métodos. Mientras tanto, verificamos la simetría (p.ej., con un saldo
entre proyecciones de entrada y salida) de conectividad estática macroscópica utilizando el Pearson
correlaciones y fracciones de cambio promedio (ver tabla 2). La conectividad se sugiere como
simétrico desde (1) Existen correlaciones positivas significativas entre TPIP y TPOP (p.ej.,
mayor que 0.9); (2) La fracción de cambio promedio del TPIP en comparación con el TPOP es suficientemente
pequeño (p.ej., menor que 1). También presentamos otra evidencia corroborativa derivada de investigaciones relacionadas.

Mesa 1.

Resultados del análisis de la ley de potencia.

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

t

/

/

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

6
3
7
6
5
2
0
3
5
9
8
5
norte
mi
norte
_
a
_
0
0
2
4
6
pag
d

t

.

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Bondad de estimación
0.0074

Sin báscula o no
Sí

Tipo
Macroscópico

Macroscópico

Microscópico

Microscópico

Variable
TPPI

TPOP

AIF

AOD

Distribución de probabilidad
PAG (TPOP = n) ∝n−2.45

PAG (TPIP = n) ∝n−2.17

PAG (AIF = n) ∝n−3.69

PAG (HABITACIÓN = n) ∝n−3.22

0.0086

0.0348

0.0623

Nota. Ser libre de escala requiere P ∝ n−α, donde α 2 (2, 3). Se espera que la bondad de la estimación sea menor que 0.05.

Neurociencia en red

Sí

No

No

768

La percolación explica la eficiencia, robustez, y economía del cerebro

Mesa 2.

Resultados del análisis de simetría.

Variable
TPPI

AIF

Variable
TPOP

AOD

Correlación de Pearson
0.9938

pag
3.31667 × 10-9

Fracción de cambio promedio
j

TPIP-TPOP
j
TPOP

= 0.8215

0.8817

< 10−10 IDA−ODA j ODA j = 0.6443 Symmetric degree Strictly strong Less strong Note. Strong symmetry requires a strong positive correlation (e.g., correlation > 0.9 y P < 10−3). Strong symmetry implies a small average change fraction (e.g., fraction < 1). The term “strictly strong” means that the strictest criterion of strong symmetry is completely satisfied. The term “less strong” means that the strictest criterion of strong symmetry is partly satisfied. variables to support these findings (please see Tables 5–6 and Figure 5 in Materials and Methods for additional information). When turn to the cell scale, we characterize microscopic static connectivity depending on the directionally adjacent relation (DA) between neurons. Two neurons are directionally adja- cent if there exists at least one synaptic connection coming from one of them to the other (see Figure 1C). Note that one DA may correspond to multiple synaptic connections because there can be more than one synaptic cleft. To offer an accurate characterization, we further subdi- vide variable DA according to input-output relations (e.g., pre- and postsynaptic relations). Specifically, we count input directionally adjacent relations (IDA) and the output directionally adjacent relations (ODA) for comparison on each neuron. Details of these variables are described in the Materials and Methods and Figure 1D. In Figure 1D and Table 1, we show the power law analysis on the above defined variables. The same analysis is also conducted on other related variables (please see Table 3 and Figure 5 in Materials and Methods for additional information). Based on these results, the potential scale-free property of microscopic static connectivity is suggested as uncertain and nonrobust. Only a few variables (e.g., additional results in Table 5 in Materials and Methods) plausibly exhibit scale-free properties while others do not (e.g., results in Table 1). Meanwhile, symmetry analysis is applied to show the approximate symmetry of microscopic static connectivity. In Table 2, significant positive correlations and small average change fractions are observed between input-related and output-related variables. Similar properties can be seen on other variables of microscopic static connectivity (please see Table 6 in Materials and Methods for additional data). These results principally suggest that microscopic static connectivity is approximately symmetric, though the symmetric degree is not as strong as macroscopic static connectivity. The above analysis conveys three important messages: during the coarse-graining process from the cell scale to the brain-region scale, potential local asymmetry and diversity gradually fade away and eventually vanish owing to the loss of information in detailed connectivity. This finding encourages us to concentrate on fine-grained microscopic static connectivity in the subsequent analysis to control information loss. Meanwhile, although asymmetric upstream- Variable PIP POP TPIP TPOP Table 3. Macroscopic variable definitions Meaning Potential input projections that a brain region can receive from another region Potential input projections that a brain region can cast to another region Total potential input projections that a brain region can receive from all other regions (macroscopic in-degree) Total potential input projections that a brain region can cast to all other regions (macroscopic out-degree) Network Neuroscience 769 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 6 3 7 6 5 2 0 3 5 9 8 5 n e n _ a _ 0 0 2 4 6 p d t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Percolation explains efficiency, robustness, and economy of the brain downstream relations can be found among brain regions during information processing, these relations may merely exist in functional connectivity (static connectivity is principally symmet- ric). This finding reminds us that functional connectivity can not be simply reflected by static connectivity. Moreover, we speculate that the uncertain scale-free property is relevant with an existing controversy of whether static brain connectivity is scale-free or not (see pieces of sup- porting (Kaiser & Hilgetag, 2004; Kaiser et al., 2007)) and opposing evidence (Breskin, Soriano, Moses, & Tlusty, 2006; Humphries, Gurney, & Prescott, 2006). Scale-free property of the brain may critically rely on the granularity and the variables used in connectivity characterization. To this point, the static connectivity of the fruit fly brain has been characterized, below we turn to formalize the formation of functional connectivity based on the static connectivity. Neural dynamics computation and coactivation probability graph. As discussed above, the fine- grained, high-throughput, and simultaneous recording of static connectivity and neural dynamics remains technically infeasible (Sporns et al., 2005). An alternative is to study the formation of functional connectivity based on the static connectivity through a theoretical way, whose first step is to analyze possible coactivation patterns among neurons. While one prerequisite of neural coactivation analysis, the static connectivity, has been obtained in the previous section, another prerequisite, the excitation-inhibition (E/I) properties of syn- apses, can not be recorded in the electron microscopy imagery of the insect brain (Xu et al., 2020). To avoid this obstacle, previous studies turn to mammalian brain regions (e.g., rat hip- pocampus) (Amini, 2010; Breskin et al., 2006; Cohen et al., 2010; Eckmann et al., 2007), where synaptic E/I properties could be easily recorded and controlled, but the connectivity imaging is much more coarse-grained and low-throughput. We, however, treat this obstacle as an opportunity to study the role of synaptic E/I balance, a global factor that reflects the E/I properties of all synapses. Although precise synaptic E/I properties remain absent, they can be randomly assigned under the restriction of E/I balance λ 2 (0, 1), the proportion of excitatory synapses in all synapses. After generating the static con- nection strength of every directionally adjacent relation Ni → Nj (here Ni and Nj are neurons), we can measure coactivation probability Pij to define the dynamic connection strength. Here the coactivation probability is estimated by the leaky integrate-and-fire (LIF) model (Gerstner et al., 2014), a standard approach in neural dynamics computation. Please see the Materials and Methods for details. 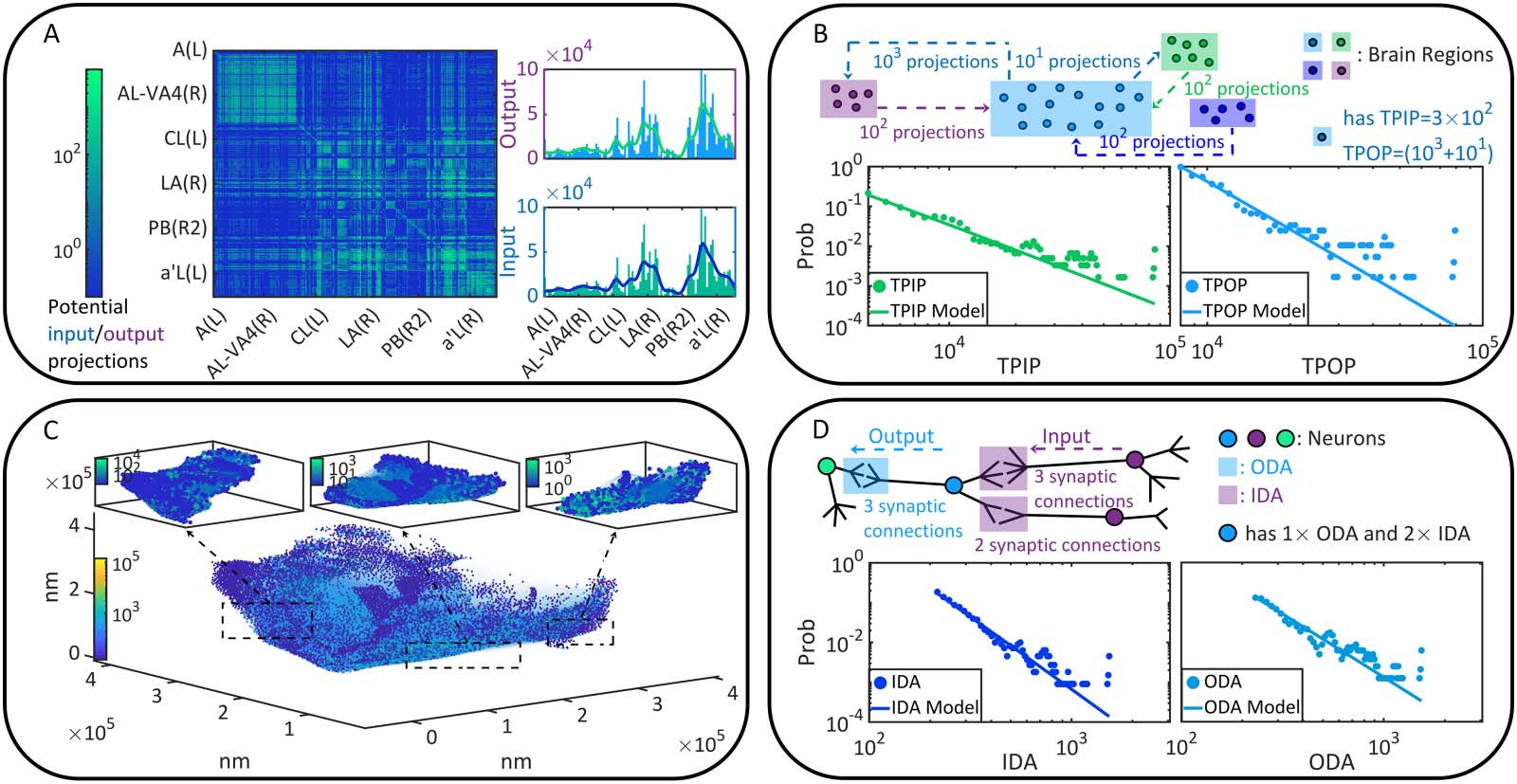Letting λ vary from 0.05 to 0.95 (Δλ = 0.05), we implement the above computation on every pair of Ni → Nj to obtain its dynamic connection strength in terms of coactivation prob- ability Pij under each λ condition. We treat Pij as a variable and sample its probability density on the whole brain (Figure 2A). According to the density concentration tendency and the first moment E(Pij), we suggest that Pij increases with λ globally. This phenomenon can be double- checked if we analyze every binomial distribution Bi(P ij) to find its peak value ^P ij and the corresponding coordinate ^ξ. The distribution is calculated in terms of a ξ-trial experiment (ξ = 100) where the success probability for each trial is P ij. Figure 2B illustrates the frequency distribution of (^ξ, ^Pij) sampled on the whole brain, revealing that ^ξ increases with λ. In Figure 2C, we show instances of coactivation patterns and their implied functional connectivity situations under each λ condition, which turn out to be denser when λ increases. Here the existence of coactivation between Ni and Nj is randomized following Bi(P ij). A directed edge Ni → Nj is added to functional connectivity when Ni and Nj are coactivated. In Figure 2D–E, we analyze the properties of the weakly connected cluster ( WCC) and the strongly connected cluster (SCC) (Bollobás, 2013) on the whole brain. It can be seen that the total numbers of WCCs and SCCs Weakly connected cluster: A subgraph of a directed graph, where each node is an endpoint of at least one directed edge coming to it or one directed edge coming out from it. Strongly connected cluster: A subgraph of a directed graph, where if any two nodes are connected by a directed path (e.g., coming from the first node to the second one), then there must exist another antidromic directed path between them (e.g., coming from the second node to the first one). Network Neuroscience 770 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 6 3 7 6 5 2 0 3 5 9 8 5 n e n _ a _ 0 0 2 4 6 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Percolation explains efficiency, robustness, and economy of the brain l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 6 3 7 6 5 2 0 3 5 9 8 5 n e n _ a _ 0 0 2 4 6 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Figure 2. Neural dynamics and coactivation probability graphs. (A) The probability densities of Pij under each λ condition are presented by colorful areas. Meanwhile, the first moment E(Pij) is shown as a function of λ. (B), The observed occurrence frequency distributions of (^ξ, ^Pij) (counted on every directionally adjacent relation, DA) and how they vary with λ. (C) Instances of coactivation patterns under each λ condition are given (upper parallel). The coactivation of neurons Ni and Nj is represented as a point (i, j ). Note that real coactivation patterns are much sparser than how they are displayed. Moreover, the implied functional connectivity by each coactivation pattern are shown (bottom parallel), where edges correspond to the DAs through which coactivation happens and neurons are colored based on the number of involved coactiva- tion relations. (D–E) The cluster number as well as the first and second moments of cluster size are presented as functions of λ. Clusters are defined in terms of WCC (see D) and SCC (see E), respectively. Although the first moment of cluster size increases with λ, its variation is sufficiently slower than the second moment and therefore less visible. Missing data points in E are 0 in a logarithmic plot. decline with λ because specific clusters become larger gradually (the first moment of cluster size maintains relatively constant while the second moment increases significantly). In sum, the com- putational costly coactivation analysis (∼1.2 × 109 times of LIF model computation) enables us to study the E/ I balance λ as a control parameter of functional connectivity formation. As expected, a higher E/I balance creates stronger functional connectivity because coactivation occurs more often. More neurons are included in the same cluster rather than maintain isolated, making it possible for large-scale communication between neurons to emerge. However, the concordant increase of dynamic connection degree with the increase of E/I balance λ discussed above is insufficient to give a whole picture of all important information. A piece of missing information lies in that the observed formation of functional connectivity is a sigmoid-like process rather than a uniform growth process. While functional connectivity forms promptly when λ is relatively small, the formation speed becomes stable at a large λ. The nonuniform speed is not a trivial consequence of λ nor of an artificially manipulation. Therefore, we conjecture it as an emergence phenomenon triggered by λ and restricted by specific mechanisms. Network Neuroscience 771 Percolation explains efficiency, robustness, and economy of the brain Functional connectivity characterized by percolation. Let us step back from the above analysis and rethink the nature of functional connectivity. Functional connectivity is rooted in the coac- tivation probability between neurons and is affected by both static connectivity and the E/I balance λ. One can interpret functional connectivity as a communication pattern between neurons, where static connectivity serves as a network of information channels, and λ modifies the information transmission probability in these channels. Although this idea has been studied previously in neuroscience computationally (Amico et al., 2021; Graham et al., 2020; Shew, Yang, Yu, Roy, & Plenz, 2011), we discuss it from a more physically fundamental perspective— percolation. Percolation is a universal characterization of critical phenomena and phase tran- sitions in a probabilistic form (Agliari, Cioli, & Guadagnini, 2011; Amini & Fountoulakis, 2014; Balogh & Pittel, 2007; Baxter, Dorogovtsev, Goltsev, & Mendes, 2010; Ben-Naim & Krapivsky, 2011; Callaway, Newman, Strogatz, & Watts, 2000; Dorogovtsev et al., 2001; Goltsev, Dorogovtsev, & Mendes, 2008; Li et al., 2021; Panagiotou, Spöhel, Steger, & Thomas, 2011; 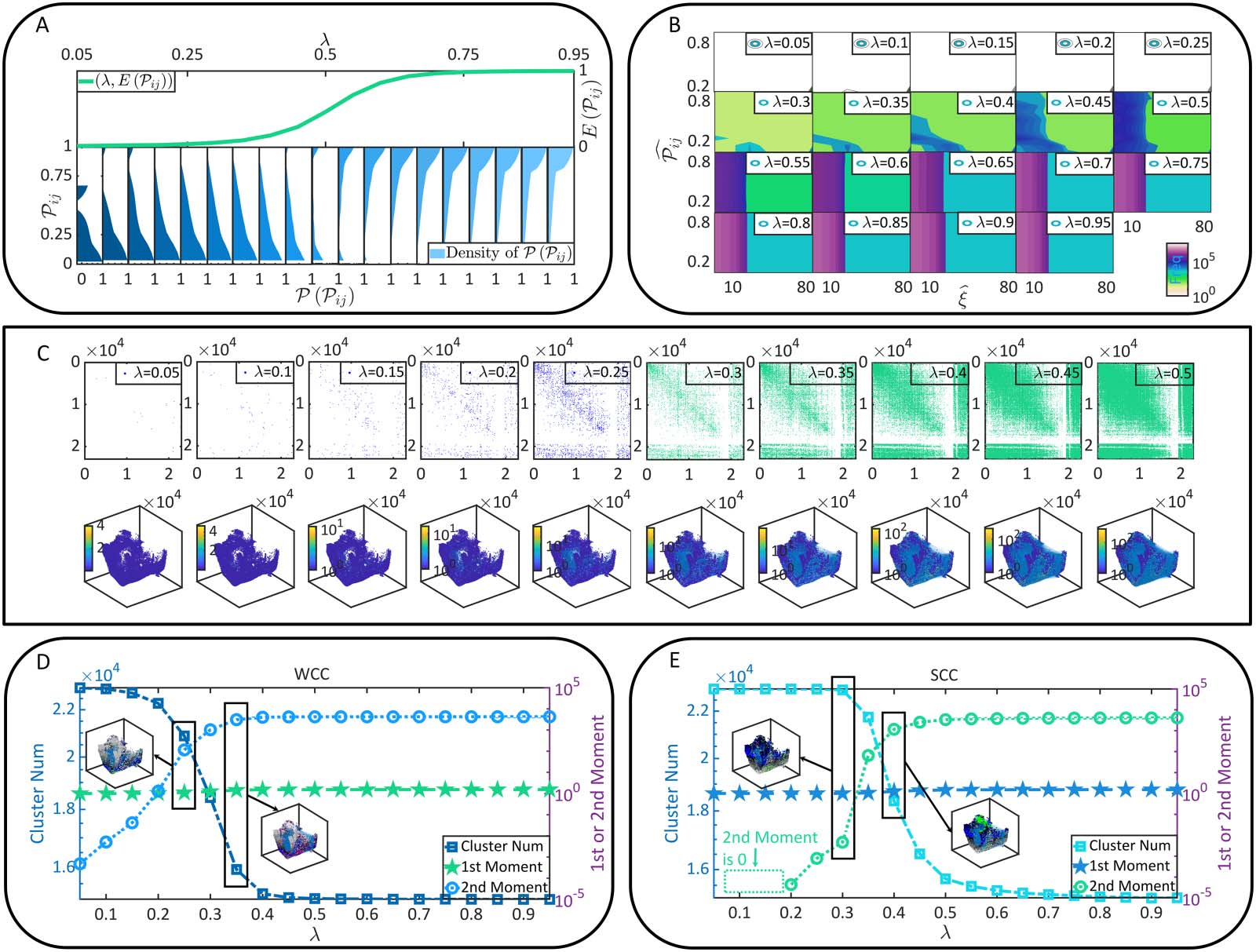Radicchi & Fortunato, 2009). To understand percolation, one can imagine that a porous stone, where pores or tiny holes are connected randomly, is immersed in water (Figure 3A). Can the water come into the core or kernel of the stone? This question can be addressed by verifying the existence of specific paths connected between pores that run through the stone. It is trivial that the stone will be wetted thoroughly when the connection probability between pores is suffi- ciently large, as connected pores can form a cluster to penetrate the stone. Replacing the stone and pores by the brain and neurons, one can see the intriguing similarity between the soaking process of porous stone and the functional connectivity of neurons (Figure 3A). The only dif- ference lies in that the space where connections can form changes from the lattice space of the stone to the random graph characterized by static connectivity. In decades, the equivalence relation between brain connectivity formation and the percolation on random graphs have attracted extensive explorations in biology (Bordier, Nicolini, & Bifone, 2017; Carvalho et al., 2020; Del Ferraro et al., 2018; Kozma & Puljic, 2015; Lucini, Del Ferraro, Sigman, & Makse, 2019; Zhou, Mowrey, Tang, & Xu, 2015) and physics (Amini, 2010; Breskin et al., 2006; Cohen et al., 2010; Costa, 2005; da Fontoura Costa & Coelho, 2005; da Fontoura Costa & Manoel, 2003; Eckmann et al., 2007; Stepanyants & Chklovskii, 2005), serving as a promis- ing direction to study brain criticality, neural collective dynamics, optimal neural circuitry, and the relation between brain anatomy and functions. In the terminology of percolation, neurons are referred to as sites. The dynamic connection formed between two neurons is called the occupation of the bond between these two sites. The central question in the following percolation analysis, as suggested above, concerns the emergence of a cluster of connected sites that penetrates the brain. The brain is referred to as percolate if such a cluster exists. Mathematically, the criterion of being percolate can be defined in terms of the giant strongly connected cluster (GSCC), a special SCC whose size approaches the whole brain size in magnitude order. In Figure 3B, we demonstrate that the size, the average in-degree, and the average out-degree of the GSCC are sigmoid-like func- tions of λ. These parameters are closing to 0 when λ is small. Then they increase dramatically after λ reaches over a specific value and approximate plateau again after λ reaches over another specific value. This phenomenon is not accidental because it shares similarities with the observations in Figure 2A and Figure 2E. To explore the underlying mechanism, we attempt to offer an analytical characterization of the GSCC rather than limit ourselves to com- putational interpretations. Note that our analysis is implemented under the framework of per- colation on directed graphs because the connectivity between neurons is unidirectional. Under each λ condition, we implement the random generation of functional connectivity l times (l = 5). Note that this setting means that all our subsequent analyses are repeated l times Percolation on random graphs: A kind of percolation process defined on random graphs, concerning the connectivity states between nodes (referred to as sites in the terminology of percolation) or edges (referred to as bonds in the terminology of percolation). Network Neuroscience 772 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 6 3 7 6 5 2 0 3 5 9 8 5 n e n _ a _ 0 0 2 4 6 p d t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Percolation explains efficiency, robustness, and economy of the brain l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 6 3 7 6 5 2 0 3 5 9 8 5 n e n _ a _ 0 0 2 4 6 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Functional connectivity formation as a percolation process. (A) The similarity between the soaking of porous stone and the Figure 3. functional connectivity of neurons. (B) The size, the average in-degree, and the average out-degree of the GSCC under different λ conditions. (C) P in and P out in brain connectome (upper parallel) and their nontrivial solutions (bottom parallel). (D) The probability ϕ predicted by Equation 7, the experimentally observed probability for a neuron to belong to the GSCC, and the upper bound (UB) of ϕ are presented as functions of λ. Meanwhile, the error between our theoretical predictions in Equation 7 and experimental observations is measured. (E) The difference between the nondilution percolation and the diluted one. (F) The percolation threshold ρc, term huvi, and term hki are shown as functions of λ. The meaningful values of threshold ρc are pointed out. Please note that D and F show l data sets of each variable indepen- dently derived from l (l = 5) times of functional connectivity generation (e.g., there are l sets of experimental data of ϕ). They highly overlap with each other to demonstrate that our observations are not accidental and keep consistency across different generated functional connectivity. (independently repeated on every generated functional connectivity). Here we do not average results across l times of analyses to show that our theory is averagely consistent with experi- ments. On the contrary, we show l sets of analysis results together to suggest that the consis- tency between our theory and experiments as well as the consistency across the results obtained on different generated functional connectivity are not accidental (e.g., see the data points that highly overlap with each other in Figure 3D, Figure 3F, and Figure 4). Given the benefits of multiple times of functional connectivity generation, let us go back to the details of generation approach. In each time, the existence of Ni → Nj is randomized following the binomial distribution Bi(P ij) (this is same as that in Figure 2B). Then we obtain statistics on functional connectivity, a directed graph, to calculate the probability P(u, v) for a neuron to have in-degree u and out-degree v. Based on the theory of percolation on directed graphs (Dorogovtsev et al., 2001; Li et al., 2021), the formation of the GSCC can be analyzed in terms of the probability Pin that a directed edge leads to the GSCC and the probability Pout that a directed edge comes from the GSCC. One can easily imagine that Pin and Pout increase with the size of GSCC. Analytically, P in and P out can be defined by their own self-consistent Network Neuroscience 773 Percolation explains efficiency, robustness, and economy of the brain Equations 1 and 2. Here self-consistency means that Pin and Pout can be represented as the functions of themselves (Dorogovtsev et al., 2001; Li et al., 2021). Pin ¼ 1− Pout ¼ 1− 1 kh i ∂ ∂x 1 kh i ∂ ∂y ð G x; y (cid:1) (cid:1) Þ x¼1;y¼1−Pin ; ð G x; y (cid:1) (cid:1) Þ x¼1−Pout;y¼1: (1) (2) The normalization term hki in Equations 1 and 2 denotes the average in-degree (or identically, the average out-degree) in Equation 3. X X kh i ¼ ð P u; v Þu ¼ ð P u; v Þv: u;v u;v (3) Equations 1 and 2 are derived based on the probability generating function (Equation 4), a standard and practical approach to study random graphs, especially in real data sets (Newman, Strogatz, & Watts, 2001). X ð G x; y Þ ¼ ð P u; v Þx uy v : (4) u;v Merely requiring the knowledge of P(u, v) in Equation 4, Equations 1 and 2 have been pow- erful enough in studying the formation of the GSCC. In other words, they can predict when the brain connectivity becomes percolate. Specifically, the sufficient and necessary condition for the GSCC to emerge is that Equations 1 and 2 have nontrivial solutions in (0, 1] (note that the trivial solution is Pin = Pout = 0). In practice, it is unnecessary to analytically study the non- trivial solutions of Equations 1 and 2. Instead, potential solutions can be numerically explored in a comprehensible way. Specifically, we only need to rewrite Equations 1 and 2 as functions Win ¼ 1 − Pin − Wout ¼ 1 − Pout − 1 kh i ∂ ∂x 1 kh i ∂ ∂y ð G x; y (cid:1) (cid:1) Þ x¼1;y¼1−Pin ; ð G x; y (cid:1) (cid:1) Þ x¼1−Pout;y¼1; (5) (6) and explore when Win and Wout go through the lines Win = 0 and Wout = 0 (see Figure 3C). When there exist non-trivial solutions ( ^Pin, ^Pout), the probability ϕ that a neuron belongs to the GSCC can be calculated in Equation 7. Otherwise, the probability maintains closing to 0. − G 1; 1 − ^Pin (cid:3) ϕ ¼ 1 − G 1 − ^Pout; 1 þ G 1 − ^Pout; 1 − ^Pin (cid:4) : (7) (cid:3) (cid:4) (cid:4) (cid:3) In Figure 3D, we compare between ϕ and the real probability that a neuron belongs to the GSCC in the experiment to quantify the error of our theoretical predictions. High consistency can be found between the predictions and experiment. As can be seen in Figure 3B and Figure 3D, a phenomenon referred to as percolation transition happens at λ = 0.3, where the GSCC emerges suddenly (ϕ = 0 when λ ≤ 0.3 and ϕ ≥ 0.06 when λ >
0.3). Esta es una transición del cerebro de estar fragmentado a filtrarse.. En otras palabras, neuronas
se acoplan ampliamente entre sí para formar una conectividad funcional a nivel de sistema después de λ
se extiende 0.3. Por lo tanto, λ = 0.3 sirve como umbral de percolación. Además, probabilidad ϕ en
Ecuación 5, así como las correspondientes observaciones experimentales, eventualmente se aproximará
a un límite superior (la velocidad creciente se acerca a 0 después de que λ se extienda 0.6). Este fenómeno
insinúa que el GSCC, reflejando la conectividad funcional, tiene un tamaño intrínsecamente limitado por estática
conectividad. La conectividad funcional se forma a través de conexiones sinápticas y, por lo tanto, debe
ser un subgrafo de conectividad estática. Recalculando las ecuaciones 1 a 5 en conectividad estática, el

Neurociencia en red

774

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

t

/

/

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

6
3
7
6
5
2
0
3
5
9
8
5
norte
mi
norte
_
a
_
0
0
2
4
6
pag
d

.

t

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

La percolación explica la eficiencia, robustez, y economía del cerebro

El límite superior de ϕ se obtiene en la Figura 3D y ϕ lo alcanza cuando λ ≥ 0.6. Nota intrínseca
coherencia entre las observaciones de la Figura 2A, Figura 2D, y la Figura 2E y que en
Figura 3D, Incluso los detalles cuantitativos son diferentes ya que se refieren a diferentes parámetros..

Además, La transición de percolación observada anteriormente también se puede confirmar a partir del análisis per-
perspectiva de percolación diluida. En condiciones de dilución, la formación de conectividad funcional es
no sólo está limitado por la probabilidad de coactivación entre neuronas sino también por la activación-
probabilidad de ción de cada neurona. En otras palabras, la condición de dilución representa una situación más
Situación realista donde las neuronas se activan condicionalmente. (p.ej., por estímulo externo) y
La conectividad funcional puede formarse sólo entre neuronas activables.. La percola sin dilución-
La solución analizada anteriormente sirve como un caso especial de la diluida. (ver Figura 3E). Considerando el
dilución de neuronas (p.ej., cada neurona se activa siguiendo una probabilidad ρ), otra versión de
umbral de percolación ρc (el parámetro de control es ρ) se puede calcular mediante ecuaciones 8 y 9
(Dorogovtsev et al., 2001; Le et al., 2021)

ρc ¼ kh i
uvh
X

;

i

uvh

yo ¼

d
pu; v

todoterreno:

(8)

(9)

tu;v

En la figura 3F, podemos ver que un ρc significativo 2 [0, 1] (la solución de una probabilidad es media-
útil si está en el intervalo de [0, 1]) emerge sólo cuando λ ≥ 0.3. Disminuye con λ hasta
alcanzando su límite inferior cuando λ ≥ 0.6. La existencia de un umbral de percolación significativo-
viejo sirve como una condición necesaria para que ocurra la transición de filtración (p.ej., cuando λ = 0.5,
La transición de percolación puede ocurrir si ρ ≥ ρc = 0.017; cuando λ = 0.2, transición de percolación nunca
sucede ya que ρc = 6.321 no tiene sentido). Por lo tanto, el GSCC puede formarse sólo después de que λ alcance
encima 0.3. Estos hallazgos son consistentes con el análisis de percolación sin dilución anterior.. En
Figura 3F, mostramos directamente la solución potencial del umbral de percolación ρc en función
de λ. Más adelante mostraremos los beneficios de tal ilustración..

En resumen, Nuestro análisis presentado anteriormente demuestra que la percolación, un universal para-
Malismo de criticidad y transiciones de fase., puede caracterizar la formación de funciones cerebrales.
conectividad sin otros modelos o suposiciones de arriba hacia abajo. Todos los cálculos analíticos únicamente.
Requieren el conocimiento de las distribuciones de grados en el conectoma cerebral., que es accesible en
práctica. Abajo, sugerimos que el análisis de percolación por sí solo es suficiente para explicar la
aparición de tres propiedades clave de las funciones cerebrales.

Propiedades de percolación y función cerebral

En la sección anterior, tenemos demonio-
La percolación explica la eficiencia de la transmisión de información.
Se demostró que la formación de conectividad funcional puede tratarse como un proceso de filtración.. A partir de
de esta sección, Estudiaremos cómo las propiedades de la función cerebral surgen como las características de
conectividad funcional formada.

Comencemos con la eficiencia de la transmisión de información., que se manifiesta como el tiempo bajo
Costo de las comunicaciones entre neuronas o alta capacidad de transmisión de información neuronal..
Tal superioridad depende fundamentalmente de los atributos topológicos de la conectividad funcional.
(Avena-Koenigsberger et al., 2018) en el cerebro real.

Aquí intentamos cuantificar la eficiencia de la transmisión de información basándonos en la teoría de grafos.
métrica. Siguiendo la misma idea en la Figura 2B y la Figura 3, aleatorizamos la conexión funcional-
actividad l veces (l = 5) bajo cada condición λ. Dada cada conectividad funcional, calculamos

Proceso de percolación:
Un proceso evolutivo del sistema.
estados de conectividad controlados por
parámetros específicos, donde cada
la unidad del sistema está ocupada aleatoriamente
y los estados de conectividad del sistema son
caracterizado por las conexiones de
unidades del sistema ocupadas.

Neurociencia en red

775

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

t

/

/

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

6
3
7
6
5
2
0
3
5
9
8
5
norte
mi
norte
_
a
_
0
0
2
4
6
pag
d

t

.

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

La percolación explica la eficiencia, robustez, y economía del cerebro

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

t

/

/

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

6
3
7
6
5
2
0
3
5
9
8
5
norte
mi
norte
_
a
_
0
0
2
4
6
pag
d

.

t

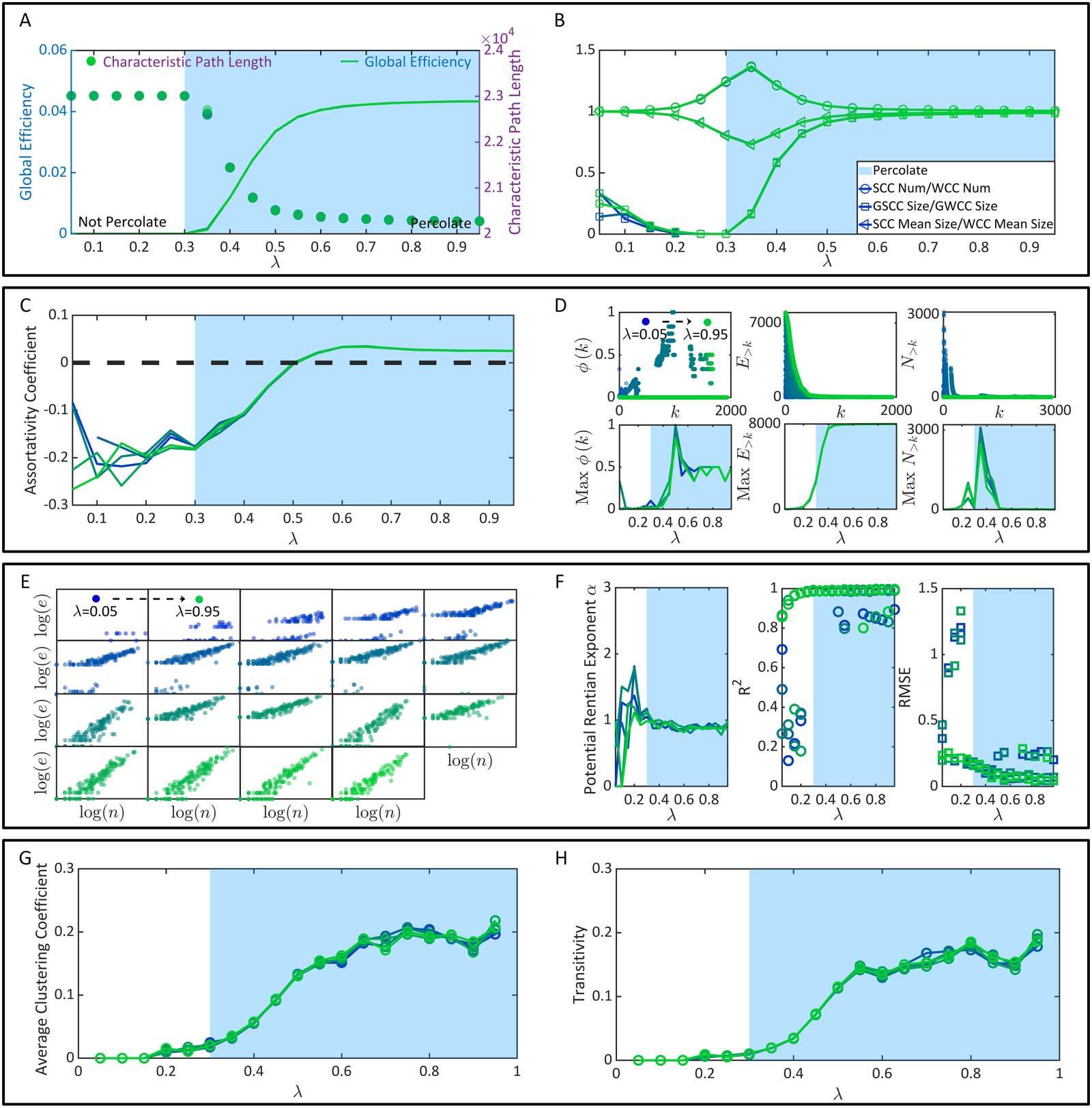
Cifra 4. El surgimiento de superioridades en la función cerebral. (A) La longitud del camino característico y la eficiencia global.. (B) Las propiedades de la estafa.-
clusters conectados. (C) El coeficiente de asortatividad. (D) las distribuciones (paralelo superior) y los máximos de ϕ(k), E>k, and N>k (paralelo inferior).
(mi) Instancias de (registro(norte), registro(mi)) bajo cada condición λ. (F) Los exponentes rentianos, el RMSE, y R2. (GRAMO) El coeficiente de agrupamiento promedio.. (h)
la transitividad. Tenga en cuenta que todas las figuras muestran l conjuntos de datos de cada variable derivados independientemente de l (l = 5) tiempos de conectividad funcional
generación.

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

su longitud de trayectoria característica (longitud promedio del camino más corto entre todas las neuronas) (Alberto &
Barrabás, 2002) y eficiencia global (longitud de camino más corta inversa promedio entre todos los neu-
ron) (latora & marchiori, 2001) (Cifra 4). En general, la longitud del camino característico refleja
el costo promedio de la transmisión óptima de información (la transmisión siempre sigue el mínimo-
principio de longitud de trayectoria imal). La eficiencia global es la transmisión de información óptima promedio.-
eficiencia de la misión. En la Figura 4A, una vez que λ supera el umbral de percolación sin dilución
0.3, La longitud del camino característico de la conectividad funcional cae drásticamente mientras que el global
la eficiencia aumenta significativamente. Una vez que λ alcanza 0.6, las velocidades de variación de estos dos
métricas aproximadas 0. Alta coherencia entre estas tendencias de variación y la filtración.
Se puede observar el proceso en la Figura 3D.. Mientras tanto, medimos la razón numérica y promediamos-
Relación de edad y tamaño entre SCC y WCC en conectividad funcional, respectivamente. Nosotros también
calcular la relación de tamaño entre el GSCC y el GWCC (cúmulo gigante débilmente conectado).

Neurociencia en red

776

La percolación explica la eficiencia, robustez, y economía del cerebro

Estas relaciones se muestran como funciones de λ en la Figura 4B.. Reflejan principalmente la proporción
de la comunidad neuronal muy unida, donde la capacidad de transmisión de información es alta, dentro
todas las neuronas comunicables (Una neurona es comunicable si puede comunicarse con al menos
otra neurona). En la Figura 4B, la relación de tamaño entre el GSCC y el GWCC tiene una
tendencia creciente similar con la eficiencia global, lo que sugiere que la gigantesca comunicación neuronal muy unida-
La comunidad ocupará más neuronas comunicables después de la transición de percolación.. Aunque el
otras dos proporciones (la proporción de números y la proporción de tamaño promedio entre SCC y WCC) no puedo
reflejar la mejora de la capacidad de transmisión de información mediante la transición de filtración, ellos
fluctúan significativamente cerca del umbral de percolación sin dilución y pueden funcionar como
marcadores observables de transición de percolación.

En resumen, La mejora de la eficiencia en la transmisión de información se demuestra como un efecto secundario.-
conducto del proceso de percolación. La transición de percolación puede ser una condición crítica para altas
eficiencia de transmisión para emerger.

La percolación explica una flexibilidad robusta. Luego pasamos a estudiar la robusta flexibilidad del control cerebral.-
conectividad, que es la capacidad del cerebro para tolerar la pérdida a gran escala de neuronas o sincronización-
conexiones apticas (p.ej., by lesions (Aerts et al., 2016; Joyce et al., 2013; Kaiser et al., 2007))
while maintaining robust brain functions.

En general, La flexibilidad robusta se puede estudiar directa e indirectamente. (Rubinov & despreciar,
2010b). El análisis directo de flexibilidad robusta generalmente compara la conectividad funcional antes
y tras presuntos ataques (p.ej., eliminando algunas neuronas) (Aerts et al., 2016; Joyce et al.,
2013; Kaiser et al., 2007). Sugerimos que estos ataques, no importa si son aleatorios o
dirigido, son equivalentes a la dilución introducida en el análisis de percolación diluida (ver
Figura 3E-F). Aquellas neuronas atacadas o relaciones direccionalmente adyacentes. (Y) nunca son
incluido en la conectividad funcional y, por lo tanto, puede tratarse como diluido. De esto por-
perspectiva, Se puede entender la motivación que subyace a la ilustración directa de la dilución por-
umbral de colación ρc en función de λ en la Figura 3F. Beneficia nuestro análisis al mostrar la
intensidad de ataque máxima tolerable 1 − ρc del cerebro manteniendo el percolado. Basado
en la Figura 3F, descubrimos que el cerebro no puede tolerar ataques hasta que λ alcance más allá 0.3. El
la flexibilidad robusta aumenta bruscamente hasta que λ supera 0.6, después de lo cual la velocidad creciente
se vuelve estable.

En cuanto al análisis indirecto de la flexibilidad robusta, Lo implementamos en términos de surtatividad.
coeficiente (Hombre nuevo, 2002) y el coeficiente del club rico (Baile et al., 2014; colizza, Llamas,
serrano, & Vespignani, 2006; Van Den Heuvel & despreciar, 2011). El coeficiente de sortatividad es
la correlación de Pearson entre los grados de todas las neuronas en dos extremos opuestos de un DA.
La conectividad cerebral con un coeficiente de asortatividad positivo puede tener un efecto comparativamente sólido
comunidad de centros de alto grado mutuamente interconectados, mientras que la conectividad cerebral con un neg-
El coeficiente de sortatividad activo puede tener centros de alto grado vulnerables y ampliamente distribuidos.
(Rubinov & despreciar, 2010b). Similarmente, el coeficiente del club rico ϕ(k) es la razón numérica de
the DAs between neurons of degree > k (denoted by E>k), cuando todas las neuronas de grado ≤ k tienen
sido eliminado, al máximo de DA que dichas neuronas pueden compartir (denoted by N>k) (Baile et al.,
2014; Colizza et al., 2006; Van Den Heuvel & despreciar, 2011). Los cálculos de estos dos
Las métricas se pueden implementar utilizando una caja de herramientas diseñada por Rubinov y Sporns. (2010b). En
Figura 4C, descubrimos que el coeficiente de asortatividad aumenta significativamente una vez que λ alcanza
encima 0.3. Se vuelve positivo después de que λ supera 0.5 y se vuelve relativamente inmutable después de λ
se extiende 0.6. También se pueden observar tendencias de variación similares en el máximo ϕ(k) (El máximo-
El valor máximo se obtiene mediante la comparación entre diferentes k). Una ligera diferencia radica en
que el máximo ϕ(k) alcanza su punto máximo cuando λ = 0.5 y luego cae hasta λ = 0.6 (Figura 4D).

Neurociencia en red

777

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

/

t

/

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

6
3
7
6
5
2
0
3
5
9
8
5
norte
mi
norte
_
a
_
0
0
2
4
6
pag
d

t

.

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

La percolación explica la eficiencia, robustez, y economía del cerebro

En suma, la robusta flexibilidad de la conectividad funcional, no importa si se analiza directamente o
indirectamente, experimenta un fuerte aumento después de la transición de percolación (λ = 0.3). Además, es
nuevamente intrínsecamente limitado por la conectividad estática y alcanza su límite después de λ ≥ 0.6.

La percolación explica la economía del cerebro. Finalmente, analizamos la economía del cerebro desde las perspectivas
del cableado de la red y funcionamiento de la red, respectivamente.

Medir la eficiencia de la integración física de la conectividad funcional es un método prometedor.
Enfoque para analizar la economía del cableado de red. (Bassett y cols., 2010). Un principio organizacional clave-
El principio compartido por varios sistemas de procesamiento de información física es la relación de escala isométrica.-
relación entre el número de unidades de procesamiento (p.ej., neuronas) y el número de conexiones
(p.ej., relaciones direccionalmente adyacentes), Conocida como la escala rentiana.. Tal propiedad revela
la relación entre la dimensionalidad de la topología del sistema y la capacidad de procesamiento de información-
idad. En general, La escala rentiana corresponde a un paradigma de cableado económico de incrustación.
una topología funcional de alta dimensión en un espacio físico de baja dimensión (Bassett y cols.,
2010; Chen, 1999; Ozactos, 1992). Para comprobar la existencia de la escala rentiana, nosotros necesitamos
dividir el espacio físico en m cubos. Luego contamos el número n de neuronas dentro
cada cubo y el número e de relaciones direccionalmente adyacentes (El) cruzando el cubo obligado-
Aries. La escala rentiana existe si existe un registro de relación de regresión lineal estadísticamente significativo
(mi) = αlog(norte) + b y a 2 (0, 1). Aquí α se conoce como el exponente físico rentiano.. Un más pequeño
Un exponente significativo corresponde a una mayor eficiencia.. Usamos la información de coordenadas de
Neuronas para incorporar conectividad funcional en un espacio físico de tamaño real., donde la partición
el número se establece como m = 300. En la Figura 4E, mostramos casos de (registro(norte), registro(mi)) distribuciones gen-
borrado de la conectividad funcional bajo cada condición λ. Cualitativamente, ya podemos encontrar
eso (registro(norte), registro(mi)) puede no seguir una relación de regresión lineal significativa cuando λ es pequeño.
Cuantitativamente, descubrimos que el rendimiento de la regresión lineal antes de la transfusión de percolación-
posición, λ = 0.3, es débil e inestable. Este fenómeno es esperable porque a nivel del sistema
la conectividad funcional aún no ha surgido, y el espacio físico está ocupado por personas aisladas
y neuronas ineficientes (ver Figura 4F). Una vez que λ se acerca y se acerca más 0.3, el
la regresión lineal se vuelve significativa con un exponente rentiano físico promedio α ∼ 0.8999
(el error estándar es ∼0.0464). Se puede observar una ligera disminución de α cuando λ 2 (0.3, 0.6),
lo que sugiere que la incrustación física se vuelve relativamente más eficiente. Excepto ser
reportado solo, el exponente rentiano físico α calculado a través de la partición del espacio físico
también se puede comparar con su mínimo teórico para sacar la misma conclusión de otro
perspectiva (p.ej., véase Bassett et al., 2010).

En cuanto a la economía del funcionamiento de la red., cabe señalar que una posible idea errónea
acerca de la economía metabólica es que la economía metabólica desaparece después de la función a nivel del sistema.-
Surge la conectividad nacional. Aquí debemos enfatizar la desigualdad entre alta
Costo metabólico y baja economía metabólica.. Conectividad funcional a nivel de sistema con alta
costo metabólico (La dinámica neuronal masiva y el alto equilibrio E/I son metabólicamente costosos.; Barta
& Costero, 2019; bullmore & despreciar, 2012) no es necesariamente ineficiente si puede soportar grandes
cantidades de funciones. La baja eficiencia corresponde a altos costos pero baja capacidad funcional. En
cerebros reales, El alto consumo metabólico es inevitable considerando miles de millones de neuronas y sintetizadores.-
álamo temblón (bullmore & despreciar, 2012); La economía metabólica está determinada principalmente por la función.
pago de capacidad. Esta recompensa en los cerebros reales suele estar determinada por la segregación funcional y
capacidades de integración (Rubinov & despreciar, 2010b). Específicamente, La segregación funcional es el hombre.-
Se manifiesta como procesamiento de información especializado y distribuido en grupos de
grupos neuronales, que se puede analizar en términos de estructura modular (Rubinov & despreciar,
2010b) y cuantificado aplicando el coeficiente de agrupamiento (Frijol, 2007; vatios & Strogatz,

Neurociencia en red

778

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

/

t

/

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

6
3
7
6
5
2
0
3
5
9
8
5
norte
mi
norte
_
a
_
0
0
2
4
6
pag
d

.

t

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

La percolación explica la eficiencia, robustez, y economía del cerebro

1998) y la transitividad (Hombre nuevo, 2003). En la Figura 4G-H, Estas dos métricas se muestran como
funciones de λ, respectivamente. Si bien aumentan considerablemente después de la transición de percolación, su
las tasas de aumento caen una vez que λ supera 0.5. En otras palabras, experiencia en estructuras modulares
fusiones masivas después de la transición de filtración, cada vez más grande y más unido. Sin embargo,
the ever-rising λ > 0.5 No se puede mejorar la segregación funcional sin limitación.. Estos mod-
Las estructuras circulares en la conectividad funcional están, en última instancia, restringidas por la conectividad estática.. Como para
integración funcional, se refiere a la capacidad de recopilar y combinar información especializada
de grupos neuronales distribuidos (Rubinov & despreciar, 2010b). La longitud del camino característico y
La eficiencia global que se muestra en la Figura 4A son métricas prácticas de esta propiedad., cual tiene
Se ha demostrado que es explicable por percolación..

Combine la información de la Figura 4E–H, podemos ver que tanto la economía del cableado de la red
y la economía de funcionamiento de la red se optimizan después de λ ≥ 0.3. Considerando que cada aumento en el
El equilibrio E/I provoca un mayor consumo de energía (Barta & Costero, 2019; bullmore & despreciar,
2012) pero puede que no traiga beneficios adicionales (p.ej., La economía de funcionamiento de la red no significa-
aumenta ligeramente después de λ ≥ 0.5), sugerimos que λ ∼ 0.5 puede ser una opción óptima para el cerebro
para mantener la economía.

DISCUSIÓN

El equilibrio sináptico E/I óptimo para las funciones cerebrales

Avancemos en nuestro análisis incorporando todos los hallazgos presentados anteriormente para resolver un problema crítico.-
Cuestión científica de interés en la neurociencia.: ¿Cuál es el equilibrio sináptico óptimo E/I??

Existen varios valores vitales del equilibrio E/I λ según nuestro análisis anterior: el
umbral de percolación sin dilución λ = 0.3 (El saldo E/I es 3:7) donde ocurre la transición de percolación-
plumas; el valor aproximado λ = 0.5 (El saldo E/I es 1:1) que concilia el tamaño real de la
GSCC con sus tarifas crecientes; el valor aproximado λ = 0.6 (El saldo E/I es 3:2), después de lo cual
la percolación se aproxima a su límite. Las características ventajosas de las funciones cerebrales.,
incluida la eficiencia (Avena-Koenigsberger et al., 2018), robustez (Aerts et al., 2016; Joyce
et al., 2013; Kaiser et al., 2007), y economía (bullmore & despreciar, 2012), principalmente expe-
rience aumentos bruscos después de la transición de percolación en λ = 0.3 y se vuelve inmutable después de λ =
0.6 porque están intrínsecamente limitados por las características de las condiciones estáticas o anatómicas.-
conectividad. Eficiencia de transmisión de información, flexibilidad robusta, y economía de cableado de red
tienen cantidades reales relativamente grandes y altas velocidades crecientes cercanas a λ = 0.5, después de lo cual
sus velocidades crecientes se aproximan gradualmente 0 y no son suficientes para actuar como pagos de
el aumento de λ. Por lo tanto, Es muy probable que el valor real de la economía de funcionamiento de la red sea óptimo.-
mizado cerca de λ = 0.5. Por encima de este valor se observa una fuerte caída. Además, un nivel significativamente alto
El equilibrio E/I puede dañar la eficiencia de codificación de información (Barta & Costero, 2019; Vocero,
2017) y estabilizador del potencial de membrana (Sadeh & Clopata, 2021; Vocero, 2017). Tomando
todas estas piezas de evidencia juntas, Se sugiere que un equilibrio E/I óptimo para que el cerebro funcione.
garantizar propiedades ventajosas simultáneamente puede ser λ ∼ 0.5, consistente con el anterior-
hallazgo experimental in vitro (Shew et al., 2011). Además, esta E/I óptima inferida
La teoría del equilibrio por percolación corrobora los hallazgos de la condición suficiente para la
La dinámica en el cerebro es crítica. (Cabello, Piedra dura, Mansvelder, & Linkenkaer-Hansen,
2012). En otras palabras, Proporciona explicaciones sobre el origen de la criticidad cortical., un generalizado
Fenómeno en el cerebro de múltiples especies. (ruega & Hora, 2012; Chialvo, 2004; Fontenele
et al., 2019; Oscuro, Williams-García, ruega, & Ortíz, 2021; Gautama, Hoang, McClanahan,
grady, & mostrar, 2015; millman, Mihalas, kirkwood, & Niebur, 2010; Williams-García, moore,
ruega, & Ortíz, 2014), desde una nueva perspectiva. En nuestra investigación, el equilibrio E/I λ se define como

Teoría de la percolación:
Una teoría física que caracteriza
fenómenos críticos y fase
transiciones desde un modelo probabilístico y
perspectiva geométrica.

Neurociencia en red

779

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

t

/

/

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

6
3
7
6
5
2
0
3
5
9
8
5
norte
mi
norte
_
a
_
0
0
2
4
6
pag
d

t

.

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

La percolación explica la eficiencia, robustez, y economía del cerebro

la fracción de sinapsis excitadoras en todas las sinapsis. Porque la fuerza de excitación/inhibición
en la ecuación 10 se genera uniformemente, el equilibrio E/I óptimo previsto λ ∼ 0.5 implica un
equilibrio entre la excitación WE y la inhibición WI fortalezas en todo el cerebro. Este resultado es
consistente con un hallazgo bien conocido de que las actividades neuronales con una entropía alta y robusta
ocurren cuando NOSOTROS y WI están equilibrados (Agrawal et al., 2018). Mientras tanto, podemos más
transformar el equilibrio óptimo E/I λ ∼ 0.5 al parámetro ψ, la fracción de neuronas excitadoras
en todas las neuronas, desde que nosotros, Wisconsin, y ψ están matemáticamente relacionados (Agrawal et al., 2018). para guarnecer-
antee entropía alta y robusta, se puede derivar una ψ grande según Agrawal et al.. (2018). Estos
Los resultados corroboran la abundancia de neuronas excitadoras en las cortezas de los mamíferos. (hendry,
Schwark, jones, & yan, 1987; Meinecke & Peters, 1987; Sáhara, yanagawa, O'Leary, & stevens,
2012).

Una dirección valiosa de exploración futura puede ser generalizar la cuantificación de la eficiencia.-
ciencia, robustez, y economía para verificar si el equilibrio óptimo E/I que simultáneamente
garantiza que estas propiedades ventajosas aún coinciden con las predicciones de la teoría de la percolación. El
La generalización es necesaria ya que las mediciones de eficiencia, robustez, y economía
en el cerebro sigue siendo un desafío abierto. Por ejemplo, las métricas teóricas de grafos consideradas
en análisis de eficiencia de transmisión de información (p.ej., eficiencia global) podría ser no ideal
porque la comunicación de señales neuronales puede no exhibir características de longitud de ruta casi mínimas
(Avena-Koenigsberger et al., 2018; Goñi et al., 2014). Métricas alternativas (Avena-Koenigsberger
et al., 2018; Seguin, tian, & Brilla, 2020; Seguin, Van Den Heuvel, & Brilla, 2018) tener
Se ha desarrollado recientemente y se puede aplicar para reflejar más la eficiencia de la transmisión.
adecuadamente.

Teoría de la percolación del cerebro: Oportunidades y desafíos

En el presente estudio, Hemos sugerido la percolación como una ventana para comprender cómo funciona el cerebro.
Las propiedades de la función surgen durante la formación de la conectividad funcional.. La relación congruente-
La relación entre la conectividad cerebral y la filtración es natural y comprensible.. Al igual que el
piedra porosa sumergida en un charco de agua, El cerebro es "poroso" en términos de neuronas y
inmerso en un “pool” de información. A través de simples cálculos analíticos, percolación anal-
ysis ha demostrado una gran coherencia tanto en las observaciones teóricas como en las experimentales.. Tal vez
debido a estas ventajas, La teoría de la percolación ha atraído un interés emergente en la neurociencia.-
ence. Desde las primeras exploraciones que combinan datos limitados de morfología neuronal con computación-
Simulaciones opcionales para analizar la percolación. (Costa, 2005; da Fontoura Costa & Coelho, 2005;
da Fontoura Costa & manuel, 2003; Stepanyants & Chklovski, 2005) a obras más recientes
que estudian la filtración directamente en la conexión cerebral de escala relativamente pequeña y de grano grueso.-
tomo y datos de dinámica neuronal estimulados eléctricamente capturados de redes neuronales vivas
(p.ej., cultivos neuronales primarios en hipocampo de rata) (Creer, 2010; Breskin et al., 2006; cohen
et al., 2010; Eckman et al., 2007), Los esfuerzos de la física han inspirado numerosos seguimientos.
exploraciones en neurociencia (Bordier et al., 2017; Carvalho et al., 2020; Del Ferraro et al.,
2018; Kozmá & Puljic, 2015; Lucini et al., 2019; Zhou y cols., 2015). Estos estudios capturan
Una visión elegante y esclarecedora sobre los circuitos neuronales óptimos., dinámica colectiva neuronal,
criticidad, y la relación entre la conectividad cerebral y las funciones cerebrales. Construido sobre estos
obras, Presentamos un marco más sistemático y biológicamente justificado para formalizar la función.-
Formación de conectividad funcional como filtración en gráficos dirigidos aleatoriamente.. El mérito de nuestra
el marco es cuádruple. Primero, diferente del bootstrap (p.ej., véase Eckmann et al., 2007) o
quórum (p.ej., véase Cohen et al., 2010) Análisis de percolación en estudios previos., dejamos el
criterio de ocupación como un trabajo de cálculo de dinámica neuronal en lugar de preestablecer la ocupación-
perfil de división de las neuronas. En el futuro, Este criterio puede optimizarse mediante neurotransmisión sincrónica.

Neurociencia en red

780

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

t

/

/

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

6
3
7
6
5
2
0
3
5
9
8
5
norte
mi
norte
_
a
_
0
0
2
4
6
pag
d

t

.

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

La percolación explica la eficiencia, robustez, y economía del cerebro

Registro de dinámica cuando madura la tecnología requerida.. Segundo, percolación dirigida
Los gráficos pueden capturar la direccionalidad de la difusión de la dinámica neuronal.. Tercero, la filtración
definido en gráficos aleatorios es un reflejo natural de la desigualdad entre estática y función.-
conectividad nacional, consistente con el hecho de que la conectividad estática sirve como plataforma del
uno dinámico. Finalmente, distinguimos entre condiciones de dilución y no dilución, permitiéndonos
Caracterizar la formación de conectividad funcional en situaciones impulsadas por estímulos o atacadas..
Estas propiedades mejoran la capacidad de nuestro marco para adaptarse al carácter real.-
ísticas de la conectividad cerebral.

Construido sobre la equivalencia entre la formación de conectividad funcional y la percolación.
controlado por el equilibrio sináptico E/I, revelamos que las propiedades de la función cerebral surgen como bypro-
conductos de transición de percolación. Aunque el actual marco de percolación es universal, nosotros
plantear la hipótesis de que las cantidades reales de umbral de percolación, el equilibrio óptimo E/I, y
el equilibrio E/I después del cual estas propiedades se aproximan a sus límites determinados por estática
conectividad, puede variar entre diferentes especies, siglos, estados corticales, y hasta poder servir
como biomarcadores de enfermedades nerviosas. Esta especulación está bien fundada porque el equilibrio E/I
oscila diariamente (Bridi et al., 2020; tao, li, & zhang, 2014) y puede cambiar debido a una disfunción-
ción (Grent et al., 2018; Ramírez-Toraño et al., 2021). Estos cambios pueden ser consecuencias de
variaciones específicas de los atributos de percolación, que quedan para futuras exploraciones.

Comprender las características de la función cerebral a través de la física

Arraigado en el emergentismo, El presente estudio intenta explorar los mecanismos de origen del cerebro.
características de la función desde una perspectiva física y evitar el modelado basado en suposiciones.
Se sugiere que los mecanismos subyacentes se describan mediante percolación., un carbón universal-
Acterización de fenómenos críticos y transiciones de fase. (Dorogovtsev et al., 2001; Le et al.,
2021). Nuestros experimentos en el conectoma cerebral más grande hasta el momento de la mosca de la fruta, Correo de Drosophila-
anogastro (Puchero de barro, 2020; Schlegel et al., 2021; Xu et al., 2020), han demostrado la
capacidad de percolación para explicar la formación de la conectividad funcional y la emer-
Gencia de las propiedades de la función cerebral sin suposiciones adicionales.. La explicación fuerte
Se observa experimentalmente el poder de la teoría de la percolación hacia estos conceptos de neurociencia.,
aunque inicialmente se estudian en diferentes campos científicos. Una conexión tan intrigante
vuelve a enfatizar la naturaleza del cerebro como un sistema físico. Recientemente, esta perspectiva física-
tive ha experimentado avances sustanciales en la neurociencia. Por ejemplo, el principio de energía libre es
demostrado como una base unificada de percepción, acción, Y aprendiendo (Friston, 2009,
2010, 2012; Friston & Kiebel, 2009; Guevara, 2021). Se descubre que la criticidad cortical
dar cuenta de la transformación eficiente entre estados corticales (ruega & Hora, 2012;
Chialvo, 2004; Fontenele et al., 2019; Oscuro et al., 2021; Gautam et al., 2015; millman
et al., 2010; Williams-García et al., 2014). Además, la termodinámica de la información es
revelado como un puente entre el cerebro físico y el informativo (Capolupo, Hombre libre,
& Vitiello, 2013; Cuello & grifo, 2015; Sartori, Granjero, Sotavento, & Horowitz, 2014; Sengupta,
votante, & Friston, 2013; Calle, 2020). En el futuro, Esta dirección ascendente puede continuar-
Homenajeando a la neurociencia como ventana para comprender las bases intrínsecas del funcionamiento cerebral.
características.

Para concluir, los paralelismos descubiertos entre la formación de conectividad funcional y la
La filtración en gráficos dirigidos al azar controlados por el equilibrio sináptico E/I sirve como un nuevo camino.-
camino hacia la comprensión del surgimiento de las características de la función cerebral. la filtración,
Un formalismo elegante de fenómenos críticos y transiciones de fase., puede dilucidar el emer-
Gencia de caracteres de función cerebral a partir de la conectividad cerebral..

Neurociencia en red

781

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

t

/

/

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

6
3
7
6
5
2
0
3
5
9
8
5
norte
mi
norte
_
a
_
0
0
2
4
6
pag
d

t

.

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

La percolación explica la eficiencia, robustez, y economía del cerebro

MATERIALES Y MÉTODOS

Adquisición del conectoma cerebral

Los datos del conectoma cerebral se publican como parte del proyecto FlyEM (Xu et al., 2020). El
La imagen del conectoma se implementa aplicando el electrón de escaneo del haz de iones enfocado.
microscopía (FIB-SEM) tecnología. Luego las imágenes se limpian y mejoran mediante una serie de tubos.-
líneas (p.ej., segmentación automatizada de la red de llenado de inundaciones), generando el grano más fino
y conectoma de alto rendimiento del cerebro central de la mosca de la fruta (∼2,5 × 105 nm en cada dimensión-
sión) hasta la fecha (Xu et al., 2020). Hay 21,662 rastreado (todas las ramas principales dentro del volumen
son reconstruidos) y sin recortar (Los cenadores principales están contenidos en el volumen.) las neuronas también
como 4,495 rastreado, recortado, y largo (≥1.000 conexiones sinápticas) neuronas en la conexión-
a mi. El complejo diagrama de cableado entre neuronas consta de aproximadamente 6 × 106 rastreado y
sitios presinápticos no recortados, así como ∼1,8 × 107 guarida postsináptica trazada y sin recortar-
ciudades (Xu et al., 2020).

Adquirir y manejar eficientemente un conjunto de datos tan grande, Google ha diseñado un sistema
neuPrint para organizar el conectoma cerebral de forma accesible. Los lectores pueden seguir el
instrucciones en Xu et al.. (2020) para descargar y procesar los datos del conectoma cerebral en neu-
Imprimir. Aunque adquirimos todo el conectoma cerebral, Incluimos neuronas y sinapsis.
en análisis sólo cuando los cuerpos celulares están posicionados con precisión (asignado con un spa de 10 nm-
coordenada de resolución espacial). La información de coordenadas se requiere expresamente porque es
Necesario en la visualización de la conectividad y el análisis de escalamiento rentiano. (Bassett y cols.,
2010; Chen, 1999; Ozactos, 1992). El conjunto de datos seleccionado contiene 23,008 neuronas,
4,967,364 conexiones sinápticas (hendiduras sinápticas), y 63,5761 pares de direccionalmente adyacentes
relaciones (Dos neuronas son direccionalmente adyacentes si una conexión sináptica sale de
una neurona y conduce a otra).

Variables en la descripción del conectoma cerebral

Presentar una caracterización sistemática del conectoma cerebral., consideramos dos informativos
escamas: escala macroscópica (regiones del cerebro) y escalas microscópicas (neuronas).

En escala macroscópica, La parcelación de las regiones del cerebro ha sido proporcionada por Xu et al..
(2020). Según la información ascendente y descendente de cada sinapsis., podemos
describir la conectividad estática macroscópica con las variables dadas en la Tabla 3.

Se puede tratar razonablemente la conectividad estática macroscópica como un gráfico dirigido.. Nodos
Son regiones del cerebro y puede haber múltiples bordes dirigidos. (PIP y POP) entre cada par
de nodos. Sumando todos los PIP o POP de una región del cerebro, podemos medir lo macroscópico
en grado (TPPI) y fuera de grado (TPOP) de ello. En nuestra investigación, Las variables TPIP y TPOP son
utilizado en nuestros principales análisis (por favor ver tablas 1 y 2 y figura 1 en el texto principal) mientras
Las variables PIP y POP se utilizan para proporcionar información adicional. (por favor ver tablas 5 y
6 y figura 5).

Similarmente, Podemos definir la conectividad estática microscópica mediante las variables dadas en

Mesa 4.

La conectividad estática microscópica corresponde a un gráfico dirigido donde los nodos son neutros.-
ron. Con una granularidad fina, Podemos tratar las conexiones sinápticas como bordes dirigidos.. De este modo, allá
pueden ser múltiples bordes (SC) entre una neurona seleccionada y una de sus neuronas adyacentes. Nosotros
puede decir además si estos bordes provienen de (OSC) o conduciendo a (ISC) este seleccionado
neurona. Con granularidad gruesa, podemos tratar las relaciones direccionalmente adyacentes como dirigidas
bordes. Bajo esta condición, solo hay un borde (Y) entre dos neuronas adyacentes

Neurociencia en red

782

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

/

t

/

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

6
3
7
6
5
2
0
3
5
9
8
5
norte
mi
norte
_
a
_
0
0
2
4
6
pag
d

t

.

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

La percolación explica la eficiencia, robustez, y economía del cerebro

Variable
CAROLINA DEL SUR

ISC

OSC

Y

AIF

AOD

SC/DA

CAI/AIF

Mesa 4. Definiciones de variables microscópicas

Significado

Todas las conexiones sinápticas que presenta una neurona.

Todas las conexiones sinápticas recibidas por una neurona de otras neuronas.

Todas las conexiones sinápticas que vienen de una neurona a otras neuronas.

Todas las relaciones direccionalmente adyacentes entre una neurona y otras neuronas.

Todas las relaciones direccionalmente adyacentes entre una neurona y sus neuronas presinápticas.

Todas las relaciones direccionalmente adyacentes entre una neurona y sus neuronas postsinápticas.

Conexiones sinápticas entre una neurona y una de sus neuronas adyacentes. (el número de SC por DA)

Conexiones sinápticas entre una neurona y una de sus neuronas presinápticas (el número de ISC por IDA)

OSC/AOD

Conexiones sinápticas entre una neurona y una de sus neuronas postsinápticas. (el número de OSC por AOD)

y podemos distinguir de manera similar entre AIF y AOD. La información detallada es
necesario en el cálculo de la dinámica neuronal, mientras que la información de grano grueso es útil en
analizando la conectividad funcional microscópica. Por lo tanto, También calculamos SC/DA, CAI/AIF,
y OSC/ODA para reflejar cómo una neurona asigna conexiones sinápticas a cada uno de sus vecinos.
Estas variables ofrecen asignaciones entre información de grano fino y de grano grueso.. En nuestro
investigación, Las variables relevantes con DA se utilizan en nuestros análisis principales. (por favor ver tablas 1 y 2
y figura 1 en el texto principal) mientras que otras variables se utilizan para proporcionar información auxiliar
(por favor ver tablas 5 y 6 y figura 5).

Análisis de ley de potencia y análisis de simetría.

En nuestra investigación, El análisis de la ley de potencia en datos empíricos agrupados se implementa aplicando un
caja de herramientas de código abierto (R. Obras & cláusula, 2014). Derivaciones matemáticas correspondientes
se puede ver en Y. Trabaja contra Clauset (2014). Primero hacemos binning en variables de interés., dónde
el número de contenedores espaciados linealmente se establece como 150. En casos reales, la ley de potencia sólo puede mantenerse
colas específicas {PAG(A)|A ≥ A0} de la distribución empírica de la variable A, donde A0 denota un
cierto límite de distribución (cláusula, shalizi, & Hombre nuevo, 2009). Aplicamos el Kolmogorov-
Enfoque basado en estadísticas de Smirnov (Y. Obras & cláusula, 2014) para estimar estas distribuciones
tejanos cortados. Luego implementamos una estimación de máxima verosimilitud de los exponentes de la ley de potencias. (Y. Obras
& cláusula, 2014) en las colas de distribución por encima de los límites. Correspondiente Kolmogorov-Smirnov
Las estadísticas se pueden calcular entre las distribuciones de probabilidad acumuladas de la potencia estimada.
modelos legales y distribuciones empíricas de probabilidad acumulativa para reflejar la bondad de la estimación.-
ción (Y. Obras & cláusula, 2014). Se espera que una estimación ideal tenga un valor suficientemente pequeño
Estadística de Kolmogorov-Smirnov (<0.05 is suggested as a strict criterion). The authors of Y. Virkar and Clauset (2014) also propose a statistic significance test based on Kolmogorov–Smirnov statistics. Although the test measures the statistic significance of rejecting the power law hypoth- esis, it cannot further imply the correctness of the estimated power law model (Y. Virkar & Clauset, 2014). Therefore, the test is unnecessary if Kolmogorov–Smirnov statistics have been sufficiently small. In Table 5 and Figure 5, we present the auxiliary results of power law analysis. These results are derived on supplementary variables in static brain connectivity descriptions and provide corroborative evidence for the main text. In general, macroscopic static connectivity is Network Neuroscience 783 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 6 3 7 6 5 2 0 3 5 9 8 5 n e n _ a _ 0 0 2 4 6 p d t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Percolation explains efficiency, robustness, and economy of the brain Table 5. Power law analysis results (supplementary information) Probability distribution P (SC = n) ∝ n−2.87 Goodness of estimation 0.0104 Scale-free or not Yes Type Microscopic Microscopic Microscopic Microscopic Microscopic Microscopic Variable SC ISC OSC DA SC/DA ISC/IDA P (ISC = n) ∝ n−2.78 P (OSC = n) ∝ n−2.81 P (DA = n) ∝ n−3.53 P (SC/DA = n) ∝ n−3.49 P (ISC/IDA = n) ∝ n−2.53 Microscopic OSC/ODA P (OSC/ODA = n) ∝ n−2.99 Note. Being scale-free requires P ∝ n−α, where α 2 (2, 3). Goodness of estimation is expected as to be less than 0.05. 0.0177 0.0172 0.0248 0.0244 0.0211 0.0183 Yes Yes No No Yes Yes l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 6 3 7 6 5 2 0 3 5 9 8 5 n e n _ a _ 0 0 2 4 6 p d t . Supplementary information of static connectivity characterization. (A) Supplementary variables of macroscopic static connectivity Figure 5. and microscopic static connectivity are graphically illustrated in an instance. (B) The power law models of synaptic connection number (SC), directionally adjacent relation number (DA), and the number of synaptic connections per directionally adjacent relation (SC/DA). (C) The power law models of input synaptic connection number (ISC) and output synaptic connection number (OSC). (D) The power law models of the number of synaptic connections between one neuron and one of its presynaptic neuron (ISC/IDA) and the number of synaptic connec- tions between one neuron and one of its postsynaptic neuron (OSC/ODA). f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 suggested as plausibly scale-free. However, the potential scale-free property of microscopic static connectivity seems to be uncertain and nonrobust. The symmetry analysis for static connectivity is implemented based on Pearson correlation and average change fraction between input-related variables and output-related variables. Pearson correlation reflects if output-related variables have similar variation trends with input-related variables. Average change fraction of output-related variables compared with input-related variables reflects if these two kinds of variables are quantitatively similar. The symmetric static connectivity is expected to have balanced input-related and output-related variables and, therefore, is required to feature significant positive correlation (e.g., larger than 0.9) and small average change fraction (e.g., smaller than 1). We refer to these two require- ments as the strictest criterion of strong symmetry. To present a more accurate analysis, we Network Neuroscience 784 Percolation explains efficiency, robustness, and economy of the brain Table 6. Symmetry analysis results (supplementary information) Variable PIP ISC Variable POP OSC ISC/IDA OSC/ODA Pearson correlation 0.9833 0.8977 0.8164 p < 10−10 < 10−10 < 10−10 Average change fraction PIP−POP = 0.6176 POP j j ISC−OSC j OSC j = 1.7042 Symmetric degree Strictly strong Relatively weak ISC=IDA−OSC=ODA j OSC=ODA j = 0.8649 Less strong Note. Strong symmetry requires a strong positive correlation (e.g., correlation > 0.9 y P < 10−3). Strong symmetry implies a small average change fraction (e.g., fraction < 1). The term “strictly strong” means that the strictest criterion of strong symmetry is completely satisfied. The term “less strong” means that the strictest criterion of strong symmetry is partly satisfied. The term “relatively weak” means that the strictest criterion of strong symmetry is not satisfied. suggest that three levels of symmetry can be specified. The symmetry is suggested as strictly strong if the strictest criterion is completely satisfied. If the criterion is partly satisfied, the sym- metry is treated as less strong. The symmetry is suggested as relatively weak if both require- ments are not satisfied (please note that this case does not imply that static connectivity is purely asymmetric, it only suggests the existence of potential local asymmetry). In Table 6, we present the symmetry analysis results of supplementary variables in static brain connectivity descriptions. These results serve as pieces of corroborative evidence to sup- port our findings in the main text. In general, macroscopic static connectivity is suggested as robustly symmetric. Although microscopic static connectivity is approximately symmetric, its symmetric degree is not as strong as the macroscopic one. Coactivation Probability Calculation Here we introduce the method of functional connectivity generation. Specifically, every direc- tionally adjacent relation (DA) Ni → Nj (here Ni and Nj are neurons) has a static connection strength Sij defined by Equation 10. In the definition, random variable Xi 2 {0, 1} determines whether Ni is an excitatory or inhibitory neuron. Random variables Yij ∼ U(0,1] and Zij 2∼ U [−1,0] are generated uniformly to measure excitation/inhibition strength (e.g., conductance). Notion αij denotes the number of synaptic connections (SC) from Ni to Nj (SC/DA, the precise number of SCs per DA) and h·i denotes the expectation. By calculating in Equation 10, we αij αijh i i;j can quantify the effects of SCs on Sij. Sij ¼ αij (cid:6) (cid:5) αij i;j (cid:7) XiYij þ 1 − Xi ð ÞZij (cid:8) : (10) Under each condition of E/I balance λ, a set of variable {X1, …, Xn} (here n denotes the number of neurons) is randomly initialized. Then, we update {X1, …, Xn} by the following algorithm: (1) measure λ^, the fraction of excitatory SCs in all SCs based on the current configuration of {X1, …, Xn}, and calculate the difference |λ^ − λ|; (2) randomly select a neuron Ni and change the corresponding Xi (e.g., change Xi from 1 to 0 or from 0 to 1). (the change will not be kept unless it reduces |λ^ − λ|); (3) repeat steps (1 and 2) until λ^ ∼ λ. Based on this algorithm, the fraction of excitatory synapses in all synapses is principally controlled by λ with reasonable errors in practice. Then, we measure coactivation probability Pij in Equation 11 to define the dynamic con- nection strength, where δ(·) denotes the Dirac delta function. Probability P ij is quantified in term of that an activated Ni can activate Nj in m times of experiments (m = 100). Pij ¼ 1 m Xm (cid:9) δ Ik i k¼1 (cid:10) : − Ik j (11) 785 Network Neuroscience l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 6 3 7 6 5 2 0 3 5 9 8 5 n e n _ a _ 0 0 2 4 6 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Percolation explains efficiency, robustness, and economy of the brain Each time all neurons are initialized at the resting potential, −70 mV. Then we continuously activate Ni (make Ik i = 1) and several other randomly selected presynaptic neurons of Nj during an interval of [0, t] (we define t = 50 ms). We ensure that at least 20% of presynaptic neurons of Nj are activated. Such activation intensity is no longer accidental and should be strong enough to affect Nj in the real brain. Any activation will be marked by Equation 12, where Ik j = 1 if Nj is activated at least one time during [0, t], otherwise Ik j = 0. The criterion of activation in Equation 12 is to verify if the actual membrane potential Vj(τ) reaches the spiking threshold ^V = −50 mV based on the unit step function ν(·). " ¼ ν Ik j (cid:4) # : Xt (cid:3) ν Vτ − ^V τ¼0 (12) We calculate the actual membrane potential Vj(τ) applying the standard leaky integrate-and- fire (LIF) model (Gerstner et al., 2014) in Equation 13, where τm is the membrane time constant (τm = 10 ms), notion Nh searches through all presynaptic neurons of Nj, and τ f h represents the arrival time of f-th spike of neuron Nh. ∂Vj τð Þ ∂τ ¼ − (cid:7) 1 τ m Vj τð Þ − ^V (cid:8) − X Shj ( X Nh f (cid:3) δ τ − τ f h (cid:4) (cid:7) (cid:4) (cid:3) Vj τ f h (cid:3) − Vh τ f h ) (cid:8) (cid:4) : (13) To make such a computationally costly experiment accessible for readers, we release our results in Tian and Sun (2021). Readers can freely download the dataset to obtain the co- activation probability Pij under each λ condition. Quantification of Efficiency, Robustness, and Economy In our research, the measurements of the characteristic path length (Albert & Barabási, 2002), the global efficiency (Latora & Marchiori, 2001), the assortativity coefficient (Newman, 2002), the rich-club coefficient (Ball et al., 2014; Colizza et al., 2006; Van Den Heuvel & Sporns, 2011), the physical Rentian exponent (Bassett et al., 2010; Chen, 1999; Ozaktas, 1992), the clustering coefficient (Watts & Strogatz, 1998), and the transitivity (Newman, 2003) are imple- mented based on the toolbox released by Rubinov and Sporns (2010b). This widely used tool- box and its instructions can be found in Rubinov and Sporns (2010a). Readers can use the adjacent matrix of functional connectivity as an input to calculate these properties. One thing to note is that the original version of the toolbox defines the graph distance between two unconnected neurons (there is no path between them) as infinity. Although this definition is mathematically justified, it may bring inconvenience in computational implementations because inf usually leads to inf or nan in computer programs. Common practices to avoid the influence of potential infinite values on target results are either excluding these infinite values during calculations or replacing them with n + 1 (here n denotes the total number of neurons). To maintain the sample size in analyses, our research chooses the second approach. ACKNOWLEDGMENTS Authors are grateful for discussions and assistance of Drs. Ziyang Zhang and Yaoyuan Wang from the Laboratory of Advanced Computing and Storage, Central Research Institute, 2012 Laboratories, Huawei Technologies Co. Ltd., Beijing, 100084, China. Network Neuroscience 786 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 6 3 7 6 5 2 0 3 5 9 8 5 n e n _ a _ 0 0 2 4 6 p d t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Percolation explains efficiency, robustness, and economy of the brain AUTHOR CONTRIBUTIONS Yang Tian: Conceptualization; Data curation; Formal analysis; Investigation; Methodology; Project administration; Software; Validation; Visualization; Writing – original draft. Pei Sun: Conceptualization; Funding acquisition; Investigation; Project administration; Resources; Supervision; Validation; Writing – review & editing. FUNDING INFORMATION Pei Sun, Artificial and General Intelligence Research Program of Guo Qiang Research Institute at Tsinghua University, Award ID: 2020GQG1017. REFERENCES Achard, S., Salvador, R., Whitcher, B., Suckling, J., & Bullmore, E. (2006). A resilient, low-frequency, small-world human brain functional network with highly connected association cortical hubs. Journal of Neuroscience, 26(1), 63–72. https://doi.org/10 .1523/JNEUROSCI.3874-05.2006, PubMed: 16399673 Aerts, H., Fias, W., Caeyenberghs, K., & Marinazzo, D. (2016). Brain networks under attack: Robustness properties and the impact of lesions. Brain, 139(12), 3063–3083. https://doi.org/10 .1093/brain/aww194, PubMed: 27497487 Agliari, E., Cioli, C., & Guadagnini, E. (2011). Percolation on cor- related random networks. Physical Review E, 84(3), 031120. https://doi.org/10.1103/ PhysRevE.84.031120, PubMed: 22060341 Agrawal, V., Cowley, A. B., Alfaori, Q., Larremore, D. B., Restrepo, J. G., & Shew, W. L. (2018). Robust entropy requires strong and balanced excitatory and inhibitory synapses. Chaos: An Interdis- ciplinary Journal of Nonlinear Science, 28(10), 103115. https:// doi.org/10.1063/1.5043429, PubMed: 30384653 Albert, R., & Barabási, A.-L. (2002). Statistical mechanics of com- plex networks. Reviews of Modern Physics, 74(1), 47. https://doi .org/10.1103/RevModPhys.74.47 Albert, R., Jeong, H., & Barabási, A.-L. (2000). Error and attack tol- erance of complex networks. Nature, 406(6794), 378–382. https://doi.org/10.1038/35019019, PubMed: 10935628 Alstott, J., Breakspear, M., Hagmann, P., Cammoun, L., & Sporns, O. (2009). Modeling the impact of lesions in the human brain. PLoS Computational Biology, 5(6), e1000408. https://doi.org/10 .1371/journal.pcbi.1000408, PubMed: 19521503 Amico, E., Abbas, K., Duong-Tran, D. A., Tipnis, U., Rajapandian, M., Chumin, E., … Goñi, J. (2021). Towards an information the- oretical description of communication in brain networks. Net- work Neuroscience, 5(3), 646–665. https://doi.org/10.1162/netn _a_00185, PubMed: 34746621 Amini, H. (2010). Bootstrap percolation in living neural networks. Journal of Statistical Physics, 141(3), 459–475. https://doi.org/10 .1007/s10955-010-0056-z Amini, H., & Fountoulakis, N. (2014). Bootstrap percolation in power-law random graphs. Journal of Statistical Physics, 155(1), 72–92. https://doi.org/10.1007/s10955-014-0946-6 Avena-Koenigsberger, A., Mišić, B., Hawkins, R. X., Griffa, A., Hagmann, P., Goñi, J., & Sporns, O. (2017). Path ensembles and a tradeoff between communication efficiency and resilience in the human connectome. Brain Structure and Function, 222(1), 603–618. https://doi.org/10.1007/s00429-016-1238-5, PubMed: 27334341 Avena-Koenigsberger, A., Misic, B., & Sporns, O. (2018). Commu- nication dynamics in complex brain networks. Nature Reviews Neuroscience, 19(1), 17–33. https://doi.org/10.1038/nrn.2017 .149, PubMed: 29238085 Ball, G., Aljabar, P., Zebari, S., Tusor, N., Arichi, T., Merchant, N., … Counsell, S. J. (2014). Rich-club organization of the newborn human brain. Proceedings of the National Academy of Sciences, 111(20), 7456–7461. https://doi.org/10.1073/pnas.1324118111, PubMed: 24799693 Balogh, J., & Pittel, B. G. (2007). Bootstrap percolation on the ran- dom regular graph. Random Structures & Algorithms, 30(1–2), 257–286. https://doi.org/10.1002/rsa.20158 Barta, T., & Kostal, L. (2019). The effect of inhibition on rate code efficiency indicators. PLoS Computational Biology, 15(12), e1007545. https://doi.org/10.1371/journal.pcbi.1007545, PubMed: 31790384 Bassett, D. S., Greenfield, D. L., Meyer-Lindenberg, A., Weinberger, D. R., Moore, S. W., & Bullmore, E. T. (2010). Efficient physical embedding of topologically complex information processing net- works in brains and computer circuits. PLoS Computational Biol- ogy, 6(4), e1000748. https://doi.org/10.1371/journal.pcbi .1000748, PubMed: 20421990 Baxter, G. J., Dorogovtsev, S. N., Goltsev, A. V., & Mendes, J. F. (2010). Bootstrap percolation on complex networks. Physical Review E, 82(1), 011103. https://doi.org/10.1103/PhysRevE.82 .011103, PubMed: 20866561 Beggs, J. M., & Timme, N. (2012). Being critical of criticality in the brain. Frontiers in Physiology, 3, 163. https://doi.org/10.3389 /fphys.2012.00163, PubMed: 22701101 Ben-Naim, E., & Krapivsky, P. (2011). Dynamics of random graphs with bounded degrees. Journal of Statistical Mechanics: Theory and Experiment, 2011(11), P11008. https://doi.org/10.1088 /1742-5468/2011/11/P11008 Betzel, R. F., Avena-Koenigsberger, A., Goñi, J., He, Y., De Reus, M. A., Griffa, A., … Sporns, O. (2016). Generative models of the human connectome. NeuroImage, 124, 1054–1064. https://doi .org/10.1016/j.neuroimage.2015.09.041, PubMed: 26427642 Network Neuroscience 787 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 6 3 7 6 5 2 0 3 5 9 8 5 n e n _ a _ 0 0 2 4 6 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Percolation explains efficiency, robustness, and economy of the brain Bollobás, B. (2013). Modern graph theory (Vol. 184). New York, NY: Springer Science & Business Media. Bordier, C., Nicolini, C., & Bifone, A. (2017). Graph analysis and modularity of brain functional connectivity networks: Searching for the optimal threshold. Frontiers in Neuroscience, 11, 441. https://doi.org/10.3389/fnins.2017.00441, PubMed: 28824364 Breskin, I., Soriano, J., Moses, E., & Tlusty, T. (2006). Percolation in living neural networks. Physical Review Letters, 97(18), 188102. https://doi.org/10.1103/ PhysRevLett.97.188102, PubMed: 17155581 Bridi, M. C., Zong, F.-J., Min, X., Luo, N., Tran, T., Qiu, J., … Kirkwood, A. (2020). Daily oscillation of the excitation- inhibition balance in visual cortical circuits. Neuron, 105(4), 621–629. https://doi.org/10.1016/j.neuron.2019.11.011, PubMed: 31831331 Bullmore, E., & Sporns, O. (2012). The economy of brain network organization. Nature Reviews Neuroscience, 13(5), 336–349. https://doi.org/10.1038/nrn3214, PubMed: 22498897 Callaway, D. S., Newman, M. E., Strogatz, S. H., & Watts, D. J. (2000). Network robustness and fragility: Percolation on random graphs. Physical Review Letters, 85(25), 5468. https://doi.org/10 .1103/PhysRevLett.85.5468, PubMed: 11136023 Capolupo, A., Freeman, W. J., & Vitiello, G. (2013). Dissipation of ‘dark energy’ by cortex in knowledge retrieval. Physics of Life Reviews, 10(1), 85–94. https://doi.org/10.1016/j.plrev.2013.01 .001, PubMed: 23333569 Carvalho, T. T., Fontenele, A. J., Girardi-Schappo, M., Feliciano, T., Aguiar, L. A., Silva, T. P., … Copelli, M. (2020). Subsam- pled directed-percolation models explain scaling relations experimentally observed in the brain. Frontiers in Neural Cir- cuits, 14. https://doi.org/10.3389/fncir.2020.576727, PubMed: 33519388 Chen, W.-K. (1999). The VLSI handbook. Boca Raton, FL: CRC Press. https://doi.org/10.1201/9781420049671 Chialvo, D. R. (2004). Critical brain networks. Physica A: Statistical Mechanics and its Applications, 340(4), 756–765. https://doi.org /10.1016/j.physa.2004.05.064 Clauset, A., Shalizi, C. R., & Newman, M. E. (2009). Power-law dis- tributions in empirical data. SIAM Review, 51(4), 661–703. https://doi.org/10.1137/070710111 Cohen, O., Keselman, A., Moses, E., Martínez, M. R., Soriano, J., & Tlusty, T. (2010). Quorum percolation in living neural networks. EPL (Europhysics Letters), 89(1), 18008. https://doi.org/10.1209 /0295-5075/89/18008 Colizza, V., Flammini, A., Serrano, M. A., & Vespignani, A. (2006). Detecting rich-club ordering in complex networks. Nature Phys- ics, 2(2), 110–115. https://doi.org/10.1038/nphys209 Collell, G., & Fauquet, J. (2015). Brain activity and cognition: A connection from thermodynamics and information theory. Fron- tiers in Psychology, 6, 818. https://doi.org/10.3389/fpsyg.2015 .00818, PubMed: 26136709 Costa, L. d. F. (2005). Morphological complex networks: Can indi- vidual morphology determine the general connectivity and dynamics of networks? arXiv preprint q-bio/0503041. https://doi .org/10.48550/arXiv.q-bio/0503041 Crossley, N. A., Mechelli, A., Scott, J., Carletti, F., Fox, P. T., McGuire, P., & Bullmore, E. T. (2014). The hubs of the human connectome are generally implicated in the anatomy of brain disorders. Brain, 137(8), 2382–2395. https://doi.org/10.1093 /brain/awu132, PubMed: 25057133 da Fontoura Costa, L., & Coelho, R. C. (2005). Growth-driven per- colations: The dynamics of connectivity in neuronal systems. The European Physical Journal B-Condensed Matter and Complex Systems, 47(4), 571–581. https://doi.org/10.1140/epjb/e2005 -00354-5 da Fontoura Costa, L., & Manoel, E. T. M. (2003). A percolation approach to neural morphometry and connectivity. Neuroinfor- matics, 1(1), 65–80. https://doi.org/10.1385/ NI:1:1:065, PubMed: 15055394 Del Ferraro, G., Moreno, A., Min, B., Morone, F., Pérez-Ramírez, Ú., Pérez-Cervera, L., … Makse, H. A. (2018). Finding influential nodes for integration in brain networks using optimal percolation theory. Nature Communications, 9(1), 1–12. https://doi.org/10 .1038/s41467-018-04718-3, PubMed: 29891915 Dorogovtsev, S. N., Mendes, J. F. F., & Samukhin, A. N. (2001). Giant strongly connected component of directed networks. Phys- ical Review E, 64(2), 025101. https://doi.org/10.1103/PhysRevE .64.025101, PubMed: 11497638 Eckmann, J.-P., Feinerman, O., Gruendlinger, L., Moses, E., Soriano, J., & Tlusty, T. (2007). The physics of living neural networks. Phys- ics Reports, 449(1–3), 54–76. https://doi.org/10.1016/j.physrep .2007.02.014 Fagiolo, G. (2007). Clustering in complex directed networks. Phys- ical Review E, 76(2), 026107. https://doi.org/10.1103/PhysRevE .76.026107, PubMed: 17930104 Fontenele, A. J., de Vasconcelos, N. A., Feliciano, T., Aguiar, L. A., Soares-Cunha, C., Coimbra, B., … Copelli, M. (2019). Criticality between cortical states. Physical Review Letters, 122(20), 208101. https://doi.org/10.1103/ PhysRevLett.122.208101, PubMed: 31172737 Fosque, L. J., Williams-García, R. V., Beggs, J. M., & Ortiz, G. (2021). Evidence for quasicritical brain dynamics. Physical Review Letters, 126(9), 098101. https://doi.org/10.1103 /PhysRevLett.126.098101, PubMed: 33750159 Friston, K. (2009). The free-energy principle: A rough guide to the brain? Trends in Cognitive Sciences, 13(7), 293–301. https://doi .org/10.1016/j.tics.2009.04.005, PubMed: 19559644 Friston, K. (2010). The free-energy principle: A unified brain theory? Nature Reviews Neuroscience, 11(2), 127–138. https://doi.org/10 .1038/nrn2787, PubMed: 20068583 Friston, K. (2012). The history of the future of the bayesian brain. NeuroImage, 62(2), 1230–1233. https://doi.org/10.1016/j .neuroimage.2011.10.004, PubMed: 22023743 Friston, K., & Kiebel, S. (2009). Predictive coding under the free-energy principle. Philosophical Transactions of the Royal Society B: Biological Sciences, 364(1521), 1211–1221. https:// doi.org/10.1098/rstb.2008.0300, PubMed: 19528002 Gautam, S. H., Hoang, T. T., McClanahan, K., Grady, S. K., & Shew, W. L. (2015). Maximizing sensory dynamic range by tuning the cortical state to criticality. PLoS Computational Biology, 11(12), e1004576. https://doi.org/10.1371/journal.pcbi.1004576, PubMed: 26623645 Gerstner, W., Kistler, W. M., Naud, R., & Paninski, L. (2014). Neu- ronal dynamics: From single neurons to networks and models of cognition. Cambridge, UK: Cambridge University Press. https:// doi.org/10.1017/CBO9781107447615 Network Neuroscience 788 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 6 3 7 6 5 2 0 3 5 9 8 5 n e n _ a _ 0 0 2 4 6 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Percolation explains efficiency, robustness, and economy of the brain Goltsev, A. V., Dorogovtsev, S. N., & Mendes, J. F. (2008). Percola- tion on correlated networks. Physical Review E, 78(5), 051105. https://doi.org/10.1103/PhysRevE.78.051105, PubMed: 19113093 Goñi, J., Van Den Heuvel, M. P., Avena-Koenigsberger, A., De Mendizabal, N. V., Betzel, R. F., Griffa, A., … Sporns, O. (2014). Resting-brain functional connectivity predicted by ana- lytic measures of network communication. Proceedings of the National Academy of Sciences, 111(2), 833–838. https://doi.org /10.1073/pnas.1315529111, PubMed: 24379387 Graham, D., Avena-Koenigsberger, A., & Misic, B. (2020). Network com- munication in the brain. Network Neuroscience, 4(4), 976–979. https://doi.org/10.1162/netn_e_00167, PubMed: 33195944 Grent, T., Gross, J., Goense, J., Wibral, M., Gajwani, R., Gumley, A. I., … Uhlhaas, P. J. (2018). Resting-state gamma-band power alterations in schizophrenia reveal E/ I-balance abnormalities across illness-stages. Elife, 7, e37799. https://doi.org/10.7554 /eLife.37799, PubMed: 30260771 Guevara, R. (2021). Synchronization, free energy and the embryo- genesis of the cortex. Physics of Life Reviews, 36, 5–6. https://doi .org/10.1016/j.plrev.2020.11.006, PubMed: 33348117 Hahn, A., Kranz, G. S., Sladky, R., Ganger, S., Windischberger, C., Kasper, S., & Lanzenberger, R. (2015). Individual diversity of functional brain network economy. Brain Connectivity, 5(3), 156–165. https://doi.org/10.1089/ brain.2014.0306, PubMed: 25411715 Hendry, S. H., Schwark, H., Jones, E., & Yan, J. (1987). Numbers and proportions of gaba-immunoreactive neurons in different areas of monkey cerebral cortex. Journal of Neuroscience, 7(5), 1503–1519. https://doi.org/10.1523/JNEUROSCI.07-05-01503 .1987, PubMed: 3033170 Hermundstad, A. M., Bassett, D. S., Brown, K. S., Aminoff, E. M., Clewett, D., Freeman, S., … Carlson, J. M. (2013). Structural foun- dations of resting-state and task-based functional connectivity in the human brain. Proceedings of the National Academy of Sci- ences, 110(15), 6169–6174. https://doi.org/10.1073/pnas .1219562110, PubMed: 23530246 Humphries, M. D., Gurney, K., & Prescott, T. J. (2006). The brain- stem reticular formation is a small-world, not scale-free, net- work. Proceedings of the Royal Society B: Biological Sciences, 273(1585), 503–511. https://doi.org/10.1098/rspb.2005.3354, PubMed: 16615219 Joyce, K. E., Hayasaka, S., & Laurienti, P. J. (2013). The human functional brain network demonstrates structural and dynamical resilience to targeted attack. PLoS Computational Biology, 9(1), e1002885. https://doi.org/10.1371/journal.pcbi.1002885, PubMed: 23358557 Kaiser, M., & Hilgetag, C. C. (2004). Edge vulnerability in neural and metabolic networks. Biological Cybernetics, 90(5), 311–317. https://doi.org/10.1007/s00422-004-0479-1, PubMed: 15221391 Kaiser, M., & Hilgetag, C. C. (2006). Nonoptimal component placement, but short processing paths, due to long-distance projections in neural systems. PLoS Computational Biology, 2(7), e95. https://doi.org/10.1371/journal.pcbi.0020095, PubMed: 16848638 Kaiser, M., Martin, R., Andras, P., & Young, M. P. (2007). Simulation of robustness against lesions of cortical networks. European Jour- nal of Neuroscience, 25(10), 3185–3192. https://doi.org/10.1111 /j.1460-9568.2007.05574.x, PubMed: 17561832 Karbowski, J. (2007). Global and regional brain metabolic scaling and its functional consequences. BMC Biology, 5(1), 1–11. https://doi.org/10.1186/1741-7007-5-18, PubMed: 17488526 Kiebel, S. J., & Friston, K. J. (2011). Free energy and dendritic self-organization. Frontiers in Systems Neuroscience, 5, 80. https://doi.org/10.3389/fnsys.2011.00080, PubMed: 22013413 Kozma, R., & Puljic, M. (2015). Random graph theory and neuro- percolation for modeling brain oscillations at criticality. Current Opinion in Neurobiology, 31, 181–188. https://doi.org/10.1016/j .conb.2014.11.005, PubMed: 25460075 Latora, V., & Marchiori, M. (2001). Efficient behavior of small-world networks. Physical Review Letters, 87(19), 198701. https://doi .org/10.1103/PhysRevLett.87.198701, PubMed: 11690461 Laughlin, S. B., van Steveninck, R. R. d. R., & Anderson, J. C. (1998). The metabolic cost of neural information. Nature Neuroscience, 1(1), 36–41. https://doi.org/10.1038/236, PubMed: 10195106 Li, M., Liu, R.-R., Lü, L., Hu, M.-B., Xu, S., & Zhang, Y.-C. (2021). Percolation on complex networks: Theory and application. Physics Reports, 907, 1–68. https://doi.org/10.1016/j.physrep .2020.12.003 Lucini, F. A., Del Ferraro, G., Sigman, M., & Makse, H. A. (2019). How the brain transitions from conscious to subliminal percep- tion. Neuroscience, 411, 280–290. https://doi.org/10.1016/j .neuroscience.2019.03.047, PubMed: 31051216 Meinecke, D. L., & Peters, A. (1987). GABA immunoreactive neurons in rat visual cortex. Journal of Comparative Neurology, 261(3), 388–404. https://doi.org/10.1002/cne.902610305, PubMed: 3301920 Millman, D., Mihalas, S., Kirkwood, A., & Niebur, E. (2010). Self- organized criticality occurs in non-conservative neuronal net- works during ‘up’ states. Nature Physics, 6(10), 801–805. https:// doi.org/10.1038/nphys1757, PubMed: 21804861 Mišić, B., Sporns, O., & McIntosh, A. R. (2014). Communication efficiency and congestion of signal traffic in large-scale brain networks. PLoS Computational Biology, 10(1), e1003427. https://doi.org/10.1371/journal.pcbi.1003427, PubMed: 24415931 Newman, M. E. (2002). Assortative mixing in networks. Physical Review Letters, 89(20), 208701. https://doi.org/10.1103 /PhysRevLett.89.208701, PubMed: 12443515 Newman, M. E. (2003). The structure and function of complex net- works. SIAM Review, 45(2), 167–256. https://doi.org/10.1137 /S003614450342480 Newman, M. E., Strogatz, S. H., & Watts, D. J. (2001). Random graphs with arbitrary degree distributions and their applications. Physical Review E, 64(2), 026118. https://doi.org/10.1103 /PhysRevE.64.026118, PubMed: 11497662 Ozaktas, H. M. (1992). Paradigms of connectivity for computer cir- cuits and networks. Optical Engineering, 31(7), 1563–1567. https://doi.org/10.1117/12.57685 Panagiotou, K., Spöhel, R., Steger, A., & Thomas, H. (2011). Explo- sive percolation in Erdős-Rényi-like random graph processes. Electronic Notes in Discrete Mathematics, 38, 699–704. https:// doi.org/10.1016/j.endm.2011.10.017 Pipkin, J. (2020). Connectomes: Mapping the mind of a fly. Elife, 9, e62451. https://doi.org/10.7554/eLife.62451, PubMed: 33030427 Poil, S.-S., Hardstone, R., Mansvelder, H. D., & Linkenkaer-Hansen, K. (2012). Critical-state dynamics of avalanches and oscillations Network Neuroscience 789 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 6 3 7 6 5 2 0 3 5 9 8 5 n e n _ a _ 0 0 2 4 6 p d t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Percolation explains efficiency, robustness, and economy of the brain jointly emerge from balanced excitation/inhibition in neuronal networks. Journal of Neuroscience, 32(29), 9817–9823. https://doi .org/10.1523/JNEUROSCI.5990-11.2012, PubMed: 22815496 Radicchi, F., & Fortunato, S. (2009). Explosive percolation in scale- free networks. Physical Review Letters, 103(16), 168701. https:// doi.org/10.1103/PhysRevLett.103.168701, PubMed: 19905730 Ramírez-Toraño, F., Bruña, R., de Frutos-Lucas, J., Rodŕıguez-Rojo, I., Marcos de Pedro, S., Delgado-Losada, M., … Maestú, F. (2021). Functional connectivity hypersynchronization in rela- tives of alzheimer’s disease patients: An early E/I balance dys- function? Cerebral Cortex, 31(2), 1201–1210. https://doi.org/10 .1093/cercor/bhaa286, PubMed: 33108468 Rubinov, M., & Sporns, O. (2010a). Brain connectivity toolbox. https://www.nitrc.org/projects/bct/. Rubinov, M., & Sporns, O. (2010b). Complex network measures of brain connectivity: Uses and interpretations. NeuroImage, 52(3), 1059–1069. https://doi.org/10.1016/j.neuroimage.2009.10.003, PubMed: 19819337 Rubinov, M., Ypma, R. J., Watson, C., & Bullmore, E. T. (2015). Wiring cost and topological participation of the mouse brain connectome. Proceedings of the National Academy of Sciences, 112(32), 10032–10037. https://doi.org/10.1073/pnas.1420315112, PubMed: 26216962 Sadeh, S., & Clopath, C. (2021). Inhibitory stabilization and cortical computation. Nature Reviews Neuroscience, 22(1), 21–37. https:// doi.org/10.1038/s41583-020-00390-z, PubMed: 33177630 Sahara, S., Yanagawa, Y., O’Leary, D. D., & Stevens, C. F. (2012). The fraction of cortical gabaergic neurons is constant from near the start of cortical neurogenesis to adulthood. Journal of Neuro- s c i en c e , 3 2 (1 4), 4 75 5 –4 7 6 1. h t t ps : / / d o i . o rg / 1 0. 1 5 2 3 /JNEUROSCI.6412-11.2012, PubMed: 22492031 Sartori, P., Granger, L., Lee, C. F., & Horowitz, J. M. (2014). Ther- modynamic costs of information processing in sensory adapta- tion. PLoS Computational Biology, 10(12), e1003974. https:// doi.org/10.1371/journal.pcbi.1003974, PubMed: 25503948 Schlegel, P., Bates, A. S., Stürner, T., Jagannathan, S. R., Drummond, N., Hsu, J., … Jefferis, G. (2021). Information flow, cell types and stereotypy in a full olfactory connectome. Elife, 10, e66018. https://doi.org/10.7554/eLife.66018, PubMed: 34032214 Seguin, C., Tian, Y., & Zalesky, A. (2020). Network communication models improve the behavioral and functional predictive utility of the human structural connectome. Network Neuroscience, 4(4), 980–1006. https://doi.org/10.1162/netn_a_00161, PubMed: 33195945 Seguin, C., Van Den Heuvel, M. P., & Zalesky, A. (2018). Naviga- tion of brain networks. Proceedings of the National Academy of Sciences, 115(24), 6297–6302. https://doi.org/10.1073/pnas .1801351115, PubMed: 29848631 Sengupta, B., Stemmler, M. B., & Friston, K. J. (2013). Information and efficiency in the nervous system—A synthesis. PLoS Compu- tational Biology, 9(7), e1003157. https://doi.org/10.1371/journal .pcbi.1003157, PubMed: 23935475 Shew, W. L., Yang, H., Yu, S., Roy, R., & Plenz, D. (2011). Information capacity and transmission are maximized in balanced cortical net- works with neuronal avalanches. Journal of Neuroscience, 31(1), 55–63. https://doi.org/10.1523/ JNEUROSCI.4637-10.2011, PubMed: 21209189 Sporns, O. (2011). The non-random brain: Efficiency, economy, and complex dynamics. Frontiers in Computational Neuroscience, 5, 5. https://doi.org/10.3389/fncom.2011.00005, PubMed: 21369354 Sporns, O., Tononi, G., & Kötter, R. (2005). The human connec- tome: A structural description of the human brain. PLoS Compu- tational Biology, 1(4), e42. https://doi.org/10.1371/journal.pcbi .0010042, PubMed: 16201007 Sprekeler, H. (2017). Functional consequences of inhibitory plastic- ity: Homeostasis, the excitation-inhibition balance and beyond. Current Opinion in Neurobiology, 43, 198–203. https://doi.org /10.1016/j.conb.2017.03.014, PubMed: 28500933 Stepanyants, A., & Chklovskii, D. B. (2005). Neurogeometry and potential synaptic connectivity. Trends in Neurosciences, 28(7), 387–394. https://doi.org/10.1016/j.tins.2005.05.006, PubMed: 15935485 Street, S. (2020). Upper limit on the thermodynamic information content of an action potential. Frontiers in Computational Neuro- science, 14, 37. https://doi.org/10.3389/fncom.2020.00037, PubMed: 32477088 Strelnikov, K. (2010). Neuroimaging and neuroenergetics: Brain activations as information-driven reorganization of energy flows. Brain and Cognition, 72(3), 449–456. https://doi.org/10.1016/j .bandc.2009.12.008, PubMed: 20092923 Tao, H. W., Li, Y.-T., & Zhang, L. I. (2014). Formation of excitation-inhibition balance: Inhibition listens and changes its tune. Trends in Neurosciences, 37(10), 528–530. https://doi.org /10.1016/j.tins.2014.09.001, PubMed: 25248294 Tian, Y., & Sun, P. (2021). Co-activation probability between neu- rons in the largest brain connectome of the fruit fly. Zenodo. https://doi.org/10.5281/zenodo.5497516 Van Den Heuvel, M. P., & Sporns, O. (2011). Rich-club organiza- tion of the human connectome. Journal of Neuroscience, 31(44), 15775–15786. https://doi.org/10.1523/ JNEUROSCI.3539-11 .2011, PubMed: 22049421 Virkar, R., & Clauset, A. (2014). Toolbox for power-law distributions in binned empirical data. https://sites.santafe.edu/~aaronc /powerlaws/bins/. Virkar, Y., & Clauset, A. (2014). Power-law distributions in binned empirical data. The Annals of Applied Statistics, 8(1), 89–119. https://doi.org/10.1214/13-AOAS710 Watts, D. J., & Strogatz, S. H. (1998). Collective dynamics of ‘small-world’ networks. Nature, 393(6684), 440–442. https://doi .org/10.1038/30918, PubMed: 9623998 Williams-García, R. V., Moore, M., Beggs, J. M., & Ortiz, G. (2014). Quasicritical brain dynamics on a nonequilibrium widom line. Physical Review E, 90(6), 062714. https://doi.org/10.1103 /PhysRevE.90.062714, PubMed: 25615136 Xu, C. S., Januszewski, M., Lu, Z., Takemura, S.-Y., Hayworth, K. J., Huang, G., … Plaza, S. M. (2020). A connectome of the adult Drosophila central brain. BioRxiv. https://doi.org/10.1101/2020 .01.21.911859 Zhou, D. W., Mowrey, D. D., Tang, P., & Xu, Y. (2015). Percolation model of sensory transmission and loss of consciousness under general anesthesia. Physical Review Letters, 115(10), 108103. https://doi.org/10.1103/ PhysRevLett.115.108103, PubMed: 26382705 Network Neuroscience 790 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 6 3 7 6 5 2 0 3 5 9 8 5 n e n _ a _ 0 0 2 4 6 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3

Descargar PDF