FUNCIÓN DE ENFOQUE:
Connectivity, Cognición, and Consciousness
Benchmarking functional connectivity by the
structure and geometry of the human brain
Zhen-Qi Liu1
, Richard F. Betzel2
, and Bratislav Misic1
1Centro de imágenes cerebrales McConnell, Montréal Neurological Institute, Universidad McGill, Montréal, Canada
2Psychological and Brain Sciences, Universidad de Indiana, Bloomington, EN, EE.UU
Palabras clave: Connectome, Conectividad funcional, Structural connectivity, Geometría, Embedding,
Degradado, Hierarchy, Transmodal
un acceso abierto
diario
ABSTRACTO
The brain’s structural connectivity supports the propagation of electrical impulses, manifesting
as patterns of coactivation, termed functional connectivity. Functional connectivity emerges
from the underlying sparse structural connections, particularly through polysynaptic
comunicación. Como resultado, functional connections between brain regions without direct
structural links are numerous, but their organization is not completely understood. Here we
investigate the organization of functional connections without direct structural links. Nosotros
develop a simple, data-driven method to benchmark functional connections with respect to
their underlying structural and geometric embedding. We then use this method to reweigh and
reexpress functional connectivity. We find evidence of unexpectedly strong functional
connectivity among distal brain regions and within the default mode network. We also find
unexpectedly strong functional connectivity at the apex of the unimodal-transmodal hierarchy.
Our results suggest that both phenomena—functional modules and functional hierarchies—
emerge from functional interactions that transcend the underlying structure and geometry.
These findings also potentially explain recent reports that structural and functional
connectivity gradually diverge in transmodal cortex. Colectivamente, we show how structural
connectivity and geometry can be used as a natural frame of reference with which to study
functional connectivity patterns in the brain.
RESUMEN DEL AUTOR
The structural connectivity of the brain supports interregional signaling, manifesting as highly
organized patterns of functional connectivity. En tono rimbombante, structural and functional
connectivity are fundamentally constrained by the spatial embedding of brain regions, semejante
that proximal regions are more likely to exhibit stronger connectivity. Here we develop a
simple method that uses robust relationships between geometry, estructura, and function as the
baseline to reweigh and reexpress functional connectivity. We use the method to identify
functional connections that are greater than expected given their structural and geometric
incrustar. We then show that the arrangement of these connections systematically follows
the functional modules and the putative unimodal-transmodal hierarchy of the brain.
Colectivamente, our findings demonstrate highly organized patterns of polysynaptic functional
connections that support the emergence of canonical features of functional connectivity
redes, including modules and hierarchies.
Citación: Liu, Z.-Q., Betzel, R. F., &
Varios, B. (2022). Benchmarking
functional connectivity by the structure
and geometry of the human brain.
Neurociencia en red, 6(4), 937–949.
https://doi.org/10.1162/netn_a_00236
DOI:
https://doi.org/10.1162/netn_a_00236
Supporting Information:
https://doi.org/10.1162/netn_a_00236
Recibió: 12 Octubre 2021
Aceptado: 18 Enero 2022
Conflicto de intereses: Los autores tienen
declaró que no hay intereses en competencia
existir.
Autor correspondiente:
Bratislav Misic
bratislav.misic@mcgill.ca
Editor de manejo:
Sean Hill
Derechos de autor: © 2022
Instituto de Tecnología de Massachusetts
Publicado bajo Creative Commons
Atribución 4.0 Internacional
(CC POR 4.0) licencia
La prensa del MIT
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
6
4
9
3
7
2
0
5
6
2
8
0
norte
mi
norte
_
a
_
0
0
2
3
6
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Estructura- and geometry-informed functional connectivity
INTRODUCCIÓN
Structural connectivity:
Anatomical projections between
neural elements.
Conectividad funcional:
Temporal coactivation among neural
elementos.
Axonal wiring among neurons and neuronal populations promotes signal exchange and informa-
tion integration. At the mesoscale, signaling via the complex network of structural connectivity
(CAROLINA DEL SUR) manifests as patterns of temporal correlations, termed functional connectivity (FC).
Functional connectivity is highly organized (Bellec, Rosa-Neto, Lyttelton, Benali, & evans,
2010; Damoiseaux et al., 2006; Yeo et al., 2011), reproducible (Gordon et al., 2017; Noble,
Scheinost, & Constable, 2019), and related to individual differences in behaviour (Músculo &
despreciar, 2016; Smith et al., 2015).
Monosynaptic:
Communication between neural
elements via a direct anatomical
projection.
Polysynaptic:
Communication between neural
elements via a sequence of multiple
anatomical projections and
intermediate neural elements.
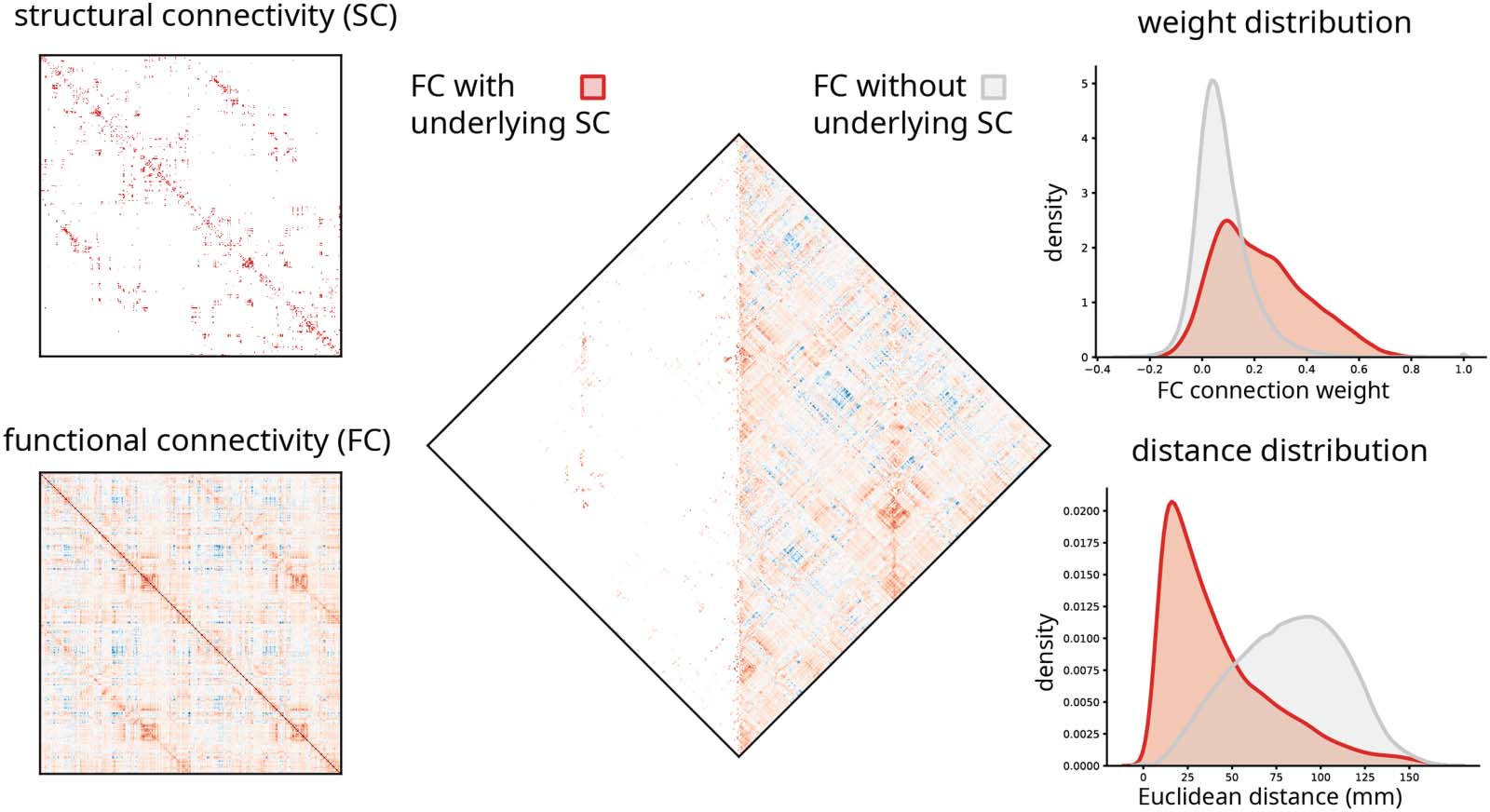
Most pairwise functional connections are not supported by a direct structural connection.
By definition, functional networks are fully connected, while structural networks are sparse
(Cifra 1). Across species, reconstruction techniques, and spatial scales, structural connection
density is typically reported to be between 2% y 40% (Van den Heuvel, bullmore, & despreciar,
2016) (but see also Markov et al., 2013), meaning that the majority of functional connections
between two regions are not accompanied by a corresponding monosynaptic structural con-
nection. These “indirect” functional connections are thought to emerge from polysynaptic
communication in the structural network (Bazinet, Vos de Wael, Hagmann, Bernhardt, &
Varios, 2021; Suárez, Markello, Betzel, & Varios, 2020).
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
En tono rimbombante, structural and functional connectivity are fundamentally constrained by the
spatial embedding of brain regions (stiso & bassett, 2018). Structural connection probability
is inversely correlated with spatial separation, such that proxmimal neural elements are more
likely to be structurally connected, while distant neural elements are less likely to be con-
nected (Horvát et al., 2016; Markov et al., 2013; Roberts et al., 2016). A similar distance
dependence is also observed for functional connectivity (Margulies et al., 2016; Mišić et al.,
2014; Salvador et al., 2005; Sepulcre et al., 2010). The overrepresentation of low-cost, corto-
range connections is thought to reflect finite material and metabolic resources (Cifra 1)
(bullmore & despreciar, 2012). Altogether, structural connectivity and spatial proximity constitute
a natural frame of reference for understanding and interpreting functional connectivity.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
6
4
9
3
7
2
0
5
6
2
8
0
norte
mi
norte
_
a
_
0
0
2
3
6
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Functional connections with and without direct structural links. Left: Structural connectivity (CAROLINA DEL SUR) and functional connectivity (FC)
Cifra 1.
matrices in the 1,000-node Lausanne parcellation (Cammoun et al., 2012). Middle: Functional connections with and without underlying struc-
tural connections. Right: The weight and anatomical (Euclidean) distance distribution of the two types of functional connections.
Neurociencia en red
938
Estructura- and geometry-informed functional connectivity
Intrinsic networks:
Subnetworks of brain areas with
coherent time courses, identified by
clustering, independent component
análisis, or community detection.
Cortical hierarchy:
A continuous axis separating
unimodal sensory-motor cortex from
transmodal association cortex.
Here we investigate the organization of functional connections without direct structural
Enlaces (Cifra 1). We develop a simple method that uses robust relationships between geometry,
estructura, and function as the baseline to reweigh and reexpress functional connectivity. Nosotros
use the method to identify functional connections that are greater than expected given their
structural and geometric embedding. We then show that the arrangement of these connections
systematically follows the functional modules (intrinsic networks) (Yeo et al., 2011) y el
putative unimodal-transmodal hierarchy of the brain (Margulies et al., 2016).
RESULTADOS
The results are organized as follows. We first establish a method to quantify how unexpectedly
strong a functional connection is given the physical Euclidean distance between its connected
areas. We then describe the organizational principles of these structurally unconnected func-
tional connections by characterizing their (1) statistical properties, (2) correspondence with
intrinsic networks, y (3) correspondence with the cortical hierarchy. Data sources include
(see Materials and Methods for detailed procedures):
▪ Structural connectivity. Structural and functional connectivity were derived from N = 66
healthy control participants (source: Lausanne University Hospital; https://doi.org/10
.5281/zenodo.2872624) using the 1,000-node Lausanne parcellation (Cammoun et al.,
2012). Participants were randomly divided into a Discovery and Validation cohort (norte =
33 cada). Structural connectivity was reconstructed using diffusion spectrum imaging
and deterministic streamline tractography. A consistency- and length-based procedure
was then used to assemble a group-representative structural connectivity matrix (Betzel,
Griffa, Hagmann, & Músculo, 2018; Mišić et al., 2015, 2018).
▪ Functional connectivity. Functional connectivity was estimated in the same individuals
by using resting-state functional MRI (rs-fMRI). A functional connectivity matrix was con-
structed using pairwise Pearson correlations among regional time courses. A group-
average functional connectivity matrix was then estimated as the mean connectivity of
pairwise connections across individuals.
Long-Range Functional Connections Are Unexpectedly Strong
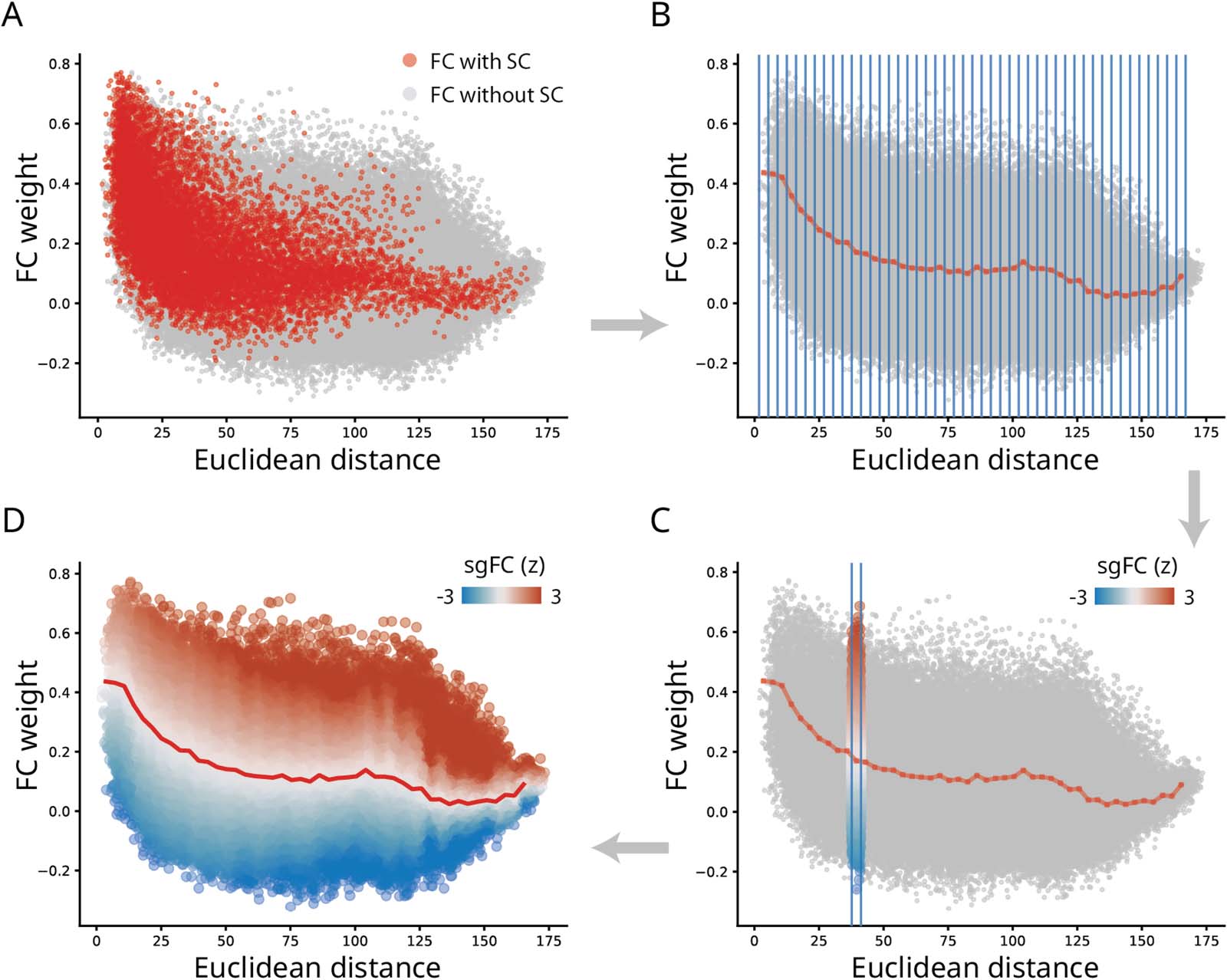
To quantify how unexpectedly strong a functional connection is, we first seek to establish a
base (for a conceptually similar approach, see Roberts et al., 2016). Figure 2A shows the
relationship between the spatial separation of two nodes (abscissa) and the functional con-
nectivity between them (ordinate). Functional connections that are supported by an under-
lying structural connection are shown in red, and all other functional connections, which we
refer to as indirect or structurally unconnected FCs, are shown in gray. We note the classical
exponential decrease in magnitude with increasing spatial separation (Roberts et al., 2016;
stiso & bassett, 2018). We also note that connected (monosynaptic) and unconnected (poly-
sináptico) FCs have similar distributions at short distances, but that they diverge considerably
at long distances. Namely, when the spatial separation between two regions is greater than
aproximadamente 125 mm, there is greater variability among unconnected FCs, with many
unconnected FCs marked by greater magnitude than connected FCs spanning comparable
distances.
We therefore set the magnitude of connected FCs at a given distance as the baseline for
unconnected FCs at a comparable distance. The goal is to identify unconnected FCs that
are unexpectedly large relative to connected FCs. To operationalize this intuition, we first
Neurociencia en red
939
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
6
4
9
3
7
2
0
5
6
2
8
0
norte
mi
norte
_
a
_
0
0
2
3
6
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Estructura- and geometry-informed functional connectivity
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
Cifra 2. Benchmarking functional connectivity by structure and geometry. (A) FC connection weight-to-distance relationship shown for FC
con (rojo) and without (gray) direct SC connections, respectivamente. (B) FCs grouped into distances bins (blue lines), and the mean value within
each bin of those with direct SCs (dotted red line). (C) Within a sample bin, unconnected (polysynaptic) FCs are expressed as a z-score relative
to connected (monosynaptic) FCs. We refer to this z-score as structure- and geometry-informed FC (sgFC). (D) sgFCs shown as a smoothly-
transitioning spectrum after the procedure is applied for each distance bin. See Methods for more technical details and Supporting Information
Figure S2 for details about smoothing and bin size selection.
F
/
/
/
/
/
6
4
9
3
7
2
0
5
6
2
8
0
norte
mi
norte
_
a
_
0
0
2
3
6
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
bin FCs according to their spatial proximity (Figura 2B). Within each bin, we record the dis-
tribution of connected FCs, including their mean and standard deviation. Finalmente, we express
each unconnected FC as a z-score relative to the distribution of connected FCs in the same
distance bin (Figura 2C). This measure reflects how unexpectedly strong a functional connec-
tion is, given its length. En tono rimbombante, z-scores for unconnected FCs are estimated based on
moments of a distribution estimated for connected FCs. Por simplicidad, we term the reexpressed
unconnected FCs as structure- and geometry-informed FC (sgFC).
Figure 2D shows the reweighing of unconnected FCs. Across the entire range of distances,
there exist many unconnected FCs that are disproportionately strong relative to their length. A
population of unconnected positive FCs spanning distances greater than 125 mm are partic-
ularly prominent, suggesting the existence of multiple strong functional interactions above and
beyond what would be expected on the basis of their length. Values of sgFC have a distribution
centered around zero, with a long positive tail (Supporting Information Figure S1). En el
following sections we explore the organization of these connections in greater detail. Para
sensitivity analyses regarding bin sizes, preprocessing choices and validation, please see
Control Analyses section and Supporting Information Figures S2 and S3. For replication in
individual participants, see Supporting Information Figure S4.
Neurociencia en red
940
Estructura- and geometry-informed functional connectivity
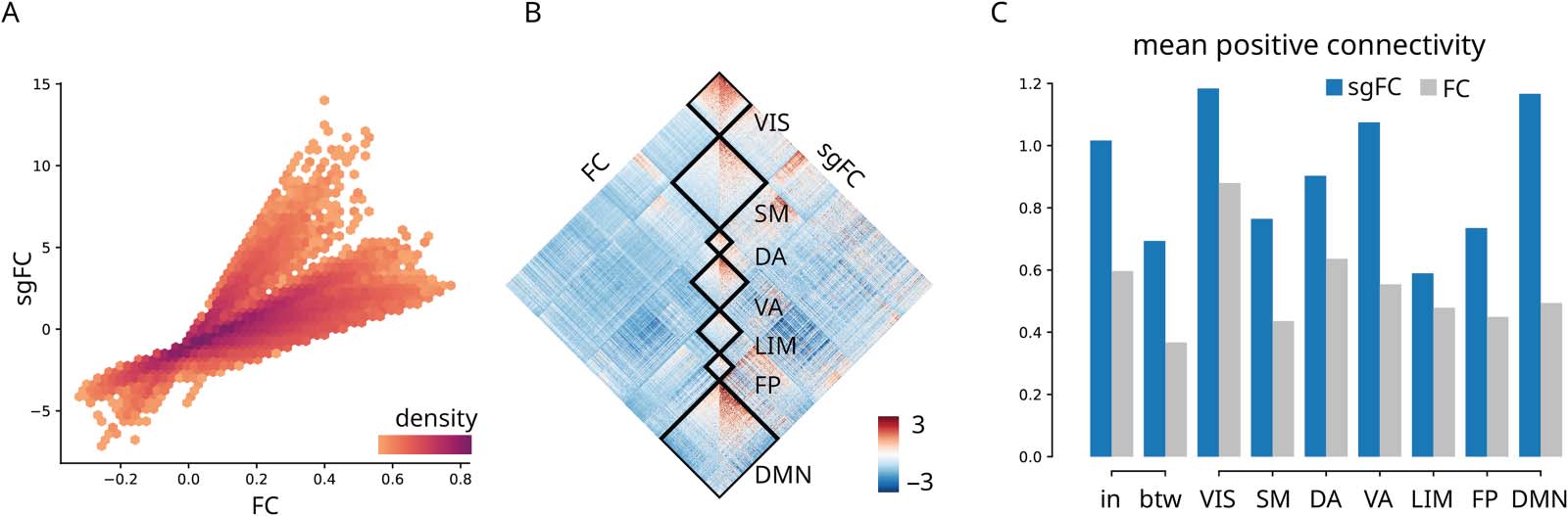
Cifra 3. Contribution to intrinsic network architecture. (A) sgFC correlated with FC, colored by scatter density. Only polysynaptic FCs are
mostrado. (B) FC and sgFC shown side-by-side, reordered according intrinsic networks (Yeo et al., 2011). VIS = visual; SM = somatomotor; DA =
atención dorsal; VA = ventral attention; LIM = limbic; FP = frontoparietal; DMN = default mode. (C) Comparison of within- and between-
network mean positive-valued connectivity with a dissection of within-network connectivity for intrinsic networks. (sgFC to FC ratios: in =
1.70; betw = 1.89; VIS = 1.35; SM = 1.75; DA = 1.42; VA = 1.94; LIM = 1.23; FP = 1.63; DMN = 2.36). In panels B and C, polysynaptic FCs are
standardized by the overall average and standard deviation of FCs with direct SCs to facilitate comparison.
Contribution to Intrinsic Network Architecture
We first ask how conventional FC and sgFC are related to each other and how they are dis-
tributed within and between intrinsic functional networks (Yeo et al., 2011). Figure 3A shows
the correlation between FC and sgFC connection weights. As expected, the reweighing of FCs
accentuates some connections and attenuates others. Supporting Information Figure S5 shows
that long-distance connections tend to be stronger than expected, confirming the intuition
developed in the previous subsection (Cifra 2).
To investigate whether the reweighing of FCs reflects any organizational features of the
cerebro, we first display FC and sgFC, now reordered by the canonical intrinsic networks
(Figura 3B) (Yeo et al., 2011). To facilitate comparison, we standardize polysynaptic FCs by
the overall average and standard deviation of FCs with direct SCs, which can be seen as FC
informed by structure but not by geometry or distance. Curiosamente, the largest differences
between uncorrected and corrected FCs are observed within transmodal networks (default
mode and ventral attention), while more modest differences are observed in the unimodal net-
obras (visual and somatomotor) (Figura 3C). This suggests that unexpectedly strong FCs may
occur more frequently between brain regions at the apex of the unimodal-transmodal cortical
hierarchy. We investigate this possibility in the next section.
Contribution to the Cortical Hierarchy
We next investigate the arrangement of unconnected FCs in macroscale cortical hierarchies.
Recent work suggests that the functional architecture of human brain networks can be sum-
marized by a small number of smooth topographic gradients, with the most prominent such
gradient spanning unimodal to transmodal cortex (Margulies et al., 2016). This putative hier-
archy is thought to support a sensory-fugal representational hierarchy (Mesulam, 1998) y
correlates with spatial variation in cytoarchitecture (Paquola et al., 2019), mielinización
(Huntenburg et al., 2017), and gene expression (Burt et al., 2018).
To place each cortical node along this putative hierarchy, we adapted the diffusion embed-
ding method described by Margulies and colleagues (Coifman et al., 2005; Margulies et al.,
2016; Vázquez-Rodríguez et al., 2019) (see Materials and Methods for more detail). Figura 4A
shows the topography of the first gradient, differentiating primary sensory and transmodal cor-
tices, replicating the original report (Margulies et al., 2016).
Neurociencia en red
941
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
6
4
9
3
7
2
0
5
6
2
8
0
norte
mi
norte
_
a
_
0
0
2
3
6
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Estructura- and geometry-informed functional connectivity
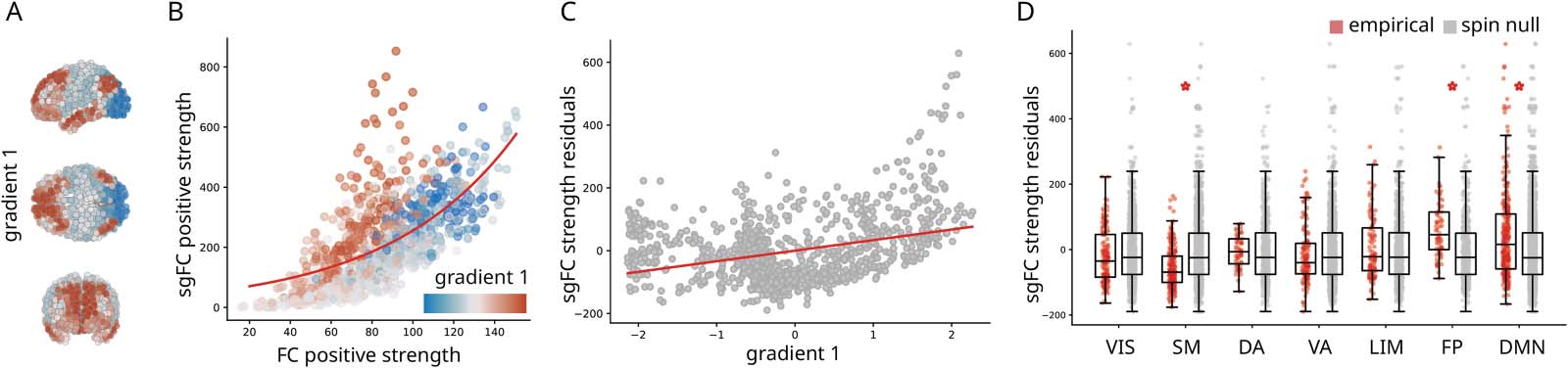
Cifra 4. Contribution to the cortical hierarchy. (A) First principal connectivity gradient estimated using diffusion map embedding applied to
the FC matrix (Margulies et al., 2016). Cold colors indicate unimodal regions and warmer colors indicate transmodal regions. (B) Correlation of
positive strengths (sum of all weights incident on a given node) between sgFC and FC. Points are regions and are colored by their position in
the unimodal-transmodal gradient. An exponential curve is fitted to the points (red line). (C) Residuals of the fitted curve in panel B correlated
with gradient 1. (D) Residuals grouped by intrinsic networks and benchmarked against spatial autocorrelation-preserving null models
(Alexander-Bloch et al., 2018; Markello & Varios, 2021). Statistically significant differences (with Bonferroni correction) are marked with a
red asterisk.
To assess the hypothesis that unexpectedly strong FCs are more concentrated in transmodal
corteza, we first compare node strengths (the sum of all weights incident on a given region)
computed using FC and sgFC. Figure 4B shows the relationship between node strength for
the original FC matrix and for the sgFC matrix. Nodes are coloured by their position in the
hierarchy (gradient 1; red = transmodal, blue = unimodal). The relationship is well-fit by an
exponential function ( y = ex; R2 = 0.44). En tono rimbombante, a cloud of red points are consistent out-
liers, residing above the curve. En otras palabras, brain regions at the apex of the hierarchy are
more likely to participate in unexpectedly strong functional interactions.
We further confirm the link between the cortical hierarchy and unexpectedly strong FCs by
computing the residual of each node relative to the exponential trend shown in Figure 4C
(Pearson’s r = 0.34). Large positive residuals indicate that the node is disproportionately central
in the sgFC functional network. Mean residuals for each intrinsic network, ordered by the
unimodal-transmodal hierarchy, are shown in Figure 4D. The greatest increases appear in
the fronto-parietal (T = 5.96, pag = 1.26 × 10−7, re = 0.62) and default mode networks (T =
5.45, pag = 1.13 × 10−7, re = 0.42), when compared to a null model that permutes region labels
while preserving their spatial autocorrelation (Alexander-Bloch et al., 2018; Markello & Varios,
2021). Colectivamente, these results show that transmodal cortex participates in polysynaptic FCs
that are stronger than expected given their length.
Control Analyses
The results presented in the preceding subsections are potentially contingent on a number of
methodological choices, which we explore in detail here. We first replicate the major
findings—the distribution of sgFC weights and their involvement in cortical hierarchies—in
a validation cohort constructed from N = 33 Participantes. Cifra 5 shows the Pearson corre-
lation of the two results in the Discovery and Validation cohorts (see Supporting Information
Figure S3 for reproduced result figures). The correlation coefficients for both measures are
greater than 0.8 en todos los casos.
We next seek to determine the extent to which global signal regression could influence the
findings. This particular preprocessing step induces negative correlations in FC, profoundly
changing the distribution of weights (Aquino, Fulcher, parque, Sabaroedin, & Proporcionó, 2020;
Murphy & Fox, 2017). We regenerated regional time series, correcting for fluctuations in
the global signal, and repeated the analysis. Cifra 5 shows the effects of the procedure, en
both the Discovery and Validation cohorts (Supporting Information Figure S3). As before, allá
Global signal:
The mean time course computed
over all voxels within the brain.
Neurociencia en red
942
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
6
4
9
3
7
2
0
5
6
2
8
0
norte
mi
norte
_
a
_
0
0
2
3
6
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Estructura- and geometry-informed functional connectivity
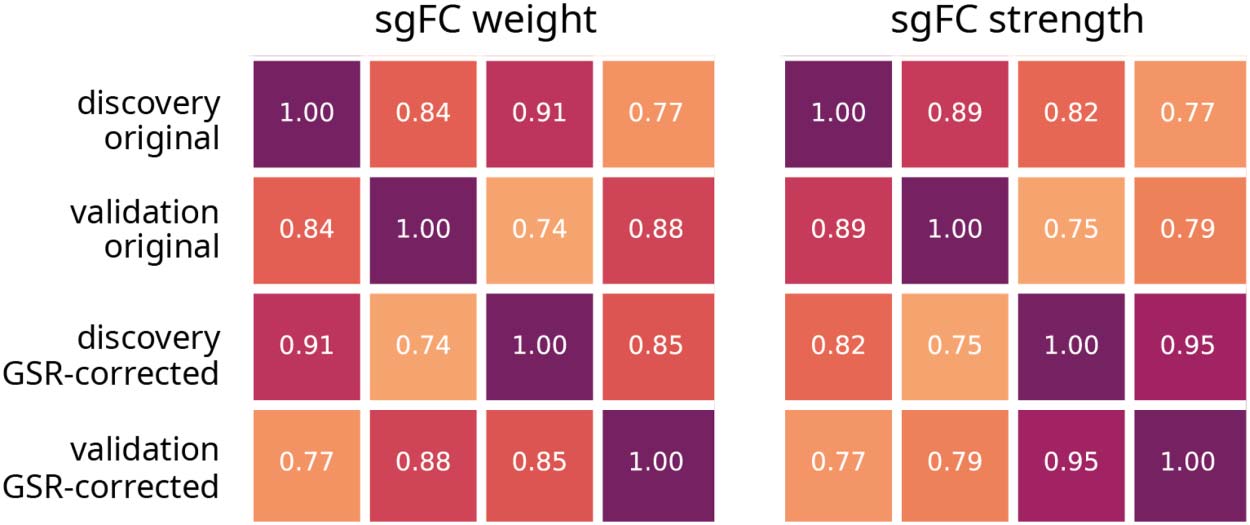
Cifra 5. Validation and global signal removal. Correlation matrices shown for sgFC weight
(values in Figure 2D) and sgFC positive node strength (values in Figure 4B) between controls. Valores
of sgFC are calculated from Discovery and Validation datasets, with and without global signal
regression (GSR). Reproduced Figure 2D and Figure 4B with these values are shown in Supporting
Information Figure S3.
appears to be minimal change in the results, with correlations at approximately 0.9 (para
weights) y 0.8 (for strength). Además, correlations between data cohorts with different
Procesando (p.ej., Discovery set with no global signal regression correlated with Validation
set with global signal regression) were also greater than 0.75.
DISCUSIÓN
In the present report we introduce a simple data-driven method to benchmark functional
connections with respect to their underlying structural and geometric embedding. We find
evidence for unexpectedly strong functional connectivity among transmodal brain regions.
These results suggest a hidden but highly organized pattern among polysnaptic FCs.
Our findings build on an emerging literature about the importance of geometry and struc-
tural connectivity for functional connectivity in the brain. Although the effect of spatial prox-
imity on the probability and weight of connections is well known (Horvát et al., 2016; Roberts
et al., 2016), in practice it is less obvious how this information should be taken into account
when representing functional connectivity. Asimismo, multiple studies report significant corre-
lations between structural and functional connectivity between regions that share direct struc-
tural links (Honey et al., 2009), but how polysynaptic or multihop structural connectivity
shapes functional connectivity is less well known. En efecto, computational models of
structure-function coupling tend to perform more poorly when predicting functional connec-
tions between regions that are not structurally connected (Goñi et al., 2014). More recent
communication models of structure-function coupling explicitly account for polysynaptic
comunicación (Seguin, tian, & Brilla, 2020; Vázquez-Rodríguez, Liu, Hagmann, & Varios,
2020). Here we show that information about structural connectivity and spatial proximity can
be naturally used as a frame of reference to describe functional connectivity between regions
without direct structural connections.
Curiosamente, we find that unexpectedly strong FCs are highly organized with respect to the
modular (despreciar & Betzel, 2016) and hierarchical (Huntenburg et al., 2017) organization of
the brain. Although both modules and hierarchies or “gradients” are robust and well-studied
features of functional networks, their anatomical origin is less clear (Suárez et al., 2020). Nuestro
results suggest that both phenomena emerge from functional interactions or coactivations that
transcend the underlying structure and geometry. En otras palabras, this class of polysynaptic
Neurociencia en red
943
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
6
4
9
3
7
2
0
5
6
2
8
0
norte
mi
norte
_
a
_
0
0
2
3
6
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Estructura- and geometry-informed functional connectivity
functional connections may be physiologically unique, and future empirical and theoretical
studies could potential stratify direct and indirect FCs prior to analysis.
The fact that unexpectedly strong FCs are overrepresented in transmodal cortex may poten-
tially explain recent reports that structure-function relationships are regionally heterogeneous.
Namely, multiple reports have found that structure-function coupling is greater in unimodal
cortex and smaller in transmodal cortex (Baum et al., 2020; Bazinet et al., 2021; Esfahlani,
Faskowitz, Slack, Músculo, & Betzel, 2021; Gu, Jamison, Jabonoso, & Kuceyeski, 2021; Preti &
Ville, 2019; Vázquez-Rodríguez et al., 2019; Wang y cols., 2019). Our results suggest that the
reason for this heterogeneity is that regions in transmodal cortex tend to participate in poly-
synaptic functional connections that are much stronger than expected given the underlying
anatomical constraints. Como resultado, models relating structural and functional connectivity
may be disadvantaged when applied to transmodal cortex relative to unimodal cortex.
More generally, the present framework is part of an emerging literature on simultaneously
representing and modeling brain geometry, structure and function. A natural extension of sgFC
is in the domain of spatially embedded null models that generate surrogate structural or func-
tional networks to benchmark the presence of specific network attributes (Esfahlani, Bertolero,
bassett, & Betzel, 2020; Roberts et al., 2016). Además, sgFC may also serve as a quality func-
tion for generative models of connectivity (Akarca, De cerca, bullmore, & Astle, 2021; Betzel
et al., 2016; Oldham et al., 2021; Shinn et al., 2021; Vértes et al., 2012). Finalmente, we envision
sgFC as the basis for more sophisticated network communication models that consider spatial
proximity as a constraint for routing signals (Seguin, Razi, & Brilla, 2019; Seguin, van den
Colina, & Brilla, 2018; Vázquez-Rodríguez et al., 2020). While these models traditionally
focus only on spatial proximity, sgFC opens the possibility for a hybrid approach that takes into
account structural connectivity and geometry.
The present results also need to be interpreted with respect to several methodological con-
siderations. Despite the fact that we adopted a robust dataset and included a replication sec-
ción, methodological choices including MRI acquisition scheme, processing pipeline, network
reconstruction, and group consensus algorithm may still be susceptible to false positives and
negatives (Jiang et al., 2021; Korhonen, Zanin, & Papo, 2021; Maier-Hein et al., 2017; Sarwar,
Ramamohanarao, & Brilla, 2021). En particular, the deterministic tractography procedure
yields relatively sparse connectomes, and future work should consider the effect of connec-
tome reconstruction and sparsity on the definition of polysynaptic FCs. Además, systematic
false positives or false negatives in connectome reconstruction could potentially emphasize or
mask some classes of connections, such as long-distance connections. En este sentido, the sgFC
procedure developed here presents a framework to comprehensively compare multiple trac-
tography pipelines with each other.
En resumen, we show how fundamental structural and geometric priors can be used to
reweigh and re-represent the functional connectivity matrix. Our results show that the canonical
features of functional connectivity—modules and hierarchies—are delineated by unexpectedly
strong functional connections between nodes without underlying structural links. The biological
origin of this class of connections remains an exciting question for future research.
MATERIALES Y MÉTODOS
Data Acquisition
A total of N = 66 healthy young adults (16 hembras, 25.3 ± 4.9 years old) were scanned at the
Department of Radiology, University Hospital Center and University of Lausanne. The scans
Neurociencia en red
944
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
6
4
9
3
7
2
0
5
6
2
8
0
norte
mi
norte
_
a
_
0
0
2
3
6
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Estructura- and geometry-informed functional connectivity
were performed in 3-Tesla MRI scanner (Trio, Siemens Medical, Alemania) using a 32-channel
head-coil. The protocol included (1) a magnetization-prepared rapid acquisition gradient echo
(MPRAGE) sequence sensitive to white/gray matter contrast (1-mm in-plane resolution,
1.2-mm slice thickness), (2) a diffusion spectrum imaging (DSI) secuencia (128 difusión-
weighted volumes and a single b0 volume, maximum b-value 8,000 s/mm2, 2.2 × 2.2 ×
3.0 mm voxel size), y (3) a gradient echo EPI sequence sensitive to BOLD contrast
(3.3-mm in-plane resolution and slice thickness with a 0.3-mm gap, TR 1,920 EM, resulting
en 280 images per participant). Participants were not subject to any overt task demands during
the fMRI scan.
Structural Network Reconstruction
Gray matter was parcellated into 68 cortical nodes according to the Desikan–Killiany atlas
(Desikan et al., 2006). These regions of interest were then further divided into four additional,
increasingly finer grained resolutions, comprising 114, 219, 448, y 1,000 aproximadamente
equally-sized nodes (Cammoun et al., 2012). Structural connectivity was estimated for indi-
vidual participants by using deterministic streamline tractography. The procedure was imple-
mented in the Connectome Mapping Toolkit (Daducci et al., 2012), initiating 32 streamline
propagations per diffusion direction for each white matter voxel.
To mitigate concerns about inconsistencies in reconstruction of individual participant con-
nectomes (jones, Knösche, & Tornero, 2013; Thomas et al., 2014), as well as the sensitive
dependence of network measures on false positives and false negatives (Zalesky et al.,
2016), we adopted a group-consensus approach (Betzel et al., 2018; de Reus & van den
Colina, 2013; Roberts, Perry, Roberts, mitchell, & romper la lanza, 2017). In constructing a con-
sensus adjacency matrix, we sought to preserve (1) the density and (2) the edge length distri-
bution of the individual participants matrices (Betzel et al., 2016, 2018; Mišić et al., 2015). Nosotros
first collated the extant edges in the individual participant matrices and binned them according
to length. The number of bins was determined heuristically, as the square root of the mean
binary density across participants. The most frequently occurring edges were then selected
for each bin. If the mean number of edges across participants in a particular bin is equal to
k, we selected the k edges of that length that occur most frequently across participants. A
ensure that interhemispheric edges are not under-represented, we carried out this procedure
separately for inter- and intrahemispheric edges. The binary density for the final whole-brain
matrix was around 2.1%.
Functional Network Reconstruction
Functional MRI data were preprocessed using procedures designed to facilitate subsequent
network exploration (Fuerza, Barnes, Snyder, Schlaggar, & Petersen, 2012). fMRI volumes were
corrected for physiological variables, including regression of white matter, cerebrospinal fluid,
as well as motion (three translations and three rotations, estimated by rigid body coregistra-
ción). BOLD time series were then subjected to a low-pass filter (temporal Gaussian filter with
full width half maximum equal to 1.92 s). The first four time points were excluded from sub-
sequent analysis to allow the time series to stabilize. Motion “scrubbing” was performed as
described by Power and colleagues (Power et al., 2012). The data were parcellated according
to the same atlas used for structural networks (Cammoun et al., 2012). Individual functional
connectivity matrices were defined as zero-lag Pearson correlation among the fMRI BOLD
time series. A group-consensus functional connectivity matrix was estimated as the mean
connectivity of pairwise connections across individuals.
Neurociencia en red
945
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
6
4
9
3
7
2
0
5
6
2
8
0
norte
mi
norte
_
a
_
0
0
2
3
6
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Estructura- and geometry-informed functional connectivity
Estructura- and Geometry-Informed Indirect FC Modeling
To construct the structure- and geometry-informed FC (sgFC), we apply equally spaced bins to
the dimension of Euclidean distance. In each bin, we acquire the mean and standard deviation
of those FCs with direct SC link. Then we take the z-score of FCs without direct SC link using
the acquired statistics. The final z-scores are smoothed to get a robust representation by
averaging over a spectrum of bin numbers (±25%) centering the optimal bin size decided
by Freedman Diaconis Estimator shown in Supporting Information Figure S2. La resultante
sgFC values corresponding to those without direct SC link are mapped back to a 1,000-by-
1,000 matrix and used for network analysis through the article.
Diffusion Map Embedding
Diffusion map embedding is a nonlinear dimensionality reduction algorithm (Coifman et al.,
2005). The algorithm seeks to project a set of embeddings into a lower dimensional Euclidean
espacio. Brevemente, the similarity matrix among a set of points (in our case, the correlation matrix rep-
resenting functional connectivity) is treated as a graph, and the goal of the procedure is to iden-
tify points that are proximal to one another on the graph. En otras palabras, two points are close
together if there are many relatively short paths connecting them. A diffusion operator, representar-
ing an ergodic Markov chain on the network, is formed by taking the normalized graph Lapla-
cian of the matrix. The new coordinate space is described by the eigenvectors of the diffusion
operator. We set the diffusion rate α = 1 and the variance of the Gaussian used in affinity com-
putation σ = 1. The procedure was implemented using the Dimensionality Reduction Toolbox
(https://lvdmaaten.github.io/drtoolbox/) (Van Der Maaten, postma, & Van den Herik, 2009).
EXPRESIONES DE GRATITUD
We thank Justine Hansen, Vincent Bazinet, Golia Shafiei, Estefany Suarez, Andrea Luppi, y
Filip Milisav for their comments and suggestions on the manuscript.
SUPPORTING INFORMATION
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
6
4
9
3
7
2
0
5
6
2
8
0
norte
mi
norte
_
a
_
0
0
2
3
6
pag
d
t
.
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00236.
CONTRIBUCIONES DE AUTOR
Zhen-Qi Liu: Conceptualización; Análisis formal; Metodología; Visualización; Writing—Original
borrador. Richard F. Betzel: Análisis formal; Writing—Review & edición. Bratislav Misic: Concep-
tualization; Metodología; Supervisión; Writing—Original draft; Writing—Review & edición.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
INFORMACIÓN DE FINANCIACIÓN
Bratislav Misic, Canada First Research Excellence Fund (https://dx.doi.org/10.13039
/501100010785). Bratislav Misic, Natural Sciences and Engineering Research Council of
Canada (NSERC Discovery Grant), Award ID: 017-04265. Bratislav Misic, Canada Research
Chairs (https://dx.doi.org/10.13039/501100001804). Award ID: SFB 936/Z3.
REFERENCIAS
Akarca, D., De cerca, PAG. MI., bullmore, mi. T., & Astle, D. mi. (2021). A gen-
erative network model of neurodevelopmental diversity in struc-
tural brain organization. Comunicaciones de la naturaleza, 12(1), 4216.
https://doi.org/10.1038/s41467-021-24430-z, PubMed: 34244490
Alexander-Bloch, A. F., shou, h., Liu, S., Satterthwaite, t. D.,
Glahn, D. C., Shinohara, R. T., … Raznahan, A. (2018). On
testing for spatial correspondence between maps of human
brain structure and function. NeuroImagen, 178, 540–551.
Neurociencia en red
946
Estructura- and geometry-informed functional connectivity
https://doi.org/10.1016/j.neuroimage.2018.05.070, PubMed:
29860082
Aquino, k. METRO., Fulcher, B. D., parque, l., Sabaroedin, K., & Proporcionó,
A. (2020). Identifying and removing widespread signal deflec-
tions from fMRI data: Rethinking the global signal regression
problema. NeuroImagen, 212, 116614. https://doi.org/10.1016/j
.neuroimage.2020.116614, PubMed: 32084564
Baum, GRAMO. l., Cual, Z., roalf, D. r., círico, r., Betzel, R. F., Larsen, B.,
… Satterthwaite, t. D. (2020). Development of structure–function
coupling in human brain networks during youth. Actas de
the National Academy of Sciences of the United States of Amer-
ica, 117(1), 771–778. https://doi.org/10.1073/pnas.1912034117,
PubMed: 31874926
Bazinet, v., Vos de Wael, r., Hagmann, PAG., Bernhardt, B. C., &
Varios, B. (2021). Multiscale communication in cortico-cortical
redes. NeuroImagen, 243, 118546. https://doi.org/10.1016/j
.neuroimage.2021.118546, PubMed: 34478823
Bellec, PAG., Rosa-Neto, PAG., Lyttelton, oh. C., Benali, h., & evans, A. C.
(2010). Multi-level bootstrap analysis of stable clusters in
resting-state fMRI. NeuroImagen, 51(3), 1126–1139. https://doi
.org/10.1016/j.neuroimage.2010.02.082, PubMed: 20226257
Betzel, R. F., Avena-Koenigsberger, A., Goñi, J., Él, y., De Reus,
METRO. A., Griffa, A., … Sporns, oh. (2016). Generative models of the
human connectome. NeuroImagen, 124, 1054–1064. https://doi
.org/10.1016/j.neuroimage.2015.09.041, PubMed: 26427642
Betzel, R. F., Griffa, A., Hagmann, PAG., & Músculo, B. (2018). Distance-
dependent consensus thresholds for generating group-
representative structural brain networks. Neurociencia en red,
3(2), 475–496. https://doi.org/10.1162/netn_a_00075, PubMed:
30984903
bullmore, MI., & despreciar, oh. (2012). The economy of brain network
organización. Naturaleza Reseñas Neurociencia, 13(5), 336–349.
https://doi.org/10.1038/nrn3214, PubMed: 22498897
Burt, j. B., Demirtaş, METRO., Eckner, W.. J., Navejar, norte. METRO., Ji, j. l.,
Martín, W.. J., … Murray, j. D. (2018). Hierarchy of transcriptomic
specialization across human cortex captured by structural neuro-
imaging topography. Neurociencia de la naturaleza, 21(9), 1251–1259.
https://doi.org/10.1038/s41593-018-0195-0 , PubMed:
30082915
Cammoun, l., Gigandet, X., Meskaldji, D., Thiran, j. PAG., despreciar, o.,
Do, k. P., … Hagmann, PAG. (2012). Mapping the human connec-
tome at multiple scales with diffusion spectrum MRI. Diario de
Neuroscience Methods, 203(2), 386–397. https://doi.org/10.1016
/j.jneumeth.2011.09.031, PubMed: 22001222
Coifman, R. r., Lafon, S., Sotavento, A. B., Maggioni, METRO., Nadler, B.,
Warner, F., & Zucker, S. W.. (2005). Geometric diffusions as a tool
for harmonic analysis and structure definition of data: Diffusion
maps. Proceedings of the National Academy of Sciences of the
United States of America, 102(21), 7426–7431. https://doi.org
/10.1073/pnas.0500334102, PubMed: 15899970
Daducci, A., Gerhard, S., Griffa, A., Lemkaddem, A., Cammoun, l.,
Gigandet, X., … Thiran, J.-P. (2012). The connectome mapper: Un
open-source processing pipeline to map connectomes with MRI.
Más uno, 7(12), e48121. https://doi.org/10.1371/journal.pone
.0048121, PubMed: 23272041
Damoiseaux, J., Rombouts, S., Barkhof, F., Scheltens, PAG., estampar, C.,
Herrero, S. METRO., & beckman, C. (2006). Consistent resting-state
networks across healthy subjects. Actas del Nacional
Academy of Sciences of the United States of America, 103(37),
13848–13853. https://doi.org/10.1073/pnas.0601417103,
PubMed: 16945915
de Reus, METRO. A., & van den heuvel, METRO. PAG. (2013). Estimating false
positives and negatives in brain networks. NeuroImagen, 70,
402–409. https://doi.org/10.1016/j.neuroimage.2012.12.066,
PubMed: 23296185
Desikan, R. S., Ségonne, F., pescado, B., quinn, B. T., Dickerson,
B. C., Blacker, D., … Killiany, R. j. (2006). An automated labeling
system for subdividing the human cerebral cortex on MRI scans
into gyral based regions of interest. NeuroImagen, 31(3), 968–980.
https://doi.org/10.1016/j.neuroimage.2006.01.021, PubMed:
16530430
Esfahlani, F. Z., Bertolero, METRO. A., bassett, D. S., & Betzel, R. F. (2020).
Space-independent community and hub structure of functional
redes cerebrales. NeuroImagen, 211, 116612. https://doi.org/10
.1016/j.neuroimage.2020.116612, PubMed: 32061801
Esfahlani, F. Z., Faskowitz, J., Slack, J., Músculo, B., & Betzel, R. F.
(2021). Local structure-function relationships in human brain
networks across the human lifespan. bioRxiv. https://doi.org/10
.1101/2021.05.23.445128
Goñi, J., van den heuvel, METRO. PAG., Avena-Koenigsberger, A., de
Mendizabal, norte. v., Betzel, R. F., Griffa, A., … Sporns, oh.
(2014). Resting-brain functional connectivity predicted by ana-
lytic measures of network communication. Actas de la
National Academy of Sciences of the United States of America,
111(2), 833–838. https://doi.org/10.1073/pnas.1315529111,
PubMed: 24379387
gordon, mi. METRO., Laumann, t. o., Gilmore, A. w., Newbold, D. J.,
verde, D. J., Iceberg, j. J., … Dosenbach, norte. Ud.. F. (2017). Precision
functional mapping of individual human brains. Neurona, 95(4),
791–807. https://doi.org/10.1016/j.neuron.2017.07.011,
PubMed: 28757305
Gu, Z., Jamison, k. w., Jabonoso, METRO. r., & Kuceyeski, A. (2021).
Heritability and interindividual variability of regional structure-
function coupling. Comunicaciones de la naturaleza, 12(1), 4894. https://
doi.org/10.1038/s41467-021-25184-4, PubMed: 34385454
Honey, C. J., despreciar, o., Cammoun, l., Gigandet, X., Thiran, j. PAG.,
Meuli, r., & Hagmann, PAG. (2009). Predicting human resting-state
functional connectivity from structural connectivity. Actas
of the National Academy of Sciences of the United States of
America, 106(6), 2035–2040. https://doi.org/10.1073/pnas
.0811168106, PubMed: 19188601
Horvát, S., Gămănut, r., Ercsey-Ravasz, METRO., Magrou, l., Gămănut,
B., VanEssen, D. C., … Kennedy, h. (2016). Spatial embedding
and wiring cost constrain the functional layout of the cortical net-
work of rodents and primates. Biología PLoS, 14(7), e1002512.
https://doi.org/10.1371/journal.pbio.1002512, PubMed:
27441598
Huntenburg, j. METRO., Bazin, P.-L., Goulas, A., Tardif, C. l., Villringer,
A., & Margulies, D. S. (2017). A systematic relationship between
functional connectivity and intracortical myelin in the human
cerebral cortex. Corteza cerebral, 27(2), 981–997. https://doi.org
/10.1093/cercor/bhx030, PubMed: 28184415
Jiang, C., Betzel, r., Él, y., Wang, Y.-S., Xing, X.-X., & Zuo, X.-N.
(2021). Toward reliable network neuroscience for mapping indi-
vidual differences. bioRxiv. https://doi.org/10.1101/2021.05.06
.442886
Neurociencia en red
947
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
6
4
9
3
7
2
0
5
6
2
8
0
norte
mi
norte
_
a
_
0
0
2
3
6
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Estructura- and geometry-informed functional connectivity
jones, D., Knösche, T., & Tornero, R. (2013). White matter integrity,
fiber count, and other fallacies: The do’s and don’ts of diffusion
resonancia magnética. NeuroImagen, 73, 239–254. https://doi.org/10.1016/j
.neuroimage.2012.06.081, PubMed: 22846632
Korhonen, o., Zanin, METRO., & Papo, D. (2021). Principles and open
questions in functional brain network reconstruction. Humano
Mapeo cerebral, 42(11), 3680–3711. https://doi.org/10.1002
/hbm.25462, PubMed: 34013636
Maier-Hein, k. h., Neher, PAG. F., Houde, J.-C., Côté, M.-A., Garyfallidis,
MI., Zhong, J., … Descoteaux, METRO. (2017). The challenge of mapping
the human connectome based on diffusion tractography. Naturaleza
Comunicaciones, 8(1), 1349. https://doi.org/10.1038/s41467-017
-01285-X, PubMed: 29116093
Margulies, D. S., Ghosh, S. S., Goulas, A., Falkiewicz, METRO., Huntenburg,
j. METRO., Langs, GRAMO., … Smallwood, j. (2016). Situating the default-mode
network along a principal gradient of macroscale cortical organiza-
ción. Proceedings of the National Academy of Sciences of the
United States of America, 113(44), 12574–12579. https://doi.org
/10.1073/pnas.1608282113, PubMed: 27791099
Markello, R. D., & Varios, B. (2021). Comparing spatial null models
for brain maps. NeuroImagen, 236, 118052. https://doi.org/10
.1016/j.neuroimage.2021.118052, PubMed: 33857618
Markov, norte. T., Ercsey-Ravasz, METRO., VanEssen, D. C., Knoblauch, K.,
Toroczkai, Z., & Kennedy, h. (2013). Cortical high-density coun-
terstream architectures. Ciencia, 342(6158), 1238406. https://doi
.org/10.1126/science.1238406, PubMed: 24179228
Mesulam, M.-M. (1998). From sensation to cognition. Cerebro, 121(6),
1013–1052. https://doi.org/10.1093/brain/121.6.1013, PubMed:
9648540
Músculo, B., Betzel, R. F., Griffa, A., De Reus, METRO. A., Él, y., Zuo, X.-N.,
… Zatorre, R. j. (2018). Network-based asymmetry of the human
auditory system. Corteza cerebral, 28(7), 2655–2664. https://doi
.org/10.1093/cercor/bhy101, PubMed: 29722805
Músculo, B., Betzel, R. F., Nematzadeh, A., Goni, J., Griffa, A.,
Hagmann, PAG., … Sporns, oh. (2015). Cooperative and competitive
spreading dynamics on the human connectome. Neurona, 86(6),
1518–1529. https://doi.org/10.1016/j.neuron.2015.05.035,
PubMed: 26087168
Músculo, B., Fatima, Z., Askren, METRO. K., Buschkuehl, METRO., Churchill, NORTE.,
Cimprich, B., … Berman, METRO. GRAMO. (2014). The functional connec-
tivity landscape of the human brain. Más uno, 9(10), e111007.
https://doi.org/10.1371/journal.pone.0111007, PubMed:
25350370
Músculo, B., & despreciar, oh. (2016). From regions to connections and
redes: New bridges between brain and behavior. Actual
Opinion in Neurobiology, 40, 1–7. https://doi.org/10.1016/j
.conb.2016.05.003, PubMed: 27209150
Murphy, K., & Fox, METRO. D. (2017). Towards a consensus regarding
global signal regression for resting state functional connectivity
resonancia magnética. NeuroImagen, 154, 169–173. https://doi.org/10.1016/j
.neuroimage.2016.11.052, PubMed: 27888059
Noble, S., Scheinost, D., & Constable, R. t. (2019). A decade of
test-retest reliability of functional connectivity: A systematic
review and meta-analysis. NeuroImagen, 203, 116157. https://
doi.org/10.1016/j.neuroimage.2019.116157, PubMed:
31494250
Oldham, S., Fulcher, B. D., Aquino, k. METRO., Arnatkeviciute, A. METRO.,
Paquola, C., Shishegar, r., & Proporcionó, A. (2021). Modeling
spatial, developmental, physiological, and topological con-
straints on human brain connectivity. bioRxiv. https://doi.org/10
.1101/2021.09.29.462379
Paquola, C., Wael, R. V. D., Wagstyl, K., Bethlehem, R. A. I., hong,
S.-J., Seidlitz, J., … Bernhardt, B. C. (2019). Microstructural and
functional gradients are increasingly dissociated in transmodal
cortices. Biología PLoS, 17(5), e3000284. https://doi.org/10
.1371/journal.pbio.3000284, PubMed: 31107870
Fuerza, j. D., Barnes, k. A., Snyder, A. Z., Schlaggar, B. l., & Petersen,
S. mi. (2012). Spurious but systematic correlations in functional
connectivity MRI networks arise from subject motion. Neuro-
Image, 59(3), 2142–2154. https://doi.org/10.1016/j.neuroimage
.2011.10.018, PubMed: 22019881
Preti, METRO. GRAMO., & Ville, D. V. D. (2019). Decoupling of brain function
from structure reveals regional behavioral specialization in
humanos. Comunicaciones de la naturaleza, 10(1), 1–7. https://doi.org/10
.1038/s41467-019-12765-7, PubMed: 31628329
Roberts, j. A., Perry, A., Lord, A. r., Roberts, GRAMO., mitchell, PAG. B., Herrero,
R. MI., … Breakspear, METRO. (2016). The acontribution of geometry to
the human connectome. NeuroImagen, 124, 379–393. https://doi
.org/10.1016/j.neuroimage.2015.09.009, PubMed: 26364864
Roberts, j. A., Perry, A., Roberts, GRAMO., mitchell, PAG. B., & romper la lanza,
METRO. (2017). Consistency-based thresholding of the human con-
nectome. NeuroImagen, 145, 118–129. https://doi.org/10.1016/j
.neuroimage.2016.09.053, PubMed: 27666386
Salvador, r., Suckling, J., Coleman, METRO. r., Pickard, j. D., menón,
D., & bullmore, mi. (2005). Neurophysiological architecture of
functional magnetic resonance images of human brain. Cerebral
Corteza, 15(9), 1332–1342. https://doi.org/10.1093/cercor
/bhi016, PubMed: 15635061
Sarwar, T., Ramamohanarao, K., & Brilla, A. (2021). A critical
review of connectome validation studies. RMN en biomedicina,
34(12), e4605. https://doi.org/10.1002/nbm.4605, PubMed:
34516016
Seguin, C., Razi, A., & Brilla, A. (2019). Inferring neural signalling
directionality from undirected structural connectomes. Naturaleza
Comunicaciones, 10(1), 1–13. https://doi.org/10.1038/s41467
-019-12201-w, PubMed: 31537787
Seguin, C., tian, y., & Brilla, A. (2020). Network communication
models improve the behavioral and functional predictive utility
of the human structural connectome. Neurociencia en red,
4(4), 980–1006. https://doi.org/10.1162/netn_a_00161,
PubMed: 33195945
Seguin, C., van den heuvel, METRO. PAG., & Brilla, A. (2018). Navigation
of brain networks. Proceedings of the National Academy of Sci-
ences of the United States of America, 115(24), 6297–6302.
https://doi.org/10.1073/pnas.1801351115, PubMed: 29848631
Sepulcro, J., Liu, h., Talukdar, T., Martincorena, I., yo, B. T., &
Buckner, R. l. (2010). The organization of local and distant
functional connectivity in the human brain. PLoS computacional
Biología, 6(6), e1000808. https://doi.org/10.1371/journal.pcbi
.1000808, PubMed: 20548945
Shinn, METRO., Hu, A., Tornero, l., Noble, S., Achard, S., Anticevic, A., …
Murray, j. D. (2021). Spatial and temporal autocorrelation weave
human brain networks. bioRxiv. https://doi.org/10.1101/2021.06
.01.446561
Herrero, S. METRO., Nichols, t. MI., Vidaurre, D., Winkler, A. METRO., Behrens,
t. MI., vidrio, METRO. F., … Miller, k. l. (2015). A positive-negative
Neurociencia en red
948
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
6
4
9
3
7
2
0
5
6
2
8
0
norte
mi
norte
_
a
_
0
0
2
3
6
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Estructura- and geometry-informed functional connectivity
mode of population covariation links brain connectivity, demo-
graphics and behavior. Neurociencia de la naturaleza, 18(11), 1565–1567.
https://doi.org/10.1038/nn.4125, PubMed: 26414616
despreciar, o., & Betzel, R. F. (2016). Modular brain networks. Annual
Review of Psychology, 67(1), 613–640. https://doi.org/10.1146
/annurev-psych-122414-033634, PubMed: 26393868
stiso, J., & bassett, D. S. (2018). Spatial embedding imposes con-
straints on neuronal network architectures. Tendencias en Cognitivo
Ciencias, 22(12), 1127–1142. https://doi.org/10.1016/j.tics.2018
.09.007, PubMed: 30449318
Suárez, l. MI., Markello, R. D., Betzel, R. F., & Varios, B. (2020). Link-
ing structure and function in macroscale brain networks. Trends
in Cognitive Sciences, 24(4), 302–315. https://doi.org/10.1016/j
.tics.2020.01.008, PubMed: 32160567
tomás, C., Franco, q. y., Irfanoglu, METRO. o., Modi, PAG., Saleem, k. S.,
Leopold, D. A., & Pierpaoli, C. (2014). Anatomical accuracy of
brain connections derived from diffusion MRI tractography is
inherently limited. Proceedings of the National Academy of Sci-
ences of the United States of America, 111(46), 16574–16579.
https://doi.org/10.1073/pnas.1405672111, PubMed: 25368179
Van den Heuvel, METRO. PAG., bullmore, mi. T., & despreciar, oh. (2016).
Comparative connectomics. Tendencias en Ciencias Cognitivas, 20(5),
345–361. https://doi.org/10.1016/j.tics.2016.03.001, PubMed:
27026480
Van Der Maaten, l., postma, MI., & Van den Herik, j. (2009). Dimen-
sionality reduction: A comparative review. Journal of Machine
Investigación del aprendizaje, 10, 66–71.
Vázquez-Rodríguez, B., Liu, Z.-Q., Hagmann, PAG., & Varios, B.
(2020). Signal propagation via cortical hierarchies. Red
Neurociencia, 4(4), 1072–1090. https://doi.org/10.1162/netn_a
_00153, PubMed: 33195949
Vázquez-Rodríguez, B., Suárez, l. MI., Markello, R. D., Shafiei, GRAMO.,
Paquola, C., Hagmann, PAG., … Misic, B. (2019). Gradients of
structure–function tethering across neocortex. Actas de la
National Academy of Sciences of the United States of America,
11 6 ( 4 2 ) , 2 1 21 9 – 2 1 2 2 7 . h t t p s : / / d o i . o rg / 1 0 . 1 0 7 3 / p n a s
.1903403116, PubMed: 31570622
De cerca, PAG. MI., Alexander-Bloch, A. F., Gogtay, NORTE., Giedd, j. NORTE.,
Rapoport, j. l., & bullmore, mi. t. (2012). Simple models of
human brain functional networks. Actas del Nacional
Academy of Sciences of the United States of America, 109(15),
5868–5873. https://doi.org/10.1073/pnas.1111738109,
PubMed: 22467830
Wang, PAG., kong, r., kong, X., Liégeois, r., Orban, C., decoración, GRAMO., …
yo, B. t. t. (2019). Inversion of a large-scale circuit model
reveals a cortical hierarchy in the dynamic resting human brain.
Science Advances, 5(1), eaat7854. https://doi.org/10.1126/sciadv
.aat7854, PubMed: 30662942
yo, B. t. T., Krienen, F. METRO., Sepulcro, J., Jabonoso, METRO. r., Ejército,
D., Hollinshead, METRO., … Buckner, R. l. (2011). The organization of
the human cerebral cortex estimated by intrinsic functional con-
conectividad. Revista de neurofisiología, 106(3), 1125–1165.
https://doi.org/10.1152/jn.00338.2011, PubMed: 21653723
Brilla, A., Proporcionó, A., cocineros, l., Perdido, l. l., van den heuvel,
METRO. PAG., & romper la lanza, METRO. (2016). Connectome sensitivity or spec-
ificity: Which is more important? NeuroImagen, 142, 407–420.
https://doi.org/10.1016/j.neuroimage.2016.06.035, PubMed:
27364472
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
6
4
9
3
7
2
0
5
6
2
8
0
norte
mi
norte
_
a
_
0
0
2
3
6
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Neurociencia en red
949