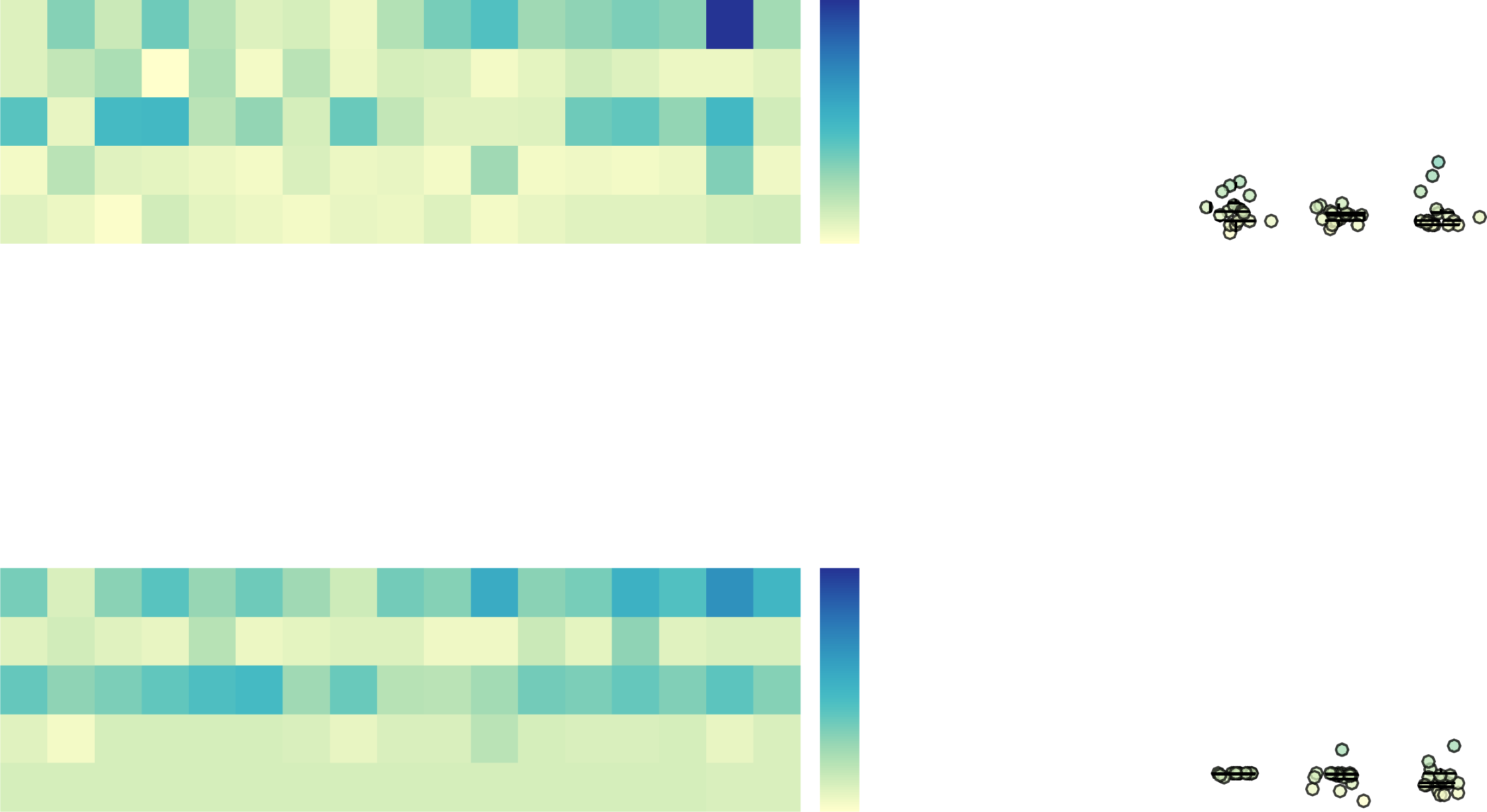FUNCIÓN DE ENFOQUE:
Network Communication in the Brain

Network communication models improve the
behavioral and functional predictive utility of the
human structural connectome

Caio Seguin1, Ye Tian1, and Andrew Zalesky1,2

1Melbourne Neuropsychiatry Centre, University of Melbourne and Melbourne Health, Melbourne, Australia
2Department of Biomedical Engineering, Melbourne School of Engineering, Universidad de Melbourne, Melbourne, Australia

Palabras clave: Brain network communication models, Neural signaling, Network neuroscience,
Connectomics, Behavioral prediction, Structure-function coupling

un acceso abierto

diario

ABSTRACTO

The connectome provides the structural substrate facilitating communication between brain
regiones. We aimed to establish whether accounting for polysynaptic communication in
structural connectomes would improve prediction of interindividual variation in behavior as
well as increase structure-function coupling strength. Connectomes were mapped for 889
healthy adults participating in the Human Connectome Project. To account for polysynaptic
signaling, connectomes were transformed into communication matrices for each of 15
different network communication models. Communication matrices were (a) used to perform
predictions of five data-driven behavioral dimensions and (b) correlated to resting-state
conectividad funcional (FC). While FC was the most accurate predictor of behavior,
communication models, in particular communicability and navigation, improved the
performance of structural connectomes. Communication also strengthened structure-function
coupling, with the navigation and shortest paths models leading to 35–65% increases in
association strength with FC. We combined behavioral and functional results into a single
ranking that provides insight into which communication models may more faithfully
recapitulate underlying neural signaling patterns. Comparing results across multiple
connectome mapping pipelines suggested that modeling polysynaptic communication is
particularly beneficial in sparse high-resolution connectomes. We conclude that network
communication models can augment the functional and behavioral predictive utility of the
human structural connectome.

RESUMEN DEL AUTOR

Brain network communication models aim to describe the patterns of large-scale neural
signaling that facilitate functional interactions between brain regions. While information can
be directly communicated between anatomically connected regions, signaling between
disconnected areas must occur via a sequence of intermediate regions. We investigated a
number of candidate models of connectome communication and found that they improved
structure-function coupling and the extent to which structural connectomes can predict
interindividual variation in behavior. Comparing the behavioral and functional predictive
utility of different models provided initial insight into which conceptualizations of network
communication may more faithfully recapitulate biological neural signaling. Nuestros resultados
suggest network communication models as a promising avenue to unite our understanding of
brain structure, brain function, and human behavior.

Citación: Seguin, C., tian, y., Brilla, A.
(2020). Network communication
models improve the behavioral and
functional predictive utility of the
human structural connectome.
Neurociencia en red, 4(4), 980–1006.
https://doi.org/10.1162/netn_a_00161

DOI:
https://doi.org/10.1162/netn_a_00161

Supporting Information:
https://doi.org/10.1162/netn_a_00161

Recibió: 21 Abril 2020
Aceptado: 3 Agosto 2020

Conflicto de intereses: Los autores tienen
declaró que no hay intereses en competencia
existir.

Autor correspondiente:
Caio Seguin
caioseguin@gmail.com

Editor de manejo:
Andrea Avena-Koenigsberger

Derechos de autor: © 2020
Instituto de Tecnología de Massachusetts
Publicado bajo Creative Commons
Atribución 4.0 Internacional
(CC POR 4.0) licencia

La prensa del MIT

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

/

t

/

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

4
4
9
8
0
1
8
6
7
0
2
6
norte
mi
norte
_
a
_
0
0
1
6
1
pag
d

t

.

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Network communication models, comportamiento, and functional connectivity

INTRODUCCIÓN

The structural connectome is a complex network that describes anatomical connections be-
tween neural elements (bassett & despreciar, 2017; Proporcionó, Brilla, & bullmore, 2016). En el
macroscale of magnetic resonance imaging (resonancia magnética), the human connectome delineates how
gray matter regions are interlinked by white matter projections (Hagmann et al., 2008; despreciar,
Tononi, & kötter, 2005). Numerous studies have demonstrated that the macroscale human
connectome is characterized by several nonrandom topological properties, including a small-
world and modular architecture (bassett & bullmore, 2006; despreciar & Betzel, 2016), heteroge-
neous degree distribution (bullmore & despreciar, 2009), and a core of densely connected hubs
(van den heuvel & despreciar, 2011). This complex anatomical scaffold both facilitates and con-
strains neural signaling between brain regions. While region pairs that share a connection
in the structural connectome may communicate directly, polysynaptic paths comprising two
or more connections are required to establish communication between anatomically uncon-
nected regions. Understanding the dynamics of polysynaptic communication in large-scale
brain networks is a key open challenge in neuroscience (Avena-Koenigsberger, Miši´c, & despreciar,
2018).

Several network communication models have been proposed to describe large-scale neu-
ral signaling, ranging from naive random walk processes to optimal routing via shortest paths
(Avena-Koenigsberger et al., 2019). By considering polysynaptic paths, these models capture
communication between both connected and unconnected nodes, thus enabling a high-order
structural description of interactions among every pair of regions in the connectome (Suárez,
Markello, Betzel, & Miši´c, 2020). Recent studies report that network communication mod-
els can improve the strength of coupling between structural and functional connectivity in
the human connectome (Goñi et al., 2014), explain established patterns of cortical lateraliza-
ción (Miši´c et al., 2018), and infer the directionality of effective connectivity from structural
connectomes (Seguin, Razi, & Brilla, 2019). These efforts provide evidence that network
communication models capture meaningful aspects of brain functioning and dynamics. Cómo-
alguna vez, the extent to which different models contribute to our understanding of neural signaling
remains unknown.

Aquí, we aimed to systematically investigate the utility of a range of candidate models of
network communication. Primero, we sought to determine whether modeling polysynaptic (multi-
hop) communication in structural brain networks would (a) improve the prediction of interindi-
vidual variation in behavior, compared with predictions based on direct structural connections
solo; y (b) improve the strength of structure-function coupling. Segundo, we aimed to estab-
lish a ranking of communication models with respect to their predictive utility, with the goal
of determining which models may more faithfully capture biological signaling patterns related
to behavior and FC.

We considered five previously proposed network communication measures: (a) shortest
paths (Kaiser & Hilgetag, 2006; latora & marchiori, 2001), (b) navigation (Boguña, Krioukov,
& Claffy, 2009; Seguin, van den heuvel, & Brilla, 2018), (C) difusión (Goñi et al., 2013), (d)
search information (Goñi et al., 2014; Rosvall, Grönlund, Minnhagen, & Sneppen, 2005), y
(v) communicability (Andreotti et al., 2014; Crofts & Higham, 2009; Estrada & Hatano, 2008).
Colectivamente, these models cover a widerange of neural signaling conceptualizations. Short-
est paths and navigation deterministically route information using centralized and decentral-
ized strategies, respectivamente. A diferencia de, diffusion and search information model communi-
cation from the stochastic perspective of random walk processes. Finalmente, communicability

Polysynaptic path:
A path between a source region and
target region that contains at least
one intermediary region; a path
between anatomically unconnected
regiones.

Brain network communication model:
A model of how neural signaling
unfolds atop the structural
conectoma; a strategy to describe
how information is communicated
between regions.

Structure-function coupling:
Relationship between structural and
conectividad funcional. Typically
quantified by the correlation
between structural and functional
connection weights.

Shortest paths efficiency:
Communication efficiency under the
shortest path routing model.
Considers that neural signaling
unfolds via optimally efficient paths.

Navigation efficiency:
Communication efficiency under the
navigation model. Considers that
neural signaling unfolds via
geometrically greedy paths.

Neurociencia en red

981

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

/

t

/

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

4
4
9
8
0
1
8
6
7
0
2
6
norte
mi
norte
_
a
_
0
0
1
6
1
pag
d

t

.

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Network communication models, comportamiento, and functional connectivity

Diffusion efficiency:
Communication efficiency under the
modelo de difusión. Considers that
neural signaling unfolds via random
walks.

Search information:
The amount of information required
for a random walker to travel via
shortest paths. Quantifies the
accessibility of efficient
communication paths in the
conectoma.

Communicability:
Weighted sum of all walk lengths
between region pairs. Considers that
neural signaling unfolds as a diffusive
broadcasting process.

Communication matrix:
A matrix quantifying communication
between every region pair under the
assumption of a certain network
communication model.

implements a broadcasting model of signaling, in which signals are simultaneously propagated
along multiple network fronts. While all these candidate models have been investigated in the
human connectome, which particular models provide the most parsimonious representation
of large-scale neural signaling remains unclear.

Using diffusion-weighted MRI and tractography, we mapped structural connectivity (CAROLINA DEL SUR)
(HCP;
matrices for 889 healthy adults participating in the Human Connectome Project
Van Essen et al., 2013). Each individual’s SC matrix was then transformed into a communica-
tion matrix, which represented the efficiency of communication between each pair of regions
under a particular candidate model of network communication. For each model, comunal-
cation matrices were fed to statistical techniques to perform out-of-sample prediction of indi-
vidual variation in five behavioral dimensions (tian, Margulies, romper la lanza, & Brilla, 2020),
and also correlated with FC matrices mapped using resting-state functional MRI. This enabled
a systematic ranking of network communication models in terms of behavior prediction and
structure-function coupling. While these criteria do not constitute direct biological validation
of signaling strategies, we hypothesize that the higher the predictive utility of a communica-
tion model, the more likely it is to parsimoniously recapitulate the signaling mechanisms of
el cerebro humano.

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

/

/

t

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

4
4
9
8
0
1
8
6
7
0
2
6
norte
mi
norte
_
a
_
0
0
1
6
1
pag
d

t

.

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

RESULTADOS

Brain Network Communication Matrices

Structural connectomes were mapped using white matter tractography applied to diffusion
MRI data acquired for 889 healthy adults participating in the Human Connectome Project
(Van Essen et al., 2013; See the Methods section). We focus on reporting results for connec-
tomes comprising N = 360 cortical regions (Glasser et al., 2016) that were thresholded to
eliminate potentially spurious connections (Zalesky et al., 2016). Results for alternative corti-
cal parcellations and connection density thresholds are reported in the Supporting Information.

Connectome mapping yielded a structural connectivity (CAROLINA DEL SUR) matrix for each individual.
These matrices represented connectivity between directly connected regions and were gen-
erally sparse because of an absence of white matter tracts between a majority of region pairs.
To model the impact of polysynaptic neural signaling, each individual’s connectivity matrix
was transformed into a communication matrix (Figura 1A). Communication matrices were of
the same dimension as the SC matrices, but fully connected in most cases, and they quan-
tified the efficiency of communication between indirectly (polysynaptic) as well as directly
connected pairs of regions under a given network communication model. A diferencia de, the SC
matrices only characterized directly connected pairs of regions.

We considered three connectivity weight definitions: (a) weighted: connection weights de-
fined as the number of tractography streamline counts between regions; (b) binario: non-zero
connection weights set to 1; y (C) distancia: nonzero connection weights set to the Euclidean
distance between regions. Network communication models computed on these connectomes
operationalize metabolic factors conjectured to shape large-scale signaling: (a) adoption of
high-volume white matter projections that putatively enable fast and reliable signal propaga-
ción (weighted); (b) reduction of the number of synaptic crossings (binario); y (C) reducción
of the physical length traversed by signals (distancia; bullmore & despreciar, 2012; Fornito et al.,
2016; Rubinov & despreciar, 2010).

Neurociencia en red

982

Network communication models, comportamiento, and functional connectivity

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

/

/

t

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

4
4
9
8
0
1
8
6
7
0
2
6
norte
mi
norte
_
a
_
0
0
1
6
1
pag
d

.

t

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

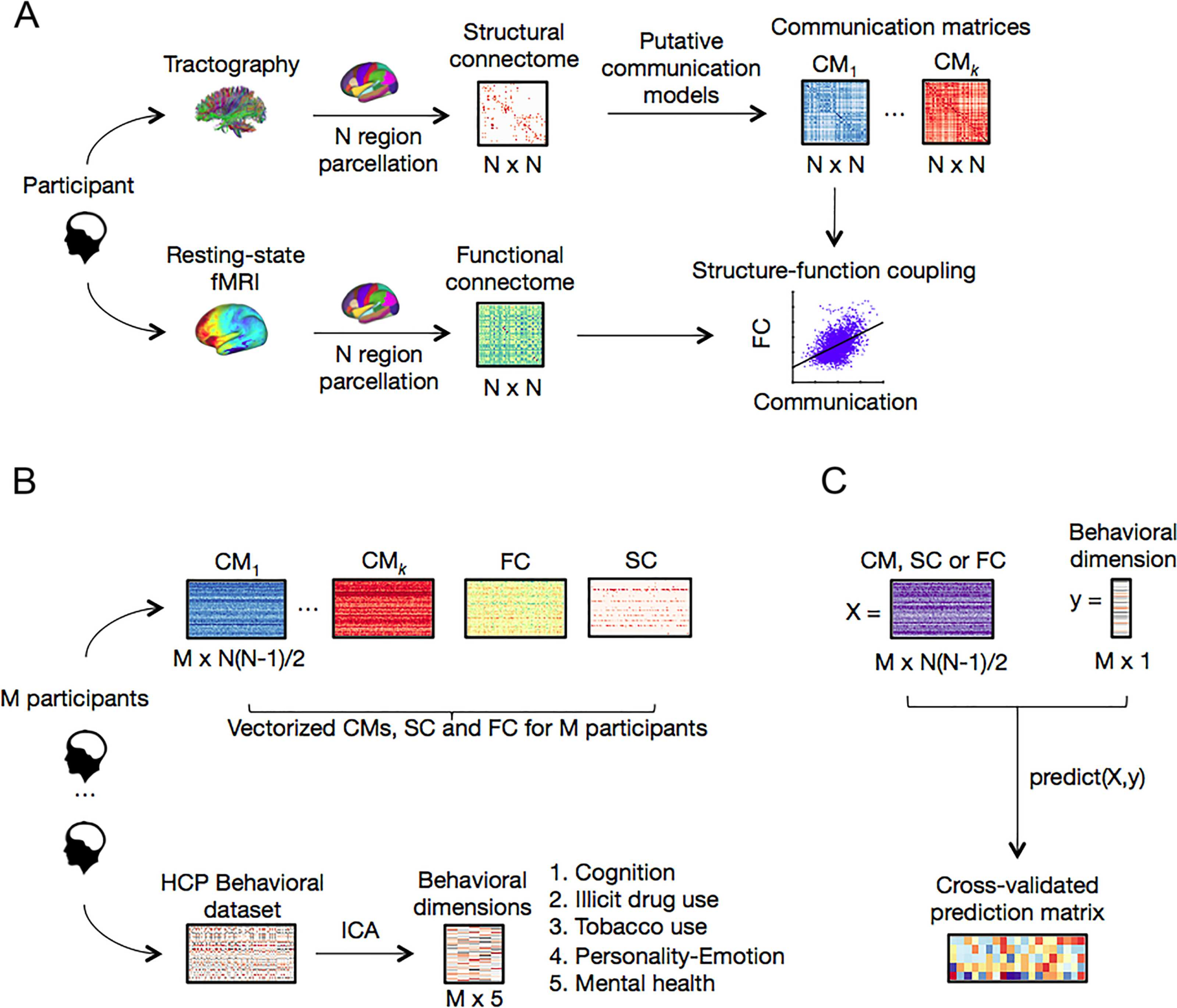
Cifra 1. Methodology overview. (A) For each participant in our sample, structural connectomes comprising N cortical regions were mapped
using white matter tractography applied to diffusion MRI. Structural connectivity matrices were transformed into communication matrices
C ∈ RN×N, where C(i, j) denotes the communication efficiency from region i to region j. Para cada participante, a total of 15 comunicación
matrices were derived representing different combinations of network communication models (shortest paths, navigation, difusión, buscar
información, communicability) and connection weight definitions (binario, weighted, distancia). To assess structure-function coupling, commu-
nication matrices were correlated with FC matrices computed from resting-state functional MRI data. (B) Comunicación, FC, and SC matrices
were vectorized and aggregated across M = 889 Participantes, Resultando en 17 M × N(N − 1)/2 matrices of explanatory variables. A set of
five behavioral dimensions was computed by applying independent component analysis (ICA) to the HCP dataset of behavioral phenotypes.
(C) Comunicación, CAROLINA DEL SUR, and FC matrices were used to predict behavior. An entry in the resulting 5 × 17 prediction matrix corresponds to the
mean cross-validated association between a communication or connectivity matrix and a behavioral dimension.

Predicting Behavior With Models of Connectome Communication

Statistical models were trained to independently predict five dimensions of behavior (cog-
nition, illicit substance use, tobacco use, personality-emotional traits, mental health) based
on features comprising an individual’s communication matrix (Figures 1B, 1C). Training and

Neurociencia en red

983

Network communication models, comportamiento, and functional connectivity

prediction were performed separately for a total of 15 communication matrices represent-
ing different connection weight definitions (binario, weighted, distancia) and network commu-
nication models (shortest paths, navigation, difusión, search information, communicability).
Además, predictions based on an individual’s SC and FC were computed to provide ac-
curacy benchmarks. The five behavioral components represent orthogonal dimensions that
were parsed from a comprehensive set of behavioral measures using independent component
análisis (see the Methods section).

Out-of-sample prediction accuracy was evaluated for 10 repetitions of a tenfold cross-
validation scheme. The Pearson correlation coefficient between the actual and out-of-sample
predicted behavior was used to quantify prediction accuracy for each behavioral dimension.
To ensure that our results were not contingent on the adoption of a particular statistical model,
predictions were independently performed using lasso regression (Tibshirani, 1996) y un
regression model based on features identified by the network-based statistic (NBS; Brilla,
Proporcionó, & bullmore, 2010; see the Methods section). Prediction accuracies were averaged
across cross-validation folds and repetitions, and visualized in the form of a matrix comprising
behavioral dimensions (filas) and communication models (columnas; Figures 2A, 2C).

We found that individual variation in some behavioral dimensions could be predicted with
greater accuracy than others (lasso: F(4,80) = 10.67, pag = 5 × 10−7; NBS: F(4,80) = 47.18,
pag = 2 × 10−20). Dimensions characterizing cognition (respective lasso and NBS accuracies
averaged across all predictors: 0.068, 0.101) and tobacco use (0.061, 0.089) could be pre-
dicted more accurately on average, whereas comparably weaker predictions of illicit substance
usar (−0,003, −0,002), personality-emotion (−0,008, −0,003), and mental health (−0.014,
−0.0003) were evident (Figures 2B, 2D).

Prediction accuracies were consistent between the two statistical models (NBS, lasso), ambos
when pooling the five behavioral dimensions (Spearman rank correlation coefficient r(83) =
0.60, pag = 2 × 10-9; Figura 2E), as well as separately for cognition (r(16) = 0.56, pag = 0.022;
Figura 2F) and tobacco use (r(16) = 0.67, pag = 0.004; Figure 2H). Lasso and NBS diverged for
the dimensions that were less accurately predicted (p.ej., pag = 0.313 for illicit substance use;
Figure 2G).

Focusing on lasso regression, we sought to determine whether behavioral predictions were
robust to variations in our methodological settings. Primero, we found that adopting the mean
square error to quantify predictive utility led to accuracies significantly associated with the
ones computed based on Pearson correlation (Supporting Information, Figure S1). Segundo,
we tested whether prediction accuracies were sensitive to changes in our connectome map-
ping pipeline. Para tal fin, we recomputed behavioral predictions for three additional sets
of connectomes: (a) norte = 360 regions without connection thresholding, (b) norte = 68 re-
gions with connection thresholding, y (C) norte = 68 regions without connection thresholding
(see the Methods section). Prediction accuracies were typically significantly correlated across
bajo- and high-resolution, as well as thresholded and unthresholded, connectomes (Secundario
Información, Figure S2). More specifically, consistency across connectome mapping pipelines
was strong when considering predictions pooled across all five behavioral dimensions and
relatively modest when focusing on cognition and tobacco use, indicating a potential effect of
parcellation and connection thresholding to the predictive utility of different communication
modelos.

Juntos, these findings suggest that network communication models (as well as SC and FC)
can explain out-of-sample interindividual variance in behavior. More specifically, cognition

Neurociencia en red

984

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

/

t

/

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

4
4
9
8
0
1
8
6
7
0
2
6
norte
mi
norte
_
a
_
0
0
1
6
1
pag
d

t

.

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Network communication models, comportamiento, and functional connectivity

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

/

t

/

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

4
4
9
8
0
1
8
6
7
0
2
6
norte
mi
norte
_
a
_
0
0
1
6
1
pag
d

t

.

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 2. Predicting individual variation in human behavioral dimensions using models of connectome communication, (norte = 360 thresh-
olded connectomes). (A) Matrix of Pearson correlation coefficients between observed and predicted behavior. Lasso regression was used to
predict five orthogonal behavioral dimensions (filas) de 15 connectome communication models, as well as SC and FC (columnas, predic-
tores). (B) Lasso regression prediction accuracies stratified by behavioral dimensions. Each boxplot summarizes a row of the prediction accuracy
matrix and the superimposed data points are colored accordingly. Top and bottom edge boxplots indicate, respectivamente, the 25th and 75th
percentiles, while the central mark shows the distribution median. Mean prediction accuracies significantly differed between the five behav-
ioral dimensions (F(4,80) = 10.67, pag = 5 × 10−7). (CD) Same as (A-B), but for predictions carried out using a regression model based on
features identified by the NBS. De nuevo, mean prediction accuracies were significantly different between behavioral dimensions (F(4,80) = 47.18,
pag = 2 × 10−20). Scatterplots showing the association (Spearman rank correlation coefficient and p value) between lasso and NBS prediction
accuracies for (mi) all behavioral dimensions, (F) cognition, (GRAMO) illicit substance use, (h) tobacco use, y (I) the average between cognition
and tobacco use prediction accuracies. SPE: shortest path efficiency, NE: navigation efficiency, DE: diffusion efficiency, SI: search information,
CMY: communicability, bin: binario, wei: weighted, dis: distancia.

Neurociencia en red

985

Network communication models, comportamiento, and functional connectivity

and tobacco use were the most accurately predicted behavioral dimensions. Por esta razón,
we henceforth focus subsequent analyses on the averaged prediction accuracy obtained for
the cognition and tobacco use dimensions. This provides us with a single measure of how
connectome communication relates to behavior by considering only the behavioral traits that
can be predicted with relevant accuracy. The obtained prediction accuracy average was also
consistent across the lasso and NBS methods (r(16) = 0.50, pag = 0.041; Figure 2I).

Communication Models Improve the Behavioral Predictive Utility of the Human Connectome

We sought to compare communication models, as well as SC and FC, in terms of their behav-
ioral prediction accuracy. Figure 3A shows the distributions of out-of-sample accuracies (10
repetitions of tenfold cross validation, averaged for the cognition and tobacco use dimensions)
obtained for the each predictor using lasso regression. Accuracy distributions were ranked
based on their medians. FC (median accuracy: 0.24) provided markedly greater accuracy than
all communication models and SC. Binary navigation (median accuracy: 0.12) and weighted
communicability (median accuracy: 0.10) followed as the second and third most predictive
communication models. Fundamentalmente, we observed that the majority of communication models
yielded greater prediction accuracy than SC (median accuracy: 0.03). This indicates that mod-
eling polysynaptic signaling through the transformation of SC into communication matrices
improved the behavioral predictive utility of structural connectomes.

We performed repeated measures t tests to assess pairwise statistical differences in the pre-
dictive utility of communication models and connectivity measures. Figure 3B shows the effect
size matrix (Cohen’s d; Bonferroni-corrected for 136 multiple comparisons with significance
threshold α = 3.67 × 10−4) of differences between mean prediction accuracies, with warm-
and cool-colored cells indicating model pairs for which a significant difference was observed.
As expected, FC outperformed all other predictors (p.ej., pag = 1 × 10−26 between FC and bi-
nary navigation). The lack of colored cells along the main diagonal of the effective size ma-
trix indicates that predictors of similar ranking seldom yielded significantly different accuracy.
En tono rimbombante, seven communication models (out of 15) significantly outperformed SC, incluir-
ing binary navigation; binario, weighted, and distance communicability; binary and distance
shortest paths; and weighted search information (all p < 10−4). This underscores the improve- ment in behavioral predictive utility gained from accounting for polysynaptic communication in structural connectomes, compared with predictions that only account for direct structural connections. The magnitude of statistical differences between communication models was better visualized when plotting effect size matrices excluding comparisons to FC (Supporting Information, Figure S3). Importantly, the behavioral prediction accuracies reported in Figure 3A were significantly larger than those obtained by computing network communication models on null sets of topo- logically randomized connectomes (Supplementary Note 1; Supporting Information, Figure S4). This corroborates the notion that network communication models are capable of predicting interindividual variation in human behavior, and that observed differences in prediction accu- racies reflect meaningful distinctions in the predictive utility of different models. Additionally, we found that the pairwise comparisons between models shown in Figure 3B were stable across each of the 10 repetitions of the performed tenfold cross validation (Supplementary Note 2; Supporting Information, Table S1). Next, we aimed to separate the effects of communication model choice and connection weight definition on prediction accuracy. To this end, accuracies were averaged over the three Network Neuroscience 986 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 4 4 9 8 0 1 8 6 7 0 2 6 n e n _ a _ 0 0 1 6 1 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Network communication models, behavior, and functional connectivity l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 4 4 9 8 0 1 8 6 7 0 2 6 n e n _ a _ 0 0 1 6 1 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 3. Comparison of the behavioral predictive utility of connectome communication models (Lasso regression, N = 360 thresholded connectomes, average cognition and tobacco use prediction accuracies). Across panels, top and bottom edge boxplots indicate, respectively, the 25th and 75th percentiles, while the central mark shows the distribution median. (A) Prediction accuracy distributions for 10 repetitions of tenfold cross validation. Communication models, SC, and FC were sorted based on their median prediction accuracy. (B) Effect size matrix of pairwise statistical comparisons between predictors. Warm- and cool-colored cells indicate predictor pairs with significantly different means, as assessed by a repeated-measures t test (Bonferroni-corrected for 136 multiple comparisons with significance threshold α = 3.67 × 10−4). A warm-colored i, j matrix entry indicates that predictor i yields significantly more accurate predictions than predictor j. (C) Prediction accuracy distributions of communication models averaged across connection weight definitions. SC and FC were not subjected to averaging and accuracies remain the same as in panel (A). (D) Effect size matrix of pairwise repeated-measures t tests between distributions in panel (C), with colored cells indicating significant differences in mean prediction accuracies (Bonferroni-corrected with significance threshold α = 0.0024). (E) Prediction accuracy distributions of connectomes with different connection weight definitions averaged across communication models. (F) Same as panel (D), but Bonferroni-corrected with significance threshold α = 0.0167. weight definitions for each communication model (Figures 3C, 3D), or averaged over the 15 models for each weight definition (Figures 3E, 3F). Prediction accuracies for FC and SC, which were not computed for multiple weight definitions, remained the same as shown in Figure 3A. With respect to the effect of communication model, we found that communicability signifi- cantly outperformed other models and SC (e.g., p = 3 × 10−5, 2 × 10−11 for comparisons of communicability to navigation and SC, respectively), although FC remained the leading pre- dictor. Navigation and shortest paths featured in second and third positions, both performing better than SC (p = 3 × 10−7, 3 × 10−5, respectively) and with no statistical difference be- tween them (p = 0.26). With respect to connection weight definition, binary connectomes yielded significantly higher prediction accuracies, on average, compared with weighted and distance connectomes (p = 0.009, 2 × 10−5, respectively), albeit with a weaker effect size than Network Neuroscience 987 Network communication models, behavior, and functional connectivity differences between communication models. This suggests that the choice of communica- tion model may be more important to behavior predictions than the definition of connection weights. To gain further insight into these results, we executed additional analyses in which we con- sidered predictions for the cognition and tobacco use dimensions separately (Supplementary Note 3; Supporting Information, Figures S5, S6). While these investigations reiterated the over- all good performance of navigation and communicability, they also revealed the presence of certain dimension-specific relationships between communication and behavior. For instance, search information yielded top- and bottom-ranking predictions for cognition and tobacco use, respectively. Finally, aiming to assess the robustness of our findings to the choice of prediction method, we analyzed behavioral predictions derived using a regression model applied to features iden- tified by the NBS. As with the lasso, we examined NBS predictions combined across the cogni- tion and tobacco use (Supporting Information, Figure S7), as well as for each of these dimension separately (Supporting Information, Figures S8, S9). As previously reported in Figure 2, NBS and lasso prediction accuracies were significantly correlated. FC remained the strongest predictor of behavior, although with a smaller margin of difference to navigation and communicability. Despite this overall agreement, we observed that SC yielded higher ranking predictions under the NBS method (5th highest ranking predictor) than the lasso (15th predictor). Interestingly, SC’s performance under the NBS diverged widely between the cognition (4th predictor) and tobacco use components (16th predictor), reiterating the dimension-specific character of brain- behavior relations observed in the lasso results. It is worth noting that the NBS feature selection process is better suited to sparse graphs (Zalesky et al., 2010), which could confer a predictive advantage to sparse SC matrices over fully connected communication and FC matrices. Taken together, the behavioral prediction analyses led to three key findings. First, behavioral predictions were more accurate when performed based on functional rather than structural attributes. Second, while navigation and communicability typically showed high predictive utility, our results did not point towards a single communication model as the best predictor of human behavior. This indicates that different communication models may be better suited to predict different behavioral dimensions, possibly suggesting the presence of behavior-specific signaling mechanisms in the human brain. Third, the transformation of SC (only direct con- nections) into communication matrices (models of polysynaptic interactions) typically led to an improvement of structural-based predictions, bringing them closer to the predictive utility of FC. Importantly, the magnitude of this improvement, as well as which and how many com- munication models conferred predictive benefits, varied depending on behavioral dimensions and prediction methods. Collectively, these findings indicate that connectome communication models capture higher order structural relations among brain regions that can better account for interindividual variation in behavior than SC alone. Communication Models Improve Structure-Function Coupling We next investigated whether accounting for network communication in the structural con- nectome can improve the strength of the relation between SC and FC, known as structure- function coupling. Classically, associations have been directly tested between structural and functional connections (Honey, Kötter, Breakspear, & Sporns, 2007). A growing body of work indicates that accounting for higher order regional interactions through models of polysynap- tic signaling (i.e., transforming structural connectomes into communication matrices) can im- prove structure-function coupling (Abdelnour, Voss, & Raj, 2014; Goñi et al., 2014; Miši´c et al., 2015; Seguin et al., 2019; Suárez et al., 2020). For two regions that are not directly Network Neuroscience 988 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 4 4 9 8 0 1 8 6 7 0 2 6 n e n _ a _ 0 0 1 6 1 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Network communication models, behavior, and functional connectivity connected with an anatomical fiber, strong FC is conjectured to indicate the presence of an efficient signaling path that facilitates communication through the underlying anatomical con- nections (Avena-Koenigsberger et al., 2018). To test this hypothesis, we computed the association between FC and communication ma- trices for each individual in our sample. Additionally, as benchmarks, we also considered the association of FC to SC and to interregional Euclidean distance. Associations were computed as the Spearman correlation between upper triangular matrix entries. In addition to individual- level associations, we also analyzed structure-function coupling derived from group-level SC and FC. Finally, associations were derived for coarse- (N = 68 regions) and fine-grained (N = 360 regions) connectomes, which were thresholded prior to the computation of com- munication models. FC matrices were not thresholded. Further details on the computation of structure-function coupling are provided in the Methods section. 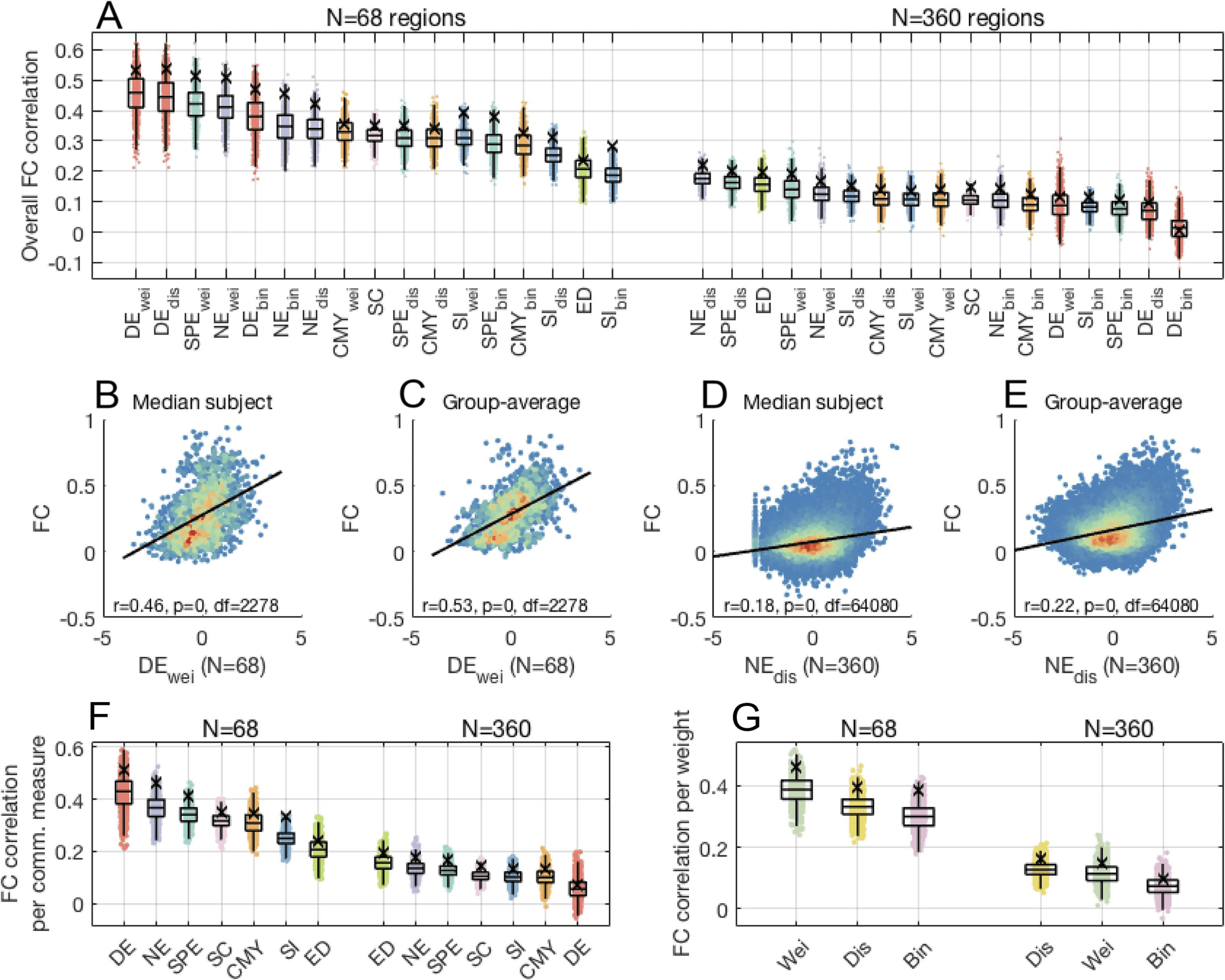As previously reported (Goñi et al., 2014), communication matrices were correlated with FC, irrespective of the particular communication model (Figure 4). In other words, FC was generally stronger between regional pairs interconnected by more efficient communication pathways. Group-level correlations (rG; black crosses) were universally stronger than those obtained for the median individual (rI; boxplots), supporting the notion that predicting population-level FC traits is less challenging than modeling idiosyncratic relationships between brain structure and function. We found that parcellation resolution had a strong influence on the strength of structure- function coupling. The link between structure and function weakened for high-resolution con- nectomes, irrespective of the communication model (Figure 4A). Moreover, the ranking of communication models in terms of structure-function coupling differed between connectome resolutions (Spearman rank correlation between low- and high-resolution FC predictions p = 0.65). For N = 68 regions, weighted and distance diffusion yielded the strongest structure- function couplings (rI = 0.46 and rG = 0.53 for weighted diffusion; Figures 4B, 4C). This recapitulates previous work indicating the functional predictive utility of random walk models applied to connectomes comprising less than 100 regions (Abdelnour et al., 2014). However, in sharp contrast, diffusion performed poorly for N = 360 regions, going from yielding the most accurate estimates of FC in low resolution to ranking as the worst overall predictor in high resolution. Conversely, the coupling between Euclidean distance and FC showed the op- posite relationship to connectome resolution, with interregional distances leading to weak and strong associations for coarse- and fine-grained parcellations, respectively. Navigation and shortest paths resulted in consistently high-ranked FC predictions regardless of connectome resolution. For N = 68 regions, weighted navigation and shortest paths showed comparable associations with the top-ranking diffusion models (e.g., rI = 0.42 for weighted shortest paths). For N = 360 regions, distance navigation was the top-ranking model (rI = 0.18 and rG = 0.22; Figures 4D, 4E), followed by distance shortest paths in second place, both outperforming the Euclidean distance benchmark in the third position. Crucially, despite the effects of connectome resolution, modeling polysynaptic communica- tion on top of structural connectomes tightened structure-function coupling. This was the case for 8 and 9 out of the 15 communication models considered, for low- and high-resolution connectomes, respectively. For instance, for the median individual, weighted diffusion in 68- region connectomes strengthened coupling by 46% compared with SC, while computing distance navigation in 360-region connectomes boosted FC predictions by 66% compared with SC. Network Neuroscience 989 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 4 4 9 8 0 1 8 6 7 0 2 6 n e n _ a _ 0 0 1 6 1 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Network communication models, behavior, and functional connectivity l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 4 4 9 8 0 1 8 6 7 0 2 6 n e n _ a _ 0 0 1 6 1 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 4. Structure-function coupling across connectome communication models (N = 68, 360 thresholded connectomes). (A) Data points show individual-level correlation of FC to communication, SC, and Euclidean distance matrices. Black crosses indicate correlations obtained for group-averaged matrices. Top and bottom edge boxplots indicate, respectively, the 25th and 75th percentiles, while the central mark shows the distribution median. Communication models, SC, and Euclidean distance were ranked according to the median structure-function coupling strength across individuals. (B) Scatterplot depicting the relationship between FC and the top-ranked communication model for connectomes comprising N = 68 regions, for the median individual. For ease of visualization, communication matrix entries were resampled to normal distributions. Warm and cool colors indicate high and low data point density, respectively. (C) Same as (B), but for group-average matrices. (D–E) Same as (B–C), but for connectomes comprising N = 360 regions. (F) Structure-function coupling for communication models, SC, and Euclidean distance, averaged across connection weight definitions. (G) Structure-function coupling obtained for binary, weighted, and distance connectomes, averaged across communication models. Grouping functional predictions by communication models reiterated differences between low- and high-resolution connectomes (Figure 4F). Grouping predictions by connection weight definitions showed that, on average, communication models computed on weighted and dis- tance connectomes led to stronger associations for coarse- and fine-grained parcellations, Network Neuroscience 990 Network communication models, behavior, and functional connectivity respectively (Figure 4G), suggesting that the established influence of interregional distance in SC and FC (Alexander-Bloch et al., 2013; Roberts et al., 2016) may be stronger for connec- tomes derived at finer levels of areal granularity. In summary, we observed that structure-function coupling is affected by connectome resolu- tion and by whether associations are computed on individual or population levels. Regardless of parcellation granularity, most connectome communication models contributed to strength- ening structure-function coupling. Moreover, navigation and shortest paths yielded the most accurate and reliable predictions of FC. While here we focused on thresholded connectomes, similar results were observed for unthresholded networks (Supporting Information, Figure S10). Rankings of functional predictive utility also remained consistent when stratifying analyses be- tween structurally connected and unconnected region pairs, as well as for intrahemispheric structure-function associations (Supplementary Note 4; Supporting Information, Figure S11). Together, these observations build on the behavioral prediction findings, further supporting the notion that connectome communication models contribute to bridging the gap between brain structure and function. Ranking Communication Models Finally, we derived a combined ranking of predictive utility, as the average of behavioral and functional prediction rankings, for the 15 communication models explored and SC (Figure 5). This was performed for the four connectome mapping pipelines explored in our analyses. Behavioral and functional results were given equal weight in the combined rankings. For N = 360 thresholded connectomes, the only case in which behavioral analyses were carried out using both lasso and NBS prediction methods, a weighted average assigning 0.25 weight to lasso behavioral rankings, 0.25 weight to NBS behavioral rankings, and 0.5 weight to structure- function coupling rankings was applied. For N = 360 thresholded connectomes, we found that distance navigation showed the highest combined predictive utility (average ranking τ = 3.7; Figure 5A), followed by a tie between distance shortest paths and weighted communicability (τ = 4.7). SC featured in the 11th position (τ = 8.7) and was outranked by most navigation, communicability, shortest paths, and search information models. Contrasting combined rankings across connectome mapping pipelines led to several inter- esting observations. First, N = 360 thresholded and unthresholded connectomes led to the only pair of significantly correlated overall rankings (Spearman rank correlation r(15) = 0.65, p = 0.007). This corroborates our previous findings that parcellation choice and connection density influence the predictive utility of network communication models. Second, network communication models were more beneficial when computed on high-resolution and thresh- olded connectomes. Intuitively, a densely connected network requires few polysynaptic sig- naling paths, since most regions can communicate via direct connections. This renders the transformation of SC into communication matrices less relevant, and therefore less advan- tageous for predictions. Third, combined rankings did not provide a clear picture on what connection weight definition may be more relevant for behavioral and functional predictions (Figures 5C, 5F, 5I, 5L). Fourth, for all connectome mapping pipelines, we found certain com- munication models that improved the predictive utility of the human connectome. In the case of unthresholded N = 68 connectomes, the scenario in which communication models provide the least benefits, we still observed that weighted navigation, shortest paths, and communica- bility outranked SC. Fifth, navigation was the top-ranking model across all connectome map- ping pipelines. This was the case when considering overall rankings (Figures 5A, 5D, 5G, 5J) as well as rankings grouped by communication models (Figures 5B, 5E, 5H, 5K). Weighted Network Neuroscience 991 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 4 4 9 8 0 1 8 6 7 0 2 6 n e n _ a _ 0 0 1 6 1 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Network communication models, behavior, and functional connectivity l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 4 4 9 8 0 1 8 6 7 0 2 6 n e n _ a _ 0 0 1 6 1 p d t . Figure 5. Rankings of communication models combining behavioral and functional predictions. Overall, communication, and weight def- inition rankings for (A–C) N = 360 thresholded, (D–F) N = 360 unthresholded, (G–I) N = 68 thresholded, and (J–L) N = 68 unthresholded connectomes. . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 navigation outranked SC in all explored scenarios, and excluding unthresholded N = 68 con- nectomes, navigation outranked SC regardless of connection weight definitions. Collectively, these results indicate that despite differences across connectome mapping pipelines, certain network communication models improved the combined behavioral and functional predictive utility of the human connectome. In particular, navigation was consis- tently positioned as the highest ranking model, indicating that the transforming of SC into nav- igation communication matrices is reliably advantageous for predictions of human behavior and FC. DISCUSSION Human cognition and behavior arise from the orchestrated activity of multiple brain regions (Friston, 2002; Laughlin & Sejnowski, 2003). Resting-state FC is currently one of the most Network Neuroscience 992 Network communication models, behavior, and functional connectivity widely used neuroimaging measures to quantify this concerted activity (Cole, Ito, Bassett, & Schultz, 2016; Sripada et al., 2019; Yeo et al., 2011). It is thus unsurprising that statistical methods trained on functional brain networks led to the most accurate predictions of human behavior. Importantly, the signaling processes that facilitate synchronous interregional activity must unfold along structural connections forming direct or indirect (polysynaptic) communi- cation paths. Therefore, brain structure, brain function, neural communication, and human behavior are tightly intertwined. This is corroborated by the key conclusion of the present study: Accounting for polysynaptic communication in SC matrices can substantially improve structure-function coupling and the predictive utility of SC. While accounting for communi- cation did not lead to SC outperforming FC with respect to behavior prediction, it narrowed the gap between the predictive utility of the two connectivity modalities. As investigators tackle the long-standing challenge of elucidating the relationship between brain structure and function (Amico & Goñi, 2018; Damoiseaux & Greicius, 2009; Park & Friston, 2013), it has become increasingly clear that FC arises from high-order regional in- teractions that cannot be explained by direct anatomical connections (Suárez et al., 2020). In line with this notion, we found that taking polysynaptic signaling into account through network communication models strengthened structure-function coupling. This observation recapitulates earlier reports on the functional predictive utility of connectome communication models (Goñi et al., 2014) and provides support to the notion that FC is facilitated by com- munication pathways in the underlying structural connectome. Taken together, the behavioral and functional prediction analyses contribute empirical evidence that connectome communi- cation models act as a bridge between structural and functional conceptualizations of brain networks (Avena-Koenigsberger et al., 2018; Miši´c, Goñi, Betzel, Sporns, & McIntosh, 2014). Importantly, brain structure-function relationships encompass a rich and diverse field of re- search, with several alternative classes of higher order models showing promise in modeling function from structure. Examples include biophysical models of neural activity (Breakspear, 2017; Deco, Kringelbach, Jirsa, & Ritter, 2017; Sokolov et al., 2018), statistical methods (Messé, Rudrauf, Benali, & Marrelec, 2014; Miši´c et al., 2016), and other approaches centered around network communication that we did not explore in the present work (Kuceyeski, Jamison, Owen, Raj, & Mukherjee, 2019; Miši´c et al., 2015; Osmanlo˘glu et al., 2019; Raj, Kuceyeski, & Weiner, 2012; Vázquez-Rodríguez, Liu, Hagmann, & Miši´c, 2020). Likewise, relating neu- roimaging data to behavior is a central goal of neuroscience (Medaglia, Lynall, & Bassett, 2015; Miši´c & Sporns, 2016). Recent studies have explored neural correlates of behavior and cogni- tion by leveraging graph measures of brain organization (Bertolero, Yeo, Bassett, & D’Esposito, 2018; van den Heuvel, Stam, Kahn, & Hulshoff Pol, 2009), dynamic patterns of FC fluctu- ations (Liégeois et al., 2019; Pedersen, Zalesky, Omidvarnia, & Jackson, 2018), multivariate correlation methods (Perry et al., 2017; Smith et al., 2015), and machine learning techniques (He et al., 2020; Li et al., 2019). Our analyses sought to complement these efforts from the perspective of connectome communication. We reiterate that the goal of this paper was not to show that network communication models lead to more accurate predictions than alternative approaches, nor that our prediction scheme and statistical methods are superior to previously adopted techniques. Rather, we were inter- ested in comparing the predictive utility of candidate models of connectome communication, as well as connectivity and distance benchmarks, in a controlled and internally consistent man- ner. Similarly, although we explored multiple brain network reconstruction pipelines, we were not primarily concerned with which mapping techniques produced connectomes with the highest predictive utility. The choice of parcellation schemes (Eickhoff, Yeo, & Genon, 2018) Network Neuroscience 993 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 4 4 9 8 0 1 8 6 7 0 2 6 n e n _ a _ 0 0 1 6 1 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Network communication models, behavior, and functional connectivity and whether to threshold structural connectomes (Buchanan et al., 2020; Civier, Smith, Yeh, Connelly, & Calamante, 2019) are both challenging open questions that fall outside the scope of this work. Comparisons Between Connectome Communication Models Communication matrices computed with the navigation and communicability models typically led to the highest ranking behavioral predictions among the candidate signaling strategies ex- plored. It is important to notice, however, that search information, shortest paths, and SC also performed well in certain scenarios. Therefore, while our behavioral results suggested the ben- efits of modeling polysynaptic signaling, they did not provide a clear answer to the question of which communication models are most associated with human behavioral dimensions. Al- ternatively, our findings may indicate the interesting possibility that large-scale information integration in the brain is not facilitated by a unique signaling mechanism, and that different communication models may find more utility in describing varied behavioral and cognitive processes. Navigation and shortest paths led to the most reliable FC predictions, featuring as the best models for high-resolution connectomes and closely following behind diffusion for low- resolution connectomes. Navigation and shortest paths computed on distance connectomes led to FC predictions that surpassed those obtained from Euclidean distance, which exerts a well-documented influence on both SC and FC (Alexander-Bloch et al., 2013; Roberts et al., 2016; Vértes et al., 2012). Furthermore, given the high efficiency of communication along navigation and shortest paths, these findings suggest that FC is facilitated primarily by effi- cient signaling pathways. This observation stands in contrast with previous work on the strong functional relevance of models that incorporate deviations from optimal routes, such as search information (Betzel et al., 2019; Goñi et al., 2014) and communicability (Osmanlo˘glu et al., 2019), underscoring the importance of further research on the validation of network commu- nication models. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 4 4 9 8 0 1 8 6 7 0 2 6 n e n _ a _ 0 0 1 6 1 p d . t We evaluated network communication models across a wide range of methodological sce- narios, including different gray matter parcellations, connection density thresholds, statisti- cal learning methods, and behavioral dimensions. While our results were stable for certain combinations of these factors, we found that the predictive utility of communication models substantially varied between some scenarios. This variability makes it difficult to draw strong conclusions about the extent to which different models are useful to understanding biological neural signaling patterns. Nonetheless, combining behavioral and functional prediction rank- ings consistently positioned navigation as the top-ranking model across connectome mapping pipelines. These findings contribute to the growing body of work supporting the neuroscien- tific utility of network navigation (Allard & Serrano, 2020; Pappas, Craig, Menon, & Stamatakis, 2020; Seguin et al., 2018; Wang et al., 2019) and highlight the potential of this signaling strat- egy as a model of information transfer in nervous systems. f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 In addition to investigating putative neural signaling strategies, we also considered different connection weight definitions. Polysynaptic transmission of neural signals entails metabolic expenditures related to the propagation of action potential along axonal projections and the crossing of synaptic junctions. Communication in the brain is thought to be metabolically fru- gal (Bullmore & Sporns, 2012; Laughlin & Sejnowski, 2003), but what aspects of structural connectivity are relevant to energy consumption in large-scale signaling remain unclear. We found that weighted and distance connectomes typically led to communication matrices with Network Neuroscience 994 Network communication models, behavior, and functional connectivity higher predictive utility. This is initial evidence that neural signaling may favor communication paths prioritizing the adoption of physically short and high-volume connections, instead of paths that reduce the number of synaptic crossings between regions. Additionally, these obser- vations warrant further investigation of the relatively unexplored distance connectome (Stiso & Bassett, 2018). Previous evidence that connection thresholding is an unnecessary step in brain network analyses is primarily based on studies considering weighted connectomes (Civier et al., 2019), for which interregional connectivity strength is determined as a function of streamline counts or fractional anisotropy (Sotiropoulos & Zalesky, 2019). Along these lines, we found that connec- tomes weighted by streamline counts led to the best performing predictors when considering unthresholded brain networks. However, we note that two thirds of the communication models explored in our analyses were based on binary and distance connectomes, which do not con- tain information on streamline counts. Therefore, it is expected that connection thresholding would impact the overall rankings of communication models. In accordance with previous reports (Messé, 2020; Messé, Rudrauf, Giron, & Marrelec, 2015), we observed that FC predictions were more accurate for low- rather than high-resolution connectomes, as well as for group- rather than individual-level analyses. This is not surpris- ing since the number of functional connections grows quadratically with the number of re- gions and capturing idiosyncrasies in FC is more challenging than modeling general principles of connectivity. Despite their simplicity, these observations are important to the validation of FC prediction methods, suggesting that models constructed and evaluated on coarse and population-level networks may not generalize to more challenging settings. Limitations and Future Directions Several methodological limitations of the present work should be discussed. First, given the sensitivity of model rankings to some aspects of connectome mapping pipelines, further work exploring alternative brain network reconstruction methods is necessary. For instance, vali- dation of our results for connectomes mapped using probabilistic tractography and/or larger numbers of streamline seeds would be valuable. We also note that white matter tractogra- phy algorithms are susceptible to a number of known biases that could potentially impact our findings (Maier-Hein et al., 2017). A conceptual limitation of our behavioral analyses was that model selection was performed on the same data used to evaluate the accuracy of single models (out-of-sample test set). In addition, we note that behavioral prediction accuracy estimates from different cross-validation folds are not independent from each other. This is a limitation of the statistical tests performed to compare the utility of communication models. Once again, these observations underscore the need for additional efforts to evaluate network communication models using alternative datasets and machine learning methods. Another interesting future research direction is to investigate the contributions of specific brain regions to the predictive utility of different communication models. This could be achieved by examining lasso regression weights and NBS connected components. Alternatively, behav- ior and functional predictions could be performed based on region-wise communication ef- ficiencies, rather than complete communication matrices (Vázquez-Rodríguez et al., 2019). Efforts in these directions could help elucidate how different communication models utilize features of connectome topology to facilitate information transfer. Network Neuroscience 995 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 4 4 9 8 0 1 8 6 7 0 2 6 n e n _ a _ 0 0 1 6 1 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Network communication models, behavior, and functional connectivity While we sought to evaluate a wide range of communication models, alternative network propagation strategies could provide valuable insight into mechanisms of neural signaling and warrant further research. These include linear transmission models (Miši´c et al., 2015), biased random walks (Avena-Koenigsberger et al., 2019), cooperative learning (Tipnis, Amico, Ventresca, & Goñi, 2018), dynamic communication models (Gilson et al., 2019), and information-theoretic approaches (Amico et al., 2019). In conclusion, we demonstrated that taking into account polysynaptic signaling via models of network communication can improve the behavioral and functional predictive utility of the human structural connectome. This work contributes to our understanding of which network communication strategies may be more useful as large-scale neural signaling models, providing novel insights to researchers interested in characterizing information processing in nervous systems. METHODS Structural Connectivity Data Minimally preprocessed high-resolution diffusion-weighted magnetic resonance imaging (MRI) data were obtained from the Human Connectome Project (HCP; Van Essen et al., 2013). De- tails about the acquisition and preprocessing of diffusion MRI data are found in Glasser et al. (2013); Sotiropoulos et al. (2013). Analyses were restricted to participants with complete HCP 3T imaging protocol, yielding a total sample of 889 healthy adults (age 22–35, 52.8% females). Whole-brain structural connectomes were mapped using diffusion tensor imaging and a deter- ministic white matter tractography pipeline implemented using MRtrix3 (Tournier, Calamante, & Connelly, 2012; FACT tracking algorithm, 5 × 106 streamlines, 0.5-mm tracking step-size, 400-mm maximum streamline length, and 0.1 fractional anisotropy cutoff for termination of tracks). Deterministic tractography is less prone to false positive than alternative reconstruction approaches (Maier-Hein et al., 2017; Sarwar, Ramamohanarao, & Zalesky, 2019), which leads to connectomes that may be better suited for network and graph-theoretical analyses (Zalesky et al., 2016). The connection weight between a pair of regions was defined as the total number of streamlines connecting them, resulting in an N × N weighted connectivity matrix for each participant. Group-level structural connectomes were computed by averaging the connectivity matrices of all subjects. We used cortical parcellations containing N = 68, 360 regions. The 68-region parcellation consists of the anatomically delineated cortical areas of the Desikan-Killiany atlas (Desikan et al., 2006). The 360-region parcellation is a multimodal atlas constructed from high-resolution structural and functional data from the HCP (Glasser et al., 2016). We also considered thresh- olded and unthresholded connectomes. Following connection density thresholding, only the top 15% and 20% strongest connections (in terms of streamline counts) were kept in con- nectomes comprising 360 and 68 regions, respectively. Connection density thresholds were chosen as the (approximate) lowest values that resulted in nonfragmented brain networks for all subjects in our sample. Unthresholded connectomes maintained all connections identified in the structural connectivity reconstruction process. Connection Weight and Length Definitions A structural connectome can be defined in terms of a N × N adjacency matrix of connectivity weights (W) or lengths (L). Connection weights provide a measure of the strength and relia- bility of anatomical connections between region pairs, while connection lengths quantify the Network Neuroscience 996 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 4 4 9 8 0 1 8 6 7 0 2 6 n e n _ a _ 0 0 1 6 1 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Network communication models, behavior, and functional connectivity distance or travel cost between region pairs. Different network communication measures are computed based on W (e.g., diffusion efficiency and communicability), L (e.g., shortest path efficiency and navigation efficiency), or a combination of both (e.g., search information). We considered three definitions of W: weighted, binary, and distance. In the weighted case, Wwei(i, j) was defined as the total number of streamlines with one endpoint in region i and the other in region j. The binary adjacency matrix was defined as Wbin(i, j) = 1 if Wwei(i, j) > 0 and Wbin(i, j) = 0 de lo contrario. Distance-based connectivity was defined as
Wdis(i, j) = 1/D(i, j) if Wwei(i, j) > 0 and Wdis(i, j) = 0 de lo contrario, where D is the Euclidean
distance matrix between region centroids.

Similarmente, L was also defined in terms of binary, weighted, and distance connection lengths.
In all three cases, l(i, j) = ∞ for ij region pairs that do not share a direct anatomical connec-
ción, ensuring that communication is restricted to unfold through the connectome. Binary (Lbin)
and distance-based (Ldis) connection lengths are straightforwardly defined from their weighted
counterparts as Lbin(i, j) = 1 if Wbin(i, j) = 1 and Lbin(i, j) = ∞ otherwise, and Ldis(i, j) =
D(i, j) if Wdis(i, j) > 0 and Ldis(i, j) = ∞ otherwise. Lengths based on the streamline count be-
tween region pairs were computed by monotonic weight-to-length transformations that remap
large connection weights into short connection lengths. This way, white matter tracts conjec-
tured to have high caliber and integrity are considered to be faster channels of communication
than weak and unreliable ones. We considered a logarithmic weight-to-length remapping such
that Lwei = −log10(Wwei/max(Wwei) + 1) (the unity addition to the denominator avoids the
remapping of the maximum weight into zero length; Seguin et al., 2018), producing normally
distributed lengths that attenuate the importance of extreme weights (Avena-Koenigsberger
et al., 2016; Rubinov, ypma, watson, & bullmore, 2015).

Network Communication Models

En esta sección, we provide details regarding the definition of the five network communication
models evaluated in this study. All computations were carried out using freely available code
provided in the Brain Connectivity Toolbox (https://sites.google.com/site/bctnet/; Rubinov &
despreciar, 2010).

Primero, we note a subtle but important distinction between network communication mod-
els and measures. A network communication model (p.ej., shortest path routing) provides a
strategy or algorithm to transfer information between node pairs. Sucesivamente, a network communi-
cation measure (p.ej., shortest path efficiency) quantifies, from a graph-theoretical standpoint,
the efficiency of information transfer achieved by a given communication model. For simplic-
idad, we used “model” throughout this paper to refer to both network communication models
and measures.

We also note that certain communication measures are inherently asymmetric, in that
Casy(i, j) 6= Casy(j, i). While this asymmetry contains meaningful information on signaling
properties of nervous systems (Seguin et al., 2019), in the present study we consider symmet-
ric communication matrices given by C(i, j) = (Casy(i, j) + Casy(j, i))/2. This simplification
allows us to take into account only the upper triangle of C, substantially reducing the dimen-
sionality of our predictive models and contributing to the computational tractability of our
analiza.

Shortest path routing proposes that neural signaling takes place along
Shortest path efficiency.
optimally efficient paths that minimize the sum of connection lengths traversed between nodes.

Neurociencia en red

997

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

/

t

/

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

4
4
9
8
0
1
8
6
7
0
2
6
norte
mi
norte
_
a
_
0
0
1
6
1
pag
d

.

t

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Network communication models, comportamiento, and functional connectivity

Let Λ∗ ∈ RN×N denote the matrix of shortest path lengths, where Λ∗(i, j) = L(i, tu) + . . . +
l(v, j) y {tu, . . . , v} is the sequence of nodes visited along the shortest path between nodes
i and j. Shortest path efficiency was defined as SPE = 1/Λ∗ (latora & marchiori, 2001). Nosotros
computed binary (SPEbin), weighted (SPEwei), and distance (SPEdis) shortest path efficiency
matrices based on Lbin, Lwei, Ldis connection length matrices, respectivamente.

Navigation efficiency. Navigation routing identifies communication paths by greedily propa-
gating information based on a measure of node (dis)semejanza (Boguña et al., 2009). Following
previous studies on brain network communication, we used the Euclidean distance between
region centroids to guide navigation (Seguin et al., 2019; Seguin et al., 2018). Navigating from
node i to node j involves progressing to i’s neighbor that is closest in distance to j. este profesional-
cess is repeated until j is reached (successful navigation) or a node is revisited (failed naviga-
ción). Successful navigation path lengths are defined as Λ(i, j) = L(i, tu) + . . . + l(v, j), dónde
{tu, . . . , v} is the sequence of nodes visited during the navigation from i to j. Failure to navigate
from i to j yields Λ(i, j) = ∞. Navigation efficiency was defined as NE = 1/Λ. Binary (NEbin),
weighted (NEwei), and distance (NEdis) navigation efficiency matrices were computed based
on Lbin, Lwei, Ldis, respectivamente.

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

Diffusion efficiency. Diffusion efficiency models neural signaling in terms of random walks.
Let T ∈ RN×N denote the transition matrix of a Markov chain process unfolding on the con-
nection weight matrix W. The probability that a naive random walker at node i will progress to
node j is given by T(i, j) = W(i, j)/ ∑N
u=1 W(i, tu). The mean first passage time H(i, j) quanti-
fies the expected number of intermediate regions visited in a random walk from i to j (details
on the mathematical derivation of H from T are given in Fornito et al., 2016; Goñi et al., 2013;
zhou, 2003). Diffusion efficiency is defined as DE = 1/H, thus capturing the efficiency of neu-
ral communication under a diffusive propagation strategy (Goñi et al., 2013). Binary (DEbin),
weighted (DEwei), and distance (DEdis) diffusion efficiency matrices were computed based on
Wbin, Wwei, Wdis, respectivamente.

/

/

t

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

4
4
9
8
0
1
8
6
7
0
2
6
norte
mi
norte
_
a
_
0
0
1
6
1
pag
d

t

.

Search information is derived from the probability of random walkers
Search information.
serendipitously traveling along the shortest paths between node pairs (Rosvall et al., 2005). Dejar
Ω(i, j) = {tu, . . . , v} be the sequence of nodes along the shortest path from node i to node j
computed from the connection length matrix L. The probability that a random walker starting
from i reaches j via Ω(i, j) is given by P(Ω(i, j)) = T(i, tu) × . . . × T(v, j), where T is the previ-
ously defined transition probability matrix computed from W. We defined search information
as SI(i, j) = log2(PAG(Ω(i, j))) (Goñi et al., 2014; Seguin et al., 2019). This definition quanti-
fies how accessible shortest paths are to naive random walkers, capturing the degree to which
efficient routes are hidden in network topology. Note that the computation of search informa-
tion depends on both L—for the identification of shortest paths—and W—for the simulation
of random walks. We used Wwei combined with Lbin, Lwei, and Ldis to compute, respectivamente,
binario, weighted, and distance versions of search information.

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Communicability models neural signaling as a diffusive process unfolding
Communicability.
simultaneously along all possible walks in a network (Estrada & Hatano, 2008). comunal-
cability between nodes i and j is defined as the weighted sum of the total number of walks
between them, with each walk weighted by its length (es decir., number of connections traversed).
In the binary case, this yields CMY(i, j) = ∑∞
n=0 Wbin(i, j)n/n!. In the limit n → ∞, este
sum converges to CMY(i, j) = eWbin(i,j). Nonbinary connection weight matrices are typically

Neurociencia en red

998

Network communication models, comportamiento, and functional connectivity

normalized as W′
wei(i, j) = Wwei(i, j)/(ps(i)pag(s(j))) prior to the computation of commu-
nicability to attenuate the influence of high strength nodes (Crofts & Higham, 2009), dónde
s(i) = ∑N
dis to compute,
respectivamente, binario, weighted, and distance versions of communicability.

u=1 Wwei(i, tu) is the total strength of node i. We used Wbin, W′

wei, and W′

Functional Connectivity Data

Minimally preprocessed resting-state functional MRI data from the same 889 individuals was
also obtained from the HCP. Participants were scanned twice (right-to-left and left-to-right
phase encodings) on two separate days, resulting in a total of four sessions per individual. En
each session, functional MRI data were acquired for a period of 14 mín. 33 s with 720 ms TR.
(Further details on resting-state functional MRI data collection and preprocessing are described
in Glasser et al., 2013; Smith et al., 2013). Functional activity in each of N = 68, 360 regiones
was computed by averaging the signal of all vertices comprised in the region. Pairwise Pearson
correlation matrices were computed from the regional time series of each session, Resultando en
four matrices per participant. Para cada participante, the four matrices were averaged to yield a
final N × N FC matrix. Group-level functional connectomes were computed by averaging the
FC matrices of all subjects.

Behavioral Dimensions

Information on HCP behavioral protocols and procedures is described elsewhere (Barch et al.,
2013). Un total de 109 variables measuring alertness, cognition, emotion, sensory-motor func-
ción, personality, psychiatric symptoms, substance use, and life function were selected from the
HCP behavioral dataset (Tian et al., 2020). Selected items consisted of raw (edad- y género-
unadjusted), total, or subtotal assessment scores. The set of 109 measures was submitted to an
independent component analysis (ICA) pipeline in order to derive latent variables summarizing
orthogonal dimensions of behavioral information. This procedure contributed to the computa-
tional tractability of our analyses by enabling behavioral inferences to be performed on a small
set of data-driven components, rather than being restricted to arbitrarily selected measures.

Behavioral dimensions were computed as follows. A rank-based inverse Gaussian transfor-
formación (Van der Waerden, 1953) was used to normalize continuous behavioral variables (87 de
109). Age and gender were regressed out from all behavioral items. ICA was performed on the
resulting residuals using the FastICA algorithm (Hyvärinen, 1999) implemented in the icasso
MATLAB package (Himberg, Hyvärinen, & Esposito, 2004). Participants were sampled with
replacement to generate a total of 500 bootstrap samples. ICA was independently performed
on each sample with randomly selected initial conditions. Agglomerative clustering with aver-
age linkage was used to derive consensus clusters of independent components across different
bootstrap samples and initial conditions. This procedure, including bootstrapping and ran-
domization of initial conditions, was repeated for 10 trials of a set of candidate ICA models
que van desde 3 a 30 independent components. The best number of components was estimated
based on the reproducibility across the 10 trials by means of a cluster quality index. Claramente
separated clusters indicate independent components were consistently and reliably estimated,
despite being computed based on different bootstrap samples and initial conditions. This cri-
terion identified the five-component model as the most robust and parsimonious set of latent
dimensions. This enabled the characterization of the five dimensions as cognitive performance,
illicit substance use, tobacco use, personality and emotion traits, and mental health. Más
details on the computation of the behavioral dimensions are provided in Tian et al. (2020).

Neurociencia en red

999

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

/

/

t

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

4
4
9
8
0
1
8
6
7
0
2
6
norte
mi
norte
_
a
_
0
0
1
6
1
pag
d

.

t

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Network communication models, comportamiento, and functional connectivity

Behavioral Prediction Framework
Let y ∈ Rn×1 be a vector of response variables corresponding to a given behavioral dimen-
sión, where n = 899 is the number of individuals in our sample. Let X ∈ Rn×p be a matrix
of p explanatory variables corresponding to the upper triangle of vectorized communication
matrices C ∈ RN×N, so that p = N(N − 1)/2. We applied two independent statistical mod-
els to predict y from X: lasso regression and a regression model based on network features
identified by the NBS. These models implement different strategies of feature selection aimed
at identifying a parsimonious set of variables in X to predict y.

The data were split into train and test sets to perform tenfold cross validation. The family
structured in the HCP dataset was taken into account by ensuring that individuals of the same
family were not separated between train and test sets (Le et al., 2019). Sensitivity to particular
train-test data splits was addressed by repeating the tenfold cross validation 10 veces. The same
train and test sets were used for lasso and NBS regressions. Model parameter estimation was
performed exclusively on train sets, while model performance was assessed exclusively on test
conjuntos.

Lasso regression.
respectivamente. We used lasso regression (Tibshirani, 1996) to compute β as

Dejar {Xa, ya} y {Xe, ye} denote a split of {X, y} into train and test sets,

mín.
β∈R p

{

1
norte

||ya − Xaβ||2

2 + λ||b||1},

dónde 0 ≤ λ ≤ 1 is a feature selection hyperparameter controlling model complexity. Para
each outer training set Xa, a nested tenfold cross validation was carried out to tune λ. Este
was performed using the MATLAB function cvglmnet (Qian, Hastie, Friedman, Tibshirani, &
Simón, 2013). For each inner training fold, solutions were computed for a decreasing sequence
of K logarithmically spaced hyperparameters from λmax to λmin, where λmax was the smallest
λ such that ||βinner||1 = 0 and λmin = ǫλmax. Values of K and ǫ were separately determined
for each inner fold by the algorithm, with typical values around K = 100 and ǫ = 0.01 (further
details are described in Friedman, Hastie, & Tibshirani, 2010). The obtained K models were
then evaluated on the inner test folds. The λ resulting in the highest accuracy averaged across
inner test folds was selected and used to compute β for the outer training set Xa. Model fit for
each outer fold was evaluated as the Pearson correlation coefficient between ˆye and ye, dónde
ˆye = Xeβ. This procedure was repeated for 100 pairs of outer train and test tests (10 repetitions
of tenfold splits).

The NBS identifies sets of connected components in a net-
Network-based statistics regression.
work that explain significant variation in a response variable (Zalesky et al., 2010). We used the
NBS as a feature selection technique to identify behaviorally relevant groups of connections.
We then fit a regression model to the average connection weight of the selected connections
in order to predict behavior. En tono rimbombante, connected components were identified exclusively
in training sets, while prediction accuracy was computed based on held-out test sets.

Dejar {Xa, ya} y {Xe, ye} denote a split of {X, y} into train and test sets, respectivamente. El
cross-validated predictive utility of NBS connected components was computed as follows.
For each column of Xa (corresponding to the value of a connection in the upper triangle of
a communication matrix C(i, j) across subjects in the train set), the interindividual Pearson
correlation between C(i, j) and ya was computed. Connections for which statistical association

Neurociencia en red

1000

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

t

/

/

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

4
4
9
8
0
1
8
6
7
0
2
6
norte
mi
norte
_
a
_
0
0
1
6
1
pag
d

.

t

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Network communication models, comportamiento, and functional connectivity

strength exceeded a t statistic threshold t > |3| were grouped into sets of positive (t > 3) y
negative (t < −3) connected components. This procedure was repeated for 1,000 random per- mutations of ya, and the likelihood of observing positive and negative connected components as large as empirical ones was assessed using a nonparametric test. Further details on the NBS are found in Zalesky et al. (2010). Let Γ+ and Γ− be, respectively, the largest positive and negative connected components ∈ R|ya|×1 as the identified by the NBS based on the train data {Xa, ya}. We computed g+,− average weight of connections belonging to the connected component Γ+,−: a g+,− a = 1 |Γ+,−| ∑ u∈Γ+,− Xa(., u), where |Γ+,−| indicates the number of connections comprising the connected component. a ]. Therefore, Ga ∈ R|ya|×2 contains the average weight of We defined the matrix Ga = [g+ connections identified as positively and negatively associated with the behavioral dimension y for subjects in the train set {Xa, ya}. Using a bivariate linear regression model, we computed the coefficients β such that a |g− { min β∈R2 1 n ||ya − Gaβ||2 2}. Analogously, we computed the average weight of connected components in the test set g+,− e = 1 |Γ+,−| ∑ u∈Γ+,− Xe(., u) e |g− and Ge = [g+ e ]. Finally, behavioral predictions were computed as ˆye = Geβ, and out-of- sample prediction accuracy was evaluated as the Pearson correlation coefficient between ˆye and ye. This procedure was repeated for 100 pairs of train and test sets (10 repetitions of tenfold splits). In cases where no significant component was identified by the NBS (|Γ+,−| = 0), model performance was set to 0. Functional Connectivity Prediction Framework FC predictions were computed as the Spearman correlation between empirical FC and ana- lytically derived communication matrices. None of the network communication models and measures used to infer FC required training, statistical estimation of weights, or parameter tun- ing (an advantage over other classes of high-order models). Hence, we oftentimes adopted the term FC “prediction” even though predictive utility was not assessed out of sample (Goñi et al., 2014). ACKNOWLEDGMENT We thank Olaf Sporns for valuable discussions. Human data were provided by the Human Connectome Project, WUMinn Consortium (1U54MH091657; principal investigators: David Van Essen and Kamil Ugurbil) funded by the 16 National Institutes of Health (NIH) institutes and centers that support the NIH Blueprint for Neuroscience Research; and by the McDonnell Center for Systems Neuroscience at Washington University. SUPPORTING INFORMATION Supporting information for this article is available at https://doi.org/10.1162/netn_a_00161. Network Neuroscience 1001 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 4 4 9 8 0 1 8 6 7 0 2 6 n e n _ a _ 0 0 1 6 1 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Network communication models, behavior, and functional connectivity AUTHOR CONTRIBUTIONS Caio Seguin: Conceptualization; Data curation; Formal analysis; Methodology; Visualization; Writing – original draft; Writing – review & editing. Ye Tian: Data curation; Formal analysis; Methodology; Writing – original draft. Andrew Zalesky: Conceptualization; Formal analysis; Methodology; Writing – original draft; Writing – review & editing. FUNDING INFORMATION Caio Seguin, Melbourne Research Scholarship, University of Melbourne (http://dx.doi.org/10 .13039/501100000987). Andrew Zalesky, National Health and Medical Research Council (AU), Award ID: 1136649. REFERENCES Abdelnour, F., Voss, H. U., & Raj, A. (2014). Network diffusion accu- rately models the relationship between structural and func- tional brain connectivity networks. NeuroImage, 90, 335–347. DOI: https://doi.org/10.1016/j.neuroimage.2013.12.039, PMID: 24384152, PMCID: PMC3951650 Alexander-Bloch, A. F., Vértes, P. E., Stidd, R., Lalonde, F., Clasen, L., Rapoport, J., . . . Gogtay, N. (2013). The anatomical dis- tance of functional connections predicts brain network topology in health and schizophrenia. Cerebral Cortex, 23(1), 127–138. DOI: https://doi.org/10.1093/cercor/bhr388, PMID: 22275481, PMCID: PMC3513955 Allard, A., & Serrano, M. Á. (2020). Navigable maps of structural brain networks across species. PLoS Computational Biology, 16(2), e1007584. DOI: https://doi.org/10.1371/journal.pcbi.1007584, PMID: 32012151, PMCID: PMC7018228 Amico, E., Abbas, K., Duong-Tran, D. A., Tipnis, U., Rajapandian, (2019). Towards a mathemat- theory of communication for the human connectome. M., Chumin, E., . . . Goñi, J. ical arXiv:1911.02601 Amico, E., & Goñi, J. (2018). Mapping hybrid functional-structural connectivity traits in the human connectome. Network Neu- roscience, 2(3), 306–322. DOI: https://doi.org/10.1162/netn_a _00049, PMID: 30259007, PMCID: PMC6145853 Andreotti, J., Jann, K., Melie-Garcia, L., Giezendanner, S., Abela, E., Wiest, R., . . . Federspiel, A. (2014). Validation of net- work communicability metrics for the analysis of brain struc- tural networks. PLoS ONE, 9(12), e115503. DOI: https://doi.org /10.1371/journal.pone.0115503, PMID: 25549088, PMCID: PMC4280193 Avena-Koenigsberger, A., Miši´c, B., Hawkins, R. X., Griffa, A., Hagmann, P., Goñi, J., & Sporns, O. (2016). Path ensembles and a tradeoff between communication efficiency and resilience in the human connectome. Brain Structure and Function, 1–16. DOI: https://doi.org/10.1007/s00429-016-1238-5, PMID: 27334341 Avena-Koenigsberger, A., Miši´c, B., & Sporns, O. (2018). Commu- nication dynamics in complex brain networks. Nature Reviews Neuroscience, 19(1), 17–33. DOI: https://doi.org/10.1038/nrn .2017.149, PMID: 29238085 Avena-Koenigsberger, A., Yan, X., Kolchinsky, A., van den Heuvel, M., Hagmann, P., & Sporns, O. (2019). A spectrum of routing strategies for brain networks. PLoS Computational Biology, 15(3), e1006833. DOI: https://doi.org/10.1371/journal.pcbi.1006833, PMID: 30849087, PMCID: PMC6426276 Barch, D. M., Burgess, G. C., Harms, M. P., Petersen, S. E., Schlaggar, B. L., Corbetta, M., . . . WU-Minn HCP Consortium. (2013). Function in the human connectome: Task-fMRI and indi- vidual differences in behavior. NeuroImage, 80, 169–189. DOI: https://doi.org/10.1016/j.neuroimage.2013.05.033, PMID: 23684877, PMCID: PMC4011498 Bassett, D. S., & Bullmore, E. (2006). Small-world brain networks. Neuroscientist, 12(6), 512–523. DOI: https://doi.org/10.1177 /1073858406293182, PMID: 17079517 Bassett, D. S., & Sporns, O. (2017). Network neuroscience. Nature Neuroscience, 20(3), 353–364. DOI: https://doi.org/10.1038/nn .4502, PMID: 28230844, PMCID: PMC5485642 Bertolero, M. A., Yeo, B. T. T., Bassett, D. S., & D’Esposito, M. (2018). A mechanistic model of connector hubs, modularity and cognition. Nature Human Behaviour, 2(10), 765–777. DOI: https://doi.org/10.1038/s41562-018-0420-6, PMID: 30631825, PMCID: PMC6322416 Betzel, R. F., Medaglia, J. D., Kahn, A. E., Soffer, J., Schonhaut, D. R., & Bassett, D. S. (2019). Structural, geometric and genetic factors predict interregional brain connectivity patterns probed by electrocorticography. Nature Biomedical Engineering, 3(11), 902–916. DOI: https://doi.org/10.1038/s41551-019-0404-5, PMID: 31133741 Boguña, M., Krioukov, D., & Claffy, K. C. (2009). Navigability of complex networks. Nature Physics, 5(1), 74–80. DOI: https://doi .org/10.1038/nphys1130 Breakspear, M. (2017). Dynamic models of large-scale brain ac- tivity. Nature Neuroscience, 20(3), 340–352. DOI: https://doi .org/10.1038/nn.4497, PMID: 28230845 Buchanan, C. R., Bastin, M. E., Ritchie, S. J., Liewald, D. C., Madole, J. W., Tucker-Drob, E. M., . . . Cox, S. R. (2020). The effect of network thresholding and weighting on structural brain networks in the UK Biobank. NeuroImage, 211, 116443. DOI: https://doi .org/10.1016/j.neuroimage.2019.116443, PMID: 31927129 Bullmore, E., & Sporns, O. (2009). Complex brain networks: Graph theoretical analysis of systems. Nature Reviews Neuroscience, 10(3), 186–198. DOI: https://doi .org/10.1038/nrn2575, PMID: 19190637 structural and functional Network Neuroscience 1002 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 4 4 9 8 0 1 8 6 7 0 2 6 n e n _ a _ 0 0 1 6 1 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Network communication models, behavior, and functional connectivity Bullmore, E., & Sporns, O. (2012). The economy of brain network organization. Nature Reviews Neuroscience, 13(5), 336–349. DOI: https://doi.org/10.1038/nrn3214, PMID: 22498897 Civier, O., Smith, R. E., Yeh, C.-H., Connelly, A., & Calamante, F. (2019). Is removal of weak connections necessary for graph- theoretical analysis of dense weighted structural connectomes from diffusion MRI? NeuroImage, 194, 68–81. DOI: https://doi .org/10.1016/j.neuroimage.2019.02.039, PMID: 30844506 Cole, M. W., Ito, T., Bassett, D. S., & Schultz, D. H. (2016). Activity flow over resting-state networks shapes cognitive task activations. Nature Neuroscience, 19(12), 1718–1726. DOI: https://doi.org /10.1038/nn.4406, PMID: 27723746, PMCID: PMC5127712 Crofts, J. J., & Higham, D. J. (2009). A weighted communicability measure applied to complex brain networks. Journal of the Royal Society Interface, 6(33), 411–414. DOI: https://doi.org/10.1098 /rsif.2008.0484, PMID: 19141429, PMCID: PMC2658663 Damoiseaux, J. S., & Greicius, M. D. (2009). Greater than the sum of its parts: A review of studies combining structural con- nectivity and resting-state functional connectivity. Brain Structure and Function, 213(6), 525–533. DOI: https://doi.org/10.1007 /s00429-009-0208-6, PMID: 19565262 Deco, G., Kringelbach, M. L., Jirsa, V. K., & Ritter, P. (2017). The dynamics of resting fluctuations in the brain: Metastability and its dynamical cortical core. Scientific Reports, 7(1), 3095. DOI: https://doi.org/10.1038/s41598-017-03073-5, PMID: 28596608, PMCID: PMC5465179 Desikan, R. S., Ségonne, F., Fischl, B., Quinn, B. T., Dickerson, B. C., Blacker, D., . . . Killiany, R. J. (2006). An automated labeling sys- tem for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. NeuroImage, 31(3), 968–980. DOI: https://doi.org/10.1016/j.neuroimage.2006.01.021, PMID: 16530430 Eickhoff, S. B., Yeo, B. T. T., & Genon, S. Imaging-based parcellations of the human brain. Nature Reviews Neuroscience, 19(11), 672–686. DOI: https://doi.org/10.1038/s41583-018 -0071-7, PMID: 30305712 (2018). Estrada, E., & Hatano, N. (2008). Communicability in complex net- works. Physical Review E, 77(3 Pt. 2), 036111. DOI: https://doi .org/10.1103/PhysRevE.77.036111, PMID: 18517465 Fornito, A., Zalesky, A., & Bullmore, E. T. (2016). Fundamentals of brain network analysis. Amsterdam, Netherlands: Elsevier. Friedman, J., Hastie, T., & Tibshirani, R. (2010). Regularization paths for generalized linear models via coordinate descent. Journal of Statistical Software, 33(1), 1–22. DOI: https://doi.org /10.18637/jss.v033.i01, PMID: 20808728, PMCID: PMC2929880 Friston, K. (2002). Beyond phrenology: What can neuroimaging tell us about distributed circuitry? Annual Review of Neuroscience, 25, 221–250. DOI: https://doi.org/10.1146/annurev.neuro.25 .112701.142846, PMID: 12052909 Gilson, M., Kouvaris, N. E., Deco, G., Mangin, J.-F., Poupon, C., Lefranc, S., . . . Zamora-López, G. (2019). Network analysis of whole-brain fMRI dynamics: A new framework based on dynamic communicability. NeuroImage, 201, 116007. DOI: https://doi .org/10.1016/j.neuroimage.2019.116007, PMID: 31306771 Glasser, M. F., Coalson, T. S., Robinson, E. C., Hacker, C. D., (2016). A multi- Harwell, J., Yacoub, E., . . . Van Essen, D. C. modal parcellation of human cerebral cortex. Nature, 536(7615), 171–178. DOI: https://doi.org/10.1038/nature18933, PMID: 27437579, PMCID: PMC4990127 Glasser, M. F., Sotiropoulos, S. N., Wilson, J. A., Coalson, T. S., Fischl, B., Andersson, J. L., . . . WU-Minn HCP Consortium. (2013). The minimal preprocessing pipelines for the Human Con- nectome Project. NeuroImage, 80, 105–24. DOI: https://doi .org/10.1016/j.neuroimage.2013.04.127, PMID: 23668970, PMCID: PMC3720813 Goñi, J., Avena-Koenigsberger, A., Velez de Mendizabal, N., van den Heuvel, M. P., Betzel, R. F., & Sporns, O. (2013). Exploring the morphospace of communication efficiency in complex networks. PLoS ONE, 8(3), e58070. DOI: https://doi .org/10.1371/journal.pone.0058070, PMID: 23505455, PMCID: PMC3591454 Goñi, J., van den Heuvel, M. P., Avena-Koenigsberger, A., Velez de Mendizabal, N., Betzel, R. F., Griffa, A., . . . Sporns, O. (2014). Resting-brain functional connectivity predicted by analytic mea- sures of network communication. Proceedings of the National Acad- emy of Sciences, 111(2), 833–838. DOI: https://doi.org/10.1073 /pnas.1315529111, PMID: 24379387, PMCID: PMC3896172 Hagmann, P., Cammoun, L., Gigandet, X., Meuli, R., Honey, C. J., Wedeen, V. J., & Sporns, O. (2008). Mapping the structural core of human cerebral cortex. PLoS Biology, 6(7), e159. DOI: https://doi .org/10.1371/journal.pbio.0060159, 18597554, PMCID: PMC2443193 PMID: He, T., Kong, R., Holmes, A. J., Nguyen, M., Sabuncu, M. R., Eickhoff, S. B., . . . Yeo, B. T. T. (2020). Deep neural networks and kernel regression achieve comparable accuracies for func- tional connectivity prediction of behavior and demograph- ics. NeuroImage, 206, 116276. DOI: https://doi.org/10.1016/j .neuroimage.2019.116276, PMID: 31610298 Himberg, J., Hyvärinen, A., & Esposito, F. (2004). Validating the independent components of neuroimaging time series via clus- tering and visualization. NeuroImage, 22(3), 1214–1222. DOI: https://doi.org/10.1016/j.neuroimage.2004.03.027, PMID: 15219593 Honey, C. J., Kötter, R., Breakspear, M., & Sporns, O. (2007). Net- work structure of cerebral cortex shapes functional connectivity on multiple time scales. Proceedings of the National Academy of Sciences, 104(24), 10240–10245. DOI: https://doi.org/10.1073 /pnas.0701519104, PMID: 17548818, PMCID: PMC1891224 Hyvärinen, A. (1999). Fast and robust fixed-point algorithms for independent component analysis. IEEE Transactions on Neural Net- works and Learning Systems, 10(3), 626–634. DOI: https://doi .org/10.1109/72.761722, PMID: 18252563 Kaiser, M., & Hilgetag, C. C. (2006). Nonoptimal component place- ment, but short processing paths, due to long-distance projec- tions in neural systems. PLoS Computational Biology, 2(7), e95. DOI: https://doi.org/10.1371/journal.pcbi.0020095, PMID: 16848638, PMCID: PMC1513269 Kuceyeski, A. F., Jamison, K. W., Owen, J. P., Raj, A., & Mukherjee, P. (2019). Longitudinal increases in structural connectome segre- gation and functional connectome integration are associated with better recovery after mild TBI. Human Brain Mapping, 40(15), 4441–4456. DOI: https://doi.org/10.1002/hbm.24713, PMID: 31294921, PMCID: PMC6865536 Network Neuroscience 1003 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 4 4 9 8 0 1 8 6 7 0 2 6 n e n _ a _ 0 0 1 6 1 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Network communication models, behavior, and functional connectivity Latora, V., & Marchiori, M. (2001). Efficient behavior of small-world networks. Physical Review Letters, 87(19), 198701. DOI: https://doi .org/10.1103/PhysRevLett.87.198701, PMID: 11690461 Laughlin, S. B., & Sejnowski, T. J. (2003). Communication in neuro- nal networks. Science, 301(5641), 1870–1874. DOI: https://doi .org/10.1126/science.1089662, PMID: 14512617, PMCID: PMC2930149 Li, J., Kong, R., Liégeois, R., Orban, C., Tan, Y., Sun, N., . . . Yeo, (2019). Global signal regression strengthens associa- B. T. T. tion between resting-state functional connectivity and behav- ior. NeuroImage, 196, 126–141. DOI: https://doi.org/10.1016/j .neuroimage.2019.04.016, PMCID: PMC6585462 30974241, PMID: Liégeois, R., Li, J., Kong, R., Orban, C., Van De Ville, D., Ge, T., . . . Yeo, B. T. T. (2019). Resting brain dynamics at different time- scales capture distinct aspects of human behavior. Nature Com- munications, 10(1), 2317. DOI: https://doi.org/10.1038/s41467- 019-10317-7, PMID: 31127095, PMCID: PMC6534566 Maier-Hein, K. H., Neher, P. F., Houde, J.-C., Côté, M.-A., Garyfallidis, E., Zhong, J., . . . Descoteaux, M. (2017). The chal- lenge of mapping the human connectome based on diffusion trac- tography. Nature Communications, 8(1), 1349. DOI: https://doi .org/10.1038/s41467-017-01285-x, PMID: 29116093, PMCID: PMC5677006 Medaglia, J. D., Lynall, M.-E., & Bassett, D. S. (2015). Cognitive network neuroscience. Journal of Cognitive Neuroscience, 27(8), 1471–14791. DOI: https://doi.org/10.1162/jocn_a_00810, PMID: 25803596, PMCID: PMC4854276 Messé, A. (2020). Parcellation influence on the connectivity- based structure-function relationship in the human brain. Human Brain Mapping, 41(5), 1167–1180. DOI: https://doi.org/10.1002 /hbm.24866, PMID: 31746083, PMCID: PMC7267927 Messé, A., Rudrauf, D., Benali, H., & Marrelec, G. (2014). Relat- ing structure and function in the human brain: Relative contri- butions of anatomy, stationary dynamics, and non-stationarities. PLoS Computational Biology, 10(3), e1003530. DOI: https://doi .org/10.1371/journal.pcbi.1003530, PMID: 24651524, PMCID: PMC3961181 Messé, A., Rudrauf, D., Giron, A., & Marrelec, G. (2015). Pre- dicting functional connectivity from structural connectivity via computational models using MRI: An extensive comparison study. NeuroImage, 111, 65–75. DOI: https://doi.org/10.1016/j .neuroimage.2015.02.001, PMID: 25682944 Miši´c, B., Betzel, R. F., de Reus, M. A., van den Heuvel, M. P., Berman, M. G., McIntosh, A. R., & Sporns, O. (2016). Network- level structure-function relationships in human neocortex. Cere- bral Cortex, 26(7), 3285–3296. DOI: https://doi.org/10.1093 /cercor/bhw089, PMID: 27102654, PMCID: PMC4898678 Miši´c, Bratislav, Betzel, Richard F., Griffa, Alessandra, de Reus, Marcel A., He, Ye, Zuo, Xi-Nian, van den Heuvel, Martijn P., Hagmann, Patric, Sporns, Olaf, & Zatorre, Robert J. (2018). Network-Based Asymmetry of the Human Auditory System. Cereb Cortex, 28(7), 2655–2664. DOI: https://doi.org/10.1101 /251827 Miši´c, B., Betzel, R. F., Nematzadeh, A., Goñi, J., Griffa, A., Hagmann, P., . . . Sporns, O. (2015). Cooperative and compet- itive spreading dynamics on the human connectome. Neuron, 86(6), 1518–1529. DOI: https://doi.org/10.1016/j.neuron.2015 .05.035, PMID: 26087168 Miši´c, B., Goñi, J., Betzel, R. F., Sporns, O., & McIntosh, A. R. (2014). A network convergence zone in the hippocampus. PLoS Computational Biology, 10(12), e1003982. DOI: https://doi.org /1v0.1371/journal.pcbi.1003982, PMID: 25474350, PMCID: PMC4256084 Miši´c, B., & Sporns, O. (2016). From regions to connections and networks: New bridges between brain and behavior. Current Opinion in Neurobiology, 40, 1–7. DOI: https://doi.org/10.1016/j .conb.2016.05.003, PMID: 27209150, PMCID: PMC5056800 Osmanlo˘glu, Y., Tunç, B., Parker, D., Elliott, M. A., Baum, G. L., Ciric, R., . . . Verma, R. (2019). System-level matching of struc- tural and functional connectomes in the human brain. NeuroIm- age, 199, 93–104. DOI: https://doi.org/10.1016/j.neuroimage .2019.05.064, PMID: 31141738 Pappas, I., Craig, M. M., Menon, D. K., & Stamatakis, E. A. (2020). Structural optimality and neurogenetic expression mediate func- tional dynamics in the human brain. Human Brain Mapping, 41(8), 2229–2243. DOI: https://doi.org/10.1002/hbm.24942, PMID: 32027077, PMCID: PMC7267953 Park, H.-J., & Friston, K. (2013). Structural and functional brain networks: From connections to cognition. Science, 342(6158), 1238411. DOI: https://doi.org/10.1126/science.1238411, PMID: 24179229 Pedersen, M., Zalesky, A., Omidvarnia, A., & Jackson, G. D. (2018). Multilayer network switching rate predicts brain performance. Proceedings of the National Academy of Sciences, 115(52), 13376–13381. DOI: https://doi.org/10.1073/pnas.1814785115, PMID: 30545918, PMCID: PMC6310789 Perry, A., Wen, W., Kochan, N. A., Thalamuthu, A., Sachdev, P. S., & Breakspear, M. (2017). The independent influences of age and education on functional brain networks and cognition in healthy older adults. Human Brain Mapping, 38(10), 5094–5114. DOI: https://doi.org/10.1002/hbm.23717, PMID: 28685910, PMCID: PMC6866868 Raj, A., Kuceyeski, A., & Weiner, M. Qian, J., Hastie, T., Friedman, J., Tibshirani, R., & Simon, N. (2013). Glmnet for matlab. http://www.stanford.edu/~hastie/glmnet_matlab (2012). A network diffu- sion model of disease progression in dementia. Neuron, 73(6), 1204–1215. DOI: https://doi.org/10.1016/j.neuron.2011.12.040, PMID: 22445347, PMCID: PMC3623298 Roberts, J. A., Perry, A., Lord, A. R., Roberts, G., Mitchell, P. B., Smith, R. E., . . . Breakspear, M. (2016). The contribution of geometry to the human connectome. NeuroImage, 124(Pt. A), 379–393. DOI: https://doi.org/10.1016/j.neuroimage.2015.09 .009, PMID: 26364864 Rosvall, M., Grönlund, A., Minnhagen, P., & Sneppen, K. (2005). Searchability of networks. Physical Review E, 72(4 Pt. 2), 046117. DOI: https://doi.org/10.1103/PhysRevE.72.046117, PMID: 16383478 Rubinov, M., & Sporns, O. (2010). Complex network measures of brain connectivity: Uses and interpretations. NeuroImage, 52(3), 1059–1069. DOI: https://doi.org/10.1016/j.neuroimage.2009 .10.003, PMID: 19819337 Rubinov, M., Ypma, R. J. F., Watson, C., & Bullmore, E. T. (2015). Wiring cost and topological participation of the mouse brain connectome. Proceedings of the National Academy of Network Neuroscience 1004 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 4 4 9 8 0 1 8 6 7 0 2 6 n e n _ a _ 0 0 1 6 1 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Network communication models, behavior, and functional connectivity Sciences, 112(32), 10032–10037. DOI: https://doi.org/10.1073 /pnas.1420315112, PMID: 26216962, PMCID: PMC4538676 Sarwar, T., Ramamohanarao, K., & Zalesky, A. (2019). Mapping connectomes with diffusion MRI: Deterministic or probabilistic tractography? Magnetic Resonance in Medicine, 81(2), 1368–1384. DOI: https://doi.org/10.1002/mrm.27471, PMID: 30303550 Seguin, C., Razi, A., & Zalesky, A. (2019). Inferring neural signalling directionality from undirected structural connectomes. Nature Com- munications, 10(1), 4289. DOI: https://doi.org/10.1038/s41467 -019-12201-w PMID: 31537787, PMCID: PMC6753104 Seguin, C., van den Heuvel, M. P., & Zalesky, A. (2018). Navigation of brain networks. Proceedings of the National Academy of Sciences, 115(24), 6297–6302. DOI: https://doi.org/10.1073/pnas .1801351115, PMID: 29848631, PMCID: PMC6004443 Smith, S. M., Beckmann, C. F., Andersson, J., Auerbach, E. J., Bijsterbosch, J., Douaud, G., . . . WU-Minn HCP Consortium. (2013). Resting-state fMRI in the Human Connectome Project. Neu- roImage, 80, 144–168. DOI: https://doi.org/10.1016/j.neuroimage .2013.05.039, PMID: 23702415, PMCID: PMC3720828 Smith, S. M., Nichols, T. E., Vidaurre, D., Winkler, A. M., Behrens, T. E. J., Glasser, M. F., . . . Miller, K. L. (2015). A positive-negative mode of population covariation links brain connectivity, demo- graphics and behavior. Nature Neuroscience, 18(11), 1565–1567. DOI: https://doi.org/10.1038/nn.4125, PMID: 26414616, PMCID: PMC4625579 Sokolov, A. A., Zeidman, P., Erb, M., Ryvlin, P., Pavlova, M. A., & Friston, K. J. (2018). Linking structural and effective brain connec- tivity: Structurally informed parametric empirical Bayes (si-PEB). Brain Structure and Function, 224, 205–217. DOI: https://doi .org/10.1007/s00429-018-1760-8, PMID: 30302538, PMCID: PMC6373362 Sotiropoulos, S. N., Jbabdi, S., Xu, J., Andersson, J. L., Moeller, S., Auerbach, E. J., . . . WU-Minn HCP Consortium. (2013). Advances in diffusion MRI acquisition and processing in the Hu- man Connectome Project. NeuroImage, 80, 125–143. DOI: https:// doi.org/10.1016/j.neuroimage.2013.05.057, PMID: 23702418, PMCID: PMC3720790 Sotiropoulos, S. N., & Zalesky, A. (2019). Building connectomes us- ing diffusion MRI: Why, how and but. NMR Biomedicine, 32(4), e3752. DOI: https://doi.org/10.1002/nbm.3752, PMID: 28654718, PMCID: PMC6491971 Sporns, O., & Betzel, R. F. (2016). Modular brain networks. Annual Re- view of Psychology, 67, 613–640. DOI: https://doi.org/10.1146 /annurev-psych-122414-033634, PMID: 26393868, PMCID: PMC4782188 Sporns, O., Tononi, G., & Kötter, R. (2005). The human connectome: A structural description of the human brain. PLoS Computational Biology, 1(4), e42. DOI: https://doi.org/10.1371/journal.pcbi .0010042, PMID: 16201007, PMCID: PMC1239902 Sripada, C., Rutherford, S., Angstadt, M., Thompson, W. K., Luciana, M., Weigard, A., . . . Heitzeg, M. (2019). Prediction of neurocognition in youth from resting state FMRI. Molecular Psychiatry. DOI: https://doi.org/10.1038/s41380-019-0481-6, PMID: 31427753 Stiso, J., & Bassett, D. S. (2018). Spatial embedding imposes con- straints on neuronal network architectures. Trends in Cognitive Sciences, 22(12), 1127–1142. DOI: https://doi.org/10.1016/j.tics .2018.09.007, PMID: 30449318 Suárez, L. E., Markello, R. D., Betzel, R. F., & Miši´c, B. (2020). Linking structure and function in macroscale brain networks. Trends in Cognitive Sciences, 24(4), 302–315. DOI: https://doi .org/10.1016/j.tics.2020.01.008, PMID: 32160567 Tian, Y., Margulies, D. S., Breakspear, M., & Zalesky, A. (2020). Hierarchical organization of the human subcortex unveiled with functional connectivity gradients. bioRxiv: 2020.01.13.903542. DOI: https://doi.org/10.1101/2020.01.13.903542 Tibshirani, R. (1996). Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society. Series B (Methodological), 58(1), 267–288. DOI: https://doi.org/10.1111/j.2517-6161.1996 .tb02080.x Tipnis, U., Amico, E., Ventresca, M., & Goñi, J. (2018). Modeling communication processes in the human connectome through cooperative learning. IEEE Transactions on Network Science and Engineering, 7(1), 476–488. DOI: https://doi.org/10.1109/TNSE .2018.2878487 Tournier, J.-D., Calamante, F., & Connelly, A. (2012). MRtrix: International Diffusion tractography in crossing fiber regions. Journal of Imaging Systems and Technology, 22. DOI: https://doi .org/10.1002/ima.22005 van den Heuvel, M. P., & Sporns, O. (2011). Rich-club organiza- tion of the human connectome. Journal of Neuroscience, 31(44), 15775–15786. DOI: https://doi.org/10.1523/JNEUROSCI.3539 -11.2011, PMID: 22049421, PMCID: PMC6623027 van den Heuvel, M. P., Stam, C. J., Kahn, R. S., & Hulshoff Pol, H. E. (2009). Efficiency of functional brain networks and intel- lectual performance. Journal of Neuroscience, 29(23), 7619–17624. DOI: https://doi.org/10.1523/JNEUROSCI.1443-09.2009, PMID: 19515930, PMCID: PMC6665421 Van der Waerden, B. (1953). Order tests for the two-sample prob- lem and their power. Indagationes Mathematicae (Proceedings), 56, 80. DOI: https://doi.org/10.1523/JNEUROSCI.1443-09.2009, PMID: 19515930, PMCID: PMC6665421 Van Essen, D. C., Smith, S. M., Barch, D. M., Behrens, T. E. J., Yacoub, E., Ugurbil, K., & WU-Minn HCP Consortium. (2013). The WU-Minn Human Connectome Project: An overview. Neu- roImage, 80, 62–79. DOI: https://doi.org/10.1016/j.neuroimage .2013.05.041, PMID: 23684880, PMCID: PMC3724347 Vázquez-Rodríguez, Bertha, Liu, Zhen-Qi, Hagmann, Patric, & Miši´c, Bratislav. (2020). Signal propagation via cortical hierar- chies. Network Neuroscience, 1–19. DOI: https://doi.org/10.1162 /netn_a_00153 Vázquez-Rodríguez, B., Suárez, L. E., Markello, R. D., Shafiei, G., Paquola, C., Hagmann, P., . . . Miši´c, B. (2019). Gradients of structure-function tethering across neocortex. Proceedings of the National Academy of Sciences, 116(42), 21219–21227. DOI: https://doi.org/10.1073/pnas.1903403116, PMID: 31570622, PMCID: PMC6800358 Vértes, P. E., Alexander-Bloch, A. F., Gogtay, N., Giedd, J. N., (2012). Simple models of Rapoport, J. L., & Bullmore, E. T. human brain functional networks. Proceedings of the National Academy of Sciences, 109(15), 5868–5873. DOI: https://doi .org/10.1073/pnas.1111738109, PMID: 22467830, PMCID: PMC3326510 Network Neuroscience 1005 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 4 4 9 8 0 1 8 6 7 0 2 6 n e n _ a _ 0 0 1 6 1 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Network communication models, behavior, and functional connectivity Wang, X., Seguin, C., Zalesky, A., Wong, W.-W., Chu, W. C.-W., & Tong, R. K.-Y. (2019). Synchronization lag in post stroke: Relation to motor function and structural connectivity. Network Neuroscience, 3(4), 1121–1140. DOI: https://doi.org/10.1162 /netn_a_00105, PMID: 31637341, PMCID: PMC6777982 Yeo, B. T. T., Krienen, F. M., Sepulcre, J., Sabuncu, M. R., Lashkari, D., Hollinshead, M., . . . Buckner, R. L. (2011). The organization of the human cerebral cortex estimated by intrinsic functional Journal of Neurophysiology, 106(3), 1125–1165. connectivity. DOI: https://doi.org/10.1152/jn.00338.2011, PMID: 21653723, PMCID: PMC3174820 Zalesky, A., Fornito, A., & Bullmore, E. T. (2010). Network-based statistic: Identifying differences in brain networks. NeuroImage, 53(4), 1197–1207. DOI: https://doi.org/10.1016/j.neuroimage .2010.06.041, PMID: 20600983 Zalesky, A., Fornito, A., Cocchi, L., Gollo, L. L., van den Heuvel, M. P., & Breakspear, M. (2016). Connectome sensitivity or spec- ificity: Which is more important? NeuroImage. DOI: https://doi .org/10.1016/j.neuroimage.2016.06.035, PMID: 27364472 Zhou, H. (2003). Network landscape from a brownian particle’s per- spective. Physical Review E, 67(4 Pt. 1), 041908. DOI: https://doi .org/10.1103/PhysRevE.67.041908, PMID: 12786397 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 4 4 9 8 0 1 8 6 7 0 2 6 n e n _ a _ 0 0 1 6 1 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Network Neuroscience 1006

Descargar PDF