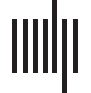INVESTIGACIÓN
Damage to the structural connectome reflected in
resting-state fMRI functional connectivity
Anirudh Wodeyar1,2, Jessica M. Cassidy3, Steven C. Cramer4, and Ramesh Srinivasan1,5
1Department of Cognitive Sciences, Universidad de California, Irvine, California, EE.UU
2Department of Statistics, Universidad de California, Irvine, California, EE.UU
3Department of Allied Health Sciences, University of North Carolina, Chapel Hill, CAROLINA DEL NORTE, EE.UU
4Department of Neurology, Universidad de California, Los Angeles, California, EE.UU
5Department of Biomedical Engineering, Universidad de California, Irvine, California, EE.UU
Palabras clave: resonancia magnética funcional, Conectividad funcional, Structural connectivity, Stroke, Partial correlation
un acceso abierto
diario
ABSTRACTO
The relationship between structural and functional connectivity has been mostly examined in
intact brains. Fewer studies have examined how differences in structure as a result of injury
alters function. In this study we analyzed the relationship of structure to function across
patients with stroke among whom infarcts caused heterogenous structural damage. Nosotros
estimated relationships between distinct brain regions of interest (ROI) from functional MRI
in two pipelines. In one analysis pipeline, we measured functional connectivity by using
correlation and partial correlation between 114 cortical ROIs. We found fMRI-BOLD partial
correlation was altered at more edges as a function of the structural connectome (CAROLINA DEL SUR)
damage, relative to the correlation. In a second analysis pipeline, we limited our analysis to
fMRI correlations between pairs of voxels for which we possess SC information. Encontramos
that voxel-level functional connectivity showed the effect of structural damage that we could
not see when examining correlations between ROIs. Más, the effects of structural damage
on functional connectivity are consistent with a model of functional connectivity, difusión,
which expects functional connectivity to result from activity spreading over multiple edge
anatomical paths.
RESUMEN DEL AUTOR
Examining the structure to function relationship at damaged edges in the structural
connectome due to lesions from stroke we find the following:
Partial correlation reflects structural connectome damage in 24% of edges tested.
Voxel-to-voxel correlation guided by structural connectivity shows the presence of SC
damage in 39% of edges tested.
Edges that show modulation when using voxel-to-voxel correlation are consistent with
diffusion as a model of functional connectivity.
Our work provides evidence that for pairs of regions that are not directly anatomically
connected due to lesions from stroke, signals must be communicated through intermediate
region-to-region steps along an anatomical path.
Citación: Wodeyar, A., Cassidy, j. METRO.,
Cramer, S. C., & Srinivasan, R. (2020).
Damage to the structural connectome
reflected in resting-state fMRI
conectividad funcional. Red
Neurociencia, 4(4), 1197–1218.
https://doi.org/10.1162/netn_a_00160
DOI:
https://doi.org/10.1162/netn_a_00160
Supporting Information:
https://doi.org/10.1162/netn_a_00160
Recibió: 12 Marzo 2020
Aceptado: 21 Julio 2020
Conflicto de intereses: Los autores tienen
declaró que no hay intereses en competencia
existir.
Autor correspondiente:
Anirudh Wodeyar
wodeyar@bu.edu
Editor de manejo:
Olaf Sporns
Derechos de autor: © 2020
Instituto de Tecnología de Massachusetts
Publicado bajo Creative Commons
Atribución 4.0 Internacional
(CC POR 4.0) licencia
La prensa del MIT
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
1
9
7
1
8
6
7
0
4
5
norte
mi
norte
_
a
_
0
0
1
6
0
pag
d
/
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Damaged SC linked to altered rs-fMRI functional connectivity
INTRODUCCIÓN
A large body of literature has demonstrated significant temporal correlations, labeled functional
conectividad, in the blood oxygen level-dependent (BOLD) signal between spatially distinct
brain regions of interest during rest (p.ej., see Greicius, Krasnow, Reiss, & menón, 2003; xiong,
Parsons, gao, & Fox, 1999). Resting-state fMRI-BOLD functional connectivity appears to have
broad use as a potential biomarker (Drysdale et al., 2017; Liem et al., 2017; Rane et al., 2015)
and has been shown to predict task-based BOLD activation (Col, Ito, bassett, & Schultz, 2016;
Tavor et al., 2016). One critical question that arises is, what mechanism gives rise to resting-
state functional connectivity? A potential answer comes from the anatomy-axonal fiber tracts
must be the backbone that supports functional connectivity. While the origin of our hypothesis
is at the scale of neurons, the fMRI-BOLD and diffusion tensor imaging (DTI) are macroscale
(neural mass scale) brain imaging techniques. Sin embargo, we can expect a persistent statistical
relationship across scales that should allow us to relate fMRI-BOLD and DTI. Recientemente, allá
have been tools developed (Johansen-Berg & Rushworth, 2009) to map the entire set of fiber
tracts and this has been termed as the structural connectome (despreciar, Tononi, & kötter, 2005).
Sin embargo, conclusively establishing an exact relationship between structural and functional
connectivity has proved difficult (Straathof, Sinke, Dijkhuizen, & Otte, 2018).
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
1
9
7
1
8
6
7
0
4
5
norte
mi
norte
_
a
_
0
0
1
6
0
pag
d
t
/
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Identifying the relationship between structural and functional connectivity requires spec-
ifying a model of how neural dynamics spread over the axonal fibers. Studies have exam-
ined different models of how simple dynamics spread over the structural connectome and
their ability to capture the functional connectivity. The simplest model one can assume is that
activity spreading over single-edge (defined as a direct structural connectome connection)
connections between two distinct regions leads to functional connectivity. Initial examina-
tions of the structural to functional connectivity relationship assuming a single-edge model
with simple Gaussian noise dynamics found that structural connectivity was indeed correlated
with functional connectivity (see Straathof et al., 2018 for a thorough review, Honey, kötter,
romper la lanza, & despreciar, 2007; Koch, Norris, & Hund-Georgiadis, 2002; O’Reilly et al., 2013;
Van Den Heuvel, Mandl, Kahn, & Hulshoff Pol, 2009) but at its best, shows shared variance in
the range of 60% with the functional connectivity. Sin embargo, another line of work has exam-
ined models that incorporate multi-edge connectivity (Abdelnour, Voss, & Raj, 2014; Avena-
Koenigsberger, Varios, & despreciar, 2018; Goñi et al., 2014; Messé, Rudrauf, Giron, & Marrelec,
2015; Miši´c et al., 2015), where multiedge connectivity between regions is defined as a con-
nected path over multiple direct structural connections. Incorporating multiedge connectivity
improves the variance of functional connectivity (FC) explained by the structural connectivity.
By extension, we might expect that we are better able to identify changes in the FC as a func-
tion of the absence of single-edge SC connectivity when we reduce the influence of multiedge
SC connectivity on the FC.
Patients who have had a stroke nearly always sustain damage to white-matter tracts, de este modo
altering the single-edge SC connectivity. We expect that there is considerable variability in
structural connectome damage across patients that arises from the uniqueness of injury (as a
function of location and volume) from stroke in each patient. We leverage the resulting hetero-
geneity in the structural connections of stroke patients to investigate the relationship between
structural connections and fMRI functional connectivity. We examined the relationship be-
tween structural connectivity and fMRI functional connectivity by using data from patients
who have suffered a stroke within a month prior to when data was collected. An estimate of
the structural connectome for each patient was obtained using virtual tractography (Kuceyeski,
Maruta, Relkin, & Raj, 2013; Pustina et al., 2017) across the pairs of 114 cortical regions of
Neurociencia en red
1198
Damaged SC linked to altered rs-fMRI functional connectivity
Diffusion:
Communication between neural
masses in distinct areas happens
through activity passing by random
walks over the structural
conectoma.
Partial correlation:
Summary statistic of conditional
dependency, es decir., it measures,
between any two areas, the linear
relationship between them when
accounting for their relationship to
all other areas.
interés (ROI) from the Lausanne parcellation (Cammoun et al., 2012). Virtual tractography
uses a template set of streamlines estimated from healthy subjects intersected with lesion masks
for each patient to identify the subset of undamaged streamlines for each patient. This set of
undamaged streamlines is used to determine the patient-specific structural connectome. Nosotros
examine the edge-by-edge relationships of the structural connectivity to fMRI functional connec-
tivity across patients, to identify how differences in structural connectivity across individuals
modulates functional connectivity, providing a strong test of the influence of communication
over multiedge pathways of the structural connectivity and fMRI functional connectivity.
en este estudio, we had the unique opportunity to examine which linear model of communica-
tion dynamics across the structural connectome best models the impact of damage to axonal
fibers from stroke. In a model that expects neural activity to spread only along direct structural
connections, functional connectivity would be expected to simply reflect the weights of the
structural connectome, eso es, damage to the strongest structural connections would have the
strongest effects of functional connectivity. In a multiedge model, there is gradient of possible
relationships between structural and functional connectivity, depending on extent of informa-
tion available about the structure. The models relating structural to functional connectivity may
be diffusion (Goni et al., 2013; Noh & Rieger, 2004), where communication happens through
random walks over the structural connectome. Under diffusion, we expect functional connec-
tivity between two regions to reflect the average number of steps taken by random walkers
passing over the structural connectome. Diffusion assumes no global information about the
structural connectome, only local information about connection strengths. Another possibil-
ity is that functional connectivity navigates the shortest path (Goñi et al., 2014), el más fuerte
weighted path between two regions through the structural connectome. Shortest path routing
requires global information about the connectome. We expect that, given the structure to func-
tion relationship mediated by multiedge pathways remains consistent across different strengths
of an SC connection, then we are able to assess the validity of the hypothesis that multedge
pathways are relevant to functional connectivity within a particularly powerful context—that
of previously existing edges.
We tested the relationship between structure and function under two analysis pipelines. En
the first approach, we estimated correlation and partial correlation by using ROI-averaged sig-
nal. Partial correlation is a measure of conditional dependency, eso es, it measures, entre
any two areas, the linear relationship between them when accounting for their relationship to
all other areas. We expected partial correlation to better measure information shared over any
single-edge path over the SC that is not passing over other edges. We hypothesized that partial
correlation would optimally reflect modulation from differences in the structural connectivity
across subjects. In our second analysis pipeline, we avoided averaging signals over an ROI by
using a voxel-level measure of correlation. Averaging signals over an ROI removes the poten-
tial variations that exist at voxel level (Korhonen, Saarimäki, Glerean, Sams, & Saramäki, 2017)
and includes voxel-level variations for which we do not possess structural connectivity infor-
formación. For each pair of ROIs, we used correlations between pairs of voxels connected by a
streamline and tested whether damage was linked to altered functional connectivity. By identi-
fying and using only the voxels representing the streamline endpoints of structural connections,
we expected that we would be able to better resolve pairs of locations in the fMRI data where
we might expect altered functional connectivity. We examined whether we could predict the
edges where damage modulated correlations by using models that incorporated only local SC
información (difusión) or a model that incorporated global SC information (shortest path rout-
En g). We expected diffusion to be a better model as it is unlikely that neurons store and utilize
information about the SC.
Neurociencia en red
1199
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
1
9
7
1
8
6
7
0
4
5
norte
mi
norte
_
a
_
0
0
1
6
0
pag
d
t
/
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Damaged SC linked to altered rs-fMRI functional connectivity
MÉTODOS
Subjects
Twenty subjects with stroke (with onset 3–26 days prior) admitted to the inpatient rehabilitation
facility at the University of California, Irvine, Medical Center participated. All subjects signed
informed consent as approved by the Institutional Review Board. Subjects were included if they
were older than 18 years with a radiologically confirmed stroke. None of the subjects had other
active major neurological or psychiatric conditions or active substance abuse likely to interfere
with study procedures along with no prior medical history of cranial surgery. Age varied, con
mean ± 1 SD between 57.5 ± 12 años (range 27–79), as did sex (4 femenino, 16 masculino) and their
extent of arm motor deficits as per their Fugl-Meyer score, which ranged from 10 a 65 (normal
score is 66, and higher scores reflect better motor status). Four patients had a hemorrhagic
Handedness
Prior to
Subject ID Stroke
l
S001
R
S002
R
S003
S004
S005
S006
S007
S008
S009
S010
S011
S012
S013
S014
S015
S016
S017
S018
S019
S020
R
R
A
R
R
R
R
R
l
l
R
R
R
R
R
l
R
Mesa 1. Participant Demographics
Lesion Site
L pons
R basal ganglia
R parietal,
R occipital
R basal ganglia
R basal ganglia
L temporal
R basal ganglia,
R posterior corona radiata,
R temporal lobe
R temporal
R Middle Cerebral Artery,
R posterior insula,
R parietal operculum
R pons
R periventricular DWM,
R PLIC
R basal ganglia
L PLIC
R pons
L pons, L caudal midbrain
L corona radiata,
L cerebellar hemisphere,
L occipital lobe
R basal ganglia
L corona radiata,
R pons,
L PLEC
R medulla,
cerebellum
L pons
Lesion Side
l
R
R
R
R
l
R
R
R
R
R
R
l
R
l
l
R
l
R
l
Stroke
lesion
volumen
(cm3)
.79
36.47
19.87
2.54
10.08
36.97
15.2
78.1
69.49
2.18
4.77
68.76
3.55
1.36
5.43
2.44
60.38
1.44
39.26
1.01
Stoke
Tipo
(I/H)
I
h
I
Time
poststroke Age
días
14
12
11
(años)
58
57
49
Sex (M/F)
METRO
F
F
FM Total
63
57
24
I
h
I
I
h
I
I
I
h
I
I
h
I
h
I
I
I
F
METRO
METRO
METRO
METRO
METRO
METRO
METRO
METRO
METRO
METRO
METRO
METRO
METRO
METRO
F
METRO
9
11
5
16
9
25
18
9
6
71
17
21
5
26
12
8
3
65
40
69
48
50
67
77
58
48
59
79
51
67
51
66
27
53
14
45
65
13
57
26
15
41
17
8
35
53
62
13
53
61
52
Nota. (Legend: L-Left, R-Right, A-Ambidextrous; FM-Fugl-Meyer; I-Ischemic, H-Hemorrhagic; PLIC-posterior limb of internal capsule).
FM Total scores range from 0–66, with higher values indicating better arm motor status.
Neurociencia en red
1200
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
1
9
7
1
8
6
7
0
4
5
norte
mi
norte
_
a
_
0
0
1
6
0
pag
d
t
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Damaged SC linked to altered rs-fMRI functional connectivity
stroke while the other 16 had suffered an ischemic stroke. Más, across all patients, promedio
lesion volume was 23.01 cm3 (range .8 a 78.1 cm3). Mesa 1 shows demographic details about
all the subjects involved in our analysis.
MRI Processing
Neuroimaging was acquired on a 3.0 T Philips Achieva (Best, Los países bajos) scanner. Un-
atomical imaging included a high-resolution T1-weighted scan that utilized a three-dimensional
magnetization-prepared rapid gradient echo sequence (repetition time (TR) = 8.1 EM, echo
tiempo (EL) = 3.7 EM, 150 slices) and a T2-weighted FLAIR scan (TR = 9,000 EM, TE = 120 EM,
33 slices).
We drew lesion masks on T1-weighted MRIs, informed by the corresponding T2 FLAIR
images. Masks were generated using techniques (Cassidy, Tran, Quinlan, & Cramer, 2018;
Riley et al., 2011) for which reliability has been described previously (Burke et al., 2014).
For one subject who was unable to complete an MRI scan, we drew the lesion mask on their
corresponding CT scan. Infarct masks were binarized and spatially transformed to MNI space.
Lesions on the right were flipped about the midline so that all lesions were in the left side
of the brain for analysis purposes. Since motor deficits from stroke in the right hemisphere
generally are not different from motor deficits with a left hemisphere stroke, we did not make
any adjustments for behavior when flipping lesions.
Subjects completed a resting-state fMRI scan: TR = 2,000 EM, TE = 30 EM, 180 volumes,
voxel size = 3.38 × 3.38 × 3 mm3. Each patient was instructed to remain still and keep eyes
open to avoid falling asleep. Structural and fMRI scans were preprocessed using the CONN
toolbox (Whitfield-Gabrieli & Nieto-Castanon, 2012). The initial eight fMRI volumes were dis-
carded. Preprocessing steps included functional slice-time correction, functional realignment
(six rigid-body motion parameters), segmentation and spatial normalization to MNI space,
functional volume coregistration with structural volumes, functional outlier detection using
the artifact removal toolbox (ART), and functional smoothing using a 6-mm3 Gaussian ker-
nel. We visually analyzed all coregistrations to ensure quality and accuracy. Functional MRI
data underwent denoising procedures to remove unwanted motion, physiological effects, y
artifacts. For denoising CONN uses an anatomical component-based noise correction proce-
dure, which includes noise components from cerebral white matter and cerebrospinal areas
(Behzadi, Restom, Liau, & Liu, 2007), estimated subject-motion parameters (Friston et al.,
1995), identified outlier scans or scrubbing (Fuerza, Schlaggar, & Petersen, 2014), and constant
and first-order linear session effects. Finalmente, global signal regression (Le et al., 2019; k. Murphy
& Fox, 2017) was applied prior to bandpass filtering (0.008–0.09 Hz).
Virtual Tractography
Virtual tractography:
Using lesions masks and structural
connectome template to estimate
structural connectomes in a stroke
population where we can expect
structural disconnection from the
lesions suffered by patients.
Virtual tractography is a new approach (Kuceyeski et al., 2013; Pustina et al., 2017) to es-
timating structural connectomes in a stroke population where we can expect structural dis-
connection from the lesions suffered by patients. This method uses a template of structural
connectivity generated from healthy subjects and lesion masks for patients to generate patient-
specific structural connectomes. In this way we are able to make maximal use of lesion mask
information when we lack diffusion imaging from patients.
For our healthy subject structural connectome template, we used streamlines (representa-
tion of the axonal fibers of the brain) generated with deterministic tractography by Yeh et al.
(2018) using diffusion imaging from the HCP842 dataset (Van Essen et al., 2013). In this dataset
Neurociencia en red
1201
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
1
9
7
1
8
6
7
0
4
5
norte
mi
norte
_
a
_
0
0
1
6
0
pag
d
/
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Damaged SC linked to altered rs-fMRI functional connectivity
experts vet the streamlines to remove potentially noisy estimates of axonal fibers. We trans-
formed the streamlines generated by Yeh et al. (2018) to the MNI152 template brain accessed
from FSL (FMRIB Software Library, https://fsl.fmrib.ox.ac.uk/fsl/fslwiki). Each streamline was
approximated by a single 100-point cubic spline using code adapted from the along-tract-
stats toolbox (Colby et al., 2012). For more details on application of tractography to the HCP
diffusion imaging data please refer to Yeh et al. (2018).
We transformed the Lausanne parcellation (Cammoun et al., 2012) de 129 ROIs to the
MNI152 template brain and generated a volumetric representation for each ROI using the
easy_lausanne toolbox (Cieslak, 2015). Estimating virtual tractography for individual patients
for subcortical regions was expected to be more difficult than for cortical ROIs as the effects of
coregistration errors may be magnified in small volumes. We removed subcortical regions to
reduce the parcellation to 114 ROI. Using the 114 ROIs and the template streamlines we built
the adjacency matrix of 114×114 ROI pairs. By identifying the streamlines that terminated in
each pair of ROIs we were able to create the structural connectome for the Lausanne parcella-
ción. We limited interhemispheric connections to white-matter tracts connecting homologous
regions to minimize the contributions of potentially noisy estimates of axonal fibers. Any edge
Wij was defined as the sum over the streamlines biased by the length of the streamline. Para
ROIs i and j connected by streamlines s of length l:
Wij = ∑
sij
1
lij
(1)
Streamlines were weighted by inverse of length to reduce the bias of tractography algorithms
toward longer streamlines (Hagmann et al., 2008). We examined the impact of different SC pre-
processing strategies—streamline count normalization by ROI sizes, no length bias applied—in
our analysis when relevant. The resulting model of structural connectivity shown in Figure 1 es
referred to as the structural connectome (CAROLINA DEL SUR). We use the abbreviation SC to exclusively refer
to our model of the structural connectome. All code to perform virtual tractography can be
found at https://github.com/wodeyara/Virtual-Tractography.
We intersected the lesion masks (whose creation is described in MRI Processing section)
with the template streamlines of the SC. For each patient we are able to identify the template
streamlines that are disconnected by the lesion and those that are not based on which stream-
lines intersect the lesion mask. We remove the streamlines that intersect the lesion mask and
use the reduced set of streamlines to define individual structural connectomes. This process
is summarized in Figure 1. Each edge for each patient was designated as either high or low
damage. High damage indicated that, for that edge, connection strength was less than the me-
dian of connection strengths seen for that edge. We show how many edges have high damage
across patients in Figure 1. We found that over half of the connections showed high damage in
few to no patients. When categorizing the damage in this way, Encontramos eso 341 bordes (afuera
de 720 total edges) showed high damage in at least three patients. The majority of the edges
showing high damage connected frontal (111)—especially motor (48)—and parietal (72) areas
in the damaged hemisphere to the rest of the brain. We show these edges by area in Figure 1.
Estimating FC at the ROI Level
In the first analysis pipeline we estimated fMRI-correlation (fMRI-C) by using conventional
linear correlation between ROI-averaged signals. By default, this measure of marginal depen-
dence between areas includes activity shared over multiedge paths over the SC and through
Neurociencia en red
1202
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
1
9
7
1
8
6
7
0
4
5
norte
mi
norte
_
a
_
0
0
1
6
0
pag
d
/
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Damaged SC linked to altered rs-fMRI functional connectivity
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
1
9
7
1
8
6
7
0
4
5
norte
mi
norte
_
a
_
0
0
1
6
0
pag
d
.
/
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 1. Virtual tractography. (A) we show the pipeline for virtual tractography. We removed from
the set of streamlines that represent the undamaged structural connectome (arriba a la izquierda) the streamlines
intersecting a given patient’s lesion(s), as shown in the top row, middle column. Using the reduced
set of streamlines we applied the Lausanne parcellation to get the final structural connectome for that
patient (shown on the top row, rightmost column). (B) Edges showing high damage across patients.
On the left column we show the number of edges where the 20 patients show high damage (ver
Virtual Tractography section for definition of high damage). We found that for over 50% of edges
there are few (1 o 2) to no patients who sustained high damage to that edge. On the right column
we show the structural connectome with edge weight representing number of subjects showing
high damage for that edge. In the current analysis we studied all edges (341) where three or more
patients had high damage.
common inputs. We can also measure functional connectivity by using partial correlations to
define the connection strengths, a measure of the conditional dependency between areas. Por
estimating the conditional dependency we expect to prioritize activity only shared over single-
edge paths and remove the influence of common inputs. We used the adaptive graphical lasso
1203
Graphical lasso:
Optimization scheme used to
estimate the inverse of covariance
while optimizing the L1 norm,
thereby pushing small values of the
precision to zero.
Neurociencia en red
Damaged SC linked to altered rs-fMRI functional connectivity
to develop an SC-based model of fMRI-partial correlation or fMRI-PC (Friston, 2011; Marrelec
et al., 2006; Reid et al., 2019; Smith et al., 2011). In the process of estimating the model based
fMRI-PC, we tested and confirmed (using cross-validation) that the SC is useful in predicting
the nonzero elements of the fMRI-PC. We compared at every edge, across patients, si
fMRI-C or fMRI-PC better reflected the impact of damage from stroke.
Partial correlation is estimated us-
Adaptive Graphical Lasso to Estimate fMRI–Partial Correlation
ing normalized inverse (precisión) of the covariance of the fMRI time series. The estimate of the
precision from direct inversion tends to be noisy due to an ill-conditioned covariance matrix.
To improve the robustness of the precision, it is estimated using the graphical model esti-
mated from the graphical lasso. The graphical lasso (Friedman, Hastie, & Tibshirani, 2008) es un
method that has been applied in multiple fields in the past decade, from genomics (Menéndez,
Kourmpetis, ter Braak, & van Eeuwijk, 2010) to fMRI functional connectivity (Ryali, Chen,
Superkar, & menón, 2012; Varoquaux, Gramfort, Poline, & Thirion, 2010) and climate models
(Zerenner, Friederichs, Lehnertz, & Hense, 2014). In order to apply the lasso, the penalized
likelihood function to estimate the precision is defined as follows (Friedman et al., 2008) (dónde
Θ is the covariance):
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
1
9
7
1
8
6
7
0
4
5
norte
mi
norte
_
a
_
0
0
1
6
0
pag
d
t
/
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
ˆΦ = argminΦ≻0
registro(detΦ) + tr(ΘΦ) + λ ∑
j
(5)
Since Θ (covariance) is frequently rank deficient, we add a small value (δ) along the diagonal
to make it full rank. We define δ as 0.001 times the maximum value along the upper triangle
of the covariance.
All of the code used to perform the analysis described above are available at https://github
.com/wodeyara/fMRI-PC.
Cross-validation to Test SC Model of Functional Connectivity We tested whether the adaptive
graphical lasso produced estimates of the precision that show reduced error relative to applying
the graphical lasso, thereby directly demonstrating the link between structural and functional
conectividad. We split the fMRI data from patients into two halves. Using graphical lasso and
adaptive graphical lasso we estimated the precision ˜Φ1 on one half of samples of fMRI-BOLD
data and estimated the deviance when using this precision as the estimate of the inverse for
the covariance of the other half Θ2 of the data (y viceversa). Deviance was estimated as:
Dev = .5(−log(det ˜Φ1) + tr(Θ2 ˜Φ1) − log(det ˜Φ2) + tr(Θ1
˜Φ2))
(6)
We applied the process of cross-validation over the same range of penalization for λ1 in the
adaptive graphical lasso (3) and for λ in the graphical lasso (Ecuación 2). For the adaptive
graphical lasso (Ecuación 3) we maintained λ2 (the penalization for non-SC edges) constant
en 0.2.
Deviance:
Cross-validated error in estimating
the precision derived from the
log-likelihood for Gaussian
Graphical Models
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
1
9
7
1
8
6
7
0
4
5
norte
mi
norte
_
a
_
0
0
1
6
0
pag
d
/
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
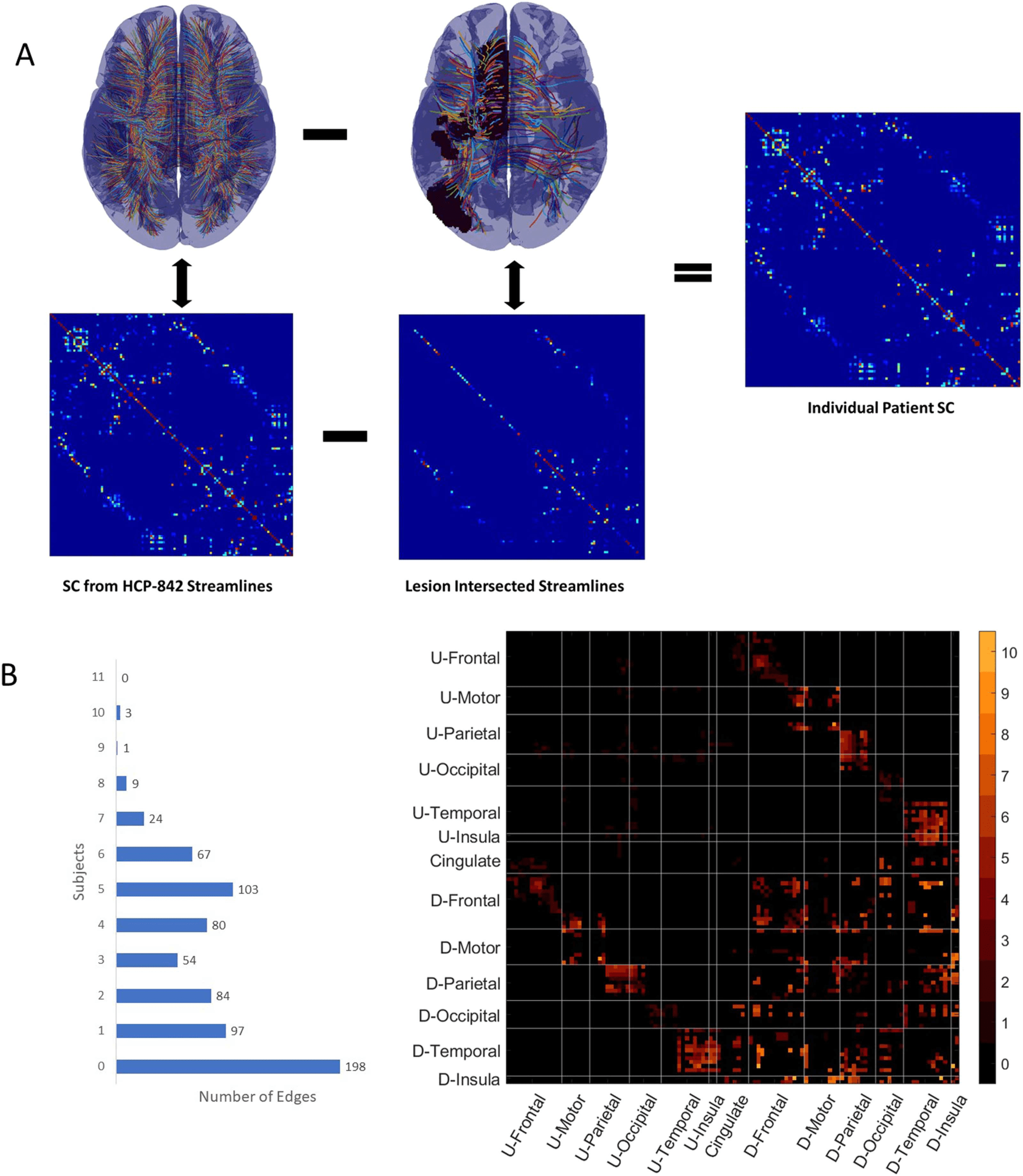
Cifra 2. Using the adaptive graphical lasso (AGL) for fMRI-PC. This figure shows the general
processing pipeline for applying the AGL to estimated patient fMRI covariance. The binarized un-
damaged SC is used to bias the penalization used when optimizing under the AGL to estimate the
precisión. We used the normalized precision to generate the partial correlation (fMRI-EC).
Neurociencia en red
1205
Damaged SC linked to altered rs-fMRI functional connectivity
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
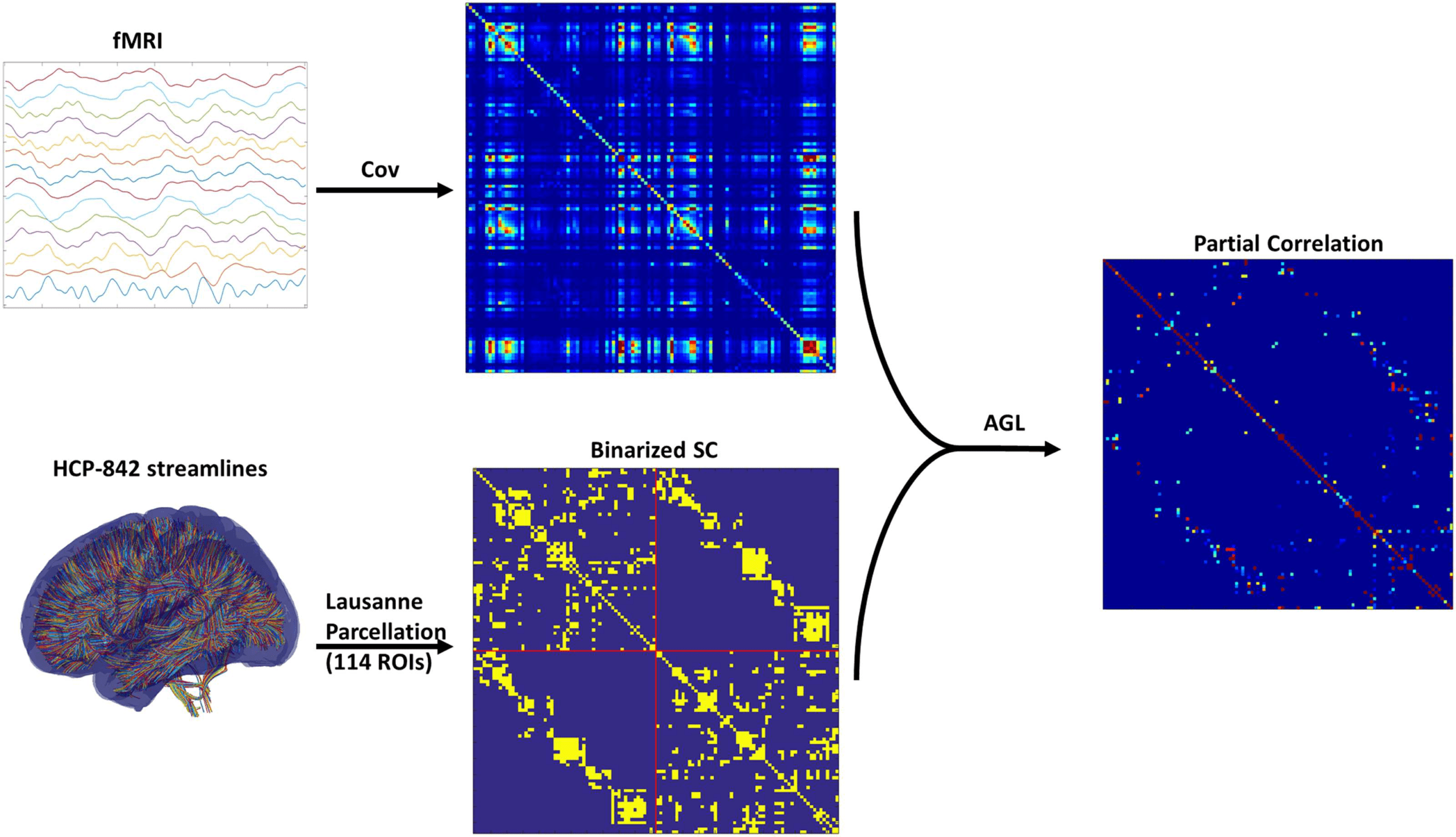
Cifra 3. Cross-validation of graphical lasso (GL) and adaptive graphical lasso (AGL). We show
actuación (cross-validated deviance) across penalization for the GL (on the left) and AGL (bien
figura). The error bars represent the standard deviation of the deviance across patients. Encontramos
that for all but very high penalization the AGL outperformed the GL. Más, the AGL shows minimal
cross-validated deviance for an optimal set of SC edges (at an SC penalization of 0.125) mientras que la
graphical lasso shows minimum deviance only for very sparse models.
We found that with the graphical lasso a sparser model (fewer connections) is always bet-
ter (indicated by the decreasing cross-validated deviance). Sin embargo, when using our adap-
tive graphical lasso, we find there is an optimal penalty which minimizes the cross-validated
deviance and consistently outperforms the graphical lasso see (Cifra 3). This clearly demon-
strates the structure-function relationship as the prior of using the SC provides useful infor-
mation in predicting the fMRI–partial correlation (evidenced by the reduced cross-validated
deviance) over and above using a uniform prior. The results from this analysis are shown in
Cifra 2. Based on the minimum deviance from cross-validation, we estimated fMRI-PC using
the adaptive graphical lasso with the penalization value of 0.125 on the SC edges (es decir., λ1 from
Ecuación 3) y 0.2 (λ2 from Equation 3) on the edges not in the SC.
Partial Correlation We estimate partial correlation as the summary statistic for the Gaussian
graphical model. We estimate the partial correlation (for any two areas x and y and estimated
precision ˜Φ):
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
1
9
7
1
8
6
7
0
4
5
norte
mi
norte
_
a
_
0
0
1
6
0
pag
d
/
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
PCxy =
Φxy
(cid:12)
(cid:12)
(cid:12)
(cid:12)
(cid:12)
Φxx ∗ Φyy (cid:12)
(cid:12)
(cid:12)
(cid:12)
(cid:12)
(7)
pag
We use PC as our estimate of the single-edge functional connectivity and refer to it as the
fMRI-PC. We use this partial correlation similarly to the correlation matrix when estimating
the impact of SC damage. This is discussed in section Estimating Functional Connectivity at
the ROI Level.
Neurociencia en red
1206
Damaged SC linked to altered rs-fMRI functional connectivity
Generalized linear model:
An extension to linear regression that
allows us to model response
variables that, given the predictors,
are not gaussian distributed, aquí,
gamma distributed.
fMRI streamline
conectividad funcional:
Using the termination points of
streamlines to determine the pair of
voxels for which we use the fMRI
data to estimate correlation.
Modeling Impact of SC Damage We transformed the correlation and partial correlation across
subjects by taking their absolute value and applying the Fisher r-to-z transform. For the partial
correlation we added a small value (10−4) to make all values nonzero since the gamma distri-
bution is undefined for 0. Let Cijk represent the transformed correlation between ROIs i and j
for subject k and Pijk the transformed partial correlation. We treat the Cijk and Pijk as gamma-
distributed variables (see Supporting Information Figure S1 for gamma distribution fit) porque
the values are positively valued and tend to be skewed toward the positive axis of the real line.
Using this notation, Cij: and Pik: represent the response vectors for gamma-(GLSM) generalized
linear models by using a log link function. We used the stratified SC damage as a predictor for
the GLM (represented as SCij:). Thus the models built for each structural connection Wij can
be represented as (E is the expectation):
ln(mi(Cij:)) = β0 + β1 ∗ SCij:
ln(mi(Pij:)) = β0 + β1 ∗ SCij:
(8)
(9)
The fMRI-C and partial correlation edge by edge models were multiple comparisons corrected
using false detection rate (FDR) correction with α set to 0.05.
Estimating Functional Connectivity at the Voxel Level
To calculate the functional connectivity estimates (correlation and partial correlation), we ini-
tially averaged over all voxels within each ROI, which averaged the fMRI data over both voxels
that contributed to the structural connectivity count and voxels that did not. We identified the
voxel-based analysis as a means of reducing this shortcoming of averaging the fMRI signal over
an ROI and instead hoped to identify the fMRI-C over single-edge paths (as a function of the
streamlines), which we expected would be a better correlate of structural connectivity from
the neural signals recorded by fMRI within each ROI.
The Lausanne estimate of any structural connectome edge aggregates structural connections
by counting the number of streamlines that connect a pair of ROIs. The termination points of
streamlines can be approximated as a voxel within each ROI, and only a subset of voxels serve
as termination points. Other voxels within the ROI have different streamline patterns, eso es,
they either connect to different ROIs or we do not have connectivity information for them
entirely.
We ran a fine-grained streamline-by-streamline analysis as we predicted we would be better
placed to then identify changes in the concomitant functional connectivity. Using the unique
pairs of voxel termination-points for every streamline, we estimated the fMRI streamline func-
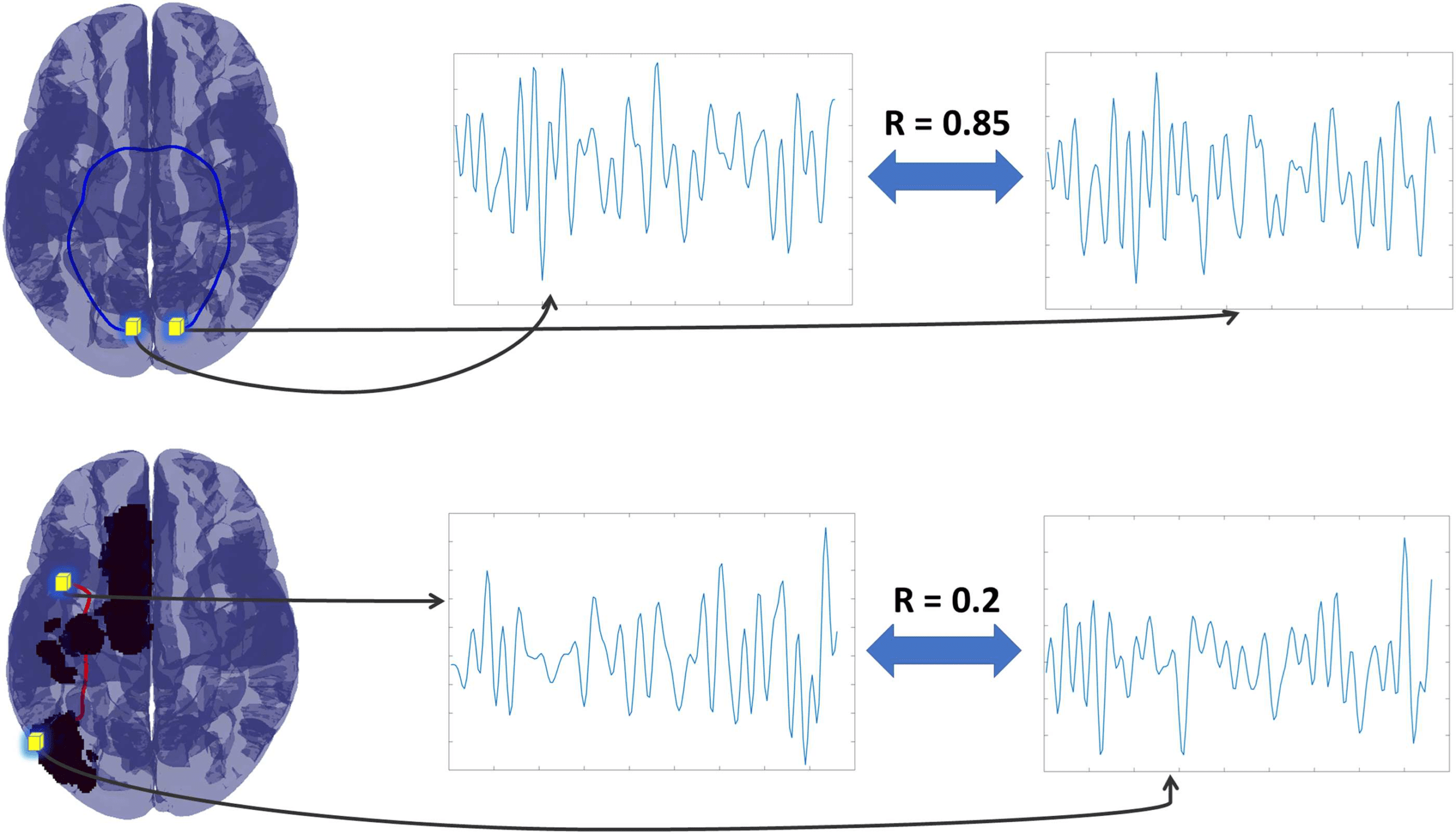
conectividad nacional (sFC) using the correlation of that pair of voxels (ver figura 4). This resulted
en, for every edge of the SC matrix for 114 ROI, a set of fMRI correlations derived for stream-
lines across subjects that were intact, and a set of fMRI correlations derived for streamlines
across subjects that were disconnected.
Finalmente, we tested different models of communication to identify which model better pre-
dicted which edges were likely to be modulated. We expected that modulated edges were more
likely to be part of multiedge pathways. So for this delimited set of edges we compared models
of functional connectivity generation (diffusion and shortest path routing) over the structural
connectome that use multiedge pathways but require different extents of information about
the structure.
Neurociencia en red
1207
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
1
9
7
1
8
6
7
0
4
5
norte
mi
norte
_
a
_
0
0
1
6
0
pag
d
/
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Damaged SC linked to altered rs-fMRI functional connectivity
Cifra 4. Streamline functional connectivity (sFC). We show how sFC was calculated for two
streamlines in two different patients. For each streamline the termination points were identified as
fMRI voxels (shown as the yellow shaded cubes in the brain in the leftmost column above), and we
estimated the correlation between these voxels. The same was done for both connected (fila superior
where the color blue indicates the streamline remained connected) and disconnected streamlines
(fila inferior, where the color red indicates a disconnected streamline). Arrows in the figure identify
the fMRI time series for the voxel termination points with the correlation between each pair of
voxels reported between the pair of time series. We repeated this process for all streamlines for
each subject.
Modeling Impact of SC Damage We took the absolute value of the streamline correlations and
applied the Fisher r-to-z transform. We again assumed that the correlation sCijkl for ROIs i and j
and streamline k for each subject l is gamma distributed (see Supporting Information Figure S2
for gamma distribution fit) and used this as the response variable. We used an indicator vari-
able sSCijkl that defined for ROIs i and j whether streamline k for a specific subject l was
disconnected (1) or connected (0) as the dependent variable. We built gamma GLMs across
subjects for each edge:
ln(mi(sCij::)) = β0 + β1 ∗ sSCij::
(10)
We corrected for multiple comparisons using FDR with α set to 0.05.
Communication Models of Functional Connectivity We tested using models of functional con-
nectivity whether we could estimate which edges showed the impact of damage when using
fMRI-sFC. We simulated functional connectivity weights (FC weights) given models of diffusion
(Goni et al., 2013) and shortest path (Goñi et al., 2014). Diffusion assumes that neural activity
randomly propagates across the connectome (with the probability of an edge being traversed
being proportional to its ROI relative weight) when passing between any two ROIs. en contra-
contraste, given a shortest path communication process, it’s assumed that neural activity takes the
shortest weighted path between any two ROIs. Note that a shortest path process depends on
global information of the structural connectome, while diffusion needs only local information
Neurociencia en red
1208
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
1
9
7
1
8
6
7
0
4
5
norte
mi
norte
_
a
_
0
0
1
6
0
pag
d
.
/
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Damaged SC linked to altered rs-fMRI functional connectivity
of the structural connectome. As the baseline case we also examine single-edge routing, el
process of activity spreading across direct SC edges.
We estimate functional connectivity under a diffusion process using the mean_first_passage_
time.m function from the Brain Connectivity Toolbox (Rubinov & despreciar, 2010). This function
estimates the “mean first passage time” (MFPT) between any two ROIs a and b—the average
number of weighted steps for a random walker going from a to b. We standardize (subtract
the mean and divide by the standard deviation) the MFPT across nodes and make it sym-
metric for analyses. A lower value of MFPT for an edge indicates it is more rapidly reached
by a random walker, indicating a higher expected functional connectivity. We estimate func-
tional connectivity under a shortest path routing process by using the betweenness centrality
(Rubinov & despreciar, 2010) for every edge. The edge betweenness centrality (BC) calculates how
many shortest paths use any edge in the structural connectome. We standardized the BC for our
análisis. A higher value of the BC indicates greater use by a shortest path routing process and
thus a higher expected functional connectivity. Finalmente, we directly used the standardized SC
weights as a third possible predictor of functional connectivity—increased structural connec-
tivity weights directly correspond to increased functional connectivity. All simulated functional
connectivity strengths were estimated using an undamaged weighted structural connectome.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
Edge betweenness centrality:
A measure of how many shortest
paths over a network use an edge.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
1
9
7
1
8
6
7
0
4
5
norte
mi
norte
_
a
_
0
0
1
6
0
pag
d
.
t
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
The set of edges (represented by Wdmg) where SC damage influenced our connectivity mea-
sure (fMRI-sFC) was assumed to be a binomially distributed random variable (with 1s when
damage significantly influenced connection strength and zero otherwise). Using Wilcoxon
rank-sum tests, we first examined whether there was a significant difference in diffusion (a nosotros-
ing MFPT), shortest path (using BC), and SCweight between edges where stroke-related damage
altered connection strength versus edges where it did not. When there was a significant differ-
ence between the two groups for multiple predictors, we built a logistic regression model as
follows (assuming for this example case that all three—MFPT/BC/SCweight—showed significant
diferencias):
logit(mi(Wdmg)) = β0 + β1 ∗ MFPT + β2 ∗ SCweight + β3 ∗ BC
(11)
RESULTADOS
ROI Level Analysis Shows that SC Damage Modulates fMRI-PC But Not fMRI-C
We averaged the fMRI data over each ROI of the Lausanne parcellation. Using this data we
computed the fMRI-C and fMRI-PC between the 114 cortical ROIs. We estimated the fMRI-PC
using the adaptive graphical lasso. We examined the models built between all pairs of appro-
priate SC edges with the response being the partial correlation/correlation, and the predictor
is the presence of white-matter damage. We initially only examined the set of edges where at
least three patients showed the presence of high damage. When examining fMRI-C we found
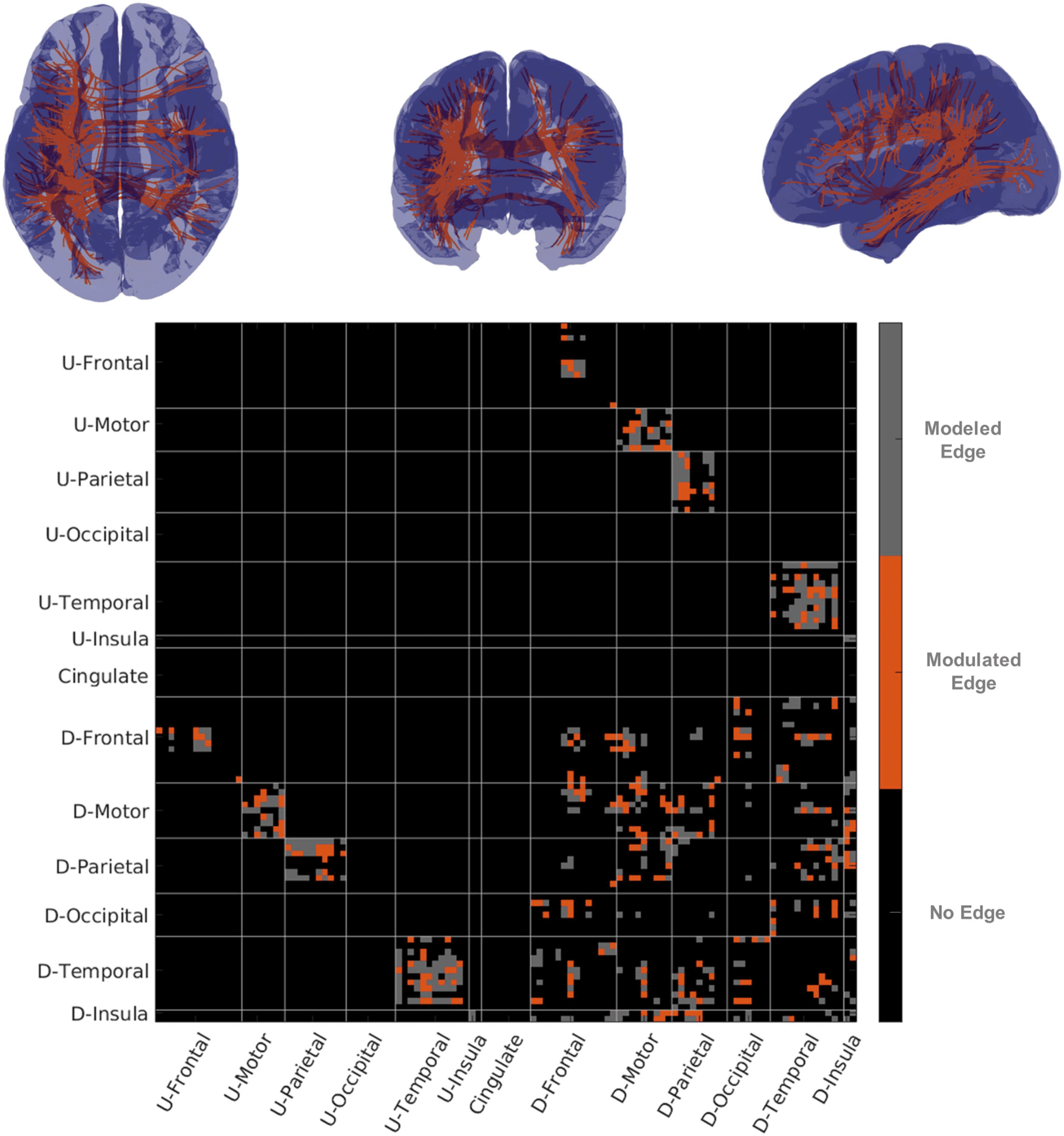
solo 1 edge out of 341 was significantly modulated by damage. When using the fMRI-PC
(Cifra 5) por otro lado, 24% (80/341) of edges were significantly modulated by damage
(applying an FDR correction for multiple comparisons). We also tested how many edges were
modulated by damage when we altered the number of patients who needed to show the pres-
ence of high damage before we modeled that edge. When we set our threshold at least five
patients showing high damage, we again only found 1 edge showing the presence of damage
in fMRI-C and 25% (52/207 bordes) using fMRI-PC. Finalmente, when we set the threshold to at least
seven patients, in fMRI-PC 22% (8/37) edges showed the presence of damage and no edges
in the fMRI-C showed the presence of damage. For an examination of all possible thresholds
and number of edges significant, please see Supporting Information Table S1.
Neurociencia en red
1209
Damaged SC linked to altered rs-fMRI functional connectivity
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
1
9
7
1
8
6
7
0
4
5
norte
mi
norte
_
a
_
0
0
1
6
0
pag
d
t
/
.
Cifra 5.
fMRI–partial correlation and structural connectivity. The top row of figures show repre-
sentative streamline connectivity (every edge where damage influenced fMRI-PC has one streamline
mostrado) for which damage influenced partial correlation. In the figure on the lower row we show a
matrix with edges modeled in gray and edges where fMRI-PC was modulated in orange. U-Areas
represent sets of areas in the undamaged (contralesional) hemisferio, and D-Areas represent groups
of areas in the damaged (ipsilesional) hemisferio.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Voxel-Level Analysis Shows that SC Damage Modulates fMRI-sFC
Similar to the analysis we used when we averaged fMRI data over ROIs, we examined the
streamline-based functional correlation. The fMRI-sFC analysis was also organized using the
114 ROI Lausanne parcellation. We built gamma GLMs between fMRI-sFC and the presence of
streamline disconnection for each edge where at least three patients showed high damage. Nosotros
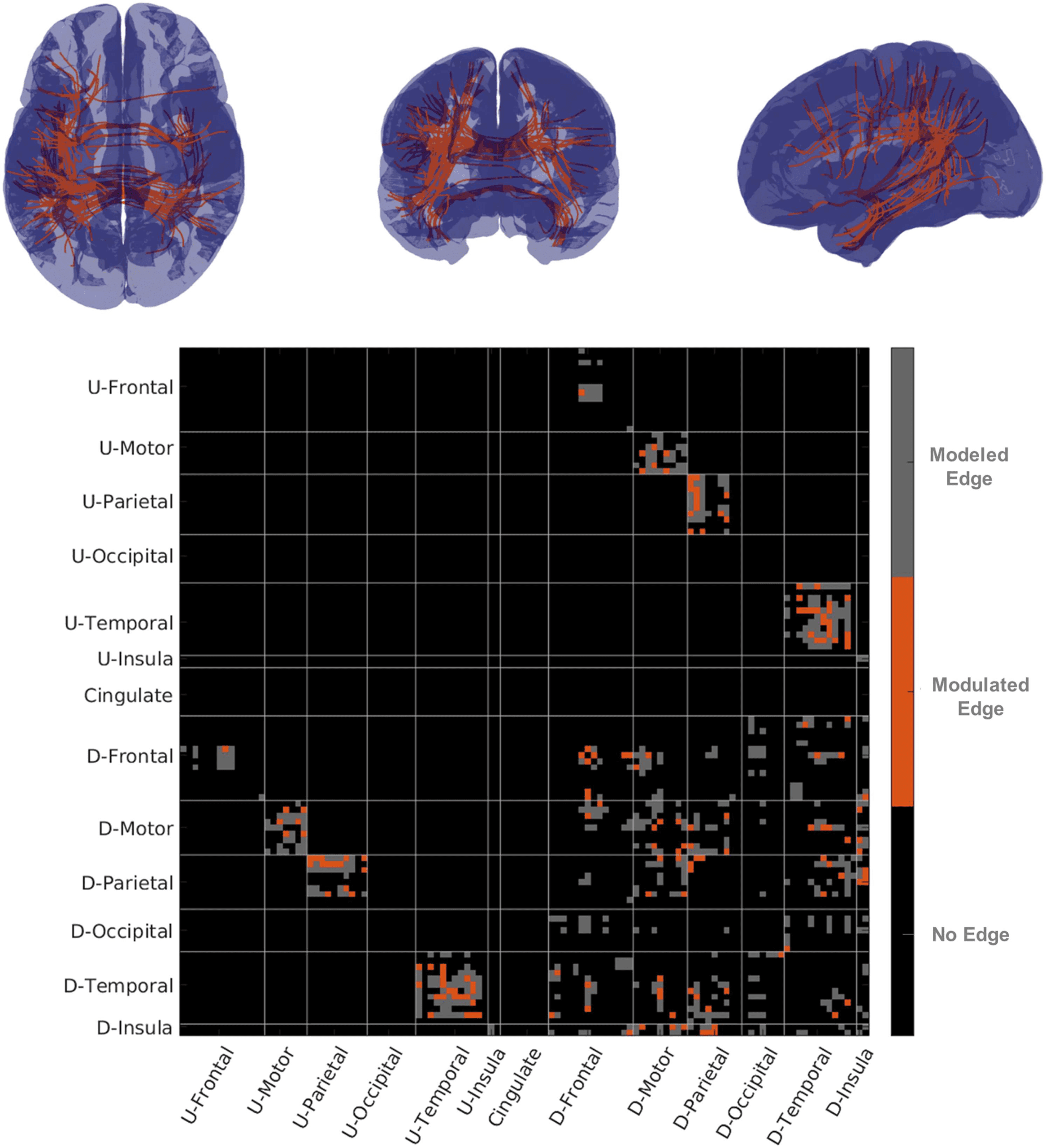
found that we could identify modulation from disconnection in the fMRI-sFC in 39% (132/341)
of the edges we modeled (ver figura 6). When at least five patients showed high damage, 38%
(79/207) of edges had sFC that was influenced by streamline disconnection, and when over
seven patients showed high damage then 15 out of 37 (41%) edges had sFC modulated by
disconnection.
Neurociencia en red
1210
Damaged SC linked to altered rs-fMRI functional connectivity
We examined the breakdown of where damage influenced fMRI-PC and fMRI-sFC by look-
ing at groups of ROIs (for a breakdown by pairs of regions, see Supporting Information Tables
S2 and S3). For the fMRI-sFC, we found that damage could be detected in 42% (37/89) of dam-
aged motor connections, 52% (16/31) of damaged occipital connections, y 39% (37/94) de
parietal connections. On the other hand for the fMRI-PC, we found that temporal (24%, 35/144
bordes), parietal (28%, 26/94 bordes) and the insula (25%, 8/32) reflected the impact of damage
the most often. For the sFC, intrahemispheric connections (42.5%, 77/181 of edges modeled)
were more easily identified relative to interhemispheric connections (31%, 50/160 of edges
modeled). Sin embargo, we saw this (weakly) reversed for the fMRI-PC where interhemispheric
connections were more easily identified 27% (43/160) relative to 20% (37/181) of intrahemi-
spheric connections modeled.
Relevance of SC Edges Modulating fMRI-sFC
Using the undamaged structural connectome, we estimated the MFPT and edge betweenness
centrality (BC) between all pairs of nodes. We extracted and standardized the SC weights
(SCweight), MFPT, and BC for the 341 edges where we modeled the impact of damage. Nosotros
treated these values as FC weight estimates and examined if they predicted the set of edges
where we could estimate the presence of damage in fMRI-sFC. Our analysis approach directly
compares these FC estimates against one another, while traditional analyses comparing differ-
ent communication models examine them across the entire connectome, including in places
where there isn’t a direct structural connection.
We found that all three FC weight estimates (MFPT, BC, and SCweight) were significantly
diferente (Wilcoxon rank-sum test, pag < 0.05) between edges where fMRI-sFC was modulated
or unmodulated by structural damage. To see their relative influence, we used them together
in a logistic regression model. The response for the model was a vector of length 341×1 with
zeroes for nonmodulated edges (fMRI-sFC did not significantly differ between damaged and
undamaged streamlines) and ones for modulated edges (fMRI-sFC significantly differed be-
tween damaged and undamaged streamlines). We found that MFPT (β MFPT = −0.63 ± 0.4,
95% CI; p = 0.003) had a stronger influence on the odds of an edge showing the impact of
damage than the betweenness centrality (βBC = 0.27 ± 0.32, 95% CI, p > 0.1) and the raw SC
weights (βSCweight = 1.5 ± 1.75, 95% CI, p > 0.1). The negative value indicates that for a unit
increase in (the standardized) MFPT, which indicates a reduced FC weight estimate, the odds
of damage impacting the fMRI-sFC are multiplicatively reduced by 0.52.
We reestimated the three FC weight estimates (MFPT, BC, and SCweight) when streamline
counts for each edge were not biased by length and also when we normalized the streamline
count by the product of ROI sizes for each pair of ROIs connected by an edge. Cuando el
SC edges were determined by the streamline counts directly (no normalization or biasing by
length), we again found the MFPT (β MFPT = −0.72 ± 0.31; pag = 7.75 × 10−6) to have a stronger
influence on the odds relative to betweenness centrality (βBC = 0.22 ± 0.32, p > 0.1) y el
SC weights (βSCweight = 0.24 ± 0.27, pag = 0.09) directly. Finalmente, when we normalized streamline
counts by the product of ROI sizes, we found that MFPT continues to have a stronger influence
on the odds, β MFPT = −0.77 ± 0.3 (pag = 1.3 × 10−6), while BC (βBC = 0.05 ± 0.26; p > 0.1)
and SC weights (βSCweight = 0.27 ± 0.3; pag = 0.09) aren’t significant predictors.
DISCUSIÓN
We found that a measure of functional connectivity averaged over ROIs that emphasized in-
formation shared over single-edge paths (partial correlation) was modulated in 24% of edges
Neurociencia en red
1211
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
1
9
7
1
8
6
7
0
4
5
norte
mi
norte
_
a
_
0
0
1
6
0
pag
d
/
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Damaged SC linked to altered rs-fMRI functional connectivity
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
1
9
7
1
8
6
7
0
4
5
norte
mi
norte
_
a
_
0
0
1
6
0
pag
d
.
/
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 6. Streamline functional connectivity and structural connectivity. In the top row figures
show representative streamline connectivity for edges for which damage influenced fMRI-sFC. On
the bottom row is a matrix with edges modeled in gray and edges where sFC was modulated in
naranja. U-Areas represents sets of areas in the undamaged (contralesional) hemisphere and D-Area
represents groups of areas in the damaged (ipsilesional) hemisferio.
with structural connectivity damage. Más, using the SC as a prior when estimating the fMRI–
partial correlation showed reduced predictive error to using a uniform prior. In parallel, nosotros
found that functional connectivity at the voxel level showed the impact of structural con-
nectivity damage in 39% of edges modeled, with the edges modulated under damage better
predicted by a multi-edge model of functional connectivity that uses only local information
about the SC (difusión). Juntos, when we considered BOLD signal at both the voxel scale
and the ROI scale, we saw how differences in structural connectivity were linked to changes
in functional connectivity. De este modo, Encontramos eso, in the brain, communication between neural
masses is mediated through anatomical connections. For pairs of regions that are not directly
anatomically connected due to lesions from stroke, signals must be communicated through
intermediate region-to-region steps along an anatomical path.
Neurociencia en red
1212
Damaged SC linked to altered rs-fMRI functional connectivity
The current study found that damage does not effectively modulate fMRI functional con-
nectivity as measured by correlation between ROIs. Partial correlation, as we hypothesized,
does show the impact of damage, though in a circumscribed set of edges. Past work employing
partial correlations to examine structural connectivity to functional connectivity relationships
have been few. In humans, partial correlation was used to study the voxel-level functional
connectivity and its relationship to the structural connectome (Horn, Ostwald, Reisert, &
Blankenburg, 2014). en este estudio (Horn et al., 2014), the authors found that while a signif-
icant relationship existed between voxel-level functional connectivity and the structural con-
nectome, the correlation between them was comparable to the correlation between voxel-
level functional and structural connectivity. Another study (Parque, Eo, & Parque, 2017) found that
structural connectome edge strength was correlated with the variability of partial correlation
across multiple sessions. Más, these authors (Park et al., 2017) found that the structural
connectome edge strength was less correlated with the fMRI-C, suggesting partial correlation
is a more robust link to structure. Finalmente, in a mouse study of the structure-to-function link
(Huebner et al., 2017), demyelination led to reduced partial correlations for long-range con-
nections. Our work is in line with the latter studies, since damage is clearly linked to fMRI-PC
rather than to fMRI-C.
Functional MRI data has millimeter-scale spatial resolution of neural activity. Sin embargo,
when estimating the fMRI-C and fMRI-PC, we removed this source of variability by averag-
ing over voxels in an ROI, which served to reduce the influence of noise, but also averaged
over heterogeneity in the neural activity present within an ROI. críticamente, averaging over vox-
els in an ROI combines fMRI data from voxels for which we have structural information with
those for which we do not have this information. By using fMRI-sFC, we tried to examine fMRI
data potentially at the scale at which we have structural connectivity information. One other
study followed a similar approach (Skudlarski et al., 2008) and found that when only exam-
ining pairs of voxels with a direct structural connection, and estimating a pseudo functional
connectivity from the structure by using all polysynaptic paths, they saw a correlation of 0.26
between the pseudo functional connectivity and empirical functional connectivity. When all
voxels were used to correlate their estimate of the pseudo functional connectivity with the
empirical functional connectivity, they saw a correlation of 0.18 across 5,000 vóxeles (nota
eso 61% of voxels were disconnected, es decir., pseudo functional connectivity was 0). Horn et al.
(2014) looked at the correlation between structural and functional connectivity at the voxel
nivel. They found the correlations were much weaker, 0.046 en 40,000 vóxeles; sin embargo, ellos
examined all-to-all voxel structural connections and voxel correlations. In our work, when ex-
amining voxel-level correlations between pairs of voxels connected by a-streamline, we saw
that the fMRI-sFC was modulated by streamline disconnection across 39% of the edges mod-
eled. Colectivamente, these findings suggest that choosing voxels by using streamlines may be a
good approach to constrain the data space for fMRI functional connectivity to that accessi-
ble to tractography applied to diffusion-weighted imaging when the goal is to link functional
connectivity to structural connectivity.
Several studies have examined what communication models most tightly link the func-
tional connectivity to structure. In a macaque study, the amygdala was inhibited using de-
signer receptors exclusively activated by designer drugs (DREADDs), which led to a reduction
in functional connectivity between amygdala and the rest of the brain (Grayson et al., 2016).
The decrease in functional connectivity could be predicted by a model of neural communica-
tion over the structural connectome that incorporated all walks (potentially repeated multiedge
pathways) across the network, requiring each node to possess only local information, capturado
by the communicability. Using communication models that incorporate all walks over the net-
work can be reexpressed as a graph eigenmode comparison problem (Tewarie et al., 2020).
Neurociencia en red
1213
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
1
9
7
1
8
6
7
0
4
5
norte
mi
norte
_
a
_
0
0
1
6
0
pag
d
t
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Damaged SC linked to altered rs-fMRI functional connectivity
Comparing the structure and function graph eigenmodes, Atasoy, Donnelly, & Pearson (2016)
and Robinson et al. (2016) demonstrated a tight relationship between the structure and func-
ción. Goñi et al. (2014) directly tested the relationship between the information about the con-
nectome needed by communication between two ROIs to occur over the shortest path and the
conectividad funcional, finding that lesser information needed to find the shortest path led to
higher functional connectivity. Other works (Abdelnour et al., 2014; Messé et al., 2015; Miši´c
et al., 2015; Osmanlıo˘glu et al., 2019) have used generative models that use only local infor-
mation about the connectome and have shown that functional connectivity is well explained
by these models. In related work to our analysis, Griffis, Metcalf, Corbetta, & Shulman (2020)
showed that using an estimate of shortest paths in a damaged structural connectome could pre-
dict altered functional connectivity. Sin embargo, they did not compare different communication
modelos. We examined whether specific communication models incorporating local informa-
ción (difusión) or global information (shortest paths) about the SC could be distinguished based
on the set of edges where damage was linked to altered fMRI-sFC. We found that edges with
rapid diffusion are more likely to show the fMRI-sFC modulation by damage, as compared
to edges that were central to the shortest paths between ROIs. By limiting our tests between
models to the actual edges of the structural connectome we provide new evidence for dif-
fusion as a relevant model of communication for functional connectivity. Finalmente, a crucial
analysis for future studies is the examination of nonzero functional connectivity at edges of
anatomical path lengths greater than 1 and their relationship to behavior and potential clinical
relevance.
For a short interval immediately following stroke (on the scale of weeks), past studies have
demonstrated an increased capacity for neural plasticity (Cramer et al., 2011; t. h. Murphy
& Corbett, 2009). Neural plasticity after a stroke can occur through new structural changes
or new functional organization of surviving neural elements, o ambos. In our work, tenemos
examined a group of patients in the subacute interval (entre 3 days to 1 mes) cuando nosotros
expected that while there is increased capacity for plasticity, the effects of plasticity are as yet
not expressed in all patients. We have treated every patient as having the same structure to
function relationship at every edge; sin embargo, this expectation may not be true. Our inability
to see the influence of damage at every edge modeled likely reflects this additionally hetero-
geneity in the data. Future work will hopefully examine the relationship between structure
and function in even more localized temporal intervals (say within the first week poststroke)
or during intervals far beyond initially elevated periods of plasticity to identify its impact (3 o
more months poststroke (Cassidy et al., 2020)). These studies will reveal in greater clarity the
structure-function relationship immediately poststroke, and the relationship after the effects of
neuroplasticity are expressed.
Our work is relevant to understanding the relationship between structure and function in
injury, pursuant to the caveats arising from our expectations of the influence of plasticity. El
fact that a large percentage of edges showed that the functional connectivity disruption will be
distinguishable in the presence of structural damage indicates that there is some constancy
in the relationship between structure and function under structural injury. There has been
simulation work (Alstott, romper la lanza, Hagmann, Cammoun, & despreciar, 2009; Cabral, Hugues,
Kringelbach, & decoración, 2012; Irimia & Van Horn, 2014; Váša et al., 2015) that found changes
to global network properties, and global functional dynamics (decrease in FC distant from le-
sión) in the presence of circumscribed lesion damage. These past studies have predominantly
assumed nonlinear associations between areas, and further, assumed that the structure-to-
function relationship is unaltered under damage, except for a change in connection strengths.
Future empirical and theoretical work would be needed to assess whether global network
Neurociencia en red
1214
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
1
9
7
1
8
6
7
0
4
5
norte
mi
norte
_
a
_
0
0
1
6
0
pag
d
/
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Damaged SC linked to altered rs-fMRI functional connectivity
consequences are simply a superposition of local SC-FC edge relationships (a linear relation-
barco) or result from nonlinear relationships. Given our knowledge of neuronal communication,
nonlinear relationships are expected at the neuronal scale; sin embargo, the SC-FC relationship
may be well approximated at the macroscale by a linear relationship. Our work (así como
that of Griffis et al., 2020) suggests weak evidence in favor of a linear relationship between SC
and FC, even under damage to the SC.
Major limitations in our work are linked to issues with tractography first, and secondly,
with virtual tractography. There are difficulties in tractography linked to overlapping fiber bun-
dles that make it hard to identify correct bundle endpoints, and strict correction of incorrect
streamlines can rapidly lead to large numbers of false negatives (Maier-Hein et al., 2017). Nuestro
decision to remove nonhomologous interhemispheric connectivity may have introduced a few
false negatives. By examining the structural connectome against a template, virtual tractogra-
phy ignores individual variability in white matter, both healthy and in relation to damage from
a lesion. While estimating structural connectivity damage with diffusion imaging for patients of
stroke is challenging (Karnath, Sperber, & Rorden, 2018), it remains plausible (Gleichgerrcht,
Fridriksson, Rorden, & Bonilha, 2017). Más, there is the potential for additional burden of
cerebrovascular risk factors within the set of subjects studied. As we do not know of their ac-
tual structure, our virtual tractography only approximates the entire extent of structural damage.
The results presented here made the best possible use of the stroke lesion imaging available via
structural MRI in conjunction with a pre-existing DTI atlas to obtain an estimate of white-matter
damage. It remains up to future work to examine the relationship of structure to function by
using individual estimates of structural connectomes drawn directly from diffusion-weighted
imaging. Another methodological limitation of this study is the use of a common space (MNI
template) to run our analyses. También, we use streamline end points to estimate fMRI-sFC. Cómo-
alguna vez, there will be cases where these end points are distant from gray matter. In our analysis
procedimiento, when this occurs, there is no fMRI signal at the voxels, and the streamline does
not contribute to discrimination of when damage influences fMRI-sFC. Finalmente, we have used
a short interval of fMRI data for our analysis (180 muestras), y, optimally, future work will
examine data collected for longer periods of time.
Despite these caveats, we found that we could see the influence of damage in 24% of SC
edges when using partial correlation and in 39% of SC edges when using streamline func-
conectividad nacional. Our work provides impetus to more deeply probe the structure-function
relationship, particularly the influence of multiedge pathways on functional connectivity both
in healthy brains and in injury.
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00160.
CONTRIBUCIONES DE AUTOR
Anirudh Wodeyar: Conceptualización; Análisis formal; Metodología; Software; Visualización;
Writing – Original Draft; Writing – Revisar & Editing. Jessica M Cassidy: Conceptualización;
Curación de datos; Adquisición de financiación; Investigación; Metodología; Writing – Revisar & Editing.
Steven C Cramer: Conceptualización; Adquisición de financiación; Metodología; Supervisión; Writing –
Revisar & Editing. Ramesh Srinivasan: Conceptualización; Adquisición de financiación; Metodología;
Recursos; Supervisión; Writing – Revisar & Editing.
Neurociencia en red
1215
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
1
9
7
1
8
6
7
0
4
5
norte
mi
norte
_
a
_
0
0
1
6
0
pag
d
/
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Damaged SC linked to altered rs-fMRI functional connectivity
REFERENCIAS
Abdelnour, F., Voss, h. Ud., & Raj, A.
(2014). Network diffusion
accurately models the relationship between structural and func-
tional brain connectivity networks. NeuroImagen, 90, 335–347.
Alstott, J., romper la lanza, METRO., Hagmann, PAG., Cammoun, l., & despreciar,
oh. (2009). Modeling the impact of lesions in the human brain.
Biología Computacional PLoS, 5(6), e1000408.
Atasoy, S., Donnelly, I., & Pearson, j.
(2016). Human brain net-
works function in connectome-specific harmonic waves. Naturaleza
Comunicaciones, 7, 10340.
Avena-Koenigsberger, A., Varios, B., & despreciar, oh. (2018). Commu-
nication dynamics in complex brain networks. Reseñas de naturaleza
Neurociencia, 19(1), 17.
Behzadi, y., Restom, K., Liau, J., & Liu, t. t. (2007). A component
based noise correction method (compcor) for bold and perfusion
based fMRI. NeuroImagen, 37(1), 90–101.
Burke, MI., Dodakian, l., Ver, J., McKenzie, A., Riley, j. D., Le, v., &
Cramer, S. C. (2014). A multimodal approach to understanding
motor impairment and disability after stroke. Journal of Neurol-
ogia, 261(6), 1178–1186.
Cabral, J., Hugues, MI., Kringelbach, METRO. l., & decoración, GRAMO. (2012). Mod-
eling the outcome of structural disconnection on resting-state
conectividad funcional. NeuroImagen, 62(3), 1342–1353.
Cammoun, l., Gigandet, X., Meskaldji, D., Thiran, j. PAG., despreciar, o.,
Do, k. P., . . . Hagmann, PAG. (2012). Mapping the human con-
nectome at multiple scales with diffusion spectrum mri. Diario
of Neuroscience Methods, 203(2), 386–397.
Cassidy, j. METRO., Tran, GRAMO., Quinlan, mi. B., & Cramer, S. C. (2018). nuevo-
roimaging identifies patients most likely to respond to a restora-
tive stroke therapy. Stroke, 49(2), 433–438.
Cassidy, j. METRO., Wodeyar, A., Wu, J., Kaur, K., Masuda, A. K.,
(2020). Low-frequency oscilla-
Srinivasan, r., & Cramer, S. C.
tions are a biomarker of injury and recovery after stroke. Stroke,
51(5), 1442–1450.
Cieslak, METRO. (2015). Easy lausanne. GitHub. Retrieved from https://
github.com/mattcieslak/easy_lausanne
Colby, j. B., Soderberg, l., Lebel, C., Dinov, I. D., Thompson, PAG. METRO.,
& Sowell, mi. R. (2012). Along-tract statistics allow for enhanced
tractography analysis. NeuroImagen, 59(4), 3227–3242.
Col, METRO. w., Ito, T., bassett, D. S., & Schultz, D. h. (2016). Activity
flow over resting-state networks shapes cognitive task activations.
Neurociencia de la naturaleza, 19(12), 1718.
Cramer, S. C., Sur, METRO., Dobkin, B. h., O’brien, C., Sanger, t. D.,
Trojanowski, j. P., . . . otros. (2011). Harnessing neuroplastic-
ity for clinical applications. Cerebro, 134(6), 1591–1609.
Drysdale, A. T., Grosenick, l., Downar, J., Dunlop, K., Mansouri, F.,
Meng, y., . . . otros. (2017). Resting-state connectivity biomark-
ers define neurophysiological subtypes of depression. Naturaleza
Medicamento, 23(1), 28.
Friedman, J., Hastie, T., & Tibshirani, R. (2008). Sparse inverse co-
variance estimation with the graphical lasso. Biostatistics, 9(3),
432–441.
Friston, k. j. (2011). Functional and effective connectivity: A review.
Brain Connectivity, 1(1), 13–36.
Friston, k. J., holmes, A. PAG., Poline, J., Grasby, PAG., williams, S.,
(1995). Analysis of fMRI time-
Frackowiak, R. S., . . . otros.
series revisited. Neuroimagen, 2(1), 45–53.
Gleichgerrcht, MI., Fridriksson, J., Rorden, C., & Bonilha, l. (2017).
Connectome-based lesion-symptom mapping (clsm): A novel
approach to map neurological function. NeuroImagen: Clinical,
16, 461–467.
Goni, J., Avena-Koenigsberger, A., de Mendizabal, norte. v., van den
Colina, METRO. PAG., Betzel, R. F., & despreciar, oh. (2013). Exploring the
morphospace of communication efficiency in complex networks.
Más uno, 8(3), e58070.
Goñi,
J., van den heuvel, METRO. PAG., Avena-Koenigsberger, A.,
de Mendizabal, norte. v., Betzel, R. F., Griffa, A., . . . despreciar, oh.
(2014). Resting-brain functional connectivity predicted by ana-
lytic measures of network communication. Actas de la
Academia Nacional de Ciencias, 111(2), 833–838.
Grayson, D. S., Bliss-Moreau, MI., Machado, C. J., bennett, J., shen,
K., Grant, k. A., . . . Amaral, D. GRAMO.
(2016). The rhesus mon-
key connectome predicts disrupted functional networks resulting
from pharmacogenetic inactivation of the amygdala. Neurona,
91(2), 453–466.
Greicius, METRO. D., Krasnow, B., Reiss, A. l., & menón, V. (2003). Func-
tional connectivity in the resting brain: A network analysis of the
default mode hypothesis. Proceedings of the National Academy
of Sciences, 100(1), 253–258.
Griffis, j. C., Metcalf, norte. v., Corbetta, METRO., & Shulman, GRAMO. l. (2020).
Damage to the shortest structural paths between brain regions is
associated with disruptions of resting-state functional connectiv-
ity after stroke. NeuroImagen, 210, 116589.
Hagmann, PAG., Cammoun, l., Gigandet, X., Meuli, r., Honey, C. J.,
Wedeen, V. J., et al. (2008). Mapping the structural core of hu-
man cerebral cortex. Biología PLoS, 6(7), e159.
Honey, C. J., kötter, r., romper la lanza, METRO., & despreciar, oh. (2007). Net-
work structure of cerebral cortex shapes functional connectivity
on multiple time scales. Proceedings of the National Academy
of Sciences, 104(24), 10240–10245.
Horn, A., Ostwald, D., Reisert, METRO., & Blankenburg, F. (2014). El
structural–functional connectome and the default mode network
of the human brain. NeuroImagen, 102, 142–151.
Hsieh, C.-J., Dhillon, I. S., Ravikumar, PAG. K., & Sustik, METRO. A. (2011).
Sparse inverse covariance matrix estimation using quadratic ap-
proximation. In Advances in neural information processing sys-
tems (páginas. 2330–2338).
Huebner, norte. S., Mechling, A. MI., Sotavento, H.-L., Reisert, METRO., Bienert, T.,
Hennig, J., . . . Harsan, L.-A. (2017). The connectomics of brain
demyelination: Functional and structural patterns in the cupri-
zone mouse model. NeuroImagen, 146, 1–18.
Irimia, A., & Van Horn, j. D.
(2014). Systematic network lesion-
ing reveals the core white matter scaffold of the human brain.
Frontiers in Human Neuroscience, 8, 51.
Johansen-Berg, h., & Rushworth, METRO. F.
(2009). Using diffusion
imaging to study human connectional anatomy. Annual Review
of Neuroscience, 32, 75–94.
Neurociencia en red
1216
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
1
9
7
1
8
6
7
0
4
5
norte
mi
norte
_
a
_
0
0
1
6
0
pag
d
/
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Damaged SC linked to altered rs-fMRI functional connectivity
Karnath, H.-O., Sperber, C., & Rorden, C. (2018). Mapping human
brain lesions and their functional consequences. NeuroImagen,
165, 180–189.
Koch, METRO. A., Norris, D. GRAMO., & Hund-Georgiadis, METRO.
(2002). Un
investigation of functional and anatomical connectivity using
magnetic resonance imaging. NeuroImagen, 16(1), 241–250.
Korhonen, o., Saarimäki, h., Glerean, MI., Sams, METRO., & Saramäki, j.
(2017). Consistency of regions of interest as nodes of fMRI func-
tional brain networks. Neurociencia en red, 1(3), 254–274.
Kuceyeski, A., Maruta, J., Relkin, NORTE., & Raj, A. (2013). The network
modification (nemo) tool: elucidating the effect of white matter
integrity changes on cortical and subcortical structural connec-
actividad. Brain Connectivity, 3(5), 451–463.
li, J., kong, r., Liegeois, r., Orban, C., Broncearse, y., Sol, NORTE., . . . yo, B. t.
(2019). Global signal regression strengthens association between
resting-state functional connectivity and behavior. NeuroImagen,
196, 126–141.
Liem, F., Varoquaux, GRAMO., Kynast, J., Beyer, F., Masouleh, S. K.,
Huntenburg, j. METRO., . . . otros. (2017). Predicting brain-age from
multimodal imaging data captures cognitive impairment. nuevo-
roImage, 148, 179–188.
J.-C., Côté, M.-A.,
Maier-Hein, k. h., Neher, PAG. F., Houde,
Garyfallidis, MI., Zhong, J., . . . otros.
(2017). El reto
of mapping the human connectome based on diffusion tractog-
raphy. Comunicaciones de la naturaleza, 8(1), 1349.
Marrelec, GRAMO., Krainik, A., Duffau, h., Pélégrini-Issac, METRO., Lehéricy,
S., Doyon, J., & Benali, h.
(2006). Partial correlation for func-
tional brain interactivity investigation in functional MRI. nuevo-
roImage, 32(1), 228–237.
Menéndez, PAG., Kourmpetis, Y. A., ter Braak, C. J., & van Eeuwijk,
(2010). Gene regulatory networks from multifactorial
F. A.
perturbations using graphical lasso: Application to the dream4
challenge. Más uno, 5(12), e14147.
Messé, A., Rudrauf, D., Giron, A., & Marrelec, GRAMO. (2015). Predict-
ing functional connectivity from structural connectivity via com-
putational models using MRI: An extensive comparison study.
NeuroImagen, 111, 65–75.
Miši´c, B., Betzel, R. F., Nematzadeh, A., Goñi,
J., Griffa, A.,
Hagmann, PAG., . . . despreciar, oh. (2015). Cooperative and compet-
itive spreading dynamics on the human connectome. Neurona,
86(6), 1518–1529.
Murphy, K., & Dunham, METRO. (2008). Pmtk: Probabilistic modeling
In Neural information processing systems (NIPS) trabajar-
toolkit.
shop on probabilistic programming.
Murphy, K., & Fox, METRO. D. (2017). Towards a consensus regarding
global signal regression for resting state functional connectivity
resonancia magnética. NeuroImagen, 154, 169–173.
Murphy, t. h., & Corbett, D. (2009). Plasticity during stroke recov-
ery: from synapse to behaviour. Naturaleza Reseñas Neurociencia,
10(12), 861–872.
Noh, j. D., & Rieger, h.
(2004). Random walks on complex net-
obras. Physical Review Letters, 92(11), 118701.
Osmanlıo˘glu, y., Tunç, B., parker, D., eliot, METRO. A., Baum, GRAMO. l.,
círico, r., . . . Verma, R. (2019). System-level matching of struc-
tural and functional connectomes in the human brain. Neuro-
Image, 199, 93–104.
O’Reilly, j. X., Croxson, PAG. l., Jbabdi, S., Sallet, J., Noonan, METRO. PAG.,
Mars, R. B., . . . otros. (2013). Causal effect of disconnection
lesions on interhemispheric functional connectivity in rhesus
monkeys. procedimientos de la Academia Nacional de Ciencias,
110(34), 13982–13987.
Parque, B., Eo, J., & Parque, H.-J. (2017). Structural brain connectivity
constrains within-a-day variability of direct functional connectiv-
idad. Frontiers in Human Neuroscience, 11, 408.
Pineda-Pardo, j. A., Bruña, r., lana rica, METRO., Marcos, A., Nobre,
A. C., Maestú, F., & Vidaurre, D.
(2014). Guiding functional
connectivity estimation by structural connectivity in meg: Un
application to discrimination of conditions of mild cognitive
impairment. NeuroImagen, 101, 765–777.
Fuerza, j. D., Schlaggar, B. l., & Petersen, S. mi.
(2014). Studying
brain organization via spontaneous fMRI signal. Neurona, 84(4),
681–696.
Pustina, D., Coslett, h. B., Ungar, l., Faseyitan, oh. K., Medalla,
j. D., Avants, B., & Schwartz, METRO. F. (2017). Enhanced estimations
of post-stroke aphasia severity using stacked multimodal predic-
ciones. Mapeo del cerebro humano, 38(11), 5603–5615.
Rane, PAG., Cochran, D., Hodge, S. METRO., Haselgrove, C., Kennedy, D.,
& Frazier, j. A. (2015). Connectivity in autism: A review of MRI
connectivity studies. Harvard Review of Psychiatry, 23(4), 223.
Reid, A. T., Headley, D. B., Mill, R. D., Sanchez-Romero, r., Uddin,
l. P., Marinazzo, D., & Col, METRO. (2019). Advancing functional
connectivity research from association to causation. Naturaleza
Neurociencia, 1(10).
Riley, j. D., Le, v., Der-Yeghiaian, l., Ver, J., Newton, j. METRO., Ward,
norte. S., & Cramer, S. C. (2011). Anatomy of stroke injury predicts
gains from therapy. Stroke, 42(2), 421–426.
robinson, PAG. A., zhao, X., Aquino, k. METRO., Griffiths, J., Sarkar, S., &
Mehta-Pandejee, GRAMO. (2016). Eigenmodes of brain activity: Neural
field theory predictions and comparison with experiment. Neuro-
Image, 142, 79–98.
Rubinov, METRO., & despreciar, oh. (2010). Complex network measures of
conectividad cerebral: uses and interpretations. NeuroImagen, 52(3),
1059–1069.
Ryali, S., Chen, T., Supekar, K., & menón, V.
(2012). Estimation
of functional connectivity in fMRI data using stability selection-
based sparse partial correlation with elastic net penalty. nuevo-
roImage, 59(4), 3852–3861.
Skudlarski, PAG., Jagannathan, K., Calhoun, V. D., Hampson, METRO.,
Skudlarska, B. A., & Pearlson, GRAMO. (2008). Measuring brain con-
conectividad: Diffusion tensor imaging validates resting state tempo-
ral correlations. NeuroImagen, 43(3), 554–561.
Herrero, S. METRO., Molinero, k. l., Salimi-Khorshidi, GRAMO., Webster, METRO.,
beckman, C. F., Nichols, t. MI., . . . lana rica, METRO. W..
(2011).
Network modelling methods for fMRI. NeuroImagen, 54(2), 875–891.
(2005). The human connec-
a mi: A structural description of the human brain. PLoS Compu-
tational Biology, 1(4), e42.
despreciar, o., Tononi, GRAMO., & kötter, R.
Straathof, METRO., Sinke, METRO. r., Dijkhuizen, R. METRO., & Otte, W.. METRO. (2018).
A systematic review on the quantitative relationship between
structural and functional network connectivity strength in mam-
Journal of Cerebral Blood Flow & Metabolism,
malian brains.
0271678X18809547.
Neurociencia en red
1217
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
1
9
7
1
8
6
7
0
4
5
norte
mi
norte
_
a
_
0
0
1
6
0
pag
d
t
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Damaged SC linked to altered rs-fMRI functional connectivity
Tewarie, PAG., Prasse, B., Meier,
Tavor, I., jones, oh. PAG., Mars, r., Herrero, S., Behrens, T., & Jbabdi,
S. (2016). Task-free MRI predicts individual differences in brain
activity during task performance. Ciencia, 352(6282), 216–220.
j. METRO., Santos, F. A., Douw, l.,
Schoonheim, METRO., . . . Hillebrand, A.
(2020). Mapping func-
tional brain networks from the structural connectome: Relating
the series expansion and eigenmode approaches. NeuroImagen,
116805.
Van Den Heuvel, METRO. PAG., Mandl, R. C., Kahn, R. S., & Hulshoff Pol,
h. mi.
(2009). Functionally linked resting-state networks reflect
the underlying structural connectivity architecture of the human
cerebro. Mapeo del cerebro humano, 30(10), 3127–3141.
VanEssen, D. C., Herrero, S. METRO., Respeto, D. METRO., Behrens, t. MI.,
Yacoub, MI., Ugurbil, K., . . . otros. (2013). The Wu-Minn human
connectome project: an overview. NeuroImagen, 80, 62–79.
Varoquaux, GRAMO., Gramfort, A., Poline, J.-B., & Thirion, B.
(2010).
Brain covariance selection: Better individual functional connec-
tivity models using population prior. In Advances in neural infor-
mation processing systems (páginas. 2334–2342).
Váša, F., Shanahan, METRO., Hellyer, PAG. J., Scott, GRAMO., Cabral, J., & Sanguijuela,
(2015). Effects of lesions on synchrony and metastability in
R.
cortical networks. NeuroImagen, 118, 456–467.
Whitfield-Gabrieli, S., & Nieto-Castanon, A.
(2012). Conn: A
functional connectivity toolbox for correlated and anticorrelated
redes cerebrales. Brain Connectivity, 2(3), 125–141.
(1999).
xiong, J., Parsons, l. METRO., gao, J.-H., & Fox, PAG. t.
Interre-
gional connectivity to primary motor cortex revealed using MRI
resting state images. Mapeo del cerebro humano, 8(2–3), 151–156.
Yeh, F.-C., Panesar, S., Fernandes, D., Meola, A., Yoshino, METRO.,
Fernandez-Miranda, j. C., . . . Petrificar, t. (2018). Population-
averaged atlas of the macroscale human structural connectome
and its network topology. NeuroImagen, 178, 57–68.
Zerenner, T., Friederichs, PAG., Lehnertz, K., & Hense, A.
(2014). A
gaussian graphical model approach to climate networks. Chaos:
An Interdisciplinary Journal of Nonlinear Science, 24(2), 023103.
Zou, h. (2006). The adaptive lasso and its oracle properties. Diario
of the American Statistical Association, 101(476), 1418–1429.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
1
9
7
1
8
6
7
0
4
5
norte
mi
norte
_
a
_
0
0
1
6
0
pag
d
t
/
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Neurociencia en red
1218