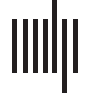FUNCIÓN DE ENFOQUE:
Network Communication in the Brain
Communicability distance reveals hidden
patterns of Alzheimer’s disease
Eufemia Lella1,2 and Ernesto Estrada
3,4
1Istituto Nazionale di Fisica Nucleare, Sezione di Bari, Barí, Italia
2Innovation Lab, Exprivia S.p.A., Molfetta, Italia
3Institute of Applied Mathematics (IUMA), Universidad de Zaragoza, Zaragoza, España
4ARAID Foundation, Government of Aragón, Zaragoza, España
un acceso abierto
diario
Palabras clave: Communicability distance, Conectividad cerebral, Alzheimer’s disease, Susceptible-infected
modelo, Graph theory
ABSTRACTO
The communicability distance between pairs of regions in human brain is used as a
quantitative proxy for studying Alzheimer’s disease. Using this distance, we obtain the
shortest communicability path lengths between different regions of brain networks from
patients with Alzheimer’s disease (ANUNCIO) and healthy cohorts (HC). We show that the shortest
communicability path length is significantly better than the shortest topological path length
in distinguishing AD patients from HC. Based on this approach, we identify 399 pairs of
brain regions for which there are very significant changes in the shortest communicability
path length after AD appears. encontramos que 42% of these regions interconnect both brain
hemispheres, 28% connect regions inside the left hemisphere only, y 20% affect vermis
connection with brain hemispheres. These findings clearly agree with the disconnection
syndrome hypothesis of AD. Finalmente, we show that in 76.9% of damaged brain regions the
shortest communicability path length drops in AD in relation to HC. This counterintuitive
finding indicates that AD transforms the brain network into a more efficient system from the
perspective of the transmission of the disease, because it drops the circulability of the disease
factor around the brain regions in relation to its transmissibility to other regions.
RESUMEN DEL AUTOR
We use a geometric measure for the separation of the different regions in the brain, cual
accounts for how well such regions communicate to each other. Our approach is based on
the consideration of a “susceptible-infected” model of the propagation of a disease factor
across the brain network. Our first important result is the finding that the shortest
communicability path length is significantly better than the shortest topological path length
in differentiating patients with Alzheimer’s disease (ANUNCIO) from healthy individuals. El segundo
and most important finding is the extraction of structural factors that seems to be responsible
for the appearance of AD. En particular, we find brain regions in which communicability
distance is significantly affected by AD. Most of them interconnect both brain hemispheres or
the vermis with them. Remarkably and counterintuitively, we found that in 76.9% de
damaged brain regions there is a drop in the communicability distance, indicating that AD
makes the brain network more efficient to the transmission of the disease between brain
regiones.
Citación: Lella, MI., & Estrada, mi. (2020).
Communicability distance reveals
hidden patterns of Alzheimer’s
enfermedad. Neurociencia en red, 4(4),
1007–1029. https://doi.org/10.1162
/netn_a_00143
DOI:
https://doi.org/10.1162/netn_a_00143
Recibió: 14 Febrero 2020
Aceptado: 29 Abril 2020
Conflicto de intereses: Los autores tienen
declaró que no hay intereses en competencia
existir.
Autor correspondiente:
Ernesto Estrada
estrada66@posta.unizar.es
Editor de manejo:
Bratislav Misic
Derechos de autor: © 2020
Instituto de Tecnología de Massachusetts
Publicado bajo Creative Commons
Atribución 4.0 Internacional
(CC POR 4.0) licencia
La prensa del MIT
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
0
0
7
1
8
6
7
0
0
5
norte
mi
norte
_
a
_
0
0
1
4
3
pag
d
t
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Communicability distance and Alzheimer’s
INTRODUCCIÓN
The human brain is arguably the most complex of all complex systems. At the most basic struc-
tural level of interest for neurosciences, the human brain consists of 1011 neurons and 1012 glial
cells, which communicate through neural projections (Herculano-Houzel, 2009). These cells
are then packed into local circuits (DeBello et al., 2014) or large gyri, which define anatomical
and functional regions in the brain. The human brain is considered to be outstanding among
mammalian brains: it is the largest than expected from body size, and it has an overdevel-
oped cerebral cortex representing over 80% of brain mass (González-Forero & jardinero, 2018;
Herculano-Houzel, 2009). Most of the complexity of these different size scales of the human
brain comes not only from the number of its components but mainly from the intricate webs
of connections linking these components. The emerging field of network neuroscience studies
the structural and dynamical properties of these webs observed at different size scales from a
variety of noninvasive neuroimaging techniques (bassett & despreciar, 2017). The term pathocon-
nectomics has been coined by Rubinov and Bullmore (2013) to describe the use of network
neuroscience techniques on the analysis of abnormal brain networks (see also Stam, 2014).
The goals of pathoconnectomics are not only of practical relevance as in the early diagnosis
of psychiatric and developmental disorders, stroke, severe brain injury, and neurodegenerative
diseases, but also in the understanding of their causal mechanisms as pointed out by Raj and
Powell (2018). Due to its societal challenge, Alzheimer’s disease (ANUNCIO) has become a major
focus of the pathoconnectomic research agenda. AD is the most common neurodegenera-
tive disorder and it represents a major growing health problem for elderly population (Head
et al., 2004; Impedovo, Pirlo, Vessio, & Angelillo, 2019; Lo et al., 2010; Rose et al., 2000).
It is characterized by a continuous degradation of the patient, which starts with a preclinical
stage, a phase of mild cognitive impairment (MCI), and finishes with dementia. The molec-
ular basis of these different stages appear to be linked to the presence of β-amyloid (Aβ) en
senile plaques and cerebral amyloid angiopathy, as well as tau proteins (tau) in neurofibrillary
tangles (Brettschneider, Del Tredici, Sotavento, & Trojanowski, 2015; Jack Jr. et al., 2013; Jucker &
Caminante, 2011). Por ejemplo, the cognitive decline in AD correlates with tauopathy (Braak &
Braak, 1991; Crystal et al., 1988; Wilcock & Esiri, 1982), while the aggregation of Aβ appears
to be critical in the early stages that trigger events conducting to tauopathy, neuronal dysfunc-
ción, and dementia (Hardy & Selkoe, 2002). Entonces, it is plausible that these proteins, Aβ and
tau, originate in a particular region of the brain and then propagate through neural fibers in a
prion-like manner (Jucker & Caminante, 2013; Mandelkow & Mandelkow, 1998; Caminante & Jucker,
2015; Warren et al., 2013).
The hypothesis of the self-propagation of AD in combination with network neurosciences
has triggered the use of epidemiological models on networks to simulate the propagation of
a disease factor as AD progresses. En particular, Peraza et al. (2019) have proposed the use of
the susceptible-infected (SI) model on networks (ver, por ejemplo, Canright & Engø-Monsen,
2006; Mei, Mohagheghi, Zampieri, & Bullo, 2017; Hombre nuevo, 2010), in which nodes are in two
possible states, infected (I) or susceptible (S). The first corresponds to brain regions wherein the
disease factor is present with high probability, while the second are those free of the disease
factor but that can be infected from any infected nearest neighbor. Similar principles have
guided Iturria-Medina et al. (2014) in modeling the progression of AD under the Network
Diffusion Model of disease progression in dementia (Raj, Kuceyeski, & Weiner, 2012).
Susceptible-infected model:
Epidemiological model where
individuals can be either susceptible
to a disease or be infected by it.
Network communicability:
A measure of how a perturbation in a
node is transmitted to another by
using all possible channels.
Here we start by adopting the SI-model for the propagation of a disease factor in AD. Cómo-
alguna vez, we use this model to connect with the theory of network communicability, which has
been widely used in network neurosciences (for some applications of communicability in
pathoconnectomics, see Crofts & Higham, 2009; Crofts et al., 2011; de Lange et al., 2019;
Neurociencia en red
1008
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
0
0
7
1
8
6
7
0
0
5
norte
mi
norte
_
a
_
0
0
1
4
3
pag
d
.
t
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Communicability distance and Alzheimer’s
Shortest communicability path:
The shortest path between two nodes
in which the edges are weighted by
the communicability distance.
Shortest topological path:
The shortest of all topological paths
between two nodes.
Topological path:
Sequence of nodes and edges
without repetition that connect two
nodos.
Disconnection syndrome:
Alteration of the connections
between different brain regions
rather than in the regions itself.
De Reus & van den heuvel, 2014; Johansen-Berg, Scholz, & Stagg, 2010; Lella et al., 2019;
Le et al., 2013; Mancini et al., 2016; Qin et al., 2015; Sanchez-Rodriguez et al., 2018; taylor
et al., 2018). Eso es, we will provide a theoretical connection between the network commu-
nicability and the probability of a disease factor of propagating from one node to another in a
network. Using this connection, we will consider a measure that accounts for the difference be-
tween the circulability of this disease factor around a given pair of nodes and its transmissibility
from one region to the other. This measure is a Euclidean distance metric—communicability
distance—for the corresponding pair of nodes in the network. We then find the length of the
shortest communicability paths between every pair of regions in human brains for cohorts of
saludable (HC) and AD individuals after appropriate normalization. We report in this work that
(i) the shortest communicability path length is orders of magnitude more significant in distin-
guishing AD from HC than the shortest topological path length, (ii) there is a set of 399 pares
of regions for which there are very significant changes in the shortest communicability path
length after AD, y (iii) 42% of these significant pairs of brain regions interconnect both brain
hemispheres, mientras 28% connect regions inside the left hemisphere only, in agreement with
findings related to the disconnection syndrome. Además, 20% of these pairs of affected
regions are connecting the vermis with any of the two brain hemispheres, in agreement with
recent results; (iv) para 76.9% of these pairs of damaged brain regions there is an increase in
the average cliquishness of the intermediate regions that connect them, which implies a sig-
nificantly higher energy consumption for communication between these regions in AD than
in HC.
THEORETICAL APPROACH
Here we will use indistinguishably the terms graph and network and follow the classical no-
tation in network theory (ver, por ejemplo, Estrada, 2012C). A graph G = (V, mi) is defined by
a set of n nodes (vertices) V and a set of m edges E = {(tu, v)|tu, v ∈ V} between the nodes.
The degree of a vertex is the number of edges incident to it. A walk of length k in G is a set of
nodes i1, i2, . . . , I, ik+1 such that for all 1 ≤ l ≤ k, (il, il+1) ∈ E. A closed walk is a walk for
which i1 = ik+1. A path is a walk with no repeated nodes. The length of a path is the number
of edges in that path. The shortest of all paths connecting the same pair of vertices is known
as the shortest topological path. A graph is connected if there is a path connecting every pair
de nodos. Here we will only consider connected graphs.
Let A be the adjacency matrix of the graph, which for simple finite graphs is symmetric, y
thus its eigenvalues are real. We label the eigenvalues of A in nonincreasing order: λ1 ≥ λ2 ≥
. . . ≥ λn. Since A is a real-valued, symmetric matrix, we can decompose A into A = UΛUT,
−→
where Λ is a diagonal matrix containing the eigenvalues of A and U = [
ψ n] es
−→
orthogonal, dónde
ψ i is an eigenvector associated with λi. Because the graphs considered
here are connected, A is irreducible and from the Perron–Frobenius theorem we can deduce
−→
that λ1 > λ2 and that the leading eigenvector
ψ 1, which will be sometimes referred to as the
Perron vector, can be chosen such that its components
−→
ψ 1(tu) are positive for all u ∈ V.
−→
ψ 1, . . . ,
Susceptible-infected model
We start by considering an SI model of propagation of a disease factor as AD progresses. En
this case the brain regions, represented as nodes of the graph, can be in two possible states,
infected or susceptible. Susceptible brain regions are those that are free of the disease factor
but that are susceptible to get infected from other regions. The infected ones are those in which
the probability of disease factor is greater than zero. Let i be a node of the graph G = (V, mi)
and let xi(t) be the probability that node i get infected at time t from any infected nearest
Neurociencia en red
1009
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
0
0
7
1
8
6
7
0
0
5
norte
mi
norte
_
a
_
0
0
1
4
3
pag
d
t
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Communicability distance and Alzheimer’s
neighbor. If the infection rate is given by γ we have, (Canright & Engø-Monsen, 2006; Mei
et al., 2017; Hombre nuevo, 2010),
dxi(t)
dt
= ~˙x(t) = γ (1 − xi(t))
norte
∑
j=1
Aijxj(t),
t ≥ t0.
(1)
It can be seen that the linearized SI model, namely ~˙x(t) = γA ~x(t), represents an upper
bound for the exact SI model, eso es,
˙xi(t) = γ[1 − xi(t)]
norte
∑
j=1
Aijxj(t) ≤ γ
norte
∑
j=1
Aijxj(t)
which in matrix-vector is given by:
~˙x(t) ≤ γA ~x(t),
(2)
(3)
with initial condition ~x(0) = ~x0, ∀i and ∀t. The solution of the linearized SI model ~˙x
⋆(t) is given by:
γA~x
⋆(t) =
⋆
~x
(t) = eγtA~x
⋆
0 .
(4)
(cid:0)
(cid:1)
etA
t≥0 is unbounded, eso es, limt→∞
Sin embargo, the solution of the linearized SI model has two important problems. The first is
= ∞, which poses a major
that the semigroup
problem for the use of this linearized model as a model of the SI propagation scheme. El
reason is that x(t) is a probability and as such it has to be bounded as 0 ≤ x(t) ≤ 1. El
second is that the solution (4) is a good approximation to the solution of the SI model only for
⋆(t) ≈ 0, which makes this solution useless for following the propagation of AD.
~x
To sort out this problem we will follow here Lee, Tenneti, and Eun (2019), who proposed
the following change of variable to avoid the aforementioned problems with the solution of
the linearized SI model:
etA
(cid:13)
(cid:13)
(cid:13)
(cid:13)
yi(t) := − log (1 − x
⋆
i (t)) ,
(5)
which is an increasing convex function. Entonces, como 1 − x⋆
is the probability that node i is not
i
infected at a given time, the new variable yi(t) can be interpreted as the information content
of the node i or surprise of not being infected (ver, p.ej., Cover & tomás, 2012). Let us then
suppose that at t = 0 the probability that every region of the brain gets infected is the same,
eso es, at the beginning every node has the same probability β to be infected and to be the
one from which the disease propagates. Eso es,
⋆
0i = β =
X
C
norte
, ∀i = 1, . . . , norte
En este caso, the solution of the upper bound of the SI model is:
~y(t) =
1
a
(cid:18)
− 1
(cid:19)
eαγtA~1 −
log α +
(cid:18)
1 − α
a (cid:19)
~1,
(6)
(7)
where α = 1 − β is a constant. También, if we fix γ and t we have that this solution can be
written as
~y(t) = m
~1 − b~1,
eζ A
(cid:16)
(cid:17)
(8)
for constants m, ζ and b. Here the constant ζ groups the previous parameters γ, α at a given
time t. We will call ˜xi(t) = 1 − e−yi(t) the approximate solution of the SI model, cual es
always bounded between zero and one as needed.
Neurociencia en red
1010
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
0
0
7
1
8
6
7
0
0
5
norte
mi
norte
_
a
_
0
0
1
4
3
pag
d
/
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Communicability distance and Alzheimer’s
Cifra 1. Simulation of the progression of a disease with the SI model (broken blue line) in an
Erd ˝os-Rényi random network with n = 100 and connection probability p = 0.1. The lineralized
solution is represented by a dotted black line and the approximate solution using the change of
variables is represented as a solid red line. The panels correspond to infectivity rates β = 0.001 (A)
and β = 0.002 (B).
In order to see the differences between the exact solution of the SI model xi(t), the lin-
earized one x⋆
i (t) and the approximate solution after the change of variable ˜xi(t), we plot the
progression of the number of infected nodes in an Erd ˝os-Rényi random network with n = 100
and connection probability p = 0.1. We simulate the progression of the disease starting the
infection with a fraction of 0.01 infected nodes in the network. The results are illustrated in
Cifra 1 for infectivity rates β = 0.001 (A) and β = 0.002 (B). As can be seen, the lineralized
modelo (dotted black line) is a bad approximation to the exact solution (broken blue line), como
it quickly diverges. Sin embargo, the approximate solution obtained by the change of variable
(solid red line) is a tight upper bound for the exact solution, and it will be used here for further
análisis.
Exponential of the adjacency matrix:
Infinite sum of powers of the
adjacency matrix divided by the
factorial of these powers.
The communicability connection
It is clear from Equation 8 that the solution ~y(t) of the upper bound of the SI model depends
~1. This term is the sum of the corresponding rows of the exponential of the
linearly of
matriz de adyacencia. For an individual node i it is known as the total communicability of the
corresponding node (Benzi & Klymko, 2013) and it can be written as
eζ A
(cid:0)
(cid:1)
eζ A
~1
(cid:17)
(cid:17)i
(cid:16)(cid:16)
=
eζ A
+ ∑
j6=i (cid:16)
eζ A
(cid:17)ij
:= Ci + ∑
j6=i
Tij,
(cid:17)ii
(cid:16)
(9)
where the first term in the right-hand side is the subgraph centrality (Estrada & Rodriguez-
Velazquez, 2005) of the node and the second one is the sum of the communicability functions
(Estrada & Hatano, 2008) from the node i to the rest of the nodes of the network (see also
Estrada, Hatano, & Benzi, 2012). In terms of the propagation of a disease factor, C
i represents
the circulability of the disease factor around the node i. The second term represents the trans-
missibility from/to the node i to/from the rest of the nodes of the network. If we concentrate
on the effect of the node i on another node j, then C
i represents the capacity of the node i
Neurociencia en red
1011
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
0
0
7
1
8
6
7
0
0
5
norte
mi
norte
_
a
_
0
0
1
4
3
pag
d
.
/
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Communicability distance and Alzheimer’s
of increasing the probability of infecting itself and Tij is the capacity of i of infecting j. De este modo,
because node j is doing the same, the term
ξij(ζ) :=
eζ A
eζ A
+
(cid:16)
(cid:17)ii
(cid:17)jj
(cid:16)
− 2
eζ A
,
(cid:17)ij
(cid:16)
(10)
represents the difference between the capacities of both nodes of increasing the probability
of infecting themself to that of infecting each other. A large value of ξij(ζ) indicates that the
disease factor gets trapped circulating at the nodes i and j, which form two islands with little
transmissibility among them. A small value, sin embargo, indicates that such transmissibility is rel-
atively large in relation to the internal circulability at the nodes, eso es, the nodes have a bridge
between them. We consider that this measure is important for the study of Alzheimer’s disease
because it should allow us to investigate whether the disease produces a patchy environment
of brain regions which form islands with little transmissibility among them. The function ξij(ζ)
2, where ~xi = eΛ/2~ϕi with ~ϕi = [ψ1,i, ψ2,i, · · · ψn,i], dónde
can be written as ξij(ζ) =
ψk,i,is the ith entry of the kth eigenvector associated with the eigenvalue λk of A. Como consecuencia,
ξij(ζ) is a Euclidean distance between the nodes i and j in the network. We call it the commu-
nicability distance between the two nodes (Estrada, 2012a, 2012b). The vector ~xi is the posi-
tion vector of the node i in a Euclidean hypersphere of dimension n (Estrada & Hatano, 2016;
Estrada, Sánchez-Lirola, & De La Peña, 2014).
~xi − ~xj
(cid:13)
(cid:13)
(cid:13)
(cid:13)
Shortest communicability paths
The communicability distance ξij(ζ) can be calculated for any pair of nodes (connected or
no) in the graph. De este modo, we can obtain a communicability distance matrix (Estrada, 2012a)
X =
~s~1T +~1~sT − 2 exp. (ζ A)
(cid:16)
(cid:17)
◦1/2
,
(11)
Euclidean distance:
The straight-line distance between
two points in a Euclidean space.
Euclidean hypersphere:
A sphere in the n-dimensional
Euclidean space.
(cid:0)
(cid:0)
(cid:1)
(cid:1)
nn
(cid:2)(cid:0)
11 ,
eζ A
eζ A
eζ A
22 , · · · ,
where ~s =
is a vector whose entries are the main diagonal
entries of the corresponding matrix function, ~1 is an all-ones vector, and ◦ indicates an en-
trywise operation. Sin embargo, we assume here that in a network “information” flows through
the edges of the graph, such that it uses certain paths connecting the corresponding pair
de nodos. In order to find the shortest communicability paths between two nodes we pro-
ceed as follows. We construct the communicability-weighted adjacency matrix of the network
(Akbarzadeh & Estrada, 2018):
(cid:1)
(cid:3)
W = A ◦ X = X ◦ A.
(12)
Entonces, the shortest communicability path between two nodes is the shortest weighted path
in W. Eso es, the shortest communicability path between two nodes i and j for a given ζ > 0 es
the path that minimizes the communicability distance between every pair of nodes in the cor-
responding path. We have proved analytically that when ζ → 0 the shortest communicability
path between any pair of nodes i and j is identical to the shortest (topological) path between
the two nodes (Silver, Akbarzadeh, & Estrada, 2018). Eso es, the shortest (topological) path is
a special case of the shortest communicability path in a network. In this work we will consider
the case ζ ≡ 1, which we will call “shortest communicability path” and the case ζ → 0 cual
we will call “shortest topological path.” Notice that the length of the shortest communicability
path is the sum of the weights (communicability distances) for the edges in that path. For an
ejemplo, ver figura 2. Here we will keep ζ = 1 due to the lack of any experimental value
that can guide us for selecting a more appropriate value. También, we should have in mind that
decreasing the values of this parameter close to zero will make the shortest communicability
paths look very similar to shortest paths, while increasing it over unity will make these paths
Neurociencia en red
1012
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
0
0
7
1
8
6
7
0
0
5
norte
mi
norte
_
a
_
0
0
1
4
3
pag
d
/
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Communicability distance and Alzheimer’s
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
0
0
7
1
8
6
7
0
0
5
norte
mi
norte
_
a
_
0
0
1
4
3
pag
d
/
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 2.
Illustration of the shortest communicability path (blue thick lines) and the shortest topo-
logical path (red thick lines) between a pair of nodes in a random geometric network. The nodes in
both shortest paths are highlighted with blue color and with sizes proportional to their degrees. El
rest of the nodes are in gray color and with a fixed size. The shortest topological path goes through
nodes averaging node degree equal to 14. The shortest communicability path goes through nodes
averaging degree 8.3. Además, the average subgraph centrality of the nodes in both paths are
18,837.3 (shortest topological path) y 4,636.6 (shortest communicability path), respectivamente.
very long indeed. De este modo, we left for a further work the analysis of the influence of this parameter
in the study of AD.
DATASET AND IMAGE PROCESSING
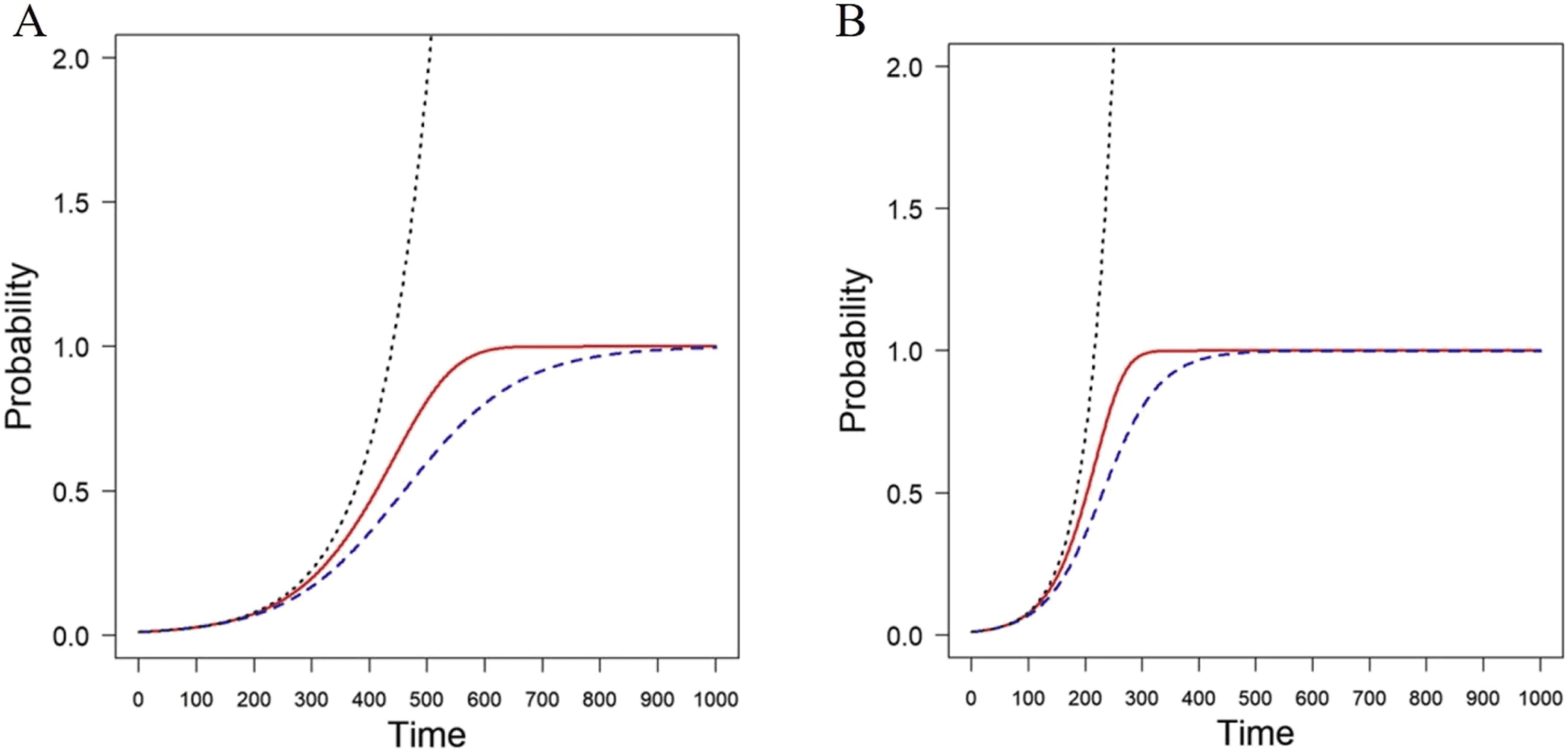
The dataset used consists of diffusion-weighted imaging (DWI) scans and anatomical T1 scans
de 88 subjects, 48 healthy controls (HC) y 40 AD patients from the publicly available Alzheimer’s
Disease Neuroimaging Initiative (ADNI) database. After preprocessing the images, a tractog-
raphy pipeline was implemented by using the MRtrix software library. The main steps of the
whole processing, which are well established in the literature, are shown in Figure 3.
Primero, a denoising step was performed in order to enhance the signal-to-noise ratio of the
diffusion-weighted MR signals in order to reduce the thermal noise due to the stochastic thermal
motion of the water molecules and their interaction with the surrounding microstructure
1013
Diffusion-weighted imaging (DWI):
A magnetic resonance imaging (resonancia magnética)
modality in which the image contrast
generation is based on the diffusion
of water molecules.
T1 anatomical scan:
Image acquired by exploiting the
spin-lattice relaxation process in
structural MRI.
Tractography:
Image processing procedure that
allows the reconstruction of fiber
tracts connecting brain region pairs.
Neurociencia en red
Communicability distance and Alzheimer’s
Cifra 3. Main steps of the image processing pipeline. DWI and T1 weighted scans are pre-
processed and co-registered. Entonces, after the fiber orientation distribution estimation, probabilístico
tractography is performed resulting in a weighted connectivity matrix.
Veraart et al. (2016). Head motion and eddy current distortions were corrected by align-
ing the DWI images of each subject to the average b0 image. The brain extraction tool was
then used for the skull stripping of the brain (S. METRO. Herrero, 2002). The bias-field correction
was used for correcting all DWI volumes. The T1-weighted scans were preprocessed by per-
forming the standard steps: reorientation to the standard image MNI152, automatic cropping,
bias-field correction, registration to the linear and nonlinear standard space, brain extraction.
The following step was the intermodal registration of the diffusion weighted and T1-weighted
imagen.
After the preprocessing and co-registration steps, the structural connectome generation
was performed. Primero, we generated a tissue-segmented image tailored to the anatomically
constrained tractography (zhang, Brady, & Herrero, 2001). Entonces, we performed an unsuper-
vised estimation of white matter, gray matter, and cerebro-spinal fluid. In the next step, el
fiber orientation distribution for spherical deconvolution was estimated (Jeurissen, Tournier,
Dhollander, connelly, & Sijbers, 2014). Then a probabilistic tractography (Tournier, Calamante,
& connelly, 2010) was performed by using dynamic seeding (R. mi. Herrero, Tournier, Calamante,
& connelly, 2015b) and anatomically constrained tractography (R. mi. Herrero, Tournier,
Calamante, & connelly, 2012), which improves the tractography reconstruction by using anatom-
ical information by means of a dynamic thresholding strategy. We applied the spherical de-
convolution informed filtering of tractograms (SIFT2) methodology (R. mi. Smith et al., 2015b),
providing more biologically meaningful estimates of the structural connection density and a
more efficient solution to the streamlines connectivity quantification problem. The obtained
streamlines were mapped through a T1 parcellation scheme by using the AAL2 atlas, (Rolls,
Joliot, & Tzourio-Mazoyer, 2015), which is a revised version of the automated anatomical at-
las (AAL) incluido 120 regiones. Finalmente, a robust structural connectome construction was per-
formed for generating the connectivity matrices (R. mi. Herrero, Tournier, Calamante, & connelly,
2015a). The pipeline here described has been used in recent structural connectivity studies,
Por ejemplo, see Amico and Goñi (2018); Lella, Amoroso, Diacono, et al. (2019); Lella et al.
(2020); Tipnis, Amico, Ventresca, and Goni (2018). The output was a weighted connectivity
matrix for each subject. Out of these 120 nodos, 24 were removed from all networks, en orden
to obtain only graphs without isolated nodes. Finalmente, a 96 × 96 matrix M for each subject was
obtained.
All matrices were binarized by considering only the edges with mij > 0 and the adjacency
matrix A was obtained. The communicability distance matrix was calculated for each binary
Streamlines:
Fiber trajectories that can be
reconstructed by means of
tractography algorithms.
Neurociencia en red
1014
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
0
0
7
1
8
6
7
0
0
5
norte
mi
norte
_
a
_
0
0
1
4
3
pag
d
/
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Communicability distance and Alzheimer’s
matrix and it was multiplied by the adjacency matrix A obtaining a weighted matrix W. A
shortest path algorithm was performed on this matrix, thus obtaining a matrix whose entries
represent the shortest communicability paths between node pairs in the network. Starting from
the adjacency matrix A, the shortest path length matrix, whose entries represent the shortest
paths between node pairs, was also calculated. A group-wise statistical analysis was performed
in order to find brain region pairs with a statistically significant difference between HC and AD
in shortest path length and shortest communicability path length. In order to make the statistical
analysis more robust, permutation tests were performed by randomly assigning subjects to the
two comparison groups 1,000 veces. Differences were considered significant if they did not
belong to 95% of the null distribution derived from the permutation tests (corrected p value
< 0.05). The false discovery rate (FDR) was used for multiple comparison correction. The same
study could also be done by considering the weighted matrix, but we follow here the more
traditional approach on binary matrix. The weighted case could be addressed in future work.
STATISTICAL ANALYSIS
Sensitivity analysis
False discovery rate:
The rate at which positives identified
by a method are truly negative ones.
(cid:0)
(cid:1)
vi, vj
and then obtain the respective average values, ¯lH
=
Our first task here is to analyze the sensitivity of the shortest communicability and the short-
est topological path lengths to detect significant changes in the brain connectivity after AD.
For that purpose we proceed as follow. For each connectivity matrix we calculate both the
shortest communicability path length and the shortest topological path length matrices. In
this case, we use permutation tests for the statistical significance analysis. For instance, let us
consider the nodes vi and vj. We then calculate the length of the communicability short-
est path between these nodes for each of the healthy lHk
and diseased individuals
. Using
lDk
these values, we obtain △l
. Now we proceed to a random-
(cid:1)
(cid:0)
ization of each individual into the two classes, that is, healthy and diseased, obtaining 1,000
=
subsets of random HC and 1,000 subsets of random AD. We then calculate △lrand
¯lHrand
are computed as before
vi, vj
(cid:1)(cid:12)
(cid:12)
(cid:1)
but using the random sets of healthy and diseased individuals, respectively. Finally, we compare
(cid:12)
(cid:12)
the null distribution of △lrand
. Therefore, we conclude
that △l
is significant if it does not belong to 95% of the null distribution, which is car-
ried out by calculating the p value of the permutation test. Here we consider significant the
nodes with corrected p value < 0.05. We use both FDR and Bonferroni correction for the mul-
tiple comparisons correction. We do these calculations for the shortest communicability path
as well as for the shortest topological path.
(cid:1)
with the true value △l
, where ¯lHrand
and ¯lDrand
(cid:0)
vi, vj
− ¯lDrand
and ¯lD
− ¯lD
(cid:1)
vi, vj
vi, vj
vi, vj
vi, vj
vi, vj
vi, vj
vi, vj
vi, vj
vi, vj
vi, vj
vi, vj
vi, vj
(cid:1)(cid:12)
(cid:12)
¯lH
(cid:12)
(cid:12)
(cid:0)
(cid:0)
(cid:0)
(cid:0)
(cid:1)
(cid:1)
(cid:0)
(cid:0)
(cid:0)
(cid:0)
(cid:1)
(cid:1)
(cid:1)
(cid:0)
(cid:1)
(cid:1)
(cid:0)
(cid:0)
(cid:0)
(cid:1)
Bonferroni correction:
A statistical method to control false
positives.
Effects of threshold selection and normalization
Here we first consider the effects of the thresholding process on the significance of the results
obtained by using the current approach. The brain networks used in this work, as usually in
many brain network studies, are constructed by using probabilistic tractography. For this reason
weak connections can introduce noisy effects. Therefore, the first thing that we need to inves-
tigate is how different thresholds to transform these weighted matrices into binary (adjacency)
matrices affect the results. The second important question is related to the comparison of net-
works with very different topological characteristics to avoid the extraction of trivial facts. That
is, it is very plausible that the brain networks of AD patients differ significantly in a few “triv-
ial” topological aspects from those of healthy individuals. For instance, the edge density can
change dramatically between HC and AD networks. This may produce the false impression
Network Neuroscience
1015
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
4
1
0
0
7
1
8
6
7
0
0
5
n
e
n
_
a
_
0
0
1
4
3
p
d
t
/
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Communicability distance and Alzheimer’s
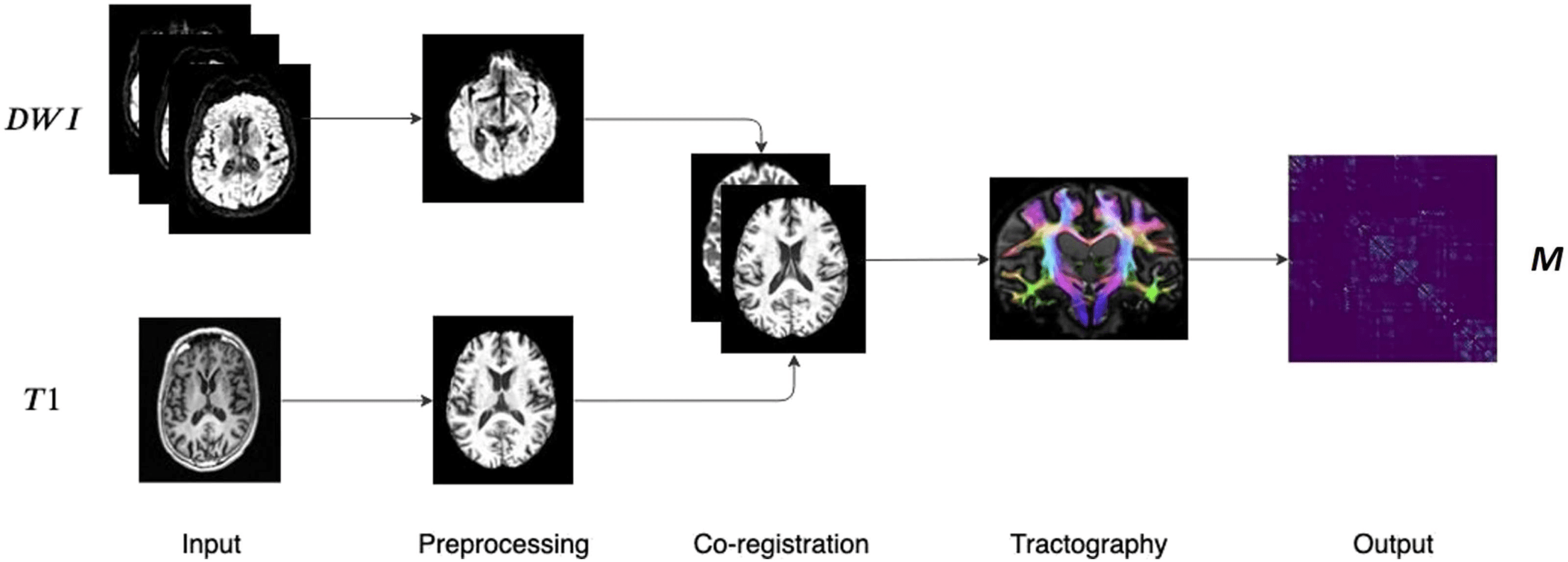
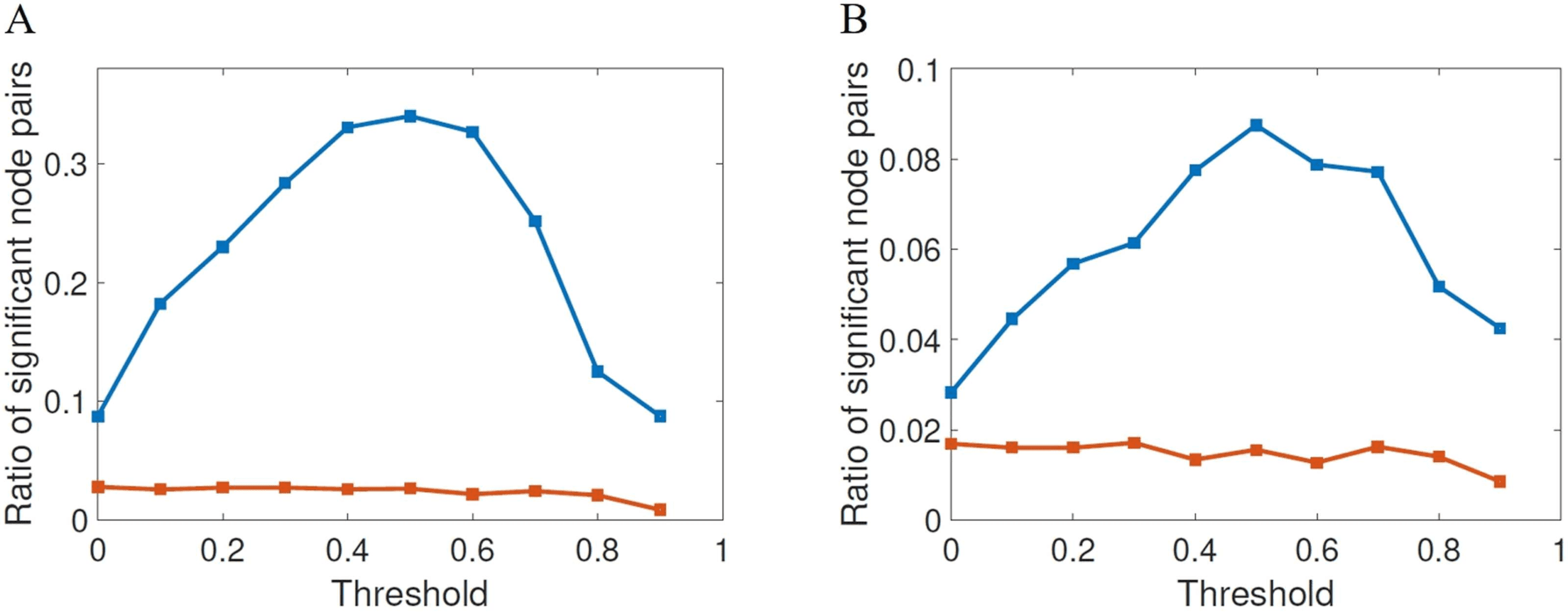
Figure 4. Fraction of node pairs with statistically significant different values of shortest commu-
nicability path length (blue squares) in HC and AD compared with the number of node pairs with
statistically significant different values of shortest path length (red squares), at different threshold
values for FDR (A) and Bonferroni correction (B).
that AD mainly produces a sparsification of the brain network that hides important structural
factors produced by the disease. To avoid these problems, we will provide a normalization of
the communicability geometric parameters used in this study as described below.
First, we will proceed to change the threshold at which the adjacency matrices are gener-
ated. We start as usual by calculating the mean matrix for the HC subjects, which results in
a weighted matrix in which entries range from 0 to 1. Each entry represents the frequency at
which the corresponding edges occur among the HC matrices. This matrix is then thresholded
by varying the threshold τ as 0 ≤ τ ≤ 0.9 obtaining a binary matrix to be used as a mask. The
adjacency matrices of all subjects are then projected onto this mask. This procedure resulted
in 10 sets of adjacency matrices, one set for each threshold value. We use the same thresh-
olding procedure described in Lella et al. (2019), which is also similar to the procedure used,
for example, in Van Den Heuvel and Sporns (2011). In Figure 4 we illustrate the results of the
statistical significance for the different thresholds studied here for both FDR (A) and Bonfer-
roni correction (B). The first shocking result is the extremely low significance of the shortest
topological paths according to both multiple comparisons correction methods for all values
of the threshold. According to FDR, for almost all values of thresholds the ratio of significant
node pairs is more than 35 times higher than that for the shortest topological paths, while ac-
cording to the most restrictive Bonferroni correction the ratio of significant node pairs is quite
dependent on the threshold value and the highest ratio of significant node pairs is obtained for
τ between 0.5 and 0.9.
Then, for each value of the threshold we calculate the communicability distance matrix
X (Pi) of subject i. We then proceed to normalize such matrix as follow. Let us call S (Pi) the
shortest communicability path length matrix of the subject Pi, let m (Pi) be the number of edges
of subject i, and let A (Pi) the adjacency matrix of subject i . The average communicability
distance of the edges of the network is then calculated for each subject:
¯ξ (Pi) =
∑n
p,q=1 ξ pq (Pi) × Apq (Pi)
m (Pi)
,
(13)
from which we obtain the normalized shortest communicability path length matrix ˆS (Pi) as:
ˆS (Pi) =
S (Pi)
¯ξ (Pi)
.
(14)
1016
Network Neuroscience
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
4
1
0
0
7
1
8
6
7
0
0
5
n
e
n
_
a
_
0
0
1
4
3
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Communicability distance and Alzheimer’s
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
4
1
0
0
7
1
8
6
7
0
0
5
n
e
n
_
a
_
0
0
1
4
3
p
d
.
t
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Figure 5.
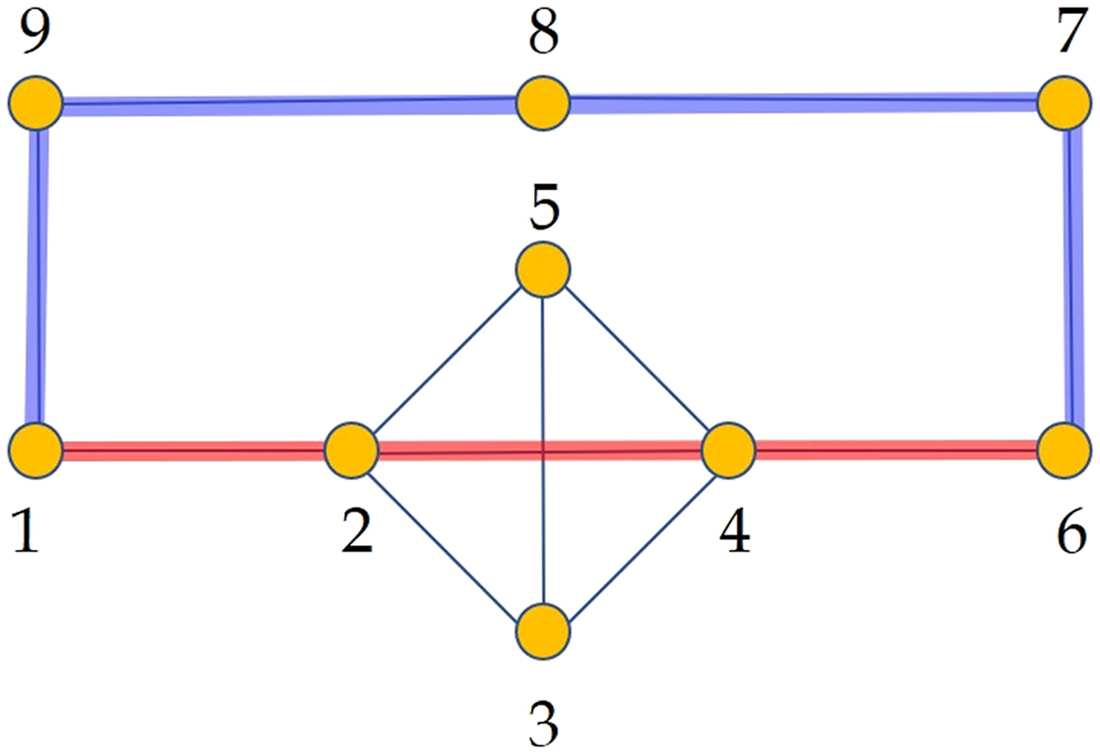
Illustration of a simple graph used to explain the normalized shortest communicability
path length. In red we illustrate the shortest path between the nodes 1 and 6 and in blue the shortest
communicability path between the same nodes. The normalized communicability shortest path
length for the path marked in blue is ˆS1,6(G) ≈ 1.939, while for that in red is ˆS1,6(G) ≈ 2.049.
For instance, for the network G in Figure 5 the value of ¯ξ(G) ≈ 2.4797, then the normalized
shortest communicability path length for the pair labeled as 1,6 is ˆS1,6(G) ≈ 1.939, which
corresponds to the path 1 − 9 − 8 − 7 − 6. In contrast, the normalized length of the commu-
nicability path 1 − 2 − 4 − 6 is 2.049, which clearly indicates that this is a longer path in term
of the communicability distance than the path 1 − 9 − 8 − 7 − 6. Notice that 1 − 2 − 4 − 6 is
the shortest topological path between the nodes 1 and 6.
We then analyze the significance for the normalized communicability distance matrices,
for each threshold studied here in the two cases of the FDR and the Bonferroni. In Figure 6A
Figure 6. Fraction of node pairs with statistically significant different values of normalized shortest
communicability path length (blue squares) in HC and AD compared with the number of node pairs
with statistically significant different values of shortest path length (red squares), at different threshold
values for FDR (A) and Bonferroni correction (B).
Network Neuroscience
1017
Communicability distance and Alzheimer’s
we illustrate the ratio of significant node pairs versus the threshold for FDR and in (B) the same
for the Bonferroni correction. We also provide the same results for the shortest topological
paths. The first interesting result is the dramatic difference between the ratios of significant
node pairs obtained from the shortest communicability paths and from the topological ones.
While for the shortest communicability paths we have very significant ratios for both statistical
parameters for certain values of the threshold, for the shortest paths we always observe very
low ratio of significant node pairs both for FDR and Bonferroni correction. The second very
interesting feature of this analysis is the fact that for both statistical criteria the normalized
shortest communicability paths makes a great differentiation of both groups for a threshold of
τ = 0.5. Notice the nonmonotonic behavior of both statistical criteria versus the threshold,
which peak at the before mentioned value.
Now we focus only on the results obtained after the normalization of the communicability
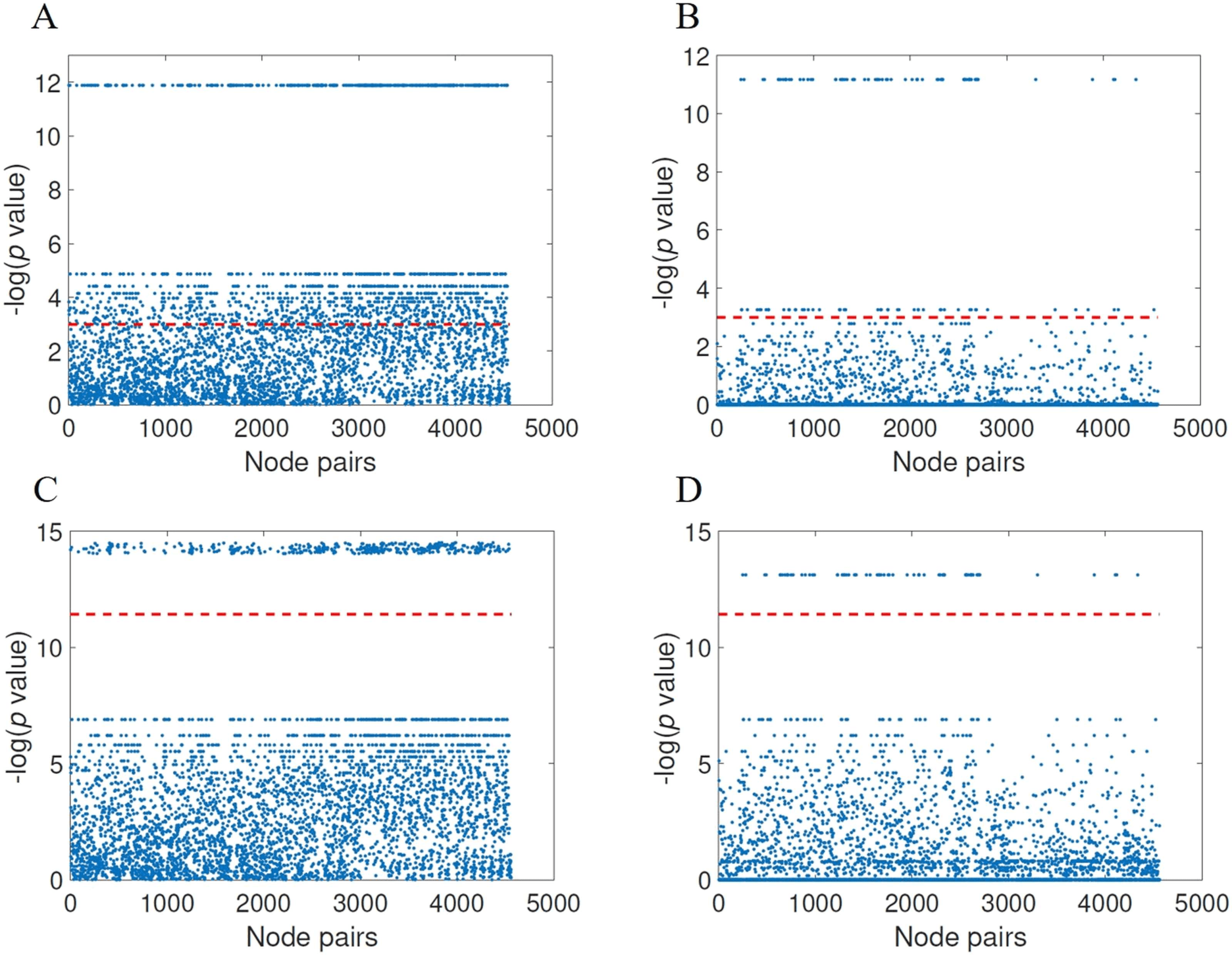
distance matrix and for the threshold found as providing the best results. In Figure 7 we illus-
trate these results using Manhattan plots for the significance of node pairs according to FDR
(panels A and B) as well as for Bonferroni correction (panels C and D). Notice that the hori-
zontal red line corresponds to the significance, that is, − ln(0.05) for FDR and − ln (0.05/κ),
where κ is the number of comparisons, for Bonferroni. All the points over the red line represent
significant node pairs. According to the FDR correction there are 1,551 significant node pairs
for the normalized communicability distance against 120 ones according to the shortest topo-
logical paths. According to the Bonferroni correction there are 399 significant node pairs for
the normalized communicability shortest paths against 71 for the topological ones. We should
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
4
1
0
0
7
1
8
6
7
0
0
5
n
e
n
_
a
_
0
0
1
4
3
p
d
/
t
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7. Results of the group-wise statistical analysis using FDR (A and B) and the Bonferroni
index (C and D) for the normalized communicability distance matrices with threshold τ = 0.5 (A
and C) as well as for the shortest topological paths (B and D). The node pairs above the red line
have significantly different values in HC and AD.
Network Neuroscience
1018
Communicability distance and Alzheimer’s
remark that FDR controls the expected proportion of false positives, while Bonferroni controls
the overall probability of making at least one false discovery. Then, because the Bonferroni
correction is a more restrictive measure, we will consider only the 399 significant node pairs
identified by this measure. Notice that even with such restrictive criterion the shortest commu-
nicability path identifies more than seven times the number of significant node pairs identified
by the topological shortest paths.
In closing, we observe a huge difference in the sensitivity of the communicability shortest
paths with respect to the shortest topological ones to the change in the brain connectivity
produced by AD. In other words, while the length of the shortest topological paths appear
almost unaltered after the appearance of AD, the length of the communicability ones is affected
in almost all the pairs of brain regions.
Before closing this section, we would like to remark on the huge differences produced by
the normalization procedure used in the current work as a way to restrict our analysis to those
highly nontrivial structural features relevant to AD. When there is no normalization in FDR
case, the shortest communicability path identifies 4,524 node pairs significantly different in
the two diagnostic groups, out of the 4,560 possible total node pairs. That is, 99.21% of the
node pairs are affected. Conversely, the topological shortest path length only identifies 124
node pairs, which represents only 2.72% of node pairs affected. Without normalization we
can also study the influence of the threshold under the ratio of significant node pairs in Bon-
ferroni case. In this case, the best results are obtained for τ = 0.8. Then, there are 4,300 node
pairs significantly different in the two diagnostic groups according to the shortest communica-
bility path, and 95 according to the shortest topological ones. These values represent 95.61%
and 2.08% node pairs affected, respectively. These results show the extraordinary value of the
normalization criterion used in reducing the number of significant node pairs to a handful set
of highly significant ones.
DISCOVERING STRUCTURAL PATTERNS OF ALZHEIMER’S DISEASE
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
4
1
0
0
7
1
8
6
7
0
0
5
n
e
n
_
a
_
0
0
1
4
3
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Considering this threshold value, the average shortest communicability path length matrix was
calculated for HC and for AD. Then, we have obtained the difference between the average
matrices for the HC minus that of AD (Figure 8A). For the sake of comparison we also obtained
such differences for the shortest path lengths between every pair of nodes (Figure 8B). We used
a divergent color map centered at zero to represent these differences, and the differences for the
shortest topological path length were set in the same scale of the differences of the normalized
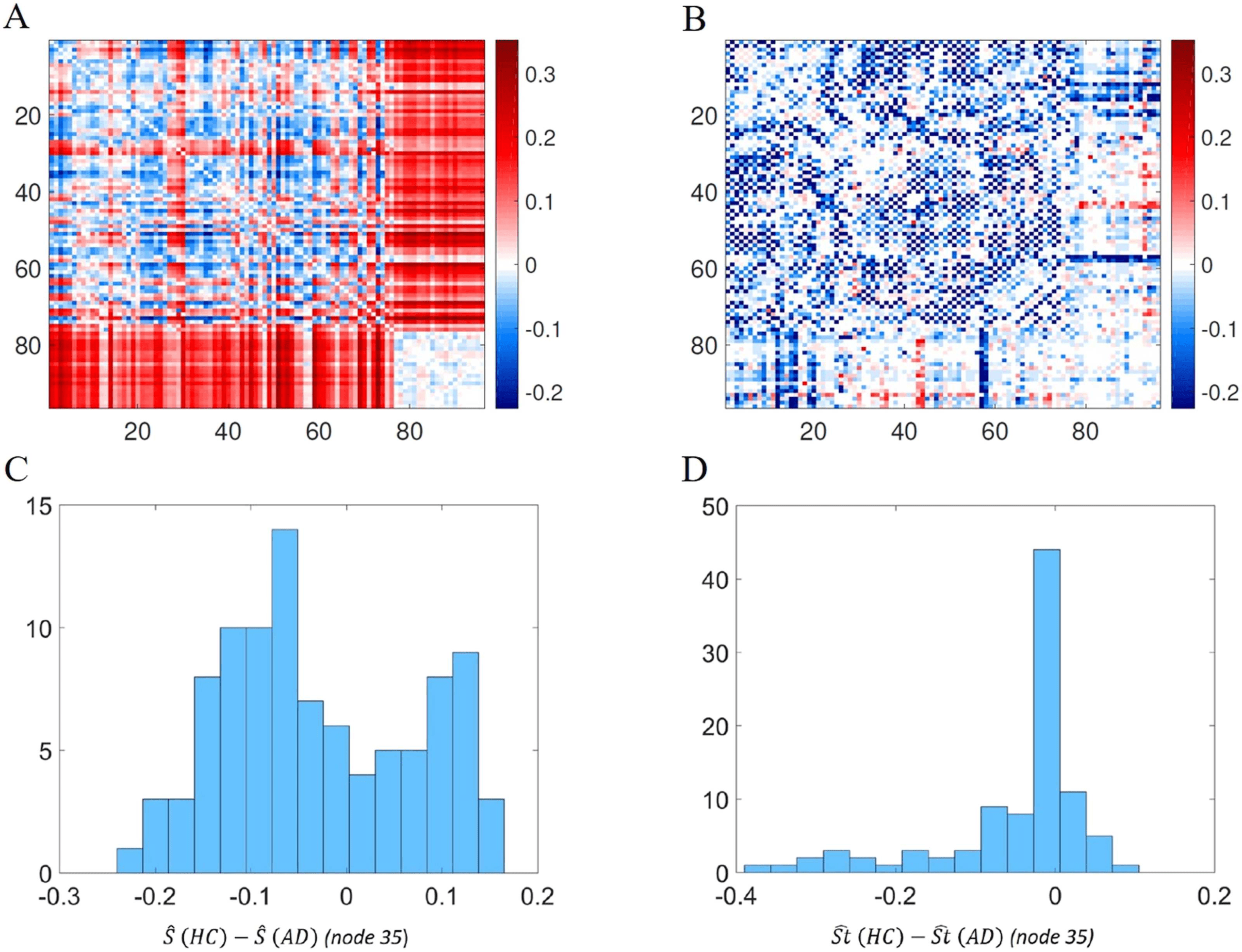
shortest communicability path length. It is interesting to note how this representation allows us
to visualize a different distribution of colors in the two heat maps. In particular, if we consider
the histogram of the values of one of the rows of the heat maps (the row corresponding to node
35 is considered as an example), the histogram derived from Figure 8A is a bimodal distribution
(Figure 8C), while the one derived from Figure 8B is a skewed distribution centered at zero
(Figure 8D). Moreover looking at Figure 8A, two different behaviors of the distribution of values
of a single row can be observed. In particular, for some rows the average difference, between
HC and AD, of normalized shortest communicability path length with the other nodes of the
network is mostly positive, while for other nodes it is mostly negative. Thus, the nodes seems
to be clustered according to this different behavior. In order to show how these two different
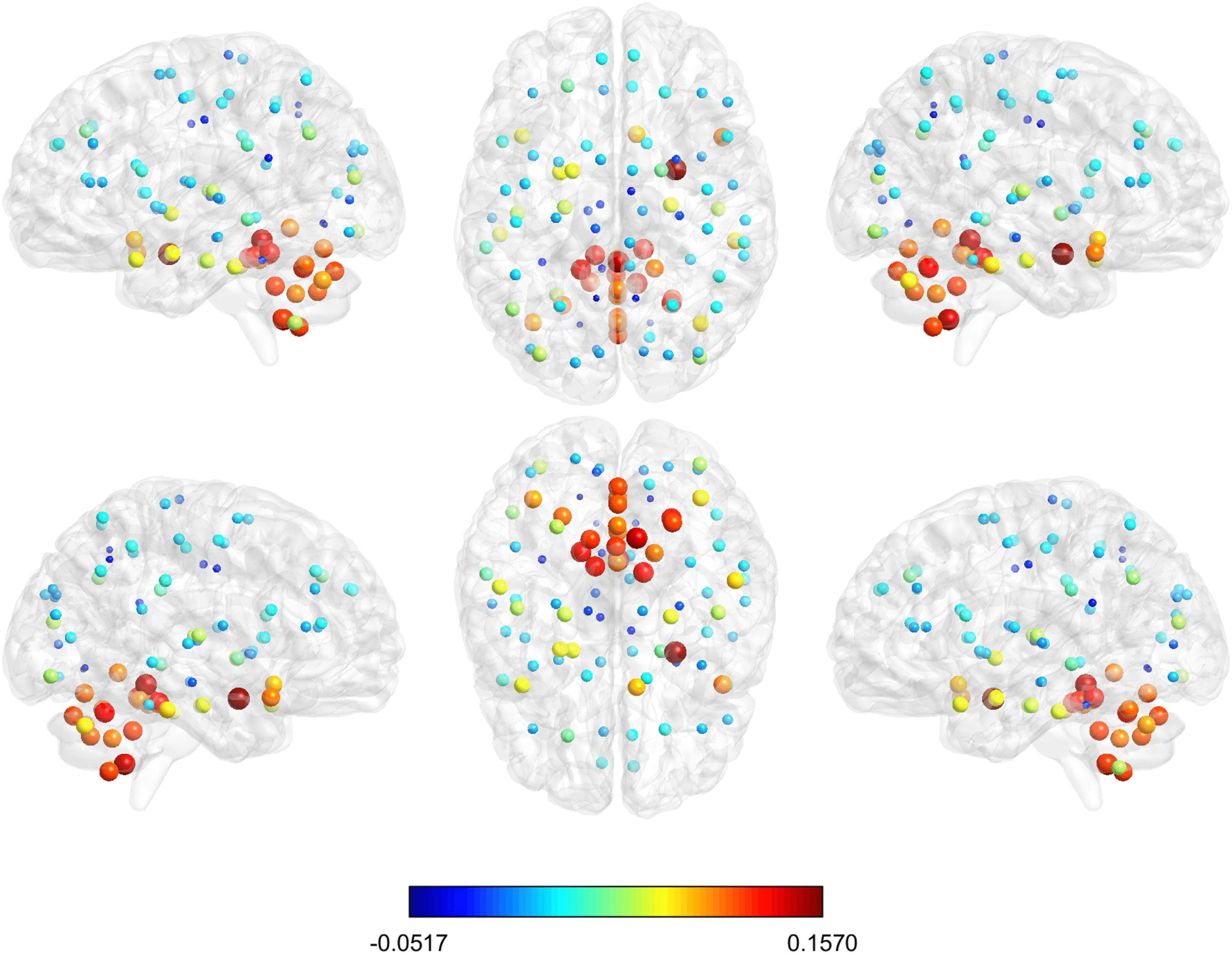
groups are distributed in the brain, we have represented the brain regions on a glass brain
coloring the corresponding nodes according to the median of the distribution of the values
over row (Figure 9). Also the dimension of the nodes is descriptive of the median value. The
cluster of nodes with the highest median values includes cerebellum, vermis, and amygdala.
Network Neuroscience
1019
Communicability distance and Alzheimer’s
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
Figure 8.
(A) Heat map of the difference between the averaged normalized shortest communi-
cability path length for HC and AD. (B) Heat map of the difference between the averaged shortest
topological paths length for HC and AD, in the same scale of A. (C) Distribution of the values of
one row (row 35 is considered as an example) of heat map A. (D) Distribution of the values of one
row (row 35 is considered as an example) of heat map B.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
4
1
0
0
7
1
8
6
7
0
0
5
n
e
n
_
a
_
0
0
1
4
3
p
d
.
t
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Figure 9. The glass brain shows for each node the median of the distribution of the difference in
HC and AD of the mean normalized shortest communicability path length with all the other nodes
of the network; the node color and dimension are descriptive of these values. The different views
show the lateral and medial sides of each hemisphere, and the dorsal and ventral side.
Network Neuroscience
1020
Communicability distance and Alzheimer’s
From these heat maps we can observe that there are pairs of nodes for which AD increases
the shortest communicability and topological paths while for others it decreases them. The
difference between the distributions of ˆS(HC) and ˆS(AD), that is, when Pi is a healthy or AD
individual, respectively, is statistically significant.
A group-wise statistical analysis using permutation tests with multiple comparison correc-
tion (both FDR and Bonferroni correction) was performed in order to find which node pairs
have a significantly different value of the normalized shortest communicability path length in
HC and AD. This can allow one to restrict the focus to only these node pairs, among all the
possible node pairs. This procedure was applied for all thresholds.
Let us call ∆ij = ˆSij(HC) − ˆSij(AD) the difference of the average normalized shortest path
communicability distance for the edge (i, j) in both the healthy and the AD cohorts. Let us then
call ∆tij = ˆStij(HC) − ˆStij(AD) the difference of the average shortest topological path length.
Then, we can observe that among the node pairs with statistically significant different values of
the average normalized shortest communicability path length, there are both node pairs with
∆ > 0 and ∆ < 0. Instead, for the node pairs with statistically significant different values of the
average shortest topological path length it is always ∆St < 0. For example, Figure 10 shows the
histograms of ∆ and ∆St (we generally call the difference of an average shortest path measure)
for the significant node pairs and for the best threshold value (τ = 0.5).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
4
1
0
0
7
1
8
6
7
0
0
5
n
e
n
_
a
_
0
0
1
4
3
p
d
/
t
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
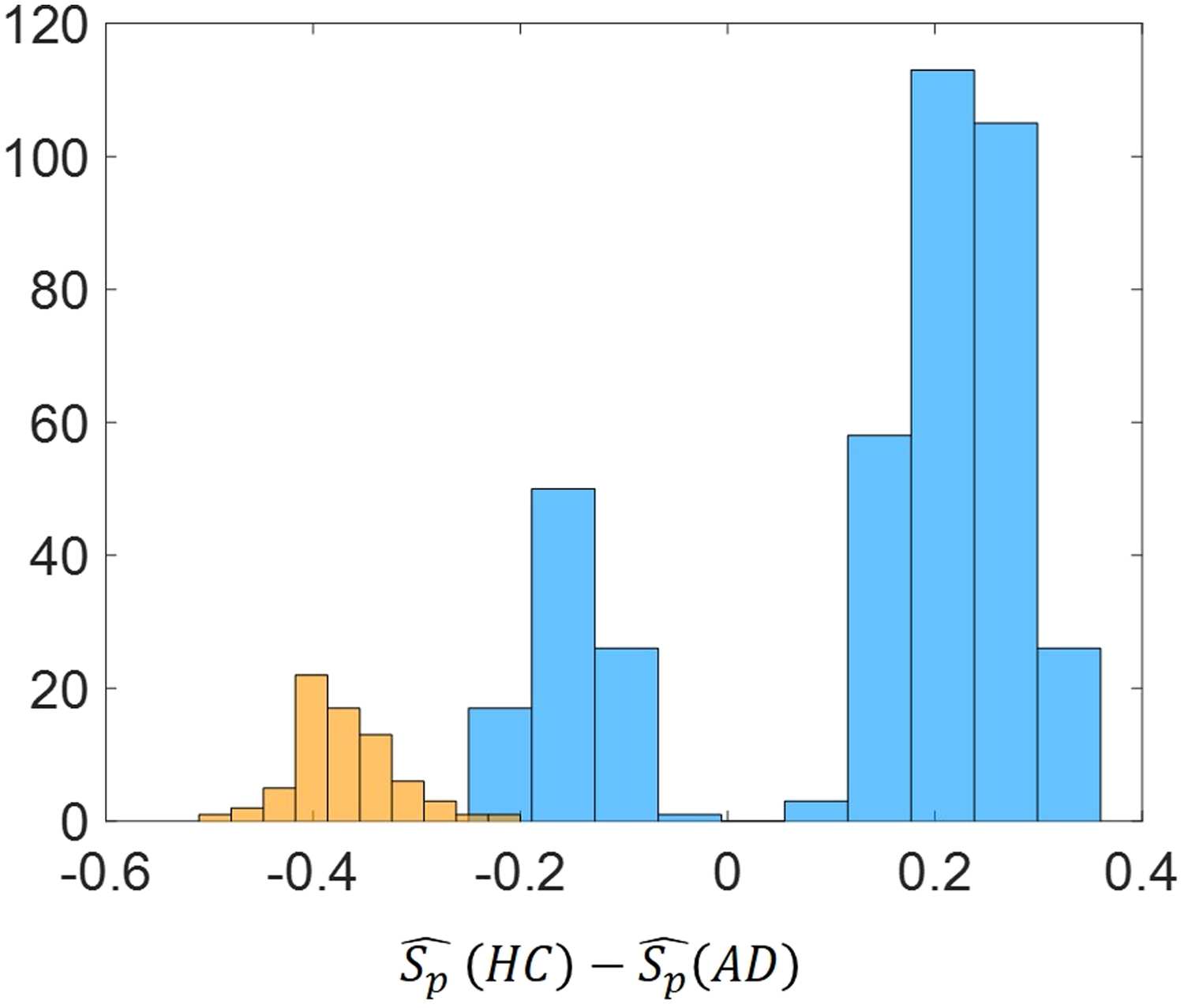
Figure 10. Histogram of ∆Sp = ˆSp(HC) − ˆSp(AD) for the significant node pairs for the best
threshold value (τ = 0.5). Blue color refers to the difference of the average normalized shortest path
communicability distance while orange color refers to difference of the average shortest topological
path length.
Network Neuroscience
1021
Communicability distance and Alzheimer’s
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
4
1
0
0
7
1
8
6
7
0
0
5
n
e
n
_
a
_
0
0
1
4
3
p
d
/
t
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
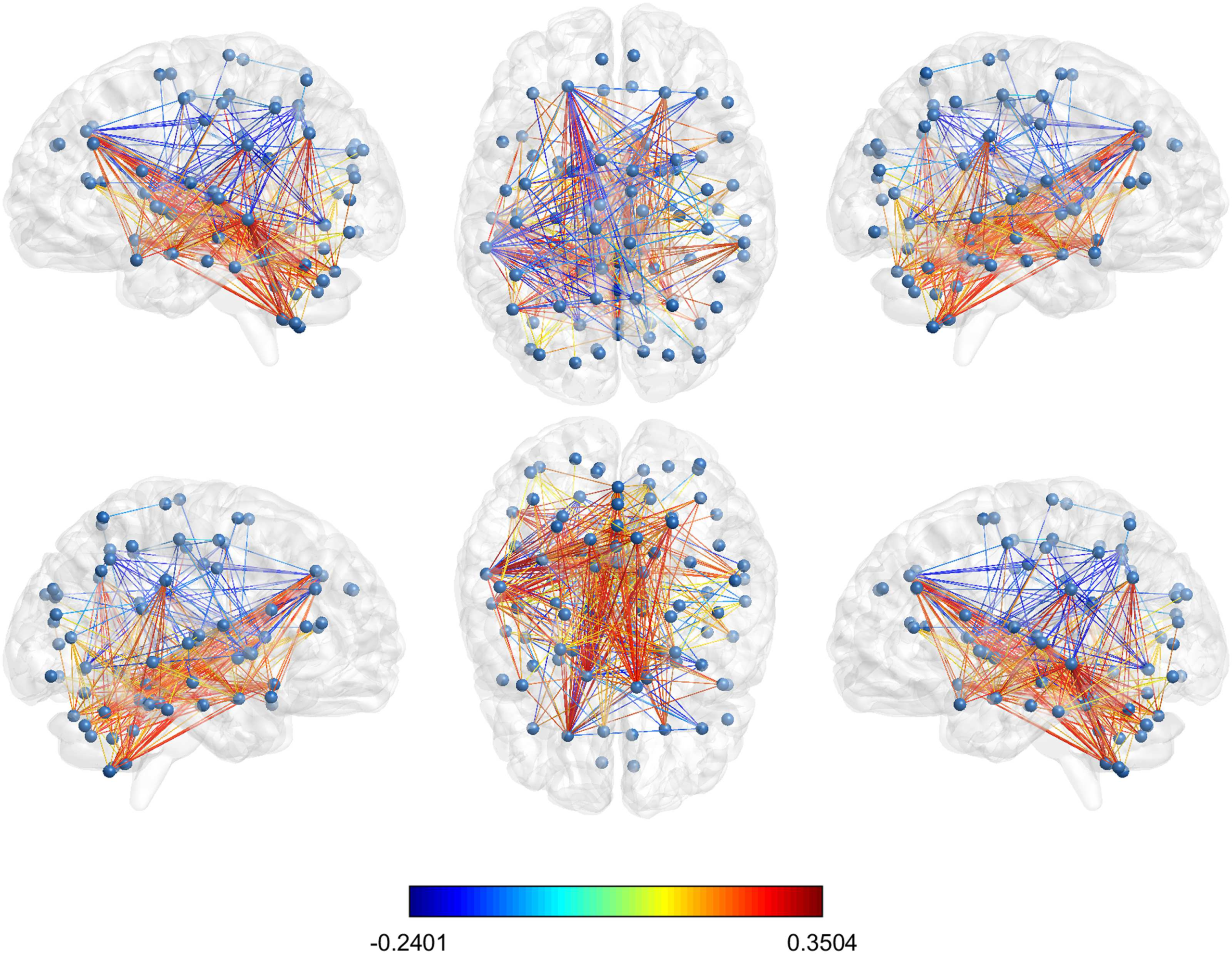
Figure 11. Glass brain visualization of the difference between the mean normalized shortest com-
municability path length of the significant edges in HC and AD; the edge colour is descriptive of
these values. The different views show the lateral and medial sides of each hemisphere, and the
dorsal and ventral side.
The values of ∆ij for the set of 399 node pairs with significantly different average normalized
shortest communicability path length for the best threshold (τ = 0.5) which were selected
according to the Bonferroni correction are illustrated in Figure 11.
A deeper analysis of these node pairs provides some illuminating information about the
structural influence of AD. Let us resume this information as follow. From the 399 significant
node pairs considered here:
1. 110 (27.6% of significant pairs) connect regions in the left hemisphere;
2. 41 (10.3% of significant pairs) connect regions in the right hemisphere;
3. 167 (41.8 of significant pairs) connect one region of the left with one region of the right
hemisphere;
4. 31 (7.8% of significant pairs) connect the vermis to the right hemisphere;
5. 50 (12.5% of significant pairs) connect the vermis to the left hemisphere.
These results indicate that almost one half of all the pairs of nodes for which there is a
significant difference in the shortest communicability paths after AD connect both brain hemi-
spheres. This result supports the disconnection hypothesis of this disease in which the damage
produced by AD can be attributed not only to specific cerebral dysfunctions but also to dis-
connection processes between different cerebral areas (Morris, 1996; Morrison et al., 1986).
In particular, the disconnection between interhemispheric regions have been widely discussed
in the literature and reviewed by Delbeuck et al. (2003). They compiled evidence about the
hypothesis of AD as a disconnection syndrome from neuropathological data, the electrophysi-
ological and neuroimaging data, as well as from neuropsychological data. Some of the earliest
Network Neuroscience
1022
Communicability distance and Alzheimer’s
evidence supporting this hypothesis point to the fact that there is a disorganized functional
activity between the two hemispheres in the early stages of AD and a loss of positive correla-
tions between the hemispheres, which suggest a breakdown of the interhemispheric functional
association. Other evidence reviewed by Delbeuck et al. (2003) are a decrease of associative
white matter fibers in the corpus callosum splenium of AD patients, the existence of a mod-
ification in the functional interactions between the hemispheres, and the existence of lower
coherence between the hemispheres in mild to moderate AD patients compared to controls,
suggesting a disturbance of the interhemispheric functional connectivity in AD. More recently,
Wang et al. (2015) obtained experimental results that demonstrate that there are “specific pat-
terns of interhemispheric functional connectivity changes in the AD and MCI, which can be
significantly correlated with the integrity changes in the midline white matter structures.” And
Qiu et al. (2016) reported homotopic interhemispheric functional connectivity disruption in
AD but not MCI.
Another third of these significant edges are located inside the left hemisphere. These re-
sults parallel those supporting the hypothesis that AD evolves first, faster, and more severely
in the left hemisphere than in the right (Giannakopoulos, Kövari, Herrmann, Hof, & Bouras,
2009; Thompson et al., 2003). As shown by Thompson et al. (2003), the spreading waves of
gray matter loss were asymmetric in both hemispheres, with the left one having significantly
larger deficits and with faster local gray matter loss rates than the right one. Their finding also
correlated with progressively declining cognitive status. Finally, we have found 81 pairs that
connect the vermis either with the right or the left hemisphere. Recently, the role of cerebel-
lar gray matter atrophy in AD has been studied (Mavroudis, et al., 2013; Jacobs et al., 2018).
Jacobs et al. (2018) have found that in the early stages of AD the vermis and posterior lobe
of the cerebellum are affected, also confirming previous results by (Mavroudis, et al., 2013),
who reported severe damage in the Purkinje cells from the vermis of the cerebellum in five
AD patients.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
4
1
0
0
7
1
8
6
7
0
0
5
n
e
n
_
a
_
0
0
1
4
3
p
d
t
/
.
Transmissibility and circulability of AD factor
As explained before, among the pairs of nodes that have significant differences between healthy
and AD cohorts, there are pairs with positive as well as with negative values of ∆ij. Pairs of
nodes for which ∆ij > 0 corresponds to brain regions that have decreased their normalized
shortest communicability path length when AD is present. Those for which ∆ij < 0 corre-
sponds to brain regions that have increased their normalized shortest communicability path
length. A resume of our results for the pairs that increase and decrease the normalized shortest
communicability path lengths is given below:
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
1. Left hemisphere: 31 pairs increased ˆS (Pi) and 79 pairs decreased it;
2. Right hemisphere: 6 pairs increased ˆS (Pi) and 35 pairs decreased it;
3. Left-Right hemispheres: 55 pairs increased ˆS (Pi) and 112 pairs decreased it;
4. Vermis-Left hemisphere: 0 pairs increased ˆS (Pi) and 31 pairs decreased it;
5. Vermis-Right hemisphere: 0 pairs increased ˆS (Pi) and 50 pairs decreased it.
These results indicate that in total 76.9% of all node pairs that display significant change
after AD have decreased the length of the shortest communicability paths connecting them.
This is a highly counterintuitive finding because it literally means that the nodes “are closer”
to each other in terms of their communicability distance after the AD has appeared. In order
to disentangle the meaning of this finding, we will consider the example provided in Figure 5.
Network Neuroscience
1023
Communicability distance and Alzheimer’s
We will consider the removal of edges which do not disconnect the graph, which are
known as cyclic edges (in the graph in Figure 5 all edges are cyclic). First we will prove the
following result.
Let Γ be a graph and let Γ − e be the same graph without the cyclic edge e = {a, b}.
we have that ¯Gpq (Γ) ≥ ¯Gpq (Γ − e), where ¯Gpq is the average
Then, if Gpq (Γ) =
eγA(Γ)
(cid:16)
(cid:17)pq
among all pairs of nodes. The proof is given by the fact that if e = {a, b} is removed, the
length of all walks between a and b will increase, and no other walk will decrease its length.
Consequently, the removal of an edge in a graph will drop both the average transmissibility
¯T (Γ) = ¯Gp6=q (Γ) and the average circulability ¯C (Γ) = ¯Gpp (Γ) of a disease factor. However,
because the communicability distance ξ pq is the difference between the circulability around
the nodes p and q, and the transmissibility between the two nodes, we have the following
situations. Let ∆ξ2
pq (Γ − e), and ∆Gpq = Gpq(Γ) − Gpq (Γ − e). Then,
pq(Γ) − ξ2
pq = ξ2
∆ξ2
pq =
Gpp(Γ) − Gpp (Γ − e)
+
Gqq(Γ) − Gqq (Γ − e)
− 2
Gpq(Γ) − Gpq (Γ − e)
(cid:2)(cid:0)
= ∆Cp + ∆Cq − 2∆Tpq.
(cid:1)
(cid:0)
(cid:1)(cid:3)
(cid:2)
(cid:3)
(15)
Consequently, when ∆ξ2
pq
while Gpq(Γ) ≫ Gpq (Γ − e). When, ∆ξ2
pq
Gqq(Γ) ≫ Gqq (Γ − e), while Gpq(Γ) ' Gpq (Γ − e).
< 0 we have that Gpp(Γ) / Gpp (Γ − e) and Gqq(Γ) ' Gqq (Γ − e),
> 0 we have that Gpp(Γ) ≫ Gpp (Γ − e) y
1. ∆ξ2
pq
< 0 implies that the drop in the transmissibility of the disease factor is bigger than
the drop in the circulability around the nodes. That is, in Γ − e dominates the circulability
to the transmissibility compared to Γ;
2. ∆ξ2
pq
> 0 implies that the drop in the circulability of the disease factor is bigger than the
drop in the transmissibility around the nodes. Eso es, in Γ − e dominates the transmissi-
bility over the circulability compared to Γ.
En mesa 1 we report the results that illustrate the previous reasoning for the graph in Figure 5.
Primero, we report the change in the average shortest path length ∆¯L after the removal of the
corresponding edges according to the node labeling in Figure 5. The removal of the edges
{1, 2}, {1, 9}, y {8, 9} produce significant increase of the communicability shortest path
Mesa 1. Values of different structural and dynamical parameters for the graph illustrated in Figure 5
to which edges have been removed. See note below.
borde
{1, 2}
{1, 9}
{8, 9}
{3, 5}
{2, 5}
{2, 4}
∆¯L (%)
−25.4
−23.2
−21.5
−0,04
+0.89
+1.42
∆ ¯Gpp (%)
10.0
15.7
17.7
14.9
15.9
18.4
∆ ¯Gpq (%)
19.2
26.5
29.6
15.6
15.0
18.7
∆tinf (%)
30.5
25.7
16.9
3.8
3.8
3.8
Nota. The edges correspond to the labeling of the nodes in the mentioned figure. ∆¯L (%)
is the percentage of change respect to the original graph in the average communicability
shortest path length. ∆ ¯Gp p (%) and ∆ ¯Gpq (%) are the percentage of change with respect to
the original graph for the values of Gp p and Gpq averaged for the nodes and edges in the
shortest communicability paths. ∆tinf (%) is the time needed by a disease factor to infect all
the nodes of the corresponding graph in an SI simulation by using the approximate solution
described below with β = 0.005 and initial condition xi(0) = 1/9 for all i.
Neurociencia en red
1024
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
0
0
7
1
8
6
7
0
0
5
norte
mi
norte
_
a
_
0
0
1
4
3
pag
d
/
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Communicability distance and Alzheimer’s
> 0. As can be seen for those graphs in which ∆ξ2
pq
< 0. The edge removals {2, 5} and {2, 4} decrease the communicability
lengths, that is, ∆ξ2
pq
< 0 the relative
shortest paths, that is, ∆ξ2
pq
drop of ∆ ¯Gpq, averaged for all edges in the shortest paths, is significantly bigger than that of
> 0, the change in ∆ ¯Gpq is of the same
∆ ¯Gpp, averaged for all nodes. In the case when ∆ξ2
pq
order than ∆ ¯Gpp. It is reasonable to think that edge removal increases the time needed by the
disease factor to infect 100% of the nodes in the network. If we designate this time change by
∆tinf and calculate it as the minimum time at which all the nodes are infected in the graph by
using the approximate solution of the SI model (upper bound), we obtain the results given in
< 0, the increase in the infection time is dramatic, ranging
Table 1. As can be seen when ∆ξ2
pq
> 0, the increase in tinf is only 3.8%.
de 17% a 30%. In remarkable contrast, when ∆ξ2
pq
> 0 the orifinal network has been transformed into a more efficient
In closing, when ∆ξ2
pq
uno, from the perspective of the transmission of the disease, because in Γ − e the circulability
around the nodes of the disease factor is sacrificed to the transmissibility to other nodes.
It is now important to analyze what are the consequences of the decrease in the lengths of
the communicability shortest paths that we have observed for AD brains. The main implication
of this observation is that AD produces some damage to the brain, not necessarily only edge
removals, which somehow improves the “efficiency” of the resulting networks to propagate
the disease in relation to other possible damage scenarios. If we constrain ourselves to the
edge-removal scenario and use the previous graph as an example, we can conclude that AD
has removed those edges which “improve” the transmissibility over the circulability of the
disease factor, by affecting as least as possible the global rate of contagion in the resulting
redes. This is an inference based on the analysis of data produced on AD patients and
comparing them with HC. In no case does it correspond to a direct observation of this effect,
and we call the attention of experimenters to try to falsify this hypothesis. We should remark
that in 2013, Tomasi et al. (2013) found by using MRI “a higher degree of connectivity was
associated with nonlinear increases in metabolism.” Recent work in network neuroscience has
proposed ways to navigate the brain avoiding the “hubs” due to their high energy consumption
(Seguin, Van Den Heuvel, & Brilla, 2018; yan, despreciar, & Avena-Koenigsberger, 2020a).
De este modo, according to our findings, AD produces damage in the connectivity of the brain, cual
drop more significantly the cliquishness—the degree is a first order approach to it—over the
transmissibility. De este modo, it is also plausible that propagating the AD through the different regions
of an already-damaged brain is less energetic than in the nondamaged one. Considerándolo todo, el
damage produced by initial stages of AD seem to improve the capacity of the disease factor to
propagate through the network more so than in the undamaged one.
CONCLUSIONS
There are two main conclusions in the current work. From a theoretical perspective for network
neurociencia, we have shown that the communicability function—widely used in this field—
can be mathematically connected to the solution of an SI model of disease factor propagation
in a brain network. En particular, we have shown that the communicability distance accounts
for the difference between the circulability of this disease factor around a brain region (nodo)
and its transmissibility to another region of the brain.
From an application point of view, we have provided solid evidences that the shortest com-
municability path length is significantly better than the shortest topological path length in
distinguishing AD patients from healthy individuals. We have identified a set of 399 pares
of regions for which there are very significant changes in the shortest communicability path
length after AD appears, 42% of which interconnect both brain hemispheres and 28% de
which connect regions inside the left hemisphere only. These findings clearly agree with the
Neurociencia en red
1025
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
0
0
7
1
8
6
7
0
0
5
norte
mi
norte
_
a
_
0
0
1
4
3
pag
d
/
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Communicability distance and Alzheimer’s
disconnection syndrome hypothesis of AD. We have also identified 20% of affected regions
that connect the vermis with any of the two brain hemispheres. The most significant result is
that in 76.9% of these pairs of damaged brain regions there is an increase in the efficiency to
transmit the disease factor across the brain network in relation to healthy individuals.
In closing, we hope that the current work helps to shed light on an important mechanistic
aspect of AD as well as to afford a better understanding of the use of communicability functions
for network neuroscience studies.
EXPRESIONES DE GRATITUD
We wish to thank Robert Smith of the Florey Institute of Neuroscience and Mental Health,
austin, for his valuable suggestions on the image processing pipeline concerning the brain
connectivity reconstruction with MRtrix. Data processing was partially carried out by using the
facilities of the ReCaS data center of the University of Bari (http://www.recas-bari.it).
INFORMACIÓN DE FINANCIACIÓN
Data collection and sharing for this project was funded by the Alzheimer’s Disease Neu-
roimaging Initiative (ADNI) (National Institutes of Health Grant U01 AG024904) and DOD
ADNI (Department of Defense award number W81XWH-12-2-0012). ADNI is funded by the
National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineer-
En g, and through generous contributions from the following: AbbVie, Alzheimer’s Association;
Alzheimer’s Drug Discovery Foundation; Araclon Biotech; BioClinica, Cª; Biogen; Bristol-
Myers Squibb Company; CereSpir, Cª; Cogstate; Eisai Inc.; Elan Pharmaceuticals, Cª; Eli Lilly
and Company; EuroImmun; F. Hoffmann-La Roche Ltd and its affiliated company Genentech,
Cª; Fujirebio; GE Healthcare; IXICO Ltd.; Janssen Alzheimer Immunotherapy Research and
Desarrollo, LLC.; Johnson and Johnson Pharmaceutical Research and Development LLC.;
Lumosity; Lundbeck; Merck and Co., Cª; Meso Scale Diagnostics, LLC.; NeuroRx Research;
Neurotrack Technologies; Novartis Pharmaceuticals Corporation; Pfizer Inc.; Piramal Imaging;
Servier; Takeda Pharmaceutical Company; and Transition Therapeutics. The Canadian Insti-
tutes of Health Research is providing funds to support ADNI clinical sites in Canada. Pri-
vate sector contributions are facilitated by the Foundation for the National Institutes of Health
(www.fnih.org). The grantee organization is the Northern California Institute for Research and
Educación, and the study is coordinated by the Alzheimer’s Therapeutic Research Institute at
the University of Southern California. ADNI data are disseminated by the Laboratory for Neuro
Imaging at the University of Southern California.
Data processing was partially carried out by using the facilities of the ReCaS data center of
the University of Bari (http://www.recas-bari.it).
CONTRIBUCIONES DE AUTOR
EE and EL designed the research. EL performed the calculations. EE and EL analyzed and dis-
cussed the results. EE wrote the paper.
REFERENCIAS
Akbarzadeh, METRO., & Estrada, mi. (2018). Communicability geometry
captures traffic flows in cities. Nature Human Behaviour, 2(9),
645–652.
Amico, MI., & Goñi, j. (2018). Mapping hybrid functional-structural
connectivity traits in the human connectome. Network Neuro-
ciencia, 2(3), 306–322.
Neurociencia en red
1026
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
0
0
7
1
8
6
7
0
0
5
norte
mi
norte
_
a
_
0
0
1
4
3
pag
d
t
/
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Communicability distance and Alzheimer’s
bassett, D. S., & despreciar, oh. (2017). Network neuroscience. Naturaleza
Neurociencia, 20(3), 353.
Benzi, METRO., & Klymko, C. (2013). Total communicability as a cen-
trality measure. Journal of Complex Networks, 1(2), 124–149.
Braak, h., & Braak, mi. (1991). Neuropathological stageing of Alzheimer-
related changes. Acta Neuropathologica, 82(4), 239–259.
Brettschneider, J., Del Tredici, K., Sotavento, V. M.-Y., & Trojanowski, j. q.
(2015). Spreading of pathology in neurodegenerative diseases: A
focus on human studies. Naturaleza Reseñas Neurociencia, 16(2),
109–120.
Canright, GRAMO. S., & Engø-Monsen, k. (2006). Spreading on networks:
A topographic view. Complexus, 3(1–3), 131–146.
Cover, t. METRO., & tomás, j. A. (2012). Elements of information the-
ory. John Wiley & Sons.
Crofts, j. J., & Higham, D. j. (2009). A weighted communicability
measure applied to complex brain networks. Journal of the Royal
Society Interface, 6(33), 411–414.
Crofts, j. J., Higham, D. J., Bosnell, r., Jbabdi, S., Matthews, PAG. METRO.,
Behrens, T., & Johansen-Berg, h. (2011). Network analysis de-
tects changes in the contralesional hemisphere following stroke.
NeuroImagen, 54(1), 161–169.
Cristal, h., Dickson, D., Fuld, PAG., Masur, D., Scott, r., Mehler,
METRO., . . . Wolfson, l.
(1988). Clinico-pathologic studies in de-
mentia: Nondemented subjects with pathologically confirmed
Alzheimer’s disease. Neurología, 38(11), 1682–1682.
DeBello, W.. METRO., McBride, t. J., Nichols, GRAMO. S., Pannoni, k. MI.,
Sanculi, D., & Totten, D. j. (2014). Input clustering and the mi-
croscale structure of local circuits. Frontiers in Neural Circuits,
8, 112.
el largo, S. C., Scholtens, l. h., van den berg, l. h., Boks, METRO. PAG.,
Bozzali, METRO., Cahn, w., & Van den Heuvel, METRO. PAG. (2019). Shared
vulnerability for connectome alterations across psychiatric and
neurological brain disorders. Nature Human Behaviour, 3(9),
988–998.
Delbeuck, X., Van der Linden, METRO., & Collette, F. (2003). Alzheimer’
disease as a disconnection syndrome? Neuropsychology Review,
13(2), 79–92.
De Reus, METRO. A., & van den heuvel, METRO. PAG.
(2014). Simulated rich
club lesioning in brain networks: a scaffold for communication
and integration? Frontiers in Human Neuroscience, 8, 647.
Estrada, mi. (2012a). The communicability distance in graphs. Lineal
Algebra and Its Applications, 436(11), 4317–4328.
Estrada, mi.
(2012b). Complex networks in the euclidean space of
communicability distances. Physical Review E, 85(6), 066122.
Estrada, mi. (2012C). The structure of complex networks: Teoría y
applications. prensa de la Universidad de Oxford.
Estrada, MI., & Hatano, norte.
(2008). Communicability in complex
redes. Physical Review E, 77(3), 036111.
Estrada, MI., & Hatano, norte. (2016). Communicability angle and the
spatial efficiency of networks. SIAM Review, 58(4), 692–715.
Estrada, MI., Hatano, NORTE., & Benzi, METRO. (2012). The physics of communi-
cability in complex networks. Physics Reports, 514(3), 89–119.
Estrada, MI., & Rodriguez-Velazquez, j. A. (2005). Subgraph central-
ity in complex networks. Physical Review E, 71(5), 056103.
Estrada, MI., Sánchez-Lirola, METRO., & De La Peña, j. A. (2014). Hyper-
spherical embedding of graphs and networks in communicability
spaces. Discrete Applied Mathematics, 176, 53–77.
Giannakopoulos, PAG., Kövari, MI., Herrmann, F. r., Hof, PAG. r., &
Bouras, C.
Interhemispheric distribution of Alzheimer
disease and vascular pathology in brain aging. Stroke, 40(3),
983–986.
(2009).
González-Forero, METRO., & jardinero, A. (2018). Inference of ecolog-
ical and social drivers of human brain-size evolution. Naturaleza,
557(7706), 554–557.
Hardy, J., & Selkoe, D. j.
(2002). The amyloid hypothesis of
Alzheimer’s disease: Progress and problems on the road to ther-
apeutics. Ciencia, 297(5580), 353–356.
Head, D., Buckner, R. l., Shimony, j. S., williams, l. MI., Akbudak, MI.,
Conturo, t. MI., . . . Snyder, A. z. (2004). Differential vulnerabil-
ity of anterior white matter in nondemented aging with minimal
acceleration in dementia of the alzheimer type: evidence from
imágenes de tensor de difusión. Corteza cerebral, 14(4), 410–423.
Herculano-Houzel, S. (2009). The human brain in numbers: A lin-
early scaled-up primate brain. Frontiers in Human Neuroscience,
3, 31.
Impedovo, D., Pirlo, GRAMO., Vessio, GRAMO., & Angelillo, METRO. t.
(2019).
A handwriting-based protocol for assessing neurodegenerative
dementia. Cognitive Computation, 11(4), 576–586.
Iturria-Medina, y., Sotero, R. C., Toussaint, PAG. J., evans, A. C., &
Alzheimer’s Disease Neuroimaging Initiative. (2014). Epidemic
spreading model to characterize misfolded proteins propagation
in aging and associated neurodegenerative disorders. PLoS Com-
putational Biology, 10(11), e1003956.
Jack Jr., C. r., Knopman, D. S., Jagust, W.. J., Petersen, R. C., Weiner,
METRO. w., Aisen, PAG. S., Lesnick T. GRAMO. (2013). Tracking pathophysio-
logical processes in Alzheimer’s disease: An updated hypotheti-
cal model of dynamic biomarkers. The Lancet Neurology, 12(2),
207–216.
Jacobs, h. I., Hopkins, D. A., Mayrhofer, h. C., Bruner, MI., camioneta
Leeuwen, F. w., Raaijmakers, w., & Schmahmann, j. D. (2018).
The cerebellum in alzheimer’ss disease: Evaluating its role in
cognitive decline. Cerebro, 141(1), 37–47.
Jeurissen, B., Tournier, J.-D., Dhollander, T., connelly, A., & Sijbers,
j.
(2014). Deconvolución esférica restringida por múltiples tejidos para
análisis mejorado de datos de resonancia magnética de difusión multicapa. NeuroIm-
edad, 103, 411–426.
Johansen-Berg, h., Scholz, J., & Stagg, C. j. (2010). Relevance of
structural brain connectivity to learning and recovery from stroke.
Frontiers in Systems Neuroscience, 4, 146.
Jucker, METRO., & Caminante, l. C. (2011). Pathogenic protein seeding in
Alzheimer disease and other neurodegenerative disorders. Un-
nals of Neurology, 70(4), 532–540.
Jucker, METRO., & Caminante, l. C. (2013). Self-propagation of patho-
genic protein aggregates in neurodegenerative diseases. Naturaleza,
501(7465), 45–51.
Sotavento, C.-H., Tenneti, S., & Eun, D. Y.
(2019). Transient dynamics
of epidemic spreading and its mitigation on large networks.
En
Proceedings of the twentieth ACM international symposium on
mobile ad hoc networking and computing (páginas. 191–200).
Lella, MI., Amoroso, NORTE., Diacono, D., Lombardi, A., Maggipinto,
T., Monaco, A., . . . Tangaro, S.
(2019). Communicability
characterization of structural DWI subcortical networks in
Alzheimer’s disease. Entropy, 21(5), 475.
Neurociencia en red
1027
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
0
0
7
1
8
6
7
0
0
5
norte
mi
norte
_
a
_
0
0
1
4
3
pag
d
/
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Communicability distance and Alzheimer’s
Lella, MI., Amoroso, NORTE., Lombardi, A., Maggipinto, T., Tangaro, S.,
Bellotti, r., . . . Initiative, A. D. norte. (2019). Communicability dis-
ruption in Alzheimer’s disease connectivity networks. Diario de
Complex Networks, 7(1), 83–100.
Lella, MI., Lombardi, A., Amoroso, NORTE., Diacono, D., Maggipinto, T.,
Monaco, A., . . . Tangaro, S. (2020). Machine learning and DWI
brain communicability networks for Alzheimer’s disease detec-
ción. Applied Sciences, 10(3), 934.
li, y., Jewells, v., kim, METRO., Chen, y., Moon, A., Armao, D., . . . shen,
D. (2013). Diffusion tensor imaging based network analysis de-
tects alterations of neuroconnectivity in patients with clinically
early relapsing-remitting multiple sclerosis. Human Brain Map-
ping, 34(12), 3376–3391.
Lo, C.-Y., Wang, P.-N., Chou, K.-H., Wang, J., Él, y., & lin, C.-P.
(2010). Diffusion tensor tractography reveals abnormal topolog-
ical organization in structural cortical networks in Alzheimer’s
enfermedad. Revista de neurociencia, 30(50), 16876–16885.
Mancini, METRO., de Reus, METRO. A., Serra, l., Bozzali, METRO., van den heuvel,
METRO. PAG., Cercignani, METRO., . . . Conforto, S. (2016). Network attack
simulations in Alzheimer’s disease: The link between network tol-
erance and neurodegeneration. En 2016 IEEE 13th international
symposium on biomedical imaging (ISBI) (páginas. 237–240).
Mandelkow, E.-M., & Mandelkow, mi.
(1998). Tau in Alzheimer’s
enfermedad. Trends in Cell Biology, 8(11), 425–427.
Mavroudis, I. A., Manani, METRO. GRAMO., Petrides, F., Petsoglou, K., Njau,
S. D., Costa, V. GRAMO., & Baloyannis, S. j.
(2013). Dendritic and
spinal pathology of the Purkinje cells from the human cerebel-
lar vermis in Alzheimer’s disease. Psychiatria Danubina, 25(3),
221–226.
Mei, w., Mohagheghi, S., Zampieri, S., & Bullo, F. (2017). Sobre el
dynamics of deterministic epidemic propagation over networks.
Annual Reviews in Control, 44, 116–128.
morris, R. GRAMO. (1996). Neurobiological correlates of cognitive dys-
In The cognitive neuropsychology of Alzheimer-type
función.
dementia. prensa de la Universidad de Oxford.
Morrison,
J., Scherr, S., Luis, D. A., Campbell, METRO., Bloom,
(1986). The laminar and regional
F., Rogers, J., & Benoit, R.
distribution of neocortical somatostatin and neuritic plaques: Im-
plications for Alzheimer’s disease as a global neocortical discon-
In The biological substrates of Alzheimer’s
nection syndrome.
enfermedad (páginas. 115–131). Prensa académica, Orlando, Florida.
Raj, A., Kuceyeski, A., & Weiner, METRO.
(2012). A network diffu-
sion model of disease progression in dementia. Neurona, 73(6),
1204–1215.
Raj, A., & Powell, F. (2018). Models of network spread and network
degeneration in brain disorders. Biological Psychiatry: Cognitivo
Neuroscience and Neuroimaging, 3(9), 788–797.
Rolls, mi. T., Joliot, METRO., & Tzourio-Mazoyer, norte. (2015). Implementa-
tion of a new parcellation of the orbitofrontal cortex in the auto-
mated anatomical labeling atlas. NeuroImagen, 122, 1–5.
Rose, S. MI., Chen, F., Chalk, j. B., Zelaya, F. o., Strugnell, W.. MI.,
Benson, METRO., . . . Doddrell, D. METRO. (2000). Loss of connectivity in
Alzheimer’s disease: an evaluation of white matter tract integrity
with colour coded MR diffusion tensor imaging. Journal of Neu-
rology, Neurosurgery & Psiquiatría, 69(4), 528–530.
Rubinov, METRO., & bullmore, mi. (2013). Fledgling pathoconnectomics
of psychiatric disorders. Tendencias en Ciencias Cognitivas, 17(12),
641–647.
Sanchez-Rodriguez, l. METRO., Iturria-Medina, y., Baines, mi. A., Mallo,
S. C., Dousty, METRO., Sotero, R. C., & Alzheimer’s Disease Neu-
roimaging Initiative.
(2018). Design of optimal nonlinear net-
work controllers for Alzheimer’s disease. PLoS computacional
Biología, 14(5).
Seguin, C., Van Den Heuvel, METRO. PAG., & Brilla, A. (2018). Naviga-
tion of brain networks. Actas de la Academia Nacional de
Ciencias, 115(24), 6297–6302.
Silver, GRAMO., Akbarzadeh, METRO., & Estrada, mi.
(2018). Tuned commu-
nicability metrics in networks. The case of alternative routes for
urban traffic. Chaos, Solitons & Fractals, 116, 402–413.
Herrero, R. MI., Tournier, J.-D., Calamante, F., & connelly, A. (2012).
Anatomically-constrained tractography: improved diffusion MRI
streamlines tractography through effective use of anatomical in-
formación. NeuroImagen, 62(3), 1924–1938.
Herrero, R. MI., Tournier, J.-D., Calamante, F., & connelly, A. (2015a).
The effects of SIFT on the reproducibility and biological accuracy
of the structural connectome. NeuroImagen, 104, 253–265.
Herrero, R. MI., Tournier, J.-D., Calamante, F., & connelly, A. (2015b).
SIFT2: Enabling dense quantitative assessment of brain white
matter connectivity using streamlines tractography. NeuroImagen,
119, 338–351.
Herrero, S. METRO. (2002). Fast robust automated brain extraction. Humano
Mapeo cerebral, 17(3), 143–155.
Hombre nuevo, METRO. (2010). Networks: An introduction. Oxford Univer-
estampar, C. j. (2014). Modern network science of neurological disor-
sity Press.
Peraza, l. r., Díaz-Parra, A., Kennion, o., Moratal, D., taylor,
J.-P., Kaiser, METRO., & Alzheimer’s Disease Neuroimaging Initiative.
(2019). Structural connectivity centrality changes mark the path
toward Alzheimer’s disease. Alzheimer’s & Dementia: Diagnosis,
Evaluación & Disease Monitoring, 11, 98–107.
Qin, J., Wei, METRO., Liu, h., Chen, J., yan, r., Yao, Z., & Lu, q. (2015).
Altered anatomical patterns of depression in relation to antide-
pressant treatment: Evidence from a pattern recognition analysis
Diario de
on the topological organization of brain networks.
Affective Disorders, 180, 129–137.
(2016).
Qiu, y., Liu, S., Hilal, S., Loke, Y. METRO., Ikram, METRO. K., Xu, X., . . .
zhou, j.
Inter-hemispheric functional dysconnectivity
mediates the association of corpus callosum degeneration with
memory impairment in AD and amnestic MCI. Scientific Reports,
6, 32573.
ders. Naturaleza Reseñas Neurociencia, 15(10), 683–695.
taylor, PAG. NORTE., Sinha, NORTE., Wang, y., vos, S. B., de Tisi, J., Miserocchi,
A., . . . Duncan, j. S. (2018). The impact of epilepsy surgery on the
structural connectome and its relation to outcome. NeuroImagen:
Clinical, 18, 202–214.
Thompson, PAG. METRO., Hayashi, k. METRO., De Zubicaray, GRAMO., Janke, A. l.,
Rose, S. MI., Semple, J., & Toga, A. W..
(2003). Dinámica de
gray matter loss in Alzheimer’s disease. Revista de neurociencia,
23(3), 994–1005.
Tipnis, Ud., Amico, MI., Ventresca, METRO., & Goni, j.
(2018). Modelo-
ing communication processes in the human connectome through
cooperative learning. IEEE Transactions on Network Science and
Ingeniería.
Tomasi, D., Wang, G.-J., & Volkow, norte. D.
(2013). Energetic cost
of brain functional connectivity. Actas del Nacional
Academia de Ciencias, 110(33), 13642–13647.
Neurociencia en red
1028
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
0
0
7
1
8
6
7
0
0
5
norte
mi
norte
_
a
_
0
0
1
4
3
pag
d
/
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Communicability distance and Alzheimer’s
Tournier, j. D., Calamante, F., & connelly, A.
Improved
probabilistic streamlines tractography by 2nd order integration
over fibre orientation distributions. In Proceedings of the Inter-
national Society for Magnetic Resonance in Medicine, 18, 1670.
(2010).
Van Den Heuvel, METRO. PAG., & despreciar, oh. (2011). Rich-club organiza-
tion of the human connectome. Revista de neurociencia, 31(44),
15775–15786.
Veraart, J., Nóvikov, D. S., Christiaens, D., Ades-Aron, B., Sijbers, J.,
& Fieremans, mi. (2016). Denoising of diffusion MRI using random
matrix theory. NeuroImagen, 142, 394–406.
Caminante, l. C., & Jucker, METRO.
(2015). Neurodegenerative diseases:
Expanding the prion concept. Revisión anual de neurociencia,
38, 87–103.
Wang, Z., Wang, J., zhang, h., Mchugh, r., Sol, X., li, K., &
Interhemispheric functional and structural
Cual, q. X.
(2015).
disconnection in alzheimer’s disease: A combined resting-state
fMRI and DTI study. Más uno, 10(5).
Warren, j. D., Rohrer, j. D., Schott, j. METRO., Fox, norte. C., Hardy, J., &
Rossor, METRO. norte. (2013). Molecular nexopathies: a new paradigm
of neurodegenerative disease. Trends in Neurosciences, 36(10),
561–569.
Wilcock, GRAMO., & Esiri, METRO. (1982). Plaques, tangles and dementia: A
quantitative study. Journal of the Neurological Sciences, 56(2–3),
343–356.
yan, X., despreciar, o., & Avena-Koenigsberger, A.
(2020). Efficient
network navigation with partial information. arXiv preimpresión arXiv:
2001.02274.
zhang, y., Brady, METRO., & Herrero, S.
(2001). Segmentation of brain
MR images through a hidden Markov random field model and
IEEE Transactions on
the expectation-maximization algorithm.
Medical Imaging, 20(1), 45–57.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
4
4
1
0
0
7
1
8
6
7
0
0
5
norte
mi
norte
_
a
_
0
0
1
4
3
pag
d
t
/
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Neurociencia en red
1029