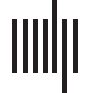INVESTIGACIÓN
Brain network constraints and recurrent neural
networks reproduce unique trajectories and state
transitions seen over the span of minutes in
resting-state fMRI
Amrit Kashyap1 and Shella Keilholz
1
1Department of Biological Engineering, Georgia Tech and Emory, Atlanta, Georgia, EE.UU
un acceso abierto
diario
Palabras clave: Networks to dynamics, Brain network models, Neural mass models, Diffusion tensor
imaging, Resting-state fMRI, Recurrent neural networks, Generative models
ABSTRACTO
Large-scale patterns of spontaneous whole-brain activity seen in resting-state functional
magnetic resonance imaging (rs-fMRI) are in part believed to arise from neural populations
interacting through the structural network (Honey, kötter, romper la lanza, & despreciar, 2007).
Generative models that simulate this network activity, called brain network models (BNM),
are able to reproduce global averaged properties of empirical rs-fMRI activity such as
conectividad funcional (FC) but perform poorly in reproducing unique trajectories and state
transitions that are observed over the span of minutes in whole-brain data (Cabral, Kringelbach,
& decoración 2017; Kashyap & Keilholz, 2019). The manuscript demonstrates that by using
recurrent neural networks, it can fit the BNM in a novel way to the rs-fMRI data and predict
large amounts of variance between subsequent measures of rs-fMRI data. Simulated data also
contain unique repeating trajectories observed in rs-fMRI, called quasiperiodic patterns
(QPP), that span 20 s and complex state transitions observed using k-means analysis on
windowed FC matrices (Allen et al., 2012; Majeed et al., 2011). Our approach is able to
estimate the manifold of rs-fMRI dynamics by training on generating subsequent time points,
and it can simulate complex resting-state trajectories better than the traditional generative
approaches.
RESUMEN DEL AUTOR
Brain network models have become a promising theoretical framework for simulating signals
that are representative of whole-brain activity such as resting-state fMRI. Sin embargo, Ha sido
difficult to compare the complex brain activity obtained from simulations with empirical
datos. Previous studies have used simple metrics to characterize coordination between regions
such as functional connectivity. In this manuscript, we extend this work by utilizing modern
machine learning techniques to fit the brain network models to observed data and train on
the mismatch between the model and observed signal. Our results show that our system
training on these new metrics generalizes to a system that is able to reproduce trajectories
and complex state transitions seen in rs-fMRI over the span of minutes. Our results will be
useful in constraining and developing more realistic simulations of whole-brain activity.
Citación: Kashyap, A., & Keilholz, S.
(2020). Brain network constraints and
recurrent neural networks reproduce
unique trajectories and state
transitions seen over the span of
minutes in resting-state fMRI.
Neurociencia en red, 4(2), 448–466.
https://doi.org/10.1162/netn_a_00129
DOI:
https://doi.org/10.1162/netn_a_00129
Recibió: 7 Octubre 2019
Aceptado: 22 Enero 2020
Conflicto de intereses: Los autores tienen
declaró que no hay intereses en competencia
existir.
Autor correspondiente:
Shella Keilholz
shella.keilholz@bme.gatech.edu
Editor de manejo:
James Shine
Derechos de autor: © 2020
Instituto de Tecnología de Massachusetts
Publicado bajo Creative Commons
Atribución 4.0 Internacional
(CC POR 4.0) licencia
La prensa del MIT
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
4
2
4
4
8
1
8
6
6
6
6
8
norte
mi
norte
_
a
_
0
0
1
2
9
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Prediciting rs-fMRI using a brain network autoencoder
Trajectories:
A sequence of observed network
actividad, where the activity evolves
from the initial state to the final state
through a well-defined path.
Brain network:
A discrete description of the brain
consisting of nodes representing
neural populations and the
connections between them.
Brain network model:
A generative model that tries to
replicate measured brain activity,
by modeling neural populations
interacting through the structural
brain network.
Structural network:
The underlying network consisting of
long-distance white matter
myelinated cables that connect
disparate neural populations.
Functional network:
Nodes of the network that act in a
coordinated way over a given period
of the time.
Recurrent neural networks:
A neural network where the last
computed output is used as feedback
for the next input.
INTRODUCCIÓN
Over the past decade, our understanding of spontaneous whole-brain activity and coordina-
tion between brain regions has largely been obtained through noninvasive resting-state func-
tional magnetic resonance imaging (rs-fMRI) estudios (Biswal, Yetkin, Haughton, & Hyde, 1995;
Margulies et al., 2016; Smith et al., 2009; Brilla, Proporcionó, cocineros, Perdido, & romper la lanza, 2014).
Resting state, a state without an explicit task or stimulus, has surprisingly complex whole-
brain trajectories that are well structured and highly dependent on the previous brain activity
(Allen et al., 2012; Billings et al., 2017; Shakil, Sotavento, & Keilholz, 2016; Zalesky et al., 2014).
Current generative models such as brain network models (BNM) attempt to characterize-whole
brain activity as the interaction between a single neural population and the activity of its net-
work neighbors defined by its structural fiber connections as measured through diffusion tensor
imaging (Cabral, Hugues, despreciar, & decoración, 2011; Honey et al., 2007). Although there are many
variants of the model that use different sets of differential equations to describe the activity at
each node, all brain network models heavily rely on the description of the structural network
through which they interact (Sanz-Leon, Knock, Spiegler, & Jirsa, 2015).
Long simulations of brain network models, starting from random initial conditions, are able
reproduce time-averaged properties of rs-fMRI. These properties such as average functional
conectividad (FC) are defined as the correlation between brain regions over long periods of
simulated time greater than 10 mín. (Cabral et al., 2017). The time-averaged properties are
thought to be more related to the structural network and are thus able to be reproduced by
many different BNMs since they all share the structural network as an input (Cabral et al.,
2017; Kashyap & Keilholz, 2019; Skudlarski et al., 2008). Sin embargo, the BNMs are worse
and more variable at reproducing transient dynamic features that occur at shorter timescales,
on the order of seconds and minutes, which are much more dependent on the exact de-
scription of the differential equations (Cabral et al., 2017; Kashyap & Keilholz, 2019). Desde
BNMs are not synchronized with actual measurements, there exists a gap in understand-
ing how much these models are able to capture the actual changes to fMRI signal between
measurements.
We propose a novel method synchronizing the BNMs to empirical data using recurrent
neural networks (RNNs) in order to learn the initial state of the BNM from measured rs-fMRI
datos. Then using a Euler integration scheme, we can use the differential equations from the
BNM to predict the next rs-fMRI data point and then evaluate directly how well it compares
against the next measured time point. By applying this technique, brain network autoencoder
(BNA), we can quantify how much of the variance of future resting-state activity can be ac-
counted for from previous brain activity using RNNs with BNM constraints as opposed to other
sources that influence large brain activity such as external stimuli. This approach of using RNNs
with constraints in order to model biological systems has been recently gaining attention as
a efficient tool in solving for and modeling unknown systems of differential equations. El
approach combines the power of machine learning and allows for the incorporation of known
biological variables that allow for interpretation on how the signal evolves (Chen, Rubanova,
Bettencourt, & Duvenaud, 2019; Pandarinath et al., 2018). Además, the approach has an
advantage over traditional methods fitting parameters of the BNM, which simulate over a large
parameter space and then use time-averaged measures such as FC for model selection. Bastante,
the mismatch between the model empirical signal at every time step is fed into the machine
learning system to fit model to the data. This approach might also help distinguish between
different variants of BNMs as it provides a useful measure in evaluating their performance
on short time predictions, as they are all able to produce time-averaged measures as average
FC (Cabral et al., 2017).
Neurociencia en red
449
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
4
2
4
4
8
1
8
6
6
6
6
8
norte
mi
norte
_
a
_
0
0
1
2
9
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Prediciting rs-fMRI using a brain network autoencoder
Dynamic analysis techniques:
Techniques that characterize
transient features of a times series,
rather than providing time-averaged
measures.
We evaluate the effectiveness of our model in its accuracy of short-term predictions (< 5s)
that are synchronized to the empirical data and the dynamic properties of the simulated signal
over long time intervals (>10 mín.). In order to train our model, we used fMRI scans from 407
Human Connectome subjects (Van Essen et al., 2013) reduced to 66 regiones de interés (ROI)
according to the Desikan-Killiany atlas (Desikan et al., 2006). The corresponding structural
connectivity to the Desikan-Killiany atlas was estimated using tractrography on five HCP sub-
jects (Kashyap & Keilholz, 2019). After we trained the model, we then evaluate our model on
a set of 40 unseen subjects and over 1,000 different initializations to see how well the system
generalizes from the training set in order to produce correct predictions on unseen brain ac-
actividad. We test two variants of this model that have different latent states, the firing rate and the
Wilson-Cowan model, in order to see whether this method can distinguish the performance
between different variants of brain network models (Cabral, Hugues, Kringelbach, & decoración,
2012a; decoración, Jirsa, McIntosh, despreciar, & kötter, 2009). We utilize an autoregressive model as
a null model to compare our effectiveness on short-term predictions. A similar linear variant
(general linear model) is currently being used to distinguish the activity between rest and task
blocks and regress out resting-state activity in order to infer task networks (Smith et al., 2009).
We test long periods of simulations of our generative model using dynamic analysis tech-
niques in a similar manner currently used for evaluating traditional BNM (Kashyap & Keilholz,
2019), in order to see whether it can reproduce dynamic properties observed in rs-fMRI that
repeat over minutes. We utilize the k-means analysis on short-windowed FCs that looks for
structure in the signal in the timescale of around a minute, and a quasiperiodic pattern (QPP)
technique that searches for a 20-s repeating pattern. We use a traditional firing rate model as
a null model to compare against the long instantiations of BNAs.
The BNA method offers three main strengths in comparison with other methods that are
currently used to simulate whole-brain signals:
1.
2.
3.
It solves the problem of comparing simulated and empirical data without using time-
averaged metrics such as average FC, by directly using real data to initialize the model
and by measuring differences in the predicted transient dynamics on a moment-to-
moment basis.
It allows us to use black-box machine learning techniques while simultaneously estimat-
ing interpretable latent variables such as firing rate or excitatory and inhibitory currents
that can be verified using multimodal recordings.
In long simulations of the BNA, the simulated signal exhibits dynamic properties seen
in empirical rs-fMRI that occur over a timescale of minutes, which are not reproducible
using traditional BNM techniques.
Por lo tanto, we believe that the brain network autoencoder will be a useful tool to help us
understand brain dynamics at the macroscale level.
RESULTADOS
One-Time-Step Prediction
Sequential autoencoders:
A deep learning architecture that
trains on predicting the next timestep
from the last observed timestep.
The sequential autoencoder is trained to predict one time step in advance. In this section we
show how the signal is reproduced across 66 regions starting from the input, then projected
onto the latent space representing the initial conditions of the BNM, and finally integrated to
predict the next time step. En figura 1, we present the results of predicting the next time step
from the previous time step for the two different variants of BNA, the firing rate model and
Neurociencia en red
450
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
4
2
4
4
8
1
8
6
6
6
6
8
norte
mi
norte
_
a
_
0
0
1
2
9
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Prediciting rs-fMRI using a brain network autoencoder
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
Cifra 1. One-step prediction. Two different Brain Network Autoencoders are able to reproduce the next time step from the previous time
step. The autoencoder takes as input the measured signal (leftmost) at time step t and outputs the predicted (second from left) signal at t + 1.
The autoencoder projects the input into a space constrained by the brain network model equations (middle panel), which are represented as
the state variables in the firing rate model (firing rate) or the Wilson-Cowan model (excitatory and inhibitory currents), and then are integrated
to produce the predicted output. The plots represent a 3D contour plot where the x-axis represents time, the y-axis represents the different
66 ROI, and the color represents the intensity that has been z-scored (see fMRI data subsection in the Methods section). The rightmost panel
shows the time series of a single ROI for the input (rs-fMRI), producción (estimated), and latent state (firing rate or excitatory/inhibitory currents).
At one time step the accuracy in terms of R2 across all ROIs is on average 0.95.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
4
2
4
4
8
1
8
6
6
6
6
8
norte
mi
norte
_
a
_
0
0
1
2
9
pag
d
.
t
the Wilson-Cowan model. Although both are able to reproduce the spatio temporal signal as
como se muestra en la figura 1 (middle top and middle bottom), they differ in the latent or hidden variables
used to represent the transitions. For the firing rate BNA, the measured data are projected
into a space with firing rate as the hidden variable for each region, as can be seen in Figure 1
(right top). The latent variable time series has a high degree of similarity to the original signal
(correlation > 0.9) como se muestra en la figura 1, top right. The latent state is then passed onto the BNM,
which integrates it according to the firing rate model to predict the next time-step. The traces
of the input, producción, and latent state for a single ROI are shown in Figure 1 (left top). Para el
Wilson-Cowan model, Cifra 1 (fila inferior), the latent state is represented by two variables,
the excitatory and the inhibitory currents, and their interaction through the Wilson-Cowan
model produces the next rs-fMRI time step. The excitatory current is positively correlated with
the measured signal and the inhibitory current is negatively correlated with the signal, a pesar de
both to lesser degrees than the firing rate model. The models perform relatively similarly in
predicting one time step in front and are able to reproduce the input signal with an R2 of 0.95
averaged across all areas.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
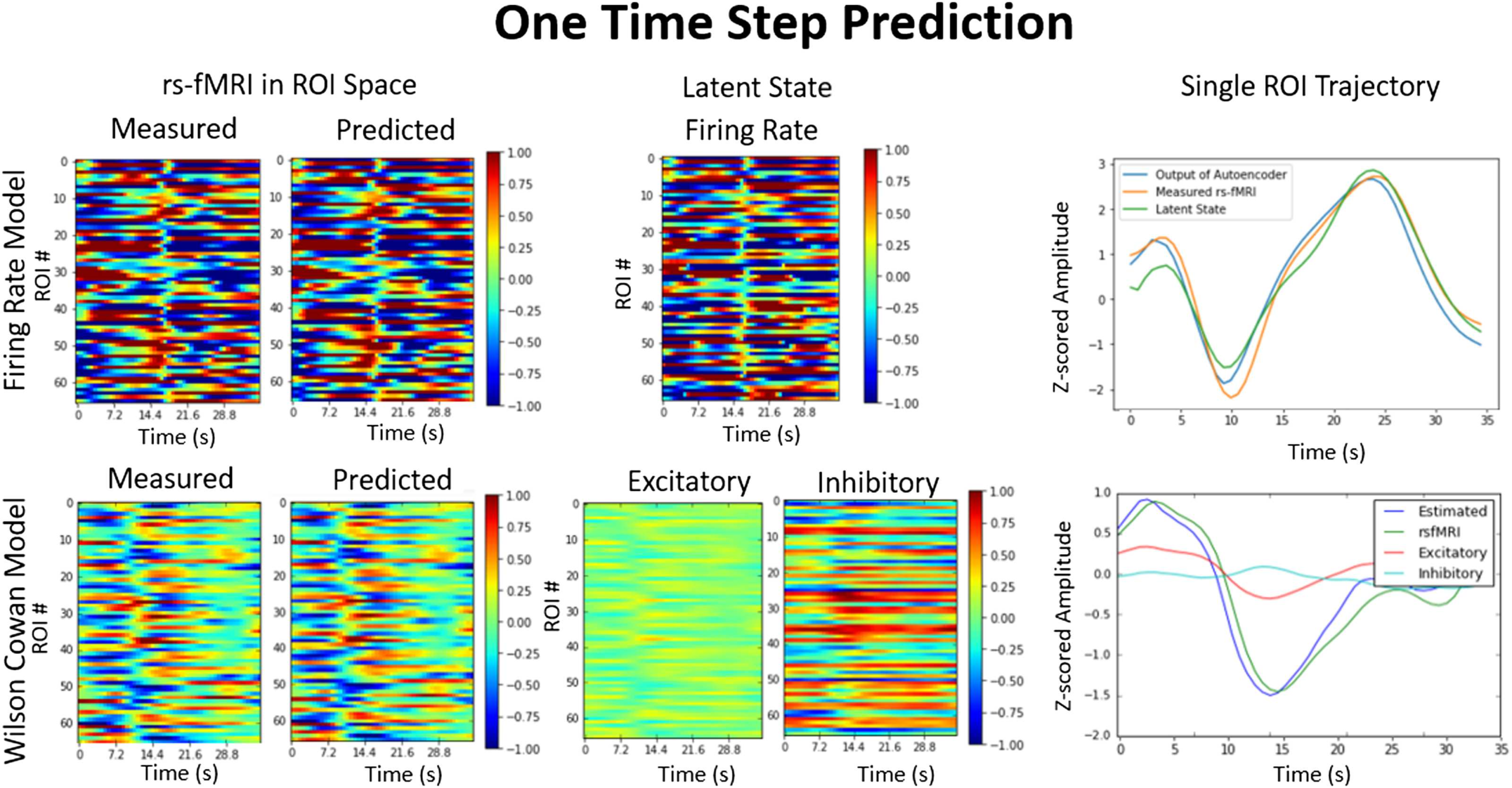
Multiple-Time-Step Prediction
The sequential autoencoder can also predict multiple steps into the future by recursively feed-
ing the predicted output in as the next input. The performance of multi-time-step forecasting
Neurociencia en red
451
Prediciting rs-fMRI using a brain network autoencoder
se muestra en la figura 2 (arriba a la izquierda), where the averaged R2 across a test and a subset of the training
data of the same size for both BNA variants are compared with a naive variant of the auto-
regressive model that assumes the next time point is the previous time point (see Methods).
The autoregressive model is similar to the current approach used to differentiate task from rest
signals, namely the generalized linear model, which uses the time steps before task activation
as a regressor to remove the resting-state activity from task responses (Smith et al., 2009). El
generalized linear and the autoregressive model resting state as a constant baseline that does
not change over time. Although the autoregressive performs as well as the BNA for the first
time point, the BNA is able to reproduce the first three time steps with an R2 of around 0.9
or higher, as opposed to autoregressive model which is only greater than 0.9 for the first time
step. The test and training performance is relatively similar for the autoencoders, only when
all the parameters are set correctly and the network is not over- or undertrained (see Methods,
Cifra 6, for more detail).
Characteristic of autoencoders, the error compounds at every time step, because the previ-
ous errors are propagated to the next time step. This causes the model to completely diverge
por 10 s from the measured signal, as shown in Figure 2, top right. The bottom left panel in
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
4
2
4
4
8
1
8
6
6
6
6
8
norte
mi
norte
_
a
_
0
0
1
2
9
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 2. Error across multi-step prediction. Top left: Accuracy of our generative model in synthesizing the first few time points. El
accuracy of the firing rate and Wilson-Cowan models are compared on training and test datasets and with the autoregressive model. The error
compounds and gradually increases until the model diverges completely from the measured signal around 10 s and continues along its own
dinámica (top right). The accuracy over time for the Wilson-Cowan and firing rate training overlap, as both models do about as well as each
other on training data. Bottom left: Histogram of R2 for each individual in test and train datasets shows that it generalizes across individuals.
Bottom right: The mean squared error (MSE) for each region of interest (ROI) in predicting the first time step. The MSE is used here to compare
differences across ROIs, because it was the error that was used to train the system and is more reproducible across instantiations.
Neurociencia en red
452
Prediciting rs-fMRI using a brain network autoencoder
Cifra 2 also shows that the BNA generalizes across individuals, as the histogram of the er-
rors is roughly the same for all the individuals in the training or the testing dataset. The two
different BNA variants, the firing rate and the Wilson-Cowan, are similar in performance as
seen in the top right of Figure 2, with the Wilson-Cowan having on average a higher R2 on
the test dataset. The BNA does not perform equally in predicting each of the ROI time series.
It predicts certain regions with a higher accuracy than the others. The mean squared error
per each ROI for the first time step is shown in Figure 2, bottom right. The mean squared
error was used here instead of R2, because the network was trained to minimize this gradient
during training and most accurately represents the performance on each ROI. The error was
largest in the ROIs in the temporal lobe, namely the entorhinal cortex, parahippocampal gyrus,
and the temporal pole. These regions are the least connected to the rest of the network and
more connected with subcortical regions, which have not been included in the simulations
(Cabral et al., 2011).
Analysis of Long Simulations
In order to assess properties of the simulated signal at longer periods, the BNA was used to
generate 1,000 time points or 12 min of data. Properties of longer simulations of BNA were
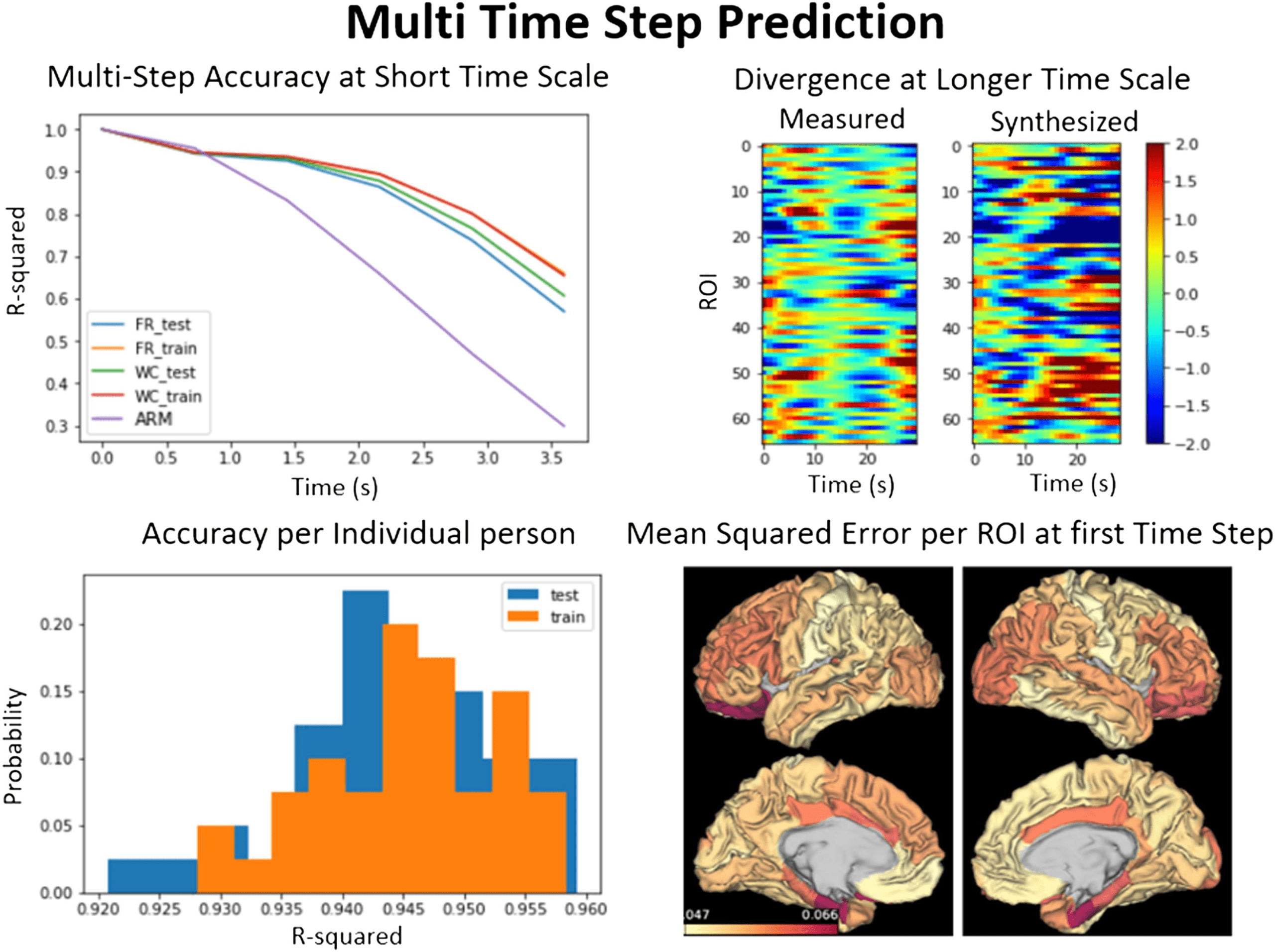
compared with those of the empirical signal. En figura 3, the average functional connectivity
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
4
2
4
4
8
1
8
6
6
6
6
8
norte
mi
norte
_
a
_
0
0
1
2
9
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 3. Average functional connectivity and power spectrum. Comparison of average functional connectivity from empirical rs-fMRI (arriba
izquierda), BNA firing rate (top left middle), BNA Wilson-Cowan (top right middle), and a traditional firing rate BNM (top right). The simulated
FC matrices have a high degree of correlation (0.7–0.85) with the empirical FC, unlike the traditional BNM that have a correlation of 0.5
(abajo a la izquierda). Each axis in the FC plots represents the regions in the ROI that are shown on the right. The frequency spectrum (abajo
bien) of the BNA follows that of the empirical signal exactly except at the higher frequencies (> 0.125 Hz), where the simulated signal has
much larger power. The traditional brain network model has less structure in the frequency range (0.01–0.1 Hz) and has equal power in most
of the range compared with the rs-fMRI and the BNA models. The traditional BNM and the empirical signal also have been filtered at 0.125 Hz,
while the BNA models are not.
Neurociencia en red
453
Prediciting rs-fMRI using a brain network autoencoder
and the power spectrum of the empirical and the BNA as well as a traditional firing rate BNM
are compared. The traditional BNM FC has a weak correlation with the empirical FC (0.35) y
is in the range of most traditional methods (0.3–0.6; Cabral et al., 2017; Kashyap & Keilholz,
2019; Sanz-Leon et al., 2015; Senden, Reuter, van den heuvel, Goebel, & decoración, 2017). El
BNA performs much better at reproducing the detailed relationship between ROIs seen in FC,
compared with the traditional model where groups of ROIs are synchronized over long periods
of time, causing blocky patches in the FC when the ROIs are ordered by highly connected
subgraphs (Cabral et al., 2011; Kashyap & Keilholz, 2019). The FC of the BNA has a high
correlation of 0.83 (firing rate) y 0.7 (Wilson-Cowan) to the actual measured signal. El
spectral power of the empirical and the simulated signal is indistinguishable in the range of
0.01 a 0.125 Hz, and has the characteristic 1/f linear slope of around 0.9. The traditional BNM
has less temporal structure and is relatively flat over the lower frequency compared with all
the other models and the empirical signal (Kashyap & Keilholz, 2019). At higher frequencies
the model tends to produce much higher levels of noise than the empirical signal and the
traditional BNM, both of which have already been filtered in the preprocessing steps. Before
analyzing the simulated signal with dynamical analysis techniques, we therefore filtered it at
0.125 Hz to minimize the high frequency power that would interfere with the dynamic analysis
algoritmos.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
4
2
4
4
8
1
8
6
6
6
6
8
norte
mi
norte
_
a
_
0
0
1
2
9
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
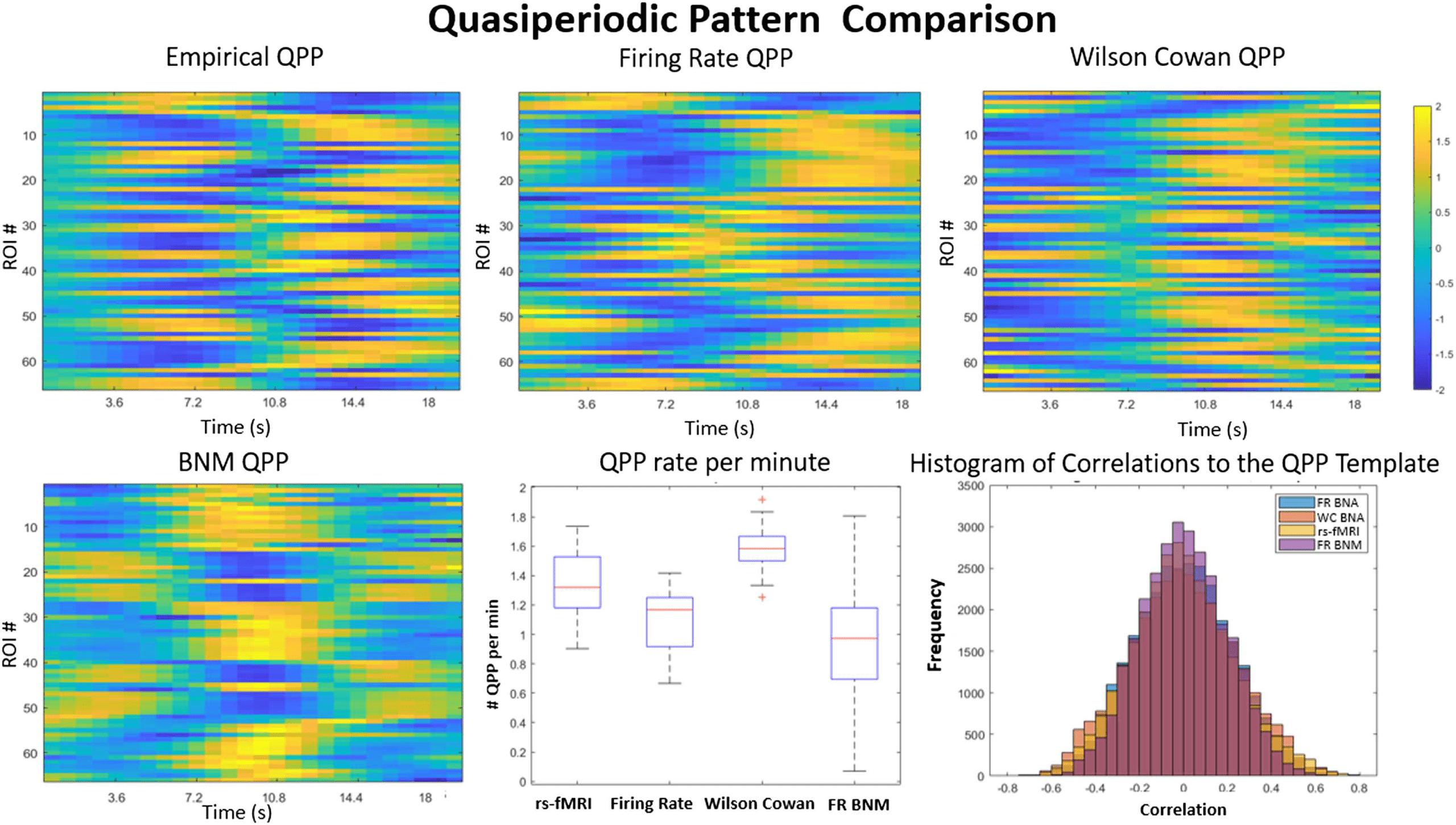
Cifra 4. QPP template comparison. Comparison of the different QPP templates is shown in the top row between measured data (arriba a la izquierda),
the brain network autoencoders (BNA; top middle and right), and the older BNM (abajo a la izquierda). The QPP templates represent a unique 18-s
trajectory of all the ROIs (y-axis) that repeats itself on average 1.3 times per minute (bottom middle). The rs-fMRI signal is highly correlated
with the template during specific time points in its trajectory, as seen in the distribution of correlations to the template (bottom right). El
Wilson-Cowan and the firing rate BNA have similar distributions, while the BNM template is least correlated with its own data. The firing
rate BNA QPP is the closest to the empirical QPP (correlation 0.73) and occurs roughly 1.19 times per minute. The Wilson-Cowan BNA QPP
occurs a little faster, alrededor 1.4 times a minute, and has a correlation of 0.43 with the original template. The older BNM QPP is more of an
on-off trajectory and does not have the intricate delays and temporal structure as seen in the QPP of the empirical signal or the BNA models.
Neurociencia en red
454
Prediciting rs-fMRI using a brain network autoencoder
We also analyzed the simulated signal for unique trajectories known as quasiperiodic pat-
charranes (QPP), which could also be considered a limit cycle (Majeed et al., 2011). Limit cycles
are a property unique to nonlinear systems, and reproducing such a property would mean that
the generative model reproduces some of the dynamics features of rs-fMRI despite its diver-
gence from measured signals. En figura 4 we have plotted the QPP for the rs-fMRI signal (arriba
izquierda), a traditional generative firing rate BNM model (abajo a la izquierda), and both of the BNA variants
(top middle and right). The empirical QPP involves a 20 s trajectory that switches from task
positive networks (first half of the template) to the more internal or default mode networks of
the brain (second half of the template; Majeed et al., 2011). After phase adjusting the tem-
plates, the maximum correlation of the firing rate BNA QPP was 0.75 and the Wilson-Cowan
BNA QPP was 0.43 to the original template. This is very different from the traditional dynam-
ics seen in BNM (abajo a la izquierda), which produce blocky limit cycles of clusters of nodes that are
highly synchronized together and activating together. The BNA produces QPP that are highly
structured spatially and temporally. The correlation between the QPP template and the signal
is plotted in the bottom middle, where certain time points show a high degree of correlation
to the trajectory in the QPP template. Thresholding at 95% significance, the occurrence of
these QPP is around 1.3 times a minute in the rs-fMRI data. The BNA models have similar
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
4
2
4
4
8
1
8
6
6
6
6
8
norte
mi
norte
_
a
_
0
0
1
2
9
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
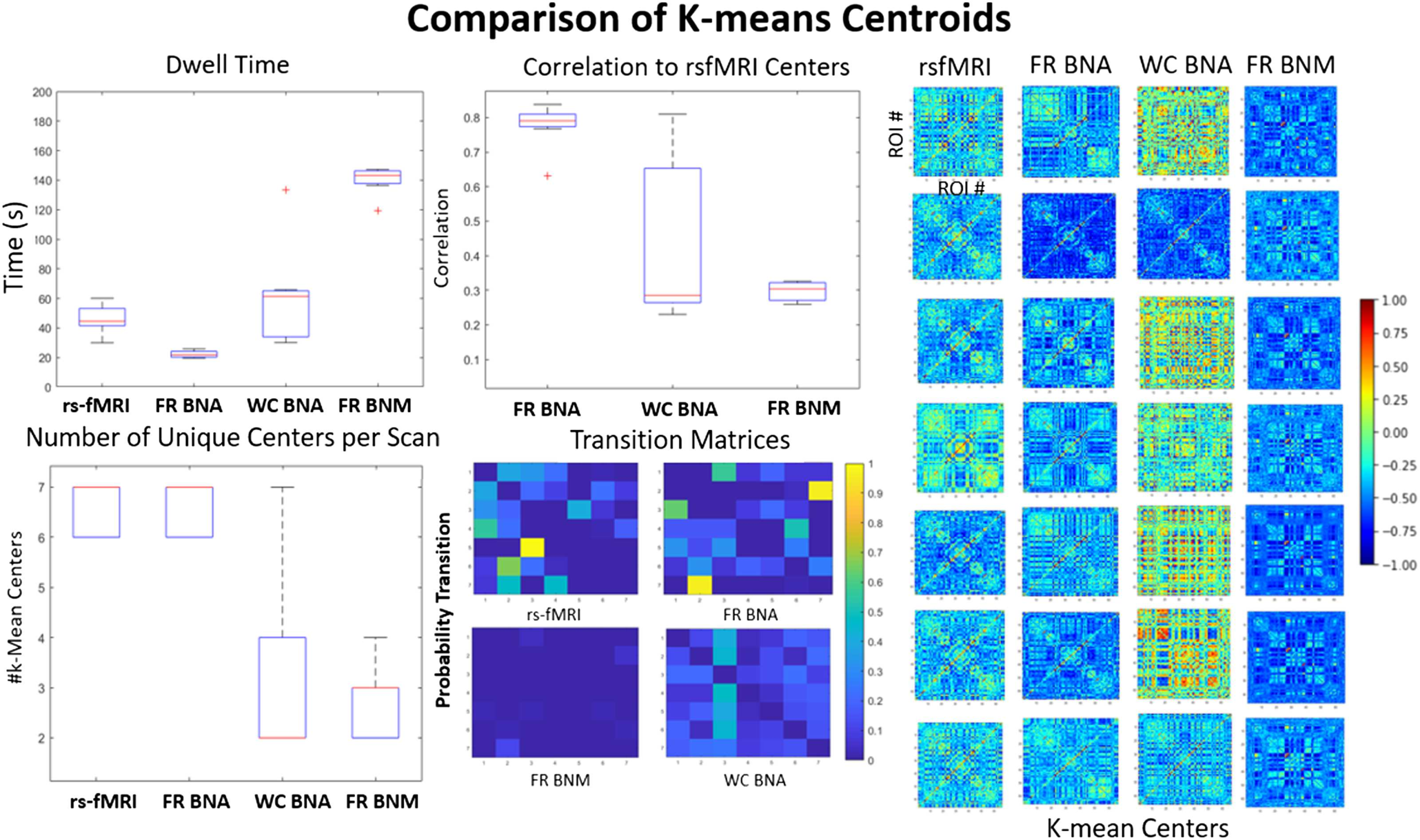
Cifra 5. K-means comparison. This figure compares the k-means centers and the transitions for the simulated (BNA and naive BNM) y
the empirical signal (30 scans of 15 mín.). The seven centers are shown in the far right for each category (FR: firing rate, WC: Wilson-Cowan).
A boxplot measuring the max correlation is shown (middle top) between each of the simulated centers to the centers from the rs-fMRI data.
The dwell time in seconds in each of these centers is shown in the top left. The rest of the transition probabilities (diagonal zeroed out) son
shown in the bottom middle. The number of centers in each of the 30 scans is also variable even though they all are defined to have seven
clusters across all scans (abajo a la izquierda).
Neurociencia en red
455
Prediciting rs-fMRI using a brain network autoencoder
tarifas, where the firing rate BNA has an occurrence of 1.19 times a minute. The firing rate brain
network model shows more variance in the number of QPP cycles per minute (bottom middle,
Cifra 4).
Another property of rs-fMRI that has been studied is the existence of brain states, cual
can be described as large scale patterns of functional organization that are stable over the
span on the order of around 40 s (Allen et al., 2012; Liu & duyn, 2013a).The brain transitions
through these states over time (Allen et al., 2012). Algorithms such as k-Means have typically
identified six or seven states. We applied k-Means clustering on short-windowed functional
connectivity matrices (50 s) to find these states in the simulated data (see methods for more
detail). En figura 5, we show the comparison between our BNA models, the firing rate brain net-
work models, and the measured signal for cluster centers as a result of the k-means algorithm.
We quantified how close the centers are to each other by taking the maximum correlation of
each center to those measured in rs-fMRI. We calculated the length of time in each state (arriba
izquierda), the transition likelihood between states (bottom middle), and how many unique states
were observed in a single scan (abajo a la izquierda). The centers of the BNA models (middle two)
compared with the traditional BNM (rightmost) are much more distinct from each other. El
Firing Rate BNA model has the highest correlation with the rs-fMRI states (0.8 on average)
and a similar number of states seen during a single scan. Sin embargo, the Firing Rate BNA has
a shorter dwell time and seems to move between states faster than observed in the measured
señal. The Wilson-Cowan model has more variable and diverse centers and tends to have
fewer of them in a single scan, but tends to dwell in them around as long as the measured
datos. The traditional firing rate brain network model is the least accurate, has few transitions
between states, and dwells in a single state for a very long time.
DISCUSIÓN
In this manuscript, we adapted the brain network model with the recurrent neural networks in
order to make short-time future predictions from observed rs-fMRI. Using this approach, nosotros
showed that using the previous measured rs-fMRI data point and an RNN in conjunction with
a network-based model, we can predict large amounts of variance in the subsequent time step.
We then showed that this system generalizes and can generate trajectories that are similar to
resting-state trajectories over larger timescales.
Predicting Moment-to-Moment Variations
We showed that a network-based model can account for up to 95% of the variance in the
fMRI signal between two adjacent time points. This reproduction is not unique, sin embargo,
and can be estimated using any number of latent variables. Although more complex architec-
tures such as variational autoencoder might be able to successfully predict future rs-fMRI data
(Pandarinath et al., 2018), the BNM provides an adequate rough guess of the system dynamics
for the autoencoder to converge. This information helps the model to converge during training
and make accurate predictions. Además, unlike a traditional machine learning approach,
this approach yields testable latent variables that can be further evaluated using multimodal
conjuntos de datos, such as magnetoencephalography (MEG) recordings that have been used to gener-
ate excitatory and inhibitory currents synchronized with concurrent rs-fMRI recordings (Ritter,
Schirner, McIntosh, & Jirsa, 2013).
Fluctuations in spontaneous whole-brain activity have been shown to be nonrandom and
highly structured (Zalesky et al., 2014). This suggests that rs-fMRI has both deterministic and
stochastic components. The variance explained by the BNA at one time prediction represents a
Neurociencia en red
456
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
4
2
4
4
8
1
8
6
6
6
6
8
norte
mi
norte
_
a
_
0
0
1
2
9
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Prediciting rs-fMRI using a brain network autoencoder
Manifold:
A set of all possible trajectories that
originate from the same system and
that describe how activity can evolve
con el tiempo.
lower bound of the amount of determinism that exists in the signal. It is not surprising that this
is the major component of rs-fMRI since the signal has been shown to be highly autocorrelated
with itself (Arbabshirani et al., 2014). The simplified first-order autoregressive model, cual
assumes a steady baseline at the last measured time step, has similar results in performance to
the BNA when compared with a single time step and has an R2 of 0.97. Sin embargo, for multiple
time steps into the future the autoregressive model performs poorly, compared with the BNA
modelos. The two different BNA models perform at short-term scales about as well as each
otro. This suggests that the trajectory in the short time span is predictable to a certain degree
regardless of the approach, but thereafter it starts diverging from the empirical measurements.
The divergence from the original trajectory could be due to a number of sources, como
unknown task or stimulus information, ruido, not incorporating higher order terms in the BNM,
the fallacy of assuming that each ROI behaves in a homogenous fashion, or simply a mismatch
between the algorithm and the data that increases over time. Note the BNA itself is not a
deterministic system. The latent space variables are modeled as distributions before they are
muestreado, resulting in a stochastic system.
Evaluation on Long-Term Dynamics
Although both rs-fMRI and the BNA models are stochastic, long-term simulations of the network-
based model are able to reproduce trajectories that are similar to those seen in rs-fMRI. Individ-
ual trajectories are varied but they repeat over time, suggesting that rs-fMRI follows a bounded
stable manifold that the model is able to estimate. Por lo tanto, random walks across this mani-
fold have shared properties in both the model and the empirical signal. Our results also suggest
that most of the resting-state manifold is strongly related to the network-based activity rather
than input or random perturbations from noise sources such as higher neural processing.
The strongest metric demonstrating this relationship is average FC, which has a large cor-
relation to the empirical dynamics (0.9 > correlation > 0.8). This is unsurprising since the
traditional BNMs do almost as well as the BNAs in this metric, and correlations as high as
0.7 have been reported in the literature (Senden et al., 2017). Average FC seems to be more
related to the structural input than the description of the dynamical system (Cabral et al., 2017;
Kashyap & Keilholz, 2019). Sin embargo, the BNA does better than most BNMs in estimating in-
terhemispheric FC correctly, which is usually challenging in network-based models because
there are far fewer interhemispheric than intrahemispheric connections detected with diffusion
resonancia magnética. The power spectrum profile is also mostly reproducible by the model, except in the very
high frequency where the model has a lot more power than the empirical signal. This might
occur because of the lack of friction in our model, namely that the signals are constantly prop-
agated through feedback loops in the network without loss of energy, unlike the real system.
Since most of predictability of the resting state comes from the structured low-frequency ac-
actividad, we can filter synthesized signal without losing too much information. Other traditional
brain network models using the virtual brain have also reported similar performance on power
spectrum profiles (Ritter et al., 2013).
Although most traditional BNMs have been able to reproduce to some degree the long-term-
averaged properties such as average FC and power spectrum, they have had a harder time in
reproducing faster scale dynamics such as reoccurring unique trajectories or the multistate
transitions seen in dynamic FC (Cabral et al., 2017; Hansen, battaglia, Spiegler, decoración, & Jirsa,
2015; Kashyap & Keilholz, 2019). The results from the QPP analysis, which extracts limit
cycles, show that the simulated signal has a similar 20-s trajectory and that pattern is repeated
over the course of minutes. The results from the k-means analysis on time-varying FC matrices
Neurociencia en red
457
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
4
2
4
4
8
1
8
6
6
6
6
8
norte
mi
norte
_
a
_
0
0
1
2
9
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Prediciting rs-fMRI using a brain network autoencoder
show that the simulated signal has similar state transition in terms of both number and the
spatial patterns to those seen in empirical rs-fMRI. This suggests that both of these properties
arise naturally in the correct nonlinear network-based representation of rs-fMRI that can be
inferred from the data using machine learning techniques. The firing rate BNA seems to fit the
data better than the Wilson-Cowan BNA. This might be because the Wilson-Cowan BNA has
additional nonlinearities due to the interaction between the excitatory and inhibitory currents.
A direct comparison between our model and other brain network models in the literature
on complex dynamical metrics is difficult because most brain network models use their own
unique metric to compare against rs-fMRI and there is no established standard. The origin
of these complex dynamics has been explained in different theoretical ways. These complex
transitions can arise because of the particular nonlinearities of the system (Hansen et al., 2015),
which can result in multiple attractors and limit cycles naturally. They can result from param-
eter changes to the network strength or Hopf bifurcations that cause the system to change its
dynamics over time (Deco et al., 2018; Senden et al., 2017). They can also be the result of
adding external input and stimuli into the system, causing a change from the zero-input man-
ifold and altering the dynamics (Ashourvan et al., 2019; Deco et al., 2019). These are not
mutually exclusive and could induce the changes at once. Our implementation is closest to
the first interpretation of rs-fMRI. We explain the observed nonlinear properties of the data
purely based on network propagation without the need for external input or a change of a
bifurcation variable.
Errors Across Different ROIs
Using our approach, it is not possible to tease apart the origin of the error that could arise
because of a mismatch between the model and the empirical data or because of intrinsic noise.
Sin embargo, looking at the error across regions shows that the error is not evenly distributed
across all regions of interest, which can give some clues to where it might arise. The error
in reproducing the dynamics at one time step is highest in the nodes of the limbic system
(Cifra 2, abajo). We believe that our model performs less accurately in this system because
they are highly connected to the amygdala and the hippocampus, which are not simulated in
el modelo, and are the least connected nodes to the rest of the network (Cabral et al., 2011).
Además, tractography has also been known to underestimate the uncinate fasciculus, el
major highway between the temporal lobe and the frontal areas, which forms the backbone
of the limbic system. The fiber has a very sharp angle that is hard to follow using tractography
(Thomas et al., 2014). The echo planar imaging (EPI) sequence used to obtain rs-fMRI data has
also known susceptibility issues at interfaces, which would affect the nodes at the proximity
such as the frontal pole and the temporal pole, both of which have larger mean squared error
compared with the other nodes.
Comparison With other Machine Learning and Time Forecasting Models
Similar time forecasting has been attempted or is being attempted by several different labs at
the time of this manuscript. A variant utilizes a variational autoencoder to find a latent space
of brain trajectories that would fit the current data (Marrón, Pasquini, Sotavento, & Seeley, 2019).
Another RNN-ICA version uses independento component analysis vectors as the latent space,
while another method uses hidden Markov model to model the hidden states (Hjelm et al.,
2018; Vidaurre et al., 2018). Sin embargo, our method is unique in using brain network models
as a latent space, whose variables are more interpretable since they represent the state of each
neural population’s activity and can be tested using multimodal data. Además, none of the
Neurociencia en red
458
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
4
2
4
4
8
1
8
6
6
6
6
8
norte
mi
norte
_
a
_
0
0
1
2
9
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Prediciting rs-fMRI using a brain network autoencoder
Memoria larga a corto plazo:
A specific implementation of a
recurrent neural network that is very
popular in modeling time series.
other architectures use their model for time series foresting or dynamical analysis, hence their
results are not directly comparable to our work, although their methods are similar.
LIMITATIONS
There are many assumptions that limit the scope of our approach. Machine learning, a pesar de
good at learning structures in datasets, has a shortcoming of arbitrarily creating a system to
fit the data, and every instantiation of the system produces slightly different properties of the
simulated system. We tried to address this issue by using various techniques such as using
structural constraints, dropout of long short-term memory (LSTM) units, using probability to
track the latent variables, and taking the results of multiple runs, in order to make the system
more reliable and reproducible. Another limitation of this model is that it needs 50 tiempo
points prior to the data point in order to solve for the initial conditions. Shorter time intervals
than 50 time points are faster to train, but are less accurate in estimating slow processes.
The longer segments required a larger LSTM network and longer training times and were less
accurate in our dataset. There are more complex architectures that could solve for the initial
conditions faster, such as a forward-backward LSTM architecture (Pandarinath et al., 2018). On
the network side, the parcellation scheme reduces the complexity of the signal and discretizes
the network. Improvements can be made by allowing for continuous propagation along the
cortical sheet, as in the neural field models. Tractography also has its limitations, and better
estimates of structural networks should make the model more realistic and improve results
especially in regions that are not very strongly connected to the rest of the network. Simulating
more of the central nervous system including subcortical regions would also lead to a more
biologically plausible model.
CONCLUSIÓN
We set out to investigate the extent to which network-based theory can explain the moment-
to-moment variations seen in rs-fMRI signal’s. Using a novel machine learning approach, nosotros
solve for the initial state of traditional network-based models and show that we can account
for most of the variation seen in the signal and predict accurately (> 0.6 R2) for at least five
consecutive time points. Longer instantiations of the system show that our model is able to
produce complex trajectories of the nonlinear dynamical system on the order of minutes. Nosotros
believe that our BNA will be useful when a generative model of rest is needed. Además,
it can be trained to predict in real time, which allows contrast against dynamics that contain
deviations from rest such as in task fMRI studies. En el futuro, it can also be used to investigate
deviations from the manifold such as in task input or due to noisy sources.
MÉTODOS
Mathematical Background
The brain network autoencoder is constructed using the constraints from the brain network
modelo, in conjunction with a recurrent neural network variant known as long short-term mem-
ory. The overall design is shown in Figure 6 and implemented using Python TensorFlow. El
architecture is a sequential autoencoder, as it is trained with the previous time point to predict
the next consecutive time point and uses a latent space where the dynamics are constrained
to a smaller space defined by BNM equations to reconstruct the next time point.
Formalmente, in order to predict the next time point, for each neural measured time point x(norte)
we map it to the space F(X(norte)). F is the transformation performed by the RNN and lives
in RM×M×T, where M represents the M distinct ROIs being modeled and T is the length of
Neurociencia en red
459
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
4
2
4
4
8
1
8
6
6
6
6
8
norte
mi
norte
_
a
_
0
0
1
2
9
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Prediciting rs-fMRI using a brain network autoencoder
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
4
2
4
4
8
1
8
6
6
6
6
8
norte
mi
norte
_
a
_
0
0
1
2
9
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
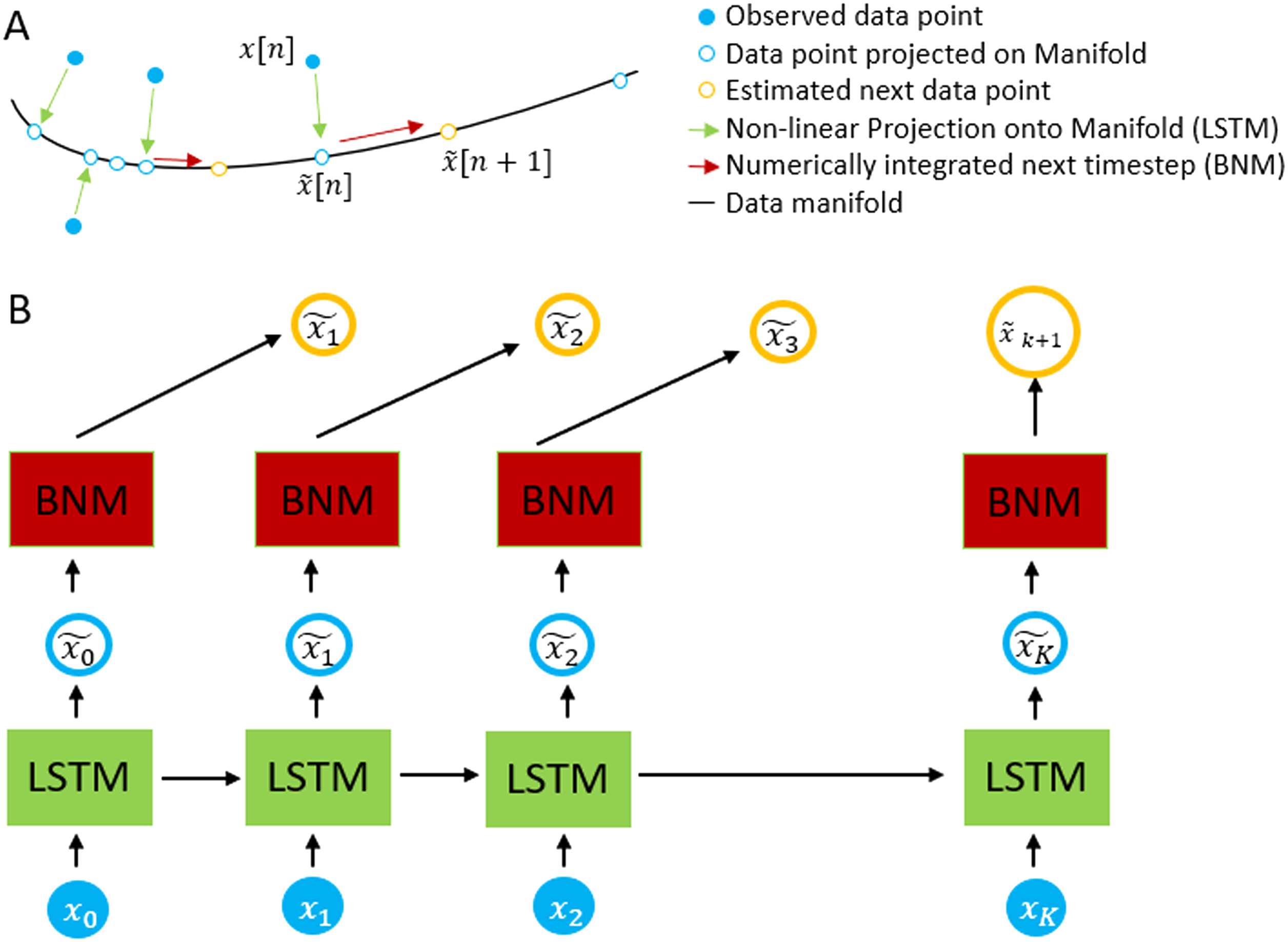
Cifra 6. Schematic of the autoencoder. The measurement x(norte) is passed into the LSTM in order
to estimate ˜x(norte), which lies in the data manifold. Using the BNM forward equations and ˜x(norte) como
our initial conditions, we estimate ˜x(norte + 1). The system is trained by difference in our predicted
versus actual measurement at x(norte + 1).
previous time points that the LSTM depends on. The next time point is computed as x(norte + 1) =
BNM(F(X(norte))). En esencia, the LSTM does a nonlinear coordinate transform of the vector
X(norte) into the brain network space where the dynamics are well defined and we can predict the
next time point. This process is shown pictorially in Figure 6A, where we show the projection
of each data point shown in filled blue circle’s into the manifold represented by the BNM
shown in hollow blue circle’s. On the manifold, we can use the BNM equations to update it
to the next time step shown in orange. Figure 6B shows the actual architecture used to update
the time steps.
For the simplest implementation of BNM, the firing rate model, we can assume the function
to be linear with the observation such that BNM(X) becomes A × x, where the matrix A is the
graph Laplacian and A = k × SN − I, where k < 1 and SN is the structural matrix as measured
through tractography using diffusion tensor imaging (see Methods section, Experimental Data,
Structural network; Hagmann et al., 2008). We use graph Laplacian because it represent’s a
well-studied dynamical system known as the consensus equation. On its own, the consensus
system does not add in any unstable dynamics because all of its eigenvalues are less than
0, if k is set to less than 1 (Mesbahi & Egerstedt, 2010). Therefore the network propagation
dies out over subsequent time steps. The eigenvectors of A have also shown similarities to rs-
fMRI networks (Atasoy, Donnelly, & Pearson, 2016). This algorithm assumes that the Jacobian
matrix representing the changes of one brain region with respect to another more or less lies
in the direction of the structural fiber network and the nonlinear discrepancies are dealt with
by the LSTM (Honey et al., 2007). This can be seen in the Results section (Figure 1), where
latent space of the firing rate model is almost identical to the measured data, suggesting that
Network Neuroscience
460
Prediciting rs-fMRI using a brain network autoencoder
the transformation is near an identity transformation. In a more complex BNM, such as the
Wilson-Cowan, the excitatory current is strongly correlated with the signal although less than
in the firing rate model, as the model has its own inbuilt nonlinearities and deviates further
from the graph Laplacian.
Implementation
The preprocessed data (see Methods section, Experimental Data, fMRI data) is first cut into
contiguous segments of length k. This whole segment is then passed into the long short term
memory unit as shown in Figure 6B. The units are built using the TensorFlow Python module,
specifically the graphics processing unit boosted version to improve speed and performance.
The LSTM units take in a series of consecutive time points, and output a sequence of the same
length of time points. The LSTM units are a form of recurrent neural networks and have memory
of previous time points by using a hidden state vector that it uses as an input to itself for the
next consecutive time point. Hence, LSTMs have become popular in the machine learning
community because of their success in using this architecture in modeling time series such
as speech and natural language processing, in self-driving cars, and even in neural Turing
computers thought to emulate biological intelligence (Graves, Mohamed, & Hinton, 2013;
Graves & Schmidhuber, 2009; Graves, Wayne, & Danihelka, 2014). Moreover, they solve the
problem of learning structure across infinite sequences of consecutive time points by using a
forget gate to truncate inputs seen from a long time ago. In practice this means that they need
to be trained with a finite sequence length of data.
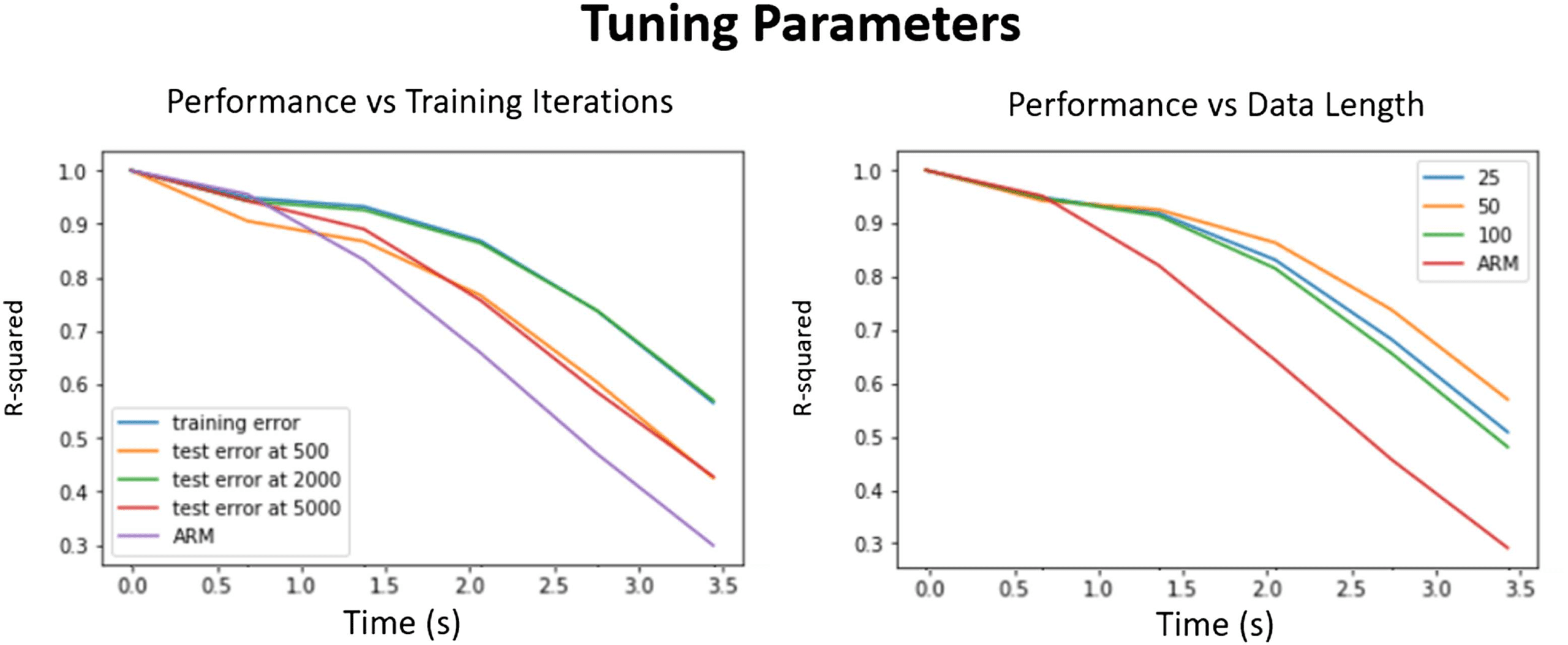
For our implementation we tested data of length 25, 50, and 100 time points (18, 36, 72 s),
as seen in Figure 7, left. The model performed best on 50-length segments, and slightly worse
for shorter and longer segments. The LSTM network was also stacked into several layers in
a similar manner that convolutional neural networks are stacked together in a series. We
In general, more layers improve
used seven identical layers to model the fMRI time series.
accuracy as long as there is enough data in the training set to scale the size of the network;
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
4
8
1
8
6
6
6
6
8
n
e
n
_
a
_
0
0
1
2
9
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7. Tuning parameters. Left: The effect of over- and undertraining the network. The perfor-
mance on the test data compared with the training data at 500 and 5,000 is much worse. For our
network size it performed best at around 2,000 iterations. It is compared with the autoregressive
model as baseline. Right: The effect of picking different length segments and the performance ac-
curacy. Again the maximum is closer to the middle, which was in our case 50. Too small and too
large networks are slightly worse at learning the relationship between past and future rs-fMRI time
points.
Network Neuroscience
461
Prediciting rs-fMRI using a brain network autoencoder
otherwise, there is a risk on overfitting. Using the inference error as a metric, we also swept
the number of training iterations until the performance on unseen cross-validated testing data
was about the same as the training data as shown in Figure 7, right. For the cross-validation
we split the data of 447 individual scans for 40 test and 407 training samples randomly. At the
right amount of training steps, the system does relatively equally in test and training sets. An
overtrained or undertrained network, on the other hand, resulted in large differences in test
In order to
and training, although all three models do equally well on the training dataset.
additionally control for overfitting, we also used the inbuilt TensorFlow dropout function that
prunes a large number of the weaker weights used in the LSTMs. This has been shown in neural
networks to better generalize to unseen test data (Srivastava, Hinton, Krizhevsky, Sutskever, &
Salakhutdinov, 2014).
To speed up the training process, we utilized minibatches, where multiple instances of
the training data are used simultaneously to train the network (Ioffe & Szegedy, 2015). The
number of instances that the network can be trained on simultaneously depends on the size
of the training data, and with 400 subjects we used 20 instances to simultaneously train the
algorithm. The LSTM network in our model is initialized to a random point, and the first time
segment supplies the initial state for the next segment. The performance on the very first block
is very poor because of the unknown hidden state and is not included in our evaluation of
the algorithm in the Results section. This is a limitation with our implementation, and more
complex architectures that solve for the initial state might circumvent this problem.
For our BNM, we choose the firing rate model and the Wilson-Cowan model described
in more detail in Box 1. Our choice of brain network models reflects the constraints of this
approach. Unlike the traditional brain network model where the simulation time step can
Box 1. Brain network models
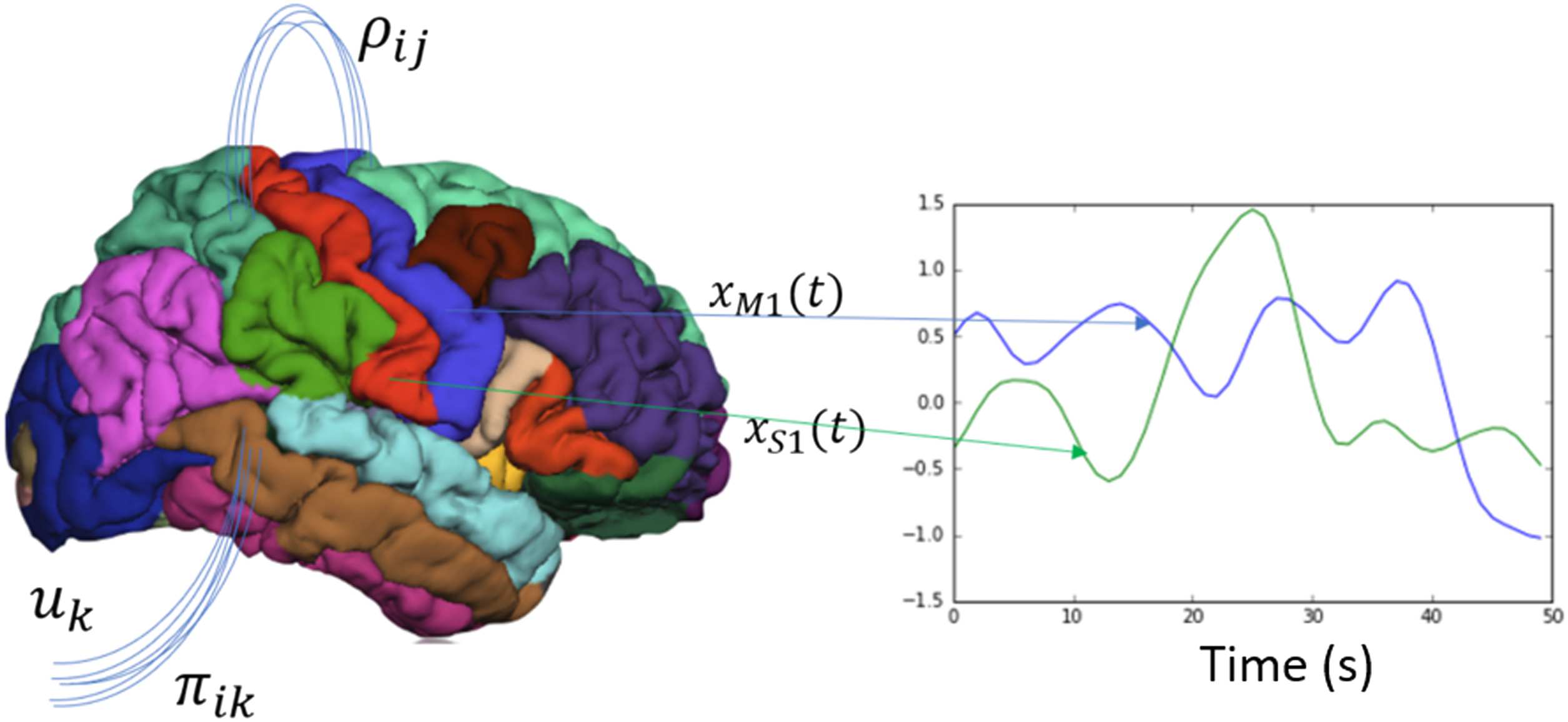
The brain network model is constructed by specifying a parcellation or atlas, and each re-
gion of interest becomes the node and the edges represent the number of fibers between
regions and is calculated using tractography. A brain network model in its most general form
(see Figure 8) describes the change in neural activity x in region of interest i as a function
of a sum of its neighbors’ j activity and its own activity and the physical properties of neu-
ral communication between i and j represented by the vector ρ (i.e., the number of fibers
between regions, the delay in propagation). The network dynamics are also mediated by a
k-dimensional vector u representing all subcortical and sensory inputs, and the vector π rep-
resenting again the physical properties that project these inputs into the brain (i.e., thalamic
tracts into cortex).
˙xi =
∑
j∈Neighbors o f i
F(xi, xj, ρij) + ∑
k∈Task inputs
G(uk, πik) + N(0, σ).
(1)
For resting-state activity, the assumption is that uk(t) = 0 ∀ t and the first term dominates the
activity. The function F for example, can be as simple as the firing rate model
˙xi = −xi + k
∑
j∈Neighbors o f i
wij × xj,
(2)
where wij represents the number of fibers between i and j, and k represents the global cou-
pling parameter. In a more complex model the state variable x can also be represented by
multiple variables such as the Wilson-Cowan model shown in the equation below, which
uses excitatory and inhibitory currents to describe the change in activity at every region of
interest. In the firing rate model the output is taken to be the firing rate, and in the Wilson-
Cowan model the fMRI signal is assumed to be just the excitatory signal since it dominates
Network Neuroscience
462
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
4
8
1
8
6
6
6
6
8
n
e
n
_
a
_
0
0
1
2
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Prediciting rs-fMRI using a brain network autoencoder
metabolically. These models are thus used to generate whole-brain signals by choosing a
random initial point and updating the next step via integration and generating the time series.
˙Ei = −Ei + α × S(ceeEi − cei Ii + k +
∑
j∈Neighbors o f i
wij × Ej + wij × Ij).
˙Ii = −Ii + α × S(cieEi − cii Ii + k +
∑
j∈Neighbors o f i
wij × Ej + wij × Ij).
S(x) =
1
1 + e−x
(3)
(4)
(5)
be arbitrary, we are constrained by the one-time-step prediction approach of synchronizing
with the measured data. Therefore, models that utilize high-frequency oscillators such as the
Hopf or the Kuramoto model and are usually simulated at a higher time resolution are more
awkward to adapt into the fMRI framework, but would be more useful for training on faster
datasets such as MEG or electroencephalogram (EEG). The two different models were also
chosen in order to characterize the approach in terms of a simpler linear firing rate model
and the more complex multistate nonlinear Wilson-Cowan model. To account for noise in the
brain network model, we chose to define the output of the LSTM as a distribution with a mean
and standard deviation. We then sample from this distribution in order to generate the initial
state. By representing the mapping as a nondeterministic process, the algorithm generalizes to
perform better on test datasets and gives more robust results between instantiations.
The output of the BNM is taken to be the next fMRI predicted time step. The loss function
then is taken as the difference between the predicted and the empirical next time points, and
the autoencoder is trained based on this gradient. By forcing the output of the BNM to be the
next predicted fMRI signal, the output of the LSTM is forced to become the closest initial time
point and the LSTM solves for the nonlinear transformation. We used the TensorFlow Adam
Optimizer with a learning rate of 0.0001 to solve for the autoencoder.
Figure 8. Brain network model. The brain network model state space is constructed by averaging
the time courses of each parcellated region. The change of one of those areas xi is a function of its
own activity and its neighbors’ activity that it is connected with ρij, and the projection of external
cortical input uk to the brain via πik.
Network Neuroscience
463
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
4
8
1
8
6
6
6
6
8
n
e
n
_
a
_
0
0
1
2
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Prediciting rs-fMRI using a brain network autoencoder
Experimental Data
To estimate the structural network we ran tractography on five HCP
Structural network.
diffusion-weighted images using the freely available software MRtrix (Kashyap & Keilholz,
2019; Van Essen et al., 2013). From the tractography we estimated the number of fibers that
intersected two ROIs in the Desikan-Killiany atlas and normalized the power by dividing by
the surface area of the receiving region (Cabral et al., 2011; Desikan et al., 2006). The matrix
is finally normalized by dividing by the largest eigenvalue in order for the graph Laplacian
(kSN − I) to have eigenvalues that are all negative (Cabral et al., 2011). This normalizes the
dynamics so that the feedback decays over time, and does not exponentially increase the sig-
nal over time. The value of k is a hyperparameter, but simulations over a few different values
around 0.9 showed that it made little difference, because the LSTM would just adjust its output
correspondingly. The algorithm is robust as long as it is biased around values that would allow
it to converge. For the Wilson-Cowan we set both the k values to 0.9 as well, and learned the
other parameters. We could also learn the value k, but since it is not unique the reproduced
latent state ends up further away from the signal. Since the autoencoder will fit the data either
way, it is important to determine the constraints from the onset and constrain the latent state
to be closer to the measurements.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
4
8
1
8
6
6
6
6
8
n
e
n
_
a
_
0
0
1
2
9
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
fMRI data. We trained our algorithm using both resting-state and task data scans. On evalu-
ation, we have only shown our results on testing resting-state data and not task data. This was
done because the algorithm was able to able to perform better on our short- and long-term
metrics when trained with more varied data such as task. Since the focus of this paper is only
on resting state, we have only shown our results on evaluating resting-state metrics on held
out resting-state data, but we are planning to address task data in a future publication.
We acquired our data from the 447 minimally processed surface files from the Human
Connectome Project (Van Essen et al., 2013). We took the MSMAII scans that were registered
to standard space and in CIFTI format and ICA-denoised them utilizing the 300 MELODIC ICA
vectors that are provided from HCP. We transform from the surface-voxel time series to the ROI
time series by averaging all voxels according to the parcellations established by the Desikan-
Killiany atlas. This was done on an individual level since the surface parcellations are provided
by HCP and FreeSurfer for each individual subject (aparc and aprac2009 files). The signal is
then bandpass filtered from 0.0008 Hz to 0.125 Hz and then global signal regressed using a
general linear model with the mean time course of all cortical parcellations. The final signal
is subsequently normalized along both axes (Kashyap & Keilholz, 2019). For the task data,
each dataset was processed separately (language, working memory, motor, social, emotional,
gambling, relational) and then concatenated together. Each task dataset was rounded to the
closest multiple of 50 and the autoencoder fed alternating segments of task and rest data. This
signal is then fed as both the input and the output to the autoencoder and is the signal that we
refer to as the empirical rs-fMRI for the rest of the paper (Kashyap & Keilholz, 2019).
Dynamical Analysis Techniques
The BNA timeseries were first filtered (0.008–0.125 Hz) before analyzing the properties us-
ing dynamical analysis techniques. The dynamical analysis techniques such as QPP and the
k-means analysis are described in detail in our previous publication, which outlines metrics in
order to compare the simulated whole-brain signal and the rs-fMRI signals (Kashyap & Keilholz,
2019). The QPP algorithm randomly picks a 20-s segment of data and correlates it with the
whole signal. At the regions of peak correlation, the algorithm sums up all segments and
Network Neuroscience
464
Prediciting rs-fMRI using a brain network autoencoder
creates a new template and iteratively converges to a repeating pattern (Majeed et al., 2011).
The k-means analysis takes in sliding-windowed (36-s) functional connectivity matrices that
are Fisher transformed and clusters them into seven different clusters (Allen et al., 2012). We
used an L1 distance to calculate the distance between matrices (Allen et al., 2012). The result-
ing transitions between clusters was then quantified.
ACKNOWLEDGMENTS
We would like to thank Dr. Chethan Pandarinath, who provided invaluable help and insight
into development and interpretation of our initial brain network autoencoder. We would also
like to thank Dr. Christopher Rozell for his insightful discussion on the interpretation of the
autoencoder.
AUTHOR CONTRIBUTIONS
Amrit Kashyap: Conceptualization; Formal analysis; Investigation; Methodology; Resources;
Software; Validation; Visualization; Writing - Original Draft; Writing - Review & Editing. Shella
Keilholz: Formal analysis; Funding acquisition; Investigation; Methodology; Project adminis-
tration; Software; Supervision; Writing - Original Draft; Writing - Review & Editing.
FUNDING INFORMATION
Shella Keilholz, National
Institutes of Health (http://dx.doi.org/10.13039/100000002),
Award ID: 1R01MH111416. Shella Keilholz, National Institutes of Health (http://dx.doi.org/
10.13039/100000002), Award ID: 1R01NS078095. Shella Keilholz, National Science Foun-
dation (http://dx.doi.org/10.13039/100000001), Award ID: 1822606.
REFERENCES
Allen, E. A., Damaraju, E., Plis, S. M., Erhardt, E. B., Eichele, T.,
(2012). Tracking whole-brain connectivity
& Calhoun, V. D.
dynamics in the resting state. Cerebral Cortex, bhs352.
Arbabshirani, M., Damaraju, E., Phlypo, R., Plis, S., Allen, E., Ma,
(2014). Impact of autocorrelation on func-
S., . . . Calhoun, V.
tional connectivity. NeuroImage, 102, 294–308.
Ashourvan, A., Pequito, S., Bertolero, M., Kim, J., Bassett, D., & Litt,
B. (2019). A dynamical systems framework to uncover the drivers
of large-scale cortical activity. bioRxiv:638718.
Atasoy, S., Donnelly, I., & Pearson, J.
(2016). Human brain net-
works function in connectome-specific harmonic waves. Nature
Communications, 7, 10340.
Billings, J., Medda, A., Shakil, S., Shen, X., Kashyap, A., Chen, S.,
. . . Keilholz, S. (2017). Instantaneous brain dynamics mapped
to a continuous state space. NeuroImage, 162, 344–352.
Biswal, B., Yetkin, F., Haughton, V., & Hyde, J. (1995). Functional
connectivity in the motor cortex of resting human brain using
echoplanar MRI. Wiley, 34, 537–541.
Brown, J., Pasquini, L., Lee, A., & Seeley, W. (2019). Brain activity
gradients dynamically interact to shape functional connectivity.
Poster presentation.
Cabral, J., Hugues, E., Kringelbach, M., & Deco, G. (2012). Mod-
eling the outcome of structural disconnection on resting-state
functional connectivity. NeuroImage, 62, 1342–1353.
Cabral, J., Hugues, E., Sporns, O., & Deco, G. (2011). Role of lo-
cal network oscillations in resting-state functional connectivity.
NeuroImage, 57(1), 130–139.
Cabral, J., Kringelbach, M., & Deco, G. (2017). Functional connec-
tivity dynamically evolves on multiple time-scales over a static
structural connectome: Models and mechanisms. NeuroImage,
160, 84–96.
Chen, R., Rubanova, Y., Bettencourt, J., & Duvenaud, D.
(2019).
Neural ordinary differential equations. arXiv:1806.07366v5.
Deco, G., Cabral, J., Saenger, V., Boly, M., Tagliazucchi, E., Laufs,
H., . . . Kringelbach, M. (2018). Perturbation of whole-brain dy-
namics in silico reveals mechanistic differences between brain
states. NeuroImage, 169, 46–56.
Deco, G., Cruzat,
J., Cabral,
J., Tagliazucchi, E., Laufs, H.,
Logothetis, N., . . . Kringelbach, M. (2019). Awakening: Predict-
ing external stimulation to force transitions between different
brain states. Proceedings of the National Academy of Sciences,
116(36), 18088–18097.
Deco, G., Jirsa, V., McIntosh, R., Sporns, O., & Kötter, R.
(2009).
Key role of coupling, delay, and noise in resting brain fluctua-
tions. Proceedings of the National Academy of Sciences, 106,
10302–10307.
Desikan, R., Segonne, F., Fischl, B., Quinn, B., Dickerson, B.,
. . . Killiany, R. (2006). An automated labeling
Blacker, D.,
Network Neuroscience
465
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
4
8
1
8
6
6
6
6
8
n
e
n
_
a
_
0
0
1
2
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Prediciting rs-fMRI using a brain network autoencoder
system for subdividing the human cerebral cortex on MRI scans
into gyral based regions of interest. NeuroImage, 31, 968–980.
Graves, A., Mohamed, A.-r., & Hinton, G. (2013). Speech recog-
nition with deep recurrent neural networks. Institute of Electrical
and Electronics Engineering.
Graves, A., & Schmidhuber, J. (2009). Offline handwriting recogni-
tion with multidimensional recurrent neural networks. Advances
in Neural Information Processing Systems, 545552.
Graves, A., Wayne, G., & Danihelka, I. (2014). Neural Turing ma-
chines. arXiv:1410.5401.
Hagmann, P., Cammoun, L., Gigandet, X., Meuli, R., Honey, C.,
Wedeen, V. J., & Sporns, O. (2008). Mapping the structural core
of human cerebral cortex. PLoS Biology, 6(7), e159.
Hansen, E., Battaglia, D., Spiegler, A., Deco, G., & Jirsa, V. (2015).
Functional connectivity dynamics: Modeling the switching be-
havior of the resting state. NeuroImage, 105, 525–535.
Hjelm, D., Damaraju, E., Cho, K., Laufs, H., Plis, S., & Calhoun, V.
(2018). Spatio-temporal dynamics of intrinsic networks in func-
tional magnetic imaging data using recurrent neural networks.
Frontiers in Neuroscience, 12(9).
Honey, C. J., Kötter, R., Breakspear, M., & Sporns, O. (2007). Net-
work structure of cerebral cortex shapes functional connectivity
on multiple time scales. Proceedings of the National Academy
of Sciences, 104(24), 10240–10245.
Ioffe, S., & Szegedy, C.
(2015). Batch normalization: Accelerat-
ing deep network training by reducing internal covariate shift.
arXiv:1502.03167v3.
Kashyap, A., & Keilholz, S. (2019). Dynamic properties of simulated
brain network models and empirical resting-state data. Network
Neuroscience, 3(2), 405–426.
Liu, X., & Duyn, J. (2013). Time-varying functional network infor-
mation extracted from brief instances of spontaneous brain activ-
ity. Proceedings of the National Academy of Sciences, 110(11),
4392–4397.
Majeed, W., Magnuson, M., Hasenkamp, W., Schwarb, H.,
Schumacher, E., Barsalou, L., & Keilholz, S. (2011). Spatiotem-
poral dynamics of low frequency BOLD fluctuations in rats and
humans. NeuroImage, 54(2), 1140–1150.
Margulies, D., Ghosh, S., Goulas, A., Falkiewicz, M., Huntenburg,
J., Langs, G., . . . Smallwood, J.
(2016). Situating the default-
mode network along a principal gradient of macroscale cortical
organization. Proceedings of the National Academy of Sciences,
113(44), 12574–12579.
Mesbahi, M., & Egerstedt, M. (2010). Graph theoretic methods in
multiagent networks (Vol. 1). Princeton Series in Applied Math-
ematics. Princeton, NJ: Princeton University Press.
Pandarinath, C., Ames, C., Russo, A., Farshchian, A., Miller, L.,
Dyer, E., & Kao, J. (2018). Latent factors and dynamics in motor
cortex and their application to brain–machine interfaces. Journal
of Neuroscience, 38(44), 9390–9401.
Ritter, P., Schirner, M., McIntosh, A., & Jirsa, V. (2013). The virtual
brain integrates computational modeling and multimodal neu-
roimaging. Brain Connectivity, 3(2), 121145.
Sanz-Leon, P., Knock, S., Spiegler, A., & Jirsa, V.
(2015). Mathe-
matical framework for large-scale brain network modeling in the
virtual brain. NeuroImage, 111, 385–430.
Senden, M., Reuter, N., van den Heuvel, M., Goebel, R., & Deco, G.
(2017). Cortical rich club regions can organize state-dependent
functional network formation by engaging in oscillatory behav-
ior. NeuroImage, 146, 561–574.
Shakil, S., Lee, C.-H., & Keilholz, S. (2016). Evaluation of sliding win-
dow correlation performance for characterizing dynamic func-
tional connectivity and brain states. Neuroimage, 133, 111–128.
Skudlarski, P., Jagannathan, K., Calhoun, V. D., Hampson, M.,
Skudlarska, B. A., & Pearlson, G. (2008). Measuring brain con-
nectivity: Diffusion tensor imaging validates resting state tempo-
ral correlations. NeuroImage, 43, 554–561.
Smith, S. M., Fox, P. T., Miller, K. L., Glahn, D. C., Fox, P. M.,
Mackay, C. E., . . . Beckmann, C. (2009). Correspondence of the
brain’s functional architecture during activation and rest. Proceed-
ings of the National Academy of Sciences, 106(31), 13040–13045.
I., &
(2014). Dropout: A simple way to prevent
Journal of Machine Learning
Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever,
Salakhutdinov, R.
neural networks from overfitting.
Research, 15, 1929–1958.
Thomas, C., Ye, F., Irfanoglu, O., Modi, P., Saleem, K., Leopold, D.,
. . . Pierpaoli, C. (2014). Anatomical accuracy of brain connec-
tions derived from diffusion MRI tractography is inherently lim-
ited. Proceedings of the National Academy of Sciences, 111(46),
16574–16579.
Van Essen, D., Smith, S., Barch, D., Behrens, T., Yacoub, E., &
Ugurbil, K. (2013). The WU-MINN Human Connectome Project:
An overview. NeuroImage, 80, 62–79.
Vidaurre, D., Abeysuriya, R., Becker, R., Quinn, A., Alfaro-
Almagro, F., Smith, S., & Woolrich, M. (2018). Discovering dy-
namic brain networks from big data in rest and task. NeuroImage,
180B, 646–656.
Zalesky, A., Fornito, A., Cocchi, L., Gollo, L. L., & Breakspear, M.
(2014). Time-resolved resting-state brain networks. Proceedings
of the National Academy of Sciences, 201400181.
Network Neuroscience
466
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
4
8
1
8
6
6
6
6
8
n
e
n
_
a
_
0
0
1
2
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3