FUNCIÓN DE ENFOQUE:
Linking Experimental and Computational Connectomics
Beyond spikes: Multiscale computational analysis
of in vivo long-term recordings in the
cockroach circadian clock
Pablo Rojas1, Jenny A. Plath2, Julia Gestrich2, Bharath Ananthasubramaniam4,
Martín E.. Garcia1,3, Hanspeter Herzel4, and Monika Stengl2,3
1Theoretical Physics, University of Kassel, Kassel, Alemania
2Animal Physiology, University of Kassel, Kassel, Alemania
3Center for Interdisciplinary Nanostructure Science and Technology (CINSaT), University of Kassel, Kassel, Alemania
4Institute for Theoretical Biology, Humboldt University of Berlin and Charité Universitätsmedizin, Berlina, Alemania
un acceso abierto
diario
Palabras clave: Circadian and ultradian rhythms, Neuropeptides, Event detection, Wavelet
ABSTRACTO
The circadian clock of the nocturnal Madeira cockroach is located in the accessory medulla,
a small nonretinotopic neuropil in the brain’s visual system. The clock comprises about
240 neurons that control rhythms in physiology and behavior such as sleep-wake cycles. El
clock neurons contain an abundant number of partly colocalized neuropeptides, entre
them pigment-dispersing factor (PDF), the insects’ most important circadian coupling signal
that controls sleep-wake rhythms. We performed long-term loose-patch clamp recordings
bajo 12:12-hr light-dark cycles in the cockroach clock in vivo. A wide range of timescales,
from milliseconds to seconds, were found in spike and field potential patterns. We developed
a framework of wavelet transform–based methods to detect these multiscale electrical events.
We analyzed frequencies and patterns of events with interesting dynamic features, como
mixed-mode oscillations reminiscent of sharp-wave ripples. Oscillations in the beta/gamma
frequency range (20–40 Hz) were observed to rise at dawn, when PDF is released, peaking
just before the onset of locomotor activity of the nocturnal cockroach. We expect that in vivo
electrophysiological recordings combined with neuropeptide/antagonist applications and
behavioral analysis will determine whether specific patterns of electrical activity recorded in
the network of the cockroach circadian clock are causally related to neuropeptide-dependent
control of behavior.
RESUMEN DEL AUTOR
We seek to understand how the neuronal network of the cockroach circadian clock controls
temporal rhythms in physiology and behavior. Circadian clocks in mammals and insects alike
employ neuropeptides for information processing that bypass synaptic information transfer.
Neuropeptides appear to work as coupling factors synchronizing and binding neuronal
circuits on multiple timescales, employing schemes of temporal encoding. Expanding known
techniques with novel approaches, we describe oscillations of electrical events on multiple
timescales in long-term in vivo electrophysiological recordings. In future studies, we will
combine experimental approaches with the construction of minimal oscillator networks to
examine how the cockroach brain controls sleep-wake cycles based on neuropeptide
signaling.
Citación: Rojas, PAG., Plath, j. A.,
Gestrich, J., Ananthasubramaniam, B.,
Garcia, METRO. MI., Herzel, h., & Stengl, METRO.
(2019). Beyond spikes: Multiscale
computational analysis of in vivo
long-term recordings in the cockroach
circadian clock. Red
Neurociencia, 3(4), 944–968.
https://doi.org/10.1162/netn_a_00106
DOI:
https://doi.org/10.1162/netn_a_00106
Supporting Information:
https://doi.org/10.1162/netn_a_00106
Recibió: 14 December 2018
Aceptado: 27 Julio 2019
Conflicto de intereses: Los autores tienen
declaró que no hay intereses en competencia
existir.
Autor correspondiente:
Monika Stengl
stengl@uni-kassel.de
Editor de manejo:
Wouter Klijn
Derechos de autor: © 2019
Instituto de Tecnología de Massachusetts
Publicado bajo Creative Commons
Atribución 4.0 Internacional
(CC POR 4.0) licencia
La prensa del MIT
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
4
9
4
4
1
8
6
6
8
9
3
norte
mi
norte
_
a
_
0
0
1
0
6
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cockroach circadian clock circuits
Accessory medulla:
A small neuropil in the optic lobe of
the insect brain that is innervated by
processes of clock neurons.
PDF (pigment-dispersing factor):
Evolutionary conserved neuropeptide
that synchronizes insect clock cells.
INTRODUCCIÓN
Rhythms in animals are generated by complex interplays of molecular and cellular feedback
loops (biological clocks) and also by network synchronizations producing temporally struc-
tured outputs. Biological circadian clocks control rhythms in physiology and behavior synchro-
nized to the 24-hr light-dark cycle of the environment. The Madeira cockroach (Rhyparobia
maderae) is an established model system for chronobiology (Nishiitsutsuji-Uwo & Pittendrigh,
1968; Página, 1984; Stengl, Werckenthin, & Wei, 2015). Madeira cockroaches are relatively
long-lived with a life span of up to 2.5 años. They are nocturnal animals, since they restrict
their activity to the dark night, while they rest (sleep) during the light phase of each day. Its cir-
cadian clock is the accessory medulla (AME), a small glomerular neuropil ventromedial to the
medulla in the brain’s optic lobes (Figura 1A; Reischig & Stengl, 2003a; Stengl & Homberg,
1994). The AME is innervated by about 240 neuropeptidergic clock neurons of mostly un-
known function (Reischig & Stengl, 2003b). Best studied are the pigment-dispersing factor
(PDF)-expressing clock neurons that control circadian sleep-wake rhythms not only in the
cockroach, but also in other insects such as the fruit fly Drosophila melanogaster (Figura 1A;
reviews: Hermann-Luibl & Helfrich-Foerster, 2015; Stengl & Arendt, 2016). The actions of
PDF in the insect circadian clock (reviews: Stengl & Arendt, 2016; Stengl et al., 2015) reflect
actions of vasoactive intestinal polypeptide (VIP) in the mammalian circadian clock (Patton
& Hastings, 2018; Vosko, Schroeder, Loh, & Colwell, 2007). Next to resemblance of PDF’s
and VIP’s circadian functions, the cellular and molecular organization of the cockroach and
the mammalian clock also resemble each other (Vansteensel, Michel, & Meijer, 2008). En-
triguingly, both clocks are abundant with neuropeptides that do not require direct synaptic
conectividad (Patton & Hastings, 2018). En cambio, neuropeptides perform volume transmission.
Neuropeptides are stored in dense core vesicles in the cells and are usually not released only
at synaptic sites into the synaptic cleft. They are released at multiple sites of the neuron, en
the respective carrier medium. In the volume of the extracellular space, the neuropeptides can
be carried very far, acting over extended time spans, depending on their life time. De este modo, neuro-
peptides bind spatially distributed neuropeptide-receptor-expressing neurons into an ensem-
ble with common, synchronous activity. Since neuropeptide-dependent ensembles of neurons
spike synchronously, they generate distinct electrical patterns that can be detected in extracel-
lular recordings (Schneider & Stengl, 2005). También, on the single cell level neuropeptidergic neu-
rons can produce characteristic electrical signatures. Neuropeptidergic neurons in mammals
and insects were shown to express ultradian membrane potential oscillations, generating bursts
of action potentials during release of their respective neuropeptides (Hatton, 1982; Kamimoto,
Nohara, & Ichikawa, 2006; Wei et al., 2014). Despite the fact that neuropeptides express
these characteristics and despite their abundant quantity in brains of evolutionary widely di-
verse species, their mechanisms of actions are not well understood. Por lo tanto, circadian clocks
with their numerous colocalized neuropeptides are well suited for the study of neuropeptide
actions/functions in general.
We aspire to understand why neuropeptidergic clock neurons express ultradian and circa-
dian rhythmicity and how rhythmic activity on multiple timescales is orchestrated to enable
circadian clock functions. The cockroach clock contains about 100 times fewer, larger neu-
rons than the mammalian clock. De este modo, it is more easily accessible to electrophysiological and
neurochemical analysis, even at the level of single identified cells (Loesel & Homberg, 2001).
Already a complete 3-D atlas of the cockroach brain was reconstructed with arborizations of
PDF-clock neurons embedded (Wei, el Jundi, Homberg, & Stengl, 2010). Based upon these
advantages we work with the cockroach for the electrophysiological analysis of neuropeptide
actions on the circadian clocks’ cellular level.
Neurociencia en red
945
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
4
9
4
4
1
8
6
6
8
9
3
norte
mi
norte
_
a
_
0
0
1
0
6
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cockroach circadian clock circuits
Zeitgeber time:
Rhythm provided by an external
environmental cue, which is able to
entrain biological clocks.
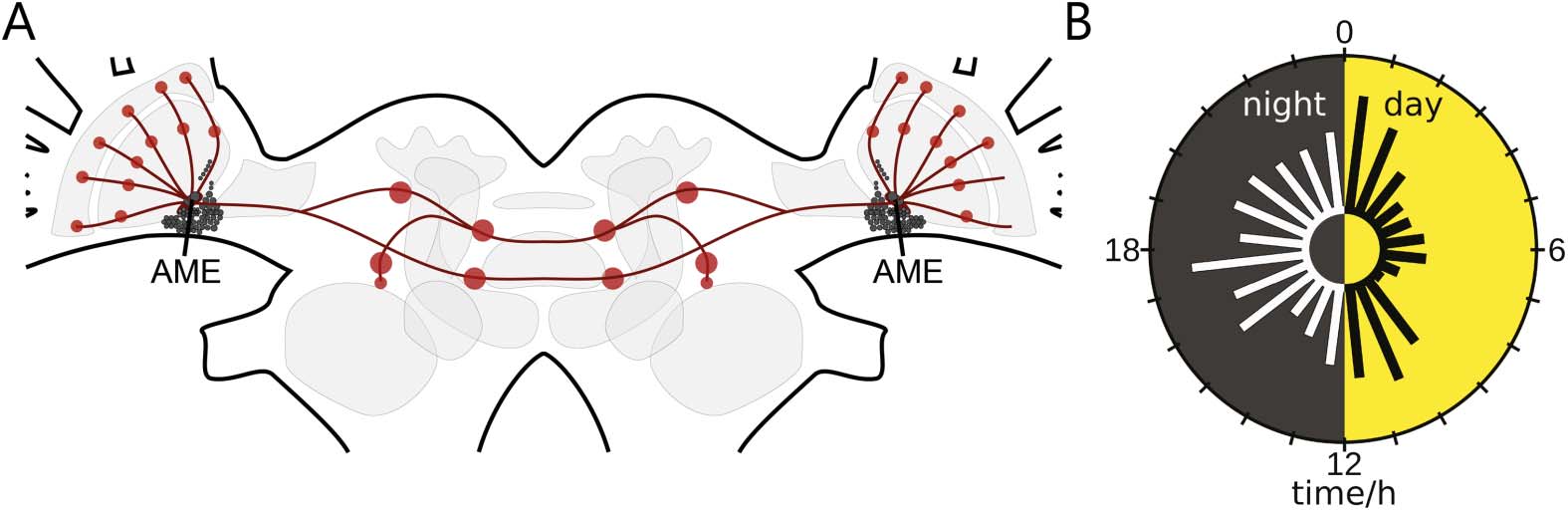
Cifra 1. The cockroach circadian clock with innervating pigment-dispersing factor (PDF)-
expressing clock neurons control circadian sleep-wake rhythms in synchrony with the light-dark
ciclo. (A) Schematic of the circadian network (red dots; neuropils) of PDF circadian clock neurons
in the cockroach brain. The circadian clock of the nocturnal Madeira cockroach is the accessory
medulla (AME) ventromedial to the medulla in the brain’s optic lobes. It is innervated by about
240 adjacent neuropeptidergic clock neurons (small black filled circles). Among them are 12 PDF
neuronas. They are clock in- and outputs; they couple the bilaterally symmetric clocks, control-
ling sleep-wake cycles (modified after Stengl et al., 2015, reprinted with permission from Elsevier).
(B) Extracellular recordings of the isolated AME in vitro revealed that endogenously generated elec-
trical activity changes systematically during the course of the day with peaks at dusk and dawn, como
well as during the middle of night and day. (modified after Stengl & Arendt, 2016, reprinted with
permission from Elsevier).
Aquí, extracellular long-term loose-patch clamp recordings from the AME were performed
in the intact animal over more than 24 hr. De este modo, for the first time, we gained information about
recurring events, oscilaciones, and network dynamics from a circadian clock receiving sensory
information from the compound eyes, as well as phase information from both bilaterally sym-
metric clocks in the cockroach. Based upon these in vivo recordings, we developed a frame-
work for the analysis of the activity of the circadian clock network over different timescales.
Scales ranged from action potential firing of a few milliseconds, to local field potentials, y
dynamic features of sequences of events ranging from seconds, to minutes, to hours. The focus
was not the analysis of action potential patterns of single neurons. Bastante, we searched for
Zeitgeber time (ZT)-specific changes in activity patterns indicative of rhythmic release of neu-
ropeptides (Figura 1B). Evidence is accumulating that during the day the clock releases the neu-
ropeptide PDF with endogenous rhythmicity. Sucesivamente, PDF generates and controls antagonistic
neuronal ensembles: the sleep and the arousal circuits, which are phase-coupled to the external
light-dark cycle (Chatterjee et al., 2018; Gestrich et al., 2018; Schneider & Stengl, 2005; Wei
& Stengl, 2011). We want to know whether the hypothesis of clock-controlled neuropeptide-
dependent ensemble formation (Schneider & Stengl, 2005; Stengl & Arendt, 2016; Stengl et al.,
2015) finds support in vivo in our noninvasive long-term recordings of the cockroach clock.
Por lo tanto, we searched for signatures of synchronized electrical activity during the light phase
consistent with light- and clock-controlled PDF-dependent ensemble formation.
RESULTADOS
To search for Zeitgeber time (ZT)-dependent changes of activity in a circadian clock that are
indicative of neuropeptide actions, we performed 24- to 48-hr-long in vivo loose-patch clamp
(∼ 1 Gigaohm seal) recordings of the accessory medulla (AME), the circadian clock of the
Madeira cockroach (norte = 18). These electrophysiological recordings contained a wide range
of events at multiple time-scales from single action potentials of 1−2 ms to second-long field
Neurociencia en red
946
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
4
9
4
4
1
8
6
6
8
9
3
norte
mi
norte
_
a
_
0
0
1
0
6
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cockroach circadian clock circuits
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
4
9
4
4
1
8
6
6
8
9
3
norte
mi
norte
_
a
_
0
0
1
0
6
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
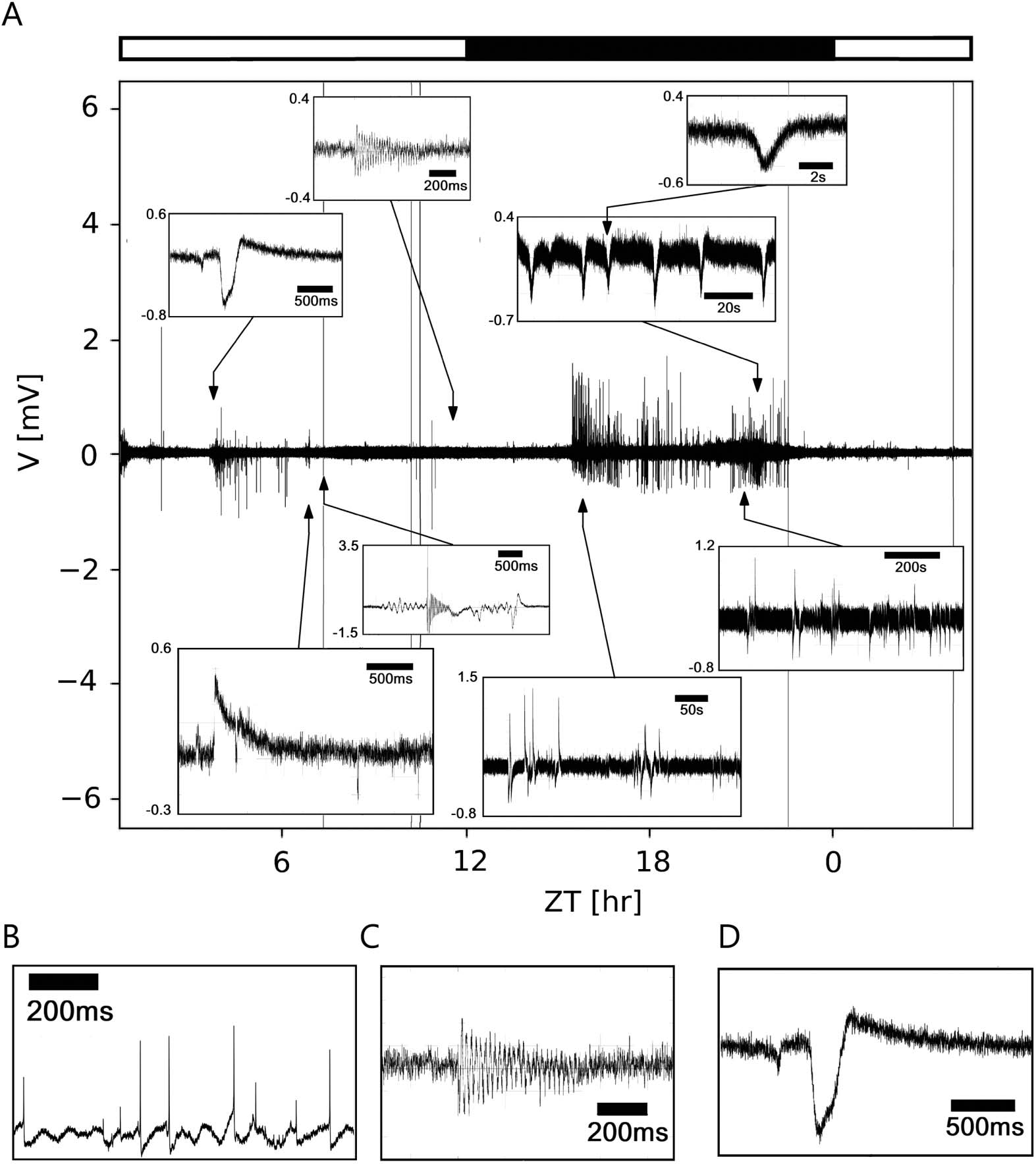
Cifra 2. Multiscale events found in an in vivo long-term loose-patch clamp recording from the
cockroach circadian clock, the accessory medulla. (A) Duration of events ranged from a few mil-
liseconds (EM) to seconds (s) and minutes (mín.), partially overlapping each other. According to their
duration and pattern three different classes of events were distinguished: primero: very fast events of a
few ms (B, action potentials); segundo: events that can be approximated by sustained sinusoidal os-
cillations occurring over hundreds of ms up to several s, or min; (C); tercero: events that are of limited
duración, between the previous two extreme cases that sometimes exhibit oscillatory behavior (D).
potentials. Además, events were found to form episodic patterns in the range of seconds
to hours (Figura 2A).
Electrophysiological recordings can be regarded as time series, composed of a sequence
of events embedded in a noisy signal, which may also contain oscillations. Event detection
methods were developed in different fields (Guralnik & Srivastava, 1999; Lilly, 2017; Merel,
Shababo, Naka, Adesnik, & paninski, 2016; Tu, Hwang, & A, 2005). Usually, they treated
an event as one of three classes of objects, depending on the support in the time and spectral
Neurociencia en red
947
Cockroach circadian clock circuits
dominios (duración, frequency): (a) events that are singularities, eso es, events of very short du-
ration (Figura 2B), such as action potentials, (b) events that can be approximated by sustained
sinusoidal oscillations and that are elongated in the time axis (Figura 2C), such as autoreceptor-
dependent neuropeptide release; o (C) events that are between those two extreme cases, lo-
calized in time, showing a limited duration, and sometimes exhibiting oscillatory behavior
(Figura 2D), as synaptic events (Guzman, Schlögl, & Schmidt-Hieber, 2014; Leise, 2013; Lilly
& Olhede, 2009; Masimore, Kakalios, & Redish, 2004; Pernía-Andrade et al., 2012; Principe
& Brockmeier, 2015; Rey, Pedreira, & Quiroga, 2015; Richardson & Silberberg, 2008; Shi,
Nenadic, & Xu, 2010; Tu et al., 2005). The detection of individual events and the measure-
ment of their specific characteristics, such as amplitude, duración, and waveform features, son
of interest in the study of electrophysiological signals that contain both synaptic events and
spikes (Guzman et al., 2014; Merel et al., 2016; Pernía-Andrade et al., 2012; Richardson &
Silberberg, 2008; Shi et al., 2010). One of the main limitations of current detection methods
is that they focus on the analysis of either action potentials or synaptic events. De este modo, the dura-
tions of events are assumed to be in a relatively narrow range, usually within the same order of
magnitude. Aquí, we relaxed this condition to events with durations over at least three orders
of magnitude.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
Wavelet transform:
Decomposition of a signal in
a set of scaled and shifted
wave-like functions called
wavelets.
Reliable Detection of Multiscale Events With Wavelet Transform–Based Methods
To quantify and analyze these complex multiscale data, we used two different approaches. Para
segments that presented a narrow range of event durations, we performed methods based on
conventional spike train analysis. For analysis of recordings containing a wider range of event
durations, we developed a multiscale approach based on the wavelet transform (Secundario
Información, Figures S2–S7). This approach allowed us to detect events at multiple timescales
of about three orders of magnitude and to extract their basic features, such as duration and
amplitude. Próximo, we examined whether event patterns and oscillations at different ultradian
timescales also expressed circadian timescales, occurring at consecutive days at the same ZT.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
4
9
4
4
1
8
6
6
8
9
3
norte
mi
norte
_
a
_
0
0
1
0
6
pag
d
t
.
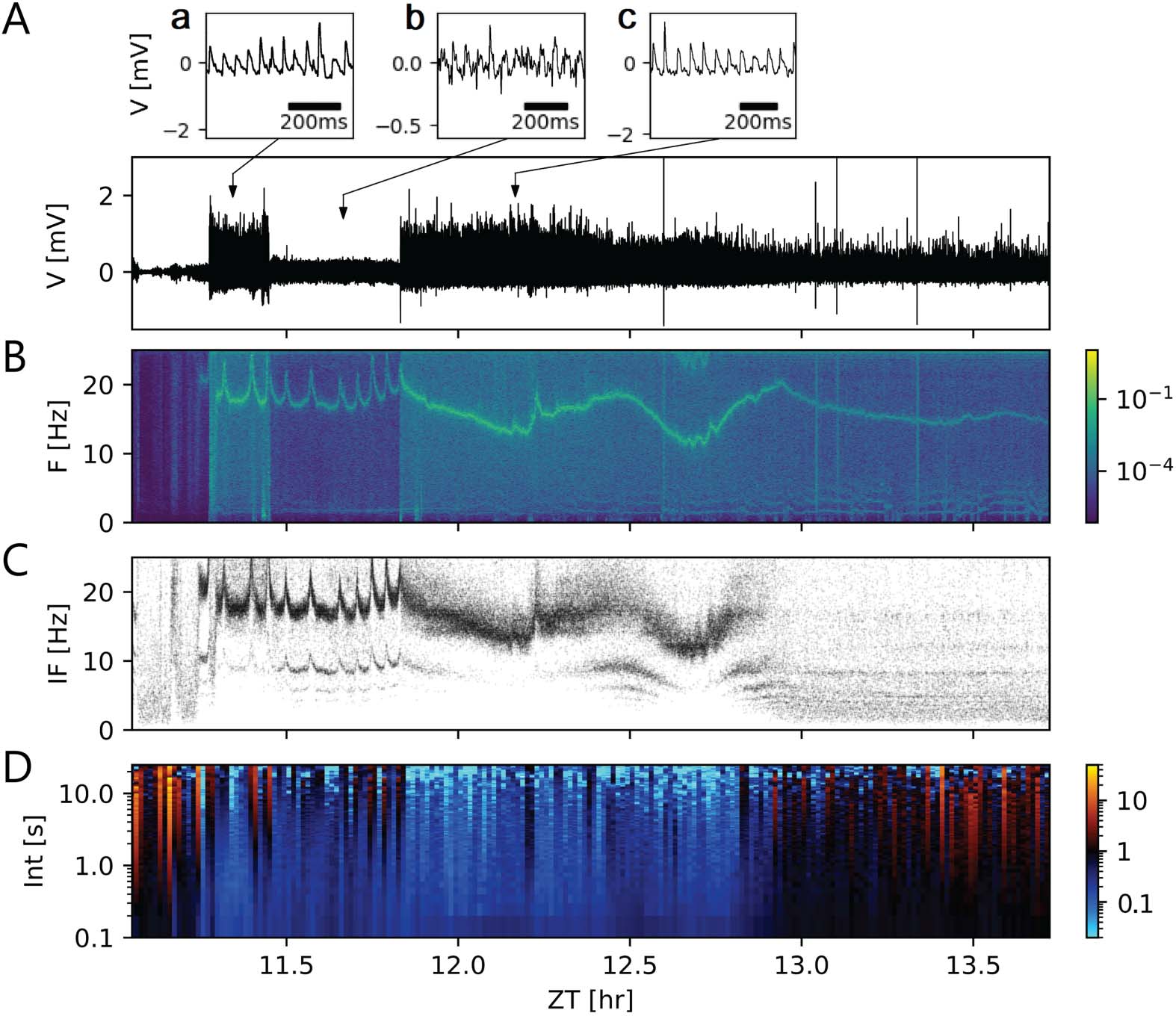
Threshold detection was applied for a recording (Figura 3A) that presented a narrow range of
timescales of events. The threshold parameter (Ecuación 3) was manually set to values between
1 y 3, where the recording showed stationarity. Compared with the usual choices in the
range 3–5, the values for the threshold parameter were smaller because the duration of events
were comparable to their interevent intervals. Despite the threshold calculation being dynamic
and adapted to properties of noise, it was not possible to set a unique threshold parameter that
worked for the whole recording. Por lo tanto, the above-mentioned manual tuning of the method
was very time-consuming.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
We performed spike train analysis on the event trains obtained. Por ejemplo, spectrogram
análisis (Figura 3B) and instantaneous frequency plots (Figura 3C) were created. The same
firing frequency at each point was clearly distinguishable, as a line of greater power density
in the spectrogram of the signal (Figura 3B). Dense bands in the instantaneous frequency plot
indicated a stable firing frequency over consecutive events and pointed towards ensembles of
neurons firing with the same frequency at the same or integer multiples of the same frequency
and the same phase (Figura 3C). This is another indication that the event durations were com-
parable to the respective interevent intervals and that the entire signal was strongly periodic.
Como consecuencia, threshold parameters had to be applied outside their usual range: As events
become wide enough, the assumption of the events being well separated and punctual was
no longer valid. Time-resolved Fano factor of the event trains supplied a metric for event train
948
Fano factor:
Metric used for variability in
interevent intervals, with a Poisson
distribution showing a Fano factor
equal to 1.
Neurociencia en red
Cockroach circadian clock circuits
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
4
9
4
4
1
8
6
6
8
9
3
norte
mi
norte
_
a
_
0
0
1
0
6
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Scale-blind analysis of events requires much manual tuning of parameters and might
Cifra 3.
not be reliable for this kind of multiscale data. (A–D) Scale-blind analysis of a segment from a
loose-patch clamp recording with nonoverlapping events of comparable scales. These events can
be detected by applying a threshold and finding the peaks that surpass it. De este modo, a single event train
is obtained, suitable for conventional spike train analysis. (A) Segment of 2.6-hr loose-patch clamp
recording between Zeitgeber time (ZT) 11.1 and ZT 13.7. Following Equation 3, threshold param-
eters required laborious manual tuning between 1 y 3, as compared with the usual 3–5 range,
because the duration of the events are comparable to their interevent intervals, as insets A–C show.
(B) Spectrogram of the in vivo recording. (C) Instantaneous firing frequency of the recording, como
the inverse of the interevent interval. A tonic stable firing frequency between 12 y 20 Hz is rec-
ognizable as a band of points. Sin embargo, missing events (false negatives) and spurious events (false
positives) produce less concentrated bands and a second band. Errors in event detection may be due
to a small signal-to-noise ratio or an incorrect threshold estimation. The firing frequency of the main
band correlates to the main frequency in the spectrogram. This also indicates that the durations of
the events are comparable to the interevent interval. This violates the assumption of well-separated
events. (D) Time-resolved Fano factor of the event train as a metric for event train variability. Menor
values are an indication of a tonic regular firing, while larger values indicate irregular firing. A Fano
factor of 1 indicates an event train variability equivalent to a Poisson process. The x-axis shows ZTs,
while the y-axis indicates the time windows taken for the Fano factor calculation.
variabilidad (Figura 3D). En este caso, both tonic regular firing as well as irregular firing, eran
present in the recording.
As the conventional methods for spike train analysis did not reliably separate events, a
wavelet transform–based method for event detection was applied to the long-term in vivo
Neurociencia en red
949
Cockroach circadian clock circuits
recordings. Events were detected by locating the maxima and minima of the modulus of the
analytical wavelet transform (AWT, Figures 4A–C). The method performed well in detecting
overlapping events of different durations and amplitudes. Además, it provided estimates
for these features and also recognized continuous events when the real part of the AWT was
used instead. As input parameters, only the maximum and minimum durations were required.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
4
9
4
4
1
8
6
6
8
9
3
norte
mi
norte
_
a
_
0
0
1
0
6
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
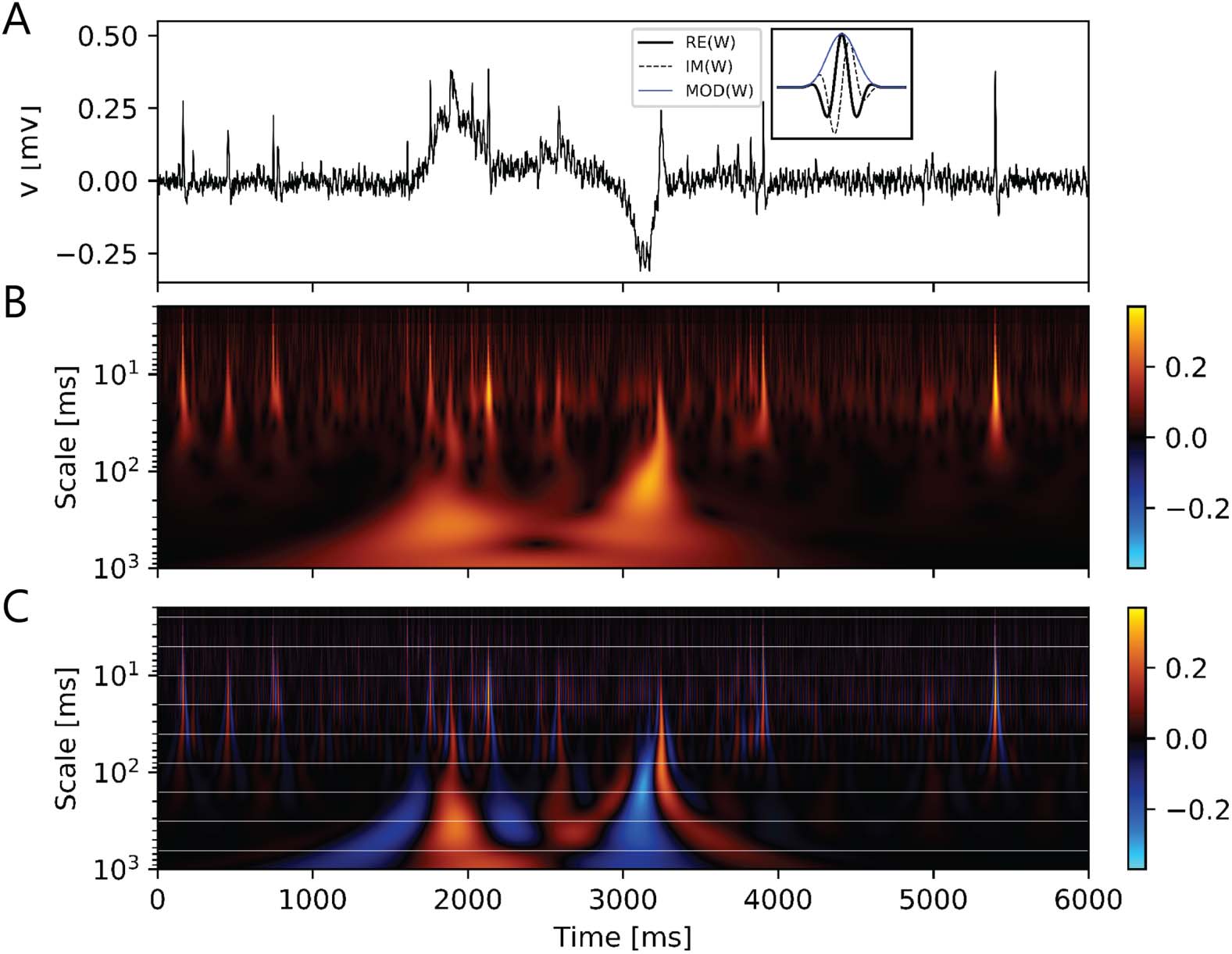
Cifra 4. Wavelet transform allows clear detection and separation of electrical events of different
durations such as fast action potentials (∼2 ms) and slower field potentials (∼50 ms to several
artículos de segunda clase). Además, it estimates polarity and amplitudes of events. Example of event detection
in the in vivo loose-patch clamp recording using wavelet transform (A). Morse wavelet (recuadro) era
used to detect time-localized events in segments of 6 s. Analytic wavelet transform (AWT) del
signal showed local maxima and minima at the time of events. (A) Six sec of neuronal activity at ZT
16.7. Inset: Modulus, real and imaginary part of an analytic Morse wavelet, using β = 2 and γ = 3.
β and γ control the shape and spectral properties of the wavelet, especially its limits in the time
and frequency domains. With higher values of β and γ, frequency components decay more sharply
from its peak frequency, leading to a narrower bandwidth. (B) Modulus of the AWT. Events could
be detected by searching for local maxima and minima in the modulus of the AWT, but the method
lost resolution in detecting individual continuous events of opposite polarity. Amplitudes of events
were indicated in the color scale. (C) Real part of the AWT. Individual continuous events could
be separately recognized. Polarity and amplitude of events were indicated in the color scale. Event
detections could also be performed using the subset of scale values shown in horizontal white lines.
By selecting only scales from a subset of s = 2jΔT, j = 0, 1, . . ., Ns, computational cost was reduced,
at the expense of less scale resolution. De este modo, each of the scales in the subset became representative
of a bandwidth of scales. This procedure enabled affordable processing times for large datasets. Para
peaks in the wavelet transform that were relevant in more than one consecutive scale, the winner
was selected based on absolute values.
Neurociencia en red
950
Cockroach circadian clock circuits
De este modo, all the scales between these extremes were automatically defined following a geometric
secuencia.
Screening of Activity Intensity Heatmaps Revealed Events, Episodes, and Network Dynamics from
Milliseconds to Hours
After identifying events using wavelet transform–based methods, we used an exploratory ap-
proach of visualizing activity at multiple timescales in activity intensity heatmaps (Figures 5A–D;
Figures 6A, D). In these maps, activity intensity is calculated for each scale as the sum of the
amplitudes of the events over a time window of 100 s. This allowed us to visually compare
the individual activity patterns and to find characteristic events at specific ZTs. Activity pat-
terns identified in the full-length heatmaps (Figures 6A, D) were magnified further to inspect
dynamics of the activity pattern in 30-min heatmap excerpts (Figures 6B, mi). In a next step,
various events with interesting patterns were isolated from the original recording trace, cual
could be indicators of specific structural configurations such as bifurcations (Baer et al., 1989)
in the underlying dynamical system (Figures 6C, F; Figures 7A–F). Por ejemplo, oscilaciones
were observed to precede the onset of large-amplitude events (Figure 6C; Figure 7C). Este
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
Bifurcation:
A sudden transition in the qualitative
behavior of a system because of
small and smooth changes in
its parameters.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
4
9
4
4
1
8
6
6
8
9
3
norte
mi
norte
_
a
_
0
0
1
0
6
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
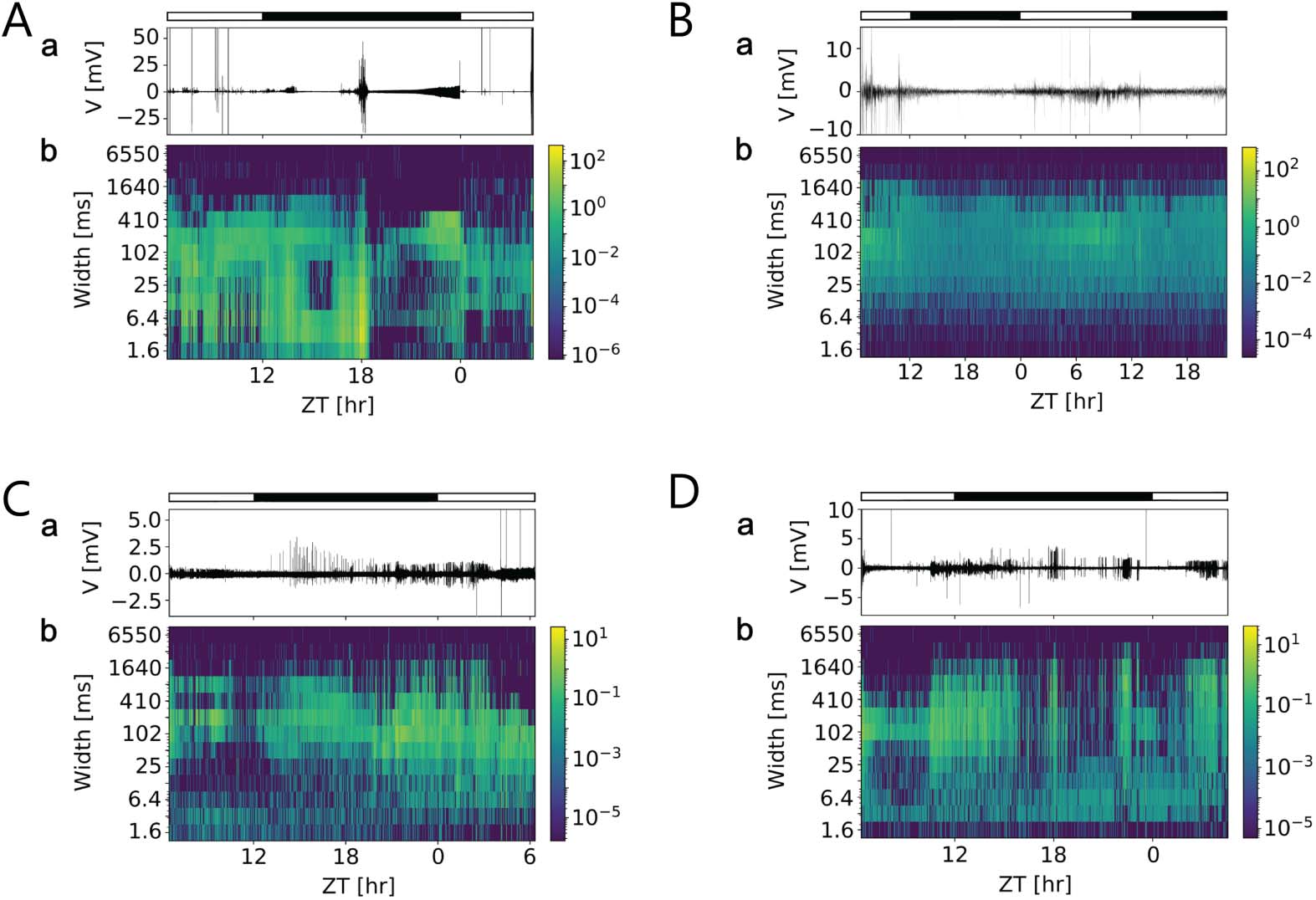
Cifra 5. Multiscale activity heatmaps of four different long-term in vivo loose-patch clamp
recordings of the cockroach clock reveal daytime-dependent changes of field potentials that were
not driven by the light-dark cycle. (A–D, a) Traces of original loose-patch clamp recordings in a
12:12-hr light (open bar) – dark (filled bar) ciclo. (A–D, b) Coarse grain activity heatmaps of events
at different durations (widths, EM) in the recordings. For each bin of 100 s, events of the same dura-
tion were counted and weighted by their amplitudes (color coded). This enabled to determination of
whether there are Zeitgeber time (ZT)-dependent events of specific durations that occur with circa-
dian periods, either directly driven by the light-dark cycle, or via endogenous rhythms. This serves
as an exploratory analysis to find events of potential biological significance such as field potential
changes at dusk when the animal starts to become active. Only in (A) some of the events coincided
with lights on or lights off. De lo contrario, either specific electrical events preceded the day (B, C) o
night phase (A, D), indicative of its endogenous rhythmicity.
Neurociencia en red
951
Cockroach circadian clock circuits
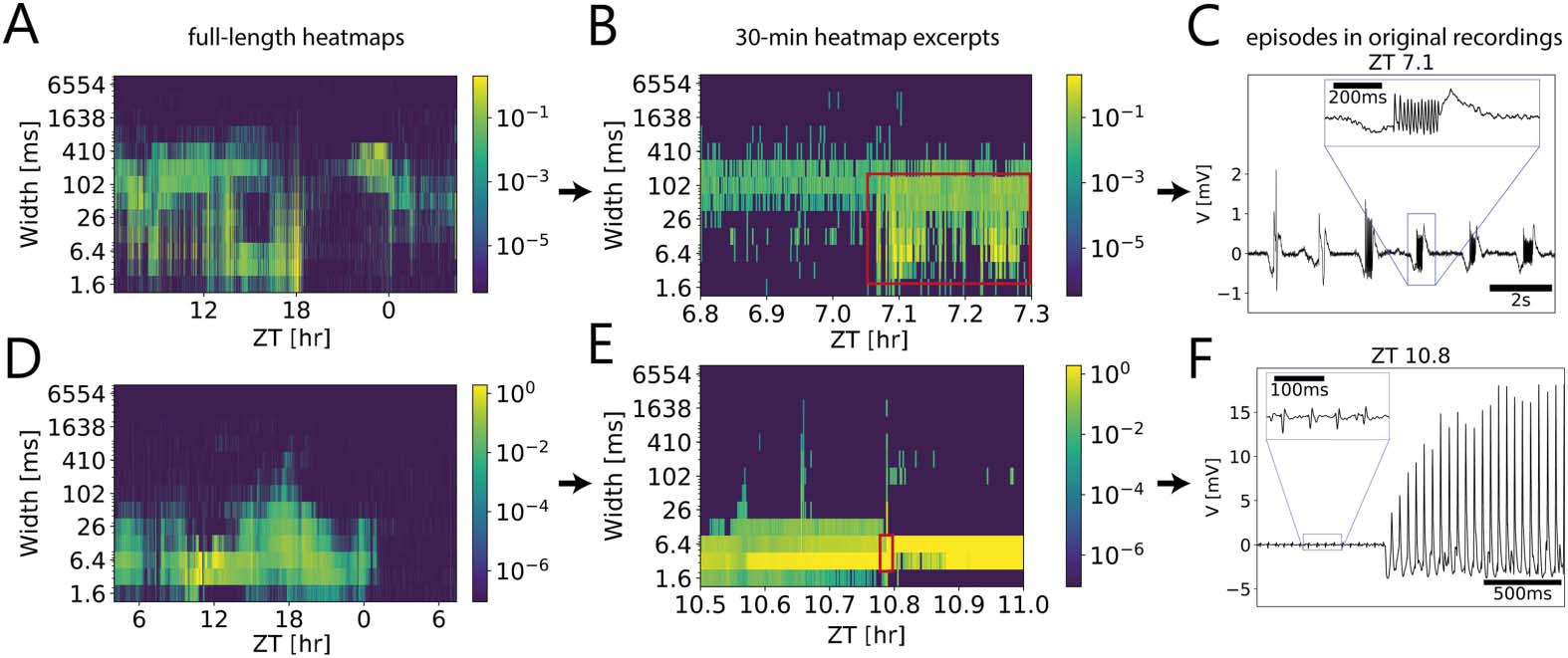
Cifra 6. Multiscale activity heatmaps as a tool for detecting interesting episodes in the underlying
dynamical system. (A, D) Full-length coarse grain activity heatmaps as well as 30-min time windows
(B, mi) that were further up-scaled (C, F) to reveal electrical events at different durations (widths) en
the in vivo long-term patch clamp recordings of the cockroach circadian clock. For each bin of
100 s, the number of events of the same duration were counted and weighted by their amplitudes
(color coded). (C.A) Larger and longer episodic events coincided with/were followed by oscillations
of increasing amplitude that could be identified by different widths (red rectangle in B). (D-F) El
onset of positive excursions resembled a Hopf bifurcation in the parameter space of the underlying
dynamical system (red renctangle in E; Baer et al., 1989. Firing frequency was constant during this
proceso.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
4
9
4
4
1
8
6
6
8
9
3
norte
mi
norte
_
a
_
0
0
1
0
6
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
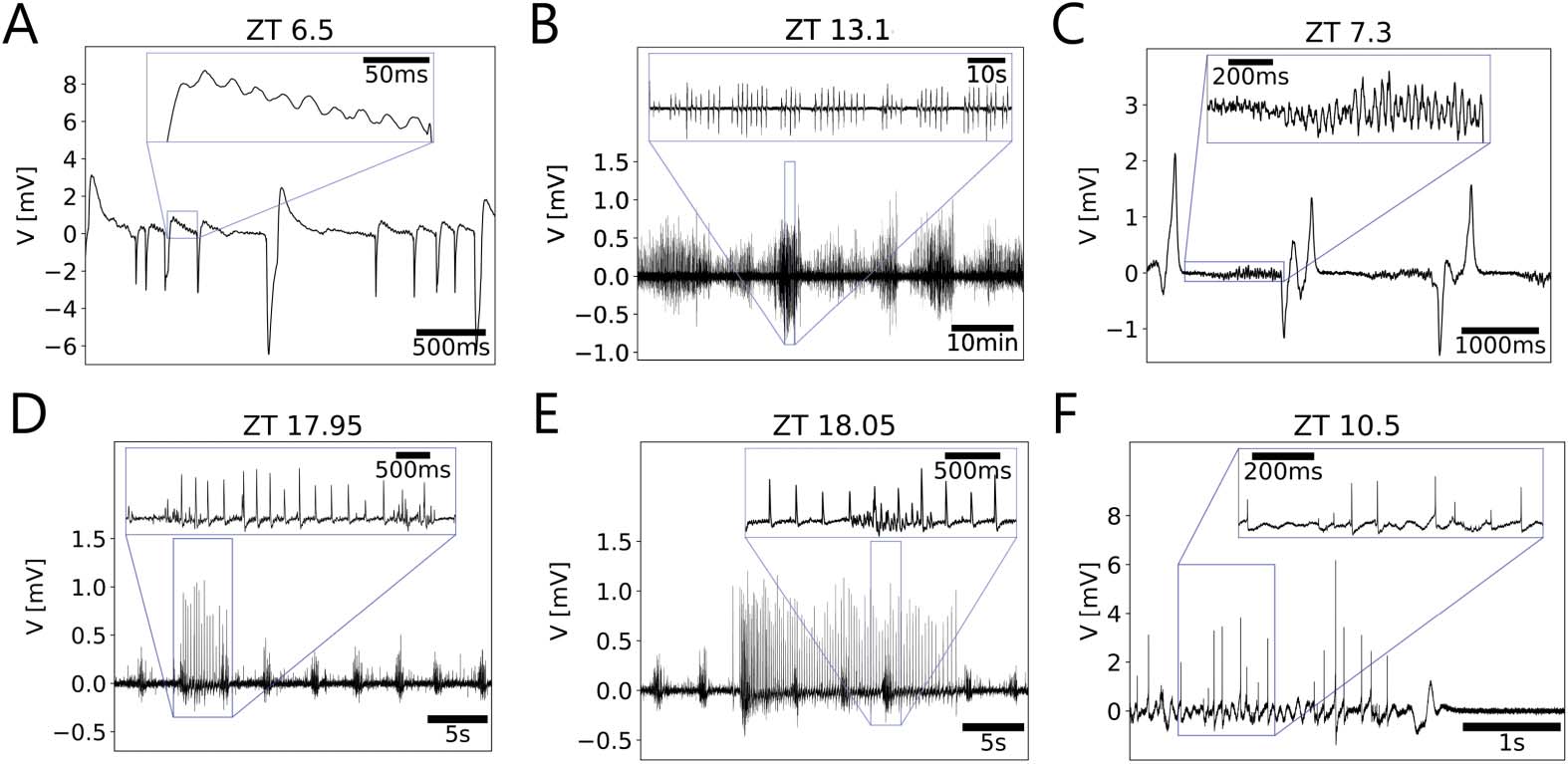
Cifra 7.
Exploratory analysis of multiscale activity heatmaps revealed episodes in the recordings,
as indications of synchronizations and bifurcations in the underlying dynamical system. (A) Oscil-
lations appeared to be followed by larger amplitude events. (B) Amplitude modulation was present
at two timescales (10 s and 10 mín.), resembling a beating-like behavior of the envelopes of the
oscilaciones. (C) Oscillations of increasing amplitudes preceded larger and broader episodic events.
(D, mi) Episodic bursts of small-amplitude events occurred phase-locked to initiation and termination
of larger amplitude tonic firing. (F) Small spikes in the range of action potentials added up to larger
events apparently due to synchronization of different neuronal units.
Neurociencia en red
952
Cockroach circadian clock circuits
Intermittency:
Intermittent transition between
regular behavior and irregular bursts.
Hopf bifurcation:
A bifurcation where sustained
oscillations arise because of a
change in the stability of an
equilibrium point.
pattern is comparable to intermittency (Stavrinides & Anagnostopoulos, 2013; ˙Zebrowski &
Baranowski, 2004). Onsets of sustained oscillations resembling Hopf bifurcations were identi-
fied (Figure 6F). Mixed-mode oscillations reminiscent of sharp-wave ripples were found to co-
exist with larger amplitude events (Figure 7A). Además, amplitude modulations of events
were identified to occur concurrently at different timescales, in the range of 10 s as well as
in the range of 10 mín. (Figure 7B). También, apparently phase coupling of two different neuronal
units was detected, one firing regularly and the other firing intermittently with low-intensity
bursts (Figures 7D, mi). Curiosamente, the firing of the tonic unit seemed to be phase-coupled to
the bursts from the other unit. These observations served to hint at the structural configuration
of the system and will be helpful for further analysis of connectivity of the cockroach circadian
clock’s neural network. To infer the possible interrelations of events, the events were grouped
additionally by similarities through a clustering process (Lara, Lizcano, Pérez, & Valente, 2014)
(Figure S1). Bayesian Gaussian mixtures were applied, using the estimated duration, amplitude,
and time localization as coordinates. Como resultado, events were clustered and labeled in groups
that were coherent with visual inspection of raw data.
Ultradian Oscillations in the Alpha, Beta, and Gamma Range Also Expressed Circadian Rhythmicity
in the Cockroach Clock
We searched for alpha (8–12 Hz), beta (12–28 Hz), and gamma (> 30 Hz) band oscillations in
the cockroach clock that were observed before in electroencephalograms (EEGs) of the mam-
malian brain (Buzsáki & Draguhn, 2004; Khanna, Pascual Leone, Michel, & Farzan, 2015). Nosotros
wanted to determine whether oscillations in different frequency bands are a general property of
neural networks with specific functional connectivity already present in the cockroach brain.
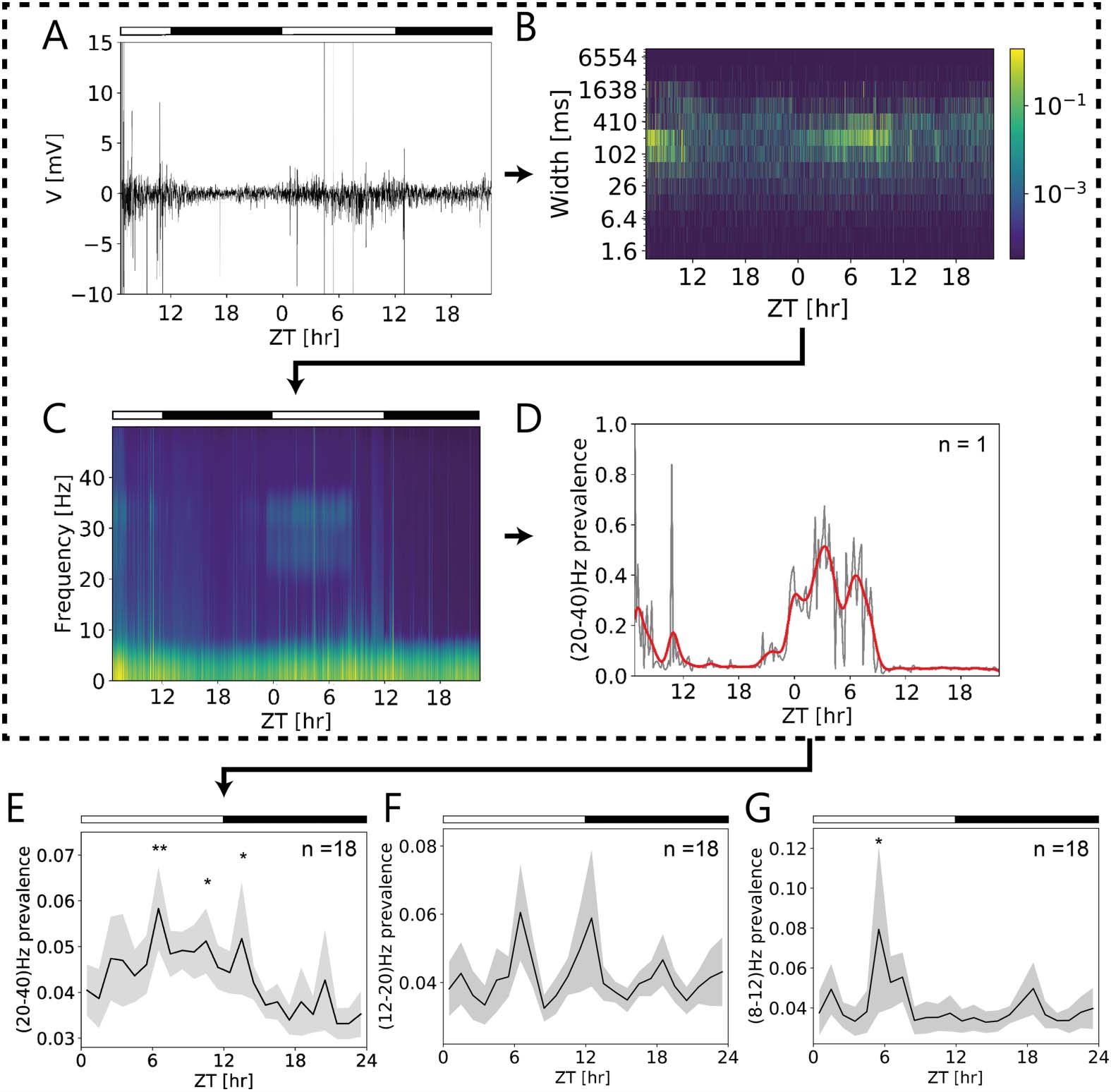
Dominating frequency bands and their prevalence at certain ZTs were extracted from overall
activity patterns of the AME recorded in vivo (Figures 8A–C). A heatmap generated from a sin-
gle 2-day-long in vivo recording (Figures 8A, B) illustrated a strong increase in activity around
midday. The spectrogram of this recording revealed a prevalence of power in a frequency band
in the beta/gamma range (20–40 Hz; Figure 8C) during the light phase. The rise of its preva-
lence preceded lights on at ZT 0 y, de este modo, was not driven by light. It sharply declined at
ZT 9, de este modo, it was not correlated with lights off at ZT 12 (Figure 8D). Several peaks of different
amplitudes at apparently regular intervals were observed at ZT 6.5 and ZT 10.5 the first day
and ZT 0.5, ZT 3, and ZT 6.5 the second day. When the prevalence of 20–40-Hz oscillations
was examined in all long-term in vivo recordings (norte = 18, Figure 8E), they were found to ex-
press rhythmicity also at circadian timescale. Significant maxima were observed at the middle
of the day and at dusk (ZT 6.5, ZT 10.5, ZT 13.5, linear mixed model, pag < 0.05, Table S1),
with a steep decline at the middle of the night (Figure 8E). Prevalence of the beta/gamma fre-
quency was significantly higher during the day compared with the night (linear mixed model,
p < 0.05, Table S1). Additionally, we found ultradian 6-hr periodicity at 12–20 Hz (beta fre-
quency band) prevalence (Figure 8F; ANOVA and sine fits, p = 0.036). In the alpha band range
(8–12 Hz) the prevalence peaked significantly at ZT 5.5 (linear mixed model, p < 0.05, Table
S1) at the middle of the day (Figure 8G). Thus, ultradian rhythms in different frequency bands
observed before in mammalian brains were present in the cockroach brain and were gated by
the circadian clock of the cockroach.
DISCUSSION
Seeking to understand neuropeptide-dependent network characteristics of circadian clocks on
multiple timescales, we employed long-term loose-patch clamp recordings in vivo of the cir-
cadian clock of the Madeira cockroach. Clock neurons of cockroaches and mammals alike
Network Neuroscience
953
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
4
9
4
4
1
8
6
6
8
9
3
n
e
n
_
a
_
0
0
1
0
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Cockroach circadian clock circuits
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
4
9
4
4
1
8
6
6
8
9
3
n
e
n
_
a
_
0
0
1
0
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 8. Multiscale frequencies at ultradian (ms) and circadian (∼24 hr) timescales present in
long-term in vivo loose-patch clamp recordings of the cockroach circadian clock. (A) Original
in vivo loose-patch clamp recording over the course of almost 2 days in12:12 hr light (open bar)–
dark (filled bar) cycle. (B) Full-length heatmap (of A) indicated strong activity increases of events
of several hundred ms durations at ∼ZT 7 at both days. (C) Spectrogram of the same recording
revealed multiple rhythms at different Zeitgeber times (ZTs), including ZT-dependent oscillations
in the beta/gamma frequency range (∼ 20–40-Hz). (D) The 20- to 40-Hz oscillations increased in
prevalence already before lights on (at dusk) with multiple peaks (∼ZTs 6.50, 10.5 (day 1), 0.5, 3,
and 6.5 (day 2)) during the day, about 2 hrs apart. It declined to zero prevalence preceding lights
off (at ∼ZT 9). (E) ZT-dependent prevalence of beta/gamma oscillations expressed significant rhyth-
micity on the circadian timescale in all long-term in vivo recordings (n = 18). Significant peaks
occurred during the day at ZTs 6.5 and 10.5, and at dusk at ZT 13.5 (p < 0.05; Table S1) (n = 18).
(F) Also, prevalence of beta oscillations (12- to 20-Hz range) changed over the course of the day
with a significant 6-hr periodicity (n = 18) (p = 0.036). (G) Furthermore, prevalence of alpha oscil-
lations (8- to 12-Hz range) expressed significant rhythmicity on the circadian timescale with a peak
at ZT 5.5 (n = 18) (p < 0.05; Table S1).
contain an astounding abundance of neuropeptides (reviews: Patton & Hastings, 2018, Stengl
& Arendt, 2016, Vosko et al., 2007). Thus, Zeitgeber time (ZT)-dependent neuropeptide release
appears to be instrumental for circadian clock functions. Consequently, rather than studying
action potential activity of single clock cells we focused on the analysis of electrical events
Network Neuroscience
954
Cockroach circadian clock circuits
that could be key signatures of neuropeptide functions, such as ensembles firing regularly and
synchronously at ultradian frequency bands. With novel approaches based on the wavelet
transform and activity heatmaps, we were able to detect and disaggregate events and event
patterns over multiple timescales. Thereby, we revealed ultradian periodicities occurring at
specific ZTs in the cockroach clock. We found ultradian rhythms in the alpha, beta, and gamma
frequency ranges that also showed rhythmicity on the 24-h circadian timescale and interme-
diate timescales. In the majority of the in vivo clock recordings, 20- to 40-Hz rhythms were
most common during the middle of the day and at dusk. Thus, they occurred at ZTs when
endogenously rhythmic release of PDF was suggested to take place, phase-controlled via dusk
and dawn (reviews: Stengl & Arendt, 2016; Stengl et al., 2015). Future analysis of long-term
in vivo recordings combined with pharmacology will test whether gamma band rhythms are
signatures of PDF actions in the cockroach clock controlling sleep during the day and arousal
at dusk. Concurrently, we model a potential circadian clock network that comprises features
found in vivo to allow for quantitative predictions of clock network characteristics and neu-
ropeptide functions in a circadian clockwork.
Wavelet Transform–Based Method Improved Reliability of Multiscale Event Detection
Our proposed method for detection of events performed well in these recordings with events
over multiple timescales and shapes. We could show events that spanned three orders of mag-
nitude in timescale. They were well recognized and characterized, even in cases where they
overlapped at multiple scales. In comparison to other existing methods for event detection in
electrophysiology recordings in the literature (Guzman et al., 2014; Merel et al., 2016; Pernía-
Andrade et al., 2012; Rey et al., 2015; Richardson & Silberberg, 2008; Shi et al., 2010), this
method required fewer restrictions and assumptions concerning the duration of events. Our
proposed method only requires defining maximum and minimum timescales, and the inter-
mediate scales will be spanned automatically. Methods that apply a threshold over a filtered
version of the original recording are very popular in spike detection. Often, the estimation of a
suitable theshold is based on the assumption that spikes are very short, compared with the in-
terspike intervals. This condition is not fulfilled in signals containing synaptic events. For those
cases, threshold methods are outperformed by techniques based on template matching (Shi
et al., 2010) and, more recently, on deconvolution of the signals (Guzman et al., 2014; Merel
et al., 2016; Pernía-Andrade et al., 2012). Deconvolution methods can be seen as more so-
phisticated versions of template matching (Merel et al., 2016). Both series of methods required
the previous extraction of representative samples from the trace (Merel et al., 2016; Pernía-
Andrade et al., 2012). While these approaches work well when the shapes are consistent over
the whole recording, they fail for multiscale, variable events (Merel et al., 2016). Widely differ-
ing durations of events are prone to cause many false positives and negatives (see Supporting
Information). Our approach avoids these problems by not using extracted templates from the
trace, and selectively highlighting the duration of the events. In addition, a greater robustness
against noise arises. Coherent with our own tests, deconvolution methods perform well un-
der the presence of low to moderate noise in the signal (deconvolution methods have been
reported to improve detection with signal-to-noise (SNR) = 5, Pernía-Andrade et al. (2012). In
contrast, the method presented here is able to detect the signature of each event even under
noise of higher amplitude (SNR = 1 and SNR = 0.5).
Activity Patterns of the Cockroach Clock Were Typical for Properties of Coupled Endogenous Oscillators
As a result of our exploratory analysis of activity intensity heatmaps (Figures 5– 7) and clus-
ter analysis (Figure S1), we found events and episodes that provided the basis for modeling
Network Neuroscience
955
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
4
9
4
4
1
8
6
6
8
9
3
n
e
n
_
a
_
0
0
1
0
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Cockroach circadian clock circuits
approaches as well as for experiments to test our hypothesis of neuropeptide actions. Phe-
nomena that were described in other dynamical systems, such as intermittency (Stavrinides
& Anagnostopoulos, 2013; ˙Zebrowski & Baranowski, 2004), are fundamental in the process
of resolving the circuit topology in the cockroach clock. The onset of large-amplitude oscil-
lations observed in the cockroach clock (Figure 6F) was reminiscent of the passage through
Hopf bifurcations under slow changes of parameters in the underlying system (Baer et al.,
1989). Concurrent amplitude modulation of events at well-separated timescales observed in
the cockroach clock (10 and 10 min; see Figure 7B) resembled a self-similar structure. Self-
similar structures (“fractals”) occur in complex networks (Gallos, Makse, & Sigman, 2012),
near bifurcations (Kwok & Smith, 2005), and also as a result of neuronal avalanches (Gireesh
& Plenz, 2008). In our modeling of the cockroach clock we currently combine the construc-
tion of minimal oscillator networks that reproduce the observed physiological features along
the lines of previous publications (Izhikevich, 2007; Tokuda et al., 2015) and that are in ac-
cordance with known neuroanatomical circuit properties (reviews: Stengl & Arendt, 2016).
Alpha, Beta, and Gamma Frequency Band Oscillations Occur in Mammalian and Insect Brains Alike
Frequency bands in the alpha range of 8 to 12 Hz were first detected in the 1920s in ex-
tracellular recordings of the cortex, in human electroencephalograms (EEGs; Berger, 1929).
Since then, different frequency bands from 0.05 to 500 Hz were described for the mammalian
brain that were associated respectively with specific cognitive functions (reviews: Buzsáki,
2015; Buzsáki & Draguhn, 2004; Engel, Fries, & Singer, 2001). Recent work described faster
oscillations in the rat clock (SCN) in vivo (Tsuji, Tsuji, Ludwig, & Leng, 2016) or in cell cul-
ture (Kononenko, Honma, & Honma, 2013). Fundamental frequencies of 32 Hz were found
in rat circadian clock neurons that responded to the onset or the offset of a light stimulus
given to the eye (Tsuji, Tsuji, Ludwig, & Leng, 2016). This fundamental gamma frequency was
present in the rat circadian clock throughout the day. It is currently unclear how these ultradian
rhythms contribute to a circadian rhythmicity. However, they seemed to be tightly linked to
environmental light input (Belle & Diekman, 2018), which is congruent with our findings. In
general, smaller compact networks with fewer neurons oscillated at higher frequencies and
lower amplitudes, while very large spatially distributed networks with synchronized activity of
many neurons produced slower oscillations at larger amplitudes (Buzsáki & Draguhn, 2004;
Csicsvari, Jamieson, Wise, & Buzsáki, 2003; Steriade, 2001).Thus, highly developed features
of connectivity in a light-dependent mammalian clock, as well as more general features of
connectivity, affected amplitude and frequency of oscillations at different frequency bands in
human/mammalian brains. Consequently, the question arose whether oscillations at different
frequency bands can be observed only in the complex mammalian brain as signature of its
unique, highly evolved functional connectivity. Alternatively, this could be an evolutionary old
property of neural networks serving specific functions that humans share with animals of differ-
ent species. In line with this hypothesis, gamma oscillations in the central brain of Drosophila
melanogaster were found to be evoked by olfactory stimulation (Paulk, Zhou, Stratton, Liu,
& van Swinderen, 2013). Electroretinograms recorded from the optic lobe of the blow fly re-
vealed a double-frequency peak around 150 Hz that corresponds to high gamma frequencies
(Kirschfeld, 1992), described also in the visual cortex of monkeys (∼ 70–80 Hz, high gamma;
Ray & Maunsell, 2010, 2011; Van Kerkoerle et al., 2014; Womelsdorf, Fries, Mitra, & Desi-
mone, 2006). Since gamma band frequencies found in mammalian brains also occurred in our
electrophysiological recordings of the cockroach clock, this suggests that network oscillations
as gamma frequency oscillations are a general property of neural networks indicative of shared
principles of connectivity between species. Integrating faster neural oscillations (alpha, beta,
Network Neuroscience
956
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
4
9
4
4
1
8
6
6
8
9
3
n
e
n
_
a
_
0
0
1
0
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Cockroach circadian clock circuits
gamma) into models of the circadian clock is still quite unexplored. As the cockroach clock is
relatively less complex and comprises a much smaller number of neurons in comparison to the
mammalian clock, exploring the interplay between faster neural oscillations and the circadian
rhythm in the cockroach clock via experiments and modeling might provide more insights into
underlying mechanisms.
Insect Clock Neurons Generate Circadian Outputs Apparently via Beta and Gamma Band Ensemble
Formation to Control Sleep-Wake Cycles
In this study, oscillations in the alpha range (8–12 Hz), lower beta range (12–20 Hz), and beta
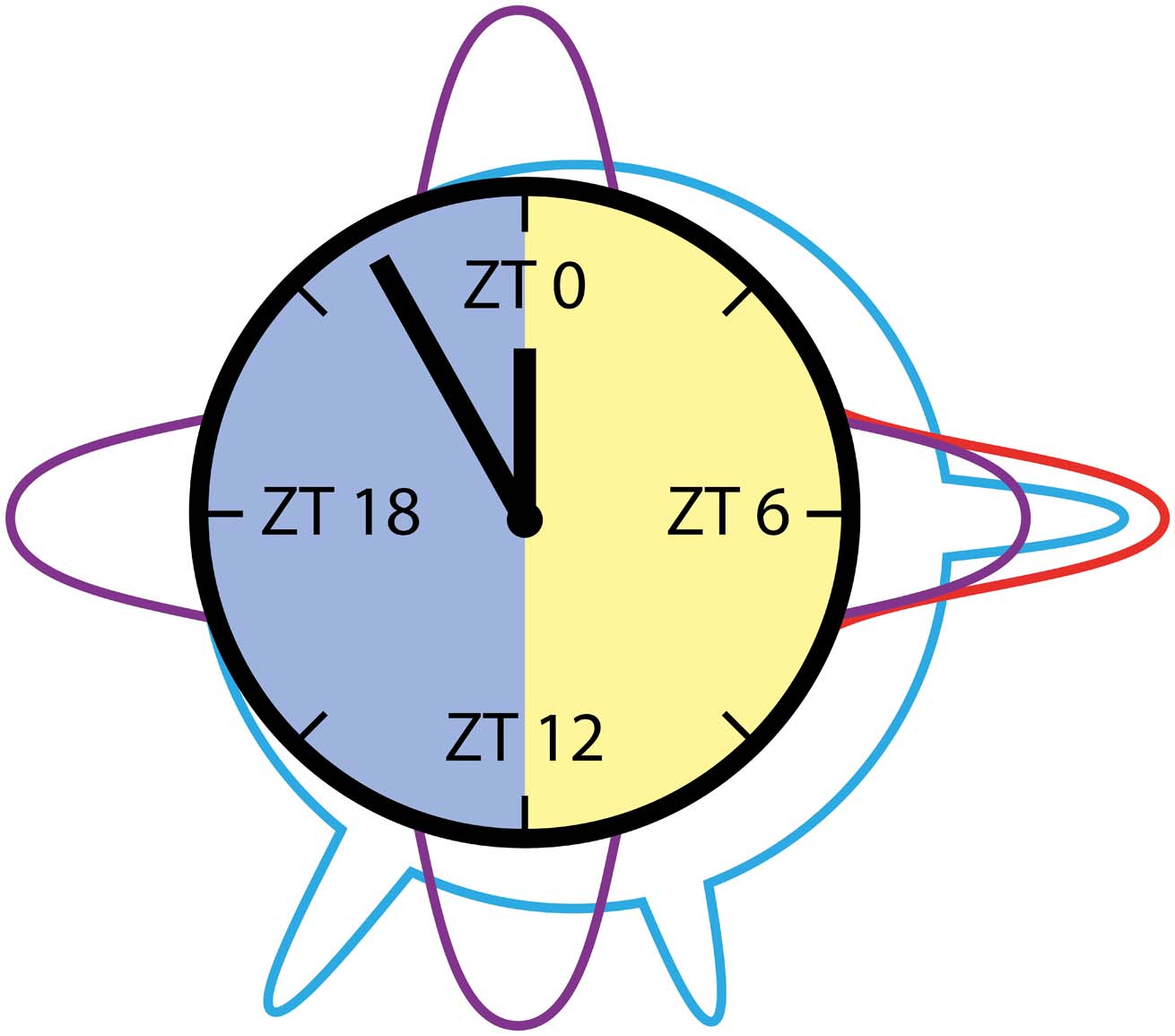
and gamma band range (20–40 Hz) exhibited distinctly different prevalence patterns (Figure 9).
Oscillations in the alpha range (8–12 Hz) peaked sharply around midday only. In mammals,
alpha oscillations were suggested to be associated with mutual inhibition (Klimesch, 2012;
Tsuji et al., 2016), since the amplitude was decreased rather than increased in response to a
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
4
9
4
4
1
8
6
6
8
9
3
n
e
n
_
a
_
0
0
1
0
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 9. Cartoon summary of main results: Beta/gamma, beta, and alpha frequencies prevailed at
different Zeitgeber times (ZTs) in long-term recordings of the cockroach clock. Beta/gamma frequen-
cies (20–40 Hz, cyan) peaked around midday, evening, and early night. They are hypothesized to be
related to PDF release. Beta frequencies (12–20 Hz, purple) with 6-hr periodicity were suggested
to be based upon clock-dependent regular neuropeptide release. Alpha frequencies (8–Hz, red),
which were dominantly present around midday, occurred during the cockroaches’ sleep. Next, we
will examine whether there are causal relationships between prevailing frequencies, neuropeptide
release, and sleep-wake phases.
Network Neuroscience
957
Cockroach circadian clock circuits
stimulus. Inhibitory GABAergic (GABA: gamma-aminobutric acid) networks play a significant
role in forming synchronized ensembles in the cockroach clock (review: Stengl et al., 2015).
Furthermore, GABA was suggested to be sleep-promoting in insects (Helfrich-Förster, 2018).
Prevalence of inhibitory GABA activity during the day would be congruent with the sleep-wake
phases of the nocturnal cockroach (Giese et al., 2018). However, whether alpha oscillations
are linked to GABA-dependent sleep-promotion in the clock network of the cockroach re-
mains to be investigated. Oscillations in the lower beta band range (12–20 Hz) exhibited a
6-hr periodic rhythm. This is congruent with extracellular recordings of an isolated accessory
medulla (AME), which revealed maximal changes of electrical activity at dawn and dusk as well
during midday and more prominently around midnight (Schneider & Stengl, 2007) with a 6-hr
periodicity. Since many other neuropeptides besides PDF are expressed in AME neurons, these
peaks could be associated with neuropeptide release via different neuronal ensembles struc-
turing sleep-wake cycles (Stengl & Arendt, 2016). Oscillations in the beta and gamma band
range (20–40 Hz) of the cockroach circadian clock were predominantly present during the day
and at dusk, correlating with the suggested time of PDF release by the AME, the insect circa-
dian clock (reviews: Hermann-Luibl & Helfrich-Foerster, 2015; Stengl & Arendt, 2016). Insect
PDF neurons are circadian clock neurons since they express circadian clock genes and inner-
vate the AME (Helfrich-Förster, 1995; Petri, Stengl, Würden, & Homberg, 1995). Controlled via
their endogenous circadian clock, they rhythmically release their neuropeptide PDF during the
day, as their light-like PDF-dependent phase response curve suggests (Eck, Helfrich-Förster, &
Rieger, 2016; Park et al., 2000; Petri & Stengl, 1997; Schulze, Schendzielorz, Neupert, Predel,
& Stengl, 2013). In the Madeira cockroach it was shown that the number of PDF-expressing
neurons increases during longer days and longer photoperiods, thus light enhanced PDF syn-
thesis (Wei & Stengl, 2011). Furthermore, in the fruitfly Drosophila melanogaster PDF neu-
rons are activated light-dependently and mediate arousal and sleep (Chatterjee et al., 2018;
Shang, Griffith, & Rosbash, 2008; Sheeba, Fogle, et al., 2008; Sheeba, Gu, Sharma, O’Dowd,
& Holmes, 2008). Also in the night-active Madeira cockroach PDF neurons control sleep-
wake cycles. During the day, they were suggested to activate sleep-promoting neuronal circuits
and inhibit arousal-promoting circuits via PDF release (Gestrich et al., 2018, review: Stengl &
Arendt, 2016). Accordingly, PDF application to an AME in vitro recruited a PDF-dependent
neuronal ensemble that fired synchronously in the beta/gamma frequency range (Schneider
& Stengl, 2005). Further in vivo experiments will test whether, indeed, timed neuropeptide
release by the cockroach circadian clock generates ensembles of neurons firing at specific
frequencies in beta and gamma frequency bands and whether alpha frequency bands could
be caused by synchronized activity of inhibitory networks. In future studies, we will challenge
our hypothesis experimentally combined with modeling that the beta/gamma band prevalence
during day and dusk is due to PDF release, controlling circadian sleep-wake cycles.
MATERIALS AND METHODS
Animals and Surgical Procedure
For all experiments, male Madeira cockroaches (Rhyparobia maderae) were collected from
laboratory colonies kept in large plastic containers. Conditions were kept constant with a tem-
C, 60% relative humidity, and a constant light-dark cycle of
perature of approximately 26
12:12 hr. Cockroaches were fed with dry dog food pellets, potatoes, and fruits, with water
provided ad libitum.
◦
For surgical preparation the animal was briefly anaesthetized on ice and inserted into a
custom-built holder. The head was fixed with wax and thorax, and the abdomen and legs were
fixed with tape. The head capsule was opened with four cuts: two cuts between both antennae
Network Neuroscience
958
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
4
9
4
4
1
8
6
6
8
9
3
n
e
n
_
a
_
0
0
1
0
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Cockroach circadian clock circuits
Loose-patch recording:
An extracellular current clamp (or
voltage clamp) recording with a
patch electrode that is attached to
the cell with low sealresistance.
and two perpendicular cuts. The head capsule was rinsed with cockroach ringer solution (NaCl
156 mM, KCl 4 mM, CaCl2 1 mM, HEPES 10 mM, glucose 5 mM; pH = 7.1; 380 mOsm) before
removing glands, large tracheal sacs, and fat bodies to expose the optic lobe of the brain. The
neurilemma was removed above the accessory medulla (AME) (recording site) with fine forceps
The location of the AME could be identified by a characteristic trachea on the brain surface
(Petri & Stengl, 1997).
Electrophysiology
Extracellular loose-patch recordings in the current clamp mode from AME neurons were per-
formed over 24–48 hr on a vibration-free table, with a MultiClamp 700B with Digidata 1550A1
(Axon Instruments, Union City, CA, USA) under a Zeiss W N-Achroplan NA 1.0 microscope.
Micromanipulators IVM-3000, Scientifica, UK, were used; additionally, in a second recording
setup bridge amplifiers BRAMP-01-R and BA-03X NPI, Tamm, Germany, with CED 1401mi-
cro, Cambridge Electronic Design, Cambridge, UK, were employed. Glass electrodes (GCF
150-7.5, Harvard Apparatus, Holliston, MA, USA) were prepared with a micropipette puller
(Flaming/Brown P-87, Sutter Instruments, Novato, CA, USA) and filled with 1 M KCl (Sigma)
with resistances of 8–12 MΩ. After recordings, the cell membrane was electrically permeabi-
lized and neurons were labeled by iontophoretic injection of neurobiotin with depolarizing
current (2–6 nA for 1–20 min). Depending on the respective seal resistance (∼ 1 GΩ, loose-
patch clamp recordings allowed to record either action potentials of single neurons (1- to
2-ms durations), or multiunit action potential activity (∼2- to 9-ms durations) of synchronized
neuronal populations, or slow field potentials indicative of synchronized excitatory/inhibitory
postsynaptic potentials (∼100- to 200-ms durations). All recordings in this study were per-
formed with a seal resistance of ∼ 1 GΩ. Long-term recordings over more than 24 hr were
very challenging and took a considerable amount of time to be accomplished. We only in-
cluded long-term recordings in our analysis that were stable for at least 24 hr, showing stable
seal resistances, no drastic drifts of the baseline, and no mechanical drift of the electrodes. Seal
resistance was checked at the beginning and at the end of the recordings via current injections.
Mechanical drift of the electrodes was checked under the microscope and were avoided with
optimization of the setup removing any mechanical load on the micromanipulators or elec-
trodes. Furthermore, stability of the in vivo recording could only be obtained with optimal
fixation of the cockroach and with minimalizing the invasiveness of the operation. Finally, po-
tential changes were monitored via an audio amplifier (12 W, Kemo Electronics, Germany) to
monitor quality of the recordings acoustically. For data acquisition pClamp10 software (Axon
Instruments) was employed and data were imported into Spike2 software (versions 7 or 9, CED,
Cambridge, UK) for analysis. Signals were digitized and sampled at frequencies of 25–50 kHz.
Aliasing was avoided according to the Nyquist theorem (Nyquist, 1928). Unfiltered recorded
data were filtered respectively afterwards during data analysis to avoid filter artefacts during
the recordings. High-pass filtering (200 Hz) eliminated electrode offset and low-pass filter-
ing (2,000 Hz) reduced high-frequency noise, if necessary. Three of the 18 recordings were
performed by Dr. HongYing Wei.
Data Preprocessing
Data files were imported and processed in a Python environment. Original files in their pro-
prietary format were converted using NEO functions (Garcia et al., 2014). Time series were
forward and backward filtered in three steps for noise removal and waveform preservation with
filtfilt function from Scipy (Jones, Oliphant, & Peterson, 2014). As a first step, power supply
interference at 50 Hz was removed using a notch filter. A low-pass filter with a cut frequency
Network Neuroscience
959
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
4
9
4
4
1
8
6
6
8
9
3
n
e
n
_
a
_
0
0
1
0
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Cockroach circadian clock circuits
of 6,000 Hz was then applied to remove high-frequency noise. A Savitzky-Golay filter was
finally used to further smooth the signal, while preserving the amplitude of the shortest peaks.
Event Detection
Our model signal can be expressed as
x(t) =
N
∑
i=1
Θ
i(t − τ
i) + B(t),
B(t) = Ω(t) + ξ(t),
(1)
i(t − τ
where x(t) is the signal, Θ
i) are the time-localized events, B(t) is the baseline of the
signal, which is noisy ( ξ(t) ), and may contain sinusoidal oscillations (Ω(t)). If the waveforms
of the events had a direct correspondence with the source processes, which they originated
from, and if the number of sources was small in comparison to the number of events, we might
find that the events Θ
i(t − τ) comply with
Θ
i(t) ∈ {Θ
R(t), Θ
1(t), Θ
2(t), ..., Θ
K(t)},
(2)
where K is the number of sources, and Θ
R is reserved for those events that are outliers or ran-
dom sources. In our approach, we used the wavelet transform to selectively highlight events
of different timescales and to infer some of their properties, such as amplitude and dura-
tion. Although the continuous wavelet transform (CWT) and analytic wavelet transform (AWT)
allowed a better resolution in time, we used a subset of the possibly present scales, prioritizing
computational affordability for large datasets. For comparison, we attempted a detection by
applying a threshold to the signal, as it is usually done in spike sorting pipelines (Rey et al.,
2015).
Threshold Detection
Detection by applying a signal threshold usually involves the following steps: (a) filter of the
signal, to remove the portion of the noise that lies in a region of the spectra we consider to
be out of interest; (b) estimate the noise properties, such as standard deviation, in order to (c)
calculate an appropriate threshold as a multiple of this noise standard deviation to set for the
signal; (d) detect peaks above this threshold. Depending on the signal-to-noise ratio (SNR),
this method is known to be sensitive to threshold estimation, leading to higher rates of false
positives when threshold is too low, and false negatives when threshold is too high. Under the
assumption that the probability of finding an event is low compared with the rest of the signal,
it is possible to estimate the noise and set the threshold (Rey et al., 2015).
Thresh = k
(cid:2)
median(|x(t)|)
0.6745
(cid:3)
,
(3)
where k is a parameter that is usually between 3 and 5. In the case presented in Figure 3, the
parameter k was manually tuned over intervals with relative stationarity, to values between 1
and 3.
Wavelet Transform
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
4
9
4
4
1
8
6
6
8
9
3
n
e
n
_
a
_
0
0
1
0
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Wavelet analyses have been successfully used to describe signals with both frequency and
time resolution. The wavelet transform of a real-valued signal x(t) is defined as
Network Neuroscience
Wx(τ, s) =
(cid:4) ∞
−∞
φ∗
1
sn
(cid:2)
(cid:3)
t − τ
s
x(t)dt,
(4)
960
Cockroach circadian clock circuits
where Wx(τ, s) is the wavelet transform of the signal x(t), φ∗(t) is the complex conjugate of
the mother wavelet, s and τ are the scale and shift with respect to the mother wavelet, and the
power sn is used as a normalization. The wavelet transform is, therefore, a convolution that can
be seen as projections onto shifted and rescaled versions of the mother wavelet. While n = 1/2
is the usual choice for normalization, it has been shown that n = 1 has some advantages, such
us making the modulus of Wx proportional to amplitudes in oscillatory signals (Lilly, 2017;
Lilly & Olhede, 2009). As this factor can be taken outside the integral, we make use of both
approaches when necessary.
Wavelets are zero-mean, square integrable functions that comply with certain requirements,
such as “admissibility” (Lilly & Olhede, 2009, 2010). A variety of wavelets have been pro-
posed (e.g., Paul, derivative of Gaussian, Daubechies, and Morlet wavelets), and the properties
of the wavelet transform differ greatly depending on the chosen wavelet. A most important
difference between different families of wavelets is the way their support is distributed in the
time/timescale plane, that is, the trade between time and timescale resolution, limited by the
Heisenberg area of the wavelet (Lilly & Olhede, 2009, 2012; Torrence & Compo, 1998). If
the wavelet is analytic, that is with support only in positive frequencies, Equation 4 is the
expression for the analytic wavelet transform (Lilly & Olhede, 2010). In the general case, that
is, when the wavelet is complex or real-valued, Wx(τ, s) is the continuous wavelet transform.
One should note that a real-valued CWT could be also obtained by taking the real part of
the AWT.
The generalized Morse wavelets have been shown to be a wavelet family, from which several
of the popular families of wavelets can be seen as special cases (Lilly & Olhede, 2012). It arises
as a solution of a joint time/frequency localization problem (Lilly & Olhede, 2009; Olhede &
Walden, 2002). It is defined in the frequency and time domain as follows:
Φβ,γ(ω) =
(cid:4) ∞
−∞
φβ,γ(t)e
−iωtdt = U(ω)aβ,γωβ
e
−ωγ
,
(5)
(cid:6) β
γ
(cid:5)
eγ
β
,
aβ,γ = 2
where U(ω) is the unit step, and β and γ are the parameters that control the wavelet shape.
It can be proven that incrementing the value of β by 1 is equivalent to performing a time
derivative. In this sense, the choice of γ defines the subfamily of wavelet that is obtained,
while β determines the wavelet within this family (Lilly & Olhede, 2012). An interesting result
is that a wavelet transform of a Morse wavelet is itself a modified Morse wavelet of the following
form (Lilly, 2017):
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
4
9
4
4
1
8
6
6
8
9
3
n
e
n
_
a
_
0
0
1
0
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
(cid:4) ∞
−∞
∗
φβ,γ
1
s
(cid:2)
t − τ
s
(cid:3)
(cid:2)
(cid:3)
φμ,γ
t
si
dt =
aβ,γaμ,γ
aβ+μ,γ
(cid:5)
(cid:5)(cid:5)
(cid:6)γ
s
si
s
si
+ 1
(cid:6)β
φβ+μ,γ
(cid:6) β+μ+1
γ
⎛
⎜
⎜
⎝
τ
si
(cid:6)γ
(cid:5)(cid:5)
s
si
(cid:6) 1
γ
+ 1
⎞
⎟
⎟
⎠
(6)
= Aβ,μ,γ f
(1)
β,μ,γ
⎛
⎝
(cid:5)
(cid:6)
s
si
φβ+μ,γ
⎞
⎠
τ
si
(cid:6)γ
(cid:6) 1γ
+1
(cid:5)(cid:5)
s
si
(for n = 1).
Network Neuroscience
961
Cockroach circadian clock circuits
It is easy to show that for the case n = 1/2;
(cid:4) ∞
−∞
1
1
2
s
∗
φβ,γ
(cid:2)
t − τ
s
(cid:3)
(cid:2)
(cid:3)
φμ,γ
t
si
dt =
aβ,γaμ,γ
aβ+μ,γ
(cid:5)(cid:5)
s
s
si
(cid:6)β+ 1
2
(cid:5)
1
2
i
(cid:6)γ
s
si
+ 1
φβ+μ,γ
(cid:6) β+μ+1
γ
⎛
⎜
⎜
⎝
τ
si
(cid:6)γ
(cid:5)(cid:5)
s
si
(cid:6) 1
γ
+ 1
⎞
⎟
⎟
⎠
(7)
= Aβ,μ,γ f
( 1
2 )
β,μ,γ
(cid:5)
(cid:6)
s
si
φβ+μ,γ
⎞
⎠
⎛
⎝
τ
si
(cid:6)γ
(cid:6) 1γ
+1
(cid:5)(cid:5)
s
si
(for n = 1/2).
By deriving these expressions, it is straightforward to see that modulus of both Equation 6
and Equation 7 are maximized for τ = 0 (center of the wavelets are coincident) and s = smax,
γ si for n = 1
being smax = si for n = 1/2 (i.e, the scales are coincident), and smax = [
(modulus is maximized when the transformation is done with a scale slightly different from 1,
for example, for β = 2, μ = 2, and γ = 3, smax = 0.87 si). Another interesting observation
is that the resulting transform also has a compact support in the time/timescale plane. This
is expected, since generalized Morse wavelets were originally constructed as solutions of a
localization problem.
β
μ+1 ]
1
Detection Using CWT or AWT
We first assumed that events were shaped with a waveform that closely resembles the selected
Morse wavelet. To detect these events in the real-valued signal, we look for maxima and min-
ima in the wavelet transform, which represent positive and negative excursions Θ
i) with
respect to the baseline signal B(t). When detected, properties of the events could be inferred
from the values at the maxima and minima. The appearance time and timescale at each max-
ima and minima could be obtained following Equations 6 and 7. Timescales could then be
transformed into an event duration. Amplitude could be inferred by taking into account that,
for n = 1, the modulus of the wavelet transform was proportional to the amplitude. Further-
more, an estimation for this proportionality was given (Lilly, 2017).
i(t − τ
Constructing the AWT or CWT might be computationally costly for long-term recordings
that last for more than 24 hr. In our approach, we selected a limited number of scales from
a geometric sequence, each of them representing a bandwidth of scales. Inspired in what is
the usual discretization in the discrete wavelet transform, we took s = 2jΔT, j = 0, 1, , Ns.
From Equations 6 and 7 it was possible to see that the modulus of AWT or CWT decay enough
between the scale where the maximum is detected and the next adjacent one, to clearly define
a “winner” scale for the event, in cases where it was detected in more than one scale.
Close and Overlapping Events
When events were separated enough from each other either in time or timescale axis, they
were reflected in AWT and CWT as separated peaks that decayed to a base level before reach-
ing the next peak. This separation was usually between three and four steps in the scale axis, or
a multiple of the scale parameter in the time axis. When events got closer in the time/timescale
plane, their support regions started to overlap. For moderate overlapping, it was still possible
to identify two distinct events, as the maxima/minima points remained clear. When the over-
lapping was larger, events started to be indistinguishable in the modulus of the AWT, but still
recognizable in the real CWT (Figure 4), which could be used in this case. If the events were
Network Neuroscience
962
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
4
9
4
4
1
8
6
6
8
9
3
n
e
n
_
a
_
0
0
1
0
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Cockroach circadian clock circuits
equally signed, they sometimes were detected as a fused larger event that is better captured
by a larger scale wavelet. This was a limitation because of the choice of a redundant base of
wavelets, compared with methods that allow for better source separation, such as independent
component analysis (ICA). In the case of opposite-signed events, it was necessary to distinguish
events from spurious oscillations in the CWT because of the second peak in the real part of
the wavelet. As a consequence, it was possible to set a minimum distance between events of
the same scale and opposite sign, choosing the one that reflects the larger amplitude when this
distance was not reached.
Procedure for Event Detection
1. Obtain a first set of pre-events by detecting maxima and minima in the real wavelet
transform for each of the scales, using n = 1/2.
2. Discard the pre-events that result from spurious oscillations, with the distance-amplitude
criteria.
3. For each of the pre-events, determine a winner scale when it is detected in more than
one consecutive scale.
4. Rescale the maxima and minima, using n = 1.
5. Estimate the duration and the amplitude for each event.
1(t), Θ
R(t), Θ
Event Clustering
K(t)}
In order to find groups of similar events, and estimate the set {Θ
posed in Equation 2, clustering was performed using estimated widths, amplitudes, and time
of each event as features. This election of features was also proposed in Lara et al. (2014)
when performing data mining of EEG recordings. These features were first rescaled, in order
to make them comparable in the calculation of Euclidean distances. Time localization was
used to account for nonstationarity in waveforms; events whose shape may change slightly in
a much slower timescale (i.e., hours) could still be recognized to be part of the same cluster.
This approach could then be complemented, if necessary, with manual merging of clusters that
showed similar behavior but showed separation in time and, therefore, were initially detected
as separate clusters.
2(t), ..., Θ
Because of the lengths of the recordings, a manual initial guess for the number of clusters
would involve a time-consuming exploration. For that reason, we opted for methods that did
not require the number of clusters as input parameters, but rather estimated them. Our tests
indicated that for the amount of overlapping between clusters, their elongated shapes, and
the choice of avoiding the initial guess of clusters, reasonable results could be obtained using
Bayesian gaussian mixtures.
Activity Descriptions
For exploratory visualization of the data, we created heatmaps for the activity at different
timescales over time (Figures 5A–D; Figures 6A, B, D, E; Figure 8B). In bins of 100 s, the
color represents the sum of the absolute values of the event amplitudes. The resulting graphs
exhibited a first good visualization of the dominant scales at each point of time.
Event Train Variability
Several metrics were developed for analyzing spike train variability. Some of these metrics
are locally defined, while others are calculated over a time window (Eden & Kramer, 2010;
Network Neuroscience
963
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
4
9
4
4
1
8
6
6
8
9
3
n
e
n
_
a
_
0
0
1
0
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Cockroach circadian clock circuits
Gabbiani & Koch, 1998; Ponce-Alvarez, Kilavik, & Riehle, 2010; Shinomoto et al., 2009).
Usually, metrics were defined in a way that they increase as the variability in the interspike
interval becomes larger. When the train shows the variability expected from a Poisson process,
metrics should be equal to 1. If it is smaller, the train is said to be more regular, up to the limit
of a constant interspike interval at the value of 0 (Gabbiani & Koch, 1998). We applied two of
these metrics for analyzing some episodes of events occurring at similar timescales: coefficient
of variation (Cv) and Fano factor (FF). Cv and FF are defined over a time window as follows:
Cv =
std(Ti)
Ti
,
FF =
var(Ti)
Ti
,
(8)
(9)
where Ti are the inter-event intervals in the selected window. By displacing a window, it is
possible to calculate time-resolved Cv and FF. Additionally, FF was calculated with variable
window sizes.
Time Series Frequency Analysis
In order to analyze frequency content of the signals over time, spectrograms were created using
the function spectrogram from SciPy (Jones et al., 2014), in windows of 26.1 s. Frequency
prevalence in the 20- to 40-Hz band, 12- to 20-Hz band, and 8- to 12-Hz band was calculated
with the following procedure: (a) columns in the spectrogram were averaged in bins of 10 min,
resulting in a periodogram for the bin; (b) for each periodogram, an exponential function was
fitted to obtain a baseline that is representative of the background noise; (c) a background
noise level was estimated as the median of the absolute values of the difference between the
spectra and the baseline; (d) a background area was estimated, as the product between the
total frequency range and the background noise level; (e) band area was calculated as the area
of the periodogram that lies above baseline in the 20- to 40-Hz, 12- to 20-Hz, or 8- to 12-Hz
bands; (f) prevalence was calculated as the ratio between band area and background area.
Statistics
Statistically significant peaks in the prevalence of 20- to 40-Hz, 12- to 20-Hz, or 8- to 12-Hz
frequencies was detected using R v. 3.6.0 and R Studio v. 1.2.1335 with a custom-written
script. Data were fitted to linear mixed models with Zeitgeber time (ZT) as fixed effect and
individual as random effect (lme function, nlme package; Pinheiro, Bates, DebRoy, Sarkar, &
R Core Team, 2019). Periodicity of 12- to 20-Hz prevalence was tested using an ANOVA and
sine fits.
ACKNOWLEDGMENTS
We thank Dr. HongYing Wei, at the Department of Biology, Animal Physiology, of the Uni-
versity of Kassel for performing three of the 18 long-term in vivo recordings. We thank André
Arand for expert animal care raising the cockroaches, Dr. Achim Werckenthin for graphical
contributions, and Dr. Susanne Neupert, Dr. Paula Kuokkanen, and Dr. Claudia Arbeitman for
their valuable comments.
SUPPORTING INFORMATION
Supporting Information for this article is available at https://doi.org/10.1162/netn_a_00106.
Network Neuroscience
964
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
4
9
4
4
1
8
6
6
8
9
3
n
e
n
_
a
_
0
0
1
0
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Cockroach circadian clock circuits
ETHICAL APPROVAL
All animal procedures were in compliance with the guidelines of the European Union (Direc-
tive 2010/63/EU) and the German Animal Welfare Act.
DATA ACCESSIBILITY STATEMENT
All raw data and statistical analyses will be made accessible upon request.
AUTHOR CONTRIBUTIONS
Pablo Rojas: Data curation; Formal analysis; Methodology; Software; Validation; Visualization; Writing –
Original Draft; Writing – Review & Editing. Jenny Plath: Visualization; Formal analysis; Writing
– Review & Editing. Julia Gestrich: Data curation;Methodology.BharathAnanthasubramaniam:
Formal analysis; Methodology; Writing – Review & Editing. Martin Garcia: Formal analysis;
Methodology; Project administration; Resources; Supervision; Writing – Review & Editing.
HanspeterHerzel: Funding acquisition; Methodology; Project administration; Resources; Su-
pervision; Writing – Review & Editing. Monika Stengl: Conceptualization; Funding acquisition;
Project administration; Resources; Supervision; Writing - Original Draft; Writing – Review &
Editing.
FUNDING INFORMATION
Monika Stengl, Deutsche Forschungsgemeinschaft (http://dx.doi.org/10.13039/501100001659),
Award ID: STE531/26-1; SPP 2041. Monika Stengl, Deutsche Forschungsgemeinschaft (http://dx.
doi.org/10.13039/501100001659), Award ID: STE531/18-2. Monika Stengl, Deutsche
(http://dx.doi.org/10.13039/501100001659), Award ID: STE531/
Forschungsgemeinschaft
18-3. Hanspeter Herzel, Deutsche Forschungsgemeinschaft
(http://dx.doi.org/10.13039/
501100001659), Award ID: HE2168/11-1; SPP 2041. Monika Stengl, University of Kassel
(http://dx.doi.org/10.13039/501100012687), Award ID: Biological clocks, graduate school
program.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
4
9
4
4
1
8
6
6
8
9
3
n
e
n
_
a
_
0
0
1
0
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
REFERENCES
Baer, S. M., Erneux, T., & Rinzel, J. (1989). The slow passage through
a Hopf bifurcation: Delay, memory effects, and resonance. SIAM
Journal on Applied mathematics, 49(1), 55–71.
Belle, M. D., & Diekman, C. O. (2018). Neuronal oscillations on
an ultra-slow timescale: Daily rhythms in electrical activity and
gene expression in the mammalian master circadian clockwork.
European Journal of Neuroscience, 48(8), 2696–2717.
Berger, H. (1929). Über das elektrenkephalogramm des menschen.
European Archives of Psychiatry and Clinical Neuroscience, 87(1),
527–570.
Buzsáki, G. (2015). Hippocampal sharp wave-ripple: A cognitive
biomarker for episodic memory and planning. Hippocampus,
25(10), 1073–1188.
Buzsáki, G., & Draguhn, A. (2004). Neuronal oscillations in cortical
networks. Science, 304(5679), 1926–1929.
Chatterjee, A., Lamaze, A., De, J., Mena, W., Chélot, E., Martin, B.,
. . . Rouyer, F. (2018). Reconfiguration of a multi-oscillator net-
work by light in the Drosophila circadian clock. Current Biology,
28(13), 2007–2017.
Csicsvari, J., Jamieson, B., Wise, K. D., & Buzsáki, G. (2003). Mech-
anisms of gamma oscillations in the hippocampus of the behav-
ing rat. Neuron, 37(2), 311–322.
Eck, S., Helfrich-Förster, C., & Rieger, D. (2016). The timed depolar-
ization of morning and evening oscillators phase shifts the circa-
Journal of Biological Rhythms, 31(5),
dian clock of Drosophila.
428–442.
Eden, U. T., & Kramer, M. A. (2010). Drawing inferences from Fano
factor calculations. Journal of Neuroscience Methods, 190(1),
149–152.
Engel, A. K., Fries, P., & Singer, W. (2001). Dynamic predictions:
Oscillations and synchrony in top-down processing. Nature
Reviews Neuroscience, 2(10), 704.
Gabbiani, F., & Koch, C. (1998). Principles of spike train analysis. In
Methods in neuronal modeling (Vol. 12, pp. 313–360). Citeseer.
Gallos, L. K., Makse, H. A., & Sigman, M. (2012). A small world of
weak ties provides optimal global integration of self-similar mod-
ules in functional brain networks. Proceedings of the National
Academy of Sciences, 109(8), 2825–2830.
Network Neuroscience
965
Cockroach circadian clock circuits
Garcia, S., Guarino, D., Jaillet, F., Jennings, T. R., Pröpper, R.,
Rautenberg, P. L., . . . Davison, A. P. (2014). Neo: An object
model for handling electrophysiology data in multiple formats.
Frontiers in Neuroinformatics, 8, 10.
Gestrich, J., Giese, M., Shen, W., Zhang, Y., Voss, A., Popov, C., . . .
Wei, H.
(2018). Sensitivity to pigment-dispersing factor (PDF)
is cell-type specific among PDF-expressing circadian clock neu-
Journal of Biological Rhythms,
rons in the Madeira cockroach.
33(1), 35–51.
Giese, M., Gestrich, J., Massah, A., Peterle, J., Wei, H., & Stengl,
M. (2018). GABA- and serotonin-expressing neurons take part in
inhibitory as well as excitatory input pathways to the circadian
clock of the Madeira cockroach Rhyparobia maderae. European
Journal of Neuroscience, 47(9), 1067–1080.
Gireesh, E. D., & Plenz, D. (2008). Neuronal avalanches organize as
nested theta- and beta/gamma-oscillations during development
of cortical layer 2/3. Proceedings of the National Academy of
Sciences, 105(21), 7576–7581.
Guralnik, V., & Srivastava, J. (1999). Event detection from time series
data. In Proceedings of the fifth ACM SIGKDD international con-
ference on knowledge discovery and data mining (pp. 33–42).
Guzman, S. J., Schlögl, A., & Schmidt-Hieber, C.
(2014). Stimfit:
Quantifying electrophysiological data with Python. Frontiers in
Neuroinformatics, 8, 16.
Hatton, G. I.
(1982). Phasic bursting activity of rat paraventricu-
lar neurones in the absence of synaptic transmission. Journal of
Physiology, 327(1), 273–284.
Helfrich-Förster, C. (1995). The period clock gene is expressed in
central nervous system neurons which also produce a neuropep-
tide that reveals the projections of circadian pacemaker cells
within the brain of Drosophila melanogaster. Proceedings of the
National Academy of Sciences, 92(2), 612–616.
Helfrich-Förster, C. (2018). Sleep in insects. Annual Review of
Entomology, 63, 69–86.
Hermann-Luibl, C., & Helfrich-Foerster, C. (2015). Clock network
in Drosophila. Current Opinion in Insect Science, 7, 65–70.
Izhikevich, E. M. (2007). Dynamical systems in neuroscience. Cam-
bridge, MA: MIT Press.
Jones, E., Oliphant, T., & Peterson, P. (2014). {SciPy}: Open source
scientific tools for {Python}.
Kamimoto, S., Nohara, R., & Ichikawa, T. (2006). Coordination be-
tween the electrical activity of developing indirect flight muscles
and the firing activity of a population of neurosecretory cells in
the silkmoth, Bombyx mori. Zoological Science, 23(5), 449–458.
Khanna, A., Pascual-Leone, A., Michel, C. M., & Farzan, F. (2015).
Microstates in resting-state EEG: Current status and future direc-
tions. Neuroscience and Biobehavioral Reviews, 49, 105–113.
Kirschfeld, K. (1992). Oscillations in the insect brain: Do they cor-
respond to the cortical gamma-waves of vertebrates? Proceedings
of the National Academy of Sciences, 89(10), 4764–4768.
Klimesch, W. (2012). Alpha-band oscillations, attention, and con-
trolled access to stored information. Trends in Cognitive Sciences,
16(12), 606–617.
Kononenko, N. I., Honma, S., & Honma, K.-I.
(2013). Fast syn-
chronous oscillations of firing rate in cultured rat suprachiasmatic
nucleus neurons: Possible role in circadian synchronization in
the intact nucleus. Neuroscience Research, 75(3), 218–227.
Kwok, T., & Smith, K. A. (2005). Optimization via intermittency with
a self-organizing neural network. Neural Computation, 17(11),
2454–2481.
Lara, J. A., Lizcano, D., Pérez, A., & Valente, J. P. (2014). A
general framework for time series data mining based on event
analysis: Application to the medical domains of electroen-
cephalography and stabilometry. Journal of Biomedical Informat-
ics, 51, 219–241.
Leise, T. L.
(2013). Wavelet analysis of circadian and ultradian
behavioral rhythms. Journal of Circadian Rhythms, 11(1), 5.
Lilly, J. M.
(2017). Element analysis: A wavelet-based method for
analysing time-localized events in noisy time series. Proceedings
of the Royal Society A: Mathematical, Physical and Engineering
Sciences, 473(2200), 20160776.
Lilly, J. M., & Olhede, S. C. (2009). Higher-order properties of
analytic wavelets. IEEE Transactions on Signal Processing, 57(1),
146–160.
Lilly, J. M., & Olhede, S. C. (2010). On the analytic wavelet
IEEE Transactions on Information Theory, 56(8),
transform.
4135–4156.
Lilly, J. M., & Olhede, S. C. (2012). Generalized Morse wavelets
as a superfamily of analytic wavelets. IEEE Transactions on Signal
Processing, 60(11), 6036–6041.
Loesel, R., & Homberg, U.
(2001). Anatomy and physiology of
neurons with processes in the accessory medulla of the cock-
roach Leucophaea maderae. Journal of Comparative Neurology,
439(2), 193–207.
Masimore, B., Kakalios, J., & Redish, A. (2004). Measuring funda-
mental frequencies in local field potentials. Journal of Neuro-
science Methods, 138(1–2), 97–105.
Merel, J., Shababo, B., Naka, A., Adesnik, H., & Paninski, L. (2016).
Bayesian methods for event analysis of intracellular currents.
Journal of Neuroscience Methods, 269, 21–32.
Nishiitsutsuji-Uwo, J., & Pittendrigh, C. S. (1968). Central nervous
system control of circadian rhythmicity in the cockroach.
Zeitschrift für vergleichende Physiologie, 58(1), 1–13.
Nyquist, H.
(1928). Certain topics in telegraph transmission the-
ory. Transactions of the American Institute of Electrical Engineers,
47(2), 617–644.
Olhede, S. C., & Walden, A. T. (2002). Generalized Morse wavelets.
IEEE Transactions on Signal Processing, 50(11), 2661–2670.
Page, T. L. (1984). Neuronal organization of a circadian clock in
the cockroach Leucophaea maderae. Photoperiodic Regulation
of Insect and Molluscan Hormones, 104, 115–131.
Park, J. H., Helfrich-Förster, C., Lee, G., Liu, L., Rosbash, M., & Hall,
J. C. (2000). Differential regulation of circadian pacemaker out-
put by separate clock genes in Drosophila. Proceedings of the
National Academy of Sciences, 97(7), 3608–3613.
Patton, A. P., & Hastings, M. H. (2018). The suprachiasmatic nu-
cleus. Current Biology, 28(15), R816–R822.
Paulk, A. C., Zhou, Y., Stratton, P., Liu, L., & van Swinderen, B.
(2013). Multichannel brain recordings in behaving Drosophila
reveal oscillatory activity and local coherence in response to sen-
sory stimulation and circuit activation. Journal of Neurophysiol-
ogy, 110(7), 1703–1721.
Pernía-Andrade, A. J., Goswami, S. P., Stickler, Y., Fröbe, U., Schlögl,
A., & Jonas, P. (2012). A deconvolution-based method with high
Network Neuroscience
966
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
4
9
4
4
1
8
6
6
8
9
3
n
e
n
_
a
_
0
0
1
0
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Cockroach circadian clock circuits
sensitivity and temporal resolution for detection of spontaneous
synaptic currents in vitro and in vivo. Biophysical Journal, 103(7),
1429–1439.
Petri, B., & Stengl, M. (1997). Pigment-dispersing hormone shifts the
phase of the circadian pacemaker of the cockroach Leucophaea
maderae. Journal of Neuroscience, 17(11), 4087–4093.
Petri, B., Stengl, M., Würden, S., & Homberg, U. (1995). Im-
munocytochemical characterization of the accessory medulla in
the cockroach Leucophaea maderae. Cell and Tissue Research,
282(1), 3–19.
Pinheiro, J., Bates, D., DebRoy, S., Sarkar, D., & R Core Team.
(2019). nlme: Linear and nonlinear mixed effects models [Com-
puter software manual]. Retrieved from https://CRAN.R-project.
org/package=nlme (R package version 3.1-140)
Ponce-Alvarez, A., Kilavik, B. E., & Riehle, A. (2010). Comparison
of local measures of spike time irregularity and relating variability
to firing rate in motor cortical neurons. Journal of Computational
Neuroscience, 29(1–2), 351–365.
Principe, J. C., & Brockmeier, A. J. (2015). Representing and de-
composing neural potential signals. Current Opinion in Neuro-
biology, 31, 13–17.
Ray, S., & Maunsell, J. H. (2010). Differences in gamma frequencies
across visual cortex restrict their possible use in computation.
Neuron, 67(5), 885–896.
Ray, S., & Maunsell, J. H. (2011). Different origins of gamma rhythm
and high-gamma activity in macaque visual cortex. PLoS Biology,
9(4), e1000610.
Reischig, T., & Stengl, M. (2003a). Ectopic transplantation of the ac-
cessory medulla restores circadian locomotor rhythms in arrhyth-
mic cockroaches (Leucophaea maderae). Journal of Experimental
Biology, 206(11), 1877–1886.
Reischig, T., & Stengl, M. (2003b). Ultrastructure of pigment-dispersing
hormone-immunoreactive neurons in a three-dimensional model
of the accessory medulla of the cockroach Leucophaea maderae.
Cell and Tissue Research, 314(3), 421–435.
Rey, H. G., Pedreira, C., & Quiroga, R. Q. (2015). Past, present and
future of spike sorting techniques. Brain Research Bulletin, 119,
106–117.
Richardson, M. J., & Silberberg, G. (2008). Measurement and analy-
sis of postsynaptic potentials using a novel voltage-deconvolution
method. Journal of Neurophysiology, 99(2), 1020–1031.
Schneider, N.-L., & Stengl, M. (2005). Pigment-dispersing factor
and GABA synchronize cells of the isolated circadian clock of
the cockroach Leucophaea maderae. Journal of Neuroscience,
25(21), 5138–5147.
Schneider, N.-L., & Stengl, M.
(2007). Extracellular long-term
recordings of
the circadian
the isolated accessory medulla,
pacemaker center of the cockroach Leucophaea maderae, re-
veal ultradian and hint circadian rhythms. Journal of Comparative
Physiology A, 193(1), 35–42.
Schulze, J., Schendzielorz, T., Neupert, S., Predel, R., & Stengl, M.
(2013). Neuropeptidergic input pathways to the circadian pace-
maker center of the madeira cockroach analysed with an im-
proved injection technique. European Journal of Neuroscience,
38(6), 2842–2852.
Shang, Y., Griffith, L. C., & Rosbash, M. (2008). Light-arousal and
circadian photoreception circuits intersect at the large PDF cells
of the Drosophila brain. Proceedings of the National Academy
of Sciences, 105(50), 19587–19594.
Sheeba, V., Fogle, K. J., Kaneko, M., Rashid, S., Chou, Y.-T., Sharma,
V. K., & Holmes, T. C. (2008). Large ventral lateral neurons mod-
ulate arousal and sleep in Drosophila. Current Biology, 18(20),
1537–1545.
Sheeba, V., Gu, H., Sharma, V. K., O’Dowd, D. K., & Holmes,
T. C. (2008). Circadian- and light-dependent regulation of rest-
ing membrane potential and spontaneous action potential firing
of Drosophila circadian pacemaker neurons.
Journal of Neuro-
physiology, 99(2), 976–988.
Shi, Y., Nenadic, Z., & Xu, X. (2010). Novel use of matched filter-
ing for synaptic event detection and extraction. PLoS ONE, 5(11),
e15517.
Shinomoto, S., Kim, H., Shimokawa, T., Matsuno, N., Funahashi, S.,
Shima, K., . . . Toyama, K. (2009). Relating neuronal firing pat-
terns to functional differentiation of cerebral cortex. PLoS Com-
putational Biology, 5(7), e1000433.
Stavrinides, S. G., & Anagnostopoulos, A. N. (2013). The route from
synchronization to desynchronization of chaotic operating cir-
In Applications of chaos and nonlinear dy-
cuits and systems.
namics in science and engineering (Vol. 3, pp. 229–275). Berlin,
Germany: Springer.
Stengl, M., & Arendt, A. (2016). Peptidergic circadian clock circuits
in the Madeira cockroach. Current Opinion in Neurobiology, 41,
44–52.
Stengl, M., & Homberg, U. (1994). Pigment-dispersing hormone-
immunoreactive neurons in the cockroach Leucophaea maderae
Journal of
share properties with circadian pacemaker neurons.
Comparative Physiology A, 175(2), 203–213.
Stengl, M., Werckenthin, A., & Wei, H. (2015). How does the cir-
cadian clock tick in the Madeira cockroach? Current Opinion in
Insect Science, 12, 38–45.
Steriade, M. (2001). Impact of network activities on neuronal prop-
erties in corticothalamic systems. Journal of Neurophysiology,
86(1), 1–39.
Tokuda,
I. T., Ono, D., Ananthasubramaniam, B., Honma, S.,
Honma, K.-I., & Herzel, H. (2015). Coupling controls the syn-
chrony of clock cells in development and knockouts. Biophysical
Journal, 109(10), 2159–2170.
Torrence, C., & Compo, G. P. (1998). A practical guide to wavelet
analysis. Bulletin of the American Meteorological Society, 79(1),
61–78.
Tsuji, T., Tsuji, C., Ludwig, M., & Leng, G. (2016). The rat suprachi-
asmatic nucleus: the Master clock ticks at 30 Hz. Journal of Phys-
iology, 594(13), 3629–3650.
Tu, C.-L., Hwang, W.-L., & Ho, J. (2005). Analysis of singularities
from modulus maxima of complex wavelets. IEEE Transactions
on Information Theory, 51(3), 1049–1062.
Van Kerkoerle, T., Self, M. W., Dagnino, B., Gariel-Mathis, M.-A.,
Poort, J., Van Der Togt, C., & Roelfsema, P. R.
(2014). Alpha
and gamma oscillations characterize feedback and feedforward
processing in monkey visual cortex. Proceedings of the National
Academy of Sciences, 111(40), 14332–14341.
Vansteensel, M. J., Michel, S., & Meijer, J. H. (2008). Organization
of cell and tissue circadian pacemakers: A comparison among
species. Brain Research Reviews, 58(1), 18–47.
Network Neuroscience
967
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
4
9
4
4
1
8
6
6
8
9
3
n
e
n
_
a
_
0
0
1
0
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Cockroach circadian clock circuits
Vosko, A. M., Schroeder, A., Loh, D. H., & Colwell, C. S. (2007). Va-
soactive intestinal peptide and the mammalian circadian system.
General and Comparative Endocrinology, 152(2–3), 165–175.
Wei, H., el Jundi, B., Homberg, U., & Stengl, M. (2010). Imple-
mentation of pigment-dispersing factor-immunoreactive neurons
in a standardized atlas of the brain of the cockroach Leucophaea
maderae. Journal of Comparative Neurology, 518(20), 4113–4133.
(2011). Light affects the branching pattern
of peptidergic circadian pacemaker neurons in the brain of the
cockroach Leucophaea maderae. Journal of Biological Rhythms,
26(6), 507–517.
Wei, H., & Stengl, M.
Wei, H., Yasar, H., Funk, N. W., Giese, M., Baz, E.-S., & Stengl,
M.
in
(2014). Signaling of pigment-dispersing factor (PDF)
the Madeira cockroach Rhyparobia maderae. PLoS ONE, 9(9),
e108757.
Womelsdorf, T., Fries, P., Mitra, P. P., & Desimone, R. (2006).
Gamma-band synchronization in visual cortex predicts speed of
change detection. Nature, 439(7077), 733.
˙Zebrowski, J., & Baranowski, R. (2004). Type I intermittency in
nonstationary systems—Models and human heart rate variability.
Physica A: Statistical Mechanics and Its Applications, 336(1–2),
74–83.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
4
9
4
4
1
8
6
6
8
9
3
n
e
n
_
a
_
0
0
1
0
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
968