PERSPECTIVE - IA de Investigación especializada en el MIT

PERSPECTIVA

Columnar connectome: toward a mathematics
of brain function

Anna Wang Roe

Institute of Interdisciplinary Neuroscience and Technology, Zhejiang University, Hangzhou, Porcelana

Palabras clave: Primate, Cerebral cortex, Functional networks, Functional tract tracing, Matrix mapping,
Brain theory, Artiﬁcial intelligence

ABSTRACTO

Understanding brain networks is important for many ﬁelds, including neuroscience,
psicología, medicine, and artiﬁcial intelligence. To address this fundamental need, hay
multiple ongoing connectome projects in the United States, Europa, and Asia producing
brain connection maps with resolutions at macro- and microscales. Sin embargo, still lacking is
a mesoscale connectome. This viewpoint (1) explains the need for a mesoscale connectome
in the primate brain (the columnar connectome), (2) presents a new method for acquiring
such data rapidly on a large scale, y (3) proposes how one might use such data to achieve
a mathematics of brain function.

THE COLUMNAR CONNECTOME

The Cerebral Cortex Is Composed of Modular Processing Units Termed “Columns”

In humans and nonhuman primates, the cerebral cortex occupies a large proportion of brain
volumen. This remarkable structure is highly organized. Anatomically, it is a two-dimensional
(2D) sheet, roughly 2mm in thickness, and divided into different cortical areas, each specializ-
ing in some aspect of sensory, motor, cognitivo, and limbic function. There is a large literature,
especially from studies of the nonhuman primate visual cortex, to support the view that the
cerebral cortex is composed of submillimeter modular functional units, termed “columns”
(Mountcastle, 1997). Columns span the 2-mm thickness of cortex and are characterized by
six input/output layers (laminae) linked together via interlaminar circuits (Cifra 1). The tens of
thousands of neurons within a single column are not functionally identical but share a common
functional preference such that single stimuli maximally activate the population and produce a
coherent columnarresponse. These coherent responses can be visualized using multiple methods,
including electrophysiology (p.ej., Hubel & Wiesel, 1977; Mountcastle, 1997; Katzner et al.,
2009), 2-deoxyglucose (p.ej., Tootell et al., 1988), optical imaging (p.ej., Blasdel & Salama,
1986; Grinvald et al., 1986), and high spatial resolution fMRI methods (p.ej., cheng, 2012;
Nasr et al., 2016; Le et al., 2019). More in-depth and scholarly articles about the deﬁnition and
existence of the column are available (p.ej., Horton & Adams, 2005; Rakic, 2008; Ts’o et al.,
2009; da Costa & Martín, 2010; Rockland, 2010).

In nonvisual cortical areas, data on columnar organization is more limited (DeFelipe et al.,
1986; Lund et al., 1993; Kritzer & Goldman-Rakic, 1995; Friedman et al., 2004; Gharbawie
et al., 2014). Sin embargo, there is accumulating evidence, as well as compelling genetic de-
velopmental (Rakic, 1988; Torii et al., 2009; Le et al., 2012), and computational reasons
(Swindale, 2004; Schwalger et al., 2017; Berkowitz & Sharpee, 2018) to believe that columnar

un acceso abierto

diario

Citación: Roe, A. W.. (2019). Columnar
conectoma: toward a mathematics of
brain function. Neurociencia en red,
3(3), 779–791. https://doi.org/10.1162/
netn_a_00088

DOI:
https://doi.org/10.1162/netn_a_00088

Recibió: 26 Octubre 2018
Aceptado: 14 Abril 2019

Conflicto de intereses: Los autores tienen
declaró que no hay intereses en competencia
existir.

Autor correspondiente:
Anna Wang Roe
annawang@zju.edu.cn

Editor de manejo:
Pedro Valdes-Sosa

Derechos de autor: © 2019
Instituto de Tecnología de Massachusetts
Publicado bajo Creative Commons
Atribución 4.0 Internacional
(CC POR 4.0) licencia

La prensa del MIT

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
3
7
7
9
1
0
9
2
4
4
9
norte
mi
norte
_
a
_
0
0
0
8
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Columnar connectome: mathematics of brain function

Columna:
A modular functional unit of cerebral
corteza.

organization may be a fundamental feature throughout cortex. Pasko Rakic (2008) writes: "El
neurons within a given column are stereotypically interconnected in the vertical dimension,
share extrinsic connectivity, and hence act as basic functional units subserving a set of common
static and dynamic cortical operations that include not only sensory and motor areas but also
association areas subserving the highest cognitive functions.” For the purposes of this view-
punto, the term “column” refers to a unit of information integration and functional speciﬁcity.

Why a Columnar Connectome Is Needed

Columns come in different ﬂavors and have very speciﬁc connections with other columns.
Por ejemplo (Cifra 2), in primary visual cortex (V1, dotted lines divide V1, V2, and V4),
different functional columns focus on visual features such as eye speciﬁcity (ocular dominance
columnas, Figura 2B), color (blobs; Figura 1C: dark dots in V1 are color “blobs,” red dot overlies
a blob), and orientation (orientation columns; Figure 1D dark and light domains in V1, yellow
dot overlies a horizontal orientation domain). In the second visual area (V2), columns within
the thin stripe (green dots) and thick/pale stripe (blue dots) types integrate columnar informa-
tion from V1 to generate higher order parameters of color (thin stripes: hue), forma (thick/pale
stripes: cue-independent orientation response), y profundidad (thick stripes: near to far binocular
disparity) (for review see Roe et al., 2009). Columns in V4 are hypothesized to perform fur-
ther abstractions such as color constancy (Kusunoki et al., 2006), invariance of shape position
and size (Rust & Dicarlo, 2010; Sharpee et al., 2013), and relative (vs. absolute) profundidad (Shiozaki
et al., 2012; Fang et al., 2019) (for review see Roe et al., 2012).

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
3
7
7
9
1
0
9
2
4
4
9
norte
mi
norte
_
a
_
0
0
0
8
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

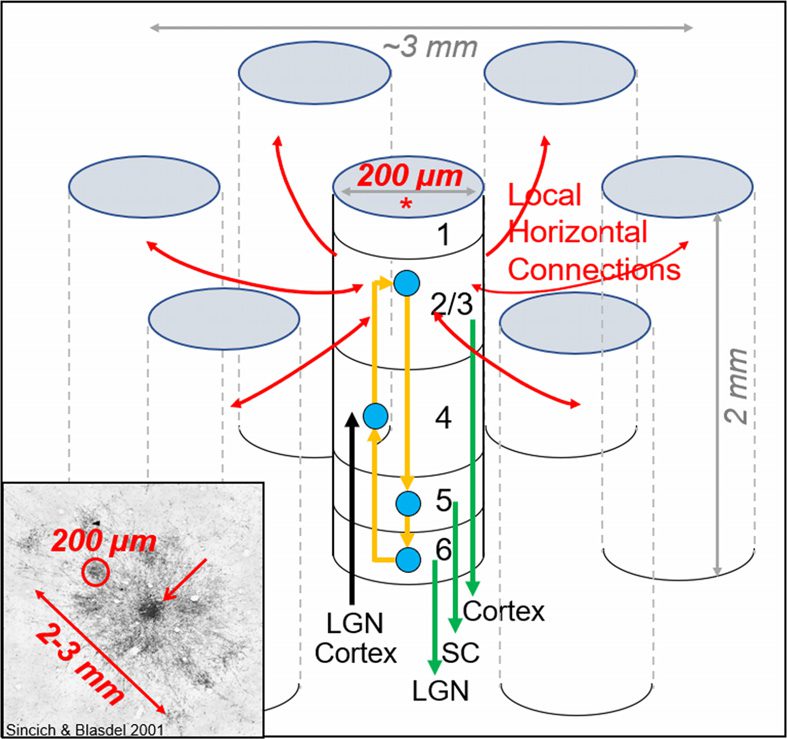
Cifra 1. The canonical cortical column and its connections (based on nonhuman primate cortex).
The cortical column (*) is a very organized input/output device, ∼200 µm in size and comprising
6 capas. Layer 4 receives inputs (black arrow, p.ej., from thalamus or other visual areas). Layers 2
y 3 provide outputs to other cortical columns within the same cortical area (red arrows) también
as to other cortical areas (green arrow from layer 2/3). Layers 5 y 6 provide outputs to subcortical
objetivos (green arrows, p.ej., LGN: lateral geniculate nucleus; CAROLINA DEL SUR: superior colliculus). Todo 6 capas
share information via interlaminar connections (yellow arrows). Through these connections, el
thousands of cells in each column share similar function; por lo tanto, each column is functionally
específico. Bottom left inset provides example of one such network (adapted from Sincich & Blasdel,
2001). Star-like arrangement of connections between columns within a local network (De arriba hacia abajo
view from surface of cortex). Labeled orientation columns (∼200 µm in size, one circled in red) tener
orientation preference similar to the injected column (red arrow). This local anatomical network
embodies the concept of orientation selectivity.

Neurociencia en red

780

Columnar connectome: mathematics of brain function

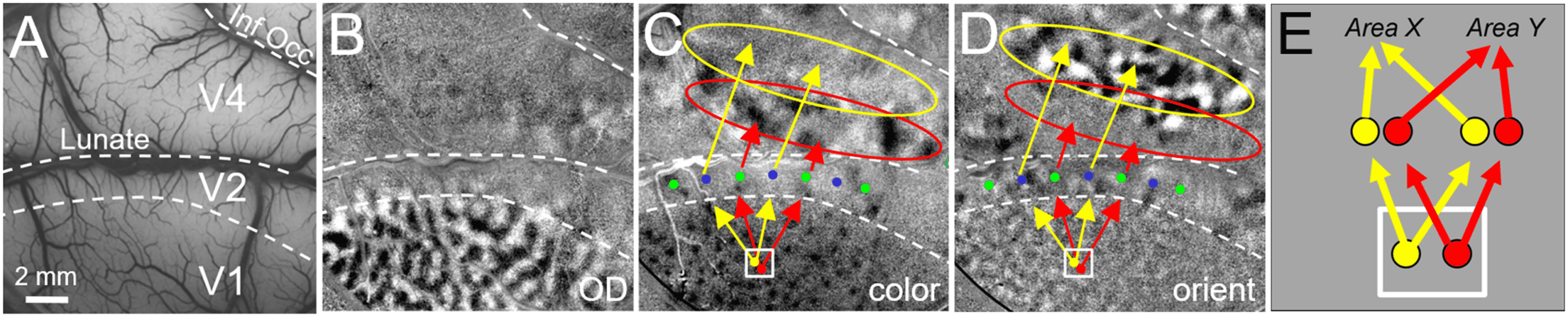
Cifra 2. Organization of columnar connections in visual cortex. (A) Cortical surface vasculature of visual areas V1, V2, and V4 in macaque
monkey brain. (B) optical image obtained by a CCD camera through window on the brain reveals ocular dominance map in V1 of macaque
monkey (dark and light columns activated by left eye and right eye, respectivamente). (C) When monkey views a color (red/green isoluminant)
grating on a monitor, this optical image reveals activated color columns (V1: dark “blobs”; V2: dark “thin stripes” indicated by green dots; V4:
domains in “color band” indicated by red oval). (D) When monkey views an achromatic grating, orientation columns are revealed (vertical
minus horizontal gratings). V1: orientation columns; V2: orientation domains in “thick/pale” stripes indicated by blue dots; V4: dominios
in “orientation band” indicated by yellow oval. Arrows are schematics of connectivity between columns in V1, V2, and V4. Red arrows:
connectivity between blobs in V1, thin stripes in V2, and color bands in V4. Yellow arrows: connectivity between orientation domains in V1,
thick/pale stripes in V2, and orientation bands in V4 (for review see Roe et al., 2012). (mi) Yellow column projects to Area X, and Red column
projects to Area Y. If connections are traced via a large anatomical tracer injection or large voxel (represented by white box), the result will
espectáculo, incorrectly, that each of the yellow and red columns project to both Area X and Area Y. Nota: por simplicidad, feedback connections, p.ej.,
from V4 to V2 and from V2 to V1, are not depicted.

A key aspect of cortical columns is their highly speciﬁc connections with other columns
(Figure 2C and 2D, red and yellow arrows). This has been demonstrated from studies using
focal injections of tracers targeted to single columns. Such studies have revealed sets of patchy
connections, both intra-areal (Cifra 1, recuadro) and inter-areal (Cifra 2, arrows) (p.ej., Livingstone
& Hubel, 1984; Sincich & Horton, 2005; Shmuel et al., 2005; Federer et al., 2013). Columna-
speciﬁc connection patterns thus embody a functionally speciﬁc (p.ej., orientation or color)
network. Sin embargo, hasta la fecha, because of the demanding nature of these experiments, hay
only a small number of such studies. Hasta ahora, there has not been a method that permits system-
atic large-scale study of columnar connectivity. De hecho, encima 40 years after Hubel and Wiesel’s
(1977) description of the organization of functional columns in V1, little is known about the
organization of cortical connectivity at the columnar level. I propose that we extend the con-
cept of the hypercolumn (all the machinery required to represent a single point in space) a
the connectional hypercolumn (all the connections of that unit of representation).

A New Mapping Method

The primary limitation of current methods are the following. (a) Lack of spatial resolution: mayoría
anatomical mapping methods employ tracer injections 2−5 mm in size. Human connectomes
are based on resting-state or diffusion methods, which typically are mapped at 2−3 mm voxel
resolution. These volumes (white rectangle in Figure 2E) encompass multiple columns and
therefore reveal connections of a population of multiple functionally distinct columns. Desde
individual nearby columns can exhibit quite distinct connectivity patterns (p.ej., Figura 2C
and 2D: color blobs to thin stripes vs. orientation columns to pale/thick stripes), connections
arising from such averages are inaccurate and misleading (Figura 2E). (b) Slow and expensive:
traditional anatomical tract tracing typically requires 2 a 3 weeks for tracer transport, animal
sacriﬁce to acquire tissue, and time-consuming weeks to map label locations and 3D recon-
estructura. (C) Not large scale: anatomical studies are limited to several tracers, and therefore
the connections of only a handful of nodes can be studied in any single brain. Other methods
such as electrophysiological stimulation with fMRI mapping have elegantly revealed networks

Neurociencia en red

781

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
3
7
7
9
1
0
9
2
4
4
9
norte
mi
norte
_
a
_
0
0
0
8
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Columnar connectome: mathematics of brain function

Optogenetics:
A method of controlling neurons by
light by viral transfection of
rhodopsin proteins.

underlying speciﬁc behaviors (p.ej., Tolias et al., 2005); sin embargo, electrical methods can suf-
fer from current spread, leading to lack of spatial speciﬁcity, as well as inability to map local
connections because of signal dropout near the electrode. Optogenetic stimulation with fMRI
mapping is a powerful cell-type speciﬁc approach (p.ej., Gerits et al., 2012); sin embargo, in pri-
compañeros, it takes weeks for viral expression and has thus far been limited by the small number
of transfected nodes, making large-scale mapping of connections in the primate brain chal-
lenging. (d) Correlation based functional connectivity: fMRI BOLD signal correlation (resting
state studies) noninvasively probes networks in human and animal brains, but are limited to
inference about correlation rather than connectivity. Such limitations also exist with neuro-
physiological cross-correlation studies of spike timing coincidence.

To overcome some of these limitations, we have developed a new rapid in vivo mapping
técnica. This method combines an optical stimulation method, termed pulsed infrared neu-
ral stimulation (INS), with high-ﬁeld fMRI (Xu et al., 2019a). INS is a method that uses pulsed
trains of light (1,875 nm) to induce heat transients in tissue (Wells et al., 2005; Cayce et al.,
2014; Chernov & Roe, 2014). Although the mechanism underlying INS is still under study, el
leading theory is that the heat transients lead to membrane capacitance change, que lleva
to induction of neuronal ﬁring. When INS is delivered with a ﬁne ﬁber optic (p.ej., 200-µm
diameter) to the cerebral cortical surface, the light distribution is highly focal (roughly the
same diameter as the ﬁber optic) and roughly ∼300 µm in penetration depth; this penetration
reaches cells in the superﬁcial layers (2/3) and apical dendrites of pyramidal cells in deep lay-
ers (5/6). Such neuronal activation, Sucesivamente, is propagated to downstream neurons at connected
sites. Similar activation can be achieved by inserting the ﬁber optic into deep brain sites (Xu
et al., 2019b). The resulting BOLD responses associated with this activation constitutes a map
of cortico-cortical connectivity arising from a single site. Por ejemplo, when INS is applied to
área 17 with ﬁne 200-µm optic ﬁbers in a high-ﬁeld MRI, INS evokes focal activations in areas
18 y 19, the ipsilateral LGN, and contralateral 17/18 (Xu et al., 2019a). This activation is
robusto, intensity dependent, and safe for long-term use (Chernov et al., 2014). One can also
use high-resolution mapping to examine BOLD activation in different cortical lamina. Esta re-
veals local connections that distinguish between feedforward (capa 4 activación) and feedback
(superﬁcial and deep laminae) connections (Xu et al., 2019a). En tono rimbombante, as no animal sac-
riﬁce is required for large dataset collection, the brain can be probed systematically with ﬁber
optic bundles applied to windows on the brain, across multiple sessions. It is also compati-
ble with other imaging, electrophysiological, and behavioral methods for multimodal dataset
correlation (Chernov & Roe, 2014; Xu et al., 2019a).

COLUMNAR MOTIFS

The long-standing notion that cortical columns perform common functional transformations
would be further bolstered by the presence of columnar connectivity motifs. The existence of
motifs would suggest that there are indeed common modes of information distribution and
integración. The true value of such motifs is the possibility of identifying a small set of gen-
eral motifs to characterize cortical function (Cifra 3). This would provide basis vectors for
constructing biological representation of information.

One could wonder why it matters what the underlying anatomical motif is. For some com-
putational neuroscientists, it matters not what the brain circuit is, as long as a circuit can
achieve the desired functional output. Sin embargo, it is a fact that our brain contains organized
anatomical constructs, and these constructs perform some pretty sophisticated functions that
so far have been difﬁcult to mimic with other architectures. Although the brain may not be the

Neurociencia en red

782

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
3
7
7
9
1
0
9
2
4
4
9
norte
mi
norte
_
a
_
0
0
0
8
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Columnar connectome: mathematics of brain function

Mesoscale:
The submilleter scale, columnar
escala.

only architecture capable of intelligent behavior, perhaps it is one optimal architecture given
existing biological and physical constraints.

Abajo, I present two possible motifs: an intra-areal motif (Motif1, binding) and an inter-
areal motif (Motif2, transformación). The basis for these motifs comes from prevous studies of
mesoscale anatomical connections.

Motif1: Intra-Areal Networks (Binding)

As shown in Figure 3, many cortical areas contain striking local “star-like” topologies in which
a central column is linked to nearby columns of similar functional preference. The columns
within these networks are typically 200–300 µms in size (red circles) (Amir et al., 1993). A
few examples from the literature illustrate the ubiquity of these constructs; areas include vi-
sual (C.A), sensorimotor (D–E), parietal (F), and prefrontal (GRAMO) areas. In V1, injection of tracer
into an orientation column labels nearby columns of similar orientation preference, thereby
forming an orientation selective network (Figura 3A, arriba). Color blobs in V1 also form star-like
redes (Figura 3A, abajo). In V2, color, forma, and disparity columns lie within separate
functional streams but are linked via interstripe connections to form single multifeature net-
obras (Figura 3B). Similar networks are seen in temporal cortex (Figura 3C). In area 3b of
somatosensory cortex, columns subserving digits D1 to D5 are linked in interdigit networks
and are hypothesized to underlie sensory co-activation during power grasp (Figura 3D). Otro
star-like networks are observed in primary motor (Figure 3E), posterior parietal (Figura 3F), y
prefrontal (Figure 3G) areas.

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
3
7
7
9
1
0
9
2
4
4
9
norte
mi
norte
_
a
_
0
0
0
8
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

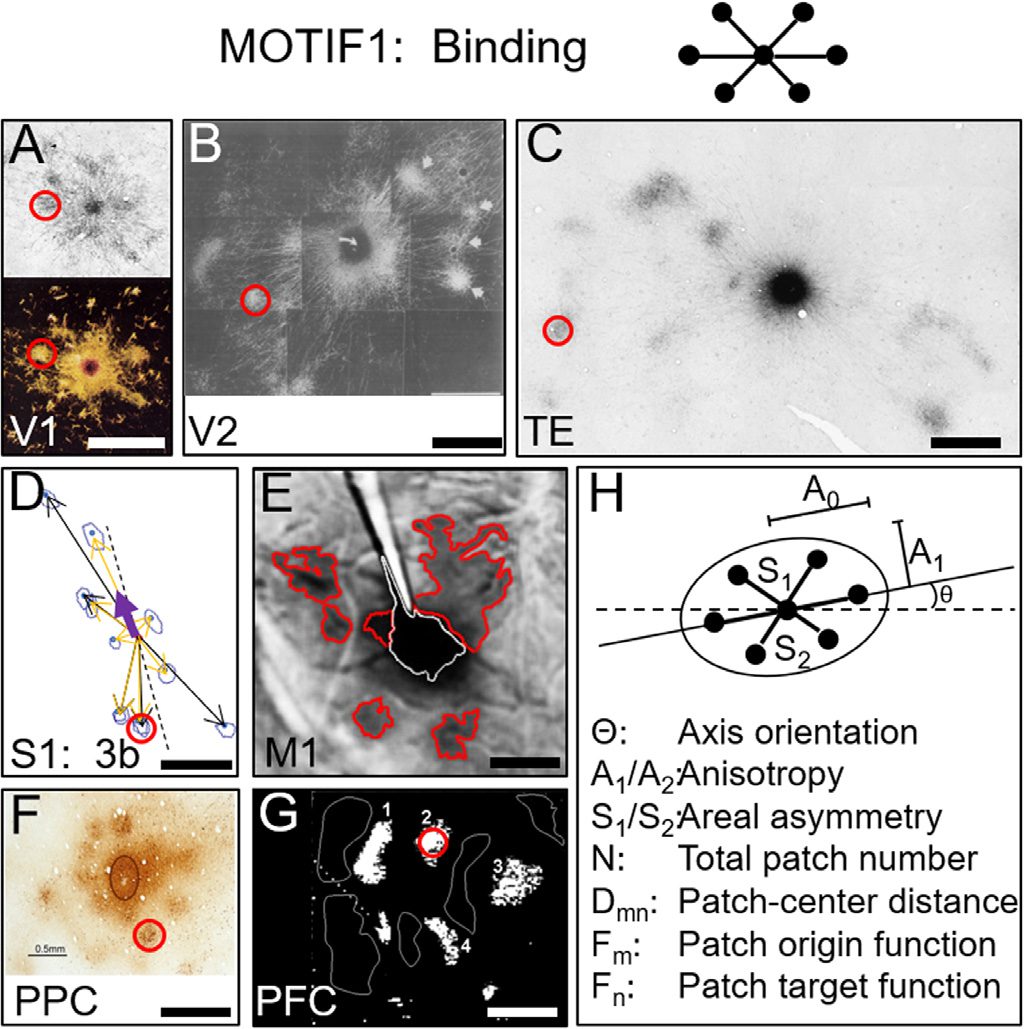
Cifra 3. Examples of Intra-areal connection motifs. Motif1: Intra-areal circuits serve binding func-
tion and display “star-like” pattern (cartoon at top). This is exempliﬁed by anatomical tract tracing.
Labeled patches are 200 µm in size (red circles). (A) V1, arriba: Sincich & Blasdel, 2001; abajo:
Livingstone & Hubel, 1984. (B) V2, Malach et al., 1993. (C) EL, inferotemporal; Tanigawa et al.,
2005. (D) S1; Pálﬁ et al., 2018, Wang y cols., 2013. (mi) M1, motor; Gharbawie et al., 2014. (F) PPC,
parietal; Stepniewska et al., 2016. (GRAMO) PFC, prefrontal; Sawaguchi, 1994. (h) Motif parameters.

Neurociencia en red

783

Columnar connectome: mathematics of brain function

Connectome:
A complete map of neural
connections in the brain, or its
“wiring diagram.”

In Motif1, the central node integrates inputs from a subset of surrounding nodes, thereby
performing a “binding” function. In some areas, nodes of similar functionality (p.ej., V1; Ts’o
et al., 1986) are linked, mientras, in others, nodes bind different modalities into a coherent
multimodal representation (p.ej., orientación, color, and disparity via interstripe connections in
V2; Levitt et al., 1994). Note that opposing networks of complementary function are similarly
“bound” via inhibitory relationships. Juntos, these interdigitated networks underlie push-pull
funciones (p.ej., white vs. outlined domains in Figure 3G; Cayce et al., 2014; Chernov et al.,
2018; cf. Sawaguchi, 1994; Weliky et al., 1995; Sato et al., 1996; Toth et al., 1996).

The speciﬁc characteristics of these networks (such as overall size, number of nodes, axis,
anisotropía; Figure 3H) may be tailored to the functional/computational purpose of each area
and may be inﬂuenced by more global factors, such as size of the cortical area or by the
number of other linked cortical areas. These possibilities remain to be explored and tested via
mesoscale connectome data.

Motif2: Inter-Areal Networks (Transformation)

This motif captures the anatomical connections underlying transformations from one cortical
area to another. It is well known that representation becomes increasingly abstract with cortical
hierarchy. Sin embargo, it is unknown whether the connections from one area to the next that
mediate functional transformations are in any way systematic or standard. En ese caso, one might be
able to systematize the transformations into functional classes, potentially reducing all cortico-
cortical projections into a small set of functions. In addition to providing a mathematical way
to represent the brain concisely, it would provide insight into the function of areas for which
there is as yet little understanding.

The idea that there are common functional transformations derives from studies in early
sensory cortical areas. Vision: From studies that simultaneously monitor responses of V2 and
V1 function to single “illusory” stimuli, we have shown that neurons in V2 domains respond to
the illusory aspect, whereas neurons in V1 respond to the “real” aspect (Roe, 2009, for review).
This “real-to-illusory” higher order transformation must be mediated by the anatomical connec-
tivity between V1 and V2. Específicamente, we observe establishment of modality-speciﬁc higher
order properties in different stripes of V2: (a) thin stripes: color representation in V1 blobs,
which is dominated by red-green/blue-yellow axes, transforms to a multicolor map of hue
columns in V2 (Conway, 2001; Xiao et al., 2003); (b) thin stripes: luminance encoding in V1
transforms to brightness encoding in V2 (Roe et al., 2005); (C) thick/pale stripes: encoding of
simple contour orientation transforms to higher order cue-invariant orientation representation
in V2 (Rasch et al., 2013); (d) thick stripes: simple motion direction detection transforms to
the detection of coherent motion in V2 (useful for ﬁgure-ground segregation, Peterhans and
von der Heydt) and to motion contrast deﬁned borders (Hu et al., 2018); y (mi) thick stripes:
segregated representation of left and right eyes in V1 to maps of near-to-far binocular disparity
columns in V2 (Chen et al., 2008, 2017). Touch: In a similar vein, in somatosensory cortex, en-
tegration of tactile pressure domains in area 3b (Friedman et al., 2004) are hypothesized to gen-
erate motion selectivity domains in area 1 (Pei et al., 2010; Wang y cols., 2013; Roe et al., 2017).
These modality-speciﬁc transformations could be achieved by integrating across multiple uni-
modal inputs in V1 and in S1.

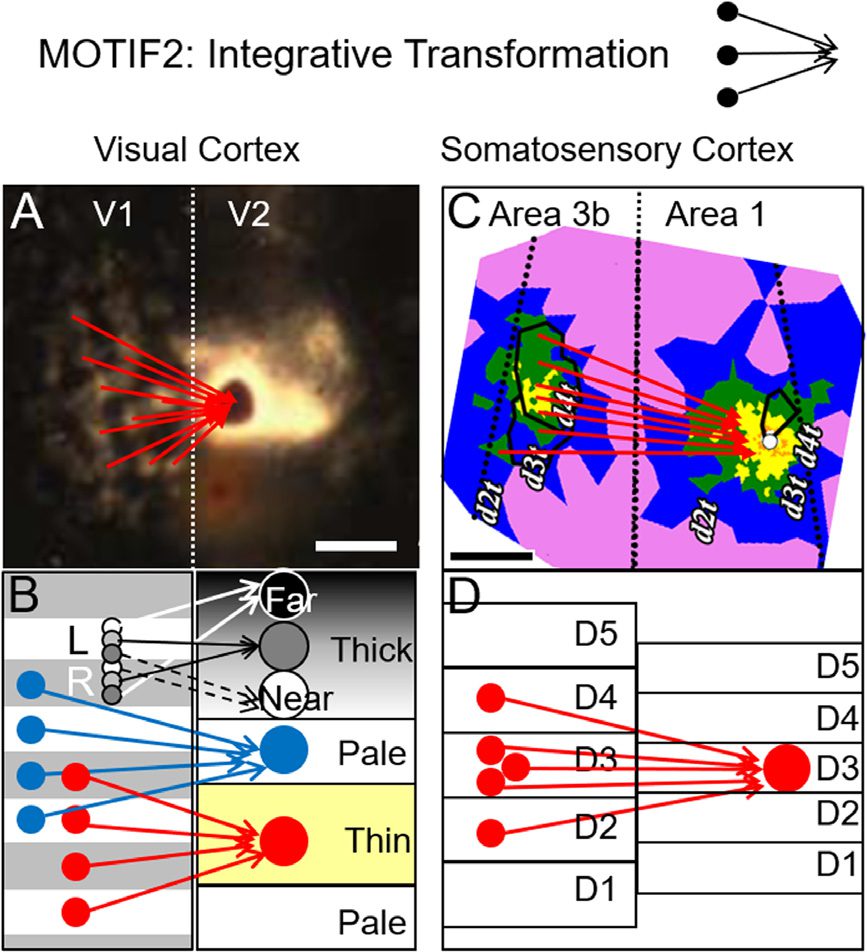
Extraordinariamente, common anatomical motifs underlie these functional computations. Injection
of tracer into V2 labels multiple columns in V1 (Cifra 4). These motifs are observed follow-
ing injections into thin stripes (Figura 4B, rojo), pale stripes (Figura 4B, azul), and thick stripes
(Figura 4B, grays). Similarmente, injection of tracer into a single digit location in area 1 labels

Neurociencia en red

784

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
3
7
7
9
1
0
9
2
4
4
9
norte
mi
norte
_
a
_
0
0
0
8
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Columnar connectome: mathematics of brain function

Cifra 4. Examples of Interareal connection motifs. Motif2: interareal circuits serve to transform
representation by integration of inputs from multiple columns. (A) Image of labeled blobs in V1
following injection of tracer in V2 (Sincich & Horton, 2005). Red arrows: interblob inputs from V1
converge onto a single pale stripe in V2. Vertical dotted line: V1/V2 border. (B) This motif is observed
de (rojo) V1 blobs to V2 thin stripes, (azul) V1 interblobs to V2 pale/thick stripes, y (grays) de
V1 ocular dominance columns to V2 thick stripes. (C, D) Red arrows: converging digit tip inputs
from Area 3b to Area 1 in somatosensory cortex (Wang y cols., 2013).

multiple (presumed) columns in area 3a (Figure 4C and 4D). Although it remains to be seen
whether such proposed transformations are also found in other sensory, motor, and cogni-
tive systems, identiﬁcation of such common motifs (along with characteristic integration size,
number, and functional type) would be important for generating an understanding of how the
anatomy of brain connections leads to and limits brain function.

SOME THOUGHTS ABOUT MATHEMATICAL FORMULATION

There is a very large gap between what is known about cortico-cortical connection patterns and
what we need to know to guide concepts about mappings in mathematical terms. Por último
we should like to know what are the organizational principles underlying cortical connec-
tion patterns. The work of investigators such as Obermayer and Blasdel (1993), Goodhill and
Cimponeriu (2000), Carreira-Perpiñán et al. (2005), Swindale (2004, 2007), and others have
beautifully demonstrated that the arrangement of multiple maps within an area arises largely
through maximizing parameters of continuity and coverage. Similar constraints need to be
identiﬁed and modelled for cortico-cortical connectivity. Progress on this front will be greatly
aided by availability of data on columnar connectivity. There are numerous efforts to char-
acterize connectomes by using mathematical topology (cf. despreciar, 2011). Sin embargo, mayor que
attention needs to be focused at the columnar scale.

Aquí, I propose one possible view of modelling cortical connections. Although represen-
tation of some parameters is continuous (p.ej., continuously shifting orientation preference), a
“binned” representation is valid from the view of functional organization; eso es, continuity

Neurociencia en red

785

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
3
7
7
9
1
0
9
2
4
4
9
norte
mi
norte
_
a
_
0
0
0
8
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Columnar connectome: mathematics of brain function

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
3
7
7
9
1
0
9
2
4
4
9
norte
mi
norte
_
a
_
0
0
0
8
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

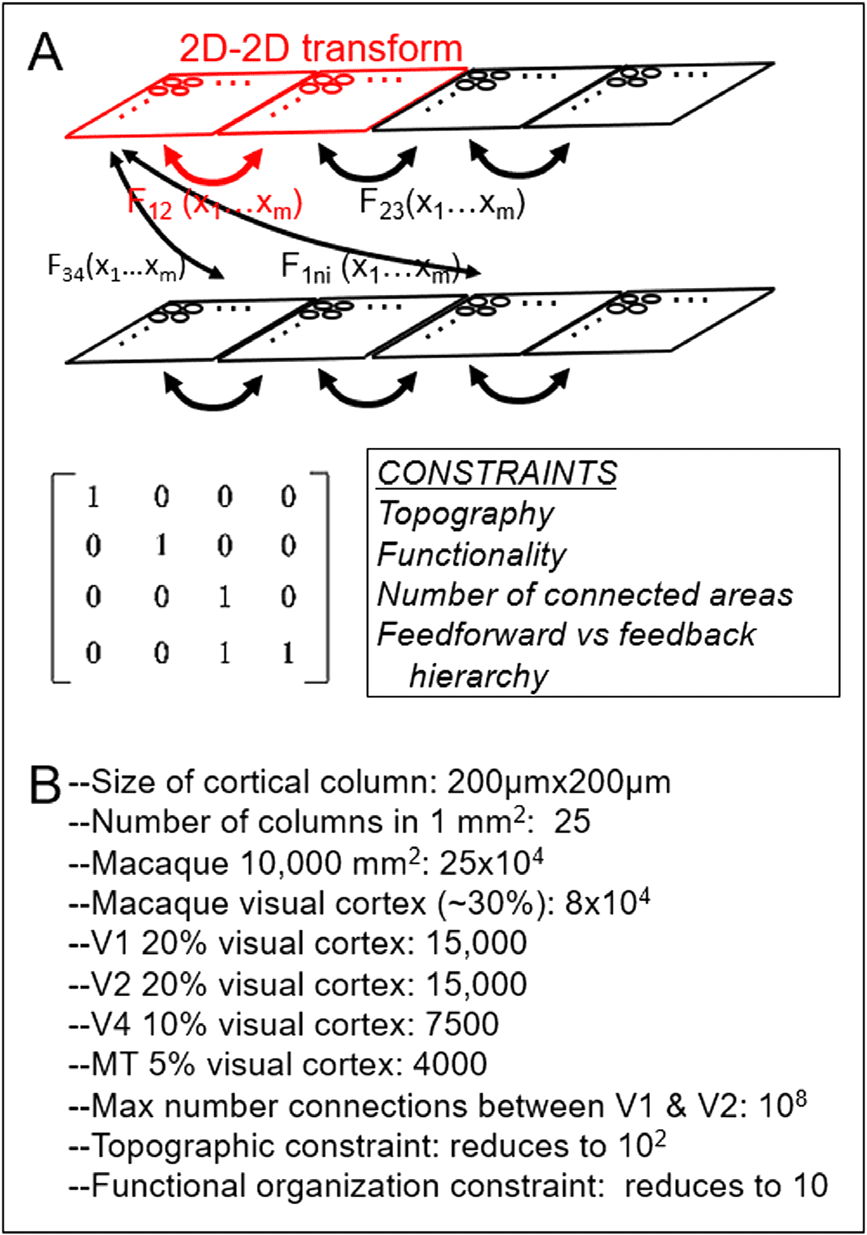
Cifra 5. Cifra 5. 2D-to-2D matrix representation of cortico-cortical mapping. (A) Each cortical
área (rectangle) is represented as a 2D array of columns (circles). Red outlined portion: mapping
between a single pair of areas. This 2D-2D mapping can be expressed as a matrix transformation
(abajo) with identiﬁed constraints such as topography and functional selectivity. The hope is that
one can reduce the mappings to a small number of motifs (Fij). (B) Some rough numbers used to
suggest that computation is manageable.

gets broken up into columnar representations by the constraint of mapping multiple parameters
within a single sheet (Obermayer & Blasdel, 1993; Swindale, 2004).

Matrix Mapping

If one views the cortical sheet as a 2D array of columns, then connections between cortical
areas can be viewed as 2D-to-2D mappings (Cifra 5, red outlined portion). El reto
to characterize connectional motifs may then be expressed as identifying generalized 2D-2D
matrix mappings that govern how two cortical areas connect (Figure 5A, Fij). For any pair of
areas, such mappings would be constrained by anatomical and functional constraints such as
continuity (topography) and functional speciﬁcity. One additional constraint to be considered
might include the number of areas with which a single area directly connects (typically this is a
small number). Once an anatomical scaffold is constructed, column-speciﬁc feedforward and
feedback modulation could be implemented to model circuit dynamics. From such treatment
of connectivity, general patterns of mappings (motifs) may emerge. Although the problem may,
at ﬁrst glance appear formidable, in my view, constraints of anatomical architecture dictate
that each cortical area maps only a few (p.ej., 3 a 4) key parameters in a continuous and
complete fashion. I make an argument below that this matrix representation may help reduce
the complexity.

Neurociencia en red

786

Columnar connectome: mathematics of brain function

Computational Feasibility

A few back-of-the-envelope estimates suggest that this mapping problem may be computa-
tionally manageable (Figure 5B). These estimates are based on published neuroanatomical
studies and inferred order-of-magnitude calculations. Usamos 200 µm as the dimension of a
2
cortical column in macaque monkey (size of orientation domains and blobs in V1); each mm
2
,
then contains 25 columnas. The macaque neocortex has an area of about 10,000–15,000 mm
roughly a third of which is visual cortex (cf. Van Essen et al., 1984; Purves & LaMantia, 1993;
Sincich et al., 2003). This means that there are on the order of 25 × 10
columns total and
acerca de (un tercio) 8 × 10
columns in visual cortex. [Nota: in humans, although visual cortex is
3 times as large, due to larger column size (roughly double), there are a comparable number
de columnas (Horton & Hedley-Whyte, 1984; Adams et al., 2007).] Out of this total of 80,000
columnas, V1, V2, and V4 occupy roughly 20%, 20%, y 10% of visual cortical area, o
15,000, 15,000, y 7,500 columnas, respectivamente (Weller et al., 1983; Sincich et al., 2003).
This is likely an underestimate as it assumes square columnar packing.

If all columns in V1 mapped to all columns in V2, the number of single node-to-single node
(15,000 × 15,000) (Figure 5B). From neuroanatom-
connections would be on the order of 10
ical studies, we estimate that a single node in V1 connects to on the order of 10 nodes in V2
(Livingstone & Hubel, 1984; Federer et al., 2013; Sincich et al., 2010). This small number is
due to (a) constraints of topography: a single point in visual space takes up roughly 2 mm of
cortical space (Hubel & Wiesel, 1977), o 4 × 25 = 100 columnas (10
); y (b) constraints
of functional speciﬁcity (Cifra 4), which further reduces this number by a ﬁfth or a tenth the
number of nodes from a single topographic point. Como ejemplo, if a full 180
cycle of orien-
tations is represented in 1-mm distance (Hubel & Wiesel, 1977) o 5 (200 µm-sized) columnas,
area there may be 5 out of 25 columns that represent a single orien-
then within a 1-mm
tation. This reduces the total number of target nodes from 100 to 10–20 or on the order of
10. This potentially reduces a problem that is on the order of 10
a 10. Such a 1:10 conver-
gence/divergence could underlie a basic architectural motif of interareal connectivity, o un
“interareal connectional hypercolumn.”

◦

Such connectional hypercolumns may be replicated at a higher level, albeit with distinct
convergence/divergence ratios and functional constraints. Por ejemplo, from V2 to V4, el
number of connections decreases (15,000 × 7,500, o 10
), producing a correspondingly
smaller cortical area (V4 is roughly half the size of V2). An area such as MT, which is only
5% the size of V1, is likely to have a greater convergence/divergence ratio from V1 to MT; este
would be consistent with the large receptive ﬁeld sizes and comparatively spatially broad inte-
grations for computation of motion direction. De este modo, interareal connectivity would be speciﬁed
by parameters such as unique topographical constraints, convergence/divergence ratios, y
functional selectivities. This set of relationships would be represented as a set of connectional
hypercolumns: F1 (x1…xm) …Fn(x1…xm). Solving how multiple connectional hypercolumns
mutually constrain the entire set of mappings will lead to a representation of total cortical
connectivity in a brain.

Columnar Organization Constrains the Global Network

Hasta ahora, topological treatment of brain networks has been based on parameters such as connec-
tion number, connectional distance, routing efﬁciency (p.ej., Joven, 1993; Avena-Koenigsberger
et al., 2019; Chaudhuri et al., 2015). These approaches have provided important advances in
our understanding of brain networks and information ﬂow at an areal level (typically with each

Neurociencia en red

787

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
3
7
7
9
1
0
9
2
4
4
9
norte
mi
norte
_
a
_
0
0
0
8
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Columnar connectome: mathematics of brain function

cortical area treated as a single node). Sin embargo, what is lacking is the concept of spatial loca-
tion within each area. Eso es, the X,Y coordinate in the matrix deﬁnes a node’s topographical
location and its functionality. Each node’s position is not independent of another nodes posi-
ción; neighbors constrain neighbors, and this impacts the organization of the global network.
Studies that address issues of multiscale constraints (p.ej., Jeub et al., 2018) could incorporate
such spatial information to further specify the resulting architecture.

CONCLUSIÓN

To summarize, I have described a column-based view of the cerebral cortex and presented a
new methodology (INS-fMRI) to map column-based networks in vivo. I suggest that acquisition
of such large-scale connectivity data may demand new ways of representing cortical networks
(p.ej., 2D-2D matrix transformations). From such data, patterns or motifs of cortical connectivity
may emerge, and give rise to basic connectivity units termed connectional hypercolumns.

My goal in this viewpoint is to encourage the connectomics ﬁeld to capture columnar con-
conectividad. New representations and mathematics need to be developed for multidimensional
treatment of nodes, one that incorporates the spatial and functional relationships between
neighboring nodes. Such representations may simplify the apparently complex connectional
relationships in the global network. Although we do not yet have enough columnar data to do
this on a large scale, one could start by using available data to generate prototype solutions.
I list a few questions here to motivate future studies. For a given cortical area, how does the
number of directly connected areas affect motif architecture? How do the number of total areas
affect the total possible mappings? Is there a general solution to the mappings of smaller brains
with fewer cortical areas versus larger brains with many? What aspects of cortical architecture
produce and simultaneously constrain our behavioral repertoire? Can one design mappings to
generate alternative artiﬁcial intelligences?

Por último, I envision a general connectional theory of brain function, complete with a
system of theorems, derivations, and corollaries (Sporns et al., 2000; despreciar, 2011). Such a
rule-based representation will lead to new understandings of brain construction and brain
evolution, and will inform our understanding of biological intelligence as well as bio-inspired
artiﬁcial intelligence.

EXPRESIONES DE GRATITUD

Thanks to Charles Gilbert and Akshay Edathodathil for useful discussions.

INFORMACIÓN DE FINANCIACIÓN

Anna Wang Roe, National Natural Science Foundation of China (http://dx.doi.org/10.13039/
501100001809), Award ID: 81430010. Anna Wang Roe, National Natural Science Foundation
of China (http://dx.doi.org/10.13039/501100001809), Award ID: 31627802. Anna Wang Roe,
National Hi-Tech Research and Development Program Grant, Award ID: 2015AA020515.

REFERENCIAS

Adams, D. l., Sincich, l. C., & Horton, j. C. (2007). Complete pat-
tern of ocular dominance columns in human primary visual cor-
tex. Revista de neurociencia, 27(39), 10391–10403. https://doi.
org/10.1523/JNEUROSCI.2923-07.2007

amir, y., Harel, METRO., & Malach, R. (1993). Cortical hierarchy re-
ﬂected in the organization of intrinsic connections in macaque

monkey visual cortex. Journal of Comparative Neurology, 334(1),
19–46. https://doi.org/10.1002/cne.903340103

Avena-Koenigsberger, A., yan, X., Kolchinsky, A., van den heuvel,
METRO. PAG., Hagmann, PAG., & despreciar, oh. (2019). A spectrum of routing
strategies for brain networks. Biología Computacional PLoS, 15(3),
e1006833. https://doi.org/10.1371/journal.pcbi.1006833

Neurociencia en red

788

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
3
7
7
9
1
0
9
2
4
4
9
norte
mi
norte
_
a
_
0
0
0
8
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Columnar connectome: mathematics of brain function

Berkowitz, J., & Sharpee, t. (2018). Decoding neural responses
with minimal information loss. BioRxiv. https://doi.org/10.1101/
273854

Blasdel, GRAMO. GRAMO. (1992). Orientation selectivity, preference, y estafa-
tinuity in monkey striate cortex. Revista de neurociencia, 12(8),
3139–3161.

Blasdel, GRAMO. GRAMO., & Salama, GRAMO. (1986). Voltage-sensitive dyes reveal
a modular organization in monkey striate cortex. Naturaleza,
321(6070), 579–85. https://doi.org/10.1038/321579a0

Carreira-Perpiñán, METRO. A., Lister, R. J., & Goodhill, GRAMO. j. (2005). A
computational model for the development of multiple maps in
primary visual cortex. Corteza cerebral, 15(8), 1222–1233. https://
doi.org/10.1093/cercor/bhi004

Cayce, j. METRO., Friedman, R. METRO., Chen, GRAMO., Jansen, mi. D., Mahadevan-
Jansen, A., & Roe, A. W.. (2014). Infrared neural stimulation of
primary visual cortex in non-human primates. Neuroimagen, 84,
181–190. https://doi.org/10.1016/j.neuroimage.2013.08.040
Chaudhuri, r., Knoblauch, K., Gariel, M.-A., Kennedy, h., &
Wang, X.-J.
(2015). A large-scale circuit mechanism for
hierarchical dynamical processing in the primate cortex. nuevo-
ron, 88(2), 419–431. https://doi.org/10.1016/j.neuron.2015.09.
008

Chen, GRAMO., Lu, h. D., & Roe, A. W.. (2008). A map for horizontal
disparity in monkey v2. Neurona, 58(3), 442–450. https://doi.org/
10.1016/j.neuron.2008.02.032

Chen, GRAMO., Lu, h. D., Tanigawa, h., & Roe, A. W.. (2017). Solv-
ing visual correspondence between the two eyes via domain-
based population encoding in nonhuman primates. Actas
of the National Academy of Sciences of the United States of
America, 114(49), 13024–13029. https://doi.org/10.1073/pnas.
1614452114

cheng, k. (2012). Revealing human ocular dominance columns
using high-resolution functional magnetic resonance imag-
En g. Neuroimagen, 62(2), 1029–1034. https://doi.org/10.1016/j.
neuroimage.2011.08.086

Chernov, METRO., & Roe, A. W.. (2014). Infrared neural stimulation: A
new stimulation tool for central nervous system applications.
Neurophotonics, 1(1), 011011. https://doi.org/10.1117/1.NPh.1.
1.011011

Chernov, METRO. METRO., Friedman, R. METRO., Chen, GRAMO., Stoner, GRAMO. r., & Roe,
A. W.. (2018). Functionally speciﬁc optogenetic modulation in
primate visual cortex. Actas de la Academia Nacional de
Ciencias de los Estados Unidos de América, 115(41), 10505–10510.
https://doi.org/10.1073/pnas.1802018115

Chernov, METRO. METRO., Chen, GRAMO., & Roe, A. W.. (2014). Histological as-
sessment of thermal damage in the brain following infrared neu-
ral stimulation. Brain Stimulation, 7(3), 476–482. https://doi.org/
10.1016/j.brs.2014.01.006

Conway, B. R. (2001). Spatial structure of cone inputs to color cells
in alert macaque primary visual cortex (V-1). Journal of Neuro-
ciencia, 21(8), 2768–2783.

da Costa, norte. METRO., & Martín, k. A. C. (2010). Whose cortical column
would that be? Frontiers in Neuroanatomy, 4, 16. https://doi.org/
10.3389/fnana.2010.00016

DeFelipe, J., Conley, METRO., & jones, mi. GRAMO. (1986). Long-range focal
collateralization of axons arising from corticocortical cells in

monkey sensory-motor cortex. Revista de neurociencia, 6(12),
3749–3766.

Fang, y., Chen, METRO., Xu, h., li, PAG., Han, C., Hu, J., . . . Lu, h. D.
(2019). An orientation map for disparity-deﬁned edges in area v4.
Corteza cerebral, 29(2), 666–679. https://doi.org/10.1093/cercor/
bhx348

Federer, F., williams, D., Ichida, j. METRO., Merlin, S., & Angelucci, A.
(2013). Two projection streams from macaque v1 to the pale
Revista de neurociencia,
cytochrome oxidase stripes of v2.
33(28), 11530–11539. https://doi.org/10.1523/JNEUROSCI.5053-
12.2013

Friedman, R. METRO., Chen, l. METRO., & Roe, A. W.. (2004). Modality
maps within primate somatosensory cortex. Actas de la
National Academy of Sciences of the United States of America,
101(34),12724–12729. https://doi.org/10.1073/pnas.0404884101
Gerits, A., Farivar, r., rosa, B. r., Wald, l. l., Boyden, mi. S.,
& Vanduffel, W.. (2012). Optogenetically induced behavioral
and functional network changes in primates. Biología actual:
CB, 22(18), 1722–1726. https://doi.org/10.1016/j.cub.2012.07.
023

Gharbawie, o., Friedman, R. METRO., & Roe, A. W.. (2014). Localization
of grasp domains in frontal and parietal cortex with intrinsic op-
tical imaging in behaving monkeys. Washington, corriente continua: Society of
Neurociencia.

Gong, h., Xu, D., Yuan, J., li, X., guo, C., Peng, J., . . . luo, q.
(2016). High-throughput dual-colour precision imaging for
brain-wide connectome with cytoarchitectonic landmarks at the
cellular level. Comunicaciones de la naturaleza, 7, 12142. https://doi.org/
10.1038/ncomms12142

Goodhill, GRAMO. J., & Cimponeriu, A. (2000). Analysis of the elastic net
model applied to the formation of ocular dominance and orien-
tation columns. Red (Bristol, Inglaterra), 11(2), 153–168.
Grinvald, A., Lieke, MI., Frostig, R. D., Gilbert, C. D., & Wiesel,
t. norte. (1986). Functional architecture of cortex revealed by op-
tical imaging of intrinsic signals. Naturaleza, 324(6095), 361–364.
https://doi.org/10.1038/324361a0

Horton, j. C., & Hedley-Whyte, mi. t. (1984). Mapping of cytochrome
oxidase patches and ocular dominance columns in human vi-
sual cortex. Philosophical Transactions of the Royal Society
of London. Serie B, Ciencias Biologicas, 304(1119), 255–272.
https://doi.org/10.1098/rstb.1984.0022

Horton, Jonathan C., & Adams, D. l. (2005). The cortical column:
A structure without a function. Philosophical, Transactions of
the Royal Society of London. Serie B, Ciencias Biologicas, 360,
837–862. https://doi.org/10.1098/rstb.2005.1623

Hu, J., Mamá, h., Zhu, S., li, PAG., Xu, h., Fang, y., Chen, METRO., Han, C.,
Fang, C., Cai, X., yan, K., & Lu, h. D. (2018). Visual Motion Pro-
cessng in Macaque V2. Cell Rep., 25(1), 157–167.e5. https://doi.
org/10.1016/j.celrep.2018.09.014

Hubel, D. h., & Wiesel, t. norte. (1977). Ferrier lecture. Funcional
architecture of macaque monkey visual cortex. Actas
of the Royal Society of London. Serie B, Ciencias Biologicas,
198(1130), 1–59. https://doi.org/10.1098/rspb.1977.0085

Jeub, l. GRAMO. S., despreciar, o., & Fortunato, S. (2018). Multiresolution
consensus clustering in networks. Scientiﬁc Reports, 8(1). https://
doi.org/10.1038/s41598-018-21352-7

Neurociencia en red

789

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
3
7
7
9
1
0
9
2
4
4
9
norte
mi
norte
_
a
_
0
0
0
8
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Columnar connectome: mathematics of brain function

Katzner, S., Nauhaus, I., Benucci, A., Bonin, v., Ringach, D. l., &
Carandini, METRO. (2009). Local origin of ﬁeld potentials in visual
corteza. Neurona, 61(1), 35–41. https://doi.org/10.1016/j.neuron.
2008.11.016

Kritzer, METRO. F., & Goldman-Rakic, PAG. S. (1995). Intrinsic circuit
organization of the major layers and sublayers of the dorsolat-
eral prefrontal cortex in the rhesus monkey. Journal of Compar-
ative Neurology, 359(1), 131–143. https://doi.org/10.1002/cne.
903590109

Kusunoki, METRO., Moutoussis, K., & Zeki, S. (2006). Effect of back-
ground colors on the tuning of color-selective cells in monkey
area v4. Revista de neurofisiología, 95(5), 3047–3059. https://
doi.org/10.1152/jn.00597.2005

Levitt, j. B., Yoshioka, T., & Lund, j. S. (1994). Intrinsic cortical con-
nections in macaque visual area v2: Evidence for interaction be-
tween different functional streams. Journal of Comparative Neurology,
342(4), 551–570. https://doi.org/10.1002/cne.903420405

li, X., Zhu, P., Janssens, T., Arsenault, j. T., & Vanduffel, W.. (2019).
In vivo identiﬁcation of thick, thin, and pale stripes of macaque
area v2 using submillimeter resolution (F)MRI at 3 t. Cerebral
Corteza, 29(2), 544–560. https://doi.org/10.1093/cercor/bhx337
li, y., Lu, h., cheng, PAG., Ge, S., Xu, h., Shi, S.-H., & Dan, Y. (2012).
Clonally related visual cortical neurons show similar stimulus
feature selectivity. Naturaleza, 486(7401), 118–121. https://doi.org/
10.1038/nature11110

Livingstone, METRO. S., & Hubel, D. h. (1984). Anatomy and physiology
of a color system in the primate visual cortex. Journal of Neuro-
ciencia, 4(1), 309–356.

Lund, j. S., Yoshioka, T., & Levitt, j. B. (1993). Comparison of intrin-
sic connectivity in different areas of macaque monkey cerebral
corteza. Corteza cerebral, 3(2), 148–162.

Malach, r., amir, y., Harel, METRO., & Grinvald, A. (1993). Relation-
ship between intrinsic connections and functional architecture
revealed by optical imaging and in vivo targeted biocytin in-
jections in primate striate cortex. Actas del Nacional
Academy of Sciences of the United States of America, 90(22),
10469–10473. https://doi.org/10.1073/pnas.90.22.10469

Mountcastle, V. B. (1997). The columnar organization of the neo-
corteza. Cerebro: A Journal of Neurology, 120(punto. 4), 701–722.
Nasr, S., Polimeni, j. r., & Tootell, R. B. h. (2016). Interdigitated
color- and disparity-selective columns within human visual corti-
cal areas v2 and v3. Revista de neurociencia, 36(6), 1841–1857.
https://doi.org/10.1523/JNEUROSCI.3518-15.2016

Obermayer, K., & Blasdel, GRAMO. GRAMO. (1993). Geometry of orientation
and ocular dominance columns in monkey striate cortex. Diario
of Neuroscience, 13(10), 4114–4129.

Pálﬁ, MI., Zalányi, l., Ashaber, METRO., Palmer, C., Kántor, o., Roe,
A. w., . . . Négyessy, l. (2018). Connectivity of neuronal popula-
tions within and between areas of primate somatosensory cortex.
Brain Structure & Function, 223(6), 2949–2971. https://doi.org/
10.1007/s00429-018-1671-8

Pei, Y.-C., Hsiao, S. S., Craig, j. C., & Bensmaia, S. j. (2010). Shape
invariant coding of motion direction in somatosensory cortex.
Biología PLoS, 8(2), e1000305. https://doi.org/10.1371/journal.
pbio.1000305

Rakic, PAG. (1988). Speciﬁcation of cerebral cortical areas. Ciencia,

241(4862), 170–176.

Rakic, Pasko (2008). Confusing cortical columns. Actas de
the National Academy of Sciences of the United States of
America, 105(34), 12099–12100. https://doi.org/10.1073/pnas.
0807271105

Rasch, METRO. J., Chen, METRO., Wu, S., Lu, h. D., & Roe, A. W.. (2013).
Quantitative inference of population response properties across
eccentricity from motion-induced maps in macaque v1. Jour-
nal of Neurophysiology, 109(5), 1233–1249. https://doi.org/10.
1152/jn.00673.2012

Rockland, k. S. (2010). Five points on columns. Frontiers in Neu-
roanatomy, 4, 22. https://doi.org/10.3389/fnana.2010.00022
Roe, A. w., Chelazzi, l., Connor, C. MI., Conway, B. r., Fujita, I.,
Gallant, j. l., . . . Vanduffel, W.. (2012). Toward a uniﬁed theory
of visual area v4. Neurona, 74(1), 12–29. https://doi.org/10.1016/
j.neuron.2012.03.011

Roe, A. w., Chen, GRAMO., & Lu, h. D.

(2009). Visual System:
Functional architecture of Area V2. En: Squire L. R. (ed.) Encyclo-
pedia of Neuroscience, volumen. 10, páginas. 331–349. Oxford: Académico
Prensa

Roe, A. w., Lu, h. D., & Hung, C. PAG. (2005). Cortical processing
of a brightness illusion. Actas de la Academia Nacional de
Ciencias de los Estados Unidos de América, 102(10), 3869–3874.
https://doi.org/10.1073/pnas.0500097102

Roe, A. w., Winberry, j. MI., & Friedman, R. METRO. (2017). Study of
single and multidigit activation in monkey somatosensory cor-
tex using voltage-sensitive dye imaging. Neurophotonics, 4(3),
031219. https://doi.org/10.1117/1.NPh.4.3.031219

Rust, norte. C., & Dicarlo, j. j. (2010). Selectivity and tolerance (“in-
variance”) both increase as visual information propagates from cor-
tical area v4 to IT. Revista de neurociencia, 30(39), 12978–12995.
https://doi.org/10.1523/JNEUROSCI.0179-10.2010

Sato, h., Katsuyama, NORTE., Tamura, h., Hata, y., & Tsumoto, t. (1996).
Mechanisms underlying orientation selectivity of neurons in the
primary visual cortex of the macaque. Revista de fisiología,
494(punto. 3), 757–771.

Sawaguchi, t.

(1994). Modular activation and suppression of
neocortical activity in the monkey revealed by optical imaging.
NeuroReport, 6(1), 185–189.

Schwalger, T., Deger, METRO., & Gerstner, W.. (2017). Towards a the-
ory of cortical columns: From spiking neurons to interacting neu-
ral populations of ﬁnite size. Biología Computacional PLoS, 13(4),
e1005507. https://doi.org/10.1371/journal.pcbi.1005507

Sharpee, t. o., Kouh, METRO., & Reynolds, j. h. (2013). Trade-off be-
tween curvature tuning and position invariance in visual area
v4. Proceedings of the National Academy of Sciences of the
United States of America, 110(28), 11618–11623. https://doi.
org/10.1073/pnas.1217479110

Shiozaki, h. METRO., Tanabe, S., Doi, T., & Fujita, I. (2012). Neural ac-
tivity in cortical area v4 underlies ﬁne disparity discrimination.
Revista de neurociencia, 32(11), 3830–3841. https://doi.org/10.
1523/JNEUROSCI.5083-11.2012

Purves, D., & LaMantia, A. (1993). Development of blobs in the
visual cortex of macaques. Journal of Comparative Neurology,
334(2), 169–175. https://doi.org/10.1002/cne.903340202

Shmuel, A., Korman, METRO., Sterkin, A., Harel, METRO., Ullman, S., Malach,
r., & Grinvald, A. (2005). Retinotopic axis speciﬁcity and selec-
tive clustering of feedback projections from v2 to v1 in the owl

Neurociencia en red

790

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
3
7
7
9
1
0
9
2
4
4
9
norte
mi
norte
_
a
_
0
0
0
8
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Columnar connectome: mathematics of brain function

monkey. Revista de neurociencia, 25(8), 2117–2131. https://doi.
org/10.1523/JNEUROSCI.4137-04.2005

Sincich, l. C., & Blasdel, GRAMO. GRAMO. (2001). Oriented axon projections
in primary visual cortex of the monkey. Revista de neurociencia,
21(12), 4416–4426.

Sincich, Lawrence C., Adams, D. l., & Horton, j. C. (2003). Com-
plete ﬂatmounting of the macaque cerebral cortex. Visual Neuro-
ciencia, 20(6), 663–686.

Sincich, Lawrence C., & Horton, j. C. (2005). Input to v2 thin
stripes arises from v1 cytochrome oxidase patches. Diario de
Neurociencia, 25(44), 10087–10093. https://doi.org/10.1523/
JNEUROSCI.3313-05.2005

Sincich, Lawrence C., Jocson, C. METRO., & Horton, j. C.

(2010). V1
interpatch projections to v2 thick stripes and pale stripes. Jour-
nal of Neuroscience, 30(20), 6963–74. https://doi.org/10.1523/
JNEUROSCI.5506-09.2010

despreciar, oh. (2011). Networks of the Brain. Cambridge, MAMÁ: CON prensa.
despreciar, o., Tononi, GRAMO., & Edelman, GRAMO. METRO. (2000). Theoretical neuro-
anatomy: Relating anatomical and functional connectivity in graphs
and cortical connectionmatrices. Corteza cerebral, 10(2), 127–141.
Stepniewska, I., Cerkevich, C. METRO., & Aquél, j. h. (2016). Cortical
connections of the caudal portion of posterior parietal cortex in
prosimian galagos. Corteza cerebral, 26(6), 2753–2777. https://
doi.org/10.1093/cercor/bhv132

Swindale, norte. V. (2004). How different feature spaces may be rep-

resented in cortical maps. Red, 15(4), 217–242.

Swindale, norte. V. (2007). A model for the thick, thin and pale stripe

organization of primate v2. Red, 18(4), 327–342.

Tanigawa, h., Wang, P., & Fujita,

(2005). Organization of
horizontal axons in the inferior temporal cortex and primary vi-
sual cortex of the macaque monkey. Corteza cerebral, 15(12),
1887–1899. https://doi.org/10.1093/cercor/bhi067

Tolias, A. S., Sultan, F., Augath, METRO., Oeltermann, A., Tehovnik,
mi. J., Schiller, PAG. h., & Logothetis, norte. k. (2005). Mapping corti-
cal activity elicited with electrical microstimulation using fMRI in
the macaque. Neurona, 48(6), 901–911. https://doi.org/10.1016/
j.neuron.2005.11.034

Tootell, R. B., Silverman, METRO. S., hamilton, S. l., De Valois, R. l., &
Switkes, mi. (1988). Functional anatomy of macaque striate cortex.
III. Color. Revista de neurociencia, 8(5), 1569–1593.

Torii, METRO., Hashimoto-Torii, K., Levitt, PAG., & Rakic, PAG. (2009). Integra-
tion of neuronal clones in the radial cortical columns by EphA
and ephrin-A signalling. Naturaleza, 461(7263), 524–528. https://
doi.org/10.1038/nature08362

Toth, l. J., Rao, S. C., kim, D. S., Somers, D., & Sur, METRO. (1996). Sub-
threshold facilitation and suppression in primary visual cortex

revealed by intrinsic signal imaging. Actas del Nacional
Academy of Sciences of the United States of America, 93(18),
9869–9874. https://doi.org/10.1073/pnas.93.18.9869

Ts’o, D. y., Gilbert, C. D., & Wiesel, t. norte. (1986). Relationships be-
tween horizontal interactions and functional architecture in cat
striate cortex as revealed by cross-correlation analysis. Diario de
Neurociencia, 6(4), 1160–1170.

Ts’o, D. y., Zarella, METRO., & Burkitt, GRAMO. (2009). Whither the hypercol-
umn? Revista de fisiología, 587(punto 12), 2791–2805. https://doi.
org/10.1113/jphysiol.2009.171082

VanEssen, D. C., nuevosome, W.. T., & Maunsell, j. h. (1984). El
visual ﬁeld representation in striate cortex of the macaque mon-
key: Asymmetries, anisotropies, and individual variability. Vision
Investigación, 24(5), 429–448.

Wang, Z., Chen, l. METRO., Négyessy, l., Friedman, R. METRO., Mishra, A.,
Sangre, j. C., & Roe, A. W.. (2013). The relationship of anatomical
and functional connectivity to resting-state connectivity in pri-
mate somatosensory cortex. Neurona, 78(6), 1116–1126. https://
doi.org/10.1016/j.neuron.2013.04.023

Weliky, METRO., Kandler, K., Fitzpatrick, D., & katz, l. C. (1995). Pat-
terns of excitation and inhibition evoked by horizontal connec-
tions in visual cortex share a common relationship to orientation
columnas. Neurona, 15(3), 541–552.

Weller, R. MI., & Aquél, j. h. (1983). Retinotopic patterns of con-
nections of area 17 with visual areas V-II and MT in macaque
monkeys. Journal of Comparative Neurology, 220(3), 253–279.
https://doi.org/10.1002/cne.902200302

Wells, J., Kao, C., Mariappan, K., Albea, J., Jansen, mi. D., Konrad,
PAG., & Mahadevan-Jansen, A. (2005). Optical stimulation of neural
tissue in vivo. Optics Letters, 30(5), 504–506.

xiao, y., Wang, y., & Felleman, D. j. (2003). A spatially organized
representation of colour in macaque cortical area v2. Naturaleza,
421(6922), 535–539. https://doi.org/10.1038/nature01372

Xu, A. GRAMO., Qian, METRO., tian, F., Xu, B., Friedman, R. METRO., Wang,
j. B., Song, X., Sol, y., Chernov, METRO. METRO., Cayce, j. METRO., Jansen,
mi. D., Mahadevan-Jansen, A., zhang, X. T., Chen, GRAMO., & Roe,
A. W.. (2019a). Focal infrared neural stimulation with high-ﬁeld
resonancia magnética funcional: A rapid way to map mesoscale brain con-
nectomes. Science Advances, 5(4):eaau7046. https://doi.org/10.
1126/sciadv.aau7046

Xu, A. GRAMO., Rui, Y. y., Wang, j. B., Song, X. METRO., Gothard, K., & Roe,
A. W.. (2019b). INS-fMRI reveals functional connections of amyg-
dalar subnuclei in the Macaque monkey. SPIE Photonics West.
San Francisco, California.

Joven, METRO. PAG. (1993). The organization of neural systems in the pri-
mate cerebral cortex. Actas. Ciencias Biologicas, 252(1333),
13–18. https://doi.org/10.1098/rspb.1993.0040

Neurociencia en red

791

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/