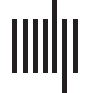INVESTIGACIÓN
High-resolution data-driven model
of the mouse connectome
José E.. Knox1,2, Kameron Decker Harris
Hongkui Zeng
1, Julie A. Harris1, Eric Shea-Brown 1,2, and Stefan Mihalas
2,3, Nile Graddis1, Jennifer D. Whitesell
1,2
1,
1Allen Institute for Brain Science, seattle, Washington, EE.UU
2Applied Mathematics, University of Washington, seattle, Washington, EE.UU
3Computer Science and Engineering, University of Washington, seattle, Washington, EE.UU
Palabras clave: Connectome, Whole-brain, Mouse
un acceso abierto
diario
ABSTRACTO
Knowledge of mesoscopic brain connectivity is important for understanding inter- y
intraregion information processing. Models of structural connectivity are typically
constructed and analyzed with the assumption that regions are homogeneous. We instead
use the Allen Mouse Brain Connectivity Atlas to construct a model of whole-brain
connectivity at the scale of 100 µm voxels. The data consist of 428 anterograde tracing
experiments in wild type C57BL/6J mice, mapping fluorescently labeled neuronal
projections brain-wide. Inferring spatial connectivity with this dataset is underdetermined,
since the approximately 2 × 105 source voxels outnumber the number of experiments.
To address this issue, we assume that connection patterns and strengths vary smoothly
across major brain divisions. We model the connectivity at each voxel as a radial basis
kernel-weighted average of the projection patterns of nearby injections. The voxel model
outperforms a previous regional model in predicting held-out experiments and compared
with a human-curated dataset. This voxel-scale model of the mouse connectome permits
researchers to extend their previous analyses of structural connectivity to much higher
levels of resolution, and it allows for comparison with functional imaging and other datasets.
RESUMEN DEL AUTOR
Anatomical tracing experiments can provide a wealth of information regarding connectivities
originating from the injection sites. Sin embargo, it is difficult to integrate all this information
into a comprehensive connectivity model. In this study we construct a high-resolution model
of the mouse brain connectome using the assumption that connectivity patterns vary
smoothly within brain regions, and we present several extensions of this model. Creemos
that this higher resolution connectome will be of great use to the community, habilitando
comparisons with other data modalities, such as functional imaging and gene expression,
as well as for theoretical studies.
INTRODUCCIÓN
Brain network structure, across many spatial scales, plays an important role in facilitating and
constraining neural computations. Models of structural connectivity have been used to inves-
tigate the relationship with functional connectivity, to compare brain structures across species,
y más (Laramée & Boire, 2015; Sethi, Zerbi, Wenderoth, Proporcionó, & Fulcher, 2017; Stafford
et al., 2014; X.-J. Wang & Kennedy, 2016). Sin embargo, most of our knowledge of neuronal
network connectivity is limited to either a detailed description of small systems (Bock et al.,
Citación: Knox, j. MI., harris, k. D.,
Graddis, NORTE., Whitesell, j. D., Zeng, h.,
harris, j. A., Shea-Brown, MI., &
Mihalas, S. (2019). High-resolution
data-driven model of the mouse
conectoma. Neurociencia en red,
3(1), 217–236. https://doi.org/
10.1162/netn_a_00066
DOI:
https://doi.org/10.1162/netn_a_00066
Supporting Information:
https://doi.org/10.1162/netn_a_00066
https://github.com/AllenInstitute/
mouse_connectivity_models
Recibió: 4 Abril 2018
Aceptado: 31 Julio 2018
Conflicto de intereses: Los autores tienen
declaró que no hay intereses en competencia
existir.
Autores correspondientes:
Kameron Decker Harris
kamdh@uw.edu
Stefan Mihalas
stefanm@alleninstitute.org
Editor de manejo:
Marcus Kaiser
Derechos de autor: © 2018
Instituto de Tecnología de Massachusetts
Publicado bajo Creative Commons
Atribución 4.0 Internacional
(CC POR 4.0) licencia
La prensa del MIT
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
1
2
1
7
1
0
9
2
3
7
3
norte
mi
norte
_
a
_
0
0
0
6
6
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
High-resolution model of the mouse connectome
2011; Glickfeld, Andermann, Bonin, & Reid, 2013; Kleinfeld et al., 2011; Blanco, Southgate,
Thomson, & Brennero, 1986) or a coarse description of connectivity between larger regions
(Felleman & VanEssen, 1991; despreciar, 2010). In between these two extremes is mesoscopic
structural connectivity: a coarser scale than that of single neurons or cortical columns but
finer than whole-brain regions (Bohland et al., 2009). Facilitated by new tracing techniques,
image-processing algorithms, and high-throughput methods, mesoscale data with partial to full
brain coverage exist in animals such as the fly (Jenett et al., 2012; Shih et al., 2015) and mouse
(G˘am˘anu¸t et al., 2018; Oh et al., 2014; Zingg et al., 2014), and such data are being collected
from other model organisms such as rat (Bota, Dong, & Swanson, 2003) and marmoset (Majka
et al., 2016).
We present a scalable regression technique for constructing spatially explicit mesoscale
connectivity from anterograde tracing experiments. Específicamente, our model estimates the pro-
jection strength between every pair of approximately 2 × 105 cubic voxels, cada 100 µm wide,
in the Allen Mouse Brain Common Coordinate Framework (CCF v3). The CCF is a fully an-
notated reference atlas space with structure/region delineations. We use data from the Allen
Mouse Brain Connectivity Atlas (Oh et al., 2014), a large dataset of viral tract-tracing exper-
iments performed across many regions of the mouse brain. All of the data processing scripts
are publicly available at https://github.com/AllenInstitute/mouse_connectivity_models (Knox,
2018).
In these mesoscale anterograde tracing experiments, a tracer virus (recombinant adeno-
associated virus) is first injected into the brain. The virus infects neurons at the site of injection
and causes them to express enhanced green fluorescent protein (eGFP) in their cytoplasm,
including throughout the entire length of their axons. Brains and labeled axons are imaged
with blockface serial two-photon tomography (Ragan et al., 2012) throughout the entire rostral-
to-caudal extent of the brain, resulting in an aligned stack of 2-D images that can easily be
transformed to 3-D space. Each brain contains one source injection only. Every image series
is registered to the 3-D CCF, using a combination of global affine and local transformations
(Kuan et al., 2015).
Combining many experiments with different injection sources in the same 3-D space re-
veals the set of pathways that connect those sources throughout the brain, the ingredients of a
“connectome.” This requires combining data across multiple animals, which appears justified
at the mesoscale (Bohland et al., 2009; Oh et al., 2014). Previous mouse connectome models
were constructed with the assumption that regions are homogeneous (G˘am˘anu¸t et al., 2018;
Oh et al., 2014; ypma & bullmore, 2016). While these have proven useful, they depend on
predefined regional parcellations and describe connectivity at a region-limited level of reso-
lution. Aquí, we go beyond the regional approach and construct a model of the whole-brain
connectivity at the scale of 100 µm voxels. Previously, k. D. harris, Mihalas, and Shea-Brown
(2016) formulated a regularized, structured regression problem for inferring voxel connectiv-
idad. This model was applied to Allen Mouse Brain Connectivity Atlas data in the visual cortex,
outperforming a regional model in prediction of held-out experiments.
Aquí, we extend the voxel approach from the visual cortex to the full mouse brain, mientras
also simplifying the mathematical model for computational efficiency. Our model relaxes the
assumption of homogeneity of connections within a region and instead assumes smoothness
across major brain divisions. We model the connectivity at each source voxel as the weighted
average of the projection patterns of nearby injections, where the weights are a monotonically
decreasing nonlinear function of distance to the injection centroid. We fit the parameters of
218
Voxel:
A 3-D cubic volume element;
the generalization of a pixel.
Major brain divisions:
The set of 12 major brain divisions
from the 3-D Allen Mouse Brain
Reference Atlas: isocortex, olfactory,
areas, hippocampus, cortical
subplate, striatum, pallidum,
thalamus, hypothalamus, midbrain,
pons, medulla, and cerebellum
(also called coarse structures).
Neurociencia en red
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
1
2
1
7
1
0
9
2
3
7
3
norte
mi
norte
_
a
_
0
0
0
6
6
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
High-resolution model of the mouse connectome
Connection strength:
The sum of the connection weights
from all voxels in a source region R
to all voxels in a target region R
denoted WR
21.
2,
1
Coarse structures:
See major brain divisions.
the model using nested cross-validation with held-out injection experiments. The new voxel-
scale model generally outpredicts a homogeneous regional model, as measured both by
cross-validation error and when compared with a human-curated dataset.
RESULTADOS
Spatial Method to Infer a Voxel Connectome
We consider the problem of fitting a weighted, directed, adjacency matrix that contains the
connection strength between any pair of points in the brain. We use n cubic voxels, 100 µm
across, to discretize the brain volume. Our goal is then to find a matrix W ∈ Rn×n
that ac-
≥0
curately captures voxel-voxel connection strength. We assume there exists some underlying
matrix W that is common across animals. Each experiment can be thought of as an injection
X, and its projections Y, where X, Y ∈ Rn
, and we want to find W so that Y ≈ WX, eso es,
we want to solve a multivariate regression problem. The details of all procedures are found in
Métodos.
:,i and W
We adopt a spatial weighting technique to combine information from multiple experiments
into one matrix, the outline of which is shown in Figure 1. As in K. D. Harris et al. (2016),
we assume that the connectivity from any given source voxel varies smoothly as a function
of distance: Columns W
:,j should be similar if the distance between voxels i and
j is small. We make the mathematically simplifying assumption that the projections we ob-
serve from a given experiment come from the center of mass of the injection ce. This allows
us to employ kernel regression to approximate the connectivity from a given voxel v as the
distance-weighted sum of injections in the major brain division containing v. We also expect
the connectivity could change sharply between the boundaries of high-level brain structures.
Por ejemplo, we know that projections arising from the thalamus and hypothalamus can be
very different, even though some areas within these divisions are near each other at the borders.
To account for this, we chose a partition of the brain into 12 nonoverlapping major brain divi-
sions or coarse structures defined in the CCF. The major brain divisions are isocortex, olfactory
areas, hippocampal formation, cortical subplate, striatum, pallidum, thalamus, hypothalamus,
midbrain, pons, medulla, and cerebellum.
Voxel-Scale Model Compared With a Regionally Homogeneous Model
Previously, Oh et al. (2014) obtained a regional mouse connectome by integrating the injection
and projection data over regions and fitting a region-by-region matrix with nonnegative least
squares. Aquí, we recomputed this matrix (see Methods) and compared it with a regionalized
Cifra 1. Cartoon illustrating our method of connectome inference. We combine the information
from viral tracing experiments with different injection sites into a model of voxel structural con-
conectividad. To predict the weight of projections Wij from the jth voxel vj to the ith voxel, we take
an average of nearby injections where the eth experiment’s projection ¯Yie is weighted by a factor
proportional to K((cid:5)vj − ce(cid:5)), ce is that injection’s center of mass, and K(·) is the kernel.
Neurociencia en red
219
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
1
2
1
7
1
0
9
2
3
7
3
norte
mi
norte
_
a
_
0
0
0
6
6
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
High-resolution model of the mouse connectome
Regions:
The set of 291 intermediate brain
structures from 3-D Allen Mouse
Brain Reference Atlas (also called
summary structures).
version of the voxel connectivity. To avoid confusion between the two models, we call the
regional connectome the homogeneous model, because it assumes homogeneity across ana-
tomical structures. We call our new model, when it has been averaged over regions, el
regionalized voxel model. En breve, we chose 291 gray matter regions, which are interme-
diate level in the CCF, and recomputed the homogeneous model. The abbreviations of all
CCF regions mentioned in this paper are given in Table S1 (Knox et al., 2019). To generate
the regionalized voxel model, voxel connectivity was integrated and averaged over regions to
produce regionalized weights (see Methods for details).
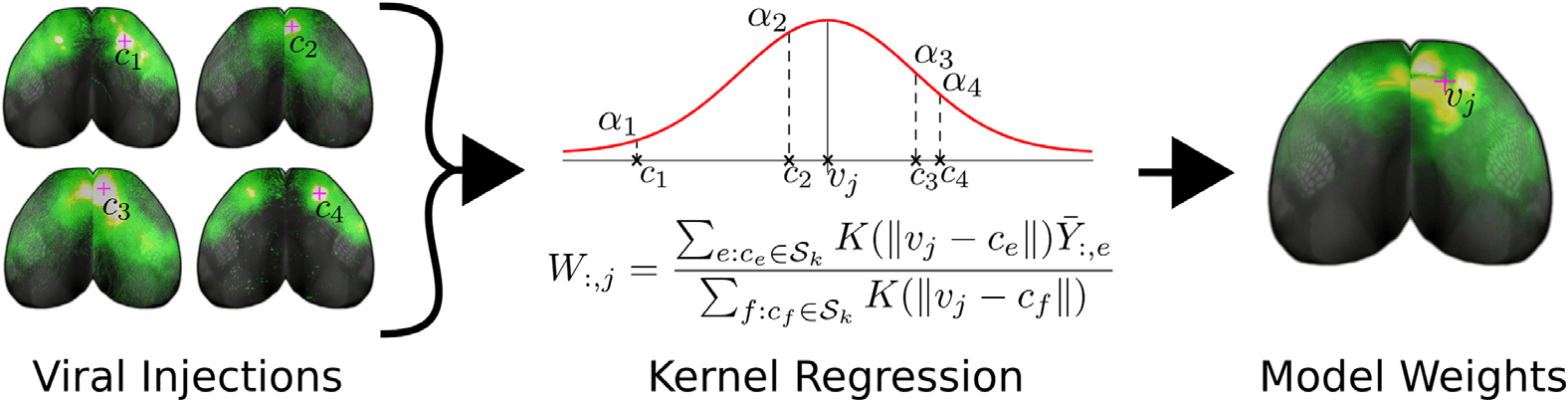
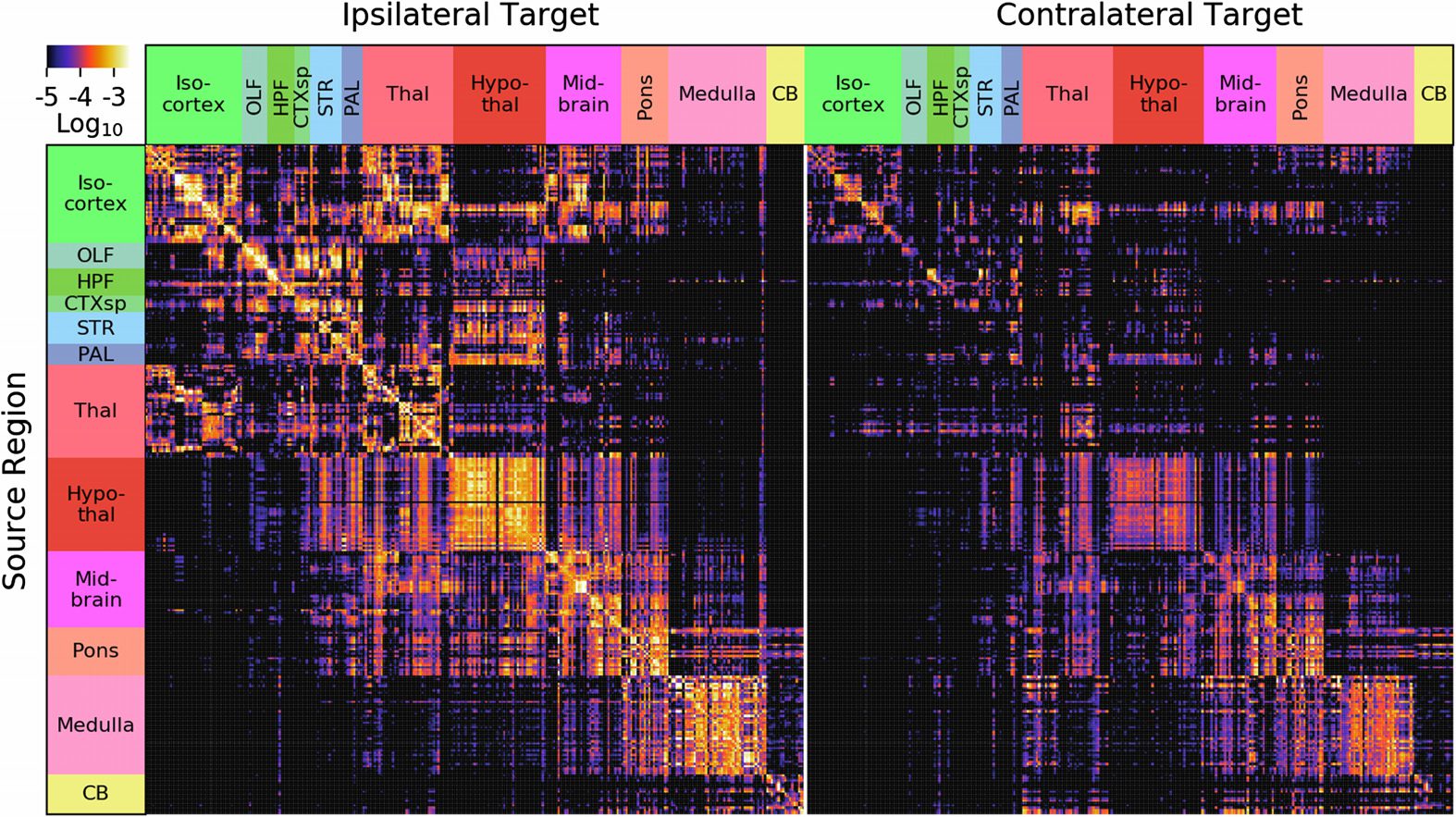
En figura 2, there is a depiction of the whole-brain regionalized weights and, En figura 3,
the regionalized weights for isocortex. Tenga en cuenta que, for visualization purposes, we depict sources
as rows and targets as columns (W.(cid:2)
), the opposite of our mathematical convention.
A number of features are evident in Figures 2 y 3. Primero, there are patterns that arise from
our smoothness assumption. The predicted projection patterns from a certain source voxel are
distance-weighted averages of injections nearby that voxel (see Methods and Figure 1). Allá-
delantero, the method we employ smooths in the source space only. The vertical banded structures
(Por ejemplo, the column near the right side of the medulla division in Figure 2) are due to
smoothing in source but not target regions, which makes the rows of W(cid:2)
correspondiente a
nearby source voxels similar. En figura 3, note that the rows PERI, ECT, and TEa (the bottom
three rows) and AUDv (upper middle) match closely. All four of these regions are very close
to each other on the posterior, ventrolateral part of the cortex, so that smoothing causes them
to be correlated. Also notice that, while the rows corresponding to these regions as sources
are very similar, the columns corresponding are not nearly as much so. This highlights that our
model interpolates only in the sources and not the targets.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
1
2
1
7
1
0
9
2
3
7
3
norte
mi
norte
_
a
_
0
0
0
6
6
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 2. Whole-brain normalized connection density obtained from the regionalized voxel
modelo. We show 291 gray matter regions divided into 12 major brain divisions. For visualization
purposes, sources are shown on the rows and targets on the columns, the opposite convention as the
mathematics in the text (W.(cid:2)
is pictured). The similarity between rows, for example in hypothalamus,
is driven both by biological similarity and as a result of the model’s interpolation in the sources. El
similarity between columns is the result of correlations in the data, as the model does not interpolate
in target space.
Normalized connection density:
The connection strength from R
R
2 divided by the product of their
1 a
sizes:
WR
|R1||R2| .
21
Neurociencia en red
220
High-resolution model of the mouse connectome
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
1
2
1
7
1
0
9
2
3
7
3
norte
mi
norte
_
a
_
0
0
0
6
6
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 3.
show sources as rows and targets as columns (W.(cid:2)
Isocortex normalized connection density from the regionalized voxel model. De nuevo, nosotros
is pictured) for visualization.
The second feature that is evident is the presence of blocks of strongly interconnected re-
gions. These correspond to modules in the network, or regions that are more highly connected
to each other than they are to the rest of the network. This is explored further in J. A. harris
et al. (2018).
En mesa 1, we show the results of comparing homogeneous and voxel models. We fit the
models using nested leave-one-out cross-validation. This allows us to evaluate both the voxel-
scale and regionalized models’ error when predicting held-out data. We report mean squared
error relative to the average squared norm of the prediction and data, which can be between
0 y 200%. See Equation 4 and the description in the Methods. The model validation and
training errors (goodness of fit, shown in parentheses) are reported at both voxel (Voxel MSErel)
and regional (Region MSErel) niveles. Además, we compare model performance using a
subset of experiments in which a given source region received at least three replicate injections.
Without another injection, the only information about that region’s projections would come
from our smoothness assumption interpolating nearby regions’ patterns. The computed relative
error MSErel for this dataset of replicated injections we call the “power to predict” (Region PTP),
and it tends to be lower than Region MSErel across divisions.
From Table 1, we see that the relative training and validation errors are higher when evalu-
ating error in the voxel space. This makes sense, because this error captures mistakes we make
in predicting spatial patterns of projections at the voxel, subregional level. That task is much
more difficult than predicting regional patterns. The lowest voxel errors are in isocortex, hy-
pothalamus, and olfactory areas, whereas the highest are in cerebellum, thalamus, and cortical
subplate. At the regional level we compare both the homogeneous model and the regionalized
voxel model, which uses the voxel connectome to make a prediction that is then integrated
across each region. At the regional level, our voxel model has lower regional validation errors
than the homogeneous model in 11/12 major brain divisions. The training error is lower in 7/12
casos, since assuming smoothness is less biased than regional homogeneity. The regional PTP
of the voxel model is lower than the PTP of the homogeneous model in 10/12 casos. Resultados
for training PTP are better for the regionalized model in 6/12.
Neurociencia en red
221
High-resolution model of the mouse connectome
Mesa 1. Table of cross-validated model errors, comparing the voxel model and the regionally
homogeneous model. In each case the training error is in parentheses. Voxel MSErel refers to relative
error, Ecuación 4, at the voxel level. This measure approximates the data normalized MSE for small
= 200%, which is achieved if either Ytrue or Ypred is
errores, but is bounded to maximum of MSErel
0 and the other is not (see Methods). Region MSErel is the error found after regionalizing the voxel
model prediction. PTP (“power to predict”) computes MSErel for only those held-out experiments
where there was another injection in that region which was not used for fitting.
Major division
Modelo
Isocortex
Olfactory areas
Hippocampus
Cortical subplate
Striatum
Pallidum
Thalamus
Hypothalamus
Midbrain
Pons
Medulla
Cerebellum
Voxel
Homogeneous
Voxel
Homogeneous
Voxel
Homogeneous
Voxel
Homogeneous
Voxel
Homogeneous
Voxel
Homogeneous
Voxel
Homogeneous
Voxel
Homogeneous
Voxel
Homogeneous
Voxel
Homogeneous
Voxel
Homogeneous
Voxel
Homogeneous
Voxel MSErel
66%
–
82%
–
92%
–
114%
–
103%
–
100%
–
115%
–
69%
–
89%
–
98%
–
96%
–
177%
–
(22%)
–
(17%)
–
(20%)
–
(40%)
–
(8%)
–
(5%)
–
(14%)
–
(46%)
–
(32%)
–
(9%)
–
(33%)
–
(9%)
–
Region MSErel
(11%)
34%
(20%)
37%
(6%)
41%
(9%)
50%
(17%)
56%
(51%)
46%
(47%)
95%
(2%)
111%
(2%)
45%
(23%)
53%
(3%)
64%
(3%)
85%
(10%)
77%
(12%)
92%
(32%)
48%
(5%)
62%
(14%)
42%
(14%)
44%
(6%)
66%
(27%)
89%
(18%)
51%
(3%)
58%
(2%)
78%
(4%)
90%
Region PTP
32%
33%
40%
44%
52%
48%
93%
99%
40%
53%
45%
74%
70%
86%
37%
77%
37%
39%
61%
87%
49%
54%
75%
63%
(9%)
(17%)
(6%)
(9%)
(17%)
(51%)
(25%)
(2%)
(1%)
(24%)
(7%)
(2%)
(12%)
(12%)
(9%)
(7%)
(13%)
(14%)
(6%)
(27%)
(21%)
(2%)
(7%)
(5%)
En general, we find the highest errors (for either model) in cortical subplate, which is the
smallest major division and has the largest distance between injections. The voxel and regional
test errors are correlated with the mean minimum distance between voxels and injection cen-
ters of mass within each major brain division (correlation coefficients of 0.50 y 0.68, respetar-
activamente). We find the smallest errors are in isocortex, which has the largest number of replicated
experimentos. The summary statistics of our data by major brain division are summarized in
Table S2 (Knox et al., 2019).
Visualizing Voxel-Scale Connectivity: Cortico-Cortical Virtual Injections
Visualization of our model faces two challenges: The matrix W contains n × n = O(1011)
entradas, and represents dense connectivities between 3-D spatial structures. In order to address
these challenges, we generated “virtual injections,” which are just the predicted projections
from a given source voxel of interest. These virtual injections allow us to visualize the average
projections from voxels of our choosing. This process is efficient, because the matrix W is
formed from m rank one components, so we never have to form the entire matrix. Estándar
herramientas, such as volume rendering and projection, can then be applied to visualize the model’s
predicciones.
Neurociencia en red
222
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
1
2
1
7
1
0
9
2
3
7
3
norte
mi
norte
_
a
_
0
0
0
6
6
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
High-resolution model of the mouse connectome
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
1
2
1
7
1
0
9
2
3
7
3
norte
mi
norte
_
a
_
0
0
0
6
6
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
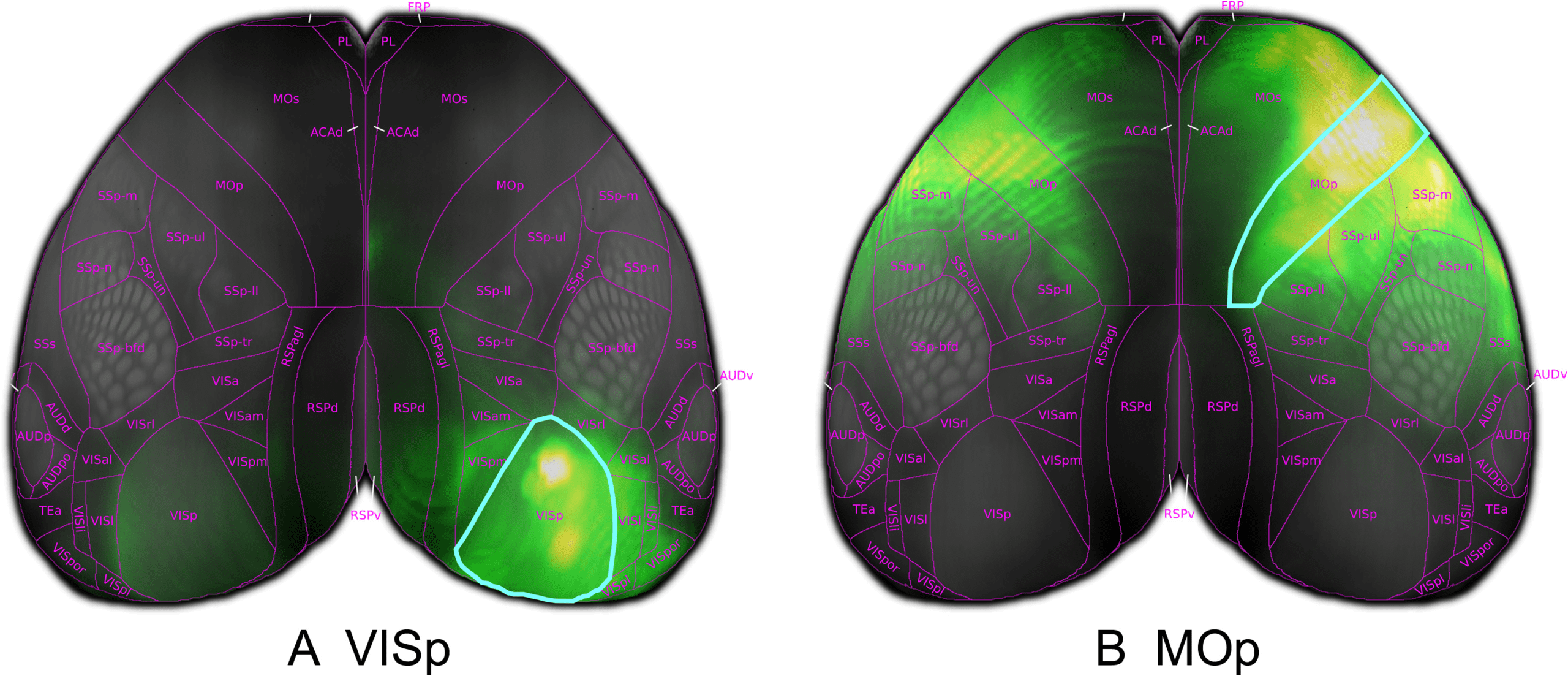
Cifra 4. Model predicted cortico-cortical projections from virtual injections into the entire primary visual area (VISp) and primary motor
área (MOp).
In order to visualize model predictions in the isocortex we make use of a curved cortical
coordinate system. This coordinate system defines two dimensions over the surface of the
cortex and one that is composed of steepest-descent paths from the pia surface to white matter.
By projecting model predictions along these paths, we can generate 2-D cortical projection
maps that are faithful to the boundaries of isocortical regions.
We display two such projections in Figure 4. Aquí, we visualize the average over the
columns of the matrix W corresponding to the projections from two isocortical regions, marked
by a cyan outline. We observe strong ipsilateral projections to nearby areas, as expected from
the experimental data. Por ejemplo, primary visual area VISp has a number of local projections
to higher visual areas, Figura 4A, and primary motor cortex MOp exhibits strong connectivity
to secondary motor and somatosensory areas, Figura 4B. We also observe weaker contralateral
projections across the midline in a similar pattern to the ipsilateral hemisphere.
Weight Distribution and Its Distance Dependence
We compared multiple models for the distribution of connection weights: lognormal (as has
been reported in Markov et al., 2014; q. Wang, despreciar, & Burkhalter, 2012), inverse gamma,
exponential, and normal. We separately construct these models for ipsilateral and contralat-
eral connections for the entire brain and for connections within isocortex. For all these weight
distributions, the best fit is for a lognormal distribution, as selected by Bayesian information
criterion (BIC). The BIC is a pseudo-likelihood that penalizes the number of model parameters.
See Table S3 (Knox et al., 2019). Sin embargo, the results from the Kolmogorov-Smirnov test show
that the fitted lognormal distributions fail to be statistically similar to the weight distributions
for any division of the connections at α = 0.05 significance. Además, the logarithmically
transformed weights fail to pass the Shapiro-Wilk test for normality at the same level of signifi-
cance. This is because the log-transformed weights, depicted on the right-hand side of Figure 5,
exhibit a skewed distribution.
Neurociencia en red
223
High-resolution model of the mouse connectome
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
1
2
1
7
1
0
9
2
3
7
3
norte
mi
norte
_
a
_
0
0
0
6
6
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
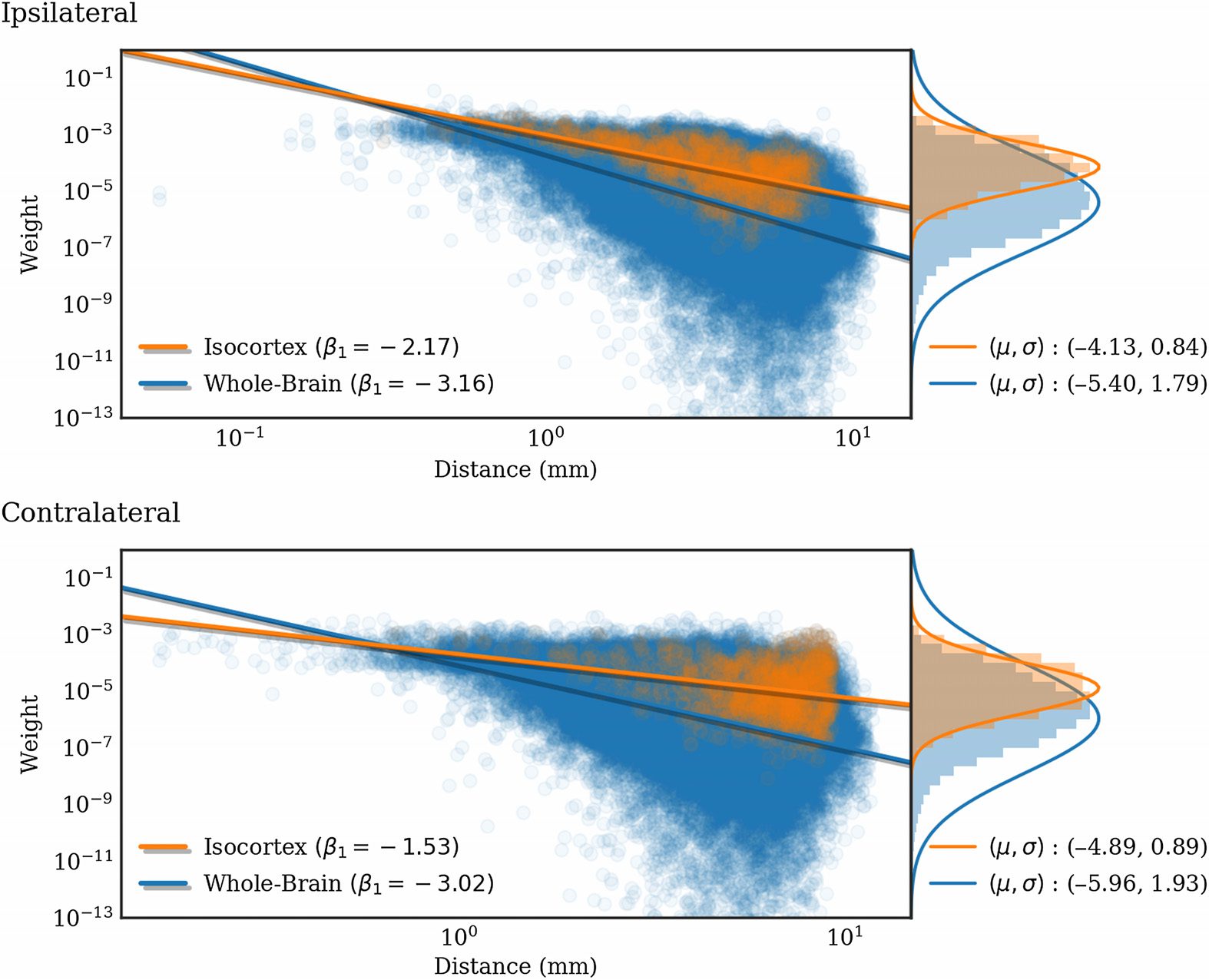
Cifra 5. Normalized connection density produced by the regionalized voxel model (log scale)
plotted against interregion distance for 291 regions in the whole-brain (azul) and for only cortico-
(weight) =
cortical connections (naranja). The lines are linear least squares of the form log10
b
0. The histograms on the right side show the distributions of weights as well as
1 log10
(weight) distribución. Note that the standard deviations are biased because
Gaussian fits of the log10
of small weight outliers.
(distancia) + b
We have previously seen that a heterogeneous set of connections can be better fit by a mix-
ture of lognormal distributions (Oh et al., 2014). In a similar manner, we find the logarithmically
transformed weights are best fit by a multiple component Gaussian mixture model (GMM). Ver
Table S4 (Knox et al., 2019). The number of components was selected to minimize the BIC.
This resulted in a five-component GMM for the whole brain, and a two- to three-component
GMM for cortico-cortical connections. With the exception of two components in each of the
whole-brain mixture models, the components have similar valued weights, suggesting that dif-
ferent regions contribute to a nonhomogeneous distribution of connection weights across the
cerebro. Sin embargo, it could also be the case that the empirical distribution of log-transformed
weights is well modeled by a skewed unimodal distribution.
En figura 5, we show the dependence of extant connection weights on distance. We com-
pared an exponential (Ercsey-Ravasz et al., 2013) and a power law fit. Using the Levenberg-
Marquardt algorithm to fit each nonlinear least squares problem, the root mean squared training
error (RMSE) was found to be slightly smaller for the power-law fit, but similar for both.
Model Performance Compared With Anatomical Data
To evaluate how closely the model predictions aligned with experimental data, we compared
the model weights from the homogeneous model and the regionalized voxel models with
Neurociencia en red
224
High-resolution model of the mouse connectome
Wild type mouse (C57BL/6J):
Mice of strain C57BL/6J that have not
been genetically altered.
Cifra 6. Fraction of whole-brain projection volume from cortical sources explained by model
weights for the regionalized voxel model (rojo) and the homogeneous model (cyan). Each of the
37 cortical source regions is plotted on the x-axis, and the transparent points are for individual
experimentos. Darker points and lines indicate the mean and 95% confidence interval across all
injections delivered to that source.
projection data for each of the 128 injections into the isocortex in wild type mice from the
Allen Mouse Brain Connectivity Atlas. For each injection experiment, we calculated the frac-
tion of explained variance for the two models by taking the square of the Pearson correlation
between the experimental normalized projection volume and the model weights in each of the
291 regiones. Cifra 6 shows the fraction of explained variance for each experiment grouped
by source structure. Although the mean predicted variance across all sources was similar be-
tween the two models, the regionalized voxel model performed better overall (mean ± SD
regionalized: 0.87 ± 0.13, homogeneous: 0.84 ± 0.17, pag < 0.0001, paired t test), but note
that each model outperformed the other for some sources.
To further explore the relationship between the model prediction and the experimental data,
we also compared the predicted weights from both models with experimental data from a
subset of experiments in which injection sites were more than 95% contained within a single
source region. There were 36 experiments that met this criterion. Of these, 35 were in the
isocortex and 1 was in the hippocampus, and this set contained in the following 10 sources
(see Table S1, Knox et al., 2019): AUDp (1), ENTl (1), MOp (3), MOs (1), RSPd (1), SSp-bfd (1),
SSp-m (4), SSp-n (1), SSs (1), and VISp (22). Note that in VISp we include four injections using
the pan-excitatory Cre line Emx1-IRES-Cre mice, which have very similar projection patterns as
wild type mice (J. A. Harris et al., 2018). Twelve of these experiments were manually checked
for segmentation errors in the regions where nonzero projections were automatically flagged.
When these manually annotated data were available, we multiplied the normalized projection
volume by 1 for true positives or 0 for true negatives. See Figure S1 (Knox et al., 2019) and the
description in Methods. For each of these 10 sources, we plotted the normalized projection
volume from the experimental data along with the predicted weights from both models for
targets in the ipsilateral isocortex.
Figure 7 shows the plot for VISp, where we had a total of 22 experiments of which eight
were checked for true positives/true negatives at all cortical targets. Four injections into Emx1-
IRES-Cre mice were included in the plot for VISp, although these were not used to fit the
model. Only the eight experiments that were manually checked are included in the plot in
the figure. The weights predicted by the regionalized voxel model were higher overall, but
generally agreed with the experimental data as well as the homogeneous model predictions.
Network Neuroscience
225
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
1
2
1
7
1
0
9
2
3
7
3
n
e
n
_
a
_
0
0
0
6
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
High-resolution model of the mouse connectome
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
1
2
1
7
1
0
9
2
3
7
3
n
e
n
_
a
_
0
0
0
6
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7. Normalized projection volume for VISp projections to ipsilateral (top) and contralateral
(bottom) cortical targets in log scale. The raw data are compared with model predictions. Normal-
ized projection volume from individual manually validated experiments (gray) and the mean and
95% confidence interval for each target are plotted as black diamonds. Note that many confidence
intervals are smaller than the markers. Corresponding weights for VISp projections to each cortical
target from the homogeneous model (cyan) and the regionalized voxel model (red) are overlaid.
The biggest difference between the two models was that the regionalized voxel model correctly
predicted nonzero weights for several targets that were missed by the homogeneous model.
All of the ipsilateral targets of VISp that had a weight of 0 in the homogeneous model were
verified true positives in at least three of the eight experiments plotted in Figure 7. All of the
contralateral targets except SSp-ll were verified true positives in at least two out of the eight
experiments. The regionalized voxel model predicted nonzero weights for all of these true
positive targets that were assigned a weight of 0 by the homogeneous model. Contralateral
SSp-ll was a true negative in all eight experiments and was incorrectly assigned a weight by
the regionalized voxel model but not the homogeneous model. Both models predicted small
but nonzero weights for several other targets that were true negatives (ipsilateral: FRP, AId, AIp,
and AIv; contralateral: FRP, SSp-n, SSp-m, SSp-ul, GU, VISC, PL, ILA, AId, AIp, AIv). Across
all 10 sources that were checked, the regionalized voxel model tended to predict nonzero
weights for connections that were assigned 0 weight in the homogeneous model.
Overall, we found the predictions of the regionalized voxel model to be more consis-
tent with the data than the homogeneous model. Even when the predicted weight from the
Network Neuroscience
226
High-resolution model of the mouse connectome
regionalized voxel model was incorrect, it was not off by a large margin. The homogeneous
model often performs well, but when its predictions differ from the experimental data they
are sometimes off by a very large margin. For example, the homogeneous model predicts zero
weight for projections from ACAv to the caudoputamen (CP), but the experimental data show
that CP is in fact the strongest projection target of ACAv with a normalized projection volume
of 4.4 and 5.0 (unitless) in the two available experiments (compared with 0.05 ± 0.28, mean
± SD for all targets of ACAv across the two experiments). The homogeneous model makes the
same error for SSp-ll, again assigning zero weight to projections in CP when the experimen-
tal data show that CP is the highest weight target of SSp-ll (normalized projection volume in
CP = 3.2 ± 1.1, mean normalized projection volume in all targets = 0.03 ± 0.2, n = 3 exper-
iments). This is reflected in the standard deviation for the fraction explained variance (0.17 for
the homogeneous model vs. 0.14 for the regionalized voxel model), and is well illustrated in
Figure 6, where the homogeneous model performs well overall, but very poorly for projections
from SSp-ll and ACAv.
DISCUSSION
In this study, we infer whole-brain connectivity at 100 µm voxel resolution from a set of brain-
wide anterograde viral tracing experiments in young adult wild type C57BL/6J mice (Oh et al.,
2014, http://connectivity.brain-map.org). The central assumption of extant voxel methods is
that brain-wide projections from nearby neurons within a brain region vary smoothly. Such a
method, and its application to the visual system, has been described by K. D. Harris et al.
(2016). Eventually, we hope to improve those mathematical methods to solve the original
source- and target-smoothed nonnegative regression problem at whole-brain scale. However,
the current implementation of that problem is computationally costly and does not scale to
the whole brain. These considerations led us to develop the simpler method presented here.
Our approach makes two simplifying assumptions (see Methods): First, we assume the in-
jection is delivered into just the center of mass voxel, rather than the entire injection volume.
This is the opposite extreme of the regionally homogeneous assumption. Second, we perform
interpolation in only the source space, rather than also in the target space. With these changes,
the model of K. D. Harris et al. (2016) becomes, essentially, the method we present here, be-
cause of the well-known “kernel trick” (Wahba, 1990). This connection is inexact because of
boundary effects, the particular choice of kernel, and the use of Nadaraya-Watson rather than
regression coefficients.
The tracing data that forms the basis of this study is based on anterograde viral tracers (Oh
et al., 2014). The viral tracing methods used to generate the Allen Mouse Brain Connectivity
Atlas dataset result in two limitations affecting our ability to resolve connections. One limita-
tion comes from the size of the injections, which have a typical radius of 0.3 mm. Table S2
(Knox et al., 2019) provides the volume distribution through different brain regions. An even
stronger limit comes from the distances between a voxel and the center of mass of an injec-
tion being typically 0.5 mm. Table S2 reports this average in the “injection distance” column.
This distance is the consequence of the number of injections (491, of which we select 428
as described in Methods) being much smaller than the number of source voxels (2.5 × 105).
The connections originating from a voxel have to be inferred from sources on average 0.5 mm
away, which average information over a radius of 0.3 mm. Spatial averaging is thus necessary
for these data.
Voxel models were fit and analyzed separately for a set of 12 major brain divisions. These
structures represent a coarse level of anatomical parcelation of mammalian brains and have
Network Neuroscience
227
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
1
2
1
7
1
0
9
2
3
7
3
n
e
n
_
a
_
0
0
0
6
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
High-resolution model of the mouse connectome
qualitatively different connection patterns. One could also take an agnostic approach and hope
that the data reveal where these differences arise. Perhaps using a total variation or similar reg-
ularization that allows for piecewise constant patterns, or working with a factored W = LR and
clustering the factors into different regions, could provide a tractable approach to this. Non-
negative matrix factorizations can also be interpreted as another way to find network modules,
as was proposed in K. D. Harris et al. (2016). However, this both increases the mathematical
difficulty and could require more experiments than are currently available.
We compared the voxel and homogeneous models’ ability to predict held-out injection ex-
periments. Although the errors for both are relatively high (but see the Supporting Information
(Knox et al., 2019) for a comparison with log-transformed errors), the voxel model on average
performs better. However, if the homogeneous model is fit with 10 µm data, it can outperform
the regionalized voxel model fit with 100 µm data (see the Supporting Information). We be-
lieve a good method to evaluate the model’s performance is to compare the predicted weights
with a human-curated ground truth metric. We were able to make this comparison for a subset
of injections well contained in 10 of 43 cortical sources. By comparing the models’ predictions
with experiments, we found two main differences between the regionalized voxel model and
the homogeneous model. First, and most importantly, the regionalized voxel model predicts
very weak but nonzero connections that the homogeneous model assigns zero weight. This is
due to the inherent tendencies of the models to increase sparsity (homogeneous model) or to
decrease sparsity (regionalized voxel model). We verified some of the connections that were
detected by the regionalized voxel model and not the homogeneous model as true positives,
but others were true negatives that were incorrectly assigned a nonzero weight by the regional-
ized voxel model. Occasionally, the homogeneous model assigns a zero weight to very strong
connections as with the projections to CP from ACAv and SSp-ll (Figure 6), but the regionalized
voxel model is less susceptible to this type of error since it tends to decrease sparsity.
The other main difference between the two models was in the prediction of weights for small
target structures. Because the regionalized voxel model is a linear smoother, it will tend to
overpredict weak connections for targets near regions with high connectivity. Some examples
of this behavior can be seen in Figure 7 where projection weight to AUDv, for example, is
overestimated by the regionalized voxel model, likely because of its spatial position between
AUDp and TEa which both receive strong projections from VISp. In choosing the appropriate
model for an application, it is therefore important to consider that weak connections have
higher uncertainty, and whether false positives or false negatives have a greater influence on
the results.
We would like to emphasize that when analyzing this connectivity, especially from a graph
theoretical perspective, one also has to be mindful of the correlations between connections
originating from nearby sources that are introduced by the method. The spatial resolution of the
connectivity is presented at 100 µm resolution. However, at source level, the average distance
to the closest injection is typically 0.5 mm (see Table S2, Knox et al., 2019), which limits the
resolution. Also, many graph statistics may not be well suited for studying such explicitly spatial
graphs as ours.
Among multiple models for unimodal weight distributions, we found the lognormal being
the best fit, in accordance with previous studies (e.g., Markov et al., 2014; Q. Wang et al.,
2012), despite failing the Kolmogorov-Smirnov test. Following this analysis, we found that a
mixture of normal distributions was an even better fit for the distribution of log weights (as
in Oh et al., 2014). A possible explanation for this is that the mixture results from combining
Network Neuroscience
228
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
1
2
1
7
1
0
9
2
3
7
3
n
e
n
_
a
_
0
0
0
6
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
High-resolution model of the mouse connectome
heterogeneous neuronal populations each with lognormal statistics, or that the log-transformed
distribution is skewed.
We analyzed the distance dependence of the connection weights and found that a power
law dependence is a marginally better fit than exponential (Ercsey-Ravasz et al., 2013), similar
to the result of Rubinov, Ypma, Watson, and Bullmore (2015). It is interesting that the power is
close to −2 for the cortex (ipsilateral), which can be roughly approximated as a 2-D “sheet,”
and close to −3 for the entire brain, which is 3-D. However, the weak scaling we observe only
holds over roughly 1.5 orders of magnitude, so we prefer not to speculate too much about this
result.
The voxel model enables quantitative characterization of the structural connectivity of the
mouse brain. It is a significant improvement over the previously published homogeneous lin-
ear model (Oh et al., 2014), with easily tractable mathematics compared with the earlier voxel
proposal (K. D. Harris et al., 2016). It offers improved predictions at region level, but, more
importantly, it provides the connectivity at a much higher spatial resolution. This new model
provides the necessary basis for studies of large-scale network structure, enabling discovery of
general organizational rules for brain-wide systems that consist of both local and long-distance
connections. For example, J. A. Harris et al. (2018) performed an analysis of modularity in the
wild type cortical subnetwork, employing the regionalized voxel model we present here. They
found that the cortical network divides into 1–14 modules, depending on the clustering pa-
rameters, but found six stable modules that were characterized as prefrontal, anterolateral,
somatomotor, visual, medial, and temporal. A better understanding of such structural rules
will lead to more accurate predictions of the directions of information flow, constrained by
anatomy, and can be used by researchers interested in questions of structure-function relation-
ships in the mouse brain.
METHODS
Summary of Data
The data were taken from 491 experiments using wild type C57BL/6J mice. These data are
available from the Allen Mouse Brain Connectivity Atlas at http://connectivity.brain-map.org/
(Oh et al., 2014). The brain is divided into a set of s = 12 major brain divisions at a high level
of the CCF ontology. These major brain divisions are isocortex, olfactory areas, hippocam-
pal formation, cortical subplate, striatum, pallidum, thalamus, hypothalamus, midbrain, pons,
medulla, and cerebellum. We also consider a finer partition (lower in the ontology) into a set
of r = 291 regions. The major brain divisions form a disjoint partition of the brain, as do the
regions. These regions are each contained within a given major brain division.
We curated experiments to exclude those in which infected cell bodies are located in mul-
tiple major brain divsions. For example, we removed experiments with large injection volumes
spanning multiple subcortical major brain divisions and subcortical injections with substantial
leakage of the tracer in the overlying cortex. Additionally, we removed four experiments hav-
ing very little to no long-distance projections (small projection volume outside of the injection
location). Overall, of the 491 experiments, we removed 63 experiments resulting in a total of
m = 428 included experiments. We summarize these experiments used to fit our connectome
in Table S2 (Knox et al., 2019).
In our mathematical framework, the brain is a subset of R3 that is discretized into a col-
lection of n cubic voxels. Subsets of these voxels then correspond to the major brain division
{Si}s
i=1. Each voxel i maps to a location in the brain, which we denote
i=1 and regions {Ri}r
Network Neuroscience
229
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
1
2
1
7
1
0
9
2
3
7
3
n
e
n
_
a
_
0
0
0
6
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
High-resolution model of the mouse connectome
by vi ∈ R3. Each injection tracing experiment produces an image stack (i.e., a 3-D image) of
fluorescently labeled neurons and axons throughout the brain. The fluorescence signal is re-
ported as injection density (fraction of fluorescing pixels per voxel for voxels in the annotated
injection site) and projection density (fraction of fluorescing pixels per voxel outside of the
injection site). For the eth experiment, let X:,e and Y:,e denote the length n vectors of injection
density and projection density, respectively. We also compute voxel coordinates of the center
of mass of the injection density ce ∈ R3. For our estimator, we also compute the normalized
projection density, normalizing by the sum of the injection density, and denote this ¯Y:,e. Note
that ¯Y:,e = (Y:,e + X:,e)/ ∑v Xve, since we also include the injection pattern in the normalized
projection density. Thus, the experimental data are this collection {(X:,e, Y:,e, ¯Y:,e, ce)}m
e=1, of
length n vectors as well as the injection centers of mass for each experiment.
Multivariate Nonparametric Regression to Infer Voxel Connectivity
We consider the problem of fitting a nonnegative, weighted adjacency matrix W ∈ Rn×n
that
≥0
is common across animals. Entry Wij is the estimated projection density of neurons in voxel j
to voxel i, if one unit of injection density were delivered to voxel j. Each experiment consists
of an injection X, and its projections Y, and we would like to find W so that so that Y ≈ WX.
Uncovering the unknown W from multiple experiments (X:,e, Y:,e) for e = 1, . . . , m is then a
multivariate regression problem. The unknown matrix W is a linear operator that takes images
of the brain (injections) and returns images of the brain (projections).
Unlike the earlier work by K. D. Harris et al. (2016), we make two crucial simplifying
approximations: First, we assume that in experiment e the injection is delivered to precisely
one voxel, the injection center of mass ce. This removes the more difficult credit assignment
problem of which voxels within each injection site contribute which projections. The method
of K. D. Harris et al. (2016) solved this problem by linear regression, essentially “dividing
out” the injection correlations across experiments. Second, we assume that projections vary
smoothly as we change the source voxel, that is, the columns of W are smooth functions of the
column voxel. However, we do not explicitly assume that the incoming projections to a target
voxel vary smoothly as we move the target voxel, or smoothness in the rows. Smoothness in
target space leads to dependencies among the output variables of the multivariate regression
problem, making it a so-called structured regression problem, which is generally more difficult
to solve. Note that, because the data tend to produce patterns of projections that are spatially
smooth, and because we enforce smoothness in the source space, some target smoothness
will arise naturally.
Nadaraya-Watson connectome estimator. With these simplifying assumptions, we can now
state the model. Our data are now the pairs of center of mass voxels ce and normalized injec-
tion densities ¯Y:,e, which we assume arise from an injection of one unit of virus to the center of
mass. Kernel regression is a standard nonparametric method for estimating a smooth univari-
ate or multivariate function. For simplicity, we use the Nadaraya-Watson estimator (Nadaraya,
1964; Watson, 1964) to estimate the connectivity:
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
1
2
1
7
1
0
9
2
3
7
3
n
e
n
_
a
_
0
0
0
6
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Wij =
∑e:ce∈Sk
∑ f :c f ∈Sk
K((cid:5)vj − ce(cid:5)) ¯Yie
K((cid:5)vj − c f (cid:5))
= ∑
e:ce∈Sk
¯Yieαej ,
where
αej =
Network Neuroscience
K((cid:5)vj − ce(cid:5))
∑ f :c f ∈Sk
K((cid:5)vj − c f (cid:5)) ,
(1)
(2)
230
High-resolution model of the mouse connectome
and k is the unique index such that vi ∈ Sk, that is, we only average over injections in the
major brain division containing the source voxel. Furthermore, we can construct the matrices
¯Y = [ ¯Y
(cid:2)
:,1, ¯Y
(cid:3)
αej
,
A =
:,2, . . . , ¯Y:,m]
so that the connectome is written compactly as a rank m matrix W = ¯YA, where ¯Y ∈ Rn×m
and A ∈ Rm×n
. Note that each column in A, the coefficients αej, has entries that sum to 1.
The Nadaraya-Watson estimator, Equation (1), has a number of nice properties: It does not
require any fitting, because the coefficients αej are given explicitly in terms of the center of
masses and kernel, Equation (2). For nonnegative data, it will produce a nonnegative connec-
tivity matrix, which we require. Furthermore, it forms a compressed rank m representation of
W that is only as large as the data. However, it does suffer some drawbacks; for example,
it is well known that the Nadaraya-Watson estimator is biased for data that are not sampled
uniformly and near boundaries.
Note also that experiments with center of masses ce ∈ Sk do not have any influence outside
of Sk. This is because we do not want to average over experiments in vastly different brain
areas. Therefore, the coefficients αe,k are decoupled across major brain divisions. Essentially,
we fit a different model for each major brain division.
Choice of spatial kernel. We use a Gaussian radial basis function kernel:
(cid:4)
Kσ(d) = exp
−
(cid:5)
,
d2
2σ2
(3)
where σ > 0 is a hyperparameter setting the length scale or bandwidth of the kernel function.
The length scale σ is fit using nested cross-validation in the model selection phase. We search
over σ ∈ [4, 50] en 11 logarithmically spaced increments, where σ is in units of 100 µm voxels.
Note that while the kernel, Ecuación 3, has infinite support, we do not evaluate it on points
outside the coarse structure of interest.
To evaluate the performance of the model, nosotros
Evaluating performance via cross-validation.
employ nested leave-one-out cross-validation. In the inner loop, we fit m − 1 different models
on sets of m − 2 experiments in order to perform model selection, wherein we fit the hyper-
parameter σ of the kernel function K. The best model is then evaluated against the held-out
experiment from the outer loop, and this process is repeated m times. The performance metric
we choose to use is mean square error relative to the average squared norm of the prediction
and left-out data:
MSErel
= 2(cid:5)Ypred − Ytrue(cid:5)2
F
F + (cid:5)Ytrue(cid:5)2
F
(cid:5)Ypred(cid:5)2
.
(4)
This choice of normalization prevents experiments with small (cid:5)Y(cid:5) from dominating the error,
more heavily weighting experiments with larger signal (k. D. Harris et al., 2016).
The relative error in Equation (4) is approximately equal to the usual relative mean square
F when Ypred is close to Ytrue, and this is not too small. To see
error (cid:5)Ypred − Ytrue(cid:5)2
F/(cid:5)Ytrue(cid:5)2
Radial basis function:
A monotonically decreasing,
nonnegative function of distance.
Frobenius norm:
The two norm of a matrix viewed as
a vector: (cid:5) A (cid:5)F =
∑ij A2
ij.
(cid:6)
Neurociencia en red
231
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
1
2
1
7
1
0
9
2
3
7
3
norte
mi
norte
_
a
_
0
0
0
6
6
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
High-resolution model of the mouse connectome
este, let Ypred = Ytrue + δ where (cid:5)δ(cid:5)F ≤ (cid:6) y (cid:5)Ytrue(cid:5)F = O(1). Entonces, dropping the superscript
“true” for clarity,
MSErel
=
2(cid:5)δ(cid:5)2
F
F + (cid:5)Y(cid:5)2
F
(cid:5)Y + δ(cid:5)2
=
2(cid:5)δ(cid:5)2
F
F + (cid:5)δ(cid:5)2
F
2(cid:5)Y(cid:5)2
=
(cid:5)δ(cid:5)2
F
(cid:5)Y(cid:5)2
F
⎞
⎟
⎠ =
⎛
⎜
⎝
1
1 + (cid:5)δ(cid:5)2
F
2(cid:5)Y(cid:5)2
F
(cid:13)
(cid:5)δ(cid:5)2
F
(cid:5)Y(cid:5)2
F
(cid:14)
1 − O((cid:6)2)
.
Sin embargo, if Y is close to 0, our metric can be different. Por ejemplo, if Ypred = 1 and Ytrue =
= 2(1 − 0.25)2/(12 + (0.25)2) = 106%. The usual relative mean square
0.25, then MSErel
error would be (1 − 0.25)2/(0.25)2 = 900%. If either Ytrue or Ypred is 0 and the other is not,
then MSErel
= 200%, its maximum value.
Consider a set of experiments {(ce, ¯Y:,mi)}metro
e=1, where ce is the center of mass of the eth injec-
ción. Let C ∈ Rn×m
be the matrix of injection center indicators, with entries Cie = 1{ce=vi}. De-
fine the kernel matrix Ac ∈ Rm×m
as the kernel evaluated at the centers of mass; then this is just
Ac = AC. Thus the model prediction of the center of mass projections is WC = ¯Y AC = ¯Y Ac.
We can perform leave-one-out cross-validation efficiently after computing the coefficients
predicts that
has the eth diagonal entry
Ac for a given set of data. If we leave out experiment e, the new model W(−e)
the projections from ce are ˆY = W(−e)C:,e = ¯YA(−e)
equal to 0 and the corresponding column renormalized to sum to 1. Por lo tanto,
, where A(−e)
C
C
(A(−e)
C
)ij =
⎧
⎪⎪⎪⎨
⎪⎪⎪⎩
(C.A)ij,
(C.A)ij
1−(C.A)ee ,
0,
j (cid:7)= e,
j = e and i (cid:7)= j,
i = j = e.
Extending the above result to compute the leave-one-out predictions for all of the experiments,
we find that these are equal to ¯Y ACV
C
, dónde
⎧
⎨
(ACV
C )ij =
⎩
(C.A)ij
1−(C.A)jj ,
0,
i (cid:7)= j,
i = j.
De este modo, once we compute the coefficients Ac, we set the diagonals equal to 0 and renormalize
the columns to obtain ACV
. The leave-one-out cross-validation relative error of the voxel model
is then
C
2(cid:5) ˆY − ¯Y(cid:5)2
F
F + (cid:5) ¯Y(cid:5)2
(cid:5) ˆY(cid:5)2
F
,
(5)
where ˆY = ¯Y ACV
C
are the leave-one-out predictions.
Regionalized and Homogeneous Models
The application of Equation (1) results in a very large n × n voxel-scale connectivity matrix.
Recall that we defined a parcellation of the brain into r regions R. We would like to be able to
compare this with extant regional connectomes, which are smaller r × r matrices. With this,
we can define the regional projection matrix, Π ∈ Rr×n
, with entries:
Πij = 1{vj∈Ri}.
Eso es, the ith row of Π has ones in entries corresponding to voxels in region i. Por lo tanto,
for some vector x ∈ Rn
corresponding to a voxel image of the brain, the vector xR = Π x
Neurociencia en red
232
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
1
2
1
7
1
0
9
2
3
7
3
norte
mi
norte
_
a
_
0
0
0
6
6
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
High-resolution model of the mouse connectome
has entries corresponding to the sum of x over regions. Además, consider another matrix
Π† ∈ Rn×r
, with entries:
Π†
ij =
1{vi∈Rj}
|Rj|
,
dónde |Rj| is the number of voxels in region j. Then Π†, operating from the left on a length r
vector, spreads the entries evenly over all of the voxels in a given region. Operating from the
bien, it averages over the voxels in a region. Note that Π Π† = Ir, so it is a right inverse of Π
and in fact is a Moore-Penrose pseudoinverse.
With this notation, it becomes simple to convert voxel vectors and matrices into regional
unos. We refer to the sum of the connection weights between two regions as the connection
strength between the regions. De este modo, the regional connection strength is given by
WR = Π W Π(cid:2)
.
Sin embargo, these regions may be vastly different sizes, in which case a measure normalized
by source and/or target region size is more appropriate. We define the normalized projection
density as the connection strength between two regions divided by the size of the source and
target region. En este caso, the matrix becomes
WR,norm density = Π†(cid:2) W Π†.
Finalmente, our last normalization only normalizes by the size of the source region, which we call
normalized connection strength:
WR,norm strength = Π W Π†.
This normalization is necessary to compare directly with the homogeneous model.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
1
2
1
7
1
0
9
2
3
7
3
norte
mi
norte
_
a
_
0
0
0
6
6
pag
d
.
t
Normalized connection strength:
The connection strength from R
R
1 a
2 divided by the size of the source
región:
WR
21
|R1|
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
As in Oh et al. (2014), one could also fit a regional
Fitting a homogeneous regional model.
model where connection strengths are fixed across regions by working directly with data that
have been regionalized. We performed this for comparison and refer to the result as the homo-
geneous model. Let XR = Π X and YR = Π Y. Then the model fit to these regional data is
found via nonnegative least squares as
Whomog = arg min
W. (cid:8)≥0
(cid:5)W.(cid:8)XR − YR(cid:5)2
F.
(6)
Note that the output Whomog is a normalized connection strength, since entry (i, j) es el
expected volume of fluorescence in region i per unit of virus in region j.
Let ˆY ∈ Rn
be the voxel
Comparing the regionalized voxel model to the homogeneous model.
predicción; we can compute the regionalized prediction ˆYR ∈ Rr
by projecting the voxel
predictions into the regional space: ˆYR = Π ˆY. It is important to note that although the com-
parison between the regionalized voxel model and the homogeneous model are done in the
same space Rr
, the predictions themselves are slightly different. The regionalized voxel predic-
tions ˆYR
:,e are the predicted result of a unit injection into the center of mass of the injection ce,
whereas the regional prediction ˆYR
:,e = Whomog X:,e is the regional prediction of the projection
from the full injection X:,mi.
Neurociencia en red
233
High-resolution model of the mouse connectome
To check individual experiments for segmentation er-
Manual checks of regional projections.
rors, we used the interactive projection experiment detail view page of the Allen Mouse Brain
Connectivity Atlas (p.ej., http://connectivity.brain-map.org/projection/experiment/100141219).
We first set the “projection volume” threshold to 0 so that all targets were displayed, then se-
lected the bar graph for all ipsilateral and contralateral targets to align the raw image viewer
for each. The viewer automatically centers on the area with the highest signal in each anatom-
ical region. Sin embargo, when no projections were initially apparent we checked several sec-
tions rostral and caudal to the initial location as well as the surrounding region. Target regions
that contained eGFP-expressing axons were labeled 1 (true positive). If no projections were
observed the target was assigned a 0 (true negative). In cases where there were a small num-
ber of axons that appeared to be passing fibers without branches or boutons, we assigned
the target a 0. Most segmentation errors were caused by tissue edges or blood vessels that
were detected by the automatic segmentation algorithm. See Figure S1 (Knox et al., 2019).
The following manually validated experiments were used to compare model weights to exper-
imental data: 100141219, 100147853, 309113907, 479756361, 500836840, 500837552,
522409371, 546103149, 112424813, 117298988, 126908007, y 180916954. el primero
eight are the VISp injections plotted in Figure 7.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
EXPRESIONES DE GRATITUD
This work was supported by the Allen Institute for Brain Science. The authors wish to thank
the Allen Institute founder, Paul G. allen, for his vision, encouragement, and support. adi-
cionalmente, the project described was supported in part by the National Institute on Aging of the
Institutos Nacionales de Salud. Its contents are solely the responsibility of the authors and do not
necessarily represent the official views of the National Institutes of Health. We would like to
thank Lydia Ng and Nathan Gouwens for assistance with the cortical flattening.
SUPPORTING INFORMATION
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
1
2
1
7
1
0
9
2
3
7
3
norte
mi
norte
_
a
_
0
0
0
6
6
pag
d
.
t
All of the data used to construct these models are available at http://connectivity.brain-map.
org. The data used in this analysis were cached in March 2017. The curved coordinate
system is described in http://help.brain-map.org/download/attachments/2818171/Mouse_
Common_Coordinate_Framework.pdf, with the specific data available from http://download.
alleninstitute.org/informatics-archive/current-release/mouse_ccf/cortical_coordinates/ccf_2017.
All code used to build this model is available from https://github.com/AllenInstitute/mouse_
connectivity_models (Knox, 2018).
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
CONTRIBUCIONES DE AUTOR
José E.. Knox: Análisis formal;
Investigación; Metodología; Software; Visualización;
Escritura – borrador original; Escritura – revisión & edición. Kameron Decker Harris: Conceptualiza-
ción; Análisis formal; Investigación; Metodología; Software; Visualización; Writing – original
borrador; Escritura – revisión & edición. Nile Graddis: Software; Escritura – revisión & edición. Jennifer
D. Whitesell: Validación; Visualización; Escritura – borrador original; Escritura – revisión & edición.
Hongkui Zeng: Supervisión. Julie A. harris: Curación de datos; Supervisión; Validación; Writing –
revisar & edición. Eric Shea-Brown: Conceptualización; Supervisión; Escritura – revisión & edit-
En g. Stefan Mihalas: Conceptualización; Supervisión; Escritura – borrador original; Escritura – revisión
& edición.
Neurociencia en red
234
High-resolution model of the mouse connectome
INFORMACIÓN DE FINANCIACIÓN
Julie A. harris, National Institute on Aging (http://dx.doi.org/10.13039/100000049), Award ID:
R01AG047589. Kameron Decker Harris, Directorate for Mathematical and Physical Sciences
(http://dx.doi.org/10.13039/100000086), Award ID: 1122106. Eric Shea-Brown, Directorate
for Mathematical and Physical Sciences (http://dx.doi.org/10.13039/100000086), Award ID:
1514743. Kameron Decker Harris, Big Data for Genomics & Neuroscience Training Grant,
Award ID: 1T32CA206089-01A1.
REFERENCIAS
Bock, D. D., Sotavento, W.-C. A., Kerlin, A. METRO., Andermann, METRO. l., Hood,
GRAMO., Wetzel, A. w., . . . Reid, R. C. (2011). Network anatomy and
in vivo physiology of visual cortical neurons. Naturaleza, 471(7337),
177–182. https://doi.org/10.1038/nature09802
Bohland, j. w., Wu, C., Barbas, h., Bokil, h., Bota, METRO., Breiter, h. C.,
. . . Mitra, PAG. PAG. (2009). A proposal for a coordinated effort for
the determination of brainwide neuroanatomical connectivity in
model organisms at a mesoscopic scale. PLoS computacional
Biología, 5(3), e1000334. https://doi.org/10.1371/journal.pcbi.
1000334
Bota, METRO., Dong, H.-W., & Swanson, l. W.. (2003). From gene net-
works to brain networks. Neurociencia de la naturaleza, 6(8), 795–799.
https://doi.org/10.1038/nn1096
Ercsey-Ravasz, METRO., Markov, norte. T., lamy, C., VanEssen, D. C.,
Knoblauch, K., Toroczkai, Z., & Kennedy, h. (2013). A predic-
tive network model of cerebral cortical connectivity based on a
distance rule. Neurona, 80(1), 184–197. https://doi.org/10.1016/
j.neuron.2013.07.036
Felleman, D. J., & VanEssen, D. C. (1991). Distributed hierarchical
processing in the primate. Corteza cerebral, 1(1), 1–47. https://
doi.org/10.1093/cercor/1.1.1
G˘am˘anu¸t, r., Kennedy, h., Toroczkai, Z., Ercsey-Ravasz, METRO.,
VanEssen, D. C., Knoblauch, K., & Burkhalter, A. (2018). El
mouse cortical connectome, characterized by an ultra-dense cor-
tical graph, maintains specificity by distinct connectivity profiles.
Neurona, 97(3), 698–715.e10. https://doi.org/10.1016/j.neuron.
2017.12.037
Glickfeld, l. l., Andermann, METRO. l., Bonin, v., & Reid, R. C. (2013).
Cortico-cortical projections in mouse visual cortex are func-
tionally target specific. Neurociencia de la naturaleza, 16(2), 219–226.
https://doi.org/10.1038/nn.3300
harris, j. A., Mihalas, S., Hirokawa, k. MI., Whitesell, j. D., Knox,
J., Bernard, A., . . . Zeng, h. (2018). The organization of intra-
cortical connections by layer and cell class in the mouse brain.
bioRxiv:292961. https://doi.org/10.1101/292961
harris, k. D., Mihalas, S., & Shea-Brown, mi. (2016). High resolution
neural connectivity from incomplete tracing data using nonnega-
tive spline regression. In D. D. Sotavento, METRO. Sugiyama, Ud.. V. Luxburg,
I. Guyon, & R. Garnett (Editores.), Advances in Neural Information
Sistemas de procesamiento 29.
Jenett, A., Frotar, GRAMO. METRO., Ngo, T.-T. B., Shepherd, D., Murphy, C.,
Dionne, h., . . . Zugates, C. t. (2012). A GAL4-driver line
resource for Drosophila neurobiology. Informes celulares, 2(4),
991–1001. https://doi.org/10.1016/j.celrep.2012.09.011
Kleinfeld, D., Bharioke, A., Blinder, PAG., Bock, D. D., Briggman,
k. l., Chklovski, D. B., . . . Sakmann, B. (2011). Large-scale
automated histology in the pursuit of connectomes. Diario de
Neurociencia, 31(45), 16125–16138. https://doi.org/10.1523/
JNEUROSCI.4077-11.2011
Knox, j.
(2018). Python package providing mesoscale connectiv-
ity models for mouse, Github, https://github.com/AllenInstitute/
mouse_connectivity_models
Knox, j. MI., Decker Harris, K., Graddis, NORTE., Whitesell, j. D., Zeng, h.,
harris, j. A., . . . Mihalas, S. (2019). Supporting information for
“High-resolution data-driven model of the mouse connectome.”
Neurociencia en red, 3(1), 217–236. https://doi.org/10.1162/
netn_a_00066
Kuan, l., li, y., Lau, C., feng, D., Bernard, A., Sunkin, S. METRO.,
. . . Ng, l. (2015). Neuroinformatics of the Allen Mouse Brain
Connectivity Atlas. Métodos, 73, 4–17. https://doi.org/10.1016/
j.ymeth.2014.12.013
Laramée, M.-E., & Boire, D. (2015). Visual cortical areas of the
mouse: Comparison of parcellation and network structure with
primates. Frontiers in Neural Circuits, 8, 149. https://doi.org/10.
3389/fncir.2014.00149
Majka, PAG., Chaplin, t. A., Yu, H.-H., Tolpygo, A., Mitra, PAG. PAG.,
Wójcik, D. K., & Rosa, METRO. GRAMO. PAG. (2016). Towards a comprehen-
sive atlas of cortical connections in a primate brain: Cartografía
tracer injection studies of the common marmoset into a reference
digital template. Journal of Comparative Neurology, 524(11),
2161–2181. https://doi.org/10.1002/cne.24023
Markov, norte. T., Ercsey-Ravasz, METRO. METRO., Ribeiro Gomes, A. r., lamy,
C., Magrou, l., Vezoli, J., . . . Kennedy, h. (2014). A weighted
and directed interareal connectivity matrix for macaque cerebral
corteza. Corteza cerebral, 24(1), 17–36. https://doi.org/10.1093/
cercor/bhs270
Nadaraya, mi. A. (1964). On estimating regression. Theory of Prob-
ability and Its Applications, 9(1), 141–142.
Oh, S. w., harris, j. A., Ng, l., Winslow, B., Cain, NORTE., Mihalas, S.,
(2014). A mesoscale connectome of the mouse
. . . Zeng, h.
cerebro. Naturaleza, 508(7495), 207–214. https://doi.org/10.1038/
nature13186
Ragan, T., Kadiri, l. r., Venkataraju, k. Ud., Bahlmann, K., Sutin, J.,
Taranda, J., . . . Osten, PAG. (2012). Serial two-photon tomography
for automated ex vivo mouse brain imaging. Nature Methods,
9(3), 255–258. https://doi.org/10.1038/nmeth.1854
Rubinov, METRO., ypma, R.
j. F., watson, C., & bullmore, mi. t.
(2015). Wiring cost and topological participation of the mouse
Neurociencia en red
235
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
1
2
1
7
1
0
9
2
3
7
3
norte
mi
norte
_
a
_
0
0
0
6
6
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
High-resolution model of the mouse connectome
brain connectome. Actas de la Academia Nacional de
Ciencias, 112(32), 10032–10037. https://doi.org/10.1073/pnas.
1420315112
Sethi, S. S., Zerbi, v., Wenderoth, NORTE., Proporcionó, A., & Fulcher, B. D.
(2017). Structural connectome topology relates to regional BOLD
signal dynamics in the mouse brain. Chaos: An Interdisciplinary
Journal of Nonlinear Science, 27(4), 047405. https://doi.org/10.
1063/1.4979281
Shih, C.-T., despreciar, o., Yuan, S.-L., Su, T.-S., lin, Y.-J., Chuang,
C.–C., . . . Chiang, A.–S.
(2015). Connectomics-based analy-
sis of information flow in the Drosophila brain. Biología actual,
25(10), 1249–1258. https://doi.org/10.1016/j.cub.2015.03.021
despreciar, oh. (2010). Networks of the brain. Cambridge, MAMÁ: CON prensa.
Stafford, j. METRO., Jarrett, B. r., Miranda-Dominguez, o., Mills, B. D.,
Cain, NORTE., Mihalas, S., . . . Fair, D. A. (2014). Large-scale topol-
ogy and the default mode network in the mouse connectome.
procedimientos de la Academia Nacional de Ciencias, 111(52),
18745–18750.
Wahba, GRAMO. (1990). Spline models for observational data. Filadelfia,
Pensilvania: SIAM.
Wang, P., despreciar, o., & Burkhalter, A. (2012). Network analysis
of corticocortical connections reveals ventral and dorsal pro-
cessing streams in mouse visual cortex. Revista de neurociencia,
32(13), 4386–4399. https://doi.org/10.1523/JNEUROSCI.6063-
11.2012
Wang, X.-J., & Kennedy, h. (2016). Brain structure and dynamics
across scales: In search of rules. Current Opinion in Neurobiol-
ogia, 37(Suplemento. C), 92–98. https://doi.org/10.1016/j.conb.2015.
12.010
watson, GRAMO. S.
(1964). Smooth regression analysis. Sankhy ¯a: El
Indian Journal of Statistics, Series A (1961–2002), 26(4), 359–372.
(1986).
The structure of the nervous system of the nematode Caenorhab-
ditis elegans. Philosophical Transactions of the Royal Society of
London B: Ciencias Biologicas, 314(1165), 1–340. https://doi.
org/10.1098/rstb.1986.0056
Blanco, j. GRAMO., Southgate, MI., Thomson, j. NORTE., & Brennero, S.
ypma, R. j. F., & bullmore, mi. t. (2016). Statistical analysis of
tract-tracing experiments demonstrates a dense, complex corti-
cal network in the mouse. Biología Computacional PLoS, 12(9),
e1005104. https://doi.org/10.1371/journal.pcbi.1005104
Zingg, B., Hintiryan, h., Gou, l., Song, METRO., Bay, METRO., Bienkowski,
METRO., . . . Dong, H.-W. (2014). Neural networks of the mouse neo-
corteza. Cell, 156(5), 1096–1111. https://doi.org/10.1016/j.cell.
2014.02.023
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
1
2
1
7
1
0
9
2
3
7
3
norte
mi
norte
_
a
_
0
0
0
6
6
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Neurociencia en red
236