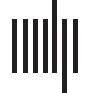FUNCIÓN DE ENFOQUE:
New Trends in Connectomics
Putting the “dynamic” back into dynamic
conectividad funcional
Stewart Heitmann
1
and Michael Breakspear
1,2
1QIMR Berghofer, Brisbane, Australia
2Metro North Mental Health Service, Brisbane, Australia
Palabras clave: Dynamic functional connectivity, Nonlinear dynamics, Metastability, Multistability
un acceso abierto
diario
ABSTRACTO
The study of fluctuations in time-resolved functional connectivity is a topic of substantial
current interest. As the term “dynamic functional connectivity” implies, such fluctuations
are believed to arise from dynamics in the neuronal systems generating these signals.
While considerable activity currently attends to methodological and statistical issues
regarding dynamic functional connectivity, less attention has been paid toward its candidate
causes. Aquí, we review candidate scenarios for dynamic (functional) connectivity that arise
in dynamical systems with two or more subsystems; generalized synchronization, itinerancy
(a form of metastability), and multistability. Each of these scenarios arises under different
configurations of local dynamics and intersystem coupling: We show how they generate time
series data with nonlinear and/or nonstationary multivariate statistics. The key issue is that
time series generated by coupled nonlinear systems contain a richer temporal structure
than matched multivariate (linear) stochastic processes. Sucesivamente, this temporal structure
yields many of the phenomena proposed as important to large-scale communication and
computation in the brain, such as phase-amplitude coupling, complejidad, and flexibility.
The code for simulating these dynamics is available in a freeware software platform, el
Brain Dynamics Toolbox.
RESUMEN DEL AUTOR
The study of network fluctuations in time-resolved functional connectivity is a topic of
substantial current interest. Sin embargo, the topic remains hotly disputed, with both positive
and negative reports. A number of fundamental issues remain disputed, including statistical
benchmarks and putative causes of nonstationarities. Dynamic models of large-scale brain
activity can play a key role in this field by proposing the types of instabilities and dynamics
that may be present. The purpose of the present paper is to employ simple dynamic models
to illustrate the basic processes (“primitives”) that can arise in neuronal ensembles and that
might, under the right conditions, cause true nonlinearities and nonstationarities in empirical
datos.
INTRODUCCIÓN
The brain is a dynamic machine par excellence,
tuned through the principles of self-
organization to anticipate the statistics and movement of the external milieu (k. Friston, 2013;
Citación: Heitmann, S., & romper la lanza,
METRO. (2018). Putting the “dynamic” back
into dynamic functional connectivity.
Neurociencia en red, 2(2), 150–174.
https://doi.org/10.1162/netn_a_00041
DOI:
https://doi.org/10.1162/netn_a_00041
Supporting Information:
https://doi.org/10.1162/netn_a_00041
Recibió: 27 Agosto 2017
Aceptado: 30 December 2017
Autor correspondiente:
Michael Breakspear
mjbreaks@gmail.com
Editor de manejo:
Danielle Bassett
Derechos de autor: © 2018
Instituto de Tecnología de Massachusetts
Publicado bajo Creative Commons
Atribución 4.0 Internacional
(CC POR 4.0) licencia
La prensa del MIT
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
0
2
0
2
1
5
0
1
0
9
2
1
8
4
norte
mi
norte
_
a
_
0
0
0
4
1
pag
d
/
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Putting the “dynamic” back into dynamic functional connectivity
Skarda & Hombre libre, 1987). Its unceasing dynamics and cycle of prediction-action-perception
mark it as distinct from even the most advanced deep learning platforms despite impressive
advances in machine learning. Systems neuroscience is likewise incorporating dynamic algo-
rithms into its core methodologies (romper la lanza, 2017; k. j. Friston, harrison, & Penny, 2003),
in the design of hierarchical models of perception and inference (Mathys, Daunizeau, Friston,
& Esteban, 2011); dynamic approaches to clinical disorders (Roberts, Friston, & romper la lanza,
2017); dynamic models of functional neuroimaging data (Stephan et al., 2008; lana rica &
Esteban, 2013); and dynamic frameworks for the analysis of resting state fMRI data (decoración,
Jirsa, & McIntosh, 2011). Dynamic models are at the heart of the distinction between func-
tional connectivity and effective connectivity (see Box 1; k. j. Friston, 2004) and can help
disambiguate correlated activity due to mutual interactions from that caused by input from a
common source.
Box 1. Definitions
Conectividad funcional: The statistical correlation between remote neurophysiological
recordings (fMRI voxels, EEG channels, reconstructed sources). May be symmetrical (p.ej.,
Pearson’s correlation coefficient) or asymmetrical (p.ej., partial correlation coefficient).
Effective connectivity: The inferred influence of one neuronal population on another. Ef-
fective connectivity cannot be directly estimated from linear or nonlinear metrics of time
series interdependence but rests upon estimation of a generative model of causal interactions
(k. j. Friston, 2004).
Autonomous dynamical system: A group of interacting units (such as neurons) evolving over
time whose interactions do not depend on a time parameter. Mathematically, those states can
be approximated by an evolution equation of the following form:
dX
dt
= f (X) ,
where f is a function that captures the interactions in the system and X is a vector of the
variables {X, y, …}.
Nonlinear dynamical system: The evolution equations for the system contain at least one
nonlinear term (p.ej., f = x2y). En general, nonlinear systems exhibit complex dynamics (semejante
as chaos) that cannot be closely approximated by a suitable linear reduction (as in noise-
driven fluctuations near an equilibrium point).
Stationarity: We adopt the simple notion of so-called weak-sense stationarity (Liegeois et al.,
2017), namely that the time-lagged autocorrelation and cross-correlation functions are invari-
ant to time shifts. Eso es, if Xt and if Yt are random processes for t = 1, 2, …, then for any
arbitrary integers k, yo, metro, y N,
k − l = m − n → Cov (Xk, Yl ) = Esos (Xn, Ym) ,
(cid:2)
(cid:3)
(cid:4)
(cid:2)
(cid:2)
(cid:3)(cid:3)(cid:5)
Xi, Yj
= mi
(Xi − E (Xi))
Yj − E
Yj
is the covariance function between
where Cov
Xt and Yt.
Research into the dynamics of resting-state fMRI data is currently very active, and takes
its form largely through the study of nonstationarities in time-resolved functional con-
conectividad (Chang & guantero, 2010; Hutchison et al., 2013; Brilla, Proporcionó, cocineros, Perdido, &
romper la lanza, 2014). Sin embargo, the topic remains hotly disputed, with both positive (Abrol et al.,
2017; Nomi et al., 2017; Zalesky et al., 2014) and negative (Laumann et al., 2016) reports.
Además, fundamental statistical issues continue to be contested, including the utility of
Neurociencia en red
151
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
0
2
0
2
1
5
0
1
0
9
2
1
8
4
norte
mi
norte
_
a
_
0
0
0
4
1
pag
d
.
/
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Putting the “dynamic” back into dynamic functional connectivity
Time series:
Time-dependent measurements of a
dynamic system, such as EEG and
fMRI data from the cortex.
Metastability:
The behavior of a system without
any stable attractors, but rather a
sequence of weakly attracting
saddles; conjuntos (such as fixed points or
periodic attractors) that are attracting
in some directions, but are repelling
in at least one direction.
Multistability:
The behavior of a system with
multiple attractors which is then
driven by sufficient noise to make
the states jump erratically from one
attractor to the next. In the absence
of noise, the system will settle
indefinitely onto one attractor.
Neural mass:
A local population of excitatory
(and/or inhibitory) neurons whose
states are not treated individually, pero
rather averaged together and treated
as a single collective entity.
sliding-window analyses (Hindriks et al., 2016; Leonardi & Van De Ville, 2015; Brilla &
romper la lanza, 2015) as well as core definitions of stationarity (Liegeois, Laumann, Snyder, zhou,
& yo, 2017). Another issue of substance pertains to the causes of putative nonstationarities
(assuming they exist); En particular, whether nonstationarities reflect subtle cognitive processes
(random episodic spontaneous thought, es decir., “rest”; romper la lanza, williams, & estampar, 2004);
whether they are slower processes that nonetheless retain cognitive salience (such as drifts
in attention and arousal; Verano, Hove, Esterman, hutchison, & Valera, 2016); or whether they
are nuisance physiological and head motion covariates that have been inadequately removed
from fMRI time series (Laumann et al., 2016). Regardless of these debates, the overarching
motivation of the field is that resting-state brain activity is endowed with functionally relevant
complex neuronal dynamics—either as the substrate for ongoing “thought,” or to prime the
cortex for perception and action (k. Friston, romper la lanza, & decoración, 2012). So, the central ques-
tion seems not whether such neuronal dynamics exist, but to what extent they can be detected
in functional neuroimaging data.
Dynamic models of large-scale brain activity can play a key role in this field by propos-
ing the types of instabilities and dynamics that may be present (Cabral, Kringelbach, & decoración,
2014; decoración, Jirsa, McIntosh, despreciar, & kötter, 2009; Perdido, Brilla, hutchison, van den
Colina, & romper la lanza, 2015; Hansen, battaglia, Spiegler, decoración, & Jirsa, 2015; C. j. Honey,
kötter, romper la lanza, & despreciar, 2007). The purpose of the present paper is to employ simple
dynamic models to illustrate the basic processes (“primitives”) that can arise in neuronal
ensembles and that might, under the right conditions, cause true nonlinearities and non-
Al hacerlo, we also aim to disambiguate some key terms
stationarities in empirical data.
in the field: primero, the differences between nonstationarity and nonlinearity—both can herald
underlying dynamics, cause rejection of common nonparametric nulls, y (as we will see)
occur individually or together; segundo, the distinctions between key terms in dynamic systems
theory, especially the catchphrase terms of metastability and multistability (which are often
used interchangeably). Hopefully this is a constructive step toward a more definitive resolu-
tion of the uncertainties in the field.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
0
2
0
2
1
5
0
1
0
9
2
1
8
4
norte
mi
norte
_
a
_
0
0
0
4
1
pag
d
t
/
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
MÉTODOS
Coupled Dynamical Systems
To illustrate the breadth of synchronization dynamics, we study an autonomous, nonlinear
system of coupled neural masses. This model has been previously employed to study whole-
brain dynamics (C. j. Honey et al., 2007; Zalesky et al., 2014). The system is composed of
local subsystems (“neural mass,” or nodes) coupled together to form a larger ensemble (for a
revisar, see Breakspear, 2017). Each local node comprises a population of excitatory neurons
and a slow variable incorporating the (simplified) response of a local inhibitory pool of neu-
ron. Inhibitory activity is driven by local excitatory activity, to which it feeds back via a slow
inhibitory current. The dynamics of neural masses are determined by a conductance-based
proceso, with fast (instantaneous) sodium membrane currents and slower potassium currents.
The dynamics within each node takes the form of a low-dimensional nonlinear differential
equation,
dX
dt
= fa (X) ,
(1)
where X is a vector of the system’s variables (cell membrane potentials, firing rates, mem-
brane channel currents). The system has a number of physiologically derived time-invariant
parameters a, such as synaptic connection strengths, membrane channel conductances, y
Neurociencia en red
152
Putting the “dynamic” back into dynamic functional connectivity
Chaos:
A form of dynamical behavior that
can arise from an autonomous
nonlinear system. Chaos is
characterized by sustained aperiodic
(nonrepeating) oscilaciones, leading
to extreme sensitivity of future states
to slight changes in present values of
the system.
Structural connectivity:
Neuronal connections, típicamente
mediated by direct axonal
projections from one neuron
(or neural population) a otro.
Structural connectivity can be
described at the microscopic
(neuronal and neural circuit) a través de
to the large scale macroscopic scale
of whole-brain tractography.
neural gain (romper la lanza, Terry, & Friston, 2003). Depending upon the choice of these parame-
ters, single-node dynamics may range from a steady-state fixed-point attractor, to fast periodic
oscillations and chaos. Here we choose the parameters so that the autonomous behavior of
each neural mass is described in mathematical terms as a nonlinear dynamical system with a
chaotic attractor. This chaotic regime arises from the intrinsic constants and variables within
the local (uncoupled) neural population—specifically from the mixing of the fast timescales of
the pyramidal cells and the slow responses of the inhibitory population. These dynamics do
not depend upon the coupled interactions.
A mesoscopic neural ensemble is constructed by permitting two or more of such local
neural masses {X1, X2, . . .} to interact through a coupling function (romper la lanza & estampar, 2005).
These interactions are parameterized by the matrix of internode coupling C =
,where i
is the source node and j is the receiver node. Connections may be reciprocal but asymmetric
(cij (cid:3)= cji). Hence each node’s dynamics are governed by
cij
(cid:7)
(cid:6)
dXi
dt
= fa(Xi) + Hcij
(cid:8)
(cid:9)
,
Xj
(2)
where i indexes the node and the coupling function H embodies the nature of the internode
influences among all nodes in the system, eso es, the model of effective connectivity. Internode
coupling in this framework is classically composed of excitatory-to-excitatory connectivity.
Sin embargo, there are no restrictions on the general nature of Equation 2 that prohibit inhibitory
internode coupling parameterized in C.
For simulations of empirical macroscopic network behaviors, the connectivity C between
neural masses can be defined by structural connectivity (despreciar, Tononi, & kötter, 2005) rep-
resenting the network of white matter fiber tracts mediating internode connectivity in the brain.
The structural connectomes can be obtained from postmortem tracing studies (Stephan et al.,
2001) or from in vivo human MRI-based tractography. Because of technical limitations of
current state of the art tractography, connectivity matrices derived from MR-based tractography
are symmetric cij = cji.
Although we employ a particular model to illustrate synchronization dynamics, many of the
underlying principles hold for any local system with chaotic dynamics (Pikovsky, Rosenblum,
& Kurths, 2003). Periodic dynamics permit a narrower range of dynamic scenarios. For most
of our simulations, we focus on dyads (pares) of coupled nodes. Complex dynamics on motifs
with three or more nodes derive from the principles of two nodes, but add an additional layer of
complejidad, depending on their connectivity as well as the nature of axonal time delays (Atay,
2010; Cabral, Luckhoo, et al., 2014; Deco et al., 2009; Perdido & romper la lanza, 2014; Perdido,
Mirasso, despreciar, & romper la lanza, 2013). For the moment, we do not consider the role of time
delays in the resulting synchronization dynamics. We return to these issues below.
All simulations in this paper are performed using the Brain Dynamics Toolbox (https://
bdtoolbox.blogspot.com.au/), an open-source Matlab-based toolbox for interactive simu-
lations of neuronal dynamics (as described in Supplementary Information II, Heitmann &
romper la lanza, 2018). The Brain Dynamics Toolbox allows scaling up to simulate large ensem-
bles, the employment of other local node dynamics, the introduction of local stochastic in-
fluences, and the treatment of internode time delays. Readers may also wish to explore The
Virtual Brain (Leon et al., 2013; Sanz-Leon, Knock, Spiegler, & Jirsa, 2015), an open-source
Python-based toolbox specifically designed for simulating whole-brain dynamics according
to the principles explored here.
Neurociencia en red
153
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
0
2
0
2
1
5
0
1
0
9
2
1
8
4
norte
mi
norte
_
a
_
0
0
0
4
1
pag
d
t
/
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Putting the “dynamic” back into dynamic functional connectivity
Quantifying and Testing Time Series Dynamics
The detection and quantification of the linear correlations or nonlinear interdependence in
time series data rests upon two related steps: (a) the employment of a metric that captures
estos (linear or nonlinear) propiedades; y (b) the application of a statistical test to ascertain
whether the value of this metric is statistically significant according to an appropriate null
hypothesis. The second of these steps recognizes the fact that such metrics are never exactly
zero when applied to noisy time series of finite length. en este documento, we use the method of
surrogate data to achieve the latter goal. Both steps are now described in further detail.
Dynamic metrics. We employ two metrics of internode interactions: the traditional Pearson’s
correlation coefficient, and a measure of nonlinear interdependence based upon time series
forecasting methods (Schiff, So, Chang, Burke, & Sauer, 1996; Terry & romper la lanza, 2003).
These are sensitive to stationary linear correlations (traditional time-averaged functional con-
conectividad) and stationary nonlinear interdependence, respectivamente. The latter estimates a (nor-
malized) prediction error based upon forward projections of each system’s dynamic trajectory:
It approaches 0 for highly structured, completely predictable nonlinear time series and di-
verges quickly toward a maximum error of 1 when the time series have no structure. Fundamentalmente,
the measure is sensitive to nonlinearities in the time series, possessing higher values for non-
linear time series than for random time series with the same (cross- and autocorrelation) linear
propiedades. There are two versions: Self-predictions are sensitive to nonlinearities within a
time series, whereas cross-predictions are sensitive to nonlinear interdependences between
subsystems.
Estimates of dynamic, instantaneous interactions are obtained by examining the behavior
of phase differences between time series. The Hilbert transform is first applied to each system’s
time series, allowing an estimate of the instantaneous phase (and amplitude) of a signal (Tass
et al., 1998). The Hilbert transform of a time series x(t) is given by
Y(t) =
(cid:10)
1
Pi
X(t)
t − τ
dτ,
which can be used to compose the analytic signal,
Λ(t) = x(t) + iY(t) = A(t)eiφ(t),
(3)
(4)
which uniquely defines the instantaneous amplitude A(t) and phase φ(t) of the signal x(t). Phase
dynamics between two signals xi(t) and xj(t) are then given by
(cid:11)
ϕ(t) =
φi(t) − φj(t)
(cid:12)
mod 2π.
(5)
In finite length, autocorrelated time series, measures of (linear and non-
Surrogate algorithms.
linear) sample correlations are generally not 0, even for uncoupled, independent systems.
Measures of correlation taken from large numbers of samples do center at 0, but the vari-
ance across individual samples can be substantial. To perform statistical inference on the
typically modest number of data available, it is thus necessary to compare empirical mea-
sures of coupling to a null distribution derived from ensembles of surrogate data: These are
pseudo time series derived from empirical data by resampling methods that preserve the time
series length, autocorrelation structure, and amplitude distribution but have had the property of
interés (nonstationarity, nonlinearity) destroyed. If the empirical measure falls outside of the
null distribution, then the data can be inferred to contain that property of interest.
Neurociencia en red
154
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
0
2
0
2
1
5
0
1
0
9
2
1
8
4
norte
mi
norte
_
a
_
0
0
0
4
1
pag
d
.
/
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Putting the “dynamic” back into dynamic functional connectivity
For the present study, we employ a nonparametric phase-randomization method (Theiler,
Eubank, Longtin, Galdrikian, & Doyne Farmer, 1992). Briefly, multivariate data are mapped
into the frequency domain by application of the Fourier transform. The phase of each fre-
quency is then independently rotated by a random increment between 0 and 2π. Los datos
are then transformed back to the time domain. By leaving the amplitude of each frequency
untouched, this process preserves the power spectrum of the time series and hence the lin-
ear autocorrelations. By rotating the phases of different time series (in a multivariate stream)
by the same random increment, the cross-correlations are also preserved (Prichard & Theiler,
1994). An additional step restores the amplitude distribution of the original time series, cual
is otherwise rendered Gaussian (Schreiber & Schmitz, 1996). This resampling approach can
be adapted for complex three-dimensional data enclosed within a bounded spatial domain,
such as whole-brain fMRI, by using the wavelet transform (romper la lanza, Brammer, bullmore,
El, & williams, 2004).
Phase randomization works because trajectories in smooth continuous dynamical systems
(Ecuación 1) generate time series with highly structured phase relationships across frequencies.
To test for significant linear cross-correlations, we simply shift the time series relative to one
otro (thus preserving auto- but destroying cross-correlations) and test the original against
the correlations from the time-shifted surrogate data. To test for nonlinearities within a single
time series, we perform phase randomization and compare the nonlinear self-prediction errors
of the original time series to the ensuing surrogate distribution. Finalmente, to establish nonlinear
interdependence, we apply a multivariate phase randomization and compare the nonlinear
cross-predictions of original and surrogate ensemble.
RESULTADOS
We first explore the emergence of dynamic synchrony between two interacting neural masses,
each with three dynamical variables X (t) = {V, W., z} exhibiting local chaotic dynamics.
Específicamente, we examine the dynamics of two uncoupled nodes,
then two nodes with
strong and weak coupling. We plot and analyze the time series corresponding to the average
membrane potential of each system, V1 and V2. In later sections, we consider the principles
underlying larger ensembles and the translation of these dynamics into the setting of noisy
experimental data.
Uncoupled Systems
In the absence of coupling cij = cji = 0, the two coupled neural subsystems evolve inde-
pendently (Cifra 1). Because of their intrinsic aperiodic dynamics, the two systems evolve in
and out of phase even if their parameters are identical. Plotting the time series of one system
V1 directly against the other V2 reveals the lack of any underlying synchronization structure
(Figura 1B). Como resultado, the difference between the two systems’ phase (modulus 2p) unwinds
(Figura 1C). Es, sin embargo, important to note that because of the autocorrelations within each
time series, the linear correlation coefficient is often not close to 0 for any particular finite
length sample: The correlation coefficient for the time series shown in Figure 1A is 0.08.
Sin embargo, the distribution of the linear correlation coefficient from an ensemble of repeated
realizations of the time series is centered at 0 (Figure 1D). This is a reminder that anecdotal
observations of nonzero correlations can easily be misinterpreted as functional connectivity
in the data, where there is none.
Surrogate data generated from the time series in Figure 1A by (multivariate) phase random-
ization are shown in Figure 1E. The distribution of linear correlations between time series
Neurociencia en red
155
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
0
2
0
2
1
5
0
1
0
9
2
1
8
4
norte
mi
norte
_
a
_
0
0
0
4
1
pag
d
.
/
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Putting the “dynamic” back into dynamic functional connectivity
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
0
2
0
2
1
5
0
1
0
9
2
1
8
4
norte
mi
norte
_
a
_
0
0
0
4
1
pag
d
t
/
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 1. Uncoupled systems. (A) Time series for two uncoupled neural masses (V1 is black, V2 is
gray) in the chaotic regime. (B) The same time series with V1 plotted against V2. Transients (t < 100)
have been omitted. (C) Hilbert phase of V1 relative to V2. Plotted in cylindrical coordinates with unit
radius. (D) Distribution of linear correlations between V1 and V2 for multiple simulation runs with
random initial conditions. (E) Amplitude-adjusted surrogates for the time series from panel A. (F)
Distribution of linear correlations between surrogate data drawn from the same instances of V1 and
V2 (i.e., one simulation run, multiple shuffles of the surrogate data). (G) Nonlinear self-prediction
of V1 from itself (black) and from surrogate data (red). Note that both errors grow toward one with
longer prediction horizons, but the original data falls well below the null distribution. (H) Nonlinear
cross-prediction of V1 from V2 (black) and from surrogate data (red). Here the empirical data falls
within the surrogate distribution, reflecting the absence of intersystem coupling.
generated by repeated application of phase randomization are shown in Figure 1F: It can be
seen that the empirical correlation (0.08) falls within the surrogate distribution. This observa-
tion confirms that the ensemble of surrogate data does adequately represent the null distribu-
tion of trivial linear correlations that arise because of the finite sample length.
Do these data contain further (i.e., nonlinear) structure? This can be tested by studying
the nonlinear prediction errors, specifically how forward projections of one system’s orbits
Network Neuroscience
156
Putting the “dynamic” back into dynamic functional connectivity
predict the actual evolution of either that same system (nonlinear self-prediction error) or
the other system (nonlinear cross-prediction error; Schiff et al., 1996; Terry & Breakspear,
2003). Because this approach is based upon a low-dimensional phase space reconstruction, it
is sensitive to nonlinear, as well as linear, correlations within the data. Here we see that such
forward predictions (of one system predicting itself, Figure 1G, and of one system predicting
the other, Figure 1H) are less than their theoretical maximal value of 1 (black lines). The non-
linear (self-) prediction errors fall well below the forward predictions arising from surrogate
data (red lines), because the original time series have internal nonlinear structure, arising from
the local chaotic dynamics. However, the nonlinear cross-prediction errors fall within the null
distribution, because there is no coupling and thus no nonlinear interdependence.
In sum, uncoupled chaotic neuronal dynamics give rise to autocorrelated time series with
trivial linear cross-correlations that distribute around 0. Nonlinear self-prediction errors lie
outside the null distribution, confirming that each time series contains nonlinear (chaotic)
structure. However, nonlinear cross-prediction errors fall within the null distribution generated
by surrogate data that contain the same linear correlations. That is, these data arise from
independent (uncoupled) stationary nonlinear processes.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
0
2
0
2
1
5
0
1
0
9
2
1
8
4
n
e
n
_
a
_
0
0
0
4
1
p
d
.
/
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Generalized synchronization:
Two or more coupled systems exhibit
generalized synchronization when
there exists a smooth and continuous
mapping between the states of one
system and the states of the other.
Synchronization manifold:
A smooth (continuous and
differentiable) surface that lies within
a complex system’s phase space,
onto which its orbits settle once
generalized synchronization is
achieved.
Network Neuroscience
Generalized Synchronization
In the presence of strong unidirectional coupling, such as c12 = 0.6, c21 = 0, two neural sub-
systems with identical parameters exhibit a rapid convergence to complete synchrony; that is,
the second (slave) system rapidly adjusts its dynamics to match those of the first (master) system
(Figure 2). Thereafter the two systems pursue identical orbits; that is, they exhibit identical syn-
chronization, evidenced by their rapid convergence to perfect phase synchrony (Figure 2C),
and their states approach the hyperdiagonal in phase space, V1 = V2, W1 = W2, Z1 = Z2. For
simplicity, we plot a two-dimensional cross section through the full dimensional phase space
spanned by V1 and V2 (Figure 2C). It can be seen that the initial transient (gray line) rapidly
converges onto the hyperdiagonal (black line).
The onset of identical synchrony occurs for much weaker internode coupling if it is bidirec-
tional, c12 = 0.05, c21 = 0.05. This is because both systems are able to simultaneously adjust
their internal dynamics according to the state of the other system, leading to a more stable,
integrated system.
Biological systems are obviously not composed of identical subsystems because some de-
gree of asymmetry is inevitable. However, two neural masses with modestly mismatching
parameters continue to exhibit strong, rapid, and stable synchrony if the internode coupling is
sufficiently strong, for example, c12 = 0.6, c21 = 0 (Figure 2B). These dynamics are accompa-
nied by stable 1:1 phase locking between the two systems (Figure 2D). That is, following an
initial transient of phase unwinding (until t = ∼150 ms), the phase difference remains close
to 0, although it shows brief, bounded excursions. Rather than contracting onto the (hyper-)
diagonal linear subspace, the orbits of this system converge toward a smooth manifold that
lies just off the diagonal (Figure 2F). This phenomenon, known as generalized synchroniza-
tion, arises in a broad variety of coupled asymmetric chaotic systems (Afraimovich, Verichev,
& Rabinovich, 1986; Hunt, Ott, & Yorke, 1997; Pecora & Carroll, 1990; Rulkov, Sushchik,
Tsimring, & Abarbanel, 1995). The smooth surface onto which the orbits converge is known
as the synchronization manifold.
157
Putting the “dynamic” back into dynamic functional connectivity
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
0
2
0
2
1
5
0
1
0
9
2
1
8
4
n
e
n
_
a
_
0
0
0
4
1
p
d
.
/
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 2. Generalized synchrony. (A) Time series for two coupled identical neural masses (V1 is
black, V2 is gray) exhibiting identical synchronization. (B) Time series for two coupled nonidentical
neural masses (V1 is black, V2 is gray) exhibiting generalized synchronization. (C) Hilbert phase of
V1 relative to V2 for the case of identical synchronization. Note the rapid approach to stable 1:1
phase synchrony. (D) Hilbert phase of V1 relative to V2 for the case of generalized synchronization.
Brief, but incomplete, phase slips continue to occur following the transient. (E) V1 plotted against
V2 for the cases of identical synchronization. After a brief transient, the system approaches the
diagonal. (F) V1 plotted against V2 for the cases of generalized synchronization. Transients have
been omitted. (G) Nonlinear self-prediction of V1 from itself (black) and from surrogate data (red).
(H) Nonlinear cross-prediction of V1 from V2 (black) and from surrogate data (red).
The time series generated in this scenario embody several instructive properties. The pres-
ence of synchrony gives rise to linear correlations that are close to unity. After a brief transient
of less than 150 ms, the correlation coefficient is above 0.99 for all successive time windows.
That is, the system has stationary linear cross-correlations. In the presence of static measure-
ment noise, such a system would give rise to stationary functional connectivity (that is, the
Network Neuroscience
158
Putting the “dynamic” back into dynamic functional connectivity
ensemble linear statistics are stationary over successive time windows). However, these time
series also contain deeper structure than multivariate surrogate data that possess the same
linear (auto- and cross-) correlations. That is, the nonlinear prediction error (Figure 2G) and
nonlinear cross-prediction (Figure 2H) of the original data are both smaller than prediction
errors of the corresponding linear null distributions. This arises because the system traverses
phase space on the highly structured and smooth synchronization manifold.
In addition to the presence of stationary linear statistics, these data thus contain nonlinear
correlations previously termed “dynamic connectivity” (Breakspear, 2004). This property of the
data permits rejection of the null hypothesis represented by the multivariate surrogate data,
namely that the time series are generated by a stationary multivariate linear process. Since
trivial analysis of the stable and very high linear correlations shows that the linear statistics are
stationary, then the preceding analyses point to the (true) alternative hypothesis that the data
are generated by a stationary multivariate nonlinear process.
Metastability
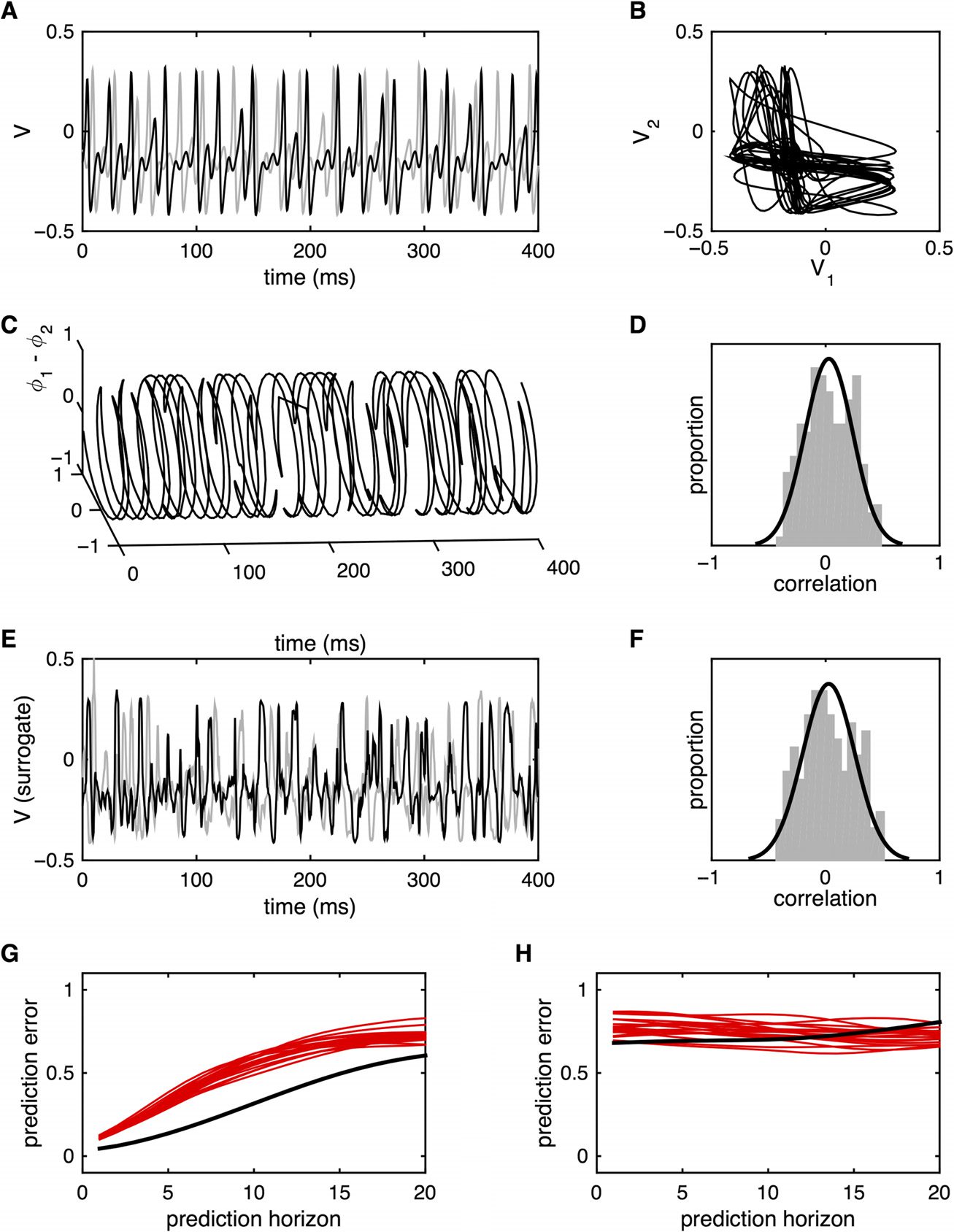
We next study the development of generalized synchrony in the presence of increasingly strong
unidirectional coupling c12 > 0, c21 = 0, eso es, as the second system gradually adjusts its
dynamics to those of the first. Increasing coupling c12 from 0 leads to a monotonic increase in
the time-averaged correlation coefficient until the onset of stable generalized synchronization.
Sin embargo, the accompanying dynamic behavior is quite complex (Ashwin, Buescu, & Stewart,
1996). When the coupling is not sufficiently strong, the two systems show instances of desyn-
chronization, evident as a separation of the states of each system (see example in Figure 3A)
and a complete unwinding of the relative phase. For weak levels of unidirectional coupling
(p.ej., c12 = 0.1), brief periods of generalized synchrony (and corresponding phase locking)
appear among longer intervals of phase unwinding (Figura 3B). If the coupling is increased,
the duration of synchronous epochs lengthens, and the instances of phase unwinding become
confined to brief, erratic bursts (Figura 3C). Even in the presence of reasonably strong coupling
(p.ej., c12 = 0.5), such bursts continue to (infrequently) appear if one waits for a sufficiently long
period of time (p.ej., a single burst over a 20-s duration, Figura 3D). Mientras tanto, as the cou-
pling increases, the synchronization manifold contracts toward the hyperdiagonal, with asyn-
chronous bursts corresponding to brief, disorganized, large amplitude excursions (Figure 3E).
The occurrence of such bursts corresponds to a dynamical phenomenon known as meta-
stability. In brief, for strong coupling, the system possesses a single, low-dimensional chaotic
attractor that is embedded within the synchronization manifold: Although the dynamics
of this chaotic attractor are reasonably complex (Supplementary Information I, Heitmann &
romper la lanza, 2018), both systems converge onto the same manifold, corresponding to sta-
ble (and stationary) generalized synchronization (Ashwin, 1995). The dynamics considered
within the full (six-dimensional) space spanned by both systems become relatively simple.
Sin embargo, if the coupling is slowly weakened from this scenario, there appears a critical
value ck below which instabilities appear within the synchronization manifold and the sys-
tem “blows out” into the full phase space for brief instances (this is formally called a blowout
bifurcation; Ashwin, Aston, & Nicol, 1998; Ott & Sommerer, 1994).
In the vicinity of this
blowout bifurcation c12 ≈ ck, the intervals between asynchronous bursts can be very long,
following a heavy-tailed process (Ott & Sommerer, 1994).
Metastability is perhaps better known when there are multiple competing states (cocineros,
I.
Perdido, Brilla, & romper la lanza, 2017; METRO. Rabinovich, Huerta, & Laurent, 2008; METRO.
Neurociencia en red
159
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
0
2
0
2
1
5
0
1
0
9
2
1
8
4
norte
mi
norte
_
a
_
0
0
0
4
1
pag
d
/
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Putting the “dynamic” back into dynamic functional connectivity
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
0
2
0
2
1
5
0
1
0
9
2
1
8
4
norte
mi
norte
_
a
_
0
0
0
4
1
pag
d
.
t
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 3. Metastability. (A) Time series for two weakly coupled neural masses (V1 is black, V2
is gray) showing a single instance of desynchronization. (B) Hilbert phase of V1 relative to V2
with relatively weak coupling. Periods of generalized synchronization are interspersed by erratic
desynchronization. The gray shaded region (bottom of panel) shows the point-wise correlations
between V1(t) and V2(t) smoothed over a 1-s moving window. (C) Hilbert phase of V1 relative to V2
with medium coupling. The instances of desynchronization have become relatively infrequent and
briefer. (D) With strong coupling, instances of desynchronization are relatively rare. (mi) Plot of V1
versus V2 for the case of strong coupling. The desynchronization is seen as a brief, erratic excursion
from the synchronization manifold. (F) Nonlinear self-predictions of V1 from itself (negro), y (GRAMO)
nonlinear cross-predictions of V1 from V2 (negro). Predictions of V1 from surrogate versions of V2 are
shown in red. The time series retain nonlinear structure despite the instances of desynchronization.
Rabinovich, Huerta, Varona, & Afraimovich, 2008). Such a system cycles between such
estados, exhibiting a broad variety of synchronous behaviors (such as a variety of cluster so-
lutions; Ashwin & Field, 1999). In the present setting, there is only one such unstable state
and the system hence jumps away, then returns back toward the same synchronous state.
This specific type of behavior is known in the literature as itinerancy (Kaneko, 1985; Kaneko
In more technical parlance, it is an example of homoclinic
& Tsuda, 2003; Tsuda, 2001).
itinerancy (“homo” referring to a single system that is both attracting and repelling).
Itinerancy endows the time series with highly nonstationary properties: The unstable bursts
yield a loss of phase synchrony and a corresponding local decrease in the linear correlation
coefficient, both of which return to high values during the longer periods of generalized syn-
chronization. Como resultado, fluctuations in time-dependent linear correlations from the original
time series are greater than those arising from multivariate (stationary) surrogate data. No-
linear prediction errors and cross-prediction errors both remain outside the null distributions
Neurociencia en red
160
Putting the “dynamic” back into dynamic functional connectivity
(from multivariate surrogate data) even if these are obtained from long windows that contain
several of the bursts (Figures 3F and 3G).
A final summary description of these data is therefore quite nuanced. Recall that they are
generated by a coupled nonlinear dynamic system whose parameters are all constant and, en
particular, do not depend upon time. These data are hence generated by an autonomous, multi-
variate nonlinear process. They yield data whose nonlinear properties (Por ejemplo, phase
locking) are highly dynamic. The linear properties of these dynamics are also highly non-
stationary; eso es, they possess fluctuating time-resolved functional connectivity. Además,
because the itineracy has long-tailed (non-Poisson) Estadísticas, these properties cannot be cap-
tured by a classic finite state Markov model and hence may, in certain circumstances, violate
formal definitions of weak-sense stationarity (Liegeois et al., 2017).
The term “dynamic functional connectivity” is arguably a poor term to summarize these
properties and to disambiguate metastability from the stationary but nonlinear properties
that arise in the setting of generalized synchronization, both of which permit rejection of the
stationary, linear null. We return to this issue in the Discussion section.
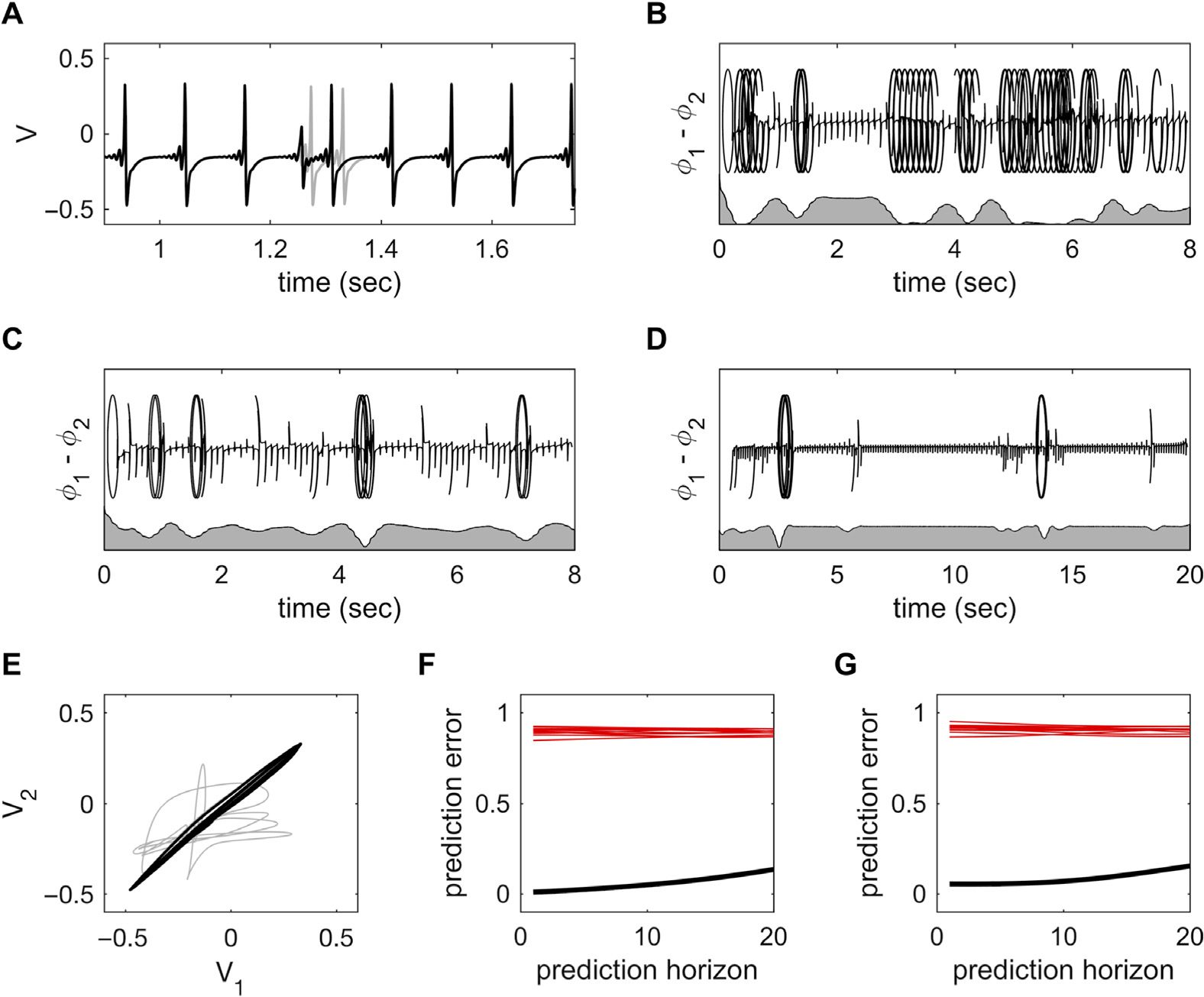
Multistability
We consider one further dynamical scenario that yields nontrivial, dynamical interdependence
between two or more systems, namely multistability. In a multistable system there exist two
or more stable attractors. Eso es, there are dynamical regimes that, in the absence of noise,
trap the behavior of a system indefinitely. Spontaneous switching between the coexisting states
then arises when there is noise ζ added dynamically to the states,
dXi
dt
= fa (Xi) + Hcij
(cid:9)
(cid:8)
Xj
+ b.ζi,
(6)
where ζi is a stationary zero mean stochastic process scaled in amplitude by the parameter b.
When the noise is of sufficient amplitude, a multistable system is able to escape the basin of
each attractor, and jump from one to the other. This is a subtle, albeit important, diferencia
between multistability and metastability. A metastable system is composed of only unstable
nodos, and the evolution of the system cycles from one to the other (or back to itself) even if
there is no noise ζ = 0. A diferencia de, a multistable system will settle onto one stable attractor
unless external noise is injected ζ > 0. The difference may seem subtle but the mechanisms,
emergent system behavior, and resulting statistics are quite distinct (para una revisión, see Cocchi
et al., 2017).
In an array of coupled systems such as we are considering, multistability can arise when
each individual node has multiple attractors. It can also emerge when the individual nodes
are monostable, but the internode interactions introduce multiple types of synchronization
dinámica (Ashwin & Field, 1999). In the system considered above, there is only one (chaotic)
attractor per node but the coupled ensemble can exhibit multistable attractors, Por ejemplo
when there are three or more nodes and their interactions have axonal time delays (Perdido &
romper la lanza, 2014).
The emergence of multistability through the interactions of monostable elements is very
interesante, but also rather complex. For reasons of relative simplicity, we will thus illustrate
a system of coupled nodes where each single node has two attractors; a fixed point and a
co-occurring periodic limit cycle. Eso es, each individual node can exhibit either steady state
or oscillatory behavior, depending on the state to which it is initially closest. A simple—or
Neurociencia en red
161
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
0
2
0
2
1
5
0
1
0
9
2
1
8
4
norte
mi
norte
_
a
_
0
0
0
4
1
pag
d
.
t
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Putting the “dynamic” back into dynamic functional connectivity
“canonical”—form of this system has been used to model the human alpha system (Freyer,
Roberts, Ritter, & romper la lanza, 2012) and is a mathematical approximation to a complex neural
field model (Freyer et al., 2011). The equation for the amplitude dynamics of a single node
according to this simplified model are given by
dr
dt
= −r5 + λr3 + βr + b1.ζ1 + b2.ζ2r,
(7)
where r is the amplitude, λ and β are parameters that control the size and depth of the fixed-
point and limit-cycle attractor basins. The parameters b1 and b2 control the influence of the
additive ζ1 and multiplicative noise ζ2x, respectivamente (see Supplementary Information III for
full details; Heitmann & romper la lanza, 2018).
When the attractor basins of each system are large (es decir., the basin boundaries are distant
from the attractors) and the noise has low amplitude, the two coupled systems exhibit either
noise-driven low-amplitude fluctuations (Cifra 4) or high-amplitude oscillations (Figura 4B).
When the noise is of sufficient strength or the attractor basins are shallow, the dynamics at
each node jump from one attractor to the other. In the absence of internode coupling, estos
transitions occur independently (Figura 4C). The introduction of intersystem coupling increases
the coincidence in the timing of the state transitions (Figure 4E). Sin embargo, debido a la
presence of system noise, these do not always co-occur, even for relatively strong coupling.
To illustrate the corresponding interactions between two coupled multistable nodes, nosotros
focus on their amplitude fluctuations and ignore their phases.
In the absence of coupling
(cij = cji = 0), linear correlations between the amplitude fluctuations converge toward 0 para
sufficiently long samples. Sin embargo, linear correlations taken from brief samples do fluctuate
importantemente. Locally, the noise-driven amplitude fluctuations are highly incoherent because
the noisy inputs are independent (es decir., ζi (cid:3)= ζ j). Sin embargo, if the two systems do transition, por
chance at similar times, then the local linear correlations are driven by these large amplitude
changes in the variance, giving rise to large (but spurious) correlations (both positive and neg-
ative). Over time, these fluctuations center on 0 (Figure 4F), although they have high variance
(DE = 0.17) as a consequence of coincidental state switches. Además, the distribution of
sample correlations (taken from short time windows) is not substantially influenced if one of
the time series is randomly shifted in time compared with the other: The distribution of values
is thus a reflection of the stochastic timing of the erratic amplitude jumps within each system,
and whether both systems happen to switch within the same time window.
In the presence of coupling, the local fluctuations remain uncorrelated. This is due to the
(cid:3)= ζ j. Even though the function f is nonlinear, el
independence of the noise sources, ζi
system evolves in a largely linear fashion within each attractor, and the intersystem coupling
is overwhelmed by the independent noisy perturbations around each attractor. Sin embargo, si
one system jumps between basins, it then exerts a strong pull on the other system, until it too
jumps to the corresponding attractor. The ensuing coincidence of such large-amplitude state
changes then skews the sample linear correlation toward the right (es decir., positively) so that they
center at a value greater than 0 (Figure 4H). Linear correlations from long time series converge
to a positive value that is typically larger than the average of the sample correlations, porque
such long windows are increasingly dominated by the large-amplitude state changes. Notablemente,
the average of the sample correlations and the long-term correlation coefficient converge
toward 0 if one time series is independently rotated in time with respect to the other, y-
derscoring the effect of intersystem coupling on sample correlations.
Neurociencia en red
162
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
0
2
0
2
1
5
0
1
0
9
2
1
8
4
norte
mi
norte
_
a
_
0
0
0
4
1
pag
d
t
/
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Putting the “dynamic” back into dynamic functional connectivity
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
0
2
0
2
1
5
0
1
0
9
2
1
8
4
norte
mi
norte
_
a
_
0
0
0
4
1
pag
d
t
/
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 4. Multistability. (A) Time series of the noisy subcritical Hopf model with one node. Con
β = −10 the system exhibits a stable (noise perturbed) fixed point at r = 0. (B) With β = −6 the
system exhibits a stable limit cycle with amplitude r = 2. Oscillations are shown in gray. Negro
represents the noise-driven amplitude fluctuations, with close-up shown in panel D. (C) With β =
−7.5, the system exhibits bistability with noise-driven switching between the fixed point and limit
ciclo. Por simplicidad, el (gray) oscillations are not shown. (mi) System with two nodes and β = −7.5
but zero coupling (c = 0). The systems jump between the fixed point and limit cycles independently.
(F) Histogram of the linear correlations between the time series generated by the two nodes from
panel E. The simulation was repeated for N = 200 trials with random initial conditions for each trial.
The correlations center at 0 but with substantial intertrial variability. (GRAMO) System with two nodes and
β = −7.5 and strong coupling (c = 1). The jumps between the fixed point and limit cycles occur in
similar time windows. (F) Histogram of the linear correlations between the time series generated by
the two nodes from panel E. The correlations center well above 0 with reduced intertrial variability.
As raised above, the local (very short-term) fluctuations are dominated by the independent
noise sources, even in the presence of coupling. These data do not contain additional nonlinear
estructura (both the nonlinear prediction errors and cross-prediction errors fall within the null).
Between state transitions, the data resemble stationary stochastic fluctuations. Only when
considered on lengthy time series data do the sample statistics reflect the presence of the
underlying nonlinear multistable attractor landscape.
Neurociencia en red
163
Putting the “dynamic” back into dynamic functional connectivity
The time series generated by a coupled (noise-driven) multistable system hence show multi-
variate statistics that are locally stochastic, independiente, and stable, but are globally highly
correlated and fluctuate substantially.
If the noise term is independent of the state of the
sistema (as per Equation 6), then the switching between attractors is Poisson (Freyer et al.,
2012). The statistics of the time series can then be closely approximated by a finite state
Markov process, with a fixed likelihood Λ of jumping states at any time, thus generating
Poisson statistics with an exponential distribution of dwell times. Despite the erratic nature
of the state transitions, this result theoretically renders the statistics weak-sense stationary
(WSS) because the expected correlation and cross-correlations are independent of time
(Liegeois et al., 2017).
Sin embargo, there is one final nuance that is conceptually important. In many situations, el
influence of the state noise ζ is state dependent, in which case a more general differential
equation pertains:
dXi
dt
= fa (Xi) + Hcij
(X) + Gb (X, ζi) ,
(8)
where the influence of the state noise ζ is dependent on the states X via the function G. Cuando
the noise is state dependent, (p.ej., Gb (X, ζi) = bX.ζi, as in the case of Figure 4), then the
system typically gets trapped near each of the attractors in a nonstationary manner (Freyer et al.,
2012). More technically, in a setting of purely additive noise, transitions probabilities are time
invariant and follow a stationary Poisson process. But with multiplicative noise, the chance of
a state transition decreases as the time since the last transition increases. This nonstationarity
gives rise to a heavy-tailed (stretched exponential) distribution of dwell times (Freyer et al.,
2012). Long dwell times are more likely than in the case of purely additive noise. Más
crucialmente, the dwell time is dependent on the history of the system. Como consecuencia, sample
statistics cannot be well approximated by a standard finite state Markov process. This is a
system for which the covariance between the two nodes is not time invariant and the process
is thus not weak-sense stationary.
En suma, the system governed by Equation 6 for cij > 0 yields stochastic (linear) time series
that fluctuate considerably. Sin embargo, the statistics are only nonstationary in the strict sense
if the noise is multiplicative (state dependent) so that system gets trapped within each state
and the ensuing statistics are non-Poisson, which better resemble the statistics of physiological
fluctuations.
Complex Dynamics in Larger Ensembles
We have thus far restricted our analyses to coupled dyads in order to illustrate dynamic
“primitives”—generalized synchronization, metastability, and multistability. Sin embargo, saber-
tive function inevitably involves exchanges between a substantial number of cortical regions—
certainly more than two (Frässle et al., 2017; Razi & Friston, 2016; Seghier & Friston, 2013;
despreciar, 2010). To what extent do dynamics in dyads inform our understanding of dynamics in
larger ensembles, particularly as time delays (t) between nodes become an indispensable part
of modeling larger systems?
In some circumstances, the complex dynamics that occur between two nodes are inher-
ited “upwards” when a large array of nodes are coupled together using the same principles of
coupling. De este modo, a system expressing multistability during the interaction between two nodes
will often exhibit noise-driven multistable switching when more nodes are added. In this sit-
uation, nodes may cluster into “up” and “down” states; eso es, nodes may cluster into similar
states within the same attractor basin, likewise segregated from other clusters which co-occupy
Neurociencia en red
164
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
0
2
0
2
1
5
0
1
0
9
2
1
8
4
norte
mi
norte
_
a
_
0
0
0
4
1
pag
d
t
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Putting the “dynamic” back into dynamic functional connectivity
a distinct state. De hecho, in many coupled oscillator systems, such multistable clustering is quite
generic (Hansel, Mato, & Meunier, 1993) and can theoretically encode complex perceptual
información (Ashwin & Borresen, 2005).
Por otro lado, introducing more nodes can lead to additional complexities and dy-
namic patterns that are not possible with two nodes. A classic example is the nature of phase
relationships between nodes in the presence of time-delayed coupling: With two nodes, el
time delays cause a phase lag between the coupled nodes’ oscillations. Sin embargo, when three
nodes are coupled in an open chain (or “V”) formación, then the outer nodes can exhibit stable
zero-lag synchrony, with the middle node jumping erratically between leading and lagging the
outer nodes (Vicente, Perdido, Mirasso, pescador, & Pipa, 2008). Although first described in arrays
of coupled lasers (Fischer et al., 2006), considerable work has since shown that such zero-lag
configurations arise in small V-shaped motifs of coupled neural systems, including spiking
neuronas (Vicente et al., 2008) and neural mass models (Perdido, Mirasso, despreciar, & romper la lanza,
2014). En tono rimbombante, stable zero-lag synchrony between the outer nodes of a V motif can sur-
vive immersion into larger arrays, where they increase the stability of the system as a whole
(Gollo et al., 2015). Such observations support the notion that these coupled triplets underlie
the emergence of zero-lag correlations that have been observed in diverse neurophysiological
recordings (Gray, König, ángel, & Cantante, 1989; Cantante & Gray, 1995). Sin embargo, closing the
three-node motif by adding a link between the outer nodes (hence turning the V into a cycle)
destroys stable zero-lag synchrony, instead promoting “frustrated” metastable dynamics (Perdido
& romper la lanza, 2014).
Time delays can generate many complex phenomena at the network level—especially when
the time delays are heterogeneous—even when the uncoupled (individual) nodes have linear
or limit-cycle behaviors (Atay, 2010). In addition to the emergence of metastability (Hansel
et al., 1993), time delays can also introduce slow collective frequencies (es decir., ensemble oscil-
lations that are much slower than the frequencies of the uncoupled individual units; Cabral,
Kringelbach, et al., 2014, Niebur, Schuster, & Kammen, 1991). Other complex dynamics
that can emerge through the influence of time delays include traveling waves (romper la lanza,
Heitmann, & Daffertshofer, 2010) and chimera states—ensemble dynamics whereby there is
a domain of coherent nodes and a separate domain of chaotic, incoherent nodes (Abrams &
Strogatz, 2004; Breakspear et al., 2010; Laing, 2009; Shanahan, 2010).
While considerable progress has been made in this area, the full armory of complex dy-
namics in large systems of coupled neural subsystems is far from understood. For illustrative
purposes, we consider a number of candidate scenarios that arise in larger arrays,
specifically when simulating neural mass dynamics on a matrix of 47 cortical regions derived
from CoCoMac (Stephan et al., 2001), a compilation of tracing studies from the macaque brain
that yields a sparse (22%) binary directed graph (available in the Brain Connectivity Toolbox,
Rubinov & despreciar, 2010). We employ a coupling function Hcij that mimics a competitive
(agonist) feedback between local self-excitation and input from distant regions such that as the
influence of external nodes is scaled up by a coupling constant c, local recurrent feedback is
correspondingly scaled down by (1 − k). All internode influences occur through the coupling
matrix Cij.
The neural mass model employed here possesses two timescales—a fast local field oscilla-
tion of approximately 100 Hz nested within a slower timescale of approximately 10 Hz (pendiente
to the slow inhibitory feedback; see Supplementary Information I, Heitmann & romper la lanza,
2018). When parameterized with strong internode coupling (p.ej., c = 0.75) and a time delay
Neurociencia en red
165
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
0
2
0
2
1
5
0
1
0
9
2
1
8
4
norte
mi
norte
_
a
_
0
0
0
4
1
pag
d
/
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Putting the “dynamic” back into dynamic functional connectivity
that approaches the period of the fast oscillations of the neural mass model (τ = 6–10 ms), el
ensemble dynamics break into a number of phase-coupled clusters (Cifra 5).
Each cluster is constituted by phase entrainment to a common beat of the faster rhythm.
The full array of cluster states then recur over the course of the slow oscillation. Tenga en cuenta que
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
0
2
0
2
1
5
0
1
0
9
2
1
8
4
norte
mi
norte
_
a
_
0
0
0
4
1
pag
d
.
/
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
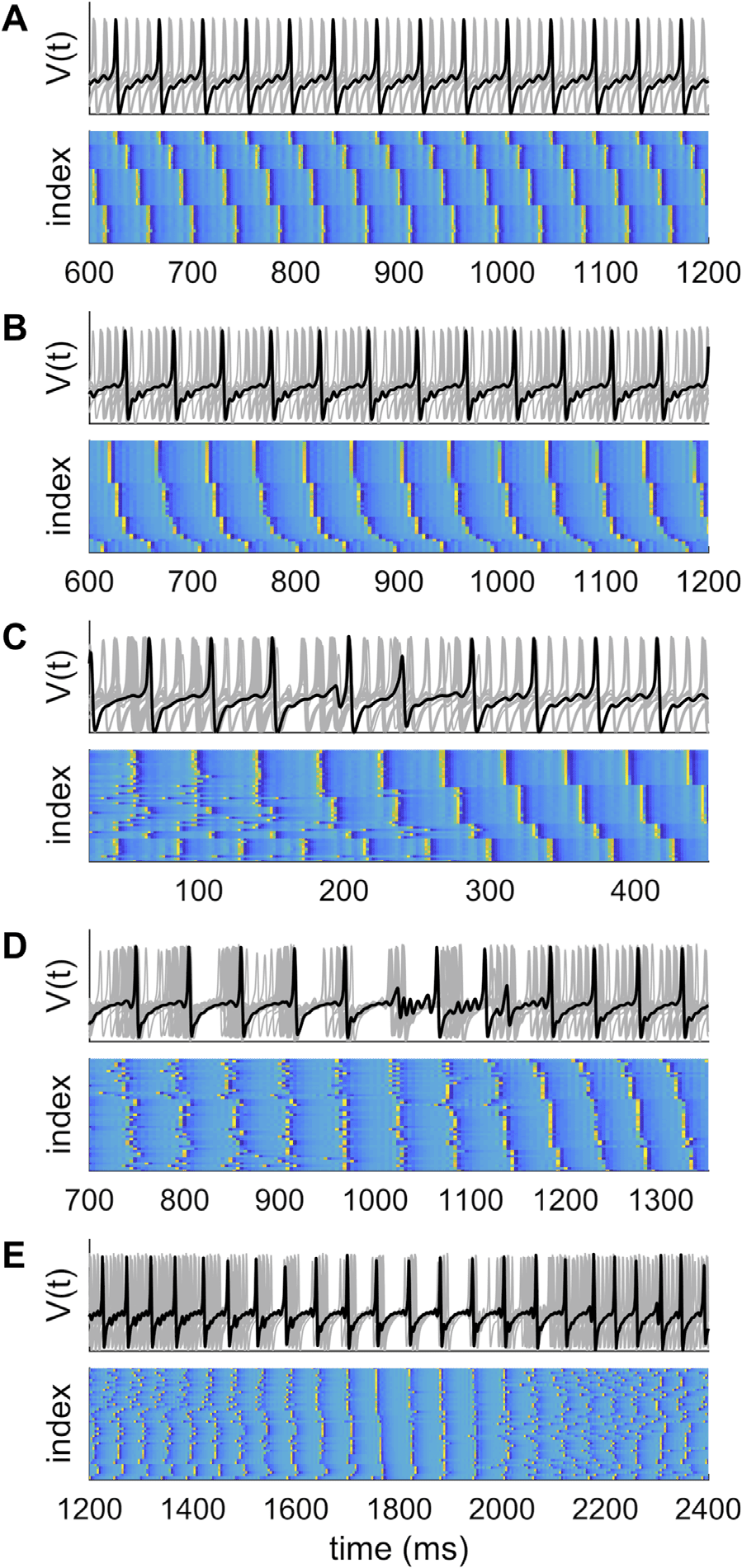
(A) Stable partitioning of ensemble dynam-
Cifra 5. Complex dynamics in larger ensembles.
ics into four phase-coupled clusters with τ = 10 ms and coupling c = 0.75.
(B) Partitioning of
ensemble dynamics into six phase-coupled clusters with τ = 6 ms and coupling c = 0.75. There is
slightly greater disorder in some of the clusters compared with those in panel A. (C, D) With weaker
coupling and/or shorter time delays (τ = 5.5 EM, c = 0.45), there are brief phase slips, leading to a
reorganization of the cluster configuration. (mi) With briefer time delays (τ = 5 EM), clustering does
not occur. Instead the system shows instances of global synchrony interspersed among spatiotem-
poral chaos.
Neurociencia en red
166
Putting the “dynamic” back into dynamic functional connectivity
the number of clusters may differ according to the time delay (four clusters for τ = 10 EM,
Figure 5A; and six clusters are apparent for τ = 6 EM, Figure 5B). In this scenario, the nodes
within clusters show stable, stationary generalized synchronization. Nodes in different clus-
ters also show generalized synchronization, albeit with a constant phase offset. This is an
ensemble equivalent of stable generalized synchrony in coupled dyads.
This example illustrates the self-organization of coupled neural systems into dynamic com-
munities, an example of functional segregation. Of interest, if the coupling is weaker (p.ej., c =
0.45) or the time delay shorter (τ ∼ 5–6 ms), the ensemble dynamics show brief instances of
desynchronization, such that the global coherence of regions into clusters decreases and nodes
switch alliances between clusters (Figure 5C). Similar occasions of desynchronization can her-
ald a reconfiguration from a poorly organized state to highly clustered dynamics (Figure 5D).
In these settings, the ensemble shows some dynamic flexibility in addition to segregation. Semejante
instances render the ensemble statistics nonstationary around the point of transition.
If a shorter time delay (τ ∼ 5 EM) is incorporated into the model, then a clean de-
marcation into distinct phase-coupled clusters does not arise. The ensemble rather shows in-
stances of near global synchrony interspersed by longer periods of relatively dispersed
dinámica (Figure 5E). During the epochs of high global synchrony, zero-lag synchrony emerges,
and as a result, the ensemble has highly ordered (low entropy) dinámica: Outside of these
windows, the amount of order among the nodes is low. The ensemble statistics in this setting
are both nonlinear and nonstationary.
If the time delays approach 0, the state of global synchronization becomes increasingly
stable, even for very weak couplings—resembling the scenario for coupled dyads (Cifra 2).
En cambio, if the time delays are increased, the synchronized cluster solutions become unsta-
ble. So, there is a finite range of delays (related to the fast dynamics of the neural masses) para
which clustering and metastable dynamics occur. In simple systems, such as coupled Kuramoto
(phase) oscillators, this relationship can be derived analytically (Yeung & Strogatz, 1999). En
systems with nontrivial local dynamics and highly asymmetric connectivity matrices, como
the CoCoMac graph employed here, there are added layers of complexity that remain poorly
comprendido.
These scenarios illustrate the capacity of neuronal ensembles to exhibit a diversity of dy-
namic behaviors that yield nonlinear and nonstationary statistics. In some scenarios, dynami-
cal primitives that characterize coupled pairs (generalized synchronization, metastability, y
multistability) dominate the ensemble dynamics, yielding their characteristic dynamic finger-
prints. New phenomena also appear, including zero-lag synchrony (despite the presence of
time delays) and clustering. Typically, these new behaviors compliment the basic dynamics
present in coupled dyads, hence metastable bursts yielding spontaneous reconfiguration of
cluster states.
DISCUSIÓN
The growth of interest in “dynamic” resting-state functional connectivity motivates a deeper
understanding of synchronization dynamics in neural systems. Our objective was to illustrate
the breadth of synchronization dynamics that emerge in pairs and ensembles of coupled neu-
ral populations, and to propose these as putative causes of empirical observations. To recap,
coupled dyads exhibit several basic forms—dynamic “primitives”—that yield nontrivial statis-
tics in the ensuing time series. Generalized synchronization yields stationary nonlinear time
series. Metastable dynamics, which arise when the intersystem coupling is below a critical
Neurociencia en red
167
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
0
2
0
2
1
5
0
1
0
9
2
1
8
4
norte
mi
norte
_
a
_
0
0
0
4
1
pag
d
/
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Putting the “dynamic” back into dynamic functional connectivity
límite, yield nonstationary and nonlinear statistics. Multistability yields a nonstationary
process that is locally linear (es decir., on short timescales) but evidences strong nonlinear prop-
erties globally (over long timescales). When such pairs are integrated into a larger ensemble
and the coupling is imbued with time delays, then these basic primitives combine with new
phenomena, such as phase clustering, to cause complex dynamics that spontaneously switch
between different network configurations. This yields time series whose statistics violate the
assumptions of a stationary stochastic process and which hence yield nontrivial fluctuations
in time-resolved functional connectivity. The dynamics primitives of generalized synchroni-
zación, metastability, or multistability may thus account for the spontaneous fluctuations
observed in resting-state fMRI data.
It is also interesting to consider the computational potential of these synchronization
dinámica. Neural mass models describe the local average of neural activity, namely local
field potentials and average spike rates, not individual spikes.
It has been proposed that
coherent oscillations in the local field potentials of disparate brain regions promotes informa-
tion transfer (Palmigiano, Geisel, Lobo, & battaglia, 2017) and spike time–dependent plasticity
(Fries, 2005). Respectivamente, the dynamics illustrated in this paper would allow such neuronal
binding (ángel, Fries, König, Brecht, & Cantante, 1999) to occur across multiple timescales, y
among dynamic cortical assemblies that form and dissolve through active, nonlinear processes
(romper la lanza, williams, et al., 2004; Kirst, Hora, & battaglia, 2016). Dynamic synchroni-
zación, and desynchronization, could also underlie the spontaneous shifts in attention that
co-occur with changes in neuronal oscillations (Jensen, Kaiser, & Lachaux, 2007; Womelsdorf
& Fries, 2007) and in the absence of changes in task context (Kucyi et al., 2016). The nesting of a
fast oscillation in a slower one—as occurs for our neural mass model—yields phase-amplitude
and phase-phase interactions, which have been proposed supporting cognitive processes re-
quiring complex spatial and temporal coordination (Canolty et al., 2006; Miller et al., 2010;
Mormann et al., 2005; Tort, Komorowski, Manns, Kopell, & Eichenbaum, 2009). More deeply,
the presence of weak instabilities (such as brief desynchronizations) in cortical dynamics
has been proposed as a means by which cortex can be primed to respond sensitively to sen-
sory perturbations and thus to optimize perceptual performance (Cocchi et al., 2017; k. Friston
et al., 2012). Future work is required to elucidate the effects of exogenous stimulation and
endogenous parameter modulation on neural dynamics, and thus to more directly address
these issues (decoración & Kringelbach, 2017).
There are several important caveats of the present study. Más destacado, functional connec-
tivity denotes correlations between neurophysiological recordings (see Box 1): We have inter-
rogated the time series of simulated neuronal states X. Neural states are not directly evident
in empirical functional imaging data, which rather arise from noisy and indirect observation
procesos. We can somewhat crudely represent this as
Yv (t) = M (XI (tT)) + ηv,
(9)
where Yv is the empirical signal in channel/voxel v, M is a complex measurement process
(a nonlinear convolution over a set of regions i ∈ I and time τ ∈ T), and ηv is the added
measurement noise. Functional connectivity is defined as Cov (Yv, Yw) not Cov
. En
the case of fMRI, the BOLD signal arises from the summed effect of neuronal activity signaling
slow changes in blood flow, mediated by neurovascular coupling (Buxton, Wong, & Franco,
1998). The net effect of this hemodynamic response function (HRF) is a broad low-pass filter
(k. j. Friston, Mechelli, Tornero, & Precio, 2000), which also includes some spatiotemporal
mixing if sampled at sufficiently high spatial resolution (Aquino, Schira, robinson, Drysdale,
Xi, Xj
(cid:9)
(cid:8)
Neurociencia en red
168
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
0
2
0
2
1
5
0
1
0
9
2
1
8
4
norte
mi
norte
_
a
_
0
0
0
4
1
pag
d
.
t
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Putting the “dynamic” back into dynamic functional connectivity
& romper la lanza, 2012). Empirical functional connectivity in rs-fMRI experiments thus reflect
slow changes (<0.1 Hz) in synchronization dynamics plus the effect of local spatial mixing.
Although we do not explicitly model the observation function, it is worth noting that both meta-
and multistability yield fluctuations that are substantially slower than the timescales of the
single-node neural dynamics (see Figures 4B–4D), clearly extending into the slow timescales
of the HRF. Explicitly incorporating an observation function into a computational framework is
crucial to any definitive resolution of fMRI fluctuations. Recent work, using neural mass models
that capture the essential internal connectivity and timescales of cortical microcircuits, driving
an observational HRF, mark an important step in this direction (Bastos et al., 2012; K. J. Friston
et al., 2017). However, the appearance of slow fluctuations in synchrony from fast dynamics
lies at the core of the body of work using neural mass models to study fMRI (Cabral, Hugues,
Sporns, & Deco, 2011; Deco et al., 2009; Deco & Jirsa, 2012; Gollo, Zalesky et al., 2015;
C. J. Honey et al., 2007; Zalesky et al., 2014).
In comparison, EEG and MEG directly detect field fluctuations and do not suffer the
same temporal filtering as fMRI. Analyses of resting-state EEG (Breakspear, 2002; Breakspear
& Terry, 2002; C. Stam, Pijn, Suffczynski, & Da Silva, 1999) and MEG (C. J. Stam, Breakspear,
van Cappellen van Walsum, & van Dijk, 2003) data using nonlinear time series techniques
have shown that the human alpha rhythm is imbued with substantial nonlinear structure. Inte-
grating these findings with use of biophysical models has shown that the alpha rhythm arises
from multistable switching between a fixed point and periodic attractor in the presence of
multiplicative noise (Freyer et al., 2011; Freyer et al., 2012)—precisely the scenario illustrated
in Figure 3. This process yields fluctuations in alpha power whose timescales clearly extend
into those of the HRF (Freyer, Aquino, Robinson, Ritter, & Breakspear, 2009). Crucially, the
presence of multiplicative noise in the model (and non-Poisson dwell times for each attractor)
imply, as discussed above, that the system statistics are history dependent and are not (weak-
sense) stationary according to formal, quite restrictive definitions (Liegeois et al., 2017). By
this we can infer that the statistics of resting-state cortex are nonstationary.
Despite their superior temporal fidelity, EEG and MEG sensor data involve substantial spatial
summation of source activity. Although “off the shelf” (Oostenveld, Fries, Maris, & Schoffelen,
2011; Tadel, Baillet, Mosher, Pantazis, & Leahy, 2011) source reconstruction methods are
now available, they inevitably incorporate assumptions about the covariance structure of the
sources and the measurement noise (Baillet, Mosher, & Leahy, 2001). As such, and despite
post hoc unmixing steps (orthogonalization; Hipp, Hawellek, Corbetta, Siegel, & Engel, 2012),
there does not yet exist a definitive account of the contribution of synchronization dynamics
to source-level M/EEG activity. Given recent accounts of complex multinetwork switching in
such data (Baker et al., 2014), substantial steps toward this end seem within reach.
In addition to spatial and temporal filtering, empirical data are also corrupted by extrane-
ous “noise,” including physiological effects (EMG, respiratory confounds) and measurement
noise (thermal fluctuations, etc.). These external (nuisance) noise sources (η in Equation 9)
are conceptually distinct from intrinsic system noise (ζ in Equation 7), which are an essential
part of neuronal dynamics. Prior assumptions regarding the amplitude and temporal cor-
relation structure of measurement noise are a crucial prelude to a formal Bayes-based model
inversion scheme (Stephan et al., 2008). While resolving the contribution of measurement
noise to resting-state fluctuations is largely a methodological and empirical issue (Laumann
et al., 2016; Uddin, 2017), computational modeling can also assist. As we have seen above,
multistable and metastable processes yield specific heavy-tailed statistics. Most nuisance
confounds either have a specific timescale (such as respiratory effects; Chang & Glover, 2009),
Network Neuroscience
169
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
0
2
0
2
1
5
0
1
0
9
2
1
8
4
n
e
n
_
a
_
0
0
0
4
1
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Putting the “dynamic” back into dynamic functional connectivity
or have very short-range correlations (such as thermal effects). The hope here is to use the
statistical fingerprints of synchronization dynamics to help disambiguate true from spurious
fluctuations in observed data. Given the salience of brain-body interactions (as indexed
by physiological and behavioral interdependences; Allen et al., 2016), it should also be
considered that some physiological correlates will index true neuronal dynamics (Nguyen,
Breakspear, Hu, & Guo, 2016) and not simply artifacts. Computational models that incorpo-
rate somatic and physiological dynamics—which thus embody and not merely eschew these
signals—may be required here (Petzschner, Weber, Gard, & Stephan, 2017).
Complex network dynamics are a topic of substantial interest (Boccaletti, Latora, Moreno,
Chavez, & Hwang, 2006), particularly in computational and network neuroscience
(Ashourvan, Gu, Mattar, Vettel, & Bassett, 2017; Khambhati, Sizemore, Betzel, & Bassett, 2017;
Sizemore & Bassett, 2017; Stitt et al., 2017). Network fluctuations co-occur with a variety of
fluctuating cognitive processes within and across resting-state fMRI sessions (Shine, Koyejo,
& Poldrack, 2016; Shine & Poldrack, 2017). To understand how basic dynamics between
pairs of coupled systems scale up, we simulated network dynamics on a structural connec-
tome using connectivity data from CoCoMac. This approach—of dissecting network activity
into basic synchronization dynamics among coupled dyads (Gollo & Breakspear, 2014; Gollo
et al., 2015)—contrasts with the engagement of emergent network dynamics without recourse
to the dynamics among the basic elements (Cabral et al., 2011; Deco et al., 2009; Deco &
Jirsa, 2012; C. J. Honey et al., 2007; Zalesky et al., 2014). Our simulations showed how dy-
namical primitives mix with new ensemble phenomena to inform global dynamics, including
the presence of clustering and global synchronization. We did not explore the specific role
of the CoCoMac connectome network topology in shaping these dynamics, nor correlations
between functional and structural connectivity, which has been the subject of substantial prior
work (C. Honey et al., 2009). However, modeling work in this field—mirroring empirical
resting-state research—has focused on structural correlates of time-averaged functional con-
nectivity. Future work is required to build upon the early forays in this direction by examining
multiple timescales in more detail (Cabral, Kringelbach, & Deco, 2017; Deco & Jirsa, 2012;
Gollo et al., 2015).
Although it has intuitive appeal, the term “dynamic functional connectivity” is arguably a
clumsy one as it suggests, perhaps naively, that dynamic processes exist within the stream of
observable data. Dynamics occur in the underlying neuronal system. If they extend into the
temporal and spatial aperture of a particular functional neuroimaging modality (in sufficient
strength to survive corruption by measurement effects), then they cause nontrivial statistics
in time-resolved data samples. From this perspective, it would be preferable to use simple
descriptive terms to capture the fluctuating properties of these time-resolved data and reserve
the notion of dynamics to refer to their underlying causes.
AUTHOR CONTRIBUTIONS
Stewart Heitmann: Conceptualization; Formal analysis; Methodology; Resources; Software;
Visualization; Writing – original draft; Writing – review & editing. Michael Breakspear:
Conceptualization; Formal analysis; Methodology; Supervision; Visualization; Writing –
original draft; Writing – review & editing.
FUNDING INFORMATION
This manuscript was supported by the National Health and Medical Research Council (118153,
10371296, 1095227) and the Australian Research Council (CE140100007).
Network Neuroscience
170
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
0
2
0
2
1
5
0
1
0
9
2
1
8
4
n
e
n
_
a
_
0
0
0
4
1
p
d
t
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Putting the “dynamic” back into dynamic functional connectivity
REFERENCES
Abrams, D. M., & Strogatz, S. H. (2004). Chimera states for coupled
oscillators. Physical Review Letters, 93(17), 174102.
Abrol, A., Damaraju, E., Miller, R. L., Stephen,
J. M., Claus,
E. D., Mayer, A. R, Calhoun, V. D. (2017). Replicability of
time-varying connectivity patterns in large resting state fMRI
samples. bioRxiv, 172866.
Afraimovich, V., Verichev, N., & Rabinovich, M. I. (1986). Stochas-
tic synchronization of oscillation in dissipative systems. Radio-
physics and Quantum Electronics, 29(9), 795–803.
Allen, M., Frank, D., Schwarzkopf, D. S., Fardo, F., Winston, J. S.,
Hauser, T. U., & Rees, G. (2016). Unexpected arousal modulates
the influence of sensory noise on confidence. eLife, 5, e18103.
Aquino, K. M., Schira, M. M., Robinson, P., Drysdale, P. M., &
Breakspear, M. (2012). Hemodynamic traveling waves in human
visual cortex. PLoS Computational Biology, 8(3), e1002435.
Ashourvan, A., Gu, S., Mattar, M. G., Vettel, J. M., & Bassett, D. S.
(2017). The energy landscape underpinning module dynamics
in the human brain connectome. NeuroImage, 157, 364–380.
Ashwin, P.
(1995). Attractors stuck on to invariant subspaces.
Physics Letters A, 209(5), 338–344.
Ashwin, P., Aston, P. J., & Nicol, M. (1998). On the unfolding of a
blowout bifurcation. Physica D: Nonlinear Phenomena, 111(1),
81–95.
Ashwin, P., & Borresen, J. (2005). Discrete computation using a per-
turbed heteroclinic network. Physics Letters A, 347(4), 208–214.
Ashwin, P., Buescu, J., & Stewart, I. (1996). From attractor to chaotic
saddle: A tale of transverse instability. Nonlinearity, 9(3), 703.
Ashwin, P., & Field, M.
(1999). Heteroclinic networks in cou-
pled cell systems. Archive for Rational Mechanics and Analysis,
148(2), 107–143.
Atay, F. M. (2010). Complex time-delay systems: Theory and appli-
cations. Berlin, Germany: Springer.
Baillet, S., Mosher, J. C., & Leahy, R. M.
(2001). Electromagnetic
brain mapping. IEEE Signal Processing Magazine, 18(6), 14–30.
Baker, A. P., Brookes, M. J., Rezek, I. A., Smith, S. M., Behrens, T.,
(2014). Fast transient networks
Smith, P. J. P., & Woolrich, M.
in spontaneous human brain activity. eLife, 3, e01867.
Bastos, A. M., Usrey, W. M., Adams, R. A., Mangun, G. R., Fries,
P., & Friston, K. J. (2012). Canonical microcircuits for predictive
coding. Neuron, 76(4), 695–711.
Boccaletti, S., Latora, V., Moreno, Y., Chavez, M., & Hwang,
(2006). Complex networks: Structure and dynamics.
D.-U.
Physics Reports, 424(4), 175–308.
Breakspear, M.
(2002). Nonlinear phase desynchronization in
human electroencephalographic data. Human Brain Mapping,
15(3), 175–198.
Breakspear, M. (2004). “Dynamic” connectivity in neural systems.
Neuroinformatics, 2(2), 205–224.
Breakspear, M. (2017). Dynamic models of large-scale brain activ-
ity. Nature Neuroscience, 20(3), 340–352.
Breakspear, M., Brammer, M. J., Bullmore, E. T., Das, P., & Williams,
L. M. (2004). Spatiotemporal wavelet resampling for functional
neuroimaging data. Human Brain Mapping, 23(1), 1–25.
Breakspear, M., Williams, L. M., & Stam, C. J.
(2004). A novel
method for the topographic analysis of neural activity reveals for-
mation and dissolution of “dynamic cell assemblies”. Journal of
Computational Neuroscience, 16(1), 49–68.
Breakspear, M., Heitmann, S., & Daffertshofer, A. (2010). Genera-
tive models of cortical oscillations: Neurobiological implications
of the kuramoto model. Frontiers in Human Neuroscience, 4,
190. https://doi.org//10.3389/fnhum.2010.00190
Breakspear, M., & Stam, C. J. (2005). Dynamics of a neural system
with a multiscale architecture. Philosophical Transactions of the
Royal Society B: Biological Sciences, 360(1457), 1051–1074.
Breakspear, M., & Terry, J.
(2002). Detection and description of
non-linear interdependence in normal multichannel human EEG
data. Clinical Neurophysiology, 113(5), 735–753.
Breakspear, M., Terry, J. R., & Friston, K. J.
(2003). Modulation
of excitatory synaptic coupling facilitates synchronization and
complex dynamics in a biophysical model of neuronal dynamics.
Network: Computation in Neural Systems, 14(4), 703–732.
Buxton, R. B., Wong, E. C., & Frank, L. R. (1998). Dynamics of blood
flow and oxygenation changes during brain activation: The Bal-
loon model. Magnetic Resonance in Medicine, 39(6), 855–864.
Cabral, J., Hugues, E., Sporns, O., & Deco, G. (2011). Role of local
network oscillations in resting-state functional connectivity.
NeuroImage, 57(1), 130–139.
Cabral, J., Kringelbach, M. L., & Deco, G.
(2014). Exploring the
network dynamics underlying brain activity during rest. Progress
in Neurobiology, 114, 102–131.
Cabral,
J., Kringelbach, M. L., & Deco, G.
(2017). Func-
tional connectivity dynamically evolves on multiple time-scales
over a static structural connectome: Models and mechanisms.
NeuroImage, 160, 84–96.
Cabral, J., Luckhoo, H., Woolrich, M., Joensson, M., Mohseni, H.,
Baker, A., . . . Deco, G. (2014). Exploring mechanisms of spon-
taneous functional connectivity in MEG: How delayed network
interactions lead to structured amplitude envelopes of band-pass
filtered oscillations. NeuroImage, 90, 423–435.
Canolty, R. T., Edwards, E., Dalal, S. S., Soltani, M., Nagarajan, S. S.,
Kirsch, H. E., . . . Knight, R. T.
(2006). High gamma power is
phase-locked to theta oscillations in human neocortex. Science,
313(5793), 1626–1628.
Chang, C., & Glover, G. H.
(2009). Relationship between res-
piration, end-tidal CO 2, and BOLD signals in resting-state fMRI.
NeuroImage, 47(4), 1381–1393.
Chang, C., & Glover, G. H.
(2010). Time-frequency dynamics of
resting-state brain connectivity measured with fMRI. Neuro-
Image, 50(1), 81–98.
Cocchi, L., Gollo, L. L., Zalesky, A., & Breakspear, M. (2017). Criti-
cality in the brain: A synthesis of neurobiology, models and cog-
nition. Progress in Neurobiology, 158, 132–152.
Deco, G., Jirsa, V., McIntosh, A., Sporns, O., & Kötter, R.
(2009).
Key role of coupling, delay, and noise in resting brain fluctua-
tions. Proceedings of the National Academy of Sciences, 106(25),
10302–10307.
Network Neuroscience
171
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
0
2
0
2
1
5
0
1
0
9
2
1
8
4
n
e
n
_
a
_
0
0
0
4
1
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Putting the “dynamic” back into dynamic functional connectivity
Deco, G., & Jirsa, V. K.
(2012). Ongoing cortical activity at
Journal of
rest: Criticality, multistability, and ghost attractors.
Neuroscience, 32(10), 3366–3375.
Deco, G., Jirsa, V. K., & McIntosh, A. R.
(2011). Emerging con-
cepts for the dynamical organization of resting-state activity in
the brain. Nature Reviews. Neuroscience, 12(1), 43.
Deco, G., & Kringelbach, M. L.
(2017). Hierarchy of information
processing in the brain: A novel “intrinsic ignition” framework.
Neuron, 94(5), 961–968.
Engel, A. K., Fries, P., König, P., Brecht, M., & Singer, W. (1999).
Temporal binding, binocular rivalry, and consciousness. Con-
sciousness and Cognition, 8(2), 128–151.
Fischer, I., Vicente, R., Buldú, J. M., Peil, M., Mirasso, C. R.,
Torrent, M., & García-Ojalvo, J.
(2006). Zero-lag long-range
synchronization via dynamical relaying. Physical Review Letters,
97(12), 123902.
Frässle, S., Lomakina, E. I., Razi, A., Friston, K. J., Buhmann, J. M.,
& Stephan, K. E. (2017). Regression DCM for fMRI. NeuroImage,
155, 406–421.
Freyer, F., Aquino, K., Robinson, P. A., Ritter, P., & Breakspear, M.
(2009). Bistability and non-gaussian fluctuations in spontaneous
cortical activity. Journal of Neuroscience, 29(26), 8512–8524.
Freyer, F., Roberts, J. A., Becker, R., Robinson, P. A., Ritter, P., &
Breakspear, M. (2011). Biophysical mechanisms of multistability
in resting-state cortical rhythms. Journal of Neuroscience, 31(17),
6353–6361.
Freyer, F., Roberts, J. A., Ritter, P., & Breakspear, M.
(2012). A
canonical model of multistability and scale-invariance in biolog-
ical systems. PLoS Computational Biology, 8(8), e1002634.
Fries, P.
(2005). A mechanism for cognitive dynamics: Neuronal
communication through neuronal coherence. Trends in Cogni-
tive Sciences, 9(10), 474–480.
Friston, K. (2013). Life as we know it. Journal of the Royal Society
Interface, 10(86), 20130475.
Friston, K., Breakspear, M., & Deco, G. (2012). Perception and self-
organized instability. Frontiers in Computational Neuroscience,
6, 44. https://doi.org/10.3389/fncom.2012.00044 https://doi.
org/10.1016/j.neuroimage.2017.02.045
Friston, K. J.
(2004).
Functional and effective connectivity in
neuroimaging: A synthesis. Human Brain Mapping, 2(1–2),
56–78.
Friston, K. J., Harrison, L., & Penny, W.
(2003). Dynamic causal
modelling. NeuroImage, 19(4), 1273–1302.
Friston, K. J., Mechelli, A., Turner, R., & Price, C. J. (2000). Non-
linear responses in fMRI: The Balloon model, Volterra kernels,
and other hemodynamics. NeuroImage, 12(4), 466–477.
Friston, K. J., Preller, K. H., Mathys, C., Cagnan, H., Heinzle,
(2017). Dynamic causal modelling
J., Razi, A., & Zeidman, P.
revisited. NeuroImage. https://doi.org/10.1016/j.neuroimage.
2017.02.045
Gollo, L. L., & Breakspear, M.
(2014). The frustrated brain: From
dynamics on motifs to communities and networks. Philosophical
Transactions of the Royal Society B, 369(1653), 20130532.
Gollo, L. L., Mirasso, C., & Sporns, M., O. Breakspear.
(2014).
Mechanisms of zero-lag synchronization in cortical motifs. PLoS
Computational Biology, 10(4), e1003548.
Gollo, L. L., Mirasso, C., Sporns, O., & Breakspear, M.
(2013).
Mechanisms of zero-lag synchronization in cortical motifs.
arXiv:1304.5008
Gollo, L. L., Mirasso, C., Sporns, O., & Breakspear, M.
(2014).
Mechanisms of zero-lag synchronization in cortical motifs. PLoS
Computational Biology, 10(4), e1003548.
Gollo, L. L., Zalesky, A., Hutchison, R. M., van den Heuvel, M.,
& Breakspear, M.
(2015). Dwelling quietly in the rich club:
Brain network determinants of slow cortical fluctuations. Philo-
sophical Transactions of
the Royal Society B, 370(1668),
20140165.
Gray, C. M., König, P., Engel, A. K., & Singer, W.
(1989). Oscil-
latory responses in cat visual cortex exhibit inter-columnar syn-
chronization which reflects global stimulus properties. Nature,
338(6213), 334–337.
Hansel, D., Mato, G., & Meunier, C. (1993). Clustering and slow
switching in globally coupled phase oscillators. Physical Review
E, 48(5), 3470.
Hansen, E. C., Battaglia, D., Spiegler, A., Deco, G., & Jirsa,
V. K.
(2015). Functional connectivity dynamics: Modeling
the switching behavior of the resting state. NeuroImage, 105,
525–535.
Heitmann, S., & Breakspear, M. (2018). Supplemental material for
“Putting the ‘dynamic’ back into dynamic functional connectiv-
ity.” Network Neuroscience. Advance publication. https://doi.
org/10.1162/netn_a_00041
Hindriks, R., Adhikari, M. H., Murayama, Y., Ganzetti, M., Mantini,
D., Logothetis, N. K., & Deco, G. (2016). Can sliding-window
correlations reveal dynamic functional connectivity in resting-
state fMRI? NeuroImage, 127, 242–256.
Hipp, J. F., Hawellek, D. J., Corbetta, M., Siegel, M., & Engel, A. K.
(2012). Large-scale cortical correlation structure of spontaneous
oscillatory activity. Nature Neuroscience, 15(6), 884–890.
Honey, C., Sporns, O., Cammoun, L., Gigandet, X., Thiran, J.-P.,
Meuli, R., & Hagmann, P. (2009). Predicting human resting-state
functional connectivity from structural connectivity. Proceedings
of the National Academy of Sciences, 106(6), 2035–2040.
Honey, C. J., Kötter, R., Breakspear, M., & Sporns, O. (2007). Net-
work structure of cerebral cortex shapes functional connectivity
on multiple time scales. Proceedings of the National Academy
of Sciences, 104(24), 10240–10245.
Hunt, B. R., Ott, E., & Yorke, J. A. (1997). Differentiable generalized
synchronization of chaos. Physical Review E, 55(4), 4029.
Hutchison, R. M., Womelsdorf, T., Allen, E. A., Bandettini, P. A.,
Calhoun, V. D., Corbetta, M., . . . Gonzalez-Castillo, J. (2013).
Dynamic functional connectivity: Promise, issues, and interpre-
tations. NeuroImage, 80, 360–378.
Jensen, O., Kaiser, J., & Lachaux, J.-P.
(2007). Human gamma-
frequency oscillations associated with attention and memory.
TRENDS in Neurosciences, 30(7), 317–324.
Kaneko, K. (1985). Spatiotemporal intermittency in coupled map
lattices. Progress of Theoretical Physics, 74(5), 1033–1044.
Kaneko, K., & Tsuda, I.
(2003). Chaotic itinerancy. Chaos: An
Interdisciplinary Journal of Nonlinear Science, 13(3), 926–936.
Khambhati, A. N., Sizemore, A. E., Betzel, R. F., & Bassett,
(2017). Modelling and interpreting mesoscale network
D. S.
Network Neuroscience
172
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
0
2
0
2
1
5
0
1
0
9
2
1
8
4
n
e
n
_
a
_
0
0
0
4
1
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Putting the “dynamic” back into dynamic functional connectivity
dynamics. NeuroImage. https://doi.org/10.1016/j.neuroimage.
2017.06.029
Kirst, C., Timme, M., & Battaglia, D. (2016). Dynamic information
Palmigiano, A., Geisel, T., Wolf, F., & Battaglia, D.
(2017).
Flexible information routing by transient synchrony. Nature
Neuroscience, 20(7), 1014–1022.
routing in complex networks. Nature Communications, 7.
Pecora, L. M., & Carroll, T. L. (1990). Synchronization in chaotic
Kucyi, A., Hove, M.
J., Esterman, M., Hutchison, R. M., &
Valera, E. M.
(2016). Dynamic brain network correlates of
spontaneous fluctuations in attention. Cerebral Cortex, 27(3),
1831–1840.
Laing, C. R.
(2009). The dynamics of chimera states in heteroge-
neous Kuramoto networks. Physica D: Nonlinear Phenomena,
238(16), 1569–1588.
Laumann, T. O., Snyder, A. Z., Mitra, A., Gordon, E. M., Gratton,
(2016). On the stability of
C., Adeyemo, B., . . . Greene, D. J.
BOLD fMRI correlations. Cerebral Cortex.
Leon, P. S., Knock, S. A., Woodman, M. M., Domide, L.,
Mersmann, J., McIntosh, A. R., & Jirsa, V. (2013). The Virtual
Brain: A simulator of primate brain network dynamics. Frontiers
in Neuroinformatics, 7.
Leonardi, N., & Van De Ville, D.
(2015). On spurious and
real fluctuations of dynamic functional connectivity during rest.
NeuroImage, 104, 430–436.
Liegeois, R., Laumann, T. O., Snyder, A. Z., Zhou, H. J., & Yeo,
Interpreting temporal fluctuations in resting-state
B. T.
functional connectivity MRI. bioRxiv:135681
(2017).
Mathys, C., Daunizeau, J., Friston, K. J., & Stephan, K. E.
(2011).
A Bayesian foundation for individual learning under uncertainty.
Frontiers in Human Neuroscience, 5.
Miller, K. J., Hermes, D., Honey, C. J., Sharma, M., Rao, R. P.,
Den Nijs, M., . . . Ojemann, J. G.
(2010). Dynamic mod-
ulation of local population activity by rhythm phase in human
occipital cortex during a visual search task. Frontiers in Human
Neuroscience, 4.
Mormann, F., Fell,
J., Axmacher, N., Weber, B., Lehnertz, K.,
Elger, C. E., & Fernández, G. (2005). Phase/amplitude reset and
theta–gamma interaction in the human medial temporal lobe dur-
ing a continuous word recognition memory task. Hippocampus,
15(7), 890–900.
Nguyen, V. T., Breakspear, M., Hu, X., & Guo, C. C.
(2016).
The integration of the internal and external milieu in the in-
sula during dynamic emotional experiences. NeuroImage, 124,
455–463.
Niebur, E., Schuster, H. G., & Kammen, D. M.
(1991). Collec-
tive frequencies and metastability in networks of limit-cycle
Physical Review Letters, 67(20),
oscillators with time delay.
2753.
Nomi, J. S., Vij, S. G., Dajani, D. R., Steimke, R., Damaraju,
E., Rachakonda S.,
(2017). Chronnec-
. . . Uddin, L. Q.
tomic patterns and neural flexibility underlie executive function.
NeuroImage, 147, 861–871.
Oostenveld, R., Fries, P., Maris, E., & Schoffelen, J.-M.
(2011).
FieldTrip: Open source software for advanced analysis of MEG,
EEG, and invasive electrophysiological data. Computational
Intelligence and Neuroscience, 2011, 1.
Ott, E., & Sommerer, J. C. (1994). Blowout bifurcations: The occur-
rence of riddled basins and on-off intermittency. Physics Letters
A, 188(1), 39–47.
systems. Physical Review Letters, 64(8), 821.
Petzschner, F. H., Weber, L. A., Gard, T., & Stephan, K. E. (2017).
Computational psychosomatics and computational psychiatry:
Toward a joint framework for differential diagnosis. Biological
Psychiatry, 82(6), 421–430.
Pikovsky, A., Rosenblum, M., & Kurths, J. (2003). Synchronization:
A universal concept in nonlinear sciences (Vol. 12). New York,
NY: Cambridge University Press.
Prichard, D., & Theiler, J. (1994). Generating surrogate data for time
series with several simultaneously measured variables. Physical
Review Letters, 73(7), 951.
Rabinovich, M., Huerta, R., & Laurent, G.
(2008). Transient dy-
namics for neural processing. Science, 321(5885), 48–50.
Rabinovich, M. I., Huerta, R., Varona, P., & Afraimovich, V. S.
(2008). Transient cognitive dynamics, metastability, and decision
making. PLoS Computational Biology, 4(5), e1000072.
Razi, A., & Friston, K.
J.
sality, models, and intrinsic dynamics.
Magazine, 33(3), 14–35.
(2016). The connected brain: Cau-
IEEE Signal Processing
Roberts, J. A., Friston, K. J., & Breakspear, M. (2017). Clinical
applications of stochastic dynamic models of the brain, part I:
A primer. Biological Psychiatry: Cognitive Neuroscience and
Neuroimaging, 2(3), 216–224.
Rubinov, M., & Sporns, O.
(2010). Complex network measures
of brain connectivity: Uses and interpretations. NeuroImage,
52(3), 1059–1069. https://doi.org/10.1016/j.neuroimage.2009.
10.003
Rulkov, N. F., Sushchik, M. M., Tsimring, L. S., & Abarbanel,
H. D. (1995). Generalized synchronization of chaos in direc-
tionally coupled chaotic systems. Physical Review E, 51(2),
980.
Sanz-Leon, P., Knock, S. A., Spiegler, A., & Jirsa, V. K.
(2015).
Mathematical framework for large-scale brain network modeling
in the virtual brain. NeuroImage, 111, 385–430.
Schiff, S. J., So, P., Chang, T., Burke, R. E., & Sauer, T.
(1996).
interdependence and generalized syn-
Detecting dynamical
chrony through mutual prediction in a neural ensemble. Physical
Review E, 54(6), 6708.
Schreiber, T., & Schmitz, A.
Improved surrogate data for
(1996).
nonlinearity tests. Physical Review Letters, 77(4), 635.
Seghier, M. L., & Friston, K. J. (2013). Network discovery with large
DCMs. NeuroImage, 68, 181–191.
Shanahan, M.
(2010). Metastable chimera states in community-
structured oscillator networks. Chaos: An Interdisciplinary Jour-
nal of Nonlinear Science, 20(1), 013108.
Shine, J. M., Koyejo, O., & Poldrack, R. A. (2016). Temporal metas-
tates are associated with differential patterns of time-resolved
connectivity, network topology, and attention. Proceedings of
the National Academy of Sciences, 201604898.
Shine, J. M., & Poldrack, R. A. (2017). Principles of dynamic net-
work reconfiguration across diverse brain states. NeuroImage.
https://doi.org/10.1016/j.neuroimage.2017.08.010
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
0
2
0
2
1
5
0
1
0
9
2
1
8
4
n
e
n
_
a
_
0
0
0
4
1
p
d
t
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
173
Putting the “dynamic” back into dynamic functional connectivity
Singer, W., & Gray, C. M.
(1995). Visual feature integration
and the temporal correlation hypothesis. Annual Review of
Neuroscience, 18(1), 555–586.
Sizemore, A. E., & Bassett, D. S. (2017). Dynamic graph metrics:
Tutorial, toolbox, and tale. arXiv:1703.10643
Skarda, C. A., & Freeman, W. J. (1987). How brains make chaos in
order to make sense of the world. Behavioral and Brain Sciences,
10(2), 161–173.
Sporns, O.
Press.
(2010). Networks of the Brain. Cambridge, MA: MIT
Sporns, O., Tononi, G., & Kötter, R.
(2005). The human
connectome: A structural description of the human brain. PLoS
Computational Biology, 1(4), e42.
Stam, C., Pijn, J., Suffczynski, P., & Da Silva, F. L. (1999). Dynamics
of the human alpha rhythm: Evidence for non-linearity? Clinical
Neurophysiology, 110(10), 1801–1813.
Stam, C. J., Breakspear, M., van Cappellen van Walsum, A. M., &
van Dijk, B. W. (2003). Nonlinear synchronization in EEG and
whole-head MEG recordings of healthy subjects. Human Brain
Mapping, 19(2), 63–78.
Stephan, K. E., Kamper, L., Bozkurt, A., Burns, G. A., Young, M. P., &
Kötter, R. (2001). Advanced database methodology for the Col-
lation of Connectivity data on the Macaque brain (CoCoMac).
Philosophical Transactions of the Royal Society of London B:
Biological Sciences, 356(1412), 1159–1186.
Stephan, K. E., Kasper, L., Harrison, L. M., Daunizeau, J., den
Ouden, H. E., Breakspear, M., & Friston, K. J. (2008). Nonlinear
dynamic causal models for fMRI. NeuroImage, 42(2), 649–662.
https://doi.org/10.1016/j.neuroimage.2008.04.262
Stitt, I., Hollensteiner, K. J., Galindo-Leon, E., Pieper, F., Fiedler, E.,
(2007). Dynamic reconfiguration
Stieglitz, T., . . . Engel, A. K.
of cortical functional connectivity across brain states. Scientific
Reports, 7.
Tadel, F., Baillet, S., Mosher, J. C., Pantazis, D., & Leahy, R. M.
(2011). Brainstorm: A user-friendly application for MEG/EEG
analysis. Computational Intelligence and Neuroscience, 2011, 8.
Tass, P., Rosenblum, M. G., Weule, J., Kurths, J., Pikovsky, A.,
Volkmann, J., . . . Freund, H.-J. (1998). Detection of n:m phase
locking from noisy data: Application to magnetoencephalogra-
phy. Physical Review Letters, 81(15), 3291.
Terry, J. R., & Breakspear, M. (2003). An improved algorithm for the
detection of dynamical interdependence in bivariate time-series.
Biological Cybernetics, 88(2), 129–136.
Theiler, J., Eubank, S., Longtin, A., Galdrikian, B., & Doyne Farmer,
(1992). Testing for nonlinearity in time series: The method
Physica D: Nonlinear Phenomena, 58(1),
J.
of surrogate data.
77–94.
Tort, A. B., Komorowski, R. W., Manns, J. R., Kopell, N. J., &
Eichenbaum, H. (2009). Theta–gamma coupling increases dur-
ing the learning of item–context associations. Proceedings of the
National Academy of Sciences, 106(49), 20942–20947.
Tsuda, I. (2001). Toward an interpretation of dynamic neural activ-
ity in terms of chaotic dynamical systems. Behavioral and Brain
Sciences, 24(05), 793–810.
Uddin, L. Q.
(2017). Mixed signals: On separating brain signal
from noise. Trends in Cognitive Sciences, 21(6), 405–406.
Vicente, R., Gollo, L. L., Mirasso, C. R., Fischer, I., & Pipa, G.
(2008). Dynamical relaying can yield zero time lag neuronal
synchrony despite long conduction delays. Proceedings of the
National Academy of Sciences, 105(44), 17157–17162.
Womelsdorf, T., & Fries, P. (2007). The role of neuronal synchro-
nization in selective attention. Current Opinion in Neurobiology,
17(2), 154–160.
Woolrich, M. W., & Stephan, K. E.
(2013). Biophysical network
models and the human connectome. NeuroImage, 80, 330–338.
Yeung, M. S., & Strogatz, S. H. (1999). Time delay in the Kuramoto
model of coupled oscillators. Physical Review Letters, 82(3), 648.
Zalesky, A., & Breakspear, M. (2015). Towards a statistical test for
functional connectivity dynamics. NeuroImage, 114, 466–470.
Zalesky, A., Fornito, A., Cocchi, L., Gollo, L. L., & Breakspear, M.
(2014). Time-resolved resting-state brain networks. Proceedings
of the National Academy of Sciences, 111(28), 10341–10346.
Network Neuroscience
174
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
0
2
0
2
1
5
0
1
0
9
2
1
8
4
n
e
n
_
a
_
0
0
0
4
1
p
d
.
t
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3