INVESTIGACIÓN

Spontaneous brain network activity:
Analysis of its temporal complexity

Mangor Pedersen1∗

, Amir Omidvarnia1, Jennifer M. Walz1,

Andrew Zalesky2,3, and Graeme D. Jackson1,4

1The Florey Institute of Neuroscience and Mental Health, The University of Melbourne, Melbourne, Victoria, Australia
2Department of Psychiatry, Melbourne Neuropsychiatry Centre, The University of Melbourne, Victoria, Australia
3Melbourne School of Engineering, The University of Melbourne, Victoria, Australia
4Department of Neurology, Austin Health, Melbourne, Victoria, Australia

Palabras clave: Instantaneous phase synchrony, Sample entropy, Brain networks, resonancia magnética funcional, Graph theory

un acceso abierto

diario

ABSTRACTO

The brain operates in a complex way. The temporal complexity underlying macroscopic and
spontaneous brain network activity is still to be understood. en este estudio, we explored the
brain’s complexity by combining functional connectivity, graph theory, and entropy analyses
en 25 healthy people using task-free functional magnetic resonance imaging. We calculated
the pairwise instantaneous phase synchrony between 8,192 brain nodes for a total of 200
time points. This resulted in graphs for which time series of clustering coefficients (el
“cliquiness” of a node) and participation coefficients (the between-module connectivity of a
nodo) were estimated. For these two network metrics, sample entropy was calculated. El
procedure produced a number of results: (1) Entropy is higher for the participation coefficient
than for the clustering coefficient. (2) The average clustering coefficient is negatively related
to its associated entropy, whereas the average participation coefficient is positively related to
its associated entropy. (3) The level of entropy is network-specific to the participation
coefficient, but not to the clustering coefficient. High entropy for the participation coefficient
was observed in the default-mode, visual, and motor networks. These results were further
validated using an independent replication dataset. Our work confirms that brain networks
are temporally complex. Entropy is a good candidate metric to explore temporal network
alterations in diseases with paroxysmal brain disruptions, including schizophrenia and
epilepsy.

RESUMEN DEL AUTOR

En años recientes, connectomics has provided significant insights into the topological
complexity of brain networks. Sin embargo, the temporal complexity of brain networks still
remains somewhat poorly understood. In this study we used entropy analysis to demonstrate
that the properties of network segregation (the clustering coefficient) and integration (el
participation coefficient) are temporally complex, situated between complete order and
disorder. Our results also indicated that “segregated network nodes” may attempt to
minimize the network’s entropy, whereas “integrated network nodes” require a higher
information load, and therefore need to increase entropy. We believe that combining
temporal information from functional brain networks and entropy can be used to test the
decomplexification theory of disease, especially in neurological and psychiatric conditions
characterized by paroxysmal brain abnormalities (p.ej., schizophrenia and epilepsy).

Citación: Pedersen, METRO., Omidvarnia, A.,
Walz, j. METRO., Brilla, A., Jackson, GRAMO. D.
(2017). Spontaneous brain network
actividad: Analysis of its temporal
complejidad. Neurociencia en red,
1(2), 100–115.
https://doi.org/10.1162/netn_a_00006

DOI:
https://doi.org/10.1162/netn_a_00006

Supporting Information:
http://www.mitpressjournals.org/doi/
suppl/10.1162/netn_a_00006

Recibió: 15 Septiembre 2016
Aceptado: 23 December 2016

Conflicto de intereses: Los autores tienen
declaró que no hay intereses en competencia
existir.

Autor correspondiente:
Mangor Pedersen
m.pedersen@brain.org.au

Editor de manejo:
Olaf Sporns

Derechos de autor: © 2017
Instituto de Tecnología de Massachusetts
Publicado bajo Creative Commons
Atribución 4.0 Internacional
(CC POR 4.0) licencia

La prensa del MIT

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

/

t

/

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

1
2
1
0
0
1
0
9
1
9
1
0
norte
mi
norte
_
a
_
0
0
0
0
6
pag
d

t

.

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Temporal complexity of brain networks

Functional magnetic resonance
imaging (resonancia magnética funcional):
An imaging technique capturing
hemodynamic interactions in the
brain with millimeter resolution.

Graph theory:
A mathematical research field aiming
to quantify the topological aspects of
redes.

Clustering coefficient:
Estimate the proportion of connected
triangles surrounding a node; a high
clustering coefficient is an indicator
of network segregation.

Module:
A collection of segregated nodes in
the brain thought to subserve distinct
funciones.

Participation coefficient:
Estimate of how well-connected the
nodes within a given module are to
other brain-wide modules; a measure
of intermodular diversity.

Instantaneous phase synchrony:
A measure that quantifies the
functional relationships between
brain nodes at each fMRI time point.

Sample entropy (SampEn):
The rate of generation of new
information in a signal; a measure of
signal complexity.

The brain is complex. One of the most convincing examples of this is the neuron, con su
lognormal firing rate and critical states (Chialvo, 2010). Sin embargo, not much is known about
the spatiotemporal complexity underlying large-scale brain networks. Sin embargo, it is fea-
sible to estimate the complexity of brain networks in functional magnetic resonance imag-
En g (resonancia magnética funcional) by using measures of signal entropy (bassett, nelson, Mueller, Camchong, & Lim,
2012). Entropy reveals the extent to which a signal is temporally ordered (low entropy), y-
correlacionado (high entropy), or complex (medium entropy). Entropy has been used in a variety
of settings, with notable contributions to cardiovascular disease markers such as heart-rate
variabilidad (Lago, Richman, Griffin, & Moorman, 2002). The entropy of spontaneous brain ac-
tivity signals has received increasing attention, and a few empirical studies have started to
explore the entropy of fMRI signals in healthy people (McDonough & Nashiro, 2014; Wang,
li, Childress, & Detre, 2014) and in disease populations (Bassett y cols., 2012; Sokunbi et al.,
2014).

Connectomics is a relatively new field in which the structure and function of brain
networks is studied (despreciar, Tononi, & kötter, 2005). Several graph-theoretic measures exist
that quantify network properties, including measures of node degree, betweenness centrality,
clustering coefficient, modularity, participation coefficient, and efficiency (Rubinov & despreciar,
2010). Given this wealth of options, a reductionist approach is appropriate when selecting
the network measures for a study. In the present work, we wanted to use measures that may
reflect topologically “segregated” and “integrated” network activity. The clustering coefficient
(the “cliquiness” of a node) and participation coefficient (the intermodular connectivity of a
nodo) are graph-theoretic measures that quantify, respectivamente, brain network segregation and
integración (Guimerà & Nunes Amaral, 2005; vatios & Strogatz, 1998).

To obtain a realistic characterization of the temporal evolution of brain networks, tiempo-
varying functional connectivity information has been collected using fMRI (Chang & guantero,
2010; Handwerker, Roopchansingh, Gonzalez-Castillo, & Bandettini, 2012; Brilla, Proporcionó,
cocineros, Perdido, & romper la lanza, 2014). Moment-to-moment changes that occur in the brain are
challenging to capture with fMRI-based network measures, due to the low-frequency nature
of the hemodynamic response function (guantero, 2011). A commonly used approach for this
purpose is sliding-window analysis, in which correlations within narrow segments of fMRI
data are estimated over time. A promising alternative to sliding-window analysis is instan-
taneous phase synchrony analysis, which considers concurrent functional relationships be-
tween brain regions at the same temporal resolution of fMRI time series (Omidvarnia et al.,
2016; Ponce-Alvarez et al., 2015).

To examine the temporal complexity of brain network properties, we estimated the sam-
ple entropy (SampEn) of clustering-coefficient and participation-coefficient time series, cual
were derived from fMRI connectivity matrices using instantaneous phase synchrony. We showed
that quantifying the entropy of brain network properties enables us to link the temporal com-
plexity and topology of functional brain networks, which may be used to characterize (altered)
brain networks in disease.

RESULTADOS

Participation Coefficient and Clustering Coefficient Are Inversely Related

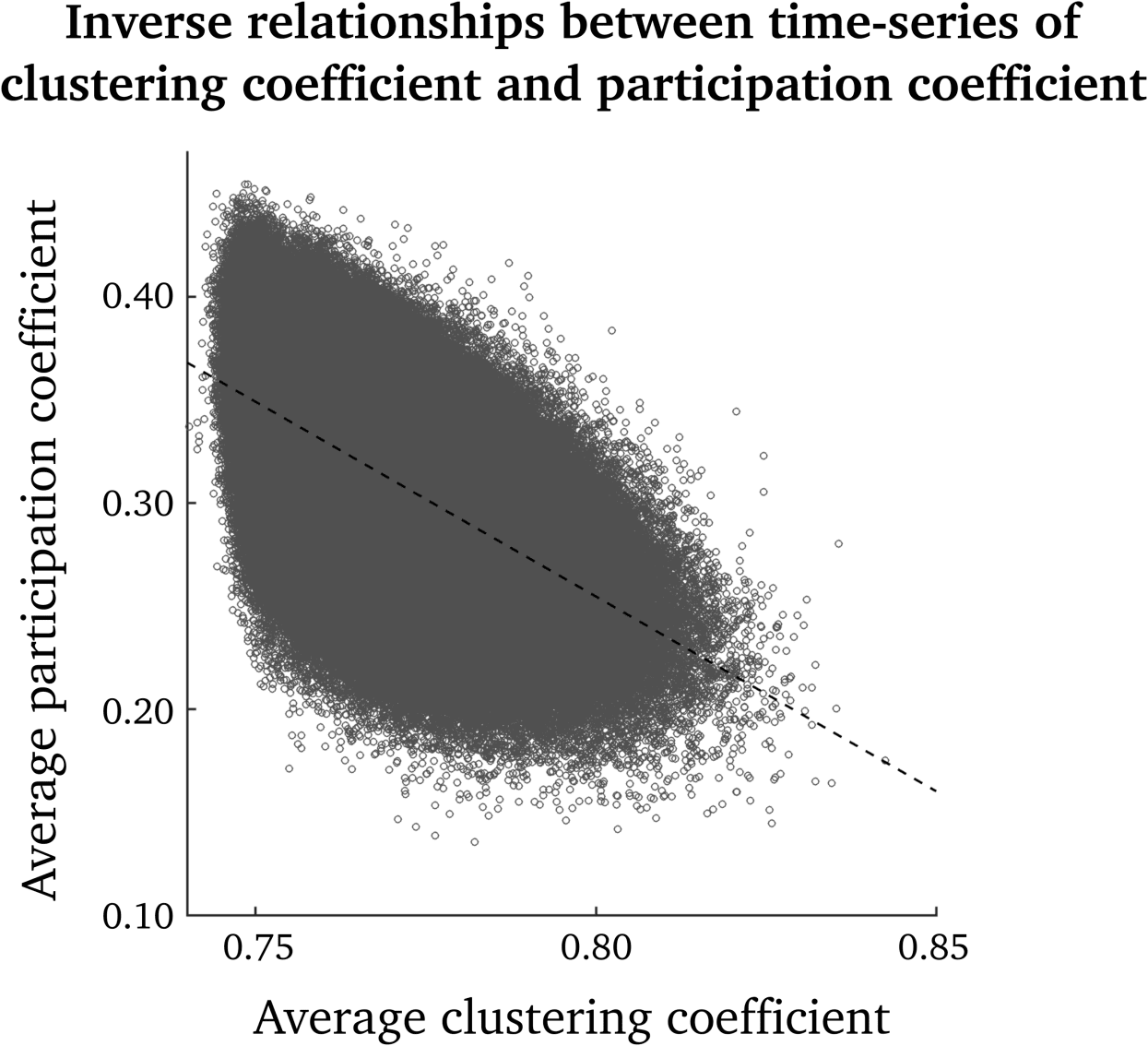
As can be seen in Figure 1, there is an inverse relationship between clustering-coefficient and
participation-coefficient time series (es decir., time points with high clustering coefficients generally

Neurociencia en red

101

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

t

/

/

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

1
2
1
0
0
1
0
9
1
9
1
0
norte
mi
norte
_
a
_
0
0
0
0
6
pag
d

t

.

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Temporal complexity of brain networks

have low participation coefficients, y viceversa). Pearson’s correlation coefficient between
the clustering coefficient and participation coefficient, pooled over all nodes and time points,
was –0.56.

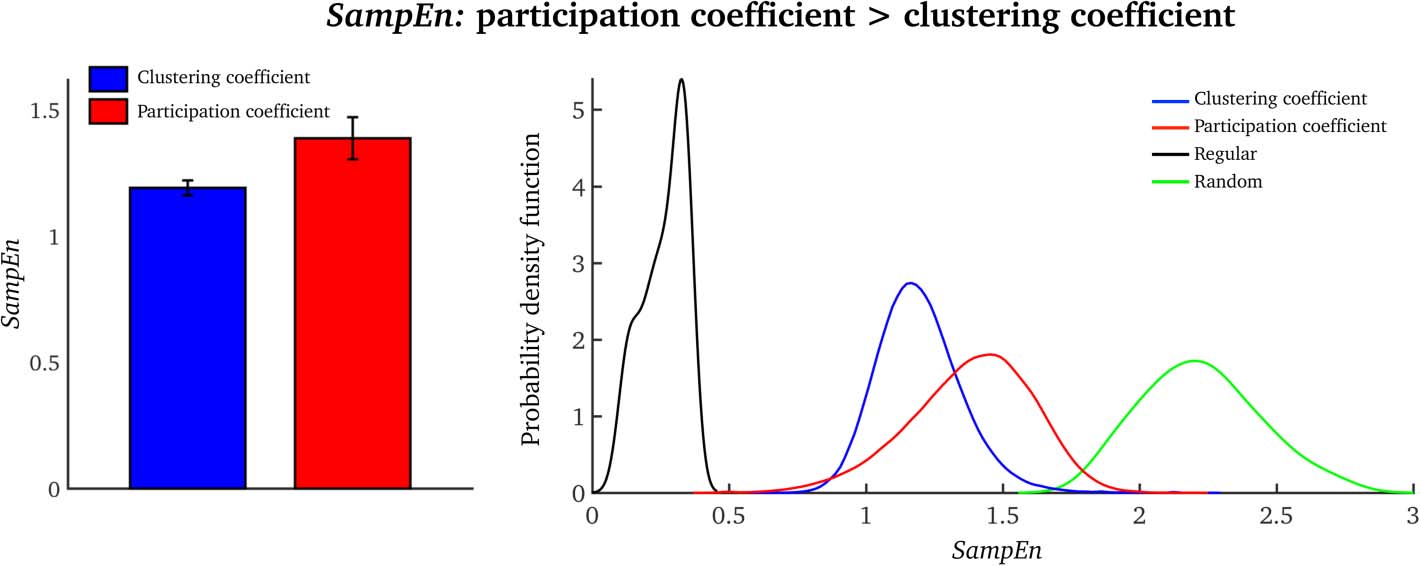
SampEn Is Higher for the Participation Coefficient Than for the Clustering Coefficient

SampEn was significantly higher for the participation coefficient than for the clustering coeffi-
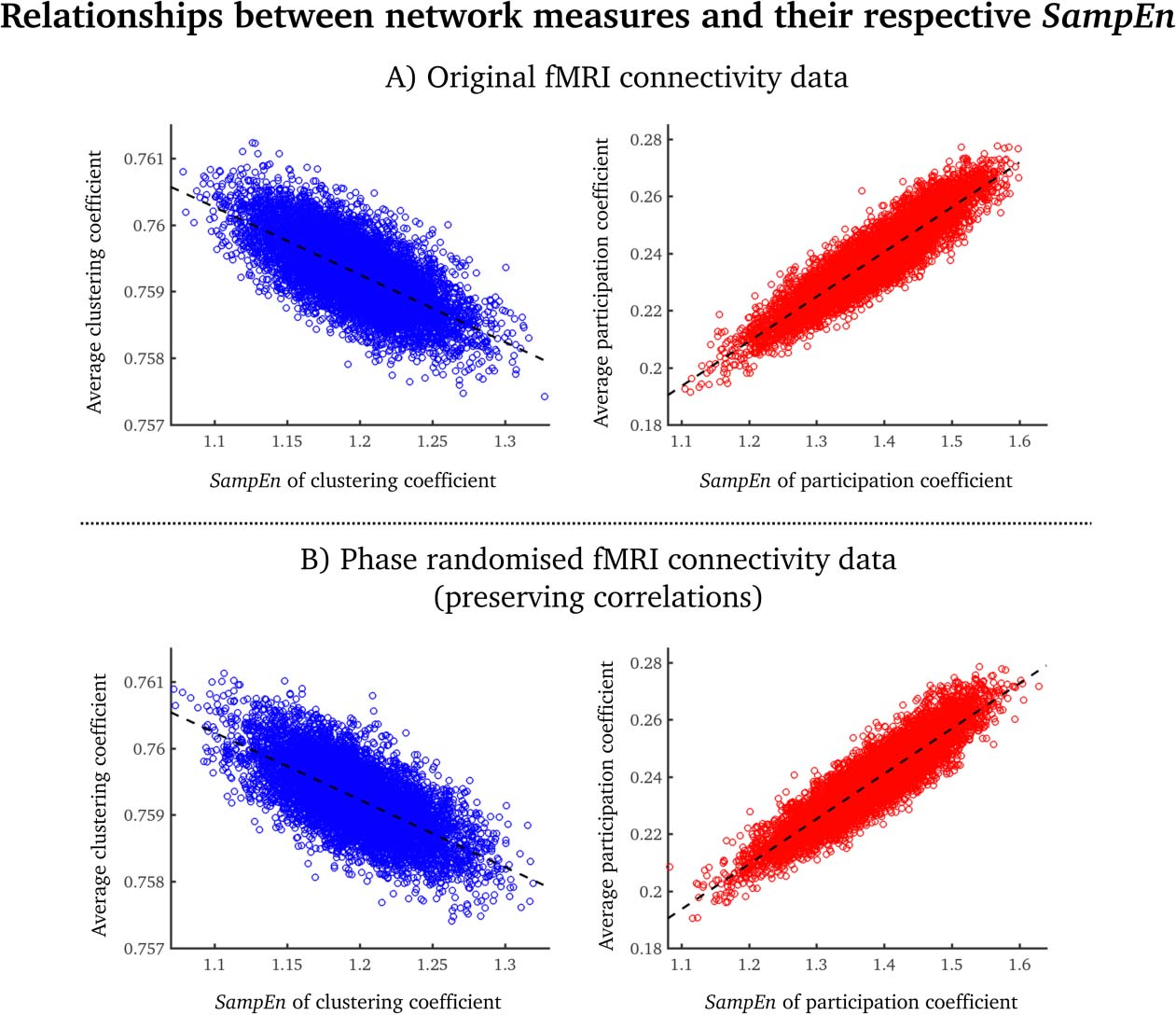
cient (two-sample t-test = 11.06, pag < 0.0001; see Figure 2, left). For both network measures, SampEn values were placed in-between completely regular and random time series (Figure 2, right). Relationships Between SampEn and the Participation Coefficient/Clustering Coefficient The average clustering coefficient was inversely related to the SampEn of clustering coeffi- cient (Pearson’s correlation coefficient = –0.67; Figure 3A, left). The average participation coefficient was positively related to the SampEn of a participation coefficient (Pearson’s corre- lation coefficient = 0.90; Figure 3A, right). Near identical results were obtained from phase- randomized data where the correlation structure is preserved, and thus the relations between SampEn and the static measures are preserved. The relationship between SampEn and net- work activity are therefore likely to be due to the zero-lag correlation structure between nodes, rather than to nonstationarities. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 1 2 1 0 0 1 0 9 1 9 1 0 n e n _ a _ 0 0 0 0 6 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 1. Scatterplot of participation-coefficient versus clustering-coefficient time series. Shown are all time points and nodes over the group of subjects. The dashed line corresponds to the best linear fit. Network Neuroscience 102 Temporal complexity of brain networks (Left) Average SampEn values over all nodes for the clustering coefficient and partici- Figure 2. (Right) Node-wise SampEn distributions for all pation coefficient (a single value per subject). 25 subjects for the clustering coefficient (blue) and the participation coefficient (red). The regu- lar distribution (black) was generated using sine waves of different frequencies, and the random distribution (green) was generated with MATLAB’s rand function (akin to the illustrative example seen in Figure 6). For the regular and random data, we generated signals equal in number and length to those in the fMRI data (blue and red). l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . 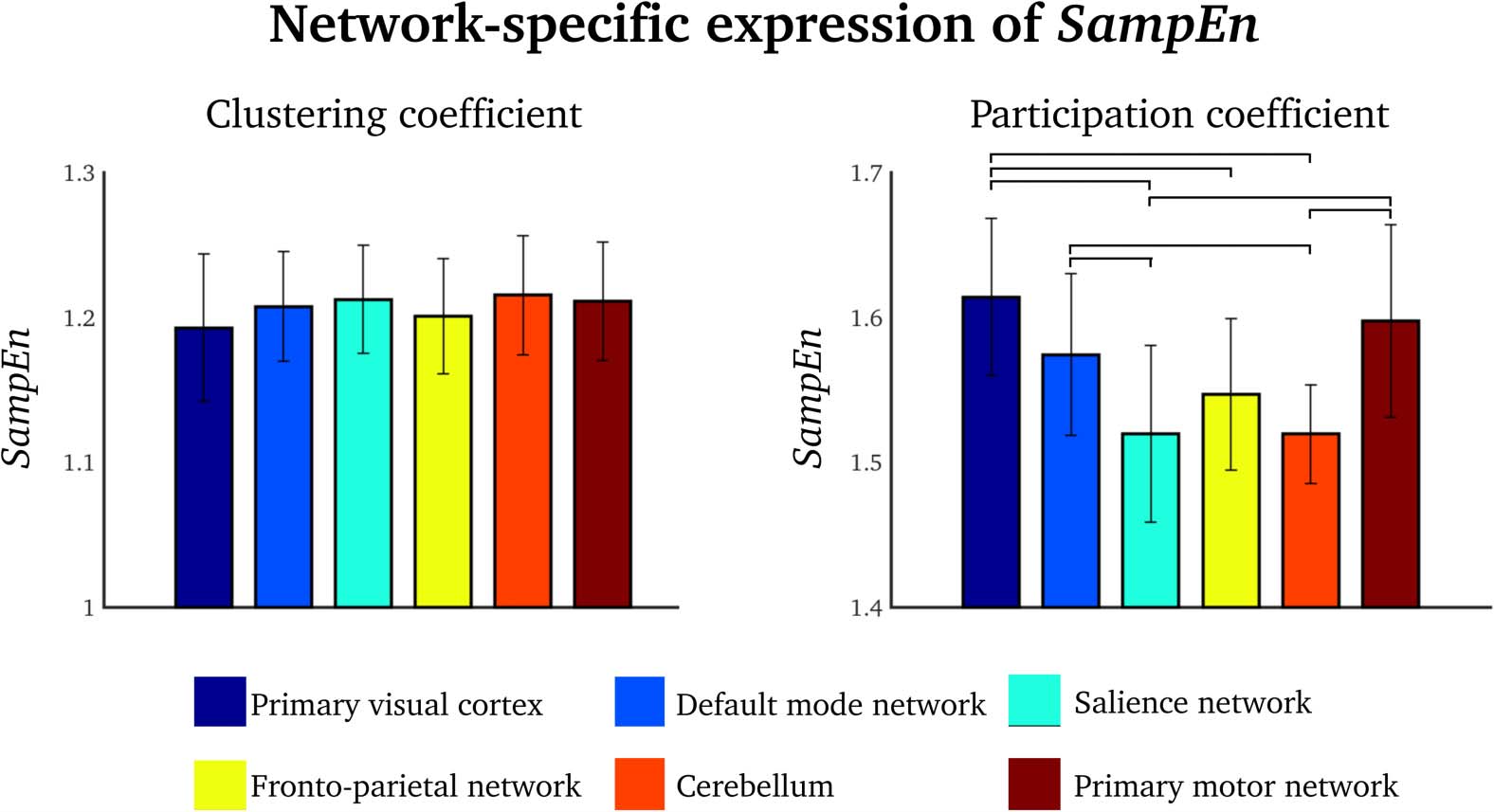SampEn Is Only Network-Specific for the Participation Coefficient We evaluated the average SampEns of the clustering coefficient and the participation coef- ficient within a number of functionally well-defined brain network nodes from the default mode network, salience network, frontoparietal network, primary sensory (visual and motor) t / / e d u n e n a r t i c e - p d l f / / / / / 1 2 1 0 0 1 0 9 1 9 1 0 n e n _ a _ 0 0 0 0 6 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 3. Scatterplots of average clustering coefficients (blue)/participation coefficients (red) and the SampEn of each network measure for the original fMRI data (A) and the phase-randomized fMRI data (B). Each point denotes a group-averaged node value. The dashed lines correspond to the best linear fit. Network Neuroscience 103 Temporal complexity of brain networks networks, and cerebellum. These network nodes were defined using principal component analysis. This was done by calculating the first five principal components of the average group-level instantaneous phase synchrony data obtained in Step 3 in Materials and Meth- ods (see Supplementary Information 1 (Pedersen et al., 2017) for more information). SampEn varied between specific network nodes for the participation coefficient (one-way ANOVA: F = 13.2, p < 0.0001), but not for the clustering coefficient (one-way ANOVA: F = 1.1, p = 0.39). Bonferroni-corrected post-hoc analysis revealed seven out of 15 significant compar- isons, mostly in the primary visual cortex, default mode network, and primary motor network (see the paired differences in Figure 4, right). 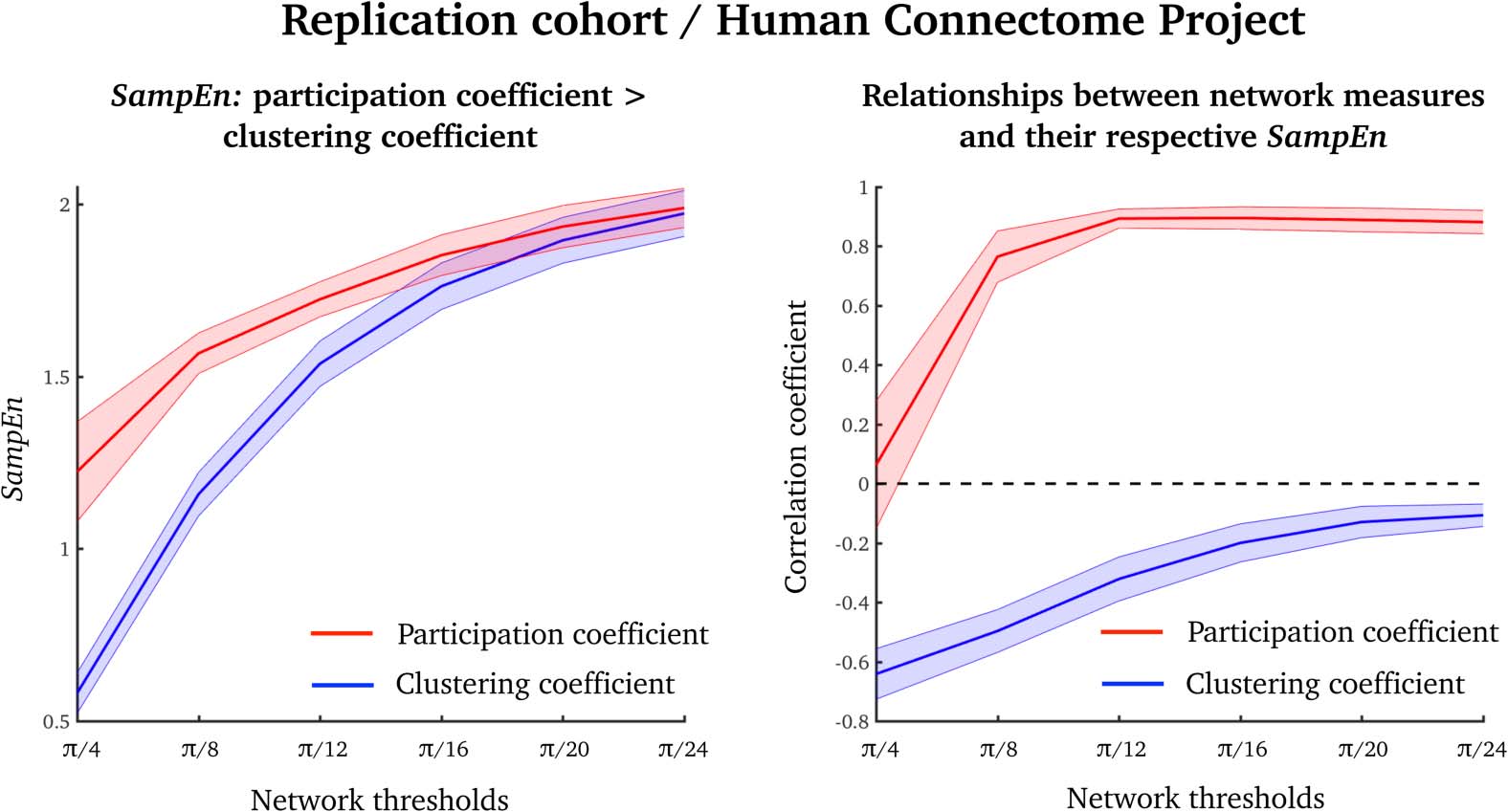Replication Dataset: Human Connectome Project To test whether our results were reproducible, we used task-free fMRI data from the Human Connectome Project (Van Essen et al., 2013). In this analysis we used a network parcellation scheme with fewer nodes (than in the analyses above), which allowed us to estimate SampEn over a range of network density thresholds. The results from this replication dataset were similar to our original results. That is, partic- ipation coefficients had higher SampEn over a range of thresholds than did clustering coeffi- cients (Figure 5, left). Also, the average clustering coefficient was negatively correlated with its SampEn, and the average participation coefficient was positive correlated with its SampEn (Figure 5, right). DISCUSSION In this study, we combined functional connectivity, graph theory, and entropy to elucidate the temporal complexity of brain network properties. Although a few studies have previ- ously measured complexity and SampEn on the basis of fMRI signals (e.g., Bassett et al., 2012; l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 1 2 1 0 0 1 0 9 1 9 1 0 n e n _ a _ 0 0 0 0 6 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 4. Group-level SampEn values of specific brain networks for the clustering coefficient (left) and the participation coefficient (right). Error bars = standard deviations. Lines = Bonferroni- corrected statistically significant pair-wise difference. Network Neuroscience 104 Temporal complexity of brain networks Figure 5. Results from a replication dataset over a range of network density thresholds (from π/4 to π/24). (Left) SampEn values of the participation coefficient (red) and clustering coefficient (blue), averaged over all nodes (akin to the results in Figure 2). (Right) Pearson’s correlation coefficients between the average clustering coefficient (blue) and participation coefficient (red) and their asso- ciated SampEns (akin to the results in Figure 3). Means and standard deviations are displayed as lines and shaded colors, respectively. McDonough & Nashiro, 2014; Sokunbi et al., 2014; Wang et al., 2014), the present study was, to our knowledge, the first to directly assess the complexity of temporal fMRI network prop- erties. We observed that the clustering-coefficient and participation-coefficient signals were more complex than regular, predictable systems (minimal entropy: see Figure 2, black distribu- tion), but less uncertain than a random, uncorrelated system (maximal entropy: see Figure 2, green distribution). This is further evidence that human brain networks are situated between temporal order and disorder—that is, at a high level of complexity. The wider implications of the divergent relationship between the clustering coefficient and the participation coefficient, and their associated temporal complexity, will be discussed in the following sections. SampEns of the Clustering Coefficient and the Participation Coefficient Are Differentially Expressed The inverse relationship between the clustering coefficient and the participation coefficient suggests that the brain transits between network “segregation” and “integration.” This is in line with a recent study demonstrating that the brain switches between two distinct states of network segregation or integration (Shine et al., 2016). Thus, the entropy of these processes may be of significance, since the “segregated” brain may attempt to minimize its own entropy—that is, nodes with high clustering coefficients display low SampEn (Figure 3, left). These particular nodes have a temporal pattern that is inclined toward temporal regularity, or predictability. This is consistent with existing theories of entropy in living systems. According to Erwin Schrödinger, any living system operates on the basis of negentropy—it will strive to minimize its own entropy (see What Is Life: The Physical Aspect of the Living Cell, published in 1944). In other words, living systems may need to be temporally ordered to function optimally in an otherwise chaotic world (Mahulikar & Herwig, 2009). Network Neuroscience 105 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 1 2 1 0 0 1 0 9 1 9 1 0 n e n _ a _ 0 0 0 0 6 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Temporal complexity of brain networks On the other hand, when the brain displays high “integration” (a high participation co- efficient), SampEn is also high (Figure 3A, right). This finding may relate to the excessive information load imposed on these particular nodes when capturing between-module con- nectivity. This result resembles findings by Bassett et al. (2012), who found that wavelet en- tropy was positively related to node-wise fMRI strength (i.e., connectivity between a node and all other nodes in the network) in both healthy people and patients with schizophrenia. Us- ing resting-state electroencephalogram recordings, Miši´c, Vakorin, Paus, and McIntosh (2011) demonstrated that nodal measures of distributed connectivity (global efficiency, degree, and betweenness centrality) were positively correlated with SampEn. These studies reinforce the notion that the extent (or diversity) of network information may be related to the entropy, or unpredictability, of brain signals. Network-specific entropy was a feature of participation-coefficient, but not of clustering- coefficient, time series (Figure 4). This finding implies that the participation coefficient is a metric that enables network-specific characterization. This is in line with the seminal work of Guimerà and Nunes Amaral (2005) on the participation coefficient. These authors demon- strated that is not able to capture network-specific processes, but on the contrary, the participation coefficient was important for quantifying between-network connectivity in a range of networks (Guimerà & Nunes Amaral, 2005). In line with previous fMRI studies, we believe that the participation coefficient may be a unique and alternative measure of brain network activity (see Power, Schlaggar, Lessov- Schlaggar, & Petersen, 2013). in several network types, the clustering coefficient On the Dynamics of fMRI Connectivity Instantaneous phase synchrony is a relatively new way of deriving time-resolved connectivity using fMRI (see Glerean, Salmi, Lahnakoski, Jääskeläinen, & Sams, 2012; Omidvarnia et al., 2016; Ponce-Alvarez et al., 2015). Glerean et al. (2012) showed that instantaneous phase synchrony and correlation-based sliding window analysis detected comparable temporal prop- erties. But they demonstrated that instantaneous phase synchrony was superior at achiev- ing optimal temporal resolution (a single repetition time), especially since the reliability of correlation-based sliding windows decreases as the temporal window shrinks. This was also the case in our data. As can be seen in Supplementary Information 2 (Pedersen et al., 2017), we observed that instantaneous phase synchrony time series are similar to correlation-based sliding windows time series at short window lengths (<60 s). The phase-randomized fMRI analysis that preserved the underlying correlational nature of our data suggests results were not predominantly driven by nonstationarities inherent in the data. This finding is concordant with Allen et al. (2014), who observed no changes in time- varying functional connectivity after applying same phase randomization procedure that we used (Prichard & Theiler, 1994). ties a recent Hindriks al. (2016), argued dynamic methods may detect nonstationarities in short resting-state scans of (∼ 10 min). Although main point present study was to generate network time series appropriate for SampEn analysis, it will remain important for future studies statistically evaluate Nevertheless, it is possible our entropy findings signify persistent relationships between nodes that facilitate spontaneous brain activity. It also tempting speculate may be partly constrained structural topology, given significant role of structure shaping (Deco al., 2013; Honey 2009; Shen, Hutchison, Bezgin, Everling, McIntosh, 2015). Network Neuroscience 106 l D o w n o a d e d f r o m h t t p : >1) and is consistent with
other studies combining graph theory and fMRI. Small-worldness was calculated by dividing
the whole-brain averaged normalized clustering coefficient and the characteristic path length
(across time points and subjects). Un total de 500 random networks were calculated for these
two normalized metrics. None of the resulting binary networks were fragmented, and the size
=8, 192 for all
of the largest subgraph (es decir., the largest network component) was equal to Nnode
subjects and time points.

Step 5: Network Analysis and Null Model

To calculate network properties from the thresholded brain graphs, we used MATLAB-
implemented functions from the Brain Connectivity Toolbox (www.brain-connectivity-toolbox.
net/) and Boost Graph Library (https://www.cs.purdue.edu/homes/dgleich/packages/matlab_
bgl/). We chose two biologically interpretable graph measures of brain connectivity—that is,
the clustering coefficient and the participation coefficient.

The clustering coefficient, or CC (vatios & Strogatz, 1998), quantifies the proportion of neigh-
boring nodes of a given node i that are clustered together. This measure is mathematically
described for node i as

Neurociencia en red

=

CCi

2de
− 1) ,
(ki

ki

(5)

109

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

/

t

/

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

1
2
1
0
0
1
0
9
1
9
1
0
norte
mi
norte
_
a
_
0
0
0
0
6
pag
d

.

t

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Temporal complexity of brain networks

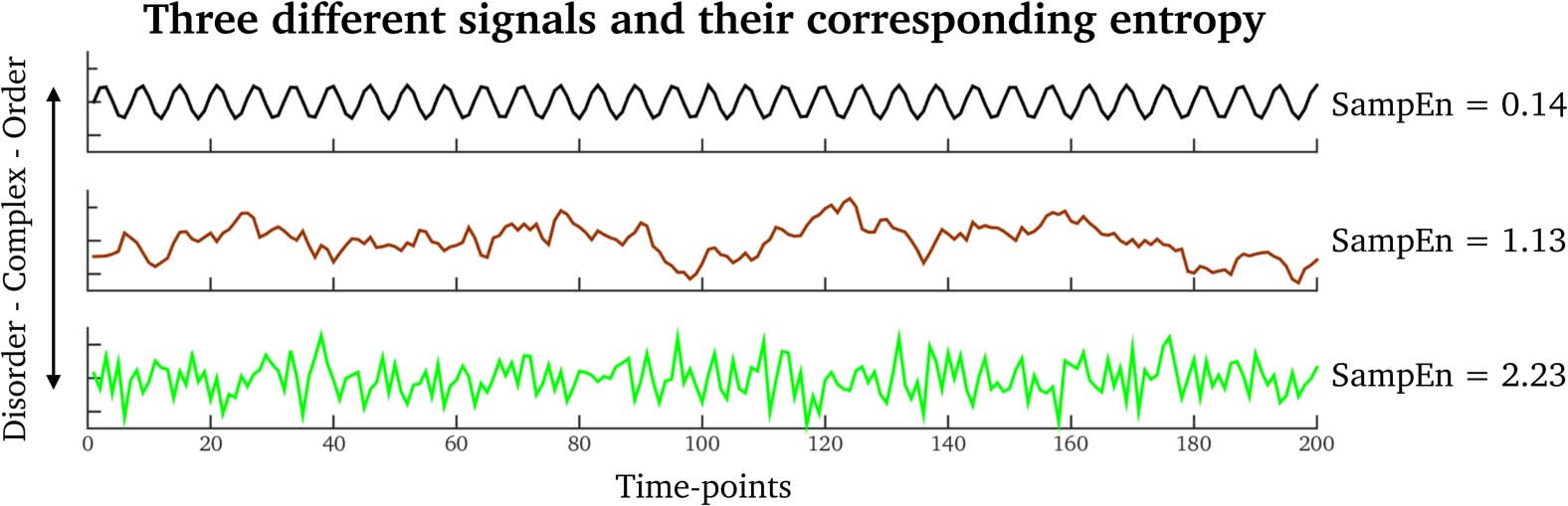
Cifra 6. Examples of signals having different SampEn values. Top row (black signal): A regular
señal. Middle row (brown signal): A fractal Brownian-motion signal. Bottom row (green signal): A
random signal.

where ti denotes the number of triangles surrounding node i and ki is its degree (es decir., number
of network-wide links connected to it). The values CCi always range within [0, 1].

The participation coefficient, or PC (Guimerà & Nunes Amaral, 2005), quantifies the

diversity of information between network modules. For node i, the metric is written as

PCi

= 1 − ∑

m∈M

(cid:3)

(cid:4)

2

,

ki

(metro)
ki

(6)

where the parameter M denotes a set of modules that subdivide the network into nonoverlap-
(metro) counts the number of connections between node i
ping partitions, and the parameter ki
and all nodes in module m. The participation coefficient always takes values in the range [0,
1]; 0 means that all nodal connections are either intramodular or intermodular to the same
module. A value of 1 means that all nodal connections are intermodular (with connections
to a variety of modules). en este estudio, M was calculated for each time point and subject, a nosotros-
ing a Louvain community structure algorithm with a community affiliation vector of γ = 2
(rubia, Guillaume, Lambiotte, & Lefebvre, 2008). We chose γ = 2 in contrast to γ = 1 a
allow for a finer spatial distinction between modules, since this reduces the probability of zero
values for the participation coefficient (es decir., a node having only intranetwork connections). Este
clustering method contains heuristics that may cause run-to-run variability. To estimate the ex-
tent of this variability, we randomly selected 50 of the instantaneous phase synchrony matrices
used in this study and calculated the average modularity of each (the Q-score) 200 veces. El
average Q-score over the runs was 0.59 with a standard deviation of 0.002 (coefficient of vari-
ance = 0.003). De este modo, the run-to-run variability of the Louvain community structure algorithm
used in this study appears to be low. The median number of modules across subjects was
6 (minimum number of modules = 1; maximum number of modules = 14).

Our main results were also compared to results generated from fMRI phase-randomized data
in which the fMRI time series were phase-shuffled in the Fourier domain while preserving the
power spectral magnitude and the correlational nature of the data (Prichard & Theiler, 1994).
De este modo, the only aspect we changed was the inherent dynamics of the original fMRI time series.
This manipulation therefore tested whether the underlying fMRI connectivity data were likely
to be nonstationary—that is, did the statistical distribution change over time?

Neurociencia en red

110

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

/

/

t

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

1
2
1
0
0
1
0
9
1
9
1
0
norte
mi
norte
_
a
_
0
0
0
0
6
pag
d

.

t

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Temporal complexity of brain networks

Step 6: Entropy Analysis in the Time Domain

The last analysis step was devoted to the extraction of SampEn (Richman & Moorman, 2000)
from the clustering-coefficient and participation-coefficient time series, from the original fMRI
data as well as from the phase-randomized surrogates. SampEn is related to “the rate of gen-
eration of new information” in a signal. Por ejemplo, periodic signals with high self-similarity
will generate trivial “new” information by evolving in time (es decir., low SampEn), whereas biolog-
ical signals with less self-similarity will have more information (es decir., high SampEn). Cifra 6
illustrates three signals with different SampEn values. See also Supplementary Information 5
(Pedersen et al., 2017) for example time series of real fMRI clustering coefficients and partici-
pation coefficients.

Mathematically, SampEn(metro, r, norte) estimates the conditional probability that two templates
of a signal will remain similar over time, when self-matches have been already excluded (ver
Richman & Moorman, 2000, and Sokunbi et al., 2013, for overviews). Aquí, the term “tem-
plate” refers to m-dimensioanal vectors made by the delayed time points in the original signal.
This is governed by four parameters: norte, metro, t, and r, where N denotes the number of time
points in the entire signal, m and τ specify the segmented and delayed templates in the original
señal, and r is a threshold controlling the level of similarity between templates. The measure
is defined as

SampEn(metro, r, norte) = −ln

(cid:3)

(cid:4)

Um+1(r)
Um(r)

where ln denotes the natural logarithm and Um(r) is defined as

1

Um(r) =

N − mτ ∑N−mτ
Ecuación (8) is based on the probability functions Cm
i
m-length templates Xj
similar to the template Xi

(r) formed by the average number of
= [xj, xj+τ, . . . , xj+(m−1)t] (1 ≤ j ≤ N − mτ), which are closely
(i (cid:8)= j):

i=1 Cm

(r).

i

,

(7)

(8)

Cm
i

(r) =

Bi
N − (metro + 1) t .

(9)

The level of “similarity” is quantified by the value Bi as the number of templates Xj whose
distance to the template Xi is less than or equal to r:
(cid:5)
(cid:5) ≤ r.

(10)

(cid:5)
(cid:5)

d

Xi, Xj

(cid:5)
(cid:5)

Xi, Xj

− Xj+k

(cid:5)
(cid:5)
(cid:5)Xi+k

(cid:5)
(cid:5) = max0≤k

Descargar PDF