Communicated by James V. Piedra
On Suspicious Coincidences and Pointwise
Mutual Information
Christopher K. I. williams
ckiw@inf.ed.ac.uk
School of Informatics, University of Edinburgh, Edinburgh EH8 9AB, REINO UNIDO.
Barlow (1985) hypothesized that the co-occurrence of two events A and
B is “suspicious” if P(A, B) (cid:2) PAG(A)PAG(B). We first review classical mea-
sures of association for 2 × 2 contingency tables, including Yule’s Y (Yule,
1912), which depends only on the odds ratio λ and is independent of the
marginal probabilities of the table. We then discuss the mutual informa-
ción (MI) and pointwise mutual information (PMI), which depend on the
ratio P(A, B)/PAG(A)PAG(B), as measures of association. We show that once the
effect of the marginals is removed, MI and PMI behave similarly to Y
as functions of λ. The pointwise mutual information is used extensively
in some research communities for flagging suspicious coincidences. Nosotros
discuss the pros and cons of using it in this way, bearing in mind the
sensitivity of the PMI to the marginals, with increased scores for sparser
events.
1 Introducción
Barlow (1985) hypothesized that “the cortex behaves like a gifted de-
tective, noting suspicious coincidences in its afferent input, and thereby
gaining knowledge of the non-random, causally related, features in its
environment.” More specifically, he wrote (pag. 40):
The coincident occurrence of two events A and B is “suspicious” if they
occur jointly more than would be expected from the probabilities of their
individual occurrence, es decir. the coincidence A&B is suspicious if P(A&B) (cid:2)
PAG(A) × P(B).1 Any detective knows that, for a coincidence to be suspi-
cious, the events themselves must be rare ones, and that if they are rare
suficiente, even a single occurrence is significant.
Edelman, Hiles, Cual, and Intrator (2002) refer to the principle of suspi-
cious coincidences as where “two candidate fragments A and B should be
combined into a composite object if the probability of their joint appearance
PAG(A, B) is much higher than P(A)PAG(B)."
1
In fact in Barlow (1985), the inequality is written (cid:3) en vez de (cid:2), but it is clear
the latter was intended. The same paper was also published as Barlow (1987); allá, el
inequality is the correct way round.
Computación neuronal 34, 2037–2046 (2022) © 2022 Instituto de Tecnología de Massachusetts
https://doi.org/10.1162/neco_a_01533
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
4
1
0
2
0
3
7
2
0
4
2
4
2
2
norte
mi
C
oh
_
a
_
0
1
5
3
3
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
2038
C. williams
The fundamental problem here is to detect if there is a significant associa-
tion between events A and B. This can arise in many different contexts—for
ejemplo:
• An animal detecting that eating a certain plant is associated with sub-
sequent illness
• Detecting that a certain drug is associated with a particular adverse
drug reaction
• Detecting the association between a visual stimulus that contains an
image of the subject’s grandmother or not and the response of a pu-
tative “grandmother cell”
• Detecting that particular successive words in text are associated more
frequently than by chance—called a collocation, an example being the
bigram “carbon dioxide”
• A geneticist determining that two genes are in linkage disequilibrium
(Lewontin, 1964)
• Detecting that the pattern of two edges in a visual scene making a
corner junction occurs more frequently than by chance
Below we review various measures of association from the literature, No-
tably Yule’s Y (Yule, 1912), which depends solely on the odds ratio and is
invariant to the marginal distributions of the two variables. We then dis-
cuss measures of association based on the mutual information and point-
wise mutual information, which make use of the ratio P(A, B)/PAG(A)PAG(B), como
proposed by Barlow and others across diverse literatures. Finalmente, nosotros estafamos-
sider the pros and cons of using pointwise mutual information (PMI) to flag
suspicious coincidences and discuss its estimation from data when (alguno
de) the counts in the table are low.
2 2 × 2 Contingency Tables
Consider two random variables X and Y that take on values of 0 o 1. El
2 × 2 contingency table has the form
(cid:2)
P =
(cid:3)
,
p00
p10
p01
p11
(2.1)
= p(X = 0, Y = 1). We will also say the event x oc-
dónde, Por ejemplo, p01
curs if X = 1, and similarly for y. We denote the marginals with “dot” no-
tation, de modo que, Por ejemplo, p1· = p(X = 1) = p10
+ p11.
P is defined by 3 degrees of freedom (as the entries sum to 1). Two of
these are taken up by the marginals, leaving 1 additional degree of free-
dominación. Given a table P, we can manipulate the marginals by multiplying the
rows and columns with positive numbers and renormalizing. Such a trans-
formation is shown in, Por ejemplo, Hasenclever and Scholz (2016, eq. 1):
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
4
1
0
2
0
3
7
2
0
4
2
4
2
2
norte
mi
C
oh
_
a
_
0
1
5
3
3
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
On Suspicious Coincidences and Pointwise Mutual Information
2039
gμ,norte (PAG) =
1
z(μ, norte)
(cid:2)
(cid:3)
,
μν p00
ν p10
μp01
p11
where Z(μ, norte) = μν p00
+ μp01
+ ν p10
+ p11. The odds ratio
λ = p00 p11
p01 p10
(2.2)
(2.3)
can be seen to be invariant to the action of this margin manipulation trans-
formation and thus defines the third degree of freedom. An odds ratio of 1
implies that there is no association and that P is equal to the product of the
marginals.
The “canonical” table with marginals of 1/2 but with the same odds ratio
as P is given by
Pcan =
⎛
⎜
⎝
√
λ
√
2(1+
λ)
1
√
2(1+
λ)
⎞
λ)
⎟
⎠ ,
λ)
1
√
2(1+
√
λ
√
2(1+
(2.4)
as shown by Yule (1912). Like a copula for continuous variables, this allows
a separation of the marginals from the dependence structure between X
and Y.
The table P can also be expressed in terms of a deviation from the product
of the marginals (see Hasenclever & Scholz, 2016, pag. 24) como
(cid:2)
P =
p0· p·0
p1· p·0
+ D p0· p·1
− D p1· p·1
(cid:3)
− D
+ D
,
(2.5)
where D = p00 p11
= p11
as the coefficient of linkage disequilibrium for two genes.
− p1· p·1, etcétera. In genetics, D is known
− p01 p10
2.1 Estimation from Data. Ecuación 2.1 is given in terms of probabili-
ties such as p01. Sin embargo, observational data do not directly provide such
probabilities but counts associated with the corresponding cells. The max-
/norte, where ni j is
imum likelihood estimator (MLE) for pi j is, por supuesto, ni j
the count associated with cell i j, and n is the total number of counts. El
MLE has well-known issues when (algunos de) the counts are small. Bayesian
approaches to address this are discussed in section 5.
3 Classical Measures of Association
For two gaussian continuous random variables, there is a natural measure
of their association, the correlation coefficient. This is independent of the
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
4
1
0
2
0
3
7
2
0
4
2
4
2
2
norte
mi
C
oh
_
a
_
0
1
5
3
3
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
2040
C. williams
individual (marginal) variances of each variable, and lies in the interval
[−1, 1].
Para el 2 × 2 mesa, many measures of association have been devised.
One is Yule’s Y (Yule, 1912), dónde
Y =
√
√
λ − 1
λ + 1
.
(3.1)
Like the correlation coefficient, Y also lies in the range of [−1, 1], con un
value of 0 reflecting that there is no association. Its dependence only on
λ means that it is invariant to the marginals in the table. Y(1/λ) = −Y(λ),
so Y is an odd function of log(λ). Edwards (1963) argued that measures of
association must be functions of the odds ratio.
There are a number of desirable properties for a measure of association
η between binary variables. Por ejemplo, Hasenclever and Scholz (2016,
pag. 22) list these:
1. η is zero on independent tables.
2. η is a strictly increasing function of the odds ratio when restricted to
tables with fixed margins.
3. η respects the symmetry group D4, a saber, η is symmetric in the
markers (es decir., invariant to matrix transposition), and η changes
sign when the states of a marker are transposed (row or column
transposition).
4. The range of the function is restricted to (−1, 1).
As well as Yule’s Y,2 several other measures of association have been pro-
planteado; indeed Tan, Kumar, and Srivastva (2004) lista 21. Other measures of
association include Lewontin’s D(cid:5)
(1964), which standardizes D from equa-
ción 2.5 by dividing it by the maximum value it can take on, which depends
on the marginals of the table, and the binary correlation coefficient r, cual
standardizes D by
p0· p·0 p1· p·1. For the canonical table, it turns out that
D(cid:5) = r = Y.
√
4 Information-Theoretic Measures of Association
Barlow’s definition of a suspicious coincidence suggests consideration of
the quantity
i(X, y) = log
pag(X, y)
pag(X)pag(y)
.
(4.1)
2
Yule (1900) had earlier proposed Q = (λ − 1)/(λ + 1) as a measure of association, pero
his discussion on p. 592 of Yule (1912) gives a number of reasons for preferring Y to Q.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
4
1
0
2
0
3
7
2
0
4
2
4
2
2
norte
mi
C
oh
_
a
_
0
1
5
3
3
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
On Suspicious Coincidences and Pointwise Mutual Information
2041
Indeed i(X, y) has been proposed in different literatures. Por ejemplo,
Church and Hanks (1990) studied it for word associations in linguistics.
i(X, y) is termed the pointwise mutual information (PMI) en, Por ejemplo, el
statistical natural language processing textbook of Manning and Schütze
(1999). In pharmacovigilance, Bate et al. (1998) call i(X, y) the information
component (IC), as it is one component of the mutual information calcula-
tion in a 2 × 2 mesa, and it is also studied in DuMouchel (1999). And in
the data mining literature, Silverstein, Brin, and Motwani (1998) define the
interest to be the ratio p(X, y)/(pag(X)pag(y)) (es decir., without the log).
Note that while Y, D(cid:5)
=
pag(X, y) − p(X)pag(y), i(X, y) considers the log ratio of these terms. De este modo, i(X, y)
considers the ratio of the observed and expected probabilities for the event
(X, y), where the expected model is that of independence.
, and r consider the difference, D = p11
− p1· p·1
The mutual information (MI) is defined as
I(X; Y) =
(cid:10)
i, j∈{0,1}
pag(X = i, Y = j) registro
PAG(X = i, Y = j)
PAG(X = i)PAG(Y = j)
.
(4.2)
We have that I(X; Y) ≥ 0, with I(X; Y) = 0 when X and Y are independent.
Both PMI and MI as defined above depend on the marginal probabili-
ties in the table. To see this, use p(X, y) ≤ p(X) or p(X, y) ≤ p(y), so i(X, y) ≤
mín.(− log p(X), − log p(y)), eso es, favoring “sparsity” (low probability).
The MI is maximal for a diagonal (or antidiagonal) table with marginals
de 1/2, the opposite trend to PMI.
There have been various proposals to normalize the PMI and MI to make
them fit in the range [−1, 1] y [0, 1], respectivamente. Por ejemplo, Bouma
(2009) defined the normalized PMI (NPMI) as in(X, y) = i(X, y)/h(X, y) para
pag(X, y) > 0, where h(X, y) = − log p(X, y). NPMI ranges from +1 cuando
events x and y only occur together, a través de 0, when they are independent,
to −1 when x and y occur separately but not together. Similarly there are a
number of proposals for normalizing the mutual information, Bouma (2009)
suggests In(X; Y) = I(X; Y)/h(X, Y), where H(X, Y) is the joint entropy of
X and Y. En(X; Y) (termed the normalized MI or NMI) takes on a value of
+1 if X and Y are perfectly associated and 0 if they are independent. Alter-
native normalizations of the MI by H(X ) or H(Y) have also been proposed;
Prensa, Teukolsky, Vetterling, and Flannery (2007, segundo. 14.7.4) term these the
uncertainty coefficients. NMI is not strictly a measure of association as de-
fined above, as it does not take on negative values, but following the con-
struction in Hasenclever and Scholz (2016), one can, Por ejemplo, define the
signed NMI as sign(D)En(X; Y).
Given that the canonical table removes the effect of the marginals, es
natural to consider PMI and MI as a function of λ. Using the canonical table
from equation 2.4, we obtain
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
4
1
0
2
0
3
7
2
0
4
2
4
2
2
norte
mi
C
oh
_
a
_
0
1
5
3
3
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
2042
iλ(X, y) = log
2
1 +
√
λ
√
λ
,
C. williams
(4.3)
which takes on a value of 0 for λ = 1 (independence) and tends to a value
of log(2) as λ tends to infinity. For λ < 1 the value of iλ(x, y) becomes neg-
ative and diverges to −∞ as λ → 0. However, study of the canonical table
indicates would make more sense in this case to consider one of the
“antidiagonal” cells in Pcan, which will have a probability greater than 1/2
as the “event.” In general we can treat all four cells of the contingency table
as the joint event, compute the PMI for each, and return the maximum. For
the canonical table with λ < 1, this means that we transform λ → 1/λ and
compute iλ as per equation 4.3.
For the MI of the canonical table, we obtain (after some manipulation)
Iλ(X; Y) =
√
1 +
√
λ
√
log
λ
λ − log(1 +
√
λ) + log 2.
(4.4)
Analysis of Iλ(X; Y) shows that it is invariant if we transform λ to 1/λ, so a
plot of Iλ(X; Y) against log(λ) is symmetric around 0 and tends to the value
log(2) as λ tends to 0 or infinity.
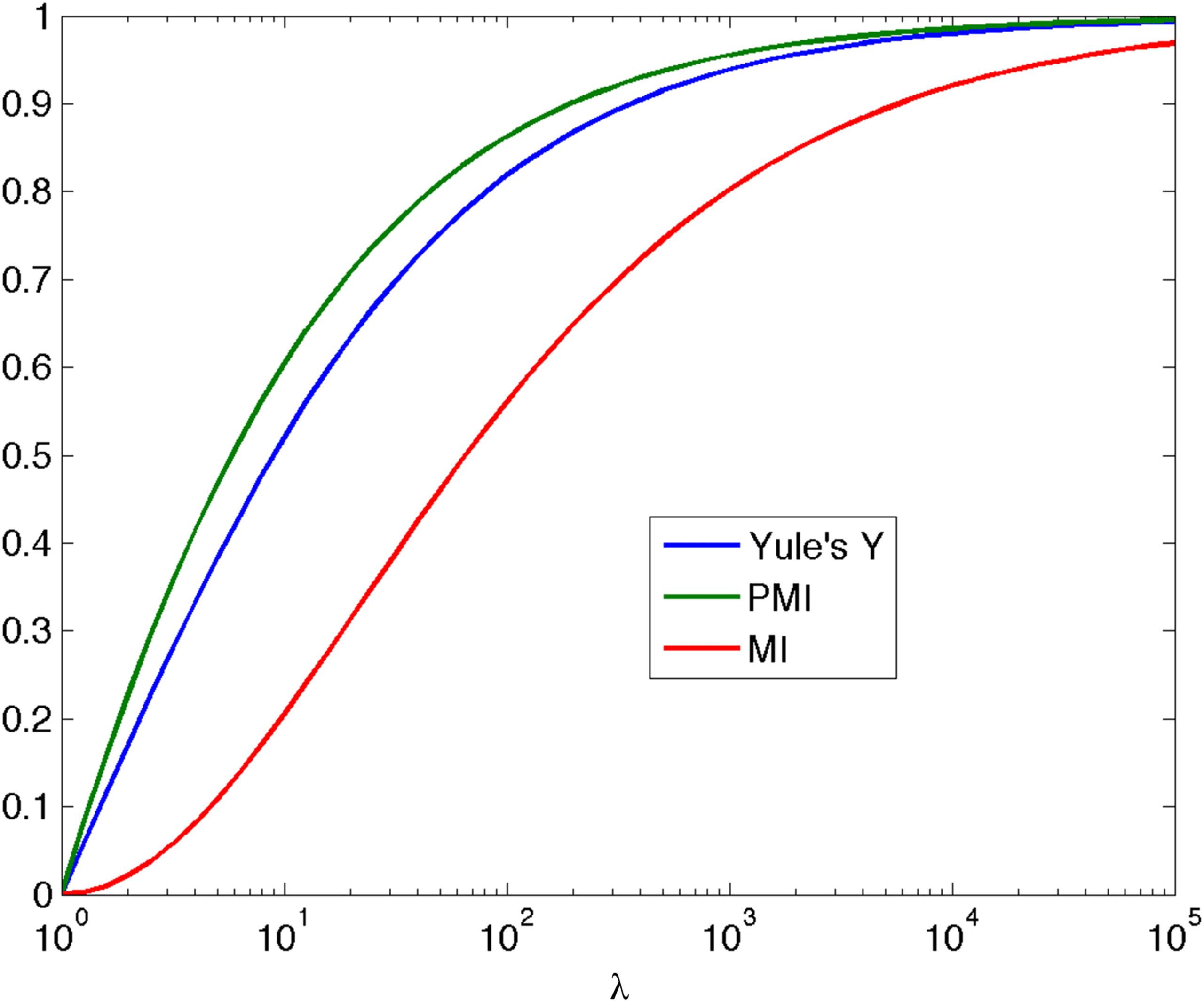
Plots of Y, iλ, and Iλ for λ ≥ 1 in Figure 1 show similar behavior, mono-
tonically increasing to a maximum value as λ → ∞. If we choose logs to
base 2, then the maximum value is 1 in all three cases. As Y is already well
established (since 1912!), it does not seem necessary to promote iλ or Iλ as
alternatives, when considering the canonical table.
5 Detecting Associations with Pointwise Mutual Information
As we have seen, the raw PMI score is not invariant to the distribution of
the marginals. This can be seen in Table 1, which concerns the association
between vaccination and death from smallpox; the original proportions in
panel a are based on the Sheffield data in Table I of Yule (1912). In panel b,
the marginals of the table with regard to vaccination have been adjusted to
50/50 (as may have happened if these data had been collected in a random-
ized, controlled trial), and in panel c, we have the canonical table where
both marginals are 50/50.3 Notice that the PMI is highest for the original
(unbalanced) table and decreases as the marginals are balanced. Conversely,
the MI is lowest in the the original (unbalanced) table and increases as the
marginals are balanced. Of course, Yule’s Y is constant throughout, by con-
struction.
3
Yule (1912) comments that on the canonical table, “These are, of course, not the actual
proportions, but the proportions that would have resulted if an omnipotent demon of
unpleasant character (no relation of Maxwell’s friend) could have visited Sheffield . . . ,
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
1
0
2
0
3
7
2
0
4
2
4
2
2
n
e
c
o
_
a
_
0
1
5
3
3
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
On Suspicious Coincidences and Pointwise Mutual Information
2043
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
Figure 1: Plots of Y, iλ (PMI), and Iλ (MI) against λ (log scale) for λ ≥ 1.
Table 1: 2 × 2 Contingency Tables for the Association between Vaccination and
Death from Smallpox.
(a) Original Table
(b) Vaccination Rate 50%
PMI = 2.300, MI = 0.108 PMI = 0.866, MI = 0.205 PMI = 0.705, MI = 0.310
(c) Canonical Table
Recover Die Marginals Recover Die Marginals Recover Die Marginals
Vaccinated
0.840
Unvaccinated 0.059
0.899
Marginals
0.043
0.058
0.101
0.883
0.117
0.476
0.252
0.728
0.024
0.248
0.272
0.500
0.500
0.408
0.092
0.500
0.092
0.408
0.500
0.500
0.500
Note: Panel a is the original table based on the data in Yule (1912), panel b adjusts the
marginals for vaccinated/unvaccinated to be 50/50, and panel c is the canonical table
where the marginals are both 50/50. In all three tables, Yule’s Y = 0.630.
As another example, consider fixing λ but adjusting the marginal prob-
abilities of events x and y. For example, for λ = 16, PMI takes on the values
of 0.678, 1.642, 2.293, 3.642, and 3.958 (using logs to base 2) as p(x) = p(y)
varies from 0.5, 0.2, 0.1, 0.01, and 0.001. This is particularly problematic as
low counts will give rise to uncertainty in the estimation of the required
and raised the fatality rate and the proportion of unvaccinated . . . to 50 per cent without
otherwise altering the facts.”
f
/
/
/
/
3
4
1
0
2
0
3
7
2
0
4
2
4
2
2
n
e
c
o
_
a
_
0
1
5
3
3
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2044
C. Williams
probabilities (especially of the joint event). In the context of word asso-
ciations, Manning and Schütze (1999, sec. 5.4) argue that PMI “does not
capture the intuitive notion of an interesting collocation very well” and
mention work that multiplies it by p(x, y) as one strategy to compensate
for the bias in favor of rare events.
Barlow (1985) suggested that sparsity is important for the detection
of suspicious coincidences, that is, that “the events themselves must be
rare ones.” It is true that a low p(y) gives more “headroom” for the ratio
p(y|x)/p(y) to be large. The PMI score is used extensively in pharmacovig-
ilance, where the aim is to detect associations between drugs taken and
adverse drug reactions (ADRs). In this context, the ratio p(x, y)/p(x)p(y) =
p(y|x)/p(y) is termed the relative reporting ratio (RRR) and compares the rel-
ative probability of an adverse drug reaction y given treatment with drug
x, compared to the base rate p(y). Another commonly used measure is the
proportional reporting ratio (PRR), defined as p(y|x)/p(y|¬x). A US Food and
Drug Administration (FDA) white paper (Duggirala et al., 2018) describes
the use of both RRR and PRR for detecting ADRs in routine surveillance
activities.
Above, we have described the maximum likelihood estimation for the
probabilities in the 2 × 2 table, based on counts. However, there are well-
known issues with the MLE when (some of) the counts are small. This
naturally suggests a Bayesian approach, and there is a considerable litera-
ture on the Bayesian analysis of contingency tables, as reviewed, for exam-
ple, in Agresti (2013). There are different sampling models depending on
how the data are assumed to be generated, as described in Agresti (2013,
sec. 2.1.5). If all four counts are unrestricted, a natural assumption is that
each ni j is drawn from a Poisson distribution with mean μ
i j, which can be
given a gamma prior. Alternatively, if n is fixed, the sampling model is a
multinomial, and the conjugate prior is a Dirichlet distribution. If one set of
marginals is fixed, then the data are drawn from two binomial distributions,
each of which can be given a beta prior. If both marginal totals are fixed, this
corresponds to Fisher’s famous “lady tasting tea” experiment, and the sam-
pling distribution of any cell in the table follows a hypergeometric distri-
bution. Section 3.6 of Agresti (2013) covers Bayesian inference for two-way
contingency tables, and Agresti and Min (2005) discuss Bayesian confidence
intervals for association parameters, such as the odds ratio.
DuMouchel (1999) applied an empirical Bayes approach to consider sam-
pling variability for PMI (a.k.a. RRR) in the context of adverse drug reac-
tions. He assumed that each n11 is a draw from a Poisson distribution with
unknown mean μ
/E11, where
11 and that the object of interest is ρ
11
E11 is the expected count (assumed known) under the assumption that the
variables are independent. Using a mixture of gamma distributions prior
for ρ
11)|n11] rather than
/E11. The mixture prior was used to
just considering the sample estimate n11
express the belief that when testing many associations, most will have a PMI
11, DuMouchel obtained the posterior mean E[log(ρ
= μ
11
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
1
0
2
0
3
7
2
0
4
2
4
2
2
n
e
c
o
_
a
_
0
1
5
3
3
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
On Suspicious Coincidences and Pointwise Mutual Information
2045
of near zero, but there will be some with significantly larger values. This
method is known as the multi-item gamma Poisson shrinker (MGPS). The
value of this approach is that Bayesian shrinkage corrects for the high vari-
ability in the RRR sample estimate n11
/E11 that results from small counts.
6 Summary
Motivated by Barlow’s hypothesis about suspicious coincidences, we have
reviewed the properties of 2 × 2 contingency tables for association analy-
sis, with a focus on the odds ratio λ and Yule’s Y. We have considered the
mutual information and pointwise mutual information as measures of asso-
ciation, along with normalized versions thereof. We have shown that, con-
sidered as functions of λ in the canonical table, MI and PMI behave similar
to Y for λ ≥ 1, increasing monotonically with λ (and can be made similar
for 0 > λ > 1).
As well as Y, the PMI measure i(X, y) = log p(X, y)/(pag(X)pag(y) puede también ser
used to identify suspicious coincidences, and it is used in practice—for ex-
amplio, in pharmacovigilance. We have discussed the pros and cons of using
it in this way, bearing in mind the sensitivity of the PMI to the marginals,
with increased scores for sparser events. When some of the counts in the
table are low, Bayesian approaches can be useful for estimating PMI from
raw counts.
Expresiones de gratitud
I thank Peter Dayan and Iain Murray for helpful comments on an early draft
of this note and the anonymous reviewers whose comments helped to im-
prove the note.
Referencias
Agresti, A. (2013). Categorical data analysis (3tercera ed.). Hoboken, Nueva Jersey: wiley.
Agresti, A., & mín., Y. (2005). Frequentist performance of Bayesian confidence inter-
vals for comparing proportions in 2 × 2 contingency tables. Biometrics, 61, 515–
523. 10.1111/j.1541-0420.2005.031228.x, PubMed: 16011699
Barlow, h. B. (1985). Cerebral cortex as model builder. In D. Rose & V. GRAMO. Dobson
(Editores.), Models of the visual cortex (páginas. 37–46). Nueva York: wiley.
Barlow, h. B. (1987). Cerebral cortex as model builder. en l. METRO. Vaina (Ed.), Matters of
Inteligencia: Conceptual structures in cognitive neuroscience (páginas. 395–406). Dordrecht:
D. Reidel.
Solución alcalina, A., Lindquist, METRO., Edwards, I. r., Olsson, S., Orre, r., Lansner, A., & De
Freitas, R. METRO. (1998). A Bayesian neural network method for adverse drug re-
action signal detection. European Journal of Clinical Pharmacology, 54, 315–321.
10.1007/s002280050466, PubMed: 9696956
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
4
1
0
2
0
3
7
2
0
4
2
4
2
2
norte
mi
C
oh
_
a
_
0
1
5
3
3
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
2046
C. williams
Bouma, GRAMO. (2009). Normalized (pointwise) mutual information in collocation extrac-
ción. In Proceedings of the Biennial GSCL Conference 2009.
Church, k. w., & Hanks, PAG. (1990). Word association norms, mutual information, y
lexicography. Comput. Linguist., 16(1), 22–29.
Duggirala, h. J., Tonning, j. METRO., Herrero, MI., Bright, r., Panadero, j. D., Ball, r., . . .
Kass-Hout, t. (2018). Data mining at FDA (White Paper). https://www.fda.gov/
science-research/data-mining/data-mining-fda-white-paper
DuMouchel, W.. (1999). Bayesian data mining in large frequency tables, with an ap-
plication to the FDA spontaneous reporting system. American Statistician, 53(3),
177–190.
Edelman, S., Hiles, B., Cual, h., & Intrator, norte. (2002). Probabilistic principles in unsu-
pervised learning of visual structure: Human data and a model. In T. Dietterich, S.
Becker, & z. Ghahramani (Editores.), Advances in neural information processing systems,
14. Cambridge, MAMÁ: CON prensa.
Edwards, A. W.. F. (1963). The measure of association in a 2 × 2 mesa. Journal of the
Royal Statistical Society, Series A (General), 126(1), 109–114. 10.2307/2982448
Hasenclever, D., & Scholz, METRO. (2016). Comparing measures of association in 2 ×
2 probability tables. Open Statistics and Probability Journal, 7, 20–35. 10.2174/
1876527001607010020
Lewontin, R. C. (1964). The interaction of selection and linkage. I. General con-
siderations; Heterotic models. Genetics, 49(1), 49–67. 10.1093/genetics/49.1.49,
PubMed: 17248194
Manning, C., & Proteger, h. (1999). Foundations of statistical natural language processing.
Cambridge, MAMÁ: CON prensa.
Prensa, W.. h., Teukolsky, S. A., Vetterling, W.. T., & Flannery, B. PAG. (2007). Numerical
recipes: The art of scientific computing (3tercera ed.). Cambridge: Cambridge University
Prensa.
Silverstein, C., Brin, S., & Motwani, R. (1998). Beyond market baskets, Generalizing
association rules to dependence rules. Data Mining and Knowledge Discovery, 2(1),
39–68. 10.1023/A:1009713703947
Broncearse, P.-N., Kumar, v., & Srivastva, j. (2004). Selecting the right objective measure
for association analysis. Information Systems, 29, 293–313. 10.1016/S0306-4379(03)
00072-3
Yule, GRAMO. Ud.. (1900). On the association of attributes in statistics. Phil. Trans. roy. Soc.,
A, 194, 257.
Yule, GRAMO. Ud.. (1912). On the methods of measuring association between two attributes.
Journal of the Royal Statistical Society, 75(6), 579–652. 10.2307/2340126
Received March 15, 2022; accepted June 2, 2022.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
4
1
0
2
0
3
7
2
0
4
2
4
2
2
norte
mi
C
oh
_
a
_
0
1
5
3
3
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3