Communicated by David Mumford - IA de Investigación especializada en el MIT

Communicated by David Mumford

Two Stages of Curve Detection Suggest Two Styles of
Visual Computation

Steven W. Zuckert
AIlan Dobbins
Lee Iverson
Computer Vision and Robotics Laboratory,
McGill Research Centre for Intelligent Machines,
McGill University, Montrkal, QuCbec, Canada

The problem of detecting curves in visual images arises in both com-
puter vision and biological visual systems. Our approach integrates
constraints from these two sources and suggests that there are two
different stages to curve detection, the first resulting in a local descrip-
ción, and the second in a global one. Each stage involves a different
style of computation: in the first stage, hypotheses are represented
explicitly and coarsely in a fixed, preconfigured architecture; in the
second stage, hypotheses are represented implicitly and more finely
in a dynamically-constructed architecture. We also show how these
stages could be related to physiology, specifying the earlier parts in a
relatively fine-grained fashion and the later ones more coarsely.

1 Introducción

An extensive mythology has developed around curve detection. In ex-
trapolating from orientation-selective neurons in the visual cortex (Hubel
and Wiesel 19621, it is now widely held that curve detection is simply a
matter of «integrating» the responses of these cells. More specifically, el
mythology holds that this integration process is global, that the initial
estimates are local, and that the relationship between them will become
clear as a more detailed understanding of cortical circuitry is uncovered.
Sin embargo, this mythical process of «integración» has turned out to be elu-
sive, the search for it has led, en cambio, to a series of dilemmas, y el
quantity of physiological data is exploding. It is rarely clear how new
details of cortical circuitry relate to different components of the curve
detection problem.

We believe that this situation is typical of vision in general, y
amounts to ascribing too little function to the earlier stages, and too

+Senior Fellow, Canadian Institute for Advanced Research.

Neural Computation 1, 68-81 (1989) @ 1989 Massachusetts Institute of Technology

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d

F
/

1
1
6
8
8
1
1
8
2
7
norte
mi
C
oh
1
9
8
9
1
1
6
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Two Stages of Curve Detection

much to the later ones. For curve detection, virtually all of the complex-
ity is delegated to the process of «integración,» so it is not surprising
that successful approaches have remained elusive. Part of the problem
is that models of integrative processes have been rich in selected detail,
but poor in abstract function. In the sense that it is often useful to see
the forest before the trees, we submit that solutions will likely be found by
considering both coarse-grained and fine-grained models, and that such
models will suggest a partitioning of function whose abstraction varies
with granularity. To make this point concretely, we here outline a coarse-
grained solution to the curve detection problem from a computational
perspectiva, and sketch how it could map onto physiology. The sketch is
coarse enough to serve as an organizational framework, but fine enough
to suggest particular physiological constraints. One of these comprises
our first, coarse-grain prediction: curve detection naturally decomposes
into two stages, the first in which a local description is computed, y el
second in which a global description is computed. These computations
are sufficiently different that we are lead to hypothesize two different
styles of visual computation.

2 The Dilemma of Curve Detection

The initial measurement of orientation information is broadly tuned,
which suggests the averaging necessary to counteract retinal (sensor)
sampling, quantization, y ruido. Sin embargo, the end result of curve de-
tection is unexpectedly precise: corners can be distinguished from arcs
of high curvature, and nearby curves can be distinguished from one an-
other to a hyperaccurate level, even though they might pass through the
same receptive field.

An analogous dilemma exists for computer vision systems, incluso con
the spectacular numerical precision of which computers are capable:
quantization and noise imply smoothing, but smoothing blurs corners,
endpoints, and nearby curves into confusion (Zucker 1986). At the foun-
dation is a chicken-and-egg problem: if the points through which the
curve passed, together with the locations of discontinuities, were known,
then the actual properties of the curve could be inferred. But initially
they are not known, so any smoothing inherent in the inference process
is potentially dangerous.

3 Two Stages of Curve Detection

We have discovered a computational solution to this dilemma, cual
involves decomposing the full problem into two stages, each of which
has a rather different character. In the first stage, the local properties of
the curve are computed: its trace (the set of retinotopic points through
which the curve passes), its tangent (or orientation at those points), y

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d

F
/

1
1
6
8
8
1
1
8
2
7
norte
mi
C
oh
1
9
8
9
1
1
6
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Steven W. Zucker, Allan Dobbins, and Lee Iverson

its curvature. In the second stage, these properties are refined to cre-
ate a global mode1 of the curve. This much – proceeding from local
to global – is standard; the style of the computations is not. The key
to the first stage is to infer the local properties coarsely – not in fine
detail – but without sacrificing reliability or robustness. Coarseness is
here related to quantization, whch must limit error propagation without
blurring over corners. Observe that this is precisely what is lacking in
the standard myth, where errors (p.ej., about placing discontinuities) poder
have far reaching consequences. The result is a style of computation in
which the different (quantized) possibilities are made explicit, and ar-
ranged in a fixed, preconfigured computational architecture that imposes
no a priori ordering over them. Each distinct hypothesis, say rough ori-
entation and curvature at every position, forms a unit in a fixed network
that strongly resembles neural-network-style models. Reliability and ro-
bustness are then maintained by the network; hence the local description
is not computed locally! A mapping onto orientation hypercolumns will
be discussed shortly.

The second stage embodies a rather different style of computation.
Now the possibilities no longer need be general, but are constrained to
be in the range dictated by the first stage. Thus the architecture can
be tailored to each problem-that
es, constructed adaptively rather than
preconfigured-and variables can be represented implicitly. With these
highly focused resources, the key limitation on precision is implemen-
tation, and it need not be hampered by uncontrolled error propagation.
From the outside, this constructive style of computation holds certain key
properties in common with later visual areas, such as V4 and IT, dónde
receptive field structure has been shown to vary with problem constraints
(p.ej., Maunsell and Newsome 1987; Moran and Desimone 1985).

4 The Model of Curve Detection

In physiological terms, neurons are said to be orientation selective if they
respond differentially to stimulus (edge or line) orientación. We take this
operational statement one step further by defining orientation selection
to be the inference of a local description of the curve everywhere along
él, and postulate orientation selection as the goal of our first stage. En el
second stage, global curves are inferred through this local description.
The various stages of our process are shown in figure 1, and expanded
abajo.

4.1 Stage 1: Inferring the Tangent Field. Formally orientation selec-
tion amounts to inferring the trace of the curve, or the set of points (en
the image) through which the curve passes, es (approximate) tangent and
curvature at those points, and their discontinuities (Zucker 1986). We re-
fer to such information as the tangent field, and note that, since the initial

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d

F
/

1
1
6
8
8
1
1
8
2
7
norte
mi
C
oh
1
9
8
9
1
1
6
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Two Stages of Curve Detection

measurements are discrete, this will impose constraints on the (inferred)
tangents, curvatures, and discontinuities (Parent and Zucker 1985).

This first stage of orientation selection is in turn modeled as a two

step process:

Step 1.1. Initial Measurement of the local fit at each point to estimate ori-
entation and curvature. These estimates derive from a model of
simple cell receptive fields instantiated at multiple scales and orien-
tations at each image position. Sin embargo, these local measurements
are inherently inaccurate (p.ej., broadly tuned), so we require:

Step 1.2. Inter~retatjon into an explicit distributed representation of tan-
gent and curvature by establishing consistency between the local
measurements. This is accomplished by modifying them according
to their geometric relationships with nearby estimates.

4.2 Stage 2 Infemng a Covering of the Curve. Since the tangent
is the first derivative of a curve (with respect to arc length), the global
curve can be recovered as an integral through the tangent field. Semejante
a view typically leads to sequential recovery algorithms (p.ej., Kass and
Witkin 1987). But these algorithms require global parameters, starting
puntos, and some amount of topological structure (es decir., which tangent
point follows which); in short, they are biologically implausible. en contra-
contraste, we propose a novel approach in which a collection of short, dy-
namically modifiable curves (”snakes” in computer vision; see Montanari
1971; Kass et al. 1988) move in parallel.

The key idea behind our approach is to recover the global curve by
computing a covering of it; es decir., a set of objects whose union is equiva-
lent to the original curve. The elements of the covering are unit-length
dynamic splines, initially equivalent to the elements of the tangent field,
but which then evolve according to a potential distribution constructed
from the tangent field. The evolution takes two forms: (i) a migration in
position to achieve smooth coverings; y (ii) a “growth to triple their
initial length. Además, since the splines are initially independent, él
is not known which should be grouped into the covering of each distinct
global curve. For graphical purposes we represent this by creating each
one with a different “color,” and include a second process which con-
verts overlapping splines to the same color. In the end, entonces, the cover
is given by a collection of overlapping splines, or short “snakes,“ each of
which is the same color.

De nuevo, there are two conceptually distinct steps to Stage 2 of the

algoritmo (David and Zucker 1989):

Step 2.1. Constructing the Potential Distribution from the discrete tangent
campo. Each entry in the tangent field actually represents a discretiza-
tion of the many possible curves in the world that could project onto
that particular (tangent, curvature) hypothesis. Now these pieces

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d

F
/

1
1
6
8
8
1
1
8
2
7
norte
mi
C
oh
1
9
8
9
1
1
6
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Steven W. Zucker, Allan Dobbins, and Lee Iverson

must be put together, so consider a measure (or envelope) en general
of these possible curves. Assuming the curves are continuous but
not necessarily differentiable everywhere, each contribution to the
potential can be modeled as a Gaussian (the Wiener measure) ori-
ented in the direction of the tangent field entry. The full potential
distribution is their pointwise sum; see figure 3.

Step 2.2. Spline Dynamics The discrete entities in the tangent field are
converted into unit splines initialized in the valleys of the potential
distribución. They evolve according to a variational scheme that
depends on spline properties (tension and rigidity) así como el
global potential.

5 Implementing the Model

Each stage of the model has different implementation requirements. A
differentiate between smooth curves, curves with corners, crossing curves
and branching curves, it is necessary to represent each possible tangent
(orientación) and curvature value at every possible position. Smooth
curves are then represented as a single (tangent, curvature) hypothesis
at each (retinotopic) trace point, corners as multiple tangents at a single
punto, and bifurcations as a single tangent but multiple curvatures at
a single point. Orientation hypercolumns in the visual cortex are thus
a natural representational substrate, with explicit representation of each
possible orientation and curvature at each position. This leads to a new
observation regarding discontinuities: explicit neurons to represent them
are unnecessary, and leads to our first physiological prediction:

Prediction 1. Crossings, corners, and bifurcations are repre-
sented at the early processing stages by multiple neurons fir-
ing within a «hypercolumn.»

5.1 Stage 1, Step 1: Intra-Columnar Initial Measurements. We first
seek a physiologically plausible mechanism for measuring orientation
and curvature. Observe that an orientation-selective cortical neuron car-
ries information about the tangent to curves as they pass through its
receptive field, and an ensemble of such cells of different size carries in-
formation about how orientation is changing over it. Such differences are
related to curvature (or deviation from straightness), and adding appro-
priate rectification leads to a model of endstopped neurons (Dobbins et al.
1987; cf. Hubel and Wiesel 1965). This model exhibits curvature-selective
response at the preferred orientation, as do endstopped neurons. De este modo

Prediction 2. Endstopped neurons carry the quantized repre-
sentation of orientation and (non-zero) curvature at each po-
posición.

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d

F
/

1
1
6
8
8
1
1
8
2
7
norte
mi
C
oh
1
9
8
9
1
1
6
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Two Stages of Curve Detection

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d

F
/

1
1
6
8
8
1
1
8
2
7
norte
mi
C
oh
1
9
8
9
1
1
6
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

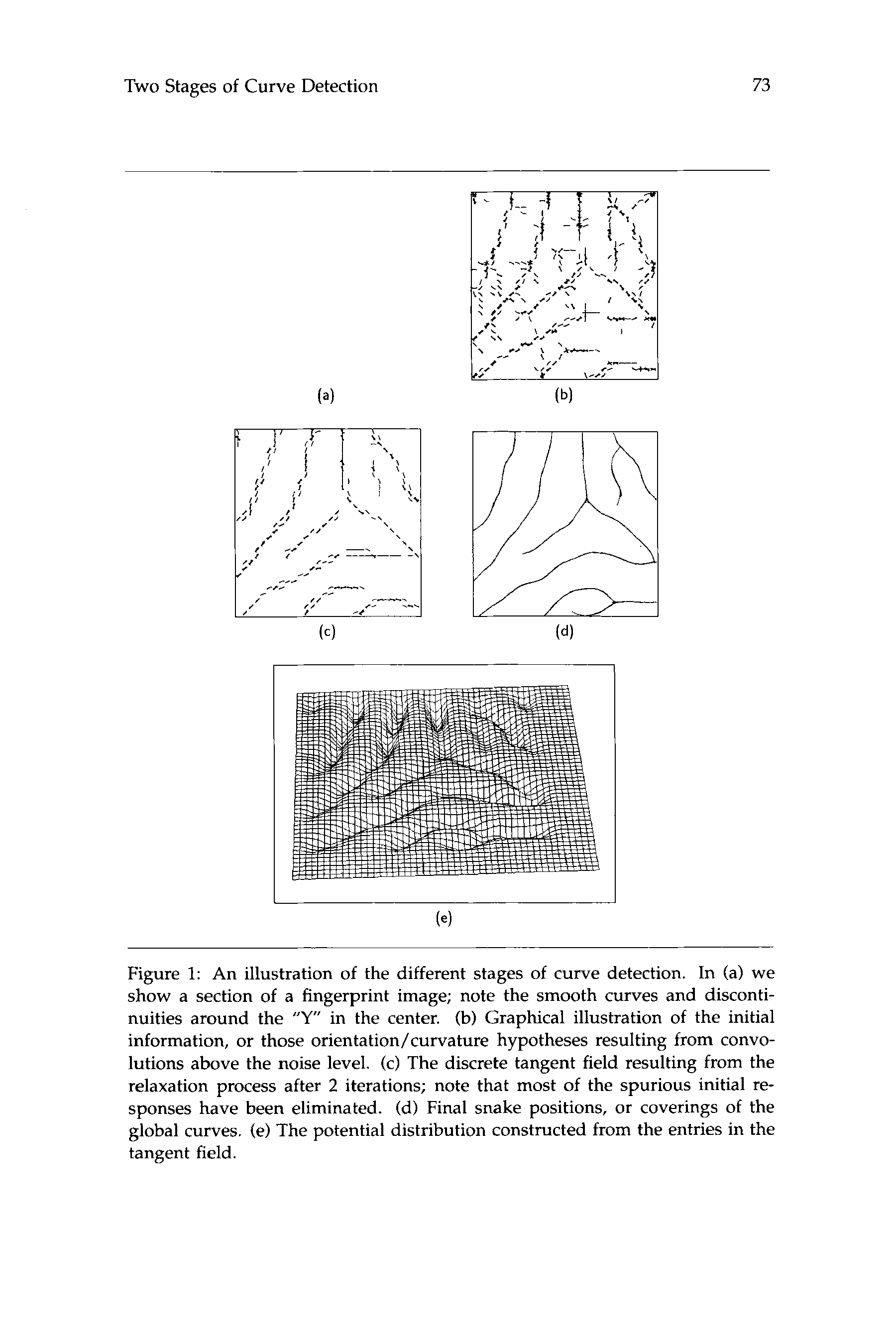
Cifra 1: An illustration of the different stages of curve detection. En (a) nosotros
show a section of a fingerprint image; note the smooth curves and disconti-
nuities around the » Y in the center. (b) Graphical illustration of the initial
información, or those orientation/curvature hypotheses resulting from convo-
lutions above the noise level. (C) The discrete tangent field resulting from the
relaxation process after 2 iterations; note that most of the spurious initial re-
sponses have been eliminated. (d) Final snake positions, or coverings of the
global curves. (mi) The potential distribution constructed from the entries in the
tangent field.

Steven W. Zucker, Allan Dobbins, and Lee Iverson

By varying the components one obtains cells selective for different ranges
and signs of curvature.

Thus the initial measurements can be built up by intra-columnar lo-
cal circuits, with the match to each (quantized) orientation and curva-
ture represented explicitly as, decir, firing rate in endstopped neurons.
Sin embargo, these measurements of orientation and curvature are broadly
tuned; nearby curves are blurred together and multiple possibilities arise
at many positions. Introducing further non-linearities into the initial
measurements eliminates some spurious responses (Zucker et al. 19881,
but the broadly-tuned smearing remains. We thus seek an abstract prin-
ciple by which these broadly tuned responses can be refined into crisper
distributions.

5.2 Stage 1, Step 2: Inter-Columnar Iterative Refinement. De nuevo
curvature enters the model, but now as a way of expressing the relation-
ship between nearby tangent (orientación) hypotheses. Consider an arc
of a curve, and observe that tangents to this arc must conform to certain
position and Orientation constraints for a given amount of curvature; nosotros
refer to such constraints geometrically as co-circularity (Higo. 2a). Dis-
cretizing all continuous curves in the world that project into the colum-
nar space of coarse (orientación, curvature) hypotheses partitions these
curves into equivalence classes, examples of which are shown in figure 2b
(Parent and Zucker 1985; Zucker et al. 1988). Interpreting the (orienta-
ción, curvature) hypotheses as endstopped neurons, such co-circularly-
consistent relationships are what is to be expected of the firing pattern
between endstopped neurons in nearby orientation hypercolumns given
such a curve as stimulus. Turning this around, when such intercolumnar
patterns arise from the initial measurements, a curve from one of the
equivalence classes is to be expected.

Such inter-columnar interactions can be viewed physiologically as ex-
citatory and inhibitory projections between endstopped cells at nearby
positions (adjacent hypercolumns), and can be used as follows. Desde
curvature is a relationship between tangents at nearby positions, two
tangents should support one another if and only if they agree under a
curvature hypothesis, and co-circularity provides the measure of such
apoyo. Además, two tangents that disagree with the curvature esti-
mate should detract support from one another. Relaxation labeling pro-
vides a formal mechanism for defining such support, and for specifying
how to use it (Hummel and Zucker 1983). Mathematically it amounts
to gradient descent; physiologically it can be viewed as a mechanism
for specifying how the response of neighboring neurons will interact. En
summary:

Prediction 3. Inter-columnar interactions exist between curva-
ture consistent (co-circular) tangent hypotheses.

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d

F
/

1
1
6
8
8
1
1
8
2
7
norte
mi
C
oh
1
9
8
9
1
1
6
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Two Stages of Curve Detection

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d

F
/

1
1
6
8
8
1
1
8
2
7
norte
mi
C
oh
1
9
8
9
1
1
6
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

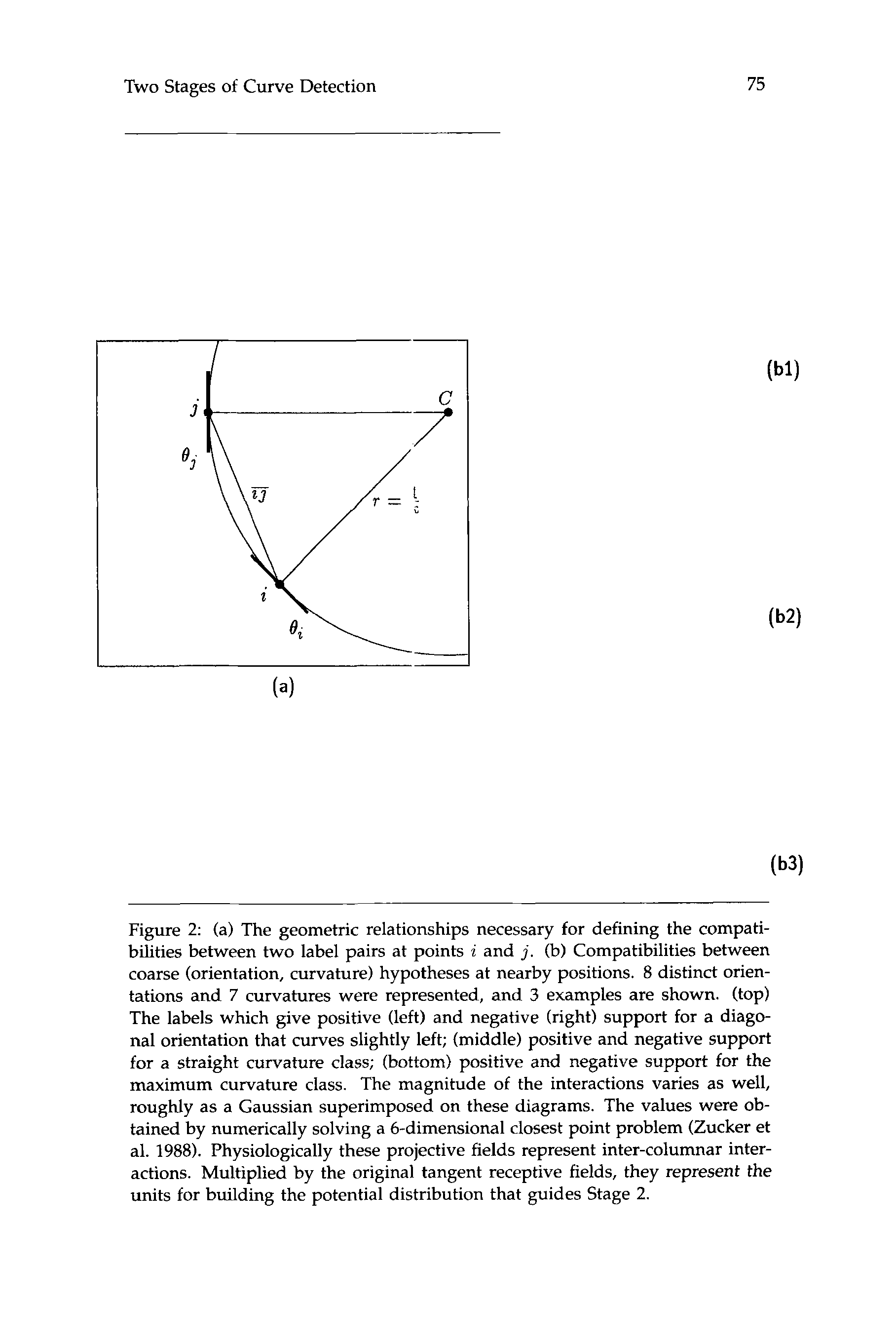
Cifra 2: (a) The geometric relationships necessary for defining the compati-
bilities between two label pairs at points i and j . (b) Compatibilities between
coarse (orientación, curvature) hypotheses at nearby positions. 8 distinct orien-
tations and 7 curvatures were represented, y 3 examples are shown. (arriba)
The labels which give positive (izquierda) and negative (bien) support for a diago-
nal orientation that curves slightly left; (middle) positive and negative support
for a straight curvature class; (abajo) positive and negative support for the
maximum curvature class. The magnitude of the interactions varies as well,
roughly as a Gaussian superimposed on these diagrams. The values were ob-
tained by numerically solving a 6-dimensional closest point problem (Zucker et
Alabama. 1988). Physiologically these projective fields represent inter-columnar inter-
comportamiento. Multiplied by the original tangent receptive fields, they represent the
units for building the potential distribution that guides Stage 2.

Steven W. Zucker, Allan Dobbins, and Lee Iverson

Given interaction, the next question relates to precision. Earlier we
hypothesized that this first stage was coarse. Both computational exper-
elementos (Zucker et al. 19881, psychophysics (Link and Zucker 19881, y
the range of receptive field sizes in striate cortex (Dobbins et al. 1988)
provide independent evidence about the quantization of curvature:

Prediction 4. The initial representation of curvature in the
visual cortex is quantized into 5 F 2 distinct classes; a saber,
straight, curved to the left a small amount, curved to the left
a large amount, and similarly to the right.

Relaxation processes can be realized iteratively, and computational
experiments suggest that about 3 interations suffice (Zucker et al. 1988).
At this time we can only speculate how these iterations relate to physiol-
ogia, but perhaps the first iteration is carried out by a recurrent network
within V1, and the subsequent iterations through the feed-forward and
-back projections to extrastriate cortex (p.ej., V2 or V4 in monkey). Allá
is no doubt, sin embargo, that interactions beyond the classical receptive field
abound (Allman et al. 1985).

The advantage of this style of ”coarse modeling” is that a number of
testable physiological hypotheses do emerge, and we are now beginning
to explore them. The requirement of initial curvature estimates led to the
connection with endstopping, and the current model suggests roles for
inter-columnar interactions. In particular, we predict that they should
be a function of position and orientation, a prediction for which some
support exists (p.ej. Nelson and Frost 1985) in the zero-curvature case;
experiments with curved stimuli remain to be done.

5.3 Stage 2: Potential Distributions and Evolving Spline Covers.
The tangent field serves as a coarse model for the curve, represented
en la zona. The next task is to infer a smooth, global curve running through
él. We perform this inference in a rather different kind of architecture,
one that involves potential distributions constructed specifically for each
instancia. It proceeds as follows.

The potential distribution is created by adding together contributions
from each element in the tangent field; see figure 3. Changing the rep-
resentation from the tangent field to the potential distribution changes
what is explicit and what is implicit in the representation. In Stage 1 allá
were discrete coarse entities; now there are smooth valleys that surround
each of the global curves, with a separation between them. The “jag-
gies’’ imposed by the initial image sampling have been eliminated, y
interpolation to sub-pixel resolution is viable.

To recover the curves through the valleys, imagine creating, at each
tangent field entry, a small spline of unit length oriented according to
the tangent and curvature estimates (Higo. 4). By construction, sabemos
that this spline will be born in a valley of the tangent field potential

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d

F
/

1
1
6
8
8
1
1
8
2
7
norte
mi
C
oh
1
9
8
9
1
1
6
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Two Stages of Curve Detection

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d

F
/

1
1
6
8
8
1
1
8
2
7
norte
mi
C
oh
1
9
8
9
1
1
6
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

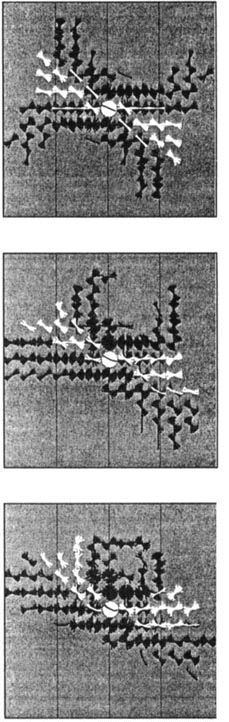
Cifra 3: Illustration of how a potential distribution is constructed from tangent
field entries. (a) A small number of tangents, showing the individual contribu-
tions from each one. (b) As more tangents are included, largo «valleys» comenzar
to form when the individual entries are added together. (C) The complete tan-
gent field and potential distribution as shown in figure 1. Physiologically one
might think of such potentials as being mapped onto neuronal membranes. No
shown is the possible effect of attention in gating the tangent field contributions,
the smallest unit for which could correspond to a tangent field entry.

distribución, so they are then permitted to migrate to both smooth out the
curve and to find the true local minima. But the inference of a cover for
the global curves requires that the splines overlap, so that each point on
every curve is covered by at least one spline. We therefore let the splines
extend in length while they migrate in position, until they each reach
a prescribed length. The covering is thus composed of these extensible
splines which have grown in the valleys of the tangent field potential.
Their specific dynamics and properties are described more fully in (David
and Zucker 1989).

It is difficult to interpret these ideas physiologically within the classi-
cal view of neurons, in which inputs are summed and transformed into

Steven W. Zucker, Allan Dobbins, and Lee Iverson

an output train of action potentials. Dendrites simply support passive
diffusion of depolarization. Recientemente, sin embargo, a richer view of neu-
ronal processing has emerged, with a variety of evidence pointing to
active dendritic computation and dendro-dendritic interaction (Schmitt
and Worden 1979). Active conductances in dendrites functionally modify
the geometry, and dendro-dendritic interactions suggest that the output
transformation is not uniquely mediated by the axon. Taken together,
these facts imply that patterns of activity can be sustained in the den-
dritic arbor, and that this membrane could be the substrate of the above
potential distribution computations. For this to be feasible, sin embargo, nosotros
require

Prediction 5. The mapping of the potential distribution onto
the neuronal membrane implies that the retinotopic coordi-
nates are similarly mapped (at least in open neighborhoods)
onto the membrane.

The large constructed potential distributions may bear some resem-
blance to the large receptive fields observed in areas V4 and IT (Maunsell
and Newsome 1987). While any such relationship is clearly speculative
at this time, it should be noted that they have two key similarities: (i)
extremely large receptive fields (potential distributions) have been cre-
ated, but they maintain about the same orientation selectivity as in V1
(Desimone et al. 1985); (ii) their structure can change. We have stressed
how structure is controlled by upward flowing information, but it should
be modifiable by «De arriba hacia abajo» attentional influences as well (Maunsell
and Newsome 1987; Moran and Desimone 1985). Attention could easily
«puerta» the tangent field entries at the creation of the potential, cual
leads to:

Prediction 6. There exists a smallest scale of attentional con-
controlar, and it corresponds (in size) to the scale of the unit poten-
tial contributions.

6 Conclusions

This paper is both constructive and speculative. On the constructive
lado, we have outlined a computational solution to the curve detection
problem that fills the wide gulf between initial broad measurements of
orientation and precise final descriptions of global curve structure. Mucho
of the mythology that has developed around curve detection is due, nosotros
believe, to ascribing too little function to the first (medición) stage,
and too much function to the second (integración) stage. Our solution
was to interpose a stable description-the
el
stages, to represent the local properties of curves (and their discontinu-
ities). Three points emerged: (i) represent the local structure coarsely,

tangent field-between

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d

F
/

1
1
6
8
8
1
1
8
2
7
norte
mi
C
oh
1
9
8
9
1
1
6
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Two Stages of Curve Detection

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d

F
/

1
1
6
8
8
1
1
8
2
7
norte
mi
C
oh
1
9
8
9
1
1
6
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

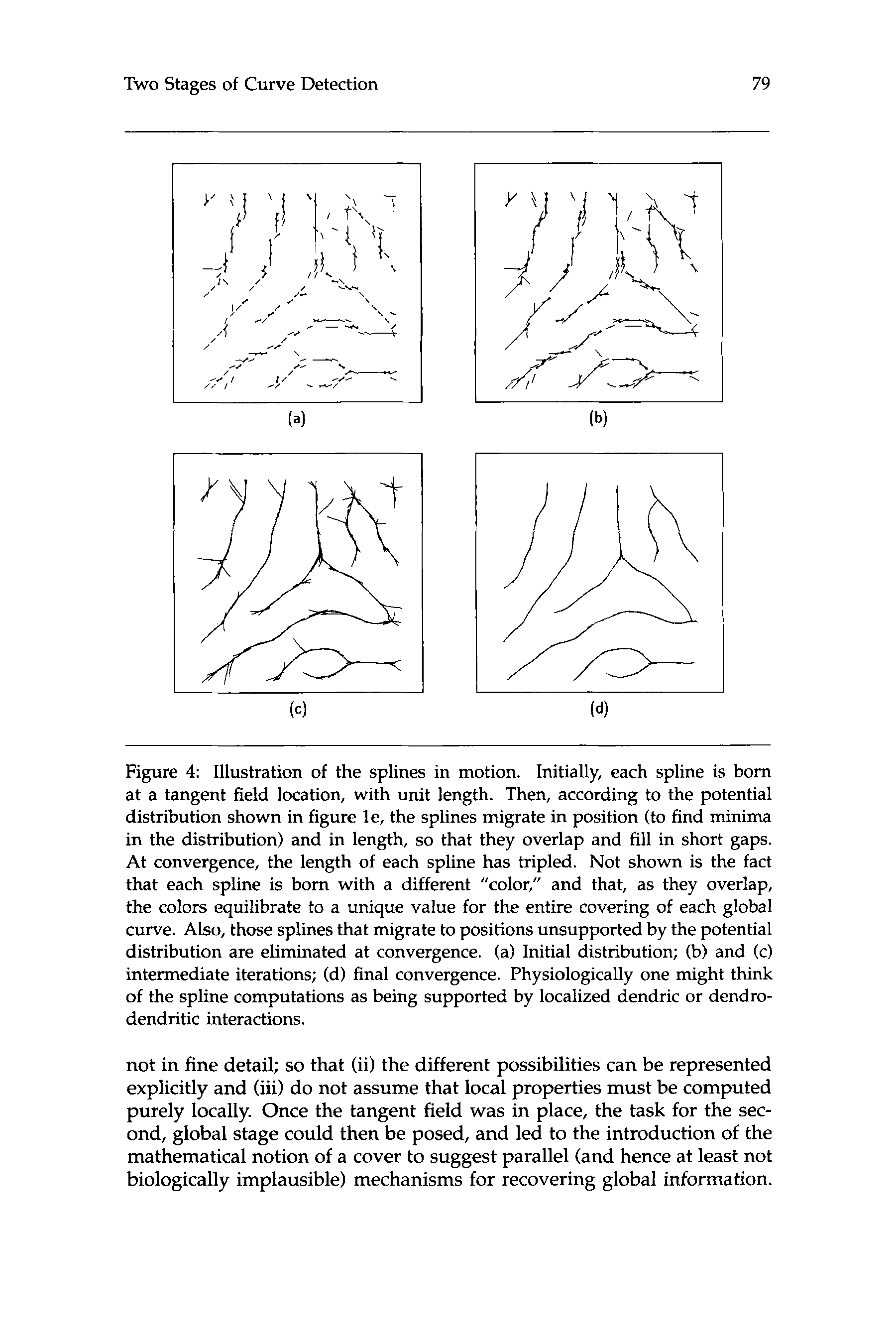
Cifra 4: Illustration of the splines in motion. Initially, each spline is born
at a tangent field location, with unit length. Entonces, according to the potential
distribution shown in figure le, the splines migrate in position (to find minima
in the distribution) and in length, so that they overlap and fill in short gaps.
At convergence, the length of each spline has tripled. Not shown is the fact
that each spline is born with a different «color,» and that, as they overlap,
the colors equilibrate to a unique value for the entire covering of each global
curve. También, those splines that migrate to positions unsupported by the potential
distribution are eliminated at convergence. (a) Initial distribution; (b) y (C)
intermediate iterations; (d) final convergence. Physiologically one might think
of the spline computations as being supported by localized dendric or dendro-
dendritic interactions.

not in fine detail; de modo que (ii) the different possibilities can be represented
explicitly and (iii) do not assume that local properties must be computed
purely locally. Once the tangent field was in place, the task for the sec-
ond, global stage could then be posed, and led to the introduction of the
mathematical notion of a cover to suggest parallel (and hence at least not
biologically implausible) mechanisms for recovering global information.

Steven W. Zucker, Allan Dobbins, and Lee Iverson

Finalmente, we introduced the notion of a potential distribution as the rep-
resentation for mediating the local to global transition between the two
stages.

The paper has also been speculative. Problems in vision are com-
complejo, and computational modeling can certainly help in understanding
a ellos. But in our view computational modeling cannot proceed without
direct constraints from the biology, and modeling – like curve detection
– should involve both coarse-grained and finer-grained theories. Nosotros
attempted to illustrate how such constraints could be abstracted by spec-
ulating how our model could map onto physiology While much clearly
remains to be done, the role for curvature at several levels now seems
evident. That such roles for curvature would have emerged from more
traditional neural network modeling seems doubtful.

Two different styles of computation emerged in the two stages of
curve detection. Although we stressed their differences in the paper,
in closing we should like to stress their similarities. Both stages enjoy
formulations as variational problems, and recognizing the hierarchy of
visual processing, we cannot help but postulate that the second, fine stage
of curve detection may well be the first, coarse stage of shape description.
The fine splines then become the coarse units of shape.

Expresiones de gratitud

This research was sponsored by NSERC grant A4470. We thank R. Milson
and especially C. David for their contributions to the second stage of this
proyecto.

Referencias

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d

F
/

1
1
6
8
8
1
1
8
2
7
norte
mi
C
oh
1
9
8
9
1
1
6
8
pag
d

Allman, J., F. Miezín, and McGuinness. 1985. Stimulus Specific Responses from
Beyond the Classical Receptive Field: Neurophysiological Mechanisms for
Local-global Comparisons in Visual Neurons. Annual Rev. neurociencias. 8,407-
430.

David, C. and S.W. Zucker. 1989. Potentials, Valleys, and Dynamic Global Cover-
ings. Reporte técnico 89-1, McGill Research Center for Intelligent Machines,
Universidad McGill, Montréal.

Desimone, r., S. Schein, j. Moran, and L. Ungerleider. 1985. Contour, Color,
and Shape Analysis Beyond the Striate Cortex. Vision Research 25, 441452.
Dobbins, A., S.W. Zucker, and M.S. Cynader. 1987. Endstopping in the Visual
Cortex as a Substrate for Calculating Curvature. Naturaleza 329, 4 3 8 4 1 .

. 1988. Endstopping and Curvature. Technical Report 88-3, McGill Re-

search Center for Intelligent Machines, Universidad McGill, Montréal.

Hubel, D.H. and T.N. Wiesel. 1962. Receptive Fields, Binocular Interaction and
Functional Architecture in the Cat’s Visual Cortex. j. Physiol. (Londres) 160,
106154.

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Two Stages of Curve Detection

. 1965. Receptive Fields and Functional Architecture in Two Non-striate

Visual Areas (18 y 19) of the Cat. j. Neurophysiol. 28, 229-89.

Hummel, R. and S.W. Zucker. 1983. On the Foundations of Relaxation Labeling
Processes. IEEE Transactions on Pattern Analysis and Machine Intelligence 5,
267-287.

Kass, METRO., A. Witkin, and D. Terzopoulos. 1988. SNAKES Active Contour

Modelos. Int. j. Computer Vision 1, 321-332.

Kass, METRO. and A. Witkin. 1987. Analyzing Oriented Patterns. Computer Vision

Graphics and Information Processing 37, 362-385.

Link, norte. and S.W. Zucker. 1988. Corner Detection in Curvilinear Dot Grouping.

Biological Cybernetics 59, 247-256.

Maunsell, j. and W. nuevosome. 3987. Visual Processing in Monkey Extrastriate

Corteza. Ann. Rev. Neurociencia 10, 363-401.

Montanari, Ud.. 1971. On the Optimum Detection of Curves in Noisy Pictures.

CACM 14, 335-345.

Moran, j. and R. Desimone. 1985. Selective Attention Gates Visual Processing

in the Extriastriate Cortex. Ciencia 229, 782-784.

nelson, J.J. and B.J. Frost. 1985. Intracortical Facilitation among Co-oriented,
Co-axially Aligned Simple Cells in Cat Striate Cortex. E x p . Br. Res. 61,
5 METRO 1 .

Padre, PAG. and S.W. Zucker. 1985. Trace Inference, Curvature Consistency, y
Curve Detection. CVaRL Technical Report CIM-86-3, Universidad McGill. I E E E
Transactions on Paftern Annlysis and Machine Intelligence, in press.

Schmitt, F. and F. Worden. 1979. The Neurosciences: Fourth Study Program,

Cambridge, MAMÁ: CON prensa.

Zucker, S.W. 1986. The Computational Connection in Vision: Early Orientation
Selection. Behaviour Research Methods, Instrumentos, and Computers 18, 608-
617.

Zucker, S.W., C. David, A. Dobbins, y yo. Iverson. 1988. The Organization of
Curve Detection: Coarse Tangent Fields and Fine Spline Coverings. Proc.
2nd Int. Conf. on Computer Vision, Tarpon Springs, Florida.