Revista de Historia Interdisciplinaria, l:1 (Verano, 2019), 91–111.
Myles Lavan
Epistemic Uncertainty, Subjective Probability, y
Ancient History Periods from which few data survive pose
a major challenge for history in the quantitative mode. Many
important historical quantities can be estimated only on the basis of
sparse and disparate information. Por ejemplo, we do not have any
census data for the population of the Roman Empire as a whole.
Yet we are hardly in a position of complete ignorance. Scattered
información, both quantitative and qualitative, allows us to reason
in terms of likelihood. The methodological question is how to report
our inevitably uncertain and subjective conclusions. Ancient histo-
rians tend to frame their debate in terms of point estimates, disputing
si 54 million or 45 million is a better estimate of the pop-
ulation of the Roman Empire in 14 C.E. Estimates of this type are
hard to interpret since they convey no information about the
margin of error, which is often large and sometimes asymmetri-
California. Historians may resort to ranges as a concession to uncertainty,
but their ranges tend to be arbitrary rather than grounded in any
measure of confidence or credibility. They signal the existence
of uncertainty without offering any real guidance regarding its
magnitude.
The problem of uncertainty becomes particularly acute when
historians combine estimates for multiple quantities. Highly uncer-
tain quantities are often estimated on the basis of other quantities
about which we have better (if still limited) conocimiento. por ejemplo-
amplio, Roman GDP has been modeled as a function of total pop-
ulation and average per capita consumption. Since these numbers
Myles Lavan is Reader in Ancient History, University of St. Andrews. He is the author of
Slaves to Rome: Paradigms of Empire in Roman Culture (Nueva York, 2013); “Pliny Epistles 10 y
Imperial Correspondence: The Empire of Letters,” in Alice König and Christopher Whitton
(editores.), Literary Interactions under Nerva, Trajan and Hadrian: Literary Interactions, AD 96–198
(Nueva York, 2018), 280–301.
The author thanks Daniel Jew, Bart Danon, and the participants in a workshop on
probabilistic modeling in ancient history, held at St. Andrews in 2017, for their help in re-
fining the approach. He also thanks Michael Papathomas and Charles Paxton for discussions
about uncertainty and the Arts and Humanities Research Council for a Fellowship support-
ing his research.
© 2019 por el Instituto de Tecnología de Massachusetts y The Journal of Interdisciplinary
Historia, Cª, https://doi.org/10.1162/jinh_a_01377
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
j
i
/
norte
h
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
5
0
1
9
1
1
7
0
2
5
9
5
/
j
i
norte
h
_
a
_
0
1
3
7
7
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
92 | M YL E S LA V AN
are themselves uncertain, the proliferating uncertainties pose a
major challenge to the credibility of any point estimate.1
This research note discusses an alternative framework that al-
lows for a more rigorous accounting of uncertainty. It formalizes
the probabilism that is already implicit in most historical reasoning
by using probability to measure degree of belief. A brief survey of
work on the population of the Roman Empire illustrates the meth-
odological problem, paving the way for a discussion of the “subjec-
tive” interpretation of probability as degree of belief and its use as
a tool of historical analysis, particularly when combining uncer-
tainties. Conceptualizing uncertainty as probability is a useful disci-
pline in itself, but its greatest value lies in the scope for aggregation.2
The probabilistic approach discussed herein is familiar to
scholars and practitioners in future-oriented fields because it
informs much current work in forecasting, risk assessment, y
decision analysis. Its unfamiliarity to many historians, even those
engaged in quantitative analysis, is probably due to a mistaken be-
lief that uncertainty about the past is qualitatively different from
that faced by other disciplines. Ancient historians are not, cómo-
alguna vez, alone in the need to base quantification on subjective assess-
ments of what is likely rather than on hard data; the problem of
reliance on subjective assessment is shared by many other fields.
Consider an observation about risk analysis from a textbook:
“Probabilistic risk analysis treats events with a low intrinsic rate
of occurrence, and large amounts of data are seldom available.
Since its inception, expert opinion in the form of subjective probabilities
has been a dominant source of data for failure probabilities” (mi
emphasis). Ancient historians can learn from the techniques that
other disciplines have developed to manage epistemic uncertainty,
eso es, uncertainty that arises from the limits of our knowledge.3
1 For the state of the art in the estimation of Roman GDP, see Walter Scheidel and Steven J.
Friesen, “The Size of the Economy and the Distribution of Income in the Roman Empire,"
Journal of Roman Studies, XCIX (2009), 61–91.
2 For an earlier article that applied this approach to a long-standing problem in ancient his-
conservador, see Lavan, “The Spread of Roman Citizenship, 14–212 C.E.: Quantification in the Face
of High Uncertainty,” Past & Present, 230 (2016), 3–46. Daniel Jew is applying it to the prob-
lem of Athenian population in The Probable Past: Agriculture and Carrying Capacity in Ancient
Greece (Nueva York, próximo). This research note expands on the theoretical premises,
particularly the underpinning conceptions of epistemic uncertainty and subjective probability.
3 For the quotation, see Tim Bedford and Roger Cooke, Probabilistic Risk Analysis: Foun-
dations and Methods (Nueva York, 2001), 191. Historians in a few sub-fields have already adopted
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
j
i
/
norte
h
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
5
0
1
9
1
1
7
0
2
5
9
5
/
j
i
norte
h
_
a
_
0
1
3
7
7
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
EPISTEM IC U NCERTAINT Y
| 93
THE POPULATION OF THE ROMAN EMPIRE Population is relevant to
a wide range of questions in the social and economic history of the
Roman Empire. Desafortunadamente, the population data that the
Roman state collected through regular censuses are almost entirely
lost to us. The most significant exception is a series of census
figures for Roman citizens that extends to the year 48 C.E. Desde
citizens were still concentrated in Italy at that point, the citizen
population should be a reasonable proxy for the population of
Italia. Yet a major ambiguity about whether these numbers com-
prise all persons or just adult males leaves even the question of
Italy’s population hotly contested. Population data that are even
more problematical exist for a few other sub-regions—such as
northwest Iberia and Egypt—but Roman historians are otherwise
dependent on estimates of carrying capacity and on crude judg-
ments about regional variation in population density and about
the trajectory of population levels relative to the late medieval
and early modern periods.4
En 1886, Beloch, a pioneer in the modern study of the Roman
población, reckoned a total of 54 million inhabitants in the Empire
en 14 C.E. He subsequently revised this number to 70 millón (como-
suming higher populations for Gaul, the Balkans, and North Africa).
a probabilistic approach by combining uncertainties through Monte Carlo simulation (dis-
cussed further below). For a pioneering application, see Donald Schaefer and Thomas Weiss,
“The Use of Simulation Techniques in Historical Analysis: Railroads versus Canals," Diario de
Economic History, XXXI (1971), 854–884, a precedent followed by several subsequent articles
in modern economic history and historical demography. For its use in the CAMSIM micro-
simulation of kin sets, see James E. Smith and Jim Oeppen, “Estimating Numbers of Kin
in Historical England Using Demographic Microsimulation,” in David S. Reher and Roger
S. Schofield (editores.), Old and New Methods in Historical Demography (Nueva York, 1993), 413–425.
Archaeologists have increasingly used the method to manage uncertainty about chronologies
(see n. 10), and ancient historians have used it in an ad hoc way to examine miscellaneous
problems in ancient history. Ver, Por ejemplo, Ellen Janssen et al., “Fuel for Debating Ancient
Economies: Calculating Wood Consumption at Urban Scale in Roman Imperial Times,"
Journal of Archaeological Science: Informes, XI (2017), 592–599, which uses Monte Carlo simula-
tion to estimate fuel consumed by pottery production and baths in Roman Sagalassos but
reverts to traditional interval analysis to estimate total fuel consumption and its impact on local
woodland—precisely the type of problem in which epistemic uncertainties could fruitfully be
construed as subjective probabilities. None of these contributions ground the method in the
Bayesian conception of uncertainty and probability. En cambio, the uncertainty tends to be inter-
preted as aleatory (eso es, related to variability or random processes).
4 For the population of Italy, see Scheidel, “Roman Population Size: The Logic of the De-
bate,” in Luuk De Ligt and Simon J. Northwood (editores.), People, Land, and Politics: Demographic
Developments and the Transformation of Roman Italy 300 antes de Cristo-AD 14 (Leiden, 2008), 17–70.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
j
i
/
norte
h
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
5
0
1
9
1
1
7
0
2
5
9
5
/
j
i
norte
h
_
a
_
0
1
3
7
7
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
94 | M YL E S LA V AN
He also suggested, offhandedly, that the population grew to a peak
of around 100 million by the end of the second century. The next
important intervention considered even his first estimate too high.
En 1978, McEvedy and Jones constructed an extraordinarily ambi-
tious model of the evolution of the global population on a country-
by-country basis from 400 a.e.c.. to the present. They significantly
reduced Beloch’s 1886 estimates for several sub-regions, particular-
larly Anatolia and the Levant, to arrive at population levels that
seemed plausible in the light of the long-term history of those
sub-regions as they understood it. They put the peak population
of the Empire c. 200 C.E. at just 46 million—10 percent lower
than Beloch’s estimate for 14 C.E. and less than half his later esti-
mate for peak population. Their work has provided the starting
point for most subsequent research in the field of Roman history.5
Reverting closer to Beloch’s figures for Anatolia and the
Levant and positing slightly higher long-term growth over the first
two centuries C.E., Frier proposed a peak population of 61 millón
en 164 C.E. (a more credible date for the peak, given the “Antonine
plague” in the 160s). More recently, Scheidel suggested a peak
de 59 a 72 million in 165 CE, assuming slightly higher pop-
ulations in the northwestern provinces and allowing for some
uncertainty.6
We need not delve more deeply into the evidence to observe
that the debate has been conducted in a way that obscures the
question of uncertainty. Most interventions have taken the form
of point estimates without any serious discussion about the margin
of error. Scheidel’s range at least signals the problem of uncer-
tainty, but it is far from clear how it should be interpreted. Hace
he mean to rule out the possibility of a population less than 59 mil-
lion or higher than 72 millón? The evidence cannot categorically
disprove either McEvedy and Jones’ minimal estimate of 46 millón
or Beloch’s maximal one of 100 millón, though both now seem
much less likely than a figure in the 60s. The proposition of this
Julius Beloch, Die Bevölkerung der griechisch-römischen Welt (Leipzig, 1886), 507; ídem, “Die
5
Bevölkerung im Altertum,” Zeitschrift für Sozialwissenschaft, II (1899), 618, 620; Colin
McEvedy and Richard M. jones, Atlas of World Population History (Londres, 1978), 22.
6 Bruce W. Frier, “Demography,” in Alan K. Bowman, Peter Garnsey, and Dominic Rathbone
(editores.), The Cambridge Ancient History. XI. The High Empire, AD 70–192 (Nueva York, 2000), 812–814;
Scheidel, “Demography,” in idem, Ian Morris, and Richard P. Saller (editores.), The Cambridge Economic
History of the Greco-Roman World (Nueva York, 2007), 45–49.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
j
i
/
norte
h
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
5
0
1
9
1
1
7
0
2
5
9
5
/
j
i
norte
h
_
a
_
0
1
3
7
7
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
EPISTEM IC U NCERTAINT Y
| 95
research note is that formal probabilities offer a better way of repre-
senting and managing the uncertainty.
KNOWLEDGE, UNCERTAINTY, AND PROBABILITY This proposition
may seem troubling at first because it contravenes our intuitions
about the nature of uncertainty and probability. Uncertainty ap-
pears to take two fundamentally different forms, which can be
illustrated by, decir, predicting the outcome of a coin toss and es-
timating the distance between Cambridge and St. Andrews. El
uncertainty in the first case is (or rather appears to be) the result
of a random process and cannot be resolved until the coin is
flipped. The uncertainty in the latter case is merely the result
of the limits of an individual’s knowledge and could be resolved
through measurement. The first type of uncertainty is often
termed aleatory (or objective) and the second type epistemic (or sub-
jective). Intuitivamente, probability seems a natural way of represent-
ing aleatory uncertainty (the chance of heads is 50 por ciento), pero
may seem an abuse to apply it to epistemic uncertainty (distancia
appears to leave no room for probability).
The association of probability with objective randomness is,
sin embargo, far less secure than it appears. The meaning of probabil-
ity is a profound and unresolved philosophical question. The two
most important positions are the frequentist and the subjective inter-
pretations. Anyone with some understanding of statistics will rec-
ognize the frequentist view, which long dominated introductory
textbooks. Frequentists see probability as an attribute of repeated
events. The probability of an event is the frequency of its occur-
rence in a long sequence of similar trials. Por eso, the probability of
heads in a coin toss is 50 percent because the frequency of heads
would approach 50 percent in a suitably long series of tosses. On
the frequentist view, it would be nonsensical to speak of the prob-
ability that some historical quantity had some value, porque
either had it or did not.7
The subjective or “Bayesian” interpretation holds that prob-
ability represents an observer’s degree of belief, given the available
información. Tal como, it is a function not just of the world but also
7 For a brief overview of interpretations of uncertainty, see M. Granger Morgan and Max
Henrion, Incertidumbre: A Guide to Dealing with Uncertainty in Quantitative Risk and Policy Analysis
(Nueva York, 1990), 48–50.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
j
i
/
norte
h
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
5
0
1
9
1
1
7
0
2
5
9
5
/
j
i
norte
h
_
a
_
0
1
3
7
7
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
96 | M YL E S LA V AN
of a particular state of knowledge. Since knowledge varies from
observer to observer, probability is always subjective or personal
(“my probability,” not “the probability”)—hence De Finetti’s
famous dictum “probability does not exist,” meaning that there
are no objective probabilities. This seemingly radical view rests
on the insight that all uncertainty has an irreducible element of
subjectivity. The apparently obvious distinction between aleatory
and epistemic uncertainty dissolves under closer inspection. Phe-
nomena that appear random are often the result of processes that
are in fact deterministic, though chaotic, in the technical sense that
the outcome is highly sensitive to small changes in the initial con-
ditions. Uncertainty about the outcome of a coin toss, Por ejemplo,
is actually epistemic uncertainty about the initial conditions and
how they determine the behavior of the coin. Most randomness
is thus a result of an observer’s lack of knowledge, not inherent
in the world itself. Además, an assessment that the probability
of heads on any coin toss is 50 percent depends on an unstated, y
possibly erroneous, assumption that the coin in question is unbi-
ased. The fundamental insight of the subjectivists is that probabil-
ities conventionally thought to be objective (a property of the
world) are always based on assumptions about the generating
mechanism (like a coin toss) and hence subjective. Their growing
influence is evident in the spread of Bayesian methods throughout
a wide variety of fields.8
Scholars in fields concerned with forecasting, risk analysis, y
decision analysis recognize that predicting the future always involves
epistemic as well as aleatory uncertainty. Many of them have em-
braced the use of probability as a measure of epistemic uncertainty.
Various alternative mathematical frameworks have been suggested
(including intervals, “imprecise probabilities,” “possibilities,” and
“belief functions”) to address doubts about the applicability of prob-
ability to all forms of uncertainty. Sin embargo, probability remains
the dominant conceptual tool for representing epistemic uncertainty
8 Bruno De Finetti, Theory of Probability: A Critical Introductory Treatment (Nueva York, 1974).
For an introduction to the subjective interpretation, see David Spiegelhalter, “Quantifying
Incertidumbre,” in Layla Skinns, Michael Scott, and Tony Cox (editores.), Risk (Darwin College Lec-
turas) (Nueva York, 2011), 17–33. Dennis V. Lindley, Understanding Uncertainty (Hoboken,
2006), provides a fuller but still accessible overview. Morgan and Henrion, Incertidumbre, 57–60,
62–64; Bedford and Cooke, Probabilistic Risk Analysis, 33–34; Terje Aven, Foundations of Risk
Análisis (Chichester, 2012), 47–49, illustrate the personalist interpretation of randomness.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
j
i
/
norte
h
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
5
0
1
9
1
1
7
0
2
5
9
5
/
j
i
norte
h
_
a
_
0
1
3
7
7
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
| 97
EPISTEM IC U NCERTAINT Y
in a wide range of fields engaged in describing the present and
predicting the future. Its strongest proponents view it as the only
rational framework to deal with uncertainty: “If you want to
handle uncertainty, then you must use probability to do it, allá
is no choice.” “It is very firmly our opinion that the uniquely suit-
able representation of uncertainty, whether aleatory or epistemic,
is probability.”9
Past, Present, and Future On this subjective interpretation,
probability is precisely the right form in which to represent uncer-
tainty about the past. Subjectivists see no qualitative difference be-
tween uncertainty about the past, present, and future, which are all
equally uncertain from the perspective of an observer in the pres-
ent. Some archaeologists and historians have already embraced
probability for the formal representation of epistemic uncertainty
about dating. Absolute chronology construction (such as carbon
dating) and phylogeny (both genetic and linguistic) are sub-fields
that routinely use Bayesian methods of inference based on subjec-
tive probability. Yet these technical fields are remote from the ex-
perience of most archaeologists and historians. A few archaeologists
have also applied a probabilistic approach to the more quotidian ex-
ercise of dating artifacts based on established chronologies of types.
Por ejemplo, the date of deposition of a sherd of African Red
Slipware of Hayes form 1—a pottery type associated with the
period from 50 a 80 C.E.—can be represented as a probability
distribution over that period (using a uniform, normal, o cualquier
other distribution depending on assumptions about the processes
9 For the quotations, see Lindley, Understanding Uncertainty, 239; Anthony O’Hagan and
Jeremy E. Oakley, “Probability Is Perfect, but We Can’t Elicit It Perfectly,” Reliability Engi-
neering & System Safety, LXXXV (2004), 247. Some theorists accept the distinction between
the two types of uncertainty and account for them separately, but they use probability in both
casos. Ver, Por ejemplo, Colin Howson and Peter Urbach, Scientific Reasoning: The Bayesian
Acercarse (chicago, 1993), 24–25; Stan Kaplan, “Formalisms for Handling Phenomenological
Uncertainties: The Concepts of Probability, Frecuencia, Variabilidad, and Probability of Fre-
quency,” Nuclear Technology, CII (1993), 137–142 (introducing the “probability of frequency”
framework in which aleatory uncertainty takes the form of frequentist probabilities and epi-
stemic uncertainty subjective probabilities); David Vose, Risk Analysis: A Quantitative Guide
(Chichester, 2008), 47–49. Others who fully embrace the subjectivist perspective that all un-
certainty contains an epistemic element and should therefore be represented by subjective
probabilities include Lindley, Understanding Uncertainty, and Aven, Foundations of Risk Analysis.
For alternatives to subjective probability, see Franz Huber, “Formal Representations of
Belief,” in Edward N. Zalt (ed.), The Stanford Encyclopedia of Philosophy (Primavera 2016), disponible
at https://plato.stanford.edu/archives/spr2016/entries/formal-belief/.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
j
i
/
norte
h
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
5
0
1
9
1
1
7
0
2
5
9
5
/
j
i
norte
h
_
a
_
0
1
3
7
7
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
98 | M YL E S LA V AN
of production and deposition). Whereas these archaeologists use
probability to represent the epistemic uncertainties about the dates
of hundreds or thousands of individual sherds or other artifacts, este
research note generalizes this approach to epistemic uncertainty
about quantities other than dates.10
The uncertainties that historians face are clearly epistemic.
They can be represented as probabilities, but only if the probabil-
ities are understood as subjective. A probability is meaningful only
in relation to a particular state of knowledge. It represents a histo-
rian’s degree of belief based on a body of evidence, not an objec-
tive randomness. Por eso, this research note speaks of assigning not
estimating probabilities and employs the term beliefs to foreground
the subjectivity that is inherent in the encounter with uncertainty.
According to this view, beliefs comprise a set of evidence-based
probabilistic judgments about historical uncertainties. “Your” be-
liefs about the past may differ from “mine” if “you” have access to
más (or less) information than “I” have or if “you” interpret it
10 For the equivalence of past, present, and future, see Lindley, Understanding Uncertainty, 2–7,
which offers twenty examples that deliberately conflate the three time frames, así como el
similar remarks of Buck et al., Bayesian Approach, 54: “The view adopted in this book is that
assessments of probability are subjective and made in the light of experience: there is no differ-
ence in kind between the bookmaker’s estimate of odds, the architectural historian’s view of a
date for a medieval building, the doctor’s diagnosis, the archaeologist’s opinion about the
provenance of a pot, or the uncertainty in a scientist’s estimate of the distance of the sun
from the earth.” For absolute chronologies, see Buck and Meson, “On Being a Good
Bayesian” and other articles in the special issue “Prehistoric Bayesian Chronologies,” World
Arqueología, XLVII (2015), 575–700. For detailed discussions about the use of probability to
date artifacts, see David L. Carlson, “Computer Analysis of Dated Ceramics: Estimating
Dates and Occupational Ranges,” Southeastern Archaeology, II (1983), 8–20; John M. Roberts
et al., “A Method for Chronological Apportioning of Ceramic Assemblages,” Journal of Ar-
chaeological Science, XXXIX (2012), 1513–1520; Enrico R. Crema, “Modelling Temporal
Uncertainty in Archaeological Analysis,” Journal of Archaeological Method and Theory, XIX
(2012), 440–461; Rinse Willet, “Experiments with Diachronic Data Distribution Methods
Applied to Eastern Sigillata A in the Eastern Mediterranean,” Herom, III (2014), 39–69; Miguel
j. Baxter and H. mi. METRO. Cool, “Reinventing the Wheel? Modelling Temporal Uncertainty
with Applications to Brooch Distributions in Roman Britain,” Journal of Archaeological Sci-
ence, LXVI (2016), 120–127. Practical applications include Elizabeth Fentress and P. Perkins,
“Counting African Red Slip Ware,” in Attilio Mastino (ed.), L’Africa Romana: Atti del V
Convegno di studio Sassari, 11–13 dicembre 1987 (Sassari, 1988), 205–14; Martin Millett, “Pot-
tery: Population or Supply Patterns? The Ager Tarraconensis Approach,” in Graeme W. W..
Barker and John Lloyd (editores.), Roman Landscapes: Archaeological Survey in the Mediterranean
Region (Londres, 1991), 18–26; Andrew Wilson, “Approaches to Quantifying Roman
Trade,” in Bowman and Wilson (editores.), Quantifying the Roman Economy: Methods and Problems
(Nueva York, 2009), 213–49.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
j
i
/
norte
h
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
5
0
1
9
1
1
7
0
2
5
9
5
/
j
i
norte
h
_
a
_
0
1
3
7
7
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
EPISTEM IC U NCERTAINT Y
differently. But describing beliefs in terms of probabilities clarifies
our differences and facilitates dialectic.11
| 99
FROM BELIEFS TO PROBABILITY DISTRIBUTIONS The uncertainty
about historical quantities such as the population of the Roman
Empire can usefully be expressed as a probability distribution. Este
distribution represents a historian’s degree of belief in different
possible values, given the available evidence.12
What do I believe about the peak population of the Roman
Empire? Without going into further detail, I am persuaded by
Frier and Scheidel that a total population in the 60 million range
is more likely than anything lower or higher. Yet identifying a
most-likely value is only part of the process of estimation. Nosotros también
need to ask how wide a range is possible. Desafortunadamente, pasado
scholarship tended to focus almost exclusively on identifying a
most-likely value rather than establishing upper and lower limits.
For the purposes of this discussion, 40 million will serve as a mini-
mum, since there is little scope to lower McEvedy and Jones’ already
minimal figure of 46 millón. Establishing a ceiling is more difficult.
Most modern scholars find Beloch’s suggestion of a population of
alrededor 100 million too high, since the combined population of
the former territories of the Empire do not appear to have exceeded
that level until 1800. Beloch’s figure can stand as a maximum, con
the proviso that the matter deserves further consideration.13
11 For this sense of belief, see Lindley, Understanding Uncertainty, 12–13. The use of sub-
jective probability should be distinguished from formal Bayesian inference, which involves
not just subjective probability but also the use of Bayes’ theorem to update a priori prob-
abilities given data: Cailtlin E. Buck et al., Bayesian Approach to Interpreting Archaeological Data
(Chichester, 1996) explores the potential of Bayesian approaches in archaeology; Buck and
Bo Meson, “On Being a Good Bayesian,” World Archaeology, XLVII (2015), 567–584, es un
recent review of progress to date. For many problems, because we lack meaningful data with
which to update our subjective beliefs, we can make only the first step, quantifying in-
formed but subjective knowledge as probabilities (analogous to the formulation of “priors”
in the Bayesian framework).
12 This research note focuses on uncertain quantities, as opposed to another type of uncertainty,
which concerns not the value of a quantity but the truth of a proposition. These uncertainties are
termed events in probability theory. Much uncertainty in history concerns events in this technical
sense. Although the discussion herein is limited to quantities, the framework can also accommo-
date uncertainty about events, by assigning a probability to the proposition that the event is true.
On the concept of event, see Lindley, Understanding Uncertainty, 12.
13 The estimate of the 1800 population of the Roman Empire’s former territories derives
from data in McEvedy and Jones, Atlas of World Population History, 43, 57, 63, 65, 87, 89, 93,
97, 105, 107, 113, 115, 135, 139, 143, 221, 225, 227.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
j
i
/
norte
h
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
5
0
1
9
1
1
7
0
2
5
9
5
/
j
i
norte
h
_
a
_
0
1
3
7
7
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
100
| MY L ES LAVA N
Higo. 1
Selecting a Distribution
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
j
i
/
norte
h
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
5
0
1
9
1
1
7
0
2
5
9
5
/
j
i
norte
h
_
a
_
0
1
3
7
7
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
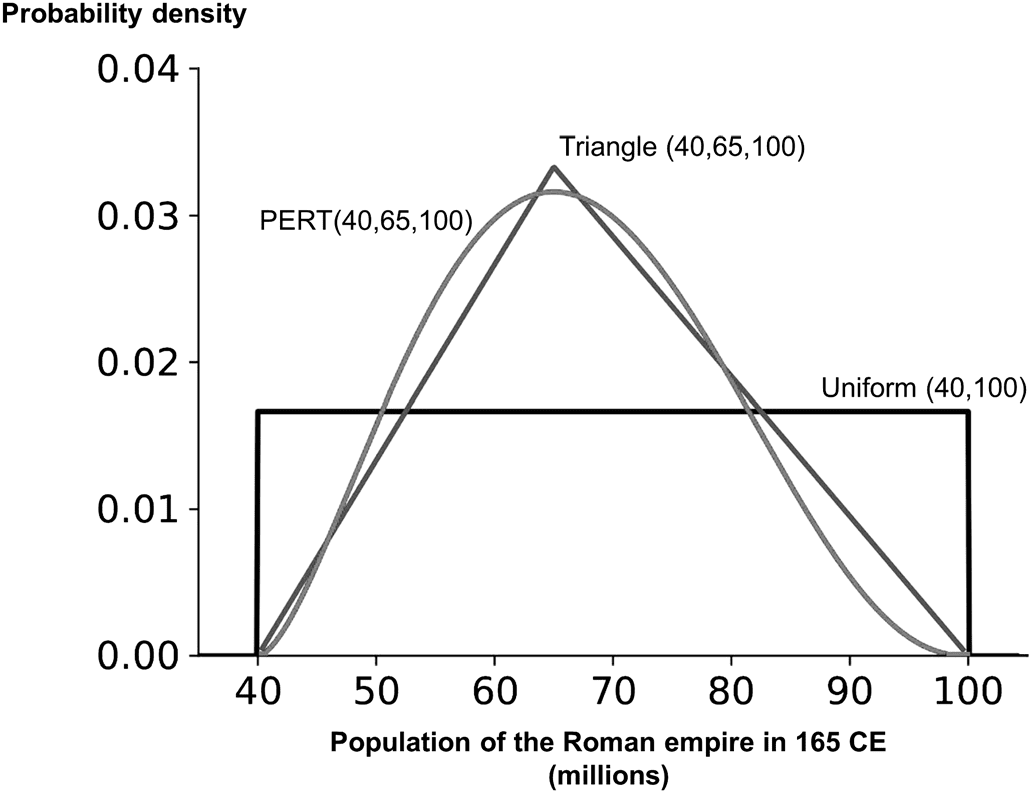
The Probability Density Function Uncertainty about a continu-
ous quantity (one that can take any value within a range) is represented
by probability density function (PDF). To facilitate computation, the PDF
implicit in our beliefs is approximated by some known mathematical
distribución. The simplest available distribution is the uniform distribution,
which assigns an equal probability to all possible values between a
minimum and maximum. Cifra 1 illustrates a uniform PDF for the peak
population of the Empire, implying that all values between 40 millón
y 100 million are equally likely. The obvious objection to this repre-
sentation of the uncertainty about the Roman population is that it fails to
take any account of my belief that a value c. 65 million is much more
likely than one around 40 o 100 millón. The uniform distribution
can be useful in expressing an absence of information or introducing
a conservative element into an analysis, but it is clearly a crude rep-
resentation of the state of knowledge in this case.14
14 With continuous variables, only intervals can be assigned a discrete probability. El
probability of an interval is represented by the area under the probability-density function
within that interval. The total area under a PDF always sums to 100 por ciento. Estrictamente hablando,
Roman population is a discrete rather than a continuous variable (since there are no fractional
persons), but the number of possibilities (in the tens of millions) is so large that it can be treated
as continuous for convenience. This brief and discursive discussion of probability is intended
only to pique the interest of historians. For a formal introduction to probability and proba-
bility distributions aimed at archaeologists, see Buck et al., Bayesian Approach, 47–65.
EPISTEM IC U NCERTAINT Y
| 101
A simpler but much better alternative is the triangle distribu-
ción, which introduces a third parameter, the most-likely value
(the point of highest probability). Cifra 1 illustrates a triangle dis-
tribution with 65 million as the most-likely value. Though still
crude, it is a much better representation of the way my degree
of belief falls away from the most-likely value toward the mini-
mum and maximum possible values.15
The graphic representation also reveals an aspect of the prob-
lem obscured by a focus on the most-likely value. Since the pos-
sible range extends further above 65 million than it does below,
the uncertainty is asymmetrical, thereby making the most-likely
value a biased estimator of the actual value. En este caso, the distor-
tion is relatively minor, but asymmetry is common in epistemic
uncertainty and can be more pronounced (the probabilistic ap-
proach has a solution to this problem, as presented below).
The triangle distribution remains imperfect in at least two
respects. It exaggerates how quickly my degree of belief declines
in the immediate area of the most-likely value (a value of 65 mil-
lion is not much more likely than a value of 60 millón), y eso
assigns too high a probability to extreme values, especially in the
90 a 100 million range. A curve with attenuated tails would be
mejor.
PERT Numerous distributions could serve that purpose, en-
cluding the beta, gamma, Weibull, and Burr distributions. Fitting
these distributions to particular beliefs can be computationally
complex, sin embargo, since the parameters that define them are ab-
stract quantities without a real-world interpretation. The most in-
tuitive to manipulate is the PERT (Program Evaluation Review
Technique) distribución (a special case of the beta distribution),
in which the three parameters have the same interpretation as
those for the triangle distribution—minimum, most-likely, y
maximum values. Cifra 1 illustrates the use of a PERT distribution
to represent the uncertainty about the Roman population. Es un
marginally better approximation because of its rounded peak and
more attenuated tails. Sin embargo, the computationally simpler tri-
angle distribution may be adequate in many cases. Practitioners in
many other fields have found triangle distributions to be a convenient
15 For the use of triangle distributions to represent epistemic uncertainty, see Vose, Risk
Análisis, 403; Morgan and Henrion, Incertidumbre, 96.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
j
i
/
norte
h
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
5
0
1
9
1
1
7
0
2
5
9
5
/
j
i
norte
h
_
a
_
0
1
3
7
7
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
102
| MY L ES LAVA N
way to represent subjective probabilities in situations of episte-
mic uncertainty. In any case, a historian is free to choose from a
wide range of distributions to find the best representation of the
uncertainty.16
This exercise of assigning probabilities is not as outlandish as it
may appear. The procedure of encoding beliefs as probability
distributions has become well established in other disciplines.
Even in fields with much better data, estimation often entails an
irreducible element of subjective judgment. Forecasting and risk
models regularly include quantities for which values are assignable
only via the subjective judgment of experts. The problem is suf-
ficiently widespread to have generated a whole literature devoted
to the “elicitation” of expert opinion in the form of probability
distributions.17
The procedure merely makes explicit a probabilism that is
already implicit in historical argument. When historians from
Beloch to Frier proposed point estimates for the population of the
Empire, they were presumably reporting the value that they judged
to be the most likely—the peak of their probability distribution for
the quantity. Their rejection of other estimates as less likely implies
their assignment of lower probabilities to those values, mientras
their rejection of other suggestions as implausible or impossible
means that their probability distributions were at, or near, zero
(otherwise their rhetoric is misleading). Making the probabilities
explicit would help to clarify the positions and focus attention
on the degree of uncertainty.
The purpose of the exercise is not to estimate some objective
probabilities but rather to use probabilities to represent uncertainty.
Kaplan, who helped to develop the probabilistic approach to risk
análisis, made the point succinctly: “People often think that putting
16 The more-familiar normal distribution, though often used to represent uncertainty aris-
ing from variation and measurement error, is unsuitable in this context since it is strictly
symmetrical—the uncertainty in this case being clearly asymmetrical—and extends infinitely
in both directions. For further discussion of distributions, see Vose, Risk Analysis, 401–410;
Paul H. Garthwaite et al., “Statistical Methods for Eliciting Probability Distributions," Diario
of the American Statistical Association, 100 ( Junio 2005), 688–689.
17 For the widespread need to rely on subjective judgments in future-oriented fields, ver,
Por ejemplo, Anthony O’Hagan et al., Uncertain Judgements: Eliciting Experts’ Probabilities
(Chichester, 2006), 97–120; Vose, Risk Analysis, 393–422; for a brief overview of the elicita-
tion of expert opinion, Garthwaite et al., “Statistical Methods for Eliciting Probability Distri-
butions”; for a fuller synthesis of research in the field, O’Hagan et al., Uncertain Judgements.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
j
i
/
norte
h
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
5
0
1
9
1
1
7
0
2
5
9
5
/
j
i
norte
h
_
a
_
0
1
3
7
7
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
| 103
EPISTEM IC U NCERTAINT Y
forth an uncertainty curve is somehow difficult, comparado con
giving a single number or ‘point estimate.’ It becomes much easier
if we remind ourselves that probability curves ‘do not exist,’ as
De Finetti said.
. . . They are only a language in which we express our
state of knowledge or state of certainty. With this understanding,
it is easy to put forth a curve (fat, if necessary) to express our un-
certeza. What is far more difficult is to put forth a single number
that people are going to believe and use for design and regulatory
decisiones, as if it were gospel truth.”18 The same argument holds
for historical estimates.
COGNITIVE BIASES Historians should be aware of two kinds of cog-
nitive bias that can affect any attempt to estimate uncertain quantities,
not just the formal probabilistic approach developed herein. The most
significant bias is overconfidence. People estimating uncertain quantities
usually produce ranges that are too narrow because they assign prob-
abilities too close to zero for values that are very low or very high. El
overconfidence becomes more pronounced as estimation becomes
more difficult (the “hard-easy effect”). Overconfidence is a major issue
for historians appraising uncertain quantities when their information is
scant. Scholars who have worked on the population of the Roman
Empire are likely to have been too quick to dismiss relatively low
or high values as implausible. The range of plausible values is probably
wider than they have suggested.19
The second important bias, the anchoring effect, arises from
one of the “heuristics” identified by Kahnemann and Tversky in
their work on the cognitive shortcuts that people take when mak-
ing decisions based on limited information. Estimates of uncertain
quantities are often distorted by preconceived values as a result of a
heuristic that first evaluates proposed estimates as high or low and
then corrects them—Kahnemann and Tversky’s “judgment by
anchoring and adjustment.” As a rule, such corrections tend to
18 Kaplan, “Formalisms for Handling Phenomenological Uncertainties," 141.
19 The study of judgment under uncertainty began with Amos Tversky and Daniel Kahneman,
“Judgment under Uncertainty: Heuristics and Biases," Ciencia, CLXXXV (1974), 1124–1131. Para
syntheses of research in the field, focusing on the implications for the formulation of expert
knowledge in probabilistic form, see O’Hagan et al., Uncertain Judgements, 33–60; Garthwaite
et al., “Statistical Methods for Eliciting Probability Distributions,” 682–684, 685; for more about
overconfidence, Ward Edwards et al., Advances in Decision Analysis: From Foundations to Applications
(Nueva York, 2007), 143–144; Garthwaite et al., “Statistical Methods for Eliciting Probability
Distributions," 685.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
j
i
/
norte
h
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
5
0
1
9
1
1
7
0
2
5
9
5
/
j
i
norte
h
_
a
_
0
1
3
7
7
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
104
| MY L ES LAVA N
be too small. The implication is that historians are likely to
anchor to previously published estimates, regardless of their qual-
idad, when forming their opinions. Every estimate of the Roman
population’s size has probably been anchored to its predecessor.
The single largest swing in the modern history of the debate was
proposed by Beloch himself, when he updated his own estimate
para 14 C.E. de 54 a 70 millón. He was presumably more
acutely aware of the uncertainties in his own estimate than later
readers would have been. Subsequent revisions tended to be
more modest. McEvedy and Jones reduced Beloch’s estimate
by around 14 million in their estimate for 1 C.E. Frier nudged
their estimate for 1 C.E. upward by just 5 millón, and Scheidel
adjusted Frier’s estimate for 164 C.E. by just 4 millón. Given the
existence of the anchoring effect, these corrections may well
have been too small.20
Considerable research has been devoted to our capacity to
suppress these biases. The most fruitful approach involves a train-
ing process in which individuals repeatedly estimate a quantity be-
fore being confronted with the actual value. It has proved effective
in calibrating the probability judgments of forecasters such as
meteorologists, but it is of little use to historians, who rarely have
the opportunity to compare their estimates to actual values. El
best that historians can do is to be aware of the biases affecting
their judgment and try to compensate for them. A formally prob-
abilistic approach provides the best framework for doing so.
COMBINING UNCERTAINTIES Conceptualizing beliefs about uncer-
tain quantities as probability distributions is a useful intellectual
discipline. Ancient historians are accustomed to confining their
disputes to point estimates, asserting a particular value or range
to be the “most likely” without stating their confidence that the
actual value was close to their proposed value and without consid-
ering how much less likely the rejected rival estimates were. El
rigor of thinking in terms of probability distributions forces histo-
rians to confront these difficult but important questions. Its real
valor, sin embargo, lies in the aggregation of uncertainties. Uno
20 For the experiment, see Tversky and Kahneman, “Judgment under Uncertainty.” O’Hagan,
et al., Uncertain Judgements, 47–49; Garthwaite et al., “Statistical Methods for Eliciting Probability
Distributions," 682.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
j
i
/
norte
h
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
5
0
1
9
1
1
7
0
2
5
9
5
/
j
i
norte
h
_
a
_
0
1
3
7
7
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
EPISTEM IC U NCERTAINT Y
| 105
key advantage of probabilities is that they are easy to combine
mathematically.
Monte Carlo Simulation Many future-oriented fields combine
uncertainties using Monte Carlo simulation. This technique in-
volves three steps: (1) the construction of a mathematical model
to represent the quantity of interest as a function of several
better-understood quantities, in which all uncertain quantities
are represented as random variables—the quantity of interest being
the output variable and the better-understood quantities the input
variables; (2) the conversion of observer’s beliefs about the input
variables to probability distributions, including the assessment of
epistemic interdependence between input variables (discussed be-
bajo); y (3) the generation of a series of scenarios through the
random selection of input values from the probability distributions
for the input variables. The output that the model produces in
each scenario can be regarded as a random sample from the prob-
ability distribution for the output variable. As the number of sce-
narios increases, the distribution of the output values in the sample
will converge on the underlying probability distribution of the
output variable.21
The Monte Carlo method, which emerged in the context of
nuclear engineering during and after World War II, has gained wide
application in forecasting, risk assessment, and decision analysis. Ser-
cause it is most often used in contexts that appear to involve aleatory
incertidumbre, its relevance to historical problems, in which the uncer-
tainty is clearly epistemic, has been underestimated. Yet it offers
historians a useful tool to aggregate epistemic uncertainties. Para
instancia, it offers a potential solution to a hitherto intractable
problem in Roman history, estimating the proportion of the pop-
ulation that had Roman citizenship before Caracalla’s universal
grant in 212/13 C.E. —crucial to the assessment of the significance
of that decision. Even though the mechanisms by which Roman
citizenship was disseminated were relatively well understood, quan-
tification seemed impossible because of the many uncertainties
involved. Any estimate of the proportion of persons who were cit-
izens in 212 would require estimates of the number of new citizens
created by 200 years of communal and personal grants, service in the
ejército, office holding in provincial cities, and the manumission of
21 For an excellent practical guide to Monte Carlo simulation, see Vose, Risk Analysis.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
j
i
/
norte
h
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
5
0
1
9
1
1
7
0
2
5
9
5
/
j
i
norte
h
_
a
_
0
1
3
7
7
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
106
| MY L ES LAVA N
slaves (the principal routes to citizenship), as well as of the total pop-
ulation of the empire, all of these variables being themselves uncer-
manchar. A traditional point estimate based on most-likely values for
each of the input quantities could never hope to command credi-
bility because of the proliferating uncertainties. A probabilistic
approach using Monte Carlo simulation makes it possible to
account for all the component uncertainties and to assess the aggre-
gate uncertainty about the prevalence of citizenship.22
INTERPRETING THE RESULTS The output of a Monte Carlo simu-
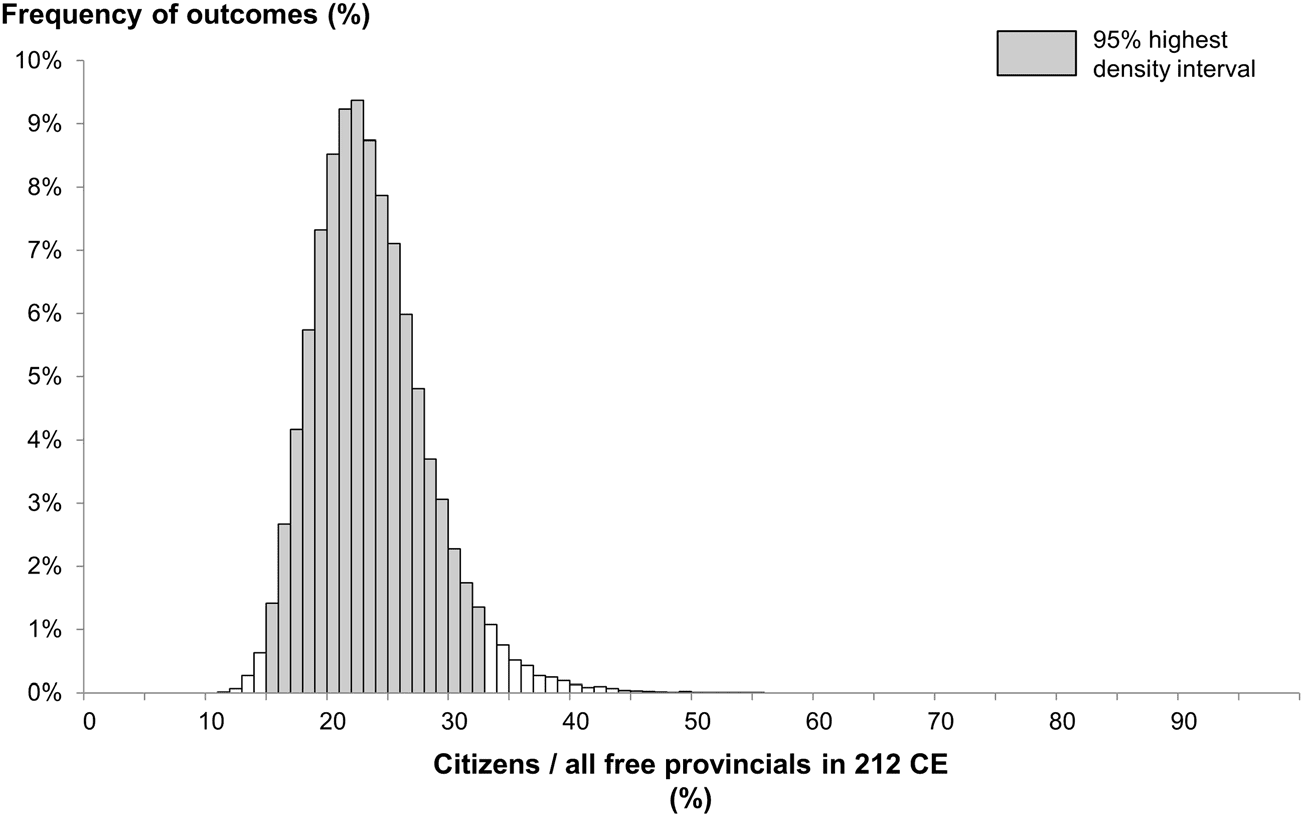
lation is most intuitively grasped through a histogram. Cifra 2
shows the result of a simulation of the spread of Roman citizen-
barco. In each random scenario, the model calculates the prevalence
of citizens in 212 CE, expressed as a percentage of the free pop-
ulación. The histogram shows how often different prevalences
occurred in a sample of 50,000 escenarios. The shape of the distri-
bution approximates the probability density function for the prev-
alence of citizens that is implied by the beliefs encoded in the
modelo. The distribution peaks in the interval 22 a 23 por ciento.
The most-likely value is thus around 22.5 por ciento. But the mean
valor, 24 por ciento, is actually the best point estimator of the quan-
tity (termed the expected value or expectation of the uncertain
quantity in probability theory), because it is the probability-
weighted average of all possible outcomes. Unlike the most-likely
valor, it takes account of any asymmetry in the uncertainty (the fact
that the distribution is slightly skewed to the right in Figure 2).
This is the best solution to the problem of asymmetry noted
earlier, which can cause problems for reasoning stemming from
most-likely values alone.23
En este caso, the improvement in point estimation is modest
(though it may be more pronounced in situations of greater asym-
metry). The overall shape of the distribution is more important. A
most-likely value would have been relatively easy to establish
using a traditional point-estimate approach. It would also be ob-
vious that a value near the most-likely value is more plausible than
any higher or lower value, but a historian would not otherwise
22 Lavan, “Spread of Roman Citizenship.”
23 For the expected value of an uncertain quantity, see Lindley, Understanding Uncertainty,
137–139.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
j
i
/
norte
h
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
5
0
1
9
1
1
7
0
2
5
9
5
/
j
i
norte
h
_
a
_
0
1
3
7
7
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
EPISTEM IC U NCERTAINT Y
| 107
Higo. 2 Monte Carlo Simulation of the Prevalence of Citizenship
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
j
i
/
norte
h
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
5
0
1
9
1
1
7
0
2
5
9
5
/
j
i
norte
h
_
a
_
0
1
3
7
7
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
have grounds to establish how much less likely outlying values are.
The benefit of the Monte Carlo simulation is that it quantifies the
decline in plausibility.
Estimation always entails a trade-off between confidence and
precisión. Ceteris paribus, the wider the range, the more confident
we can be that it includes the actual value. But a wider range also
contains less information about the quantity. Most strategies for
managing uncertainty depend on discounting some possibilities
as highly unlikely. In the case of Figure 2, which is a probability
density function representing degree of belief, this strategy means
discounting the tails of the distribution and reporting a specified
credible interval (a Bayesian credible interval—to be distinguished from
a frequentist confidence interval, which does not admit a probabilistic
interpretation—is a contiguous interval that contains a specified
proportion of the total probability mass). Which interval to report
is a matter of convention. Many disciplines operate with a 95 por-
cent threshold for estimation (though the threshold is often applied
in a frequentist rather than Bayesian framework). Some fields with
better data hold themselves to a higher standard, operating with a
99 por ciento, or even higher, límite. In a field as data-poor as
ancient history, a lower threshold of 80 percent may well be appro-
priate. Most ancient historians seem to operate with even lower
108
| MY L ES LAVA N
thresholds in the ranges that they report, but the issue is never dis-
cussed. En este caso, el 95 percent credible interval for the prevalence
of citizenship is 15 a 33 por ciento. En otras palabras, that range is suffi-
cient to enclose 95 percent of the probability mass. This estimate
incorporates the uncertainty about the population of the Empire
and the other relevant variables. The resulting range, though broad,
represents an important advance in our understanding of an im-
portant quantity that had hitherto resisted quantification entirely.24
The Monte Carlo simulation demonstrates that beliefs about
the input variables and the laws of probability together constrain
beliefs about the quantity of interest. The underlying logic is that
of coherence—the axiom that a set of probabilistic judgments has to
be internally consistent to be valid. Our beliefs about the processes
that disseminated citizenship (as encoded in the identification of
variables and the mathematical model that links them to the prev-
alence of citizenship) and about the historical values of those var-
iables (as encoded in the input probability distributions) impel us
to assign a much higher probability to some possible values of the
quantity than to others. En otras palabras, we learned that we al-
ready knew enough about the mechanisms of enfranchisement
and the demography of the Empire to be confident that the pro-
portion of the population who had citizenship in 212 was between
15 y 33 percent.25
The aggregation of probability distributions through Monte
Carlo simulation is a better method of manipulating uncertain
quantities than traditional approaches that collapse uncertainty by
treating all variables as point estimates. En algunos casos, as in this ex-
amplio, Monte Carlo simulation will produce credible intervals that
are usefully narrow, revealing that historians knew more than they
realized about the quantity of interest. En otros casos, sin embargo, incluso
un 80 percent credible interval may be too broad to be informative.
But that finding would also be significant, demonstrating the vul-
nerability of any existing point estimates for the quantity.
It is essential to consider whether
EPISTEMIC INTERDEPENDENCE
there is any interdependence between the uncertainties that are
24 For Bayesian credible intervals, see O’Hagan et al., Uncertain Judgements, 234–235.
25 For the principle of coherence, see Lindley, Understanding Uncertainty, 36–37, 236–237;
for the application discussed herein, Aven, Foundations of Risk Analysis, 97–98.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
j
i
/
norte
h
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
5
0
1
9
1
1
7
0
2
5
9
5
/
j
i
norte
h
_
a
_
0
1
3
7
7
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
EPISTEM IC U NCERTAINT Y
| 109
being combined. The Monte Carlo approach can cope with inter-
dependencia, but only if it is taken into proper account. The inter-
dependence in question is specifically epistemic, a matter of the
interdependence of historical problems. Two quantities are episte-
mically interdependent if acquiring new information about one
quantity would change the historian’s beliefs about the second
quantity.26
Returning to the problem of the Roman population, the un-
certainties about the population of Italy and the population of
Iberia are clearly not independent. All estimates for Iberia are in-
formed by an assumption that Iberia was less densely populated
than Italy was. If we were to discover that the actual peak popu-
lation of Italy was toward the top of our range of possible values,
we would have to adjust our probability distribution for the pop-
ulation of Iberia accordingly. Modeling the two variables as inde-
pendent would fail to account for this interdependence and
produce a meaningless result. But many other uncertainties can
be regarded as independent. Take the peak population of the
Empire and the proportion of slaves who were freed. En este caso,
discovering the exact value of the population would in no way
reduce my uncertainty about the freed slaves. The two can thus
be treated as independent.
Various strategies are available for managing epistemic
interdependence once it has been identified, but unacknowl-
edged epistemic interdependence is the potential Achilles heel
of any probabilistic model. The most dangerous pitfall is ignoring
strong epistemic interdependence that makes extreme outcomes
more likely. The risk of such an error is increased by historians’
desire to produce a narrower and hence more informative esti-
compañero. Epistemic interdependence needs to be accounted for
carefully.27
26 For epistemic (also termed probabilistic and subjective) interdependence, see Garthwaite
et al., “Statistical Methods for Eliciting Probability Distributions," 686; O’Hagan et al.,
Uncertain Judgements, 107–108, 243; Lindley, Understanding Uncertainty, 52–53.
27
Interdependence either reduces the variance of the resulting probability distribution (eso
es, produces a narrower credible interval), if the effect of an extreme value for one variable is
partly offset by a correspondingly extreme value for the other variable, or increases it, if the
effects of extreme values compound each other (as would be the case with the populations of
Italy and Spain with regard to the total population of the Empire). For different ways to in-
corporate interdependence, see Garthwaite et al., “Statistical Methods for Eliciting Probability
Distributions," 687; Vose, Risk Analysis, 356–364.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
j
i
/
norte
h
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
5
0
1
9
1
1
7
0
2
5
9
5
/
j
i
norte
h
_
a
_
0
1
3
7
7
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
110
| MY L ES LAVA N
SENSITIVITY ANALYSIS AND ITERATION Monte Carlo simulation is
useful not just for arriving at an estimate but also for clarifying
the structure of a problem. Various types of sensitivity analysis
can be performed to measure how much the individual input var-
iables contribute to the overall uncertainty about the output var-
iable. The point is to identify the most important components of
incertidumbre. Sensitivity analysis of this sort is particularly important
for historians because the Monte Carlo approach works best as an
iterative process. The information relevant to problems in ancient
history tends to be dispersed and difficult to interpret. Even dis-
counting the discovery of new information, an individual’s assess-
ment of the current state of knowledge can only be provisional
because it has to rely on the work of others and is likely to omit
at least some relevant information—for example, comparable data
from other regions or periods. Por eso, the assignment of probability
distributions to the input variables should be an iterative process. Él
should start with a rough set of probability distributions (erring on
the side of exaggerating the uncertainty) to identify the variables
that contribute most to the uncertainty about the quantity of
interés. The probability distributions for those variables can then
be refined through a deeper review of the evidence, etcétera,
until the probability distribution for the quantity of interest begins
to stabilize. Several iterations may be necessary before reaching a
stable estimate (stable in the sense that further analysis of the avail-
able evidence is unlikely to change it significantly).28
This research note demonstrates the value of subjective probability
as a tool of historical analysis. It provides a framework that can ac-
commodate the significant epistemic uncertainty involved in esti-
mates of historical quantities, especially (but not only) regarding
periods for which we have limited data. Thinking in terms of
probability distributions is always a good discipline because it
draws attention to complexities that traditional approaches miss
by focusing exclusively on a most-likely value. It becomes even
more useful when multiple uncertain quantities are combined in
a single analysis, a common occurrence in ancient history. Though
it may appear a radical departure from current practice, it builds
upon a probabilism that is already latent in historical reasoning.
28 For a good overview of the options for sensitivity analysis, see Vose, Risk Analysis, 80–88.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
j
i
/
norte
h
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
5
0
1
9
1
1
7
0
2
5
9
5
/
j
i
norte
h
_
a
_
0
1
3
7
7
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
EPISTEM IC U NCERTAINT Y
| 111
Most of the estimates that circulate in ancient history are implicit
expressions of their proponents’ probability distributions for the
quantities in question, insofar as they represent the value judged
to be the most likely, given the available evidence. But the tradi-
tional best-estimate approach leaves their beliefs about the likeli-
hood of other possible values unclear or unexamined.
These probabilities have to be understood as subjective, en el
technical sense. They are not estimates of objective probabilities
that exist in the world (en efecto, Bayesians admit no objective prob-
abilities) but representations of the epistemic uncertainty about
quantities that have a fixed value, albeit an unknown one. Tal como,
the probabilities are both conditional and personal. They are con-
ditional because they depend on a state of knowledge. New infor-
mation will change the probabilities. They are personal because
they rely on an individual scholar’s assessment of the evidence.
One scholar cannot dictate another’s probabilities. Yet their prob-
abilities should converge if they agree on the model and on the
probability distributions for the input variables. If they disagree,
expressing their beliefs in terms of probability distributions will
clarify the area of disagreement and focus further research and
debate.
The avowedly subjective character of the framework may
trouble some historians. But it merely makes explicit an inherent
feature of historical analysis. Historians can present their evidence
and their arguments, but they can never coerce their colleagues’
assent; other scholars may reach different conclusions from the
same evidence. The most that they can hope is that their reasoning
will prove persuasive. This condition is no different from my
expectation that other scholars will recognize in my probability
distributions a careful and honest representation of the state of
conocimiento. The subjectivity inherent in historical analysis is too
often regarded as an intellectual defect to be obfuscated through
a misleading rhetoric of objective authority. One of the great
merits of this framework is that it acknowledges the irreducible
subjectivity in all empirical disciplines and shows that it is not an
obstacle to quantitative analysis.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
j
i
/
norte
h
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
5
0
1
9
1
1
7
0
2
5
9
5
/
j
i
norte
h
_
a
_
0
1
3
7
7
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
j
i
/
norte
h
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
5
0
1
9
1
1
7
0
2
5
9
5
/
j
i
norte
h
_
a
_
0
1
3
7
7
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3