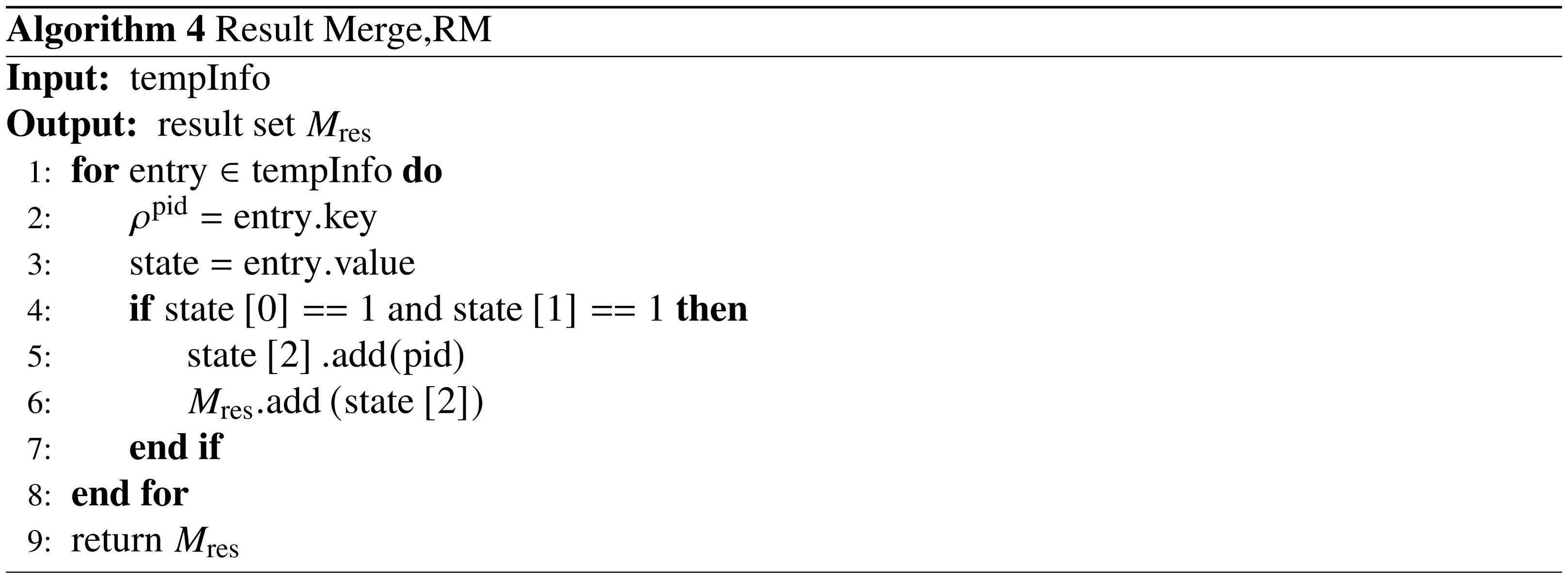RESEARCH PAPER - IA de Investigación especializada en el MIT

TRABAJO DE INVESTIGACIÓN

Fuzzy-Constrained Graph Patter n Matching in Medical
Knowledge Graphs

Lei Li1,2,3†, Xun Du3, Zan Zhang3 & Zhenchao Tao4

1Key Laboratory of Knowledge Engineering with Big Data (the Ministry of Education of China), Universidad Tecnológica de Hefei,

Hefei 230601, Porcelana

2Intelligent Interconnected Systems Laboratory of Anhui Province (Universidad Tecnológica de Hefei), Hefei 230601, Porcelana

3School of Computer Science and Information Engineering, Universidad Tecnológica de Hefei, Hefei 230601, Porcelana

4The First Affiliated Hospital of University of Science and Technology of China, Hefei 230031, Porcelana

Palabras clave: Graph pattern matching; Medical Knowledge Graphs; Fuzzy constraints; Breast cancer; Diagnostic

clasificación

Citación: li, l. et al.: Fuzzy-Constrained Graph Pattern Matching in Medical Knowledge Graphs. Data Intelligence 4(3), 599-619

(2022). DOI: 10.1162/dint_a_00153

Recibió: Oct. 10, 2021; Revised: Ene. 15, 2022; Aceptado: Apr. 10, 2022

ABSTRACTO

The research on graph pattern matching (GPM) has attracted a lot of attention. Sin embargo, most of the
research has focused on complex networks, and there are few researches on GPM in the medical field.
Por eso, with GPM this paper is to make a breast cancer-oriented diagnosis before the surgery. Technically,
this paper has firstly made a new definition of GPM, aiming to explore the GPM in the medical field,
especially in Medical Knowledge Graphs (MKGs). Entonces, in the specific matching process, this paper
introduces fuzzy calculation, and proposes a multi-threaded bidirectional routing exploration (M-TBRE)
algorithm based on depth first search and a two-way routing matching algorithm based on multi-threading.
Además, fuzzy constraints are introduced in the M-TBRE algorithm, which leads to the Fuzzy-M-TBRE
algoritmo. The experimental results on the two datasets show that compared with existing algorithms, nuestro
proposed algorithm is more efficient and effective.

†

Autor correspondiente: Lei Li (Correo electrónico: lilei@hfut.edu.cn, ORCID: 0000-0002-5374-7293).

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

t
/

a
r
t
i
C
mi
–
pag
d

F
/

4
3
5
9
9
2
0
3
8
4
4
3
d
norte
_
a
_
0
0
1
5
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Fuzzy-Constrained Graph Pattern Matching in Medical Knowledge Graphs

1. INTRODUCCIÓN

As a basic data structure, graphs are widely used in a lot of applications. Por ejemplo, as for object
anomaly checking, objects can be represented by graphs, and then anomalies can be discovered with
certain graph algorithm [1]. Mientras tanto, in order to determine whether a user is interested in a certain
webpage, the webpages can be converted into multiple graphs, and with the multiple graphs taken as a
bag, the bag can be classified and judged [2]. As a popular graph-based technology, graph pattern matching
(GPM) has attracted a lot of attentions. Específicamente, given a pattern graph, finding subgraphs from the data
graph with a similar or the same structure as the pattern graph is named as GPM. As the research field of
GPM has changed from the initial protein isomorphism [3, 4] to community detection [5, 6], expert
discovery [7], recommendation systems [8], the discovery of social groups [9–11] and the identification of
criminal groups [12], the definition of graph pattern has also changed accordingly.

Technically, GPM is originally defined based on subgraph isomorphism. Given a data graph GD and a
pattern graph GP as input, it will return whether it contains a subgraph, and whether this subgraph has
exactly the same topological structure as GP. Por ejemplo, we can guess the properties of unknown proteins
from the properties of known proteins through this matching [3, 4]. Sin embargo, this traditional subgraph
isomorphism is too strict. In order to extend the application scenarios of GPM, Fan et al. [12] propose a
bounded simulation, which extends the edge-to-edge matching to the edge-to-finite length path matching.
Sin embargo, this matching still does not make use of the rich attribute information on vertices and edges.
Por lo tanto, Liu et al. [13] propose a multi-constrained graph pattern matching (MC-GPM) problem to obtain
more effective matching results. Afterwards, Liu et al. [14] propose a multiple fuzzy constrained graph
pattern matching (MFC-GPM) based on MC-GPM, considering that some attributes do not require exact
matching. Sin embargo, the current application scenarios of GPM are mostly concentrated on complex
redes, and there are very few research applications of GPM in the medical field, especially in Medical
Knowledge Graphs.

Hoy en día, the incidence of breast cancer is getting higher and higher, and the age is getting younger
and younger. Breast cancer can be divided into ductal carcinoma in situ, lobular carcinoma in situ, invasive
ductal carcinoma, invasive lobular carcinoma, and so on. Each type of breast cancer can be divided
according to the primary tumor staging, regional lymph node staging, and distant metastasis staging. El
purpose of this paper is to make a diagnosis through GPM technology before the patient’s condition is
diagnosed with surgery.

en este documento, to introduce GPM into the medical field, we propose the problem of GPM in MKGs and
give relevant definitions. Además, the M-TBRE algorithm is proposed, which firstly divides the pattern
graph into pattern subgraphs, then obtains the matching results of the pattern subgraphs, and finally merges
the matching results of the pattern subgraphs. M-TBRE can give the diagnosis distribution of the pattern
graph, and return the best k diagnosis classification results according to the frequency of each diagnosis
clasificación. Fuzzy constraints are also introduced in the M-TBRE algorithm, which extend it to the Fuzzy-
M-TBRE algorithm, and the effectiveness of our algorithm are verified on two public data sets.

600

Data Intelligence

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

t
/

a
r
t
i
C
mi
–
pag
d

F
/

4
3
5
9
9
2
0
3
8
4
4
3
d
norte
_
a
_
0
0
1
5
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Fuzzy-Constrained Graph Pattern Matching in Medical Knowledge Graphs

The rest of this paper is organized as follows. The related work of GPM is reviewed in Section 2. Entonces
en la sección 3, the concept of pattern matching in MKGs is introduced. Sección 4 proposes a multi-threaded
bidirectional routing exploration algorithm and a Fuzzy-M-TBRE algorithm to process GPM in MKGs.
Sección 5 introduces the data sets and conducts experiments to verify our proposed Fuzzy-M-TBRE algorithm,
y Sección 6 concludes our work in this paper.

2. RELATED WORK

According to the judgment based on bijective function or based on binary relationship, the research on

GPM can be divided into isomorphism-based GPM and simulation-based GPM.

2.1 Isomorphism-Based GPM

Isomorphism-based GPM has a bijective function between the pattern graph and the data graph, y el
topological structure of the matched data subgraph and pattern graph must be the same. Ullmann [15] primero
proposes a matching algorithm based on depth-first search. Cordella et al. [16] improve Ullmann’s algorithm
in terms of matching order and pruning strategy, and propose the VF2 algorithm. Tong et al. [17] propose
the G-Ray method, which uses the goodness function to measure the degree of matching between a
subgraph and the pattern graph, so that the optimal-k subgraphs can be returned. Además, Cheng et al.
[18] also propose a top-k matching algorithm, which sorts the matched subgraphs obtained based on the
number of spanning trees, thereby returning the optimal-k subgraphs. Cheng et al. [19] propose the R-join
algorithm based on the join index of the clustering graph and optimize the algorithm. Other representative
algorithms include DDST algorithm [20], IncBMatch algorithm [21], etcétera. Generally, as an NP-complete
problema, Isomorphism-based GPM uses indexing [22,23] and parallel distributed [24–26] to improve the
efficiency of matching.

Isomorphism-based GPM is mostly used in fields with strict structural requirements such as protein
isomorphism, 3D object matching [27] and network abnormal behavior detection [28]. Sin embargo, semejante
matching is too strict for applications such as social networks or knowledge graphs that do not require strict
matching accuracy. Por lo tanto, simulation-based GPM research has emerged.

2.2 Simulation-Based GPM

As judged through binary relations, graph simulation is introduced by Henzinger et al. [29], but it is still
an edge-to-edge matching, which cannot meet the requirements of many applications. Fan et al. [12] extend
the graph simulation and propose a bounded simulation, where the edge of the pattern graph can be
matched to a path, and the length of this path does not exceed the given constraint value k. Basado en el
bounded simulation, Ma et al. [30] propose a strong simulation, which can well preserve the topological
structure of the pattern graph. There is a lot of attribute information on vertexes and edges in big graph
datos, but these existing work does not consider this information. Liu et al. [13] consider this information
to extend the bounded simulation to MC-GPM and propose a baseline algorithm based on exploration and

Data Intelligence

601

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

t
/

a
r
t
i
C
mi
–
pag
d

F
/

4
3
5
9
9
2
0
3
8
4
4
3
d
norte
_
a
_
0
0
1
5
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Fuzzy-Constrained Graph Pattern Matching in Medical Knowledge Graphs

a heuristic algorithm based on data graph compression index (HAMC). Since the HAMC algorithm only
considers the constraint conditions of the matching path, which does not consider the minimization of the
matching path length and the HAMC algorithm does not support a distributed computing structure, Liu et
Alabama. [31] propose an M-HAMC algorithm. Considering that the attribute values on vertexes and edges
sometimes do not need to be exactly matched, on the basis of MC-GPM, Liu et al. [14] propose an MFC-
GPM and an ETOF-K algorithm, which improves matching efficiency from two aspects: edge matching and
edge connection. Based on the topologically ordered sequence of pattern graph vertexes, Liu et al. [32]
propose the NTSS algorithm and optimize the algorithm by introducing two measures: caching mechanism
and reverse edge matching. The caching mechanism solves the problem of repeated calculation of the same
candidate path in multiple matching subgraphs, and the reverse edge matching prunes the candidate set
of the edge with a partial degree of entry 0 in advance.

3. GRAPH PATTERN MATCHING

GPM is to find all data subgraphs that satisfy the pattern graph GP in a given data graph GD. In this
sección, we will give the relevant definitions of data graphs, pattern graphs, and graph pattern matching in
MKGs.

3.1 Data Graph and Pattern Graph

The related definitions of the data graph and the pattern graph are as follows.

3.1.1 Data Graph

A data graph GD = (V, mi, fV

D, fE

D) is a directed graph with vertex attributes and edge attributes, dónde

•
•

V is the set of vertices of the data graph;
E is the set of edges of the data graph, y (vi, vj)  E represents the directed edge from vertex vi 
V to vertex vj  V;
− fV

D(v) is the attribute set of v. In an MKG, each vertex v has
a label rr, and rr represents the type of this vertex. The value of rr is different, and the other
D(v) are also different. The value of rr can be DI, BI, MI, GW, OC,
attributes in the attribute set fV
AL and PD;

D is a function defined on V. v  V, fV

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

t
/

a
r
t
i
C
mi
–
pag
d

F
/

4
3
5
9
9
2
0
3
8
4
4
3
d
norte
_
a
_
0
0
1
5
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

− fE

D is the function defined on E. e  E, fE
ρ .
pids
v vi

D(vi, vj), only contains

borde (vi, vj), fE
identity information of vertex which comes from those patients;

D(vi, vj) is the attribute set of e. In an MKG, for a directed
ρ is a list that stores patient numbers, eso es, el
pids
v vi

DI: When the value of rr is DI, the attribute set fV

D(v) of vertex v describes the diagnostic classification
information of breast cancer, which includes pathological information rh, T staging stage rs, tumor length
rTS, the description of regional lymph nodes N staging stage rLN, and M staging stage rDM describing distant
metastasis. The value of rh can be 0, 1, 2, y 3 respectively representing “invasive ductal carcinoma”,

602

Data Intelligence

Fuzzy-Constrained Graph Pattern Matching in Medical Knowledge Graphs

“invasive lobular carcinoma”, “ductal carcinoma in situ”, and “lobular carcinoma in situ”; the value of rs
can be 0, 1, 2, 3, y 4; rTS is a floating point number in cm. The value of rLN can be N0, N1, N2, y
N3; the value of rDM can be M0, and M1.

BI: When the value of rr is BI, the attribute set fV

D(v) of vertex v describes the basic information of the
patient, which includes rCN, rCP and rage. rCN indicates whether the patient currently needs care, and its
value is true or false; rCP indicates that the patient is currently pregnant, and its value is true or false; rage
indicates the current age of the patient, and its value is a positive integer.

MI: When the value of rr is MI, the attribute set fV

D(v) of vertex v describes the patient’s menopausal
información, and it only contains rMS. The value of rMS can be 0, 1, y 2, respectivamente, indicando
pre-menopausal, perimenopausal, and post-menopausal.

GW: When the value of rr is GW, the attribute set fV

D(v) of vertex v describes the patient’s current overall
well-being, and it only contains rGWB. The value of rGWB can be 0, 1, 2, 3, y 4, respectivamente, which means
“fully active, no complaints or symptoms”, “doing normal activities requires a little effort”, “occasionally
need help, but can meet most of the personal needs”, “needs a lot of assistance and frequent medical care”,
“completely disabled, can only lie in a bed or a chair.”

OC: When the value of rr is OC, the attribute set fV

D(v) of vertex v describes whether the patient has
cancers other than breast cancer, which includes rOCS and rOCN. When the value of rOCS is false, el valor
of rOCN is none; when the value of rOCS is true, the value of rOCN is the names of the patient’s other cancers;

AL: When the value of rr is AL, the attribute set fV

D(v) of vertex v describes the patient’s axillary lymph
nodos, which includes rLN, rLS, rIN, rSN and rCW. The value of rLS is true or false, indicating whether the
patient’s axillary lymph nodes are normal or not. The value of rIN is true or false, indicating whether the
supraclavicular lymph nodes of the patient are normal or not. The value of rSN is true or false, indicando
whether the subclavian lymph nodes of the patient are normal or not. The value of rCW is true or false,
indicating whether the patient’s chest wall is normal or not. The value of rLN is a positive integer, cual
means that several of the three of the patient’s supraclavicular lymph node, subclavian lymph node, y
chest wall have problems.

PD: When the value of rr is PD, the attribute set of vertex v describes some diagnosis information of the
patient in the past, which includes raid, rane, raut, rlun, rdia, rcar, rost and rrep. The value of raid is true or false,
indicating whether the patient has AIDS; the value of rane is true or false, indicating whether the patient has
anemia; the value of raut is true or false, indicating whether the patient has autoimmune disease; The value
of rlun is true or false, indicating whether the patient has lung cancer; the value of rdia is true or false,
indicating whether the patient has diabetes; the value of rcar is true or false, indicating whether the patient
has cardiovascular disease; The value of rost is true or false, which indicates whether the patient has
osteoporosis; the value of rrep is true or false, which indicates whether the patient’s reproductive organs are
diseased.

Data Intelligence

603

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

t
/

a
r
t
i
C
mi
–
pag
d

F
/

4
3
5
9
9
2
0
3
8
4
4
3
d
norte
_
a
_
0
0
1
5
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Fuzzy-Constrained Graph Pattern Matching in Medical Knowledge Graphs

3.1.2 Pattern Graph

A pattern graph GP = (Vp, EP, fV

PAG, fE

PAG, fl

PAG, fm

PAG ) is a directed graph with vertex attributes and edge attributes,

dónde:

•
•

•

p is a function defined on Vp, and v  VP, fV
pag(v) is the attribute set of v. In an MKG, the function
PAG(tu) corresponding to the vertex u has the same meaning as the attribute set of the above vertex in

Vp is the set of vertices of the pattern graph;
Ep is the set of edges of the pattern graph, y (ui, uj)  EP represents the directed edge from vertex
ui  VP to vertex uj  VP;
fV
fV
the data graph.
fE
(ui, uj), fE
information of the vertices comes from those patients.
fl
P is the function defined on Ep. (ui, uj)  Ep, fl
PAG(ui, uj) is the length constraint of the edge (ui, uj), y
its value is a positive integer k or a symbol *, respectivamente, indicating that the length of the interval
from vi to vj does not exceed k, or there is no length limit. In an MKG, fl
fm
P is a set of membership constraint functions defined on vertex attributes and edge attributes.

pag(mi) is the attribute set of e. In an MKG, for a directed edge
ρ is a list that stores patient numbers, eso es, the identity
pids
u ui

P is the function defined on Ep. e  EP, fE

PAG(ui, uj) only contains

PAG(ui, uj) = 1;

ρ .

pids
u ui

3.1.3 Fuzzy constraints

During matching, it would be better to get more and better matching results. Because in the actual
matching, each matched subgraph corresponds to a patient who has roughly the same health information
as the patient to be diagnosed in the pattern graph. The more obtained matches, the better experience will
be used for reference in the treatment of patients corresponding to the pattern graph. Sin embargo, en la práctica,
it is possible that a subgraph in a data graph can be well satisfied with other constraints, but because some
less important attribute constraints on a vertex cannot be satisfied, the subgraph cannot become a matching
resultado. Además, some attribute constraints on vertexes do not need to be accurately matched when
matching, and their differences only need to fall within a certain range. Por lo tanto, we introduce fuzzy
constraints to GPM in MKGs.

PAG
mf

f=
{

metro
edad

}

In the MKG, the membership function

is only considered to introduce a fuzzy constraint to
mf
represents the membership function defined on the vertex age attribute rage. El
the age attribute.
edad
mf
mf
is defined as Eq. (1), where abs is the
constraint value of age
is set to 3. The membership function age
ρ represents the age attribute constraint value of vertex v in pattern graph GP.
absolute value function,
ρ represents the age attribute constraint value of vertex u in data graph GD. During matching, edad
mf
attribute rage only needs to satisfy age

≤ .
3

edad
v

edad
tu

metro
F
edad

abs(

ρ
edad
tu

−

ρ
edad
v

)

(1)

604

Data Intelligence

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

t
/

a
r
t
i
C
mi
–
pag
d

F
/

4
3
5
9
9
2
0
3
8
4
4
3
d
norte
_
a
_
0
0
1
5
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Fuzzy-Constrained Graph Pattern Matching in Medical Knowledge Graphs

3.2 Pattern Matching

The matched subgraph

is a subgraph of the data graph GD and matches the
pattern graph GP. The number of matched subgraphs may not be unique, where Gsub  GD, Vsub  V, Esub 
mi,

; The definition of pattern matching in the MKG is as follows.

mi
sub

V
(

GRAMO

⊂

sub

)

sub

D
F
V

D
F
mi
sub

D
F
V

sub

D
F
V

D
F
mi
sub

D
F
mi

For a pattern graph GP = (Vp, EP, fV

PAG, fE

PAG, fl

PAG, fm

PAG) and a data graph GD = (V, mi, fV

D, fE

D), GD matches GP,

denoted as GP  GD, if there is a binary relationship:

•

PAG(tu). If age attribute

ρ is included,
edad
iu

for all u  VP, there is v  V such that (tu, v)  S, which means that there is a vertex v in V that
matches u, eso es, v satisfies fV
representa el
≤ . Except
ρ only needs to satisfy age
mf
membership function defined on the age attribute of u, entonces
ρ , the values corresponding to the other attributes of v must be equal to the

for the age attribute
values of the attributes corresponding to u before it can be determined that vi matches ui.
for each pair (ui, vi)  S,
* ui ~ vi, y
* for each edge (ui, uj) in EP, there is a path from vi to vj in GD such that (uj, vj)  S. Because of
PAG(ui, uj) = 1, this path can be regarded as the edge from vi to vj in GD;
fl

f=
{

edad
tu

metro
edad

PAG
mf

}

ρ . Por ejemplo, the value of

D(A1, B1) defined on the directed edge (A1, B1) in GD, fE

Ejemplo 1: As shown in Figure 1, GD is a data graph composed of related information of multiple breast
cancer patients. The attribute information of some vertexes contained in the data graph saves the diagnostic
classification information of breast cancer. In the data graph GD, each vertex represents some information
D(A1, B1) only contains
of the patient. For the function fE
ρ is 1375, which means that the relevant information on
pids
the attribute
A B
1 1
the B1 vertex comes from the breast cancer patient numbered 1375. The pattern graph GP is the health
status of a patient to be diagnosed. The vertices B, C, D, mi, F, and G respectively represent the patient’s
basic information, menopausal status, general well-being, information on cancers other than breast cancer,
axillary lymph nodes and information about past diagnoses. Vertex A is the diagnostic information of this
patient, but it is unknown and needs to be obtained through GPM. Since all vertex information in the
pattern graph comes from the same patient, we need to find a patient number as the attribute constraint
information on the edges to get the matching result of the pattern graph.

pids
A B
1 1

Data Intelligence

605

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

t
/

a
r
t
i
C
mi
–
pag
d

F
/

4
3
5
9
9
2
0
3
8
4
4
3
d
norte
_
a
_
0
0
1
5
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Fuzzy-Constrained Graph Pattern Matching in Medical Knowledge Graphs

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

t
/

a
r
t
i
C
mi
–
pag
d

F
/

4
3
5
9
9
2
0
3
8
4
4
3
d
norte
_
a
_
0
0
1
5
3
pag
d

Cifra 1. Data graph and pattern graph in an MKG

Ejemplo 2: As shown in Figure 1, it is easy to find a subgraph Msub1 from data graph GD that matches
pattern graph GP. Msub1 passes through vertexes A2, B2, C1, D2, E1, F2 and G3. Vertex A2 is the breast cancer
diagnosis result of the pattern graph GP. The attribute constraint value on the edges in Msub1 is 2384, cual
means that the patient with the number 2384 is closer to the health status of the patient corresponding to
médico de cabecera.

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

After introducing fuzzy constraints, desde

−
ρ ρ
edad
B
3
function constraint value 3 on the age attribute. Además,

abs(

metro
F
edad

edad
B

= , it does not exceed the membership
) 1
=
=
ρ ρ ρ ρ ρ ρ
=
r
CP
, and vertex B
B
B
3

CN
B
3

CN
B

CP
B

r
B
3

606

Data Intelligence

Fuzzy-Constrained Graph Pattern Matching in Medical Knowledge Graphs

matches vertex B3. We can get a new matched subgraph Msub2 that passes through vertexes A2, B3, C1, D2,
E1, F2 and G3. The attribute constraint value on the edges in Msub2 is 676.

4. GRAPH PATTERN MATCHING IN MEDICAL KNOWLEDGE GRAPHS

En esta sección, we propose a multi-threaded bidirectional routing exploration algorithm M-TBRE to solve

the GPM problem in MKGs.

4.1 Algorithm Description

The emergence of multi-core CPU can realize the parallel processing of tasks and speeds up the execution
of programs. Since the multi-constrained GPM problem is an NP-complete problem, in order to speed up
the matching speed and return the matched results quickly, here we consider adopting multi-threading to
solve this GPM problem. In the matching process, the idea of divide and conquer is adopted. For a pattern
graph GP, it can be divided into several pattern subgraphs. After the matching of each pattern subgraph is
completed in the data graph GD, the matched results of each pattern subgraph can be connected to
obtaining the matched results of the pattern graph GP. The matching of pattern subgraphs can be delivered
as subtasks to multiple threads to complete independently, so that matching results can be obtained quickly.

4.2 Algorithm Flow

In the M-TBRE algorithm, since the pattern graph of the MKG can be regarded as a path, we can segment
the pattern graph according to the intermediate vertexes of this path, divide the pattern graph into two
partes, and obtain two pattern subgraphs. Próximo, to match the two pattern subgraphs, the matched results are
connected to obtaining the matched results of the pattern graph.

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

t
/

a
r
t
i
C
mi
–
pag
d

F
/

4
3
5
9
9
2
0
3
8
4
4
3
d
norte
_
a
_
0
0
1
5
3
pag
d

PG and

The detailed steps of the M-TBRE algorithm are shown in Algorithm 1. Primero, the intermediate vertex mid
of the pattern graph GP and the candidate vertex set candmid of mid
need to be obtained, as shown in lines
1–2. In line 3, pool and tempInfo represent the thread pool and the temporary result of the matching,
respectivamente. The number of threads in pool can be set according to the actual situation. Then the pattern
sub1
graph GP is divided into two sub-pattern graphs
as the
dividing point, and the two sub-pattern graphs are matched in the data graph GD. Traversing the candidate
vertex set candmid of mid
PG , as shown
to complete the matching of the sub-pattern graphs
ρ on each forward
in lines 4–27. For each element candmid[i] in candmid, we use the attribute constraint
De to obtain rpids,
borde
De and the current
De , as shown in lines 6–25. For each patient number rpid in rpids, rpid is taken as the attribute
PG , as shown in lines 14–21. tempInfo
constraint on the edge to complete the matching of
stores the partial matched result with rpid as the edge attribute constraint, as shown in lines 15–16. El
sub 2
thread pool submits subtasks MC-SEM and MC-FEM to complete the matching of
PG

which saves the common patient number information of the current forward edge

pe
De of candmid[i] to intersect the attribute constraint

PG with intermediate vertex

ρ on each successor edge

successor edge

PG and

pids
pe

pids
ae

sub 2

sub1

mid

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Data Intelligence

607

Fuzzy-Constrained Graph Pattern Matching in Medical Knowledge Graphs

The MC-SEM algorithm can complete the matching of the pattern subgraph

respectivamente, as shown in lines 19–20. The algorithm RM merges the matched results, as shown in line 28.
, rpid
and tempInfo respectively represent the pattern vertex to be matched, the candidate vertex of the pattern

PG , dónde

curr
Pv

curr
Dv

sub1

vertex

curr
Pv

to be matched, the attribute constraint value (patient number) of the edge, and the temporary

curr
Dv

matches vertex

result of the matching. If ver tex

does not have a successor edge, eso es,
PG is completed, and the matched
when the out-degree of
result when rpid is used as the attribute constraint on the edge is saved in tempInfo, such as Algorithm 2 es
curr
Pv
shown in lines 2–7. If vertex
has a successor edge, then traverse the
De includes rpid, the matching of pattern

es 0, the matching of the pattern subgraph

. When the attribute constraint

curr
Pv
ρ on

matches vertex

y
pids
ae

successor edge

ae
De of

pero

curr
Dv

curr
Pv

sub1

curr
Pv

vertex

ae
Pe . tailNode is recursively completed, as shown in lines 8–16.

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

t
/

a
r
t
i
C
mi
–
pag
d

F
/

4
3
5
9
9
2
0
3
8
4
4
3
d
norte
_
a
_
0
0
1
5
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

608

Data Intelligence

Fuzzy-Constrained Graph Pattern Matching in Medical Knowledge Graphs

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

t
/

The MC-FEM algorithm can complete the matching of the pattern su bgraph

PG . The processing process
of the MC-FEM algorithm is similar to that of the MC-SEM algorithm, except that MC-FEM completes the
matching of the pattern subgraph

PG according to the reverse depth-first search strategy.

sub 2

a
r
t
i
C
mi
–
pag
d

F
/

4
3
5
9
9
2
0
3
8
4
4
3
d
norte
_
a
_
0
0
1
5
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Data Intelligence

609

Fuzzy-Constrained Graph Pattern Matching in Medical Knowledge Graphs

The RM algorithm can complete the connection operation of the matching results of pattern subgraphs
sub1
PG . When a given value is used as an attribute constraint on all edges, and the flag bits
PG are both 1, then combining the matching results of

PG and

sub 2

sub1

PG and
representing the matching results of
PG and

sub 2

sub1

PG is a matching result of the pattern graph GP, such as lines 4–6 in Algorithm 4.

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

t
/

a
r
t
i
C
mi
–
pag
d

F
/

4
3
5
9
9
2
0
3
8
4
4
3
d
norte
_
a
_
0
0
1
5
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

sub1

sub 2

ρ =
pids
C D
1 2

{676,2384}

PG as an example, the attribute constraint

Ejemplo 3: In this example, GP and GD in Figure 1 are the pattern graph and the data graph, respectivamente.
Primero, to obtain intermediate vertex D of pattern graph GP and candidate vertex set candmid = {D2} of D. El
pattern graph GP is divided into pattern subgraph
PG which passes through vertexes A, B and C, y
which passes through vertexes E, F and G. The forward edge (C1, D2) y el
pattern subgraph
subsequent edge (D2, E1) of D2 have the same attribute constraint rpids = {676, 2384}. Taking the matching
on edg e (C1, D2) contains rpid = 2384,
de
and C1 matches C at the same time, so edge (C1, D2, GD)  (C, D, médico de cabecera). We can get (C1, D2, GD)  (C, D,
médico de cabecera) y (A2, B2, GD)  (A, B, médico de cabecera). The matching of
PG takes rpid = 2384 as the attribute constraint, y
the attribute constraint information of vertex A2
PG . In the same
way, we can get the matched results (D2, E1, GD)  (D, mi, médico de cabecera), (E1, F2, GD)  (mi, F, médico de cabecera), (F2, G3, GD)  (F,
GRAMO, médico de cabecera) de
PG have matched
resultados, so the diagnostic classification information of GP is the diagnostic classification information of
PG , and the patient number in GD is 2384. Finalmente, two matching subgraphs are obtained through the
M-TBRE algorithm. Msub1 = {Vm, Em, fv, fe}, where VM = {A2, B2, C1, D2, E1, F2, G3}, fe = {2384} and EM = {(A2,
B2), (B2, C1), (C1, D2), (D2, E1), (E1, F2), (F2, G3)}. Msub2 = {Vm, Em, fv, fe}, where VM = {A2, B3, C1, D2, E1, F2,
G3}, fe = {676} and EM = {(A2, B3), (B3, C1), (C1, D2), (D2, E1), (E1, F2), (F2, G3)}. The patients numbered 676
y 2384 can be used for reference when treating the patients corresponding to the pattern graph GP.

PG when rpid = 2384 is the attribute constraint on edge EP. Ambos

is the diagnosis classification result of

PG and

sub 2

sub1

5. EXPERIMENTS

En esta sección, we conduct experiments on two public MKGs. The details of these two datasets are shown
en mesa 1. We propose and implement the M-TBRE algorithm to complete the pattern matching of MKG.
Since the M-TBRE algorithm divides the pattern graph into two sub-pattern graphs, for different edge

610

Data Intelligence

Fuzzy-Constrained Graph Pattern Matching in Medical Knowledge Graphs

attribute constraint values rpid, the matching of these two sub-pattern graphs is delivered to the thread pool
as a subtask for execution. More or less the number of threads in the thread pool will affect the execution
results of the algorithm. We will set a different number of threads to measure the efficiency dynamics of
the M-TBRE algorithm. Además, to obtain more matched results, we introduce the fuzzy constraint,
which is a membership function for the age attribute constraint in the vertexes. The age attribute constraint
on the data graph vertexes does not need to be the same as the attribute constraints in the pattern graph
during matching, but only needs to go through the calculated result of the membership function and satisfy
the corresponding membership constraint value. Together with the M-TBRE algorithm, we have the Fuzzy-
M-TBRE algorithm. The Fuzzy-M-TBRE and M-TBRE algorithms can be compared to prove the effectiveness
of the introduced fuzzy constraints.

Mesa 1. The detail information of two datasets.

Dataset

Female-breast-cancer-2013a
Breastcancer-femalepatient-2016A

Vertices

10812
101221

Edges

20366
200845

Descripción

A graph about breast cancer patients
A graph about breast cancer patients

5.1 Experimental Settings and Implementation

The MKG used in the experiment is about breast cancer. Dataset-1 and dataset-2 are used to represent
the dataset Female-breast-cancer-2013a and the dataset Breastcancer-femalepatient-2016A, respectivamente.
Dataset-1 is composed of the physical condition information of 10,000 breast cancer patients, and dataset-2
is composed of 100,000 breast cancer patients. In our experiment, several pattern graphs are used, pero
these pattern graphs are similar to the pattern graph shown in Figure 1. Our membership function is only
for the age attribute of the vertex, and the membership constraint value is set to 3. Both M-TBRE and Fuzzy-
M-TBRE are implemented using Java and running on a PC with Intel(R) Core(TM) i9-10900F CPU @2.81G
GHz, 32 GB RAM and Windows 10 operating system.

5.2 Experimental Results and Analysis

5.2.1 Experiments on Execution Time

This experiment studies the execution time change when we set different thread numbers for the thread
pool used in the M-TBRE algorithm, and the algorithm completes the GPM. To prevent error interference,
the results in the experiment are the arithmetic mean after 10 carreras.

As shown in Figure 2 and Figure 3, the abscissa represents different pattern graphs, and the ordinate
represents the matching time of these pattern graphs. The M-TBRE-1 algorithm represents that the number
of threads in the thread pool in the M-TBRE algorithm is set to 1. Since the pattern graph in the MKG is a
camino, and the edge join strategy proposed in the ETOF-K algorithm does not take effect in the matching,
the performance of the ETOF-K algorithm and the M-TBRE-1 algorithm is almost the same on dataset-1 and
dataset-2. The reverse matching strategy of the NTSS algorithm is invalid in the matching process, but its

Data Intelligence

611

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

t
/

a
r
t
i
C
mi
–
pag
d

F
/

4
3
5
9
9
2
0
3
8
4
4
3
d
norte
_
a
_
0
0
1
5
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Fuzzy-Constrained Graph Pattern Matching in Medical Knowledge Graphs

caching mechanism avoids the double calculation of the same path, so the NTSS algorithm is better than
the ETOF-K algorithm and the M-TBRE-1 algorithm on dataset-1 and dataset-2.

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

Cifra 2. Matching time of different pattern graphs on Female-breast-cancer-2013a.

mi
d
tu
d
norte

t
/

a
r
t
i
C
mi
–
pag
d

F
/

4
3
5
9
9
2
0
3
8
4
4
3
d
norte
_
a
_
0
0
1
5
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 3. Matching time of different pattern graphs on Breastcancer-femalepatient-2016A.

Sin embargo, our M-TBRE-1 algorithm can be extended to multithreaded algorithms, such as the M-TBRE-2
algoritmo, M-TBRE-4 algorithm, M-TBRE-8 algorithm, which means that the number of threads in the thread
pool is set to 2, 4, y 8, respectivamente. As can be seen from Figure 2 y figura 3, the effect of the M-TBRE-2
algorithm has already exceeded the NTSS algorithm, which also proves the effectiveness of our proposed
M-TBRE algorithm. Además, Mesa 2 and Table 3 show the detailed execution time in seconds. Mesa 4
shows the comparison of the average execution time of these four algorithms on the two datasets. It can
be seen that on the two data sets, as the number of threads increases, the execution time of the algorithm
continues to decrease.

612

Data Intelligence

Fuzzy-Constrained Graph Pattern Matching in Medical Knowledge Graphs

Mesa 2. Execution time on the Female-breast-cancer-2013a dataset.

ETOF-K
NTSS
M-TBRE-1
M-TBRE-2
M-TBRE-4
M-TBRE-8

0.1625
0.1398
0.1832
0.1161
0.0869
0.0750

0.1933
0.1472
0.1869
0.1097
0.0709
0.0488

0.1742
0.1109
0.1516
0.0905
0.0488
0.0430

0.1659
0.1365
0.1807
0.1059
0.0595
0.0373

0.1743
0.1247
0.1654
0.0890
0.0550
0.0366

0.1601
0.0973
0.1560
0.0785
0.0459
0.0311

0.1742
0.1148
0.1535
0.0789
0.0448
0.0294

0.1633
0.1245
0.1700
0.0979
0.0512
0.0331

Mesa 3. Execution time on the Breastcancer-femalepatient-2016A dataset.

ETOF-K
NTSS
M-TBRE-1
M-TBRE-2
M-TBRE-4
M-TBRE-8

25.1406
20.7231
27.2807
16.2298
9.4020
5.8198

26.1477
21.6519
27.6337
16.3104
9.7056
5.9732

29.3101
19.9583
28.7748
16.1557
9.8746
6.0509

28.1559
20.4127
27.8562
16.3067
9.9239
6.0256

26.7859
19.8864
27.7634
16.6475
9.7943
5.9963

27.4765
22.7456
27.1356
16.5609
9.0300
6.1483

28.6518
19.7193
26.8715
16.4358
8.9316
6.1579

27.4800
21.5986
27.3600
16.7567
8.9685
6.1895

Mesa 4. The comparison of execution time on two datasets.

Dataset

M-TBRE-1

M-TBRE-2

M-TBRE-4

M-TBRE-8

Percentage

Female-breast-cancer-2013a
Female-breast-cancer-2013a
Female-breast-cancer-2013a
Breastcancer-femalepatient-2016A
Breastcancer-femalepatient-2016A
Breastcancer-femalepatient-2016A

0.1684
—
—
27.5845
—
—

0.0958
0.0958
—
16.4254
16.4254
—

—
0.0579
0.0579
—
9.4538
9.4538

—
—
0.0418
—
—
6.0452

43.11%
39.56%
27.81%
40.45%
42.44%
36.06%

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

t
/

a
r
t
i
C
mi
–
pag
d

F
/

4
3
5
9
9
2
0
3
8
4
4
3
d
norte
_
a
_
0
0
1
5
3
pag
d

•

For dataset-1, the execution time of the M-TBRE-2 algorithm is increased by 43.11% comparado con
the M-TBRE-1, and the execution time of the M-TBRE-4 algorithm is increased by 39.56% comparado
with the M-TBRE-2 algorithm, but compared with the M-TBRE-4 algorithm, the execution time of the
M-TBRE-8 algorithm is only increased by 27.81%. This is because dataset-1 itself is small in scale,
and the time spent on thread context switching and system state transitions occupies a large proportion
of the total time.
For dataset-2, its scale is larger, and the total execution time of the algorithm is also larger. The time
spent on thread context switching and system state transition takes up a relatively small proportion
of the total time. Por lo tanto, M-TBRE-8 in dataset-2 still increased by 36.06%.

For our proposed M-TBRE algorithm, as the number of threads increases, the execution speed is also
accelerating. But when the number of threads reaches a certain level, the increase in execution speed will
slow down, as shown by M-TBRE-8 in Figure 2. If the dataset is larger, or when the M-TBRE algorithm
submits more subtasks, this slowing downtrend will become slower. Compared with the M-TBRE-4 algorithm,

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Data Intelligence

613

Fuzzy-Constrained Graph Pattern Matching in Medical Knowledge Graphs

the M-TBRE-8 algorithm in dataset-1 increased by 27.81%, while in dataset-2, the M-TBRE-8 algorithm
increased by 36.06% compared with the M-TBRE-4 algorithm.

5.2.2 Experiments on Fuzzy Constraints

This experiment studies the change in the number of matching subgraphs when our M-TBRE algorithm
introduces fuzzy constraints. The Fuzzy-M-TBRE algorithm is the algorithm after M-TBRE introduces fuzzy
constraints. Since our Fuzzy-M-TBRE algorithm can get all the matched results of the pattern graph, podemos
compare the changes in the total number of matches before and after the introduction of fuzzy constraints.

As shown in Figure 4 and Figure 5, the abscissa represents different pattern graphs, and the ordinate
represents the number of matched subgraphs. On dataset-1 and dataset-2, for the same pattern graph, el
Fuzzy-M-TBRE algorithm returns more matched results than the M-TBRE algorithm. Each matched subgraph
corresponds to a breast cancer patient. When treating the patient corresponding to the pattern graph, please
refer to the treatment plan of the corresponding patient in these matched subgraphs. Introducing fuzzy
constraints can get more treatment options. Por lo tanto, it is necessary to introduce fuzzy constraints into the
M-TBRE algorithm.

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

t
/

a
r
t
i
C
mi
–
pag
d

F
/

4
3
5
9
9
2
0
3
8
4
4
3
d
norte
_
a
_
0
0
1
5
3
pag
d

Cifra 4. The number of matched subgraphs of different pattern graphs on Female-breast-cancer-2013a.

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 5. The number of matched subgraphs of different pattern graphs on Breastcancer-femalepatient-2016A.

614

Data Intelligence

Fuzzy-Constrained Graph Pattern Matching in Medical Knowledge Graphs

6. CONCLUSIÓN

en este documento, we put forward the problem of GPM in MKGs, and provide related definitions. In order to
solve this problem, an M-TBRE algorithm is proposed, which divides the pattern graph into several pattern
subgraphs, uses multi-threaded bidirectional routing to complete the matching of the pattern subgraphs,
and then merges the matching results. Además, fuzzy constraints are introduced to obtain more matching
subgraphs. Each matched subgraph corresponds to a past patient. The patients corresponding to these
matched subgraphs have the same physical condition as the patient corresponding to the pattern graph, entonces
the treatment plan of the patients corresponding to these matched subgraphs can be used for reference in
the treatment of the patient corresponding to the pattern graph. In this way, better and more effective
treatment plans can be developed for patients corresponding to the pattern graph. We conduct verification
experiments on the M-TBRE algorithm on two public MKG datasets. Experimental results show that our
proposed M-TBRE algorithm has better performance. Además, the necessity of introducing fuzzy
constraints is also demonstrated, which leads to the outperformance of the Fuzzy-M-TBRE algorithm. En el
future, we will further research and improve the M-TBRE algorithm, and study the dynamic graph pattern
matching problem in MKGs oriented to the dynamics of pattern graph content.

EXPRESIONES DE GRATITUD

This work has been supported by the National Natural Science Foundation of China under grants
62076087 & 61906059 and the Program for Changjiang Scholars and Innovative Research Team in University
(PCSIRT) of the Ministry of Education of China under grant IRT17R32.

The first author would like to thank his wife Jun Zhang, his parents and friends during his fight with lung

adenocarcinoma. “I leave no trace of wings in the air, but I am glad I have had my flight.”

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

t
/

a
r
t
i
C
mi
–
pag
d

F
/

4
3
5
9
9
2
0
3
8
4
4
3
d
norte
_
a
_
0
0
1
5
3
pag
d

CONTRIBUCIONES DE AUTOR

All authors including L. li (lilei@hfut.edu.cn), X. Du (dlx4339@163.com), z. zhang (zanzhang@hfut.edu.
cn), and Z. tao (zctao@ustc.edu.cn) took part in writing the paper. Además, l. Li designed the algorithm
and experiments, and provided the funding; X. Du designed and conducted experiments, and analyzed the
datos; z. Tao analyzed the data.

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

REFERENCIAS

[1] Mamá, X., Wu, J., Xue, S., et al.: A comprehensive survey on graph anomaly detection with deep learning. IEEE

Transactions on Knowledge and Data Engineering (2021)

[2] Wu, J., Zhu, X., zhang, C., et al.: Bag constrained structure pattern mining for multi-graph classification. IEEE

Transactions on Knowledge and Data Engineering 26(10), 2382–2396 (2014)

Data Intelligence

615

Fuzzy-Constrained Graph Pattern Matching in Medical Knowledge Graphs

[3] Hu, J., Ferguson, A.: Global graph matching using diffusion maps. Intelligent Data Analysis 20(3), 637–654

(2016)

[4] tian, y., patel, J.: TALE: A tool for approximate large graph matching. En: Proceedings of the IEEE 24th

[5]

[6]

[7]

[8]

International Conference on Data Engineering, páginas. 963–972 (2018)
Liu, F., Xue, S., Wu, J., et al.: Deep learning for community detection: progress, challenges and opportunities.
En: Proceedings IJCAI, páginas. 4981–4987 (2020)
Su, X., Xue, S., Liu, F., et al.: A comprehensive survey on community detection with deep learning. IEEE
Transactions on Neural Networks and Learning Systems, 1–21 (2021)
Admirador, w., Wang, X., Wu, y.: Finding experts by graph pattern matching. En: Proceedings of the IEEE 29th
International Conference on Data Engineering, páginas. 1316–1319 (2008)
Admirador, w., Wang, X., Wu, y.: Incremental graph pattern matching. ACM Transactions on Database Systems
38(3), 1–47 (2013)

[9] Kan, A., Golab, l., et al.: Compact group discovery in attributed graphs and social networks. Información

Procesando & Management 57(2), 102054 (2020)

[10] Ryota, S., Hitoshi, h., et al.: Social Group Discovery Extracting Useful Features using Multiple Instance

Aprendiendo. Journal of Japan Society for Fuzzy Theory & Intelligent Informatics 28(6), 920–931 (2016)

[11] Chikhaoui, B., shimula, J., Wang, S.: Community Mining and Cross-Community Discovery in Online Social
Networks. En: Proceedings of the International Conference on Network-Based Information Systems, páginas. 176–
187 (2020)

[12] Admirador, w., li, J., et al.: Graph pattern matching: from intractable to polynomial time. Proceedings of the VLDB

Endowment 3(1–2), 264–275 (2010)

[13] Liu, GRAMO., Zheng, K., et al.: Multi-constrained graph pattern matching in large-scale contextual social graphs.

En: Proceedings of the IEEE 31st International Conference on Data Engineering, páginas. 351–362 (2015)

[14] Liu, GRAMO., li, l., Wu, X.: Multi-fuzzy-constrained graph pattern matching with big graph data. Intelligent Data

Análisis 24(4), 941–958 (2020)

[15] Ullmann, J.: An Algorithm for Subgraph Isomorphism. Revista de la ACM 23(1), 31–42 (1976)
[16] Cordella, l., Foggia, et al.: A (Sub) Graph Isomorphism Algorithm for Matching Large Graphs. IEEE

transactions on pattern analysis and machine intelligence 26(10), 1367–1372 (2004)

[17] Tong, h., Faloutsos, C., et al.: Fast best-effort pattern matching in large attributed graphs. En: Actas de
the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, páginas. 737–746
(2007)

[18] cheng, J., Zeng, X., Yu, J.: Top-k graph pattern matching over large graphs. En: Proceedings of the IEEE 29th

International Conference on Data Engineering, páginas. 1033–1044 (2013)

[19] cheng, J., Yu, J., et al.: Fast Graph Pattern Matching. En: Proceedings of the IEEE 24th International Conference

on Data Engineering, páginas. 913–922 (2008)

[20] Song, C., Ge, T., Chen, C., Wang, J.: Event pattern matching over graph streams. Proceedings of the VLDB

Endowment 8(4), 413–424 (2014)

[21] Admirador, w., li, J., luo, J., Broncearse, Z., Wang, X., Wu, X.: Incremental graph pattern matching. En: Actas de la

ACM SIGMOD International Conference on Management of Data, páginas. 925–936 (2011)

[22] yan, X., Yu, PAG., Han, J.: Graph indexing: a frequent structure-based approach. En: Actas de la 2004

ACM SIGMOD international conference on Management of data, páginas. 335–346 (2004)

[23] Shasha, D., Wang, J., Giugno, r.: Algorithmics and applications of tree and graph searching. En: Actas
of the twenty-first ACM SIGMOD-SIGACT-SIGART symposium on Principles of database systems, páginas. 39–52
(2002)

616

Data Intelligence

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

t
/

a
r
t
i
C
mi
–
pag
d

F
/

4
3
5
9
9
2
0
3
8
4
4
3
d
norte
_
a
_
0
0
1
5
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Fuzzy-Constrained Graph Pattern Matching in Medical Knowledge Graphs

[24] Afrati, F., Fotakis, D., Ullman, J.: Enumerating subgraph instances using map-reduce. En: Actas de la

IEEE 29th International Conference on Data Engineering, páginas. 62–73 (2013)

[25] shao, y., Cual, B., Chen, l., Mamá, l., Yao, J., Xu, NORTE.: Parallel subgraph listing in a large-scale graph. En: Proceed-

ings of the 2014 ACM SIGMOD International Conference on Management of Data, páginas. 625–636 (2014)
[26] Huang, J., Venkatraman, K., Abadi, D.: Query optimization of distributed pattern matching. En: Actas

del 2014 IEEE 30th International Conference on Data Engineering, páginas. 64–75 (2014)

[27] Demirci, METRO.: Graph-based shape indexing. Machine Vision and Applications 23(3), 541–555 (2012)
[28] Choudhury, S., Holder, l., Chin, GRAMO., Rayo, A., Beus, S., Feo, J.: StreamWorks: a system for dynamic graph
buscar. En: Proceedings of the 2013 ACM SIGMOD International Conference on Management of Data,
páginas. 1101–1104 (2013)

[29] Henzinger, METRO., Henzinger, T., Kopke, PAG.: Computing simulations on finite and infinite graphs. En: Actas

of the IEEE 36th Annual Foundations of Computer Science, páginas. 453–462 (1995)

[30] Mamá, S., Cao, y., Admirador, w., Huai, J., Wo, T.: Capturing topology in graph pattern matching. ACM Transactions

on Database Systems 39(1), 4:1–4:46 (2014)

[31] Liu, GRAMO., Liu, y., Zheng, K., Liu, A., li, Z., Wang, y., zhou, X.: MCS-GPM: Multi-Constrained Simulation Based
Graph Pattern Matching in Contextual Social Graphs. IEEE Transactions on Knowledge and Data Engineering
30(6), 1050–1064 (2018)

[32] Liu, GRAMO., li, l., Liu, GRAMO., Wu, X.: Social Group Query Based on Multi-Fuzzy-Constrained Strong Simulation.

Transactions on Knowledge Discovery from Data 16(3), 1–27 (2021)

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

t
/

a
r
t
i
C
mi
–
pag
d

F
/

4
3
5
9
9
2
0
3
8
4
4
3
d
norte
_
a
_
0
0
1
5
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Data Intelligence

617

Fuzzy-Constrained Graph Pattern Matching in Medical Knowledge Graphs

AUTHOR BIOGRAPHY

Lei Li received his Bachelor’s degree from Jilin University, Changchun, Porcelana,
en 2004, his Master’s degree from the Memorial University of Newfoundland,
Calle. John’s, Canada, en 2006, and his Ph.D. degree from Macquarie University,
Sídney, Australia, en 2012. He is currently an Associate Professor at Key
Laboratory of Knowledge Engineering with Big Data (the Ministry of Education
of China), Intelligent Interconnected Systems Laboratory of Anhui Province
(Hefei University of Technology), and School of Computer Science and
Information Engineering, Hefei University of Technology, Hefei, Porcelana. Su
research interests include data mining, social computing and graph computing.
He is a senior member of IEEE.
ORCID: 0000-0002-5374-7293

Xun Du received the Bachelor’s degree in 2019, and Master’s degree in 2022
from Hefei University of Technology, Porcelana. His research interests are in
graph computing and social computing. Actualmente, he works as a software
development engineer at Honor Terminals LTD.
ORCID: 0000-0002-7020-5883

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

t
/

a
r
t
i
C
mi
–
pag
d

F
/

4
3
5
9
9
2
0
3
8
4
4
3
d
norte
_
a
_
0
0
1
5
3
pag
d

Zan Zhang received his Ph.D. degree in Computer Science from Hefei
University of Technology, Porcelana, en 2018. He is currently a lecturer at the
Hefei University of Technology. His research interests include data mining
and knowledge engineering.
ORCID: 0000-0002-6383-1683

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

618

Data Intelligence

Fuzzy-Constrained Graph Pattern Matching in Medical Knowledge Graphs

Zhenchao Tao was born in Wuhu, Anhui, Porcelana, en 1985. He received the
METRO. METRO. degree in oncology from Anhui Medical University, en 2012. De
2012 a 2015, he was a Resident, and from 2015 a 2017, he was an Attending
Physician at the Department of Radiotherapy, Anhui Cancer Hospital. Desde
2017, he has been an Attending Physician with the Department of
Radiotherapy, The First Affiliated Hospital of University of Science and
Technology of China. He published five articles as first author and participated
in three provincial and national projects.
ORCID: 0000-0001-8142-9164