Jyri Pakarinen∗ and David T. Yeh†
∗Department of Signal Processing
and Acoustics
Helsinki University of Technology
P.O. Box 3000
FI-02015 TKK Finland
jyri.pakarinen@tkk.fi
†Center for Computer Research
in Music and Acoustics
Department of Music
Universidad Stanford
stanford, California 94305-8180 EE.UU
dtyeh@ccrma.stanford.edu
A Review of Digital
Techniques for Modeling
Vacuum-Tube Guitar
Amplifiers
Although semiconductor technologies have dis-
placed vacuum-tube devices in nearly all fields of
electronics, vacuum tubes are still widely used in
professional guitar amplifiers. A major reason for
this is that electric-guitar amplifiers are typically
overdriven, eso es, operated in such a way that the
output saturates. Vacuum tubes distort the signal in
a different manner compared to solid-state electron-
circuitos integrados, and human listeners tend to prefer this. Este
might be because the distinctive tone of tube am-
plifiers was popularized in the 1950s and 1960s by
early rock and roll bands, so musicians and listeners
have become accustomed to tube distortion. Alguno
studies on the perceptual aspects of vacuum-tube
and solid-state distortion have been published (p.ej.,
Hamm 1973; Bussey and Haigler 1981; Santo 1994).
Despite their acclaimed tone, vacuum-tube
amplifiers have certain shortcomings: large size and
weight, poor durability, high power consumption,
high price, and often poor availability of spare parts.
De este modo, it is not surprising that many attempts have
been made to emulate guitar tube amplifiers using
smaller and cheaper solid-state analog circuits (p.ej.,
Todokoro 1976; Sondermeyer 1984). The next step
in the evolution of tube-amplifier emulation has
been to simulate the amplifiers using computers
and digital signal processors (DSP).
A primary advantage of digital emulation is that
the same hardware can be used for modeling many
different tube amplifiers and effects. When a new
model is to be added, new parameter values or
program code are simply uploaded to the device.
Además, amplifier models can be implemented
as software plug-ins so that the musician can
connect the guitar directly to the computer’s sound
card, record the input tracks, add effects and/or
virtual instruments, and then compile the song as
a CD or upload it to the Internet. This is especially
useful for home studios and small ad hoc recording
sessions, because it eliminates several tedious
tasks of acoustic recording, such as setting up the
amplifier and recording equipment, selecting a
microphone position, finding a recording room, etc..
This article attempts to summarize real-time
digital techniques for modeling guitar tube ampli-
fiers. Although a brief overview was presented in
Pakarinen (2008), to the authors’ knowledge, allá
are no previous works that attempt a comprehensive
survey of the topic. Because this topic is relatively
new and commercially active, most of the reference
material can be found in patents rather than aca-
demic publications. Judging from the large number
of amateur musicians and home-studio owners, como
well as the huge number of discussion threads on
Internet forums, this topic is potentially interesting
for a wide spectrum of readers. De este modo, a conscious
choice has been made to try to survey the modeling
techniques at an abstracted level, without delving
into the underlying mathematics or electric circuit
análisis.
This review is organized into four sections. Nosotros
first describe the sources of the nonlinearities in
guitar amplifier circuits. Entonces, we review published
methods for modeling the linear stages of guitar
amplifiers. The heart of this survey is the review
of methods for nonlinear modeling. Finally we
Computer Music Journal, 33:2, páginas. 85–100, Verano 2009
C(cid:2) 2009 Instituto de Tecnología de Massachusetts.
Pakarinen and Yeh
85
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
3
2
8
5
1
8
5
5
3
0
8
/
C
oh
metro
j
.
.
2
0
0
9
3
3
2
8
5
pag
d
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
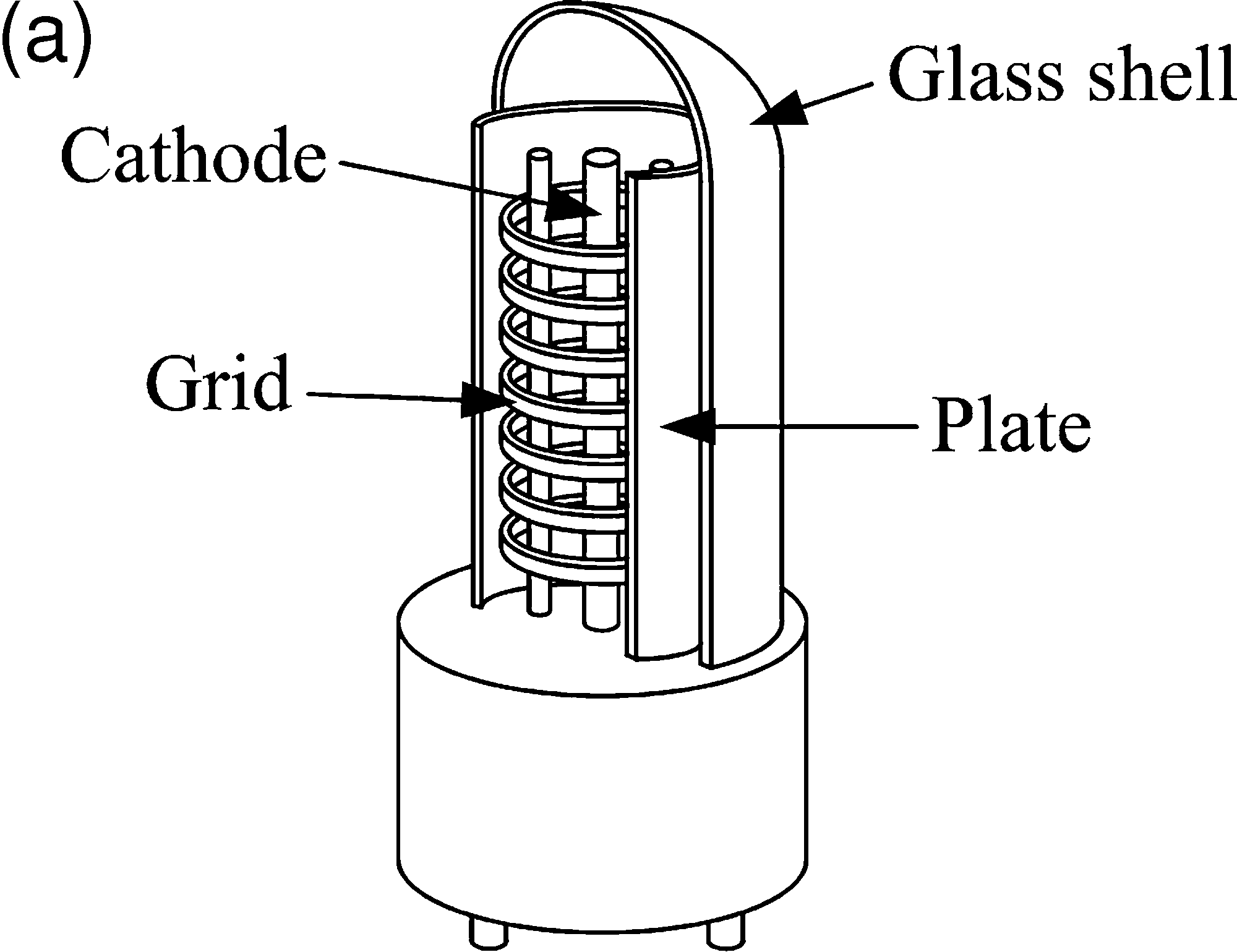
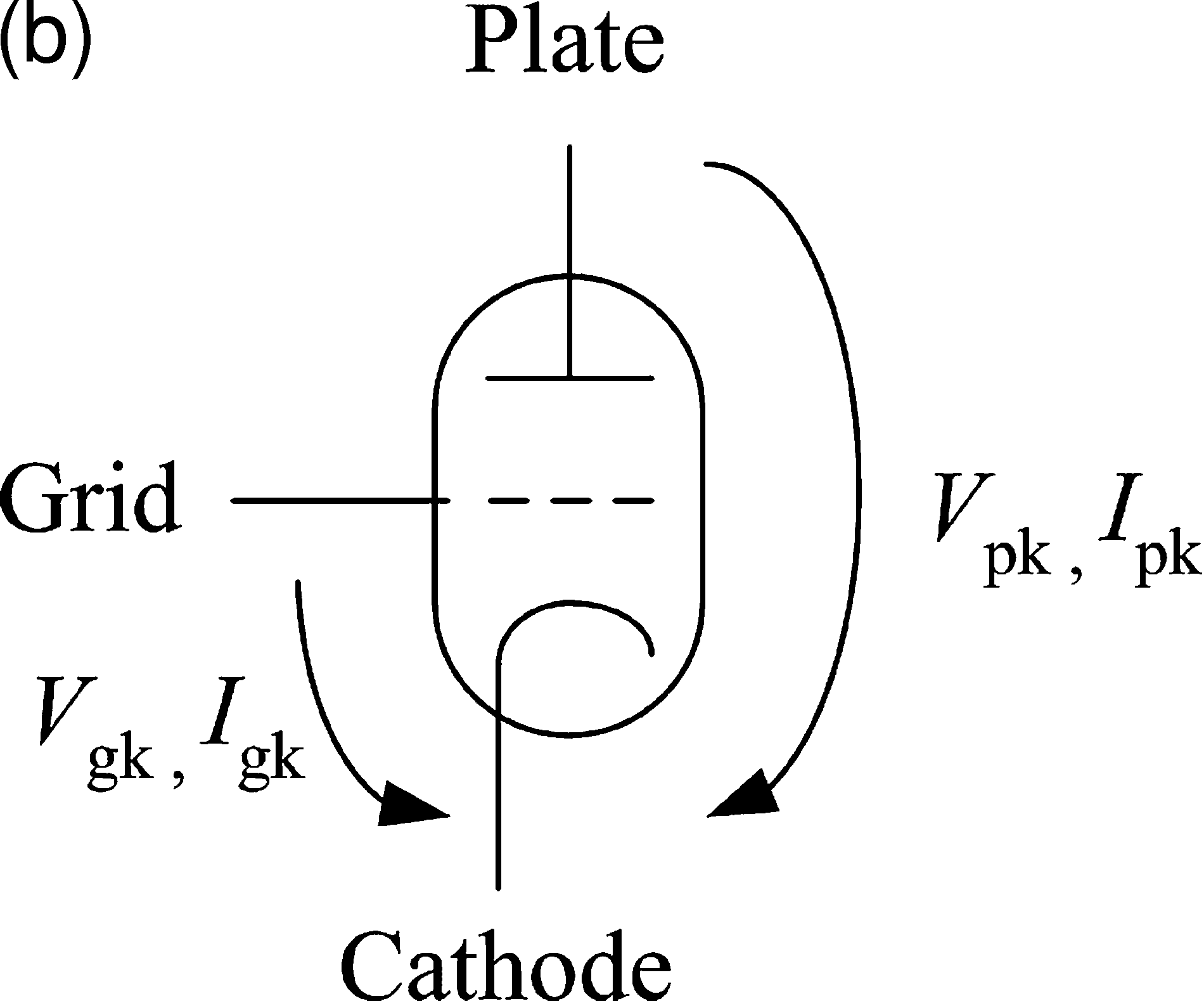
Cifra 1. Físico
construction (a) y
electrical representation
(b) of a triode tube. (Cifra
(a) is adapted from
en.wikipedia.org/wiki/Vacuum tube.)
mention various other guitar-amplifier related
technologies and present conclusions.
Vacuum-Tube Amplifiers
The purpose of this section is to present an overview
of the operation of vacuum-tube amplifiers and to
illustrate the complex nature of their important
nonlinearities. An overview of vacuum tubes used
in audio applications can be found in Barbour
(1998), and a detailed tutorial on classic vacuum-
tube circuits is provided in Langford-Smith (1954).
The physical principles governing the operation of
vacuum tubes are reviewed in Spangenberger (1948).
Excellent Internet articles discussing the design of
guitar tube amplifiers can be found online (p.ej., en
www.aikenamps.com and www.ax84.com).
A typical guitar tube amplifier consists of a
preamplifier, a tone-control circuit (es decir., tone stack),
a power amplifier, and a transformer that couples
to the loudspeaker load. The preamplifier magnifies
the relatively weak signal from the magnetic
guitar pickups and provides buffering so that the
pickup response is not altered by the amplifier
circuitry. The preamplifier is usually realized with
triode tubes. The tone stack provides a typical V-
shaped equalization for compensating the pickup’s
resonance at mid-frequencies, and it gives the
user additional tonal control. The power amplifier
boosts the signal so that it is powerful enough
to drive a loudspeaker. In the so-called all-tube
guitar amplifiers, both the pre- and power-amplifier
circuits use tubes instead of transistors in amplifying
the signal. Typically, these amplification circuits
contain one or more tube stages, a saber, circuito
blocks that consist of a tube connected to resistive
and capacitive (RC) componentes.
Vacuum Tubes
Vacuum tubes, or thermionic valves, were invented
in the early 1900s for amplifying low-level volt-
age signals. Structurally, they consist of two or
more electrodes in a vacuum enclosed in a glass
or metal shell. A two-terminal device is a diode,
commonly used for signal rectification. Three-
terminal devices are known as triodes and are
primarily used in preamplifier circuits. Four- y
five-terminal devices (tetrodes and pentodes, re-
spectively) are used mainly for power amplification
purposes to drive a loudspeaker, Por ejemplo.
The operation of vacuum tubes is analogous to
water flow on a slope. Primero, the electrode termed
the cathode is heated, and the process known as
thermionic emission acts like a pump that forms
a pool of electrons at the top of a hill. A second
terminal called the plate (or anode) is at the bottom
of a slope. Electrons will flow from the cathode to
the plate depending upon the relative height of the
plate, which is controlled by the voltage applied
lo. Note that because a pump is at the cathode,
electrodes can never flow backward from the plate
to the cathode even though the plate may be raised
uphill of the cathode. This describes the rectification
behavior of a diode tube.
The triode, illustrated in Figure 1, introduces
a third terminal called the grid between the two
terminals. With the plate downhill of the cathode,
the grid is like a raised barrier in the slope that
limits the flow of electrons from the cathode to
the plate. If this barrier controlled by the grid is
high enough, it stops the electron flow completely.
This water-flow analogy motivates the British term
referring to vacuum tubes as “valves.”
86
Computer Music Journal
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
3
2
8
5
1
8
5
5
3
0
8
/
C
oh
metro
j
.
.
2
0
0
9
3
3
2
8
5
pag
d
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Nonlinear Amplification
The plate-to-cathode current is a nonlinear function
of both the grid-to-cathode and plate-to-cathode
voltages: Ipk = f (Vgk,Vpk). Note that a change in
voltage on the grid causes a change in current
flow between the cathode and plate. Amplification
occurs when the change in current is converted to
a change in voltage by a large-valued load resistor.
Although amplification is nominally linear around
a central operating voltage known as the bias, en
extreme signal levels, the amplified output will
saturate. When the grid-to-cathode voltage Vgk is
very small, current flow cuts off sharply. Very large
Vgk causes the plate voltage to approach that of the
cathode again, limiting the current and resulting in
a nonlinearly saturating characteristic. To find the
full nonlinear transfer characteristic from input to
output requires the solution of a nonlinear system
of implicit equations, because in a typical amplifier
circuito, Vpk depends on Ipk and vice versa.
In guitar-amplifier circuits, the operating point
(inclinación), defined in terms of current through the tube
device, is often set by a resistor connecting the
cathode terminal to ground. The resistor introduces
feedback into the circuit, and its value influences
the shape of the input-output curve and determines
the offset about which the signal varies. Amplifier
designs often include an AC bypass capacitor to
recover gain in the passband lost to the feedback, pero
this introduces memory effects into the nonlinear
characteristic.
Dynamic Operation
Capacitive elements exist throughout the tube cir-
cuit, preventing it from being accurately modeled as
a static waveshaper (a memory-less nonlinearity). Si
large transients are present in the input signal—as is
often the case with the electric guitar—the grid-to-
cathode voltage could become positive, and current
Igk will flow from the grid to the cathode, eventu-
ally causing the device to cut off, introducing an
undesirable phenomenon called blocking distortion
(Aiken 2006). También, because a grid capacitor is often
used to block the direct-current (corriente continua) component
of the input signal, the grid current Igk charges the
capacitor and dynamically varies the bias point of
the tube, leading to dynamically varying transient
distortion characteristics.
The cathode bypass capacitor retains memory of
the tube bias and responds slowly to rapid changes in
signal amplitude, causing signal history–dependent
changes in distortion characteristics. Además,
there exist parasitic capacitances in the tube itself
owing to the close proximity of its electrodes. El
dominant effect, Miller capacitance, is a low-pass
filter resulting from the amplified capacitance
between plate and grid; this is discussed more
thoroughly in Aiken (1999a).
Amplifier Power Stage
The power amplifier can use either a single-ended
or push–pull topology. In the single-ended topology,
the signal is amplified in a single vacuum tube. Este
tube conducts plate-to-cathode current during the
whole signal cycle (Class A biasing). Parallel tube
stages can also be added if more output power is
required.
The push–pull topology, perhaps more commonly
usado, consists of two identical sets of output tubes
driven in opposite phases. The output of one set
is inverted and combined with the other through
transformer coupling. When a push-pull power
amplifier is operated in Class A biasing, ambos
tubes are actively amplifying during the entire
signal cycle. Alternativamente, Class AB biasing can
be used, where one tube handles the signal for
positive signal excursions while the other tube is
in a low current quiescent state, and vice versa for
negative excursions. Leaving the quiescent tube
in a low-power state gives Class AB operation
higher power efficiency, but it may also introduce
crossover distortion as the tubes transition between
quiescent and amplifying states. También, because Class
AB amplifiers draw current from the power supply
proportional to the signal amplitude, large input-
voltage bursts can cause a momentary decrease
in the supply voltage. This effect, called sagging,
introduces further dynamic range compression
(Aiken 1999b).
Pakarinen and Yeh
87
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
3
2
8
5
1
8
5
5
3
0
8
/
C
oh
metro
j
.
.
2
0
0
9
3
3
2
8
5
pag
d
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
The power amplifier is coupled to a guitar
loudspeaker through an output transformer, cual
introduces additional distortion and hysteresis (es decir.,
an increasing signal is distorted differently than a
decreasing signal). Además, the loudspeaker
itself can also contribute significant nonlinear
behavior both acoustically and electrically.
En conclusión, the complicated interdependen-
cies and dynamic nonlinearities in vacuum-tube
amplifiers make their accurate physical modeling
extremely demanding. Como resultado, approximate
models simulating only some of the most noticeable
phenomena have been developed by the amplifier-
modeling community.
Modeling of Linear Filters in Amplifiers
To better understand nonlinear distortion modeling
later in this article, we will first consider the
simulation of the linear part of the amplifier, a saber,
the tone stack. The characteristics of linear filtering
greatly influence the tonal quality of electric-guitar
amplifiers. A menudo, switches will be provided to allow
a guitarist to choose between different component
values in a circuit to vary its frequency response.
Certain frequency responses are associated with
particular genres or styles of music and are often
associated with specific guitar-amplifier models.
The unique quality of the tone stack of the
electric-guitar amplifier is significant enough to
warrant several attempts in the patent literature
to invent methods to make a digital tone-stack
modelo. The tone-stack configurations in guitar
amplifiers are all very similar. Amplifiers are mainly
differentiated by the component values of the circuit
and the mapping from the controls to these values.
The tone stack typically has up to three knobs
controlling the gains of three bands, loosely called
bass, middle, and treble. The middle band is a notch
in the frequency response.
Digital Filtering
A system that introduces no new frequencies
to the signal is linear and can be characterized
completely by its impulse response. The impulse
response describes how the system reacts to a
unit impulse. The frequency representation of this
impulse response is known as the frequency response
and describes the gain or attenuation applied to the
input signal at various frequencies. Once the impulse
response is known, p.ej., on the computer in digital
forma, convolution with this impulse response will
recreate the effect of this filter.
There are two general methodologies of modeling
linear systems in guitar circuits. The black-box
system identification approach views the system
as an abstract linear system and determines coeffi-
cients replicating the system. A white-box approach
derives a discretized frequency response transfer
function for the system based upon knowledge of its
linear, constant-coefficient differential equations.
Because the linear systems in guitar amplification
are often parametrically controlled (p.ej., by poten-
tiometers in tone or volume controls), the modeling
approach must be parametric.
Black-Box Approach
In the black-box approach, the linear system is
excited with a test signal that covers all frequencies
de interés. This signal is usually a frequency sweep
of a low-amplitude sinusoidal input or broadband
white noise. A set of measurements is obtained
for various settings of the parameters, which may
be multivariate as for the low, mid, and high tone
knobs of the guitar tone stack. Various techniques
are well known for extracting a frequency response
from these measurements (Foster 1986; Abel and
Berners 2006).
Once the impulse response is found, it can be
used directly as a finite impulse response (FIR)
filter to simulate the measured system. Because the
original systems are typically low-order infinite im-
pulse response (IIR) sistemas, it is computationally
advantageous to identify IIR filters corresponding
to the measured response. The digital filter system
identification process optimizes either the error in
impulse response (time-domain identification) o
frequency response (frequency-domain identifica-
ción) over the set of digital filter coefficients, given
a desired filter order. Preferably, optimizing over the
88
Computer Music Journal
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
3
2
8
5
1
8
5
5
3
0
8
/
C
oh
metro
j
.
.
2
0
0
9
3
3
2
8
5
pag
d
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
impulse response captures phase information and is
a simpler, more robust formulation.
Because the parameterized filter coefficients are
usually implemented as lookup tables, the patents
covering linear modeling of amplifier components
generally concern methods to reduce table size and
storage costs in a practical implementation. El
Fender tone-stack patent (Curtis, Chapman, y
Adams 2001) covers an active filter topology that
replicates the range of frequency responses of a
tone stack. Assuming this filter structure, sistema
identification comprises obtaining coefficients for
various knob settings by manual tuning to match the
resulting frequency responses. The mapping from pa-
rameters to coefficients is compressed for implemen-
tation by sparse sampling (a suggested five points per
knob) and 3D linear interpolation of the coefficients.
The Gustafsson et al. (2004) patent also de-
scribes multidimensional linear interpolation for
the compression of mapping from parameters to
filter coefficients. This approach improves upon
the accuracy of classical linear interpolation and
reduces the number of entries needed in the table
by warping each parameter dimension using non-
linear mapping functions prior to interpolated table
lookup. The patent also describes the decomposition
of the resulting filter into a linear combination of
Kautz basis filters, a particular form of second-order
digital filter, for stability in implementation. Este
is a special case of the general technique in digital
signal processing to ensure numerically stable filter
implementations by decomposition into second-
order sections. More information concerning Kautz
filters in audio applications can be found in Paatero
and Karjalainen (2003).
A gray-box approach incorporating some insight
into the structure of the circuit, described in a
patent application by Gallien and Robertson (2007),
divides the tone stack into a parallel bank of two
first-order filters, one high-pass and one low-pass,
which are weighted and added. The filters are
cleverly devised approximate equivalent circuits
comprising resistors and capacitors that allow for
implementation of the parameter mapping. El
equivalent circuits are simulated and compared to
a simulation of the full circuit to derive component
values for the equivalent circuits and the filter
weights so that the resulting response matches that
of the actual circuit. los circuitos, which are defined
using capacitors and resistors, are taken into the
discrete time domain by the bilinear transform for
digital implementation.
En resumen, black-box approaches decide on a
particular filter structure, and then they decide on
coefficients for that structure to match the response
of the target system. Ad hoc mappings from parame-
ter space to coefficient space parameterize the filter.
White-Box Approach
Yeh and Smith (2006) propose an analytical approach
to the full tone-stack circuit and suggest that the
resulting parameter update equations are not pro-
hibitively complicated. This approach derives the
full third-order transfer function with no approxi-
mations for the filter by symbolic circuit analysis.
Because the coefficients are described as algebraic
functions of the parameters, this method is fully
parametric. Yeh, Abel, and Smith (2007) applied this
approach to filters based upon operational amplifiers.
The tone stack for the Boss DS-1 distortion pedal
was implemented by interpreting the analog filter as
a weighted sum of high-pass and low-pass functions
and implementing the analogous structure digitally.
Nonlinear Modeling
Nonlinear signal processing is at the heart of
tube-amplifier modeling. Aquí, we review static
waveshaping with memoryless nonlinearities,
which is a fundamental technique in digital-
distortion implementations, and several categories
of methods to reintroduce memory into the
nonlinearity: ad hoc nonlinear filters based upon
the circuit signal path, analytical approaches,
and nonlinear filters derived from solving circuit
equations using numerical methods.
Static Waveshaping
The most straightforward method for obtaining
signal distortion with digital devices is to apply an
Pakarinen and Yeh
89
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
3
2
8
5
1
8
5
5
3
0
8
/
C
oh
metro
j
.
.
2
0
0
9
3
3
2
8
5
pag
d
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 2. Construction of
the digital effects device
described in Araya and
Suyama (1996). El
distortion block consists of
three identical
nonlinearities and suitable
scaling coefficients. El
amount of distortion can
be varied by changing the
scaling coefficients.
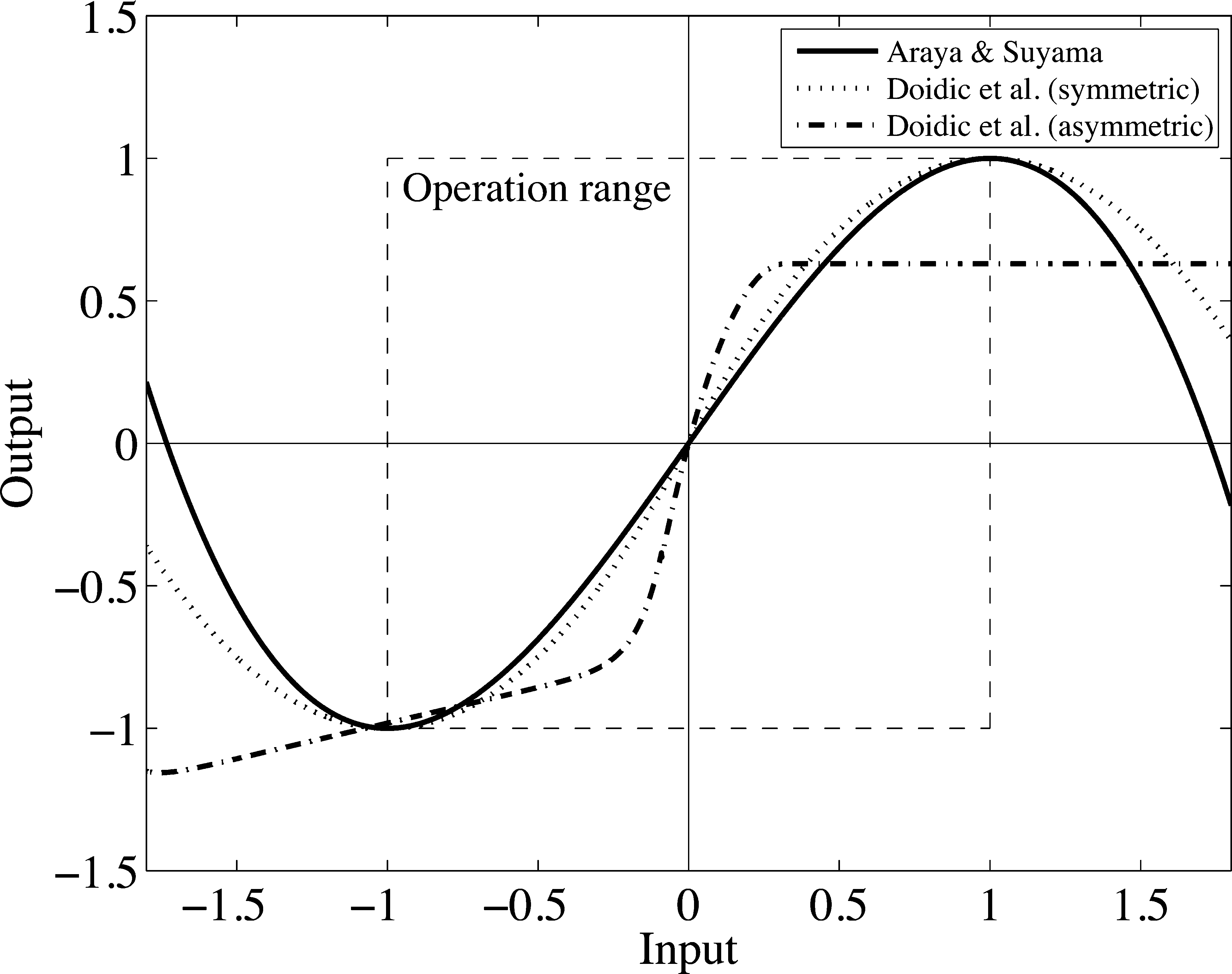
Cifra 3. Solid line:
input–output plot of the
nonlinear function of
Ecuación 1 used in Araya
and Suyama (1996); dotted
line: the input-output plot
of the symmetric
nonlinearity in Equation 2,
used in Doidic et al.
(1998). Dash-dotted line:
the asymmetric
nonlinearity in Equation 3,
also used in Doidic et al.
(1998). The allowed
operation range is denoted
with dashed lines.
Cifra 2
instantaneous nonlinear mapping from the input
variable to the output variable. This type of timbre
alteration is called waveshaping (Arfib 1979; Le
Brun 1979). If the mapping does not change in time,
this method is called static waveshaping. An early
Yamaha patent (Araya and Suyama 1996) describe
a digital guitar effects device using this technique.
This is illustrated in Figure 2.
En figura 2, the signal from the instrument
is first fed to the distortion block through an
analog-to-digital (A/D) converter (including an
analog amplifier for setting a suitable input level).
The distortion effect is obtained by feeding the
signal into a nonlinear function through a scaling
coeficiente. The nonlinear function used in Araya
and Suyama (1996) is of the form
(cid:3)
(cid:2)
1 − x2
3
y = 3x
2
(1)
where x is the input (bounded between [−1, 1]) and y
is the output signal. The nonlinear curve produced by
Ecuación 1 is illustrated in Figure 3 with a solid line.
Because the curve is fairly linear in the operation
range of the device, the scaling and nonlinearity is
applied three times in cascade (es decir., sequentially) para
obtaining more distortion. After leaving the distor-
tion block in Figure 2, the signal is fed to a collection
of linear effects (p.ej., chorus or reverberation) y
finally to a digital-to-analog (D/A) converter. Araya
and Suyama also suggest adding a digital equalizer
between the A/D converter and the distortion.
More nonlinear functions are suggested in Doidic
et al. (1998), including a symmetric function of the
forma
F (X) = (|2X| − x2) sign(X)
(2)
where sign(X) = 1 if x > 0, and sign(X) = −1 other-
wise. Alternativamente, a hard-clipping function or a
piecewise-defined asymmetric static nonlinearity of
Cifra 3
the form
F (X) = - 3
4
+ 1
3
(cid:4)
1 − [1 − (|X| − 0.032847)]12
(cid:5)
(|X| − 0.032847)
+ 0.01,
for − 1 ≤ x < −0.08905
f (x) = −6.153x2 + 3.9375x,
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
for − 0.08905 ≤ x < 0.320018,
f (x) = 0.630035, for 0.320018 ≤ x ≤ 1
and
(3)
can be used. Figure 3 illustrates the input-output
curve defined by Equation 2 using a dotted line and
the curve defined by Equation 3 using a dash-dotted
line. It must be noted that the original patent (Doidic
et al. 1998) has some typographical errors in the
equation of the asymmetric nonlinearity, and thus
it does not produce the input–output relationship
illustrated in Figure 3.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
3
2
8
5
1
8
5
5
3
0
8
/
c
o
m
j
.
.
2
0
0
9
3
3
2
8
5
p
d
.
.
.
90
Computer Music Journal
As displayed in Figure 3, all the input–output
curves are fairly linear for small-amplitude signals,
that is, signal values near the origin. This obviously
means that the smaller the signal is, the less it
is distorted. A patent by Toyama (1996) uses a
signal-dependent scaling procedure with a nonlinear
function to also distort small-amplitude signals.
This technique can add harmonic content to various
signals regardless of their amplitude levels, although
it does not resemble the behavior of vacuum-tube
distortion. A further Yamaha patent (Shibutani
1996) describes a computationally simple method
for creating piecewise-linear distortion functions by
branching the signal via various scaling coefficients
and adding the output. Graphically, this means that
each of the scaling coefficients determines a slope
for a linear segment in the input–output plot.
Another simple digital distortion circuit, “man-
tissa fuzz,” is described in Massie (1996). This exotic
algorithm uses a simple bitshifing operation in dis-
torting the input signal. Although the mantissa-fuzz
technique is computationally extremely efficient, it
seems virtually impossible to match the distortion
curve to a desired nonlinearity.
M ¨oller, Gromowski, and Z ¨olzer (2002) describe
a technique to measure static, nonlinear transfer
curves from all stages of a guitar amplifier. Their
goal is to mimic the nonlinearities and filters in
the signal path of the amplifier, approximating the
nonlinearities as static, the filters as linear, and
neglecting loading between stages. Santagata, Sarti,
and Tubaro (2007) introduce a model of the triode
preamplifier with an added hard-clipping feature.
This model uses an iterative technique for evaluating
the nonlinear tube equations, but it does not
incorporate the capacitive effects of the triode stage;
therefore, it can be considered as computing the
implicitly defined waveshaping curve “on the fly,”
based on parameters measured from an actual tube.
Lookup-Table Nonlinearity
Preceding the patent by Araya and Suyama (1996),
there had already been some studies on how to obtain
digital distortion effects. Kramer (1991) introduced
a simple method for obtaining arbitrary nonlinear
distortion in real time using a lookup table. This
means that instead of applying a nonlinear algebraic
function, such as the one in Equation 1, the system
reads the input–output relation from a pre-stored
table, for example, a digitized version of Figure 3.
The advantage of this technique is that it is easier
to obtain a desired type of input-output relation,
because the designer can freely draw the input–
output curve for the lookup table.
On the other hand, a high-resolution lookup
table would consume an excessive amount of
memory, so low-resolution lookup tables and
interpolation algorithms must be used. Also, run-
time modification of the nonlinearity becomes
difficult. Digidesign implemented this type of
lookup-table waveshaping in their early software
synthesizer Turbosynth in 1989.
In an early study by Sullivan (1990), a simple non-
linear function or a lookup table is used in distorting
the output of a synthesized guitar string. In fact,
the nonlinear function in Equation 1 can be seen
as a scaled version of the one suggested in Sullivan
(1990). Sullivan’s article also introduces a system for
simulating the acoustic feedback between synthe-
sized guitar strings, amplifier, and a loudspeaker.
Oversampling
Nonlinear signal processing blocks are known to
expand the bandwidth of the incoming signal,
which in a DSP system can cause aliasing if the
bandwidth of the output exceeds the Nyquist
frequency (i.e., half the sampling rate). An amplifier
model can distort harmonic signals such as a
guitar tone and produce many new harmonics in
the output that, through aliasing into the audio
range, are no longer harmonically related to the
original tone. The resulting noisy, “dissonant”
sound owing to aliasing is characteristic of low-
cost digital implementations of strong distortions
and is typically mitigated through running the
distortion algorithm at an oversampled rate, which
is computationally expensive.
In the late 1990s, the Line 6 Company patented a
digital guitar amplifier, i.e., an amplifier and effects
emulator combined with a loudspeaker (Doidic et al.
1998). This device used a sampling rate of 31.2 kHz
for most of the signal processing, but it included
Pakarinen and Yeh
91
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
3
2
8
5
1
8
5
5
3
0
8
/
c
o
m
j
.
.
2
0
0
9
3
3
2
8
5
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4. Tube-amplifier
modeling scheme, as
suggested in the Line 6
TubeTone patent (Doidic
et al. 1998). The
nonlinearity is evaluated
at a higher sampling rate
to avoid aliasing.
Multichannel output can
be used, for example, in
conjunction with stereo
effects.
an eight-times oversampling circuit for evaluating
a static nonlinearity at 249.6 kHz, thus attenuating
the aliased distortion components. This straightfor-
ward technique, named TubeTone Modeling, was
used in several commercially successful Line 6
digital guitar-amplifier emulators.
Figure 4 illustrates the system described in Doidic
et al. (1998). Here, the digital signal is first fed to
a collection of preamplifier effects—that is, effects
that are typically located between the guitar and
amplifier, such as a noise gate, compressor, or a
wah-wah. Next, eight-times oversampling with
linear interpolation is applied to the signal, and it
is fed to a nonlinearity. After the nonlinearity, the
signal is lowpass-filtered using an antialiasing FIR
filter, and it is downsampled back to the sampling
rate of 31.2 kHz.
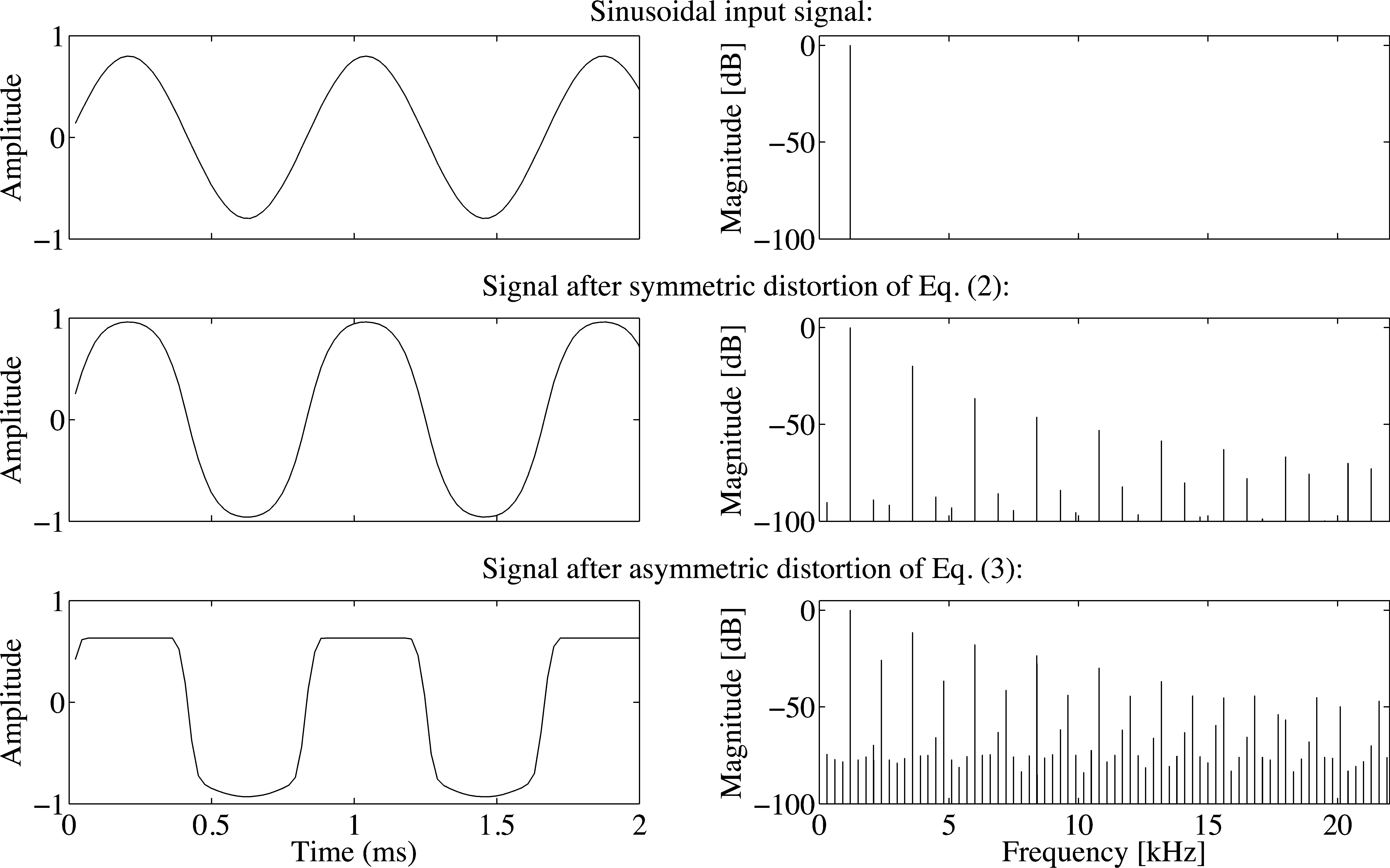
Figure 5 visualizes what happens to the waveform
and spectrum of a sinusoidal input signal when
distorted by the nonlinear Equations 2 and 3.
The top row illustrates the waveform (left) and
spectrum (right) of a 1.2-kHz sinusoidal signal with
an amplitude of 0.8. The middle row shows the
signal after the symmetric distortion defined by
Equation 2. As expected, the symmetric distortion
creates a “tail” of odd harmonics in the output
signal spectrum. For frequencies above the Nyquist
limit (a sampling frequency of 44.1 kHz was used
here), the harmonics fold back to the audio band,
resulting in frequency components that are not in
any simple harmonic relation with the input tone.
The bottom row shows the input signal after the
heavy-clipping asymmetric distortion defined by
Equation 3. As can be seen in the lower right graph,
the asymmetric distortion creates even and odd
harmonic components. The upper components are
again aliased back to the audio band, resulting in an
inharmonic spectrum.
In Doidic et al. (1998), the output signal from the
distortion is fed to a collection of linear effects, such
as tremolo, chorus, or delay. If headphones or line
output are used, a simple low-pass filter can also be
applied for simulating the effect of the loudspeaker
cabinet. Finally, the signal drives a loudspeaker (or
several loudspeakers, if for example stereo effects
are used) after a D/A conversion and amplification.
Customized Waveshaping
An interesting method for obtaining a highly
customized type of distortion has been introduced
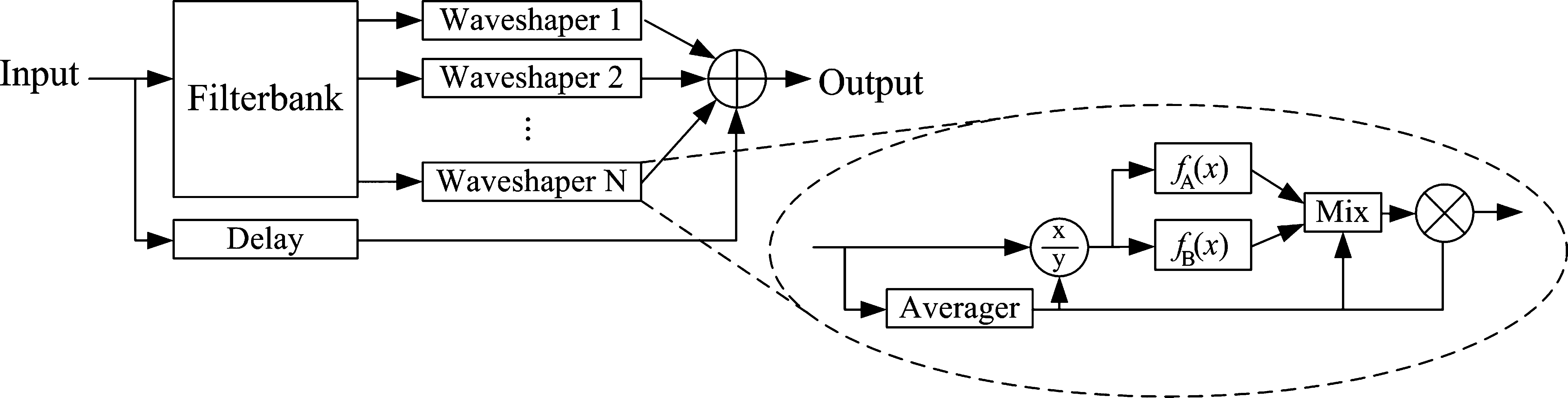
in Fern ´andez-Cid and Quir ´os (2001). This technique,
illustrated on the left of Figure 6, decomposes the
input signal into frequency bands using a filterbank,
and it then applies a different static nonlinearity
for each band separately. Thus, only narrow-band
signals are inserted to the nonlinear waveshapers,
and the perceptually disturbing intermodulation
distortion is minimized. The authors call this tech-
nique multiband waveshaping. The delay imposed
on the direct signal in Figure 6 equals the delay
caused by the filterbank, so that the signal phase is
correctly preserved after the final summation.
Fern ´andez-Cid and Quir ´os (2001) suggest using
Chebychev polynomials as the nonlinearities. These
polynomials are a special type of function allowing
the designer to individually set the amplitude of
each harmonic distortion component, provided
that the input signal is purely sinusoidal with
unity amplitude. Furthermore, using this type of
polynomial approximation, aliasing can be avoided
for sinusoidal input signals, because the designer
can simply choose not to synthesize the highest
harmonics. The right part of Figure 6 illustrates
the construction of a single Chebychev-based
waveshaper used in Fern ´andez-Cid and Quir ´os,
where the overall signal level is set between [–1, 1]
prior to the evaluation of the nonlinearity. Dynamic
nonlinearities can be imitated by using two different
polynomials ( fA(x) and fB(x) in the right part of
92
Computer Music Journal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
3
2
8
5
1
8
5
5
3
0
8
/
c
o
m
j
.
.
2
0
0
9
3
3
2
8
5
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 5. Signal waveforms
(left pane) and the
corresponding frequency
spectra (right pane) for
sinusoidal input-output
signals. Top row: a
sinusoidal input signal
with a frequency of 1.2
kHz; middle row: the input
signal after the symmetric
distortion defined by
Equation 2; bottom row:
the input signal after the
heavy-clipping asymmetric
distortion defined by
Equation 3.
Figure 6) in parallel, and varying their mix ratio
according to the signal level of the corresponding
band. Finally, the original dynamics of the signal
are restored by multiplying the polynomial output
with the signal level, as shown in the right part of
Figure 6. The authors claim that the waveshapers
perform well, even though their input is not a
sinusoid but rather a narrowband signal.
Patents by Jackson (2003) and Amels (2003)
present trigonometric functions for creating static
waveshapers where the distortion component levels
can be set by the designer. Schimmel and Misurec
(2007) implemented and analyzed static nonlinear-
ities using piecewise-linear approximations of the
nonlinear input-output curves. These three meth-
ods use oversampling to suppress aliasing. Also,
a polynomial approximation of a static nonlinear-
ity without aliasing suppression is presented in
Schimmel (2003).
Ad Hoc Nonlinear Filters
Because the assumption that the nonlinearities
are memory-less does not hold for describing the
behavior of real tube amplifiers, researchers have
proposed various dynamic waveshapers, namely,
nonlinearities that change their shape according to
the input signal or some system-state variables.
An early digital system for emulating a tube
amplifier was outlined by Pritchard (1991). He
suggested using two nonlinear distortion blocks
with a digital equalization unit in between. Ideally,
the first distortion block would have a high-pass
filter with the cutoff frequency controlled by the
input-signal polarity, and an asymmetric static
nonlinearity for producing mainly even harmonics.
The second distortion block would generate both
even and odd harmonics and emulate the sagging
effect of the power amplifier using a dynamic
nonlinearity. Aliasing problems, however, are not
addressed by Pritchard.
A more detailed description of a dynamic tube-
amplifier model has been discussed in a Yamaha
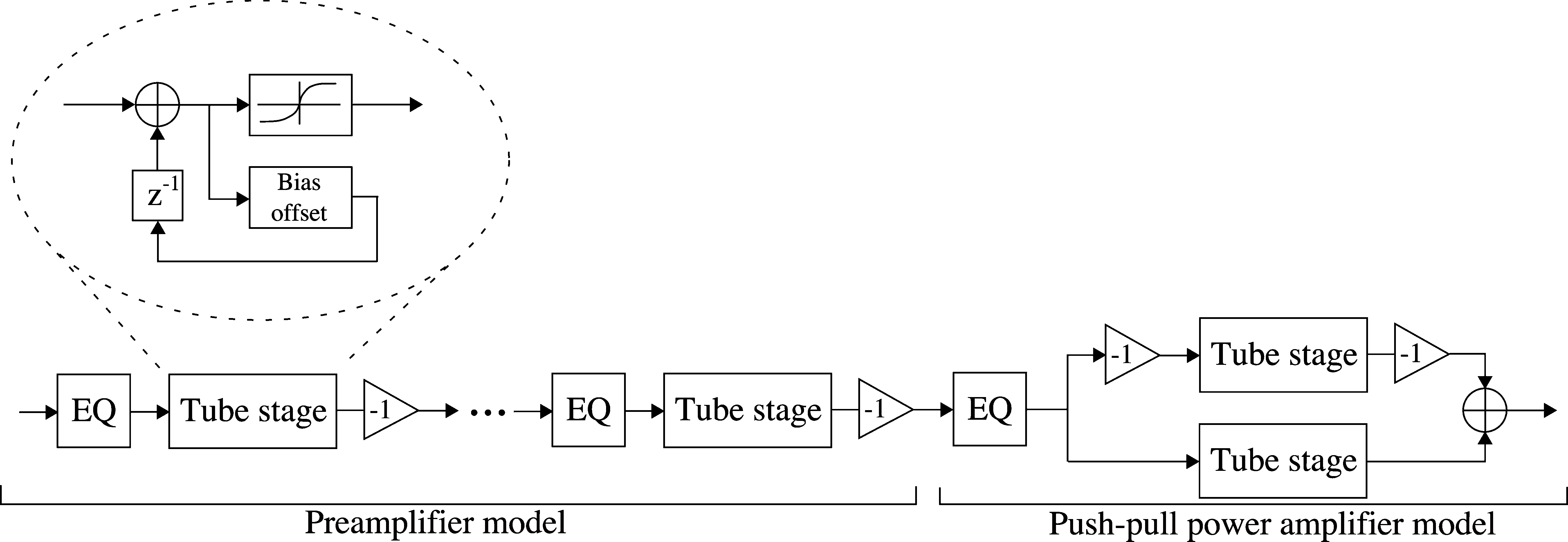
patent (Kuroki and Ito 1998). There, a single tube
stage is again modeled using a lookup table, but
the DC offset of the input is varied according to
the input-signal envelope. The authors give the
impression that this bias variation would be caused
by grid capacitor charging owing to grid current,
although a more realistic explanation would be the
variation of the cathode voltage owing to a change in
plate current. A tube preamplifier can be simulated
by connecting several tube-stage models in cascade.
Pakarinen and Yeh
93
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
3
2
8
5
1
8
5
5
3
0
8
/
c
o
m
j
.
.
2
0
0
9
3
3
2
8
5
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 6. Construction of
the multiband waveshaper
distortion, described in
Fern ´andez-Cid and Quir ´os
(2001). The overall
structure is illustrated in
the left half of the figure,
and the signaling inside an
individual waveshaper is
depicted in the right half.
In the right half, the
output of the averager can
be seen as a measure of the
overall signal level.
Sign inversion is applied between tube stages for
modeling the phase-inverting behavior of a real tube
stage. Note that, owing to the dynamic nonlineari-
ties (i.e., signal history-dependent DC offsets), the
preamplifier stages cannot be combined as a single
equivalent lookup table. A push–pull power ampli-
fier can be simulated by connecting two tube-stage
models in parallel and reversing the sign of the other
branch. With suitable DC-offset values, crossover
distortion can be emulated, if desired. The system
proposed in Kuroki and Ito is illustrated in Figure 7.
Another dynamic model of a guitar preamplifier
has been presented in Karjalainen et al. (2006). This
model assumes that the plate load of the tube stage is
constant and resistive, so that the tube nonlinearity
simplifies to a mapping from the grid voltage Vgk
to plate voltage Vp. This curve is measured from the
tube by shorting the cathode to ground and varying
the grid voltage. Grid current is also measured as
a function of the grid voltage. These curves are
combined in a single precomputed Vgk-to-Vp table.
Bias variation is simulated using a feedback loop,
as in Kuroki and Ito (1998). The filtering effect
caused by the grid resistor and Miller capacitance
is modeled with a low-pass filter at grid input,
while a high-pass filter emulates the interstage
DC-blocking filter. Three tube-stage models are
used in series and connected to a loudspeaker model
via an equalizer. A minimum-phase FIR filter is
used as a loudspeaker model.
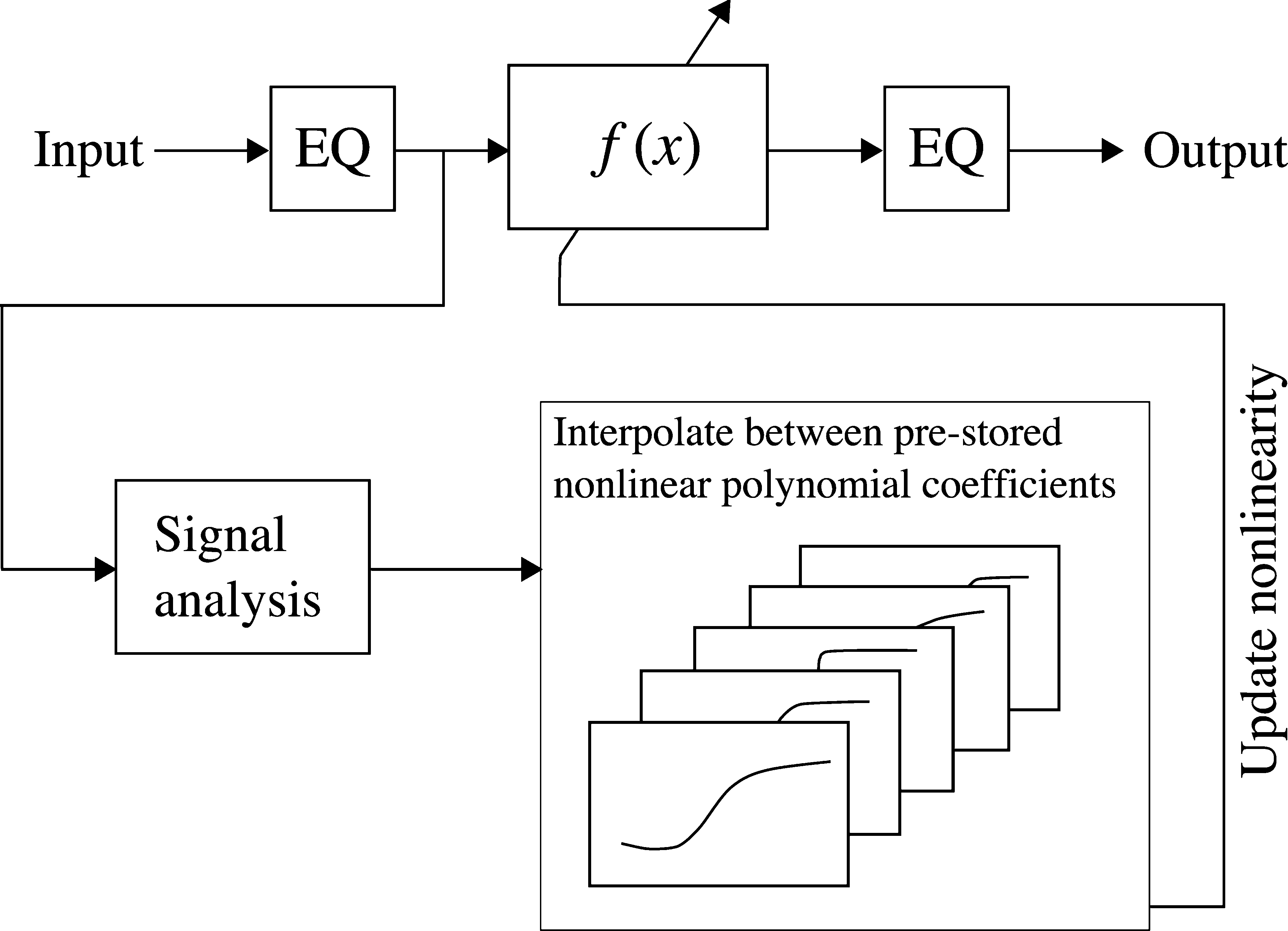
An interesting system-identification-based ap-
proach has been presented by Gustafsson et al.
(2004), the founders of the Swedish company Soft-
ube AB (producers of Amp Room software). Here,
the dynamic nonlinearity is simulated by feeding
the signal through a nonlinear polynomial function
and varying the polynomial coefficients according
to the input signal. Figure 8 illustrates this. The
signal-analysis block estimates the signal energy
for the last few milliseconds, and it checks whether
the input signal is increasing or decreasing. Next,
the polynomial coefficients are interpolated from
a set of pre-stored coefficient values according to
the signal energy. The pre-stored coefficients are
obtained from measured tube data using system-
identification techniques (see, e.g., Nelles 2000).
The hysteresis effect can be simulated by using
a different set of polynomial coefficients for in-
creasing and decreasing input signals. The authors
suggest implementing the static nonlinearities with
Chebychev polynomials to avoid aliasing, and also
because the accuracy of the Chebychev polynomial
approximation is highest near the signal extrema
(i.e., around ±1, near saturation).
Analytical Methods
Several methods exist for analyzing a nonlinearity
with memory. These are based upon Volterra series
theory and can be used to implement nonlinear
audio effects.
Volterra Series
The Volterra series expansion (Boyd 1985) is a
representation of systems based upon a nonlinear
expansion of linear systems theory. Analogous to
convolution with the impulse response vector of a
linear system, the Volterra series is a multidimen-
sional convolution with nonlinear system-response
matrices. Whereas in linear systems the impulse re-
sponse fully characterizes the system and allows its
output to be predicted given an input, Volterra sys-
tems are characterized by special functions, called
kernels, that correspond to the multidimensional
impulse response of the nonlinear terms. It can also
94
Computer Music Journal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
3
2
8
5
1
8
5
5
3
0
8
/
c
o
m
j
.
.
2
0
0
9
3
3
2
8
5
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7. A dynamic tube
amplifier model as
described in a Yamaha
patent (Kuroki and Ito
1998). The model of a
single tube stage consists
of a lookup table, added
with a signal-dependent
DC-offset. An entire
preamplifier can be
simulated by connecting
tube-stage models in
cascade with a phase
inversion in between. A
push–pull power amplifier
is simulated by connecting
the tube stage models in
parallel and in opposite
phase.
be regarded as a Taylor series expansion with the
polynomial terms replaced by multidimensional
convolution, accounting for the memory associated
with different orders of nonlinearity.
Volterra series have been used extensively to
model nonlinear acoustic systems including loud-
speakers. In particular, they can linearize low-order
distortion circuits and loudspeakers in real time (e.g.,
Katayama and Serikawa 1997). Farina, Bellini, and
Armelloni (2001) and Abel and Berners (2006) used
a technique to identify parameters for a subclass
of Volterra systems based upon a frequency-sweep
excitation of the system. A similar technique is used
in the Nebula effects sampler by Acustica Audio
(www.acusticaudio.net), which allows the user to
create soft-saturating models of several audio effects
based on the system response. H `elie (2006) applied
a specific Volterra series expansion to create a real-
time effect that includes the third-order nonlinear-
ities of the Moog ladder filter. Schattschneider and
Z ¨olzer (1999) report an efficient implementation of
a type of Volterra series and a system-identification
technique to derive parameters for their
model.
Although Volterra series are a theoretically
valid black-box method for simulating various
nonlinearities, real-time emulation of strongly
saturating distortion poses a problem. This is
because Volterra series involve a convolution of a
dimension equal to the order of the nonlinearity
for each nonlinear term in the model, making the
number of coefficients and computational cost
grow rapidly with increasing order of nonlinearity.
Because guitar distortion often involves very strong,
clipping-type nonlinearities, Volterra series are not
the preferred technology for this application.
Dynamic Convolution
Kemp (2006) has patented a black-box method,
dynamic convolution, for nonlinear system analysis
and emulation. The basic idea of this technique is
simple: several impulses with different amplitudes
are inserted into the distorting system during the
analysis, and the resulting impulse responses are
recorded. System emulation is carried out using con-
volution, so that the amplitude of each input sample
is detected and compared to the set of impulse
amplitudes used in the analysis. Once the near-
est measured impulse is found, the corresponding
impulse response is used in evaluating the convo-
lution. Because this procedure is applied for each
input sample, the convolution coefficients change
according to the input signal level during run-time.
Although a promising technique, dynamic con-
volution has some limitations. First, the amount
of stored data can be prohibitively large if a high-
amplitude resolution is used. Secondly, dynamic
convolution can be used for modeling static nonlin-
earities, but it fails to model dynamic nonlinearities,
namely, systems for which the shape of the nonlin-
earity changes due to the input signal (Berners and
Abel 2004). Note that the nonlinear convolution
introduced by Farina, Bellini, and Armelloni (2001)
can be seen as the Volterra representation of the
dynamic convolution method.
Circuit Simulation-Based Techniques
The preceding techniques have all treated the
distortion device as a nonlinear black box, possibly
with memory. Techniques based upon solving the
Pakarinen and Yeh
95
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
3
2
8
5
1
8
5
5
3
0
8
/
c
o
m
j
.
.
2
0
0
9
3
3
2
8
5
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 8. A dynamic
amplifier stage model,
described in Gustafsson et
al. (2004). The nonlinear
function f(x) is varied each
time sample according to
the input signal
characteristics. Chebychev
polynomials are suggested
for implementing the
nonlinearities. A complete
amplifier can be simulated
by connecting several
amplifier stage models in
cascade.
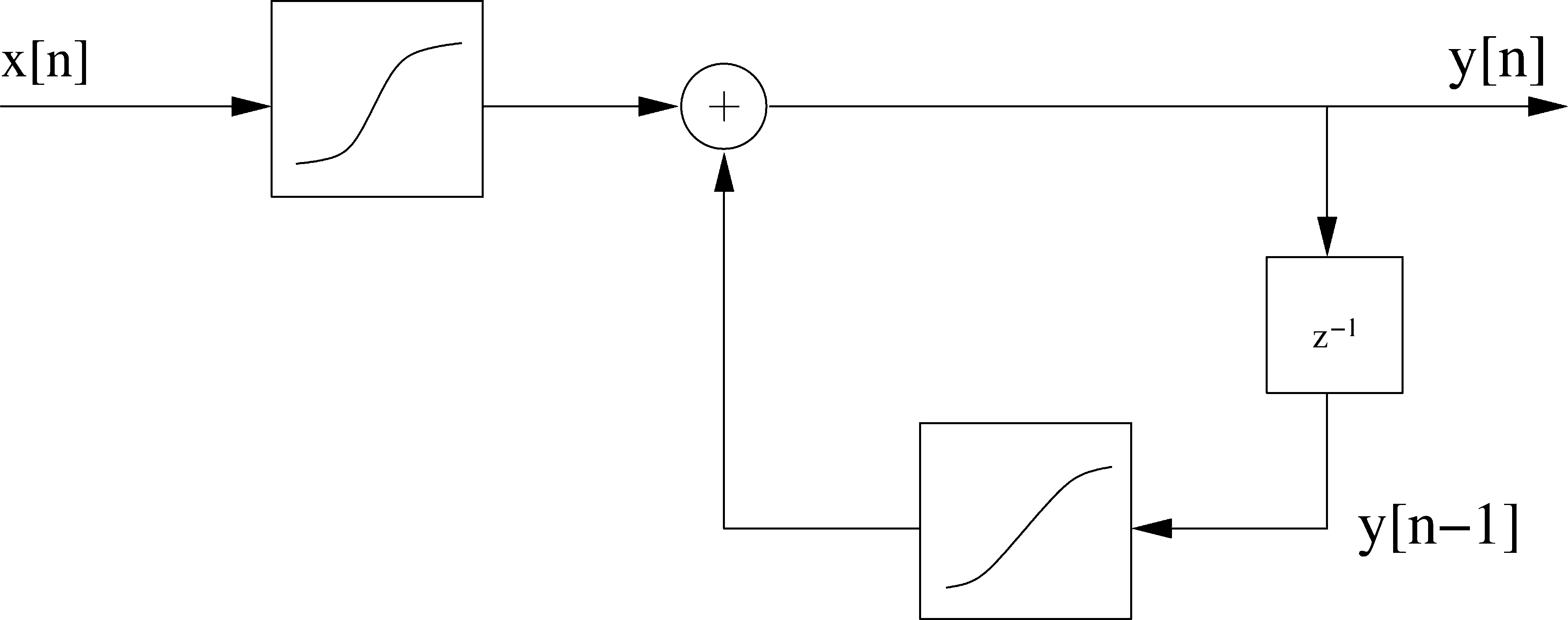
Figure 9. A single stage of
the nonlinear digital Moog
filter (Huovilainen 2004).
The nonlinearity is
embedded within the
digital filter feedback loop.
Equivalently, this is a
nonlinearity with
embedded memory,
derived by discretizing the
circuit equations.
where N is the number of rows or columns of the
square matrix G, it has been found empirically that
for typical circuits a sparse LU solve is O(N1.4),
owing to the sparse nature of the matrix equations
(White and Sangiovanni-Vincentelli 1987). As com-
putational power increases and researchers model
more complex circuits, MNA offers a simple way to
construct circuit schematic-based audio effects.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
ordinary differential equations (ODEs) that describe
the behavior of the circuit have also been attempted.
/
/
/
3
3
2
8
5
1
8
5
5
3
0
8
/
c
o
m
j
.
.
2
0
0
9
3
3
2
8
5
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Transient Modified Nodal Analysis
Integrated circuit design involves the engineer-
ing of analog and digital systems based upon
highly nonlinear integrated circuit devices such as
metal-oxide-semiconductor field-effect transistors
(MOSFETs) and bipolar transistors. Verification of
the designs depends critically on the accuracy of
numerical circuit simulators, e.g., the Simulation
Program with Integrated Circuit Emphasis (SPICE;
Vladimirescu 1994). SPICE uses transient modified
nodal analysis (MNA) with nonlinear components in
audio circuit simulation. MNA solves the equations
describing circuit behavior in matrix form, GV = I,
where V is a vector containing the node voltages;
I is a vector containing the current contributed by
the nonlinear devices, capacitors, and sources; and
G is the conductance matrix representing the linear
current-to-voltage relation of each component in the
circuit. MNA is particularly convenient, because
the computer can easily derive the circuit equations
given a circuit schematic.
The matrix G is typically sparse, because it
encodes the connections between the components
of the circuit, which are typically connected to just
a few neighbors. MNA requires the solution of this
equation, usually by LU decomposition. Although
the complexity of a general matrix solve is O(N3),
Custom, Simplified Ordinary Differential
Equation Solvers
For commercial digital audio effects, the simplest
acceptable implementation is desired, because
companies boast of their capability to provide
a multitude of real-time effects simultaneously.
To this end, several researchers have developed
effects based on simplifying the ODE model of the
circuit and trading off accuracy for efficiency in the
numerical ODE solvers.
Huovilainen reported nonlinear models of the
Moog ladder filter (2004), as well as operational
transconductance amplifier (OTA)-based all-pass
filters (2005), by deriving a minimal ODE from the
circuit equations and solving it using Forward-Euler
numerical integration. The result is a nonlinear
recursive filter structure with a nonlinearity embed-
ded in the filter loop. Huovilainen’s nonlinear Moog
filter model is illustrated in Figure 9. A simplified
version of this model has been presented in V ¨alim ¨aki
and Huovilainen (2006).
Yeh et al. (2008) extended this approach to
strongly clipping diode-based distortion circuits
and found that for circuits in general, implicit ODE
methods such as Backward Euler or Trapezoidal
Rule are needed to avoid numerical instability at
typical sampling rates. Implicit methods require the
96
Computer Music Journal
numerical solution of an implicit nonlinear equation
by iterative fixed-point methods, a general subclass
of which are the Newton–Raphson methods. Yeh
and Smith (2008) also extended this approach to
the triode preamplifier using a state-space approach
with a memory-less nonlinearity (the vacuum-tube
Ipk expression itself), demonstrating that implicit
methods transform the ODEs for audio circuits into
a recursive state-space structure with a multidimen-
sional static nonlinearity embedded in the feedback
loop. This approach accounts for both the implicit
nonlinearity of the circuit and the memory intro-
duced by bypass, coupling, and Miller capacitances
in the circuit. It can be considered a brute-force,
fixed-sampling-rate simulation of the circuit.
A recent patent by Gallo (2008), the founder of
Gallo Engineering (producers of Studio Devil soft-
ware), introduces a tube-stage emulation algorithm
using a parametric nonlinear function. The bias
variation is modeled by evaluating the cathode
voltage ODE using a numerical solver, such as
the fourth-order Runge–Kutta algorithm. The plate
voltage variation is neglected here, as in Karjalainen
et al. (2006).
Wave Digital Filters
Wave digital filters (WDFs; Fettweis 1986) are a
special class of digital filters with parameters that
directly map to physical quantities. Each of the
basic electrical circuit elements has a simple WDF
representation, and, through the use of “adaptors,”
the resulting filters connect to each other as real
electric components do. Thus, the user can build the
WDF circuit model by connecting elementary blocks
(resistors, capacitors, etc.) to each other like a real
amplifier builder. A real-time model of a WDF tube-
amplifier stage has been presented in Karjalainen
and Pakarinen (2006). Here, the tube is modeled
using a two-dimensional lookup table for simulating
the bias variation, while the effect of the grid
current is neglected. Sound examples are available
at www.acoustics.hut.fi/publications/papers/icassp-
wdftube. Yeh and Smith (2008) demonstrated that
the WDF can efficiently represent certain guitar
circuits, such as the bright switch and the two-
capacitor diode clipper.
Although WDFs are a computationally efficient,
modular physical-modeling technique—and thus
a promising method for flexible real-time audio
circuit simulation—some barriers to widespread
application of WDFs remain. Finding a general
methodology in the WDF framework to model
instantaneous feedback loops between different
parts of the amplifier circuitry presents a significant
challenge. Also, certain circuit topologies, such as
bridges, do not easily map to connections of the
adaptors commonly used for WDFs.
Other Models
A hybrid DSP/tube amplifier has been patented by
Korg (Suruga, Suzuki, and Matsumoto 2002). Their
system uses an upsampled nonlinear function in
modeling the preamplifier, while the power amplifier
is emulated using two push-pull triodes, connected
to a solid-state power circuit via a transformer. A
central processing unit (CPU) controls the biasing of
the tubes and the filtering of the feedback from the
output to the input. The power amplifier state can
be switched between class A and class AB biasing by
the CPU. Furthermore, the solid-state power circuit
couples the output transformer to the loudspeaker so
that the output power rating can be varied without
altering the interaction between the tubes and the
loudspeaker. Vox Amplification, a subsidiary of
Korg, manufactures a hybrid DSP/tube amplifier
modeling system called Valvetronix.
A recently introduced exotic sound effect
(Pekonen 2008) uses a time-varying allpass filter
in adding phase distortion to the input signal. Al-
though various types of distortion could be emulated
by suitably modulating the filter coefficients, the
current usage of this effect does not allow convincing
emulation of vacuum-tube distortion.
Summary and Discussion
Digital emulation of guitar tube amplifiers is a
vibrant area of research with many existing com-
mercial products. Linear parts of the amplifier,
such as the tone stack, are modeled using digital
Pakarinen and Yeh
97
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
3
2
8
5
1
8
5
5
3
0
8
/
c
o
m
j
.
.
2
0
0
9
3
3
2
8
5
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
filters, for which the parameters are found with
system-identification methods or by using a priori
knowledge of the underlying circuitry. In the sim-
plest case, the distortion introduced by the tube
stages is modeled using static waveshaping. Aliasing
problems can be avoided using oversampling. More-
sophisticated methods can be used for the simulation
of dynamic nonlinearities. Most of these methods
can be classified as being inspired by circuit signal
paths, which try to model the signal path from the
amplifier’s input to the output. There are also some
methods that attempt to simulate the operation of
the underlying electric circuit, but these are often
either greatly simplified or still too demanding com-
putationally for real-time modeling of complex cir-
cuits. Alternatively, some analytical methods, such
as Volterra series or dynamical convolution, have
also been suggested. Owing to the complex dynam-
ical nonlinearities of the tube-amplifier circuit, true
physics-based models for accurate real-time simula-
tion of the tube amplifier have yet to be discovered.
It must be noted that owing to the essentially
nonlinear, complex nature of tube amplifiers, objec-
tive evaluation of their sound quality—and hence
the sound quality of tube emulators—is extremely
difficult. Thus, the best way to rate different emu-
lation schemes is by listening. Marui and Martens
(2002) have presented some studies discussing per-
ceptual aspects of amplifier modeling. As a result
of the subjectivity of human listeners, one should
be careful not to underestimate certain amplifier-
modeling schemes just because the method used is
simple or physically inaccurate. Careful tuning of
the emulation parameters can make a tremendous
improvement in the resulting sound.
Existing emulation techniques are improving in
both physical accuracy and sound quality. Owing
to the easy distribution of digital media, software
amplifier emulators are also constantly gaining new
users. Although some tube-amplifier enthusiasts
might feel that digital emulation is a threat to the
tube-amplifier industry, the authors believe that it
should rather be viewed as an homage. It can also be
seen as a form of conservation, because the quantity
and quality of available tube-amplifier components
continues to dwindle. After all, the ultimate goal
of amplifier emulation is to convincingly reproduce
all the fine details and nuances of the vacuum-tube
sound, and to make it widely available for use in
artistic expression.
Acknowledgments
Jyri Pakarinen’s research is funded by Helsinki Uni-
versity of Technology. David Yeh was supported by a
National Science Foundation Graduate Fellowship.
The authors wish to thank Prof. Matti Karjalainen,
Prof. Vesa V ¨alim ¨aki, Miikka Tikander, and Jonte
Knif for helpful comments.
References
Abel, J. S., and D. P. Berners. 2006. “A Technique for
Nonlinear System Measurement.” Proceedings of the
Audio Engineering Society 121st Convention. New
York: Audio Engineering Society, paper no. 6951.
Aiken, R. 1999a. “What is Miller Capacitance?” Available
online at www.aikenamps.com/MillerCapacitance
.html (accessed Apr. 7, 2008).
Aiken, R. 1999b. “What is ‘Sag’?” Available online
at www.aikenamps.com/Sag.html (accessed Apr. 14,
2008).
Aiken, R. 2006. “What is ‘Blocking’ Distortion?” Available
online at www.aikenamps.com/BlockingDistortion
.html (accessed Apr. 7, 2008).
Amels, D. 2003. “System and Method for Distorting a
Signal.” U.S. Patent No. 6,611,854 B1. Filed Sep. 22,
2000, issued Aug. 26, 2003.
Araya, T., and A. Suyama. 1996. ”Sound Effector Capable
of Imparting Plural Sound Effects Like Distortion and
Other Effects.” U.S. Patent No. 5,570,424. Filed Nov.
24, 1993, issued Jun. 4, 1996.
Arfib, D. 1979. “Digital Synthesis of Complex Spectra
by Means of Multiplication of Nonlinear Distorted
Sine Waves.” Journal of the Audio Engineering Society
27(10):757–768.
Barbour, E. 1998. “The Cool Sound of Tubes.” IEEE
Spectrum 35(8):24–35.
Berners, D. P., and J. S. Abel. 2004. “Ask the Doc-
tors!” Universal Audio WebZine 2(6). Available on-
line at www.uaudio.com/webzine/2004/july/text/
content2.html (accessed Jun. 10, 2008).
Boyd, S. P. 1985. “Volterra Series: Engineering Fun-
damentals.” Doctoral Thesis, University of Cal-
ifornia at Berkeley. Available online at www
98
Computer Music Journal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
3
2
8
5
1
8
5
5
3
0
8
/
c
o
m
j
.
.
2
0
0
9
3
3
2
8
5
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
.stanford.edu/∼boyd/papers/pdf/boyd phd thesis.pdf
(accessed Jun. 2, 2008).
Bussey, W. S., and R. M. Haigler. 1981. “Tubes Versus
Transistors in Electric Guitar Amplifiers.” Proceedings
of the IEEE International Conference on Acoustics,
Speech, and Signal Processing. New York: Institute of
Electrical and Electronics Engineers, pp. 800–803.
Curtis, D. V., K. L. Chapman, and C. C. Adams. 2001.
“Simulated Tone Stack for Electric Guitar.” U.S. Patent
No. 6,222,110. Filed Jun. 15, 2000, issued Apr. 24, 2001.
Doidic, M., et al. 1998. “Tube Modeling Programmable
Digital Guitar Amplification System.” U.S. Patent No.
5,789,689. Filed Jan. 17, 1997, issued Aug. 4, 1998.
Farina, A., A. Bellini, and E. Armelloni. 2001. ”Non-Linear
Convolution: A New Approach for the Auralization
of Distortion Systems.” Proceedings of the Audio
Engineering Society 110th Convention. New York:
Audio Engineering Society, paper no. 5359.
Fern ´andez-Cid, P., and J. C. Quir ´os. 2001. “Distortion of
Musical Signals by Means of Multiband Waveshaping.”
Journal of New Music Research 30(3):219–287.
Fettweis, A. 1986. “Wave Digital Filters: Theory and
Practice.” Proceedings of the IEEE 74(2):270–327.
Foster, S. 1986. “Impulse Response Measurement Using
Golay Codes.” Proceedings of the IEEE International
Conference on Acoustics, Speech, and Signal Process-
ing. New York: Institute of Electrical and Electronics
Engineers, pp. 929–932.
Gallien, R. A., and K. A. Robertson. 2007. “Programmable
Tone Control Filters for Electric Guitar.” U.S. Patent
Application 2007/0168063 A1. Filed Jan. 18, 2006,
published Jul. 19, 2007.
Gallo, M. N. 2008. “Method and Apparatus for Distortion
of Audio Signals and Emulation of Vacuum Tube
Amplifiers.” U.S. Patent Application 2008/0218259 A1.
Filed Mar. 6, 2007, published Sep. 11, 2008.
Gustafsson, F., et al. 2004. “System and Method for
Simulation of Non-Linear Audio Equipment.” U.S.
Patent Application 2004/0258250 A1. Filed Jun. 21,
2004, published Dec. 23, 2004.
Hamm, R. O. 1973. ”Tubes Versus Transistors—Is
There an Audible Difference?” Journal of the Audio
Engineering Society 21(4):267–273.
H `elie, T. 2006. “On the Use of Volterra Series for
Real-Time Simulations of Weakly Nonlinear Analog
Audio Device: Application to the Moog Ladder Filter.”
Proceedings of the International Conference on Digital
Audio Effects (DAFx-06). New York: Association for
Computing Machinery, pp. 7–12.
Huovilainen, A. 2004. “Nonlinear Digital Implementation
of the Moog Ladder Filter.” Proceedings of the Interna-
tional Conference on Digital Audio Effects (DAFx-04).
New York: Association for Computing Machinery, pp.
61–64.
Huovilainen, A. 2005. “Enhanced Digital Models for Ana-
log Modulation Effects.” Proceedings of the Interna-
tional Conference on Digital Audio Effects (DAFx-05).
New York: Association for Computing Machinery, pp.
155–160.
Jackson, D. L. 2003. “Method and Apparatus for the
Modeling and Synthesis of Harmonic Distortion.” U.S.
Patent No. 6,504,935 B1. Filed Aug. 19, 1998, issued
Jan. 7, 2003.
Karjalainen, M., et al. 2006. “Virtual Air Guitar.” Journal
of the Audio Engineering Society 54(10):964–980.
Karjalainen, M., and J. Pakarinen. 2006. “Wave Digital
Simulation of a Vacuum-Tube Amplifier.” Proceedings
of the IEEE International Conference on Acoustics,
Speech, and Signal Processing. New York: Institute of
Electrical and Electronics Engineers, pp. 14–19.
Katayama, T., and M. Serikawa. 1997. “Reduction of Sec-
ond Order Non-Linear Distortion of a Horn Loudspeaker
by a Volterra Filter-Real-Time Implementation.” Pro-
ceedings of the Audio Engineering Society 103rd
Convention. New York: Audio Engineering Society,
paper no. 4525.
Kemp. M. J. 2006. “Audio Effects Synthesizer with or
without Analyzer.” U.S. Patent No. 7,039,194 B1. Filed
Aug. 8, 1997, issued May 2, 2006.
Kramer, G. 1991. “Digital Signal Processor for Providing
Timbral Change in Arbitrary Audio and Dynami-
cally Controlled Stored Digital Audio Signals.” U.S.
Patent No. 4,991,218 (continuation-in-part of U.S. Pat.
4,868,869). Filed Aug. 24, 1989, issued Feb. 5, 1991.
Kuroki, R., and T. Ito. 1998. “Digital Audio Signal
Processor with Harmonics Modification.” U.S. Patent
No. 5,841,875. Filed Jan. 18, 1996, issued Nov. 24, 1998.
Langford-Smith, F. 1954. Radiotron Designer’s Handbook,
4th ed. New York: Radio Corporation of America.
Le Brun, M. 1979. “Digital Waveshaping Synthesis.”
Journal of the Audio Engineering Society 27(4):250–
266.
Marui, A., and W. L. Martens. 2002. “Multidimensional
Perceptual Calibration for Distortion Effects Processing
Software.” Proceedings of the Audio Engineering Soci-
ety 113rd Convention. New York: Audio Engineering
Society, paper no. 5708.
Massie, D. C. 1996. “Digital Signal Processor for Adding
Harmonic Content to Digital Audio Signals.” U.S.
Patent No. 5,524,074. Filed Jun. 29, 1992, issued Jun.
4, 1996, continuation patent issued May 5, 1998 but
without an extended expiration date.
Pakarinen and Yeh
99
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
3
2
8
5
1
8
5
5
3
0
8
/
c
o
m
j
.
.
2
0
0
9
3
3
2
8
5
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M ¨oller, S., M. Gromowski, and U. Z ¨olzer. 2002.
“A Measurement Technique for Highly Non-
linear Transfer Functions.” Proceedings of the
International Conference on Digital Audio Ef-
fects (DAFx-02), Hamburg, Germany, pp. 203–
206.
Nelles, O. 2000. Nonlinear System Identification. New
York: Springer.
Paatero, T., and M. Karjalainen. 2003. “Kautz Filters and
Generalized Frequency Resolution: Theory and Audio
Applications.” Journal of the Audio Engineering Society
51(1/2):27–44.
Pakarinen, J. 2008. “Modeling of Nonlinear and Time-
Varying Phenomena in the Guitar.” Doctoral Thesis,
Helsinki University of Technology. Available online at
lib.tkk.fi/Diss/2008/isbn9789512292431 (accessed Apr.
3, 2008).
Pekonen, J. 2008. “Coefficient-Modulated First-
Order Allpass Filter as Distortion Effect.” Pro-
ceedings of the International Conference on Dig-
ital Audio Effects (DAFx-08). Available online at
www.acoustics.hut.fi/dafx08/papers/dafx08 16.pdf.
Pritchard, E. K., 1991. “Semiconductor Emulation of Tube
Amplifiers.” U.S. Patent No. 4,995,084. Filed Mar. 23,
1998, issued Feb. 19, 1991.
Santagata, F., A. Sarti, and S. Tubaro. 2007. “Non-
Linear Digital Implementation of a Parametric
Analog Tube Ground Cathode Amplifier.” Proceed-
ings of the International Conference on Digital
Audio Effects (DAFx-07). Available online at
dafx.labri.fr/main/papers/p169.pdf.
Santo, B. 1994. “Volume Cranked Up in Amp Debate.”
Electric Engineering Times Oct:24–35. Available online
at www.trueaudio.com/at eetjlm.htm (accessed May 8,
2008).
Schattschneider, J., and U. Z ¨olzer. 1999. “Discrete-
Time Models for Nonlinear Audio Systems.”
Proceedings of the 2nd COST G-6 Work-
shop on Digital Audio Effects (DAFx99).
Available online at www.hsu-hh.de/download
-1.4.1.php?brick id=ZCXQx8BdUQZKnUBW.
Schimmel, J. 2003. “Non-Linear Dynamics Processing.”
Proceedings of the Audio Engineering Society 114st
Convention. paper no. 5775. Amsterdam: Audio
Engineering Society.
Schimmel, J., and J. Misurec. 2007. “Characteristics of
Broken Line Approximation and Its Use in Distortion
Audio Effects.” Proceedings of the International
Conference on Digital Audio Effects (DAFx-07). New
York: Association for Computing Machinery, pp. 161–
164.
Shibutani, M. 1996. “Distortion Circuits for Improving
Distortion Effects to Audio Data.” U.S. Patent No.
5,528,532. Filed Jun. 6, 1995, issued Jun. 18, 1996.
Sondermeyer, J. C. 1984. “Circuit for Simulating Vacuum
Tube Compression in Transistor Amplifiers.” U.S.
Patent No. 4,439,742. Filed Sep. 4, 1981, issued Mar.
27, 1984.
Spangenberger, K. R. 1948. Vacuum Tubes. New York:
McGraw-Hill.
Sullivan, C. R. 1990. “Extending the Karplus-Strong
Algorithm to Synthesize Electric Guitar Timbres with
Distortion and Feedback.” Computer Music Journal
14(3):26–37.
Suruga, M., Y. Suzuki, and K. Matsumoto. 2002. “Electric
Instrument Amplifier.” U.S. Patent No. 6,350,943.
Filed Dec. 28, 2000, issued Feb. 26, 2002.
Todokoro, S. 1976. “Signal Amplifier Circuit Using a
Field Effect Transistor Having Current Unsaturated
Triode Vacuum Tube Characteristics.” U.S. Patent No.
4,000,474. Filed Jun. 10, 1975, issued Dec. 28, 1976.
Toyama, S. 1996. “Harmonic Tone Generator for Low
Level Input Audio Signals and Small Amplitude Input
Audio Signals.” U.S. Patent No. 5,578,948. Filed Jan.
13, 1992, issued Nov. 26, 1996.
V ¨alim ¨aki, V., and A. Huovilainen. 2006. “Oscillator
and Filter Algorithms for Virtual Analog Synthesis.”
Computer Music Journal 30(2):19–31.
Vladimirescu, A. 1994. The SPICE Book. New York: Wiley.
White, J. K., and A. Sangiovanni-Vincentelli. 1987. Relax-
ation Techniques for the Simulation of VLSI Circuits.
Boston, Massachusetts: Kluwer Academic Publishers.
Yeh, D. T., J. Abel, and J. O. Smith. 2007. “Simplified,
Physically-Informed Models of Distortion and
Overdrive Guitar Effects Pedals.” Proceedings of the
International Conference on Digital Audio Effects
(DAFx-07). New York: Association for Computing
Machinery, pp. 189–196.
Yeh, D. T., et al. 2008. “Numerical Methods for
Simulation of Guitar Distortion Circuits.” Computer
Music Journal 32(2):23–42.
Yeh, D. T., and J. O. Smith. 2006. “Discretization of the
’59 Fender Bassman Tone Stack.” Proceedings of the
International Conference on Digital Audio Effects
(DAFx-06). New York: Association for Computing
Machinery, pp. 1–6.
Yeh, D. T., and J. O. Smith. 2008. “Simulating Guitar
Distortion Circuits Using Wave Digital and Nonlinear
State-Space Formulations.” Proceedings of the
International Conference on Digital Audio Effects
(DAFx-08). New York: Association for Computing
Machinery, pp. 19–26.
100
Computer Music Journal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
3
2
8
5
1
8
5
5
3
0
8
/
c
o
m
j
.
.
2
0
0
9
3
3
2
8
5
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3