Commuted Waveguide
Synthesis of the
Clavichord
Vesa Va¨ lima¨ ki,* Mikael Laurson,†
and Cumhur Erkut*
*Laboratory of Acoustics and Audio
Signal Processing
Helsinki University of Technology
P.O. Box 3000
FIN-02015 HUT
Espoo, Finland
{Vesa.Valimaki, Cumhur.Erkut}@hut.fi
†Centre for Music and Technology
Sibelius Academy
P.O. Box 86
Helsinki, Finland
laurson@siba.fi
The clavichord is one of the oldest keyboard instru-
mentos, and it is still often used in performances
and recordings of Renaissance and Baroque music.
The sound of the instrument is pleasant and ex-
pressive but quiet. Como consecuencia, the instrument
can only be used in intimate performances for
small audiences. This is the main reason why the
clavichord was replaced by the harpsichord and fi-
nally by the modern piano, both of which produce
a considerably louder output. Attempts have been
made to amplify the sound of the clavichord using
a piezoelectric pickup (Burhans 1973).
One of our motivations in this research is to give
the clavichord a new life in the digital world,
where the faint sound level of the instrument can
be amplified by simply turning a volume knob. El
suggested synthesis model is based on digital wave-
guide modeling of string instruments (Herrero 1992,
1998; Va¨ lima¨ ki et al. 1996; Karjalainen, Va¨ lima¨ ki,
and Tolonen 1998) and uses the principle of com-
muted waveguide synthesis where the soundbox’s
response is incorporated in the excitation signal
(Herrero 1993; Karjalainen and Va¨ lima¨ ki 1993; Karja-
lainen, Va¨ lima¨ ki, and Ja´ nosy 1993). Special sam-
pling techniques are also employed. Musical
examples produced using the proposed synthesizer
will be included on a forthcoming Computer Music
Journal CD.
Acoustics of the Clavichord
A photograph of the clavichord used for the mea-
surements in this study is shown in Figure 1. El
Computer Music Journal, 27:1, páginas. 71–82, Primavera 2003
(cid:1) 2003 Instituto de Tecnología de Massachusetts.
instrument is an Anthony Sidey clavichord manu-
factured by Heugel in Paris, Francia, en 1988. Este
clavichord is an unfretted one, so any combination
of notes can be played. The range of a clavichord is
anywhere from three octaves to over five octaves.
Our clavichord has 51 keys ranging from C2 to D6.
The instrument was tuned about a whole tone
lower than the standard modern tuning
(A4 (cid:2) 440 Hz): the nominal frequency of A4 is 395
Hz. The Werkmeister tuning system was used.
For each key of the clavichord, a pair of strings is
tuned in unison, as sketched in Figure 2 (ver, para
ejemplo, Thwaites and Fletcher 1981; Campbell
and Greated 1987). Sin embargo, the two strings are al-
ways slightly detuned around the same note, ser-
cause exact tuning is impossible manually. Every
key forms one end of a lever that has a tangent at-
tached to its other end. When a key is depressed,
the tangent hits the string pair and initiates vibra-
ción. One end of the strings has been damped with
felt, and the other end goes over a bridge to the
tuning mechanism. De este modo, the strings are freely vi-
brating between the bridge and the tangent, cual
works as both a hammer and a termination. El
tangent mechanism is rather noisy, as it excites
modes of the soundboard but also itself causes
sound from its moving parts owing to friction.
When the key is released, the tangent falls back
with the aid of gravity, and the string vibration is
allowed to propagate to the felt-covered end of the
cadena, which efficiently damps the vibration. En
the end of each note, another knock is heard as the
tangent returns to its resting position. The some-
what mistuned strings of each pair are coupled via
a non-rigid bridge, and thus both beats and a two-
stage decay result (Weinreich 1977).
Va¨ lima¨ ki, Laurson, and Erkut
71
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
2
7
1
7
1
1
8
5
3
8
2
7
0
1
4
8
9
2
6
0
3
6
0
6
1
3
3
5
3
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 1. Clavichord used
in this study.
Cifra 2. Tangent mecha-
nism of one key of the
clavichord and a string
pair associated with it.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
The first thing that people usually notice about
the clavichord is that the sound level is very low.
The maximum sound pressure level at 1 meter is
only about 50 dB or 60 dB, depending on the indi-
vidual construction of the instrument. This makes
this ancient instrument a sound source less effi-
cient than a human speaker. There are many rea-
sons for the weak output (see Campbell and
Greated 1987; Fletcher and Rossing 1991). El
strings are thin and their tension is low, y ellos
radiate sound inefficiently. The soundboard is
small and light, and it cannot amplify the sound
mucho.
A particularly interesting feature in the clavi-
chord is the mechanical aftertouch known as Be-
bung. When the player increases pressure on a key,
the tangent is raised more, which in turn increases
the tension of the string pair, resulting in a raise of
pitch. This enables continuous control of vibrato,
which is a used performance style. Aftertouch has
been part of keyboard controllers since the 1980s,
and it is thus easy to include this control in the
clavichord synthesizer. Sin embargo, a fully poly-
/
/
/
/
2
7
1
7
1
1
8
5
3
8
2
7
0
1
4
8
9
2
6
0
3
6
0
6
1
3
3
5
3
pag
d
.
Felt
Tangent
Key
Lever
Bridge
String
pair
Tuning
pins
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
phonic aftertouch, which would really be needed, es
only available in high-end keyboard controllers.
As the key pressure is changed, the tangent
causes a slightly different change in the tension of
the two strings of a pair. This feature affects the
timbre of clavichord tones by introducing a flang-
ing effect. It is heard during and after the attack,
particularly in the bass register.
72
Computer Music Journal
Cifra 3. (Top) Waveform
of a clavichord tone (A3)
showing the irregular over-
all decay pattern and the
thump at the end of the
tone at 1.1 segundo, y (bot-
tom) the time history of its
fundamental frequency
(nominal fundamental fre-
quency is 197.5 Hz).
Cifra 4. Envelopes of the
lowest partials of the tone
como se muestra en la figura 1: 1st
(solid line with circles),
2nd (solid line), 3rd
(dashed line), 4th (dash-
dot line), and 5th (dotted
line).
1
0
yo
mi
v
mi
l
(cid:1)1
0
200
199
198
)
z
h
(
0
F
197
0
(cid:1)80
(cid:1)100
(cid:1)120
)
B
d
(
mi
d
tu
t
i
norte
gramo
a
METRO
0.2
0.4
0.6
0.8
1
1.2
0
0.2
0.4
0.6
Time (segundo)
0.8
0.2
0.4
0.6
Time (segundo)
0.8
1
1.2
Properties of Single Clavichord Tones
Cifra 3 shows the envelope of a recorded clavi-
chord tone. The irregular, non-exponential decay of
the tone can be observed. The key mechanism of
the clavichord generates a loud knock at the begin-
ning and end of a tone, which is characteristic to
the sound of the instrument. En figura 3, a burst lo-
cated at 1.1 sec corresponds to the thump caused
by release of the key, at the same time the signal
starts to decay quickly. The envelope curves of the
first five harmonics are presented in Figure 4. Nota
that regular exponential decay (es decir., linear decay on
a dB scale) es raro: pronounced beating and other ir-
regularities are observed in many harmonics (p.ej.,
the beating of the fourth partial).
The fundamental frequency of clavichord tones
varies over time, as illustrated by an example in
the lower part of Figure 3. This may be partly
caused by tension modulation (Tolonen, Va¨ lima¨ ki,
and Karjalainen 2000), which is a purely physical
phenomenon in vibrating strings, but also by the
pressure of the player’s finger (es decir., the mechanical
aftertouch), which directly controls string tension
during playing. A time-domain finite-difference
simulation suggests that the tension modulation ef-
fect is negligible compared to that caused by the
mechanical aftertouch (Va¨ lima¨ ki et al. 2000). En
Cifra 3, the pitch glide is about 2 Hz, cual es
lower than the threshold of audibility for this ef-
fect. According to Ja¨ rvela¨ inen and Va¨ lima¨ ki (2001),
the threshold at 196 Hz (the nearest frequency
probado) es 4.4 Hz. In the case of the clavichord used
in our measurements, during normal playing the
pitch glide can be inaudible for most listeners. Au-
dible pitch glides can be generated easily, sin embargo.
Cifra 5 gives an example of a tone that contains
an exaggerated pitch vibrato, which should be obvi-
ous for all listeners. Note that the vibrato width is
typically about 2 Hz or less, but can occasionally
peak higher. The vibrato rate is about 7 Hz in this
caso, which is slightly faster than what would be
usual in a musical context. The above fundamental
frequency measurements reflect the effective pitch,
where the contributions of both strings are present.
Impulsively driven string instrument sounds are
always at least weakly inharmonic (Fletcher and
Rossing 1991). This is caused by the stiffness of the
string material. It is well known that piano tones,
particularly in the bass range, are highly inhar-
monic, which affects both the timbre and the tun-
En g. Measurements of inharmonicity have not been
published previously for the clavichord, so we con-
ducted them ourselves. This was needed to decide
whether we had to implement the inharmonicity
using an allpass filter, as is customary to do in
waveguide synthesis (Jaffe and Smith 1983; Bank
2000). We used our parameter estimation software
to extract partial frequencies of clavichord tones as
a function of time. Using a least-squares fit, we es-
timated from the data the inharmonicity coeffi-
cient. We found that the clavichord used in our
measurements produces almost perfectly harmonic
tones. (The inharmonicity coefficient does not ex-
ceed 10–6.) De este modo, the effect of inharmonicity can be
considered inaudible (Ja¨ rvela¨ inen, Va¨ lima¨ ki, y
Va¨ lima¨ ki, Laurson, and Erkut
73
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
2
7
1
7
1
1
8
5
3
8
2
7
0
1
4
8
9
2
6
0
3
6
0
6
1
3
3
5
3
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 5. (Top) Waveform
of clavichord tone A3 with
strong vibrato (mechanical
aftertouch) y (abajo)
its fundamental frequency
as a function of time.
Cifra 6. Magnitude spec-
trum of the soundboard
excited with an impulse
hammer at the high-
frequency (arriba) and at the
low-frequency end of the
puente (abajo). Results of
two measurements (solid
and dashed line) are plot-
ted one on the other for
ambos casos.
1
0
yo
mi
v
mi
l
(cid:1)1
0
202
)
z
h
(
0
F
200
198
0.5
1
1.5
2
2.5
196
0
0.5
1
Time (segundo)
1.5
2
2.5
)
B
d
(
mi
d
tu
t
i
norte
gramo
a
METRO
)
B
d
(
mi
d
tu
t
i
norte
gramo
a
METRO
60
40
20
0
60
40
20
0
100
200
300
400
500
100
300
200
Frecuencia (Hz)
400
500
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
2
7
1
7
1
1
8
5
3
8
2
7
0
1
4
8
9
2
6
0
3
6
0
6
1
3
3
5
3
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Karjalainen 2001), and perfectly harmonic synthesis
is adequate.
Synthesis Model for the Clavichord
Soundbox
An essential part of clavichord tones is the re-
sponse of the soundbox. The box is strongly excited
every time a key is pressed. This reverberant re-
sponse will ring for about five seconds, y eso
stands out particularly in staccato notes, donde el
string vibration itself is damped quickly after the
attack.
We have conducted a series of acoustic measure-
ments on the soundbox of the instrument to iden-
tify the most prominent modes. Cifra 6 shows the
magnitude spectrum of the soundboard that was
hit with an impulse hammer when the strings were
carefully damped with soft material. Results of two
separate measurements are plotted on top of each
otro. The differences between these curves are
quite small, verifying the repeatability of the mea-
surement. Many narrow peaks are visible in Figure
6. They correspond to long ringing resonance
modes. It can also be seen that the excitation of
modes depends on the location of excitation. Para
ejemplo, el 90 Hz mode is much stronger in the
top part of the figure than in the lower part. A
similar phenomenon occurs in the case of the mode
at about 340 Hz.
Próximo, we describe the synthesis model for clavi-
chord tones. The commuted waveguide synthesis
method invented by Smith (1993) and Karjalainen
and colleagues (Karjalainen and Va¨ lima¨ ki 1993;
Karjalainen, Va¨ lima¨ ki, and Ja´ nosy 1993) is applied
by using inverse-filtered clavichord signals as exci-
tation for the synthesis model. Inverse filtering
here refers to the processing of a signal with the in-
verted transfer function of a waveguide string
modelo. En este caso, the inverse filtering essentially
cancels the partials of a recorded tone. El COM-
muted waveguide synthesis method has been for-
merly used successfully for the synthesis of the
acoustic guitar (Karjalainen, Va¨ lima¨ ki, and Ja´ nosy
1993; Va¨ lima¨ ki et al. 1996; Laurson et al. 2001) y
the piano (Smith and Van Duyne 1995).
Cifra 7 shows the structure of the synthesis
model developed in this work. The coupling of the
two basic strings models Sl(z) and S2(z) is realized
with an unconditionally stable technique suggested
by Karjalainen et al. (1998): the output of only one
of the string models is fed to the input of the other,
and hence there is no feedback. En la práctica, el
coupling coefficient gc is selected to have a small
valor, but this is not required, because there can be
no stability problems. The input and output signals
of the string models are scaled by constant multi-
74
Computer Music Journal
Cifra 7. Clavichord syn-
thesis algorithm for one
key consists of three data-
bases of samples and two
basic string models that
are coupled.
Cifra 8. Block diagram of
(a) the standard and (b)
modified string algorithm.
The latter allows control-
ling the sharpness of
attack using parameter
gattack.
Trigger at attack time
Excitation
signals
Timbre
control
Trigger at release time
Soundbox
respuestas
gi1
gi2
S1
gc
gsb
go1
go2
S2
End knocks
grelease
Sound
plying coefficients gi and go, respectivamente. In addi-
ción, two sample databases are needed for realistic
simulation of the soundbox response and the per-
cussive noise caused by key release. In the follow-
En g, we discuss the string algorithm, modelo
parameters and their control, and the sample data-
bases.
Modified String Algorithm
The strings of the clavichord can be simulated us-
ing digital waveguide string models. En principio,
two digital waveguide models should be used for
each string, since they have two polarizations of vi-
bration (es decir., horizontal and vertical with respect to
the soundboard), but at present we only use one
digital waveguide per string. For a pair of clavi-
chord strings, we thus have two digital waveguide
string models, not four. This choice results in an
efficient algorithm and still generates some beating
in the synthetic tones.
Usually, a digital waveguide string model has the
following transfer function (Jaffe and Smith 1983;
Va¨ lima¨ ki et al. 1996), as also illustrated in Figure
8(a),
S (z) (cid:2)
1
1(cid:3)F (z ) h (z)z
1
(cid:3)l
(1)
where F(z) (cid:2) h0
(cid:4) h1z –1 (cid:4) h2z –2 (cid:4) h3z –3 is a third-
order Lagrange interpolation filter (Laakso et al.
1996), l es el (integer) length of the delay line, y
)(zF
)(zF
)(zH l
)(zH l
(cid:1)
Lz
(a)
gramo
attack
Lz(cid:1)
(b)
Hl(z) is a loop filter with the following transfer func-
ción (Va¨ lima¨ ki et al. 1996):
h (z) (cid:2) gramo
1
loop
1(cid:4)aloop
zloop
1(cid:4)a
(cid:3)1
(2)
(cid:2) 1 and –1 (cid:2) aloop
con 0 (cid:2) gloop
(cid:2) 0. The values of
these parameters can be estimated for each string
using previously developed methods (Va¨ lima¨ ki et
Alabama. 1996; Erkut et al. 2000).
While testing an early version of the clavichord
synthesizer, we noticed that the contribution of the
tangent knock was not sufficiently prominent. En
particular, the attack of high notes sounded too
soft. To fix this deficiency, we modified the above
string algorithm to allow the attack sharpness to be
controlled with one parameter. The block diagram
Va¨ lima¨ ki, Laurson, and Erkut
75
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
2
7
1
7
1
1
8
5
3
8
2
7
0
1
4
8
9
2
6
0
3
6
0
6
1
3
3
5
3
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 9. Estimated values
of string model parameters
gloop (arriba) and aloop (abajo)
(dots connected with
dashed line) together with
their straight-line approxi-
mations (solid lines).
1
pag
oh
oh
1
gramo
0.995
0.99
0.985
0
0
pag
oh
oh
1
a
(cid:1)0.2
(cid:1)0.4
10
20
30
40
50
0
10
20
30
Key index
40
50
of the new algorithm is shown in Figure 8b. Its
transfer function can be written as
S (z) (cid:2) gramo
attack
(cid:4)
(cid:2)
(cid:3)l
F (z) h (z) z
yo
1(cid:3)F (z) h (z) z
gramo (cid:4)(1(cid:3)gramo
attack
attack
yo
(cid:3)l
) F (z) h (z) z
(cid:3)l
1(cid:3) F (z) h (z) z
yo
yo
(cid:3)l
(3)
(cid:2) 1, this algorithm is identi-
(cid:2) 4, may be used to imitate the aggressive at-
Note that with gattack
cal to the standard plucked-string algorithm of
Ecuación 1. A value larger than unity, como
gattack
tack of acoustic tones. In the current version, el
value of the attack sharpness parameter increases
linearly with key number, so that for C2 it is 2.0
and for D6 it is 4.0. The linear trend and the actual
values were adjusted by informal listening. There is
no physical motivation for this new model struc-
tura, other than that it enables separate control of
two different components of the tone: the tangent
knock and the vibrating string sound.
String Model Parameters
Parameter values for the synthesizer are obtained
from analysis of recorded signals. We use a method
based on the short-time Fourier transform and si-
nusoidal modeling of the clavichord tones. Estos
methods have proven successful earlier in the case
of the acoustic guitar. Details can be found else-
dónde (Va¨ lima¨ ki et al. 1996; Erkut et al. 2000).
Cifra 9 shows the gloop and aloop parameters for
todo 51 keys of the clavichord. These values were es-
timated from recorded clavichord tones. The sec-
ond string model uses the same parameters but
slightly different delay lines lengths for mistuning.
The fundamental frequencies of the lowest (#1) y
highest (#51) key are 58.7 Hz and 1056 Hz, respetar-
activamente. Note that the loop gain parameters gloop have
a nearly linear trend as a function of key index (es decir.,
logarithm of frequency) with some variations and a
few outliers. Ja¨ rvela¨ inen and Tolonen (2001) tener
investigated the tolerance of parameters value vari-
ación. Their results show that –30% to (cid:4)40%
changes in the time constant (which depends on
gloop) are inaudible. También, in the aloop parameter, variar-
ations between –17% and (cid:4)16% cannot be per-
ceived. It appears that the gloop parameters
presented in Figure 9 can be replaced with values
obtained by linear regression:
loop
gramo (cid:3) 0.989 (cid:4) 0.000189k
(4)
where k (cid:2) 1. . .51 is the key number starting from
C2 (k (cid:2) 1), and continuing up to D6 (k (cid:2) 51). Este
straight-line fit is illustrated in Figure 9 (arriba) con un
solid line.
The values of parameter aloop may be approxi-
mated by a low-order polynomial as well. Sin embargo,
a linear regression to the data shown in the lower
part of Figure 9 yields intolerably large errors. A
reduce the error, we attempt a piecewise linear re-
gression with a knee point between key indices 23
y 24:
a (cid:3)
loop
(cid:3)0.514 (cid:4) 0.0176k, for k (cid:1) 23
(cid:1)(cid:3)0.175 (cid:4) 0.00225k, for k (cid:2) 24
(5)
This two-part straight-line fit is shown in Figure 9
(abajo) with solid lines, one for the low end of the
keyboard and another for the high end. This ap-
proximation for the aloop values introduces minor
changes in timbre that can be perceived, but it does
not necessarily render the sound quality worse. En
hecho, the overall tone color behaves more uniformly
with the linear approximations than with the un-
processed parameter data.
The damping of the string vibrations as a result
of releasing a key is simulated by changing the loop
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
2
7
1
7
1
1
8
5
3
8
2
7
0
1
4
8
9
2
6
0
3
6
0
6
1
3
3
5
3
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
76
Computer Music Journal
filter characteristics (p.ej., by setting loop gain gloop
equal to 0.1 momentarily). A similar method has
been used successfully to simulate damping of a
guitar string by finger (Erkut et al. 2000; Laurson et
Alabama. 2001).
Sample Databases
Excitation signals for the synthesis have been ob-
tained by processing anechoic recordings of clavi-
chord tones using the methods described by Erkut
et al. (2000). The procedure consists of sinusoidal
análisis, subtracting partials, equalizing the resid-
ual, and truncating the resulting signals with the
right half of a Hanning window. One such excita-
tion signal is used for each of the 51 keys. Canalla-
rently, all excitation signals are 20,000 muestras
largo (acerca de 0.45 sec at a 44.1 kHz sampling rate).
It would be possible to reduce their length further,
but we have found it unnecessary in our current
implementación, since there is no lack of memory.
The reverberation caused by the soundbox is in-
corporated by triggering a soundbox response sam-
ple at a low level each time any note is played (ver
Cifra 7). This sample must be long enough (acerca de
five seconds) so that it provides the reverberant
character of the instrument. This is particularly
important for short notes, such as staccato playing,
for which the output signal would otherwise stop
suddenly in an unnatural manner. Tenga en cuenta que en
principle we could instead use very long excitation
signals for each note, in which case the full sound-
box response would automatically sound with each
nota. Sin embargo, we prefer using short excitation sig-
nal, because we can avoid certain problems related
to the inverse filtering (p.ej., ringing and beating due
to imperfectly cancelled partials). This also saves
memory, because we use fewer soundbox samples
than excitation signals. Using a separate soundbox
sample also allows adjusting the relative levels of
soundbox reverberation and string sound, cual es
an advantage.
The soundbox samples can be obtained by hitting
the bridge of the clavichord with an impulse ham-
mer at various points. The response must be edited
to remove the sharp attack caused by contact of
metals, eso es, the tip of the hammer and a tuning
pin. This is easily done with a fast fade-in. Nota
that this editing is not extremely critical, porque
the impact noise from the tangent mechanism,
which is included in the excitation signal, domi-
nates during the attack and masks the beginning of
the soundbox response. For each key, a soundbox
sample should be chosen, which is obtained close
to the point where the strings are attached. Cómo-
alguna vez, it is practically impossible to excite the bridge
of the clavichord between the tuning pins, y el
only clean samples that we could obtain are from
both ends of the bridge (ver figura 6). This leaves
us with possibilities to use one of the samples for
the left half of the keyboard and the other for the
right one, or to interpolate between the high- y
low-end samples along the keyboard. Aunque el
sampling-based reverberation modeling is clearly
simplified, it yields a natural-sounding ambience in
the synthetic output and is very cheap to imple-
ment because it requires no filtering.
The knock database for note endings consists of a
few short samples (duration less than 0.5 segundo).
These samples may be obtained from recorded long
tones, where the sound of string vibration is al-
lowed to decay below the threshold of audibility
before the key is released. Now the isolated thump
can be simply edited from the recording. One prac-
tical problem was caused by the poor signal-to-
noise ratio of the release samples. It was possible to
hear when a key release occurred from the in-
creased hiss during synthesis. This led us to apply a
de-noising algorithm to suppress the background
noise from the key release recordings, which solved
the problem.
It is unnecessary to record a release sample for
each key. Because the tangent mechanism for every
key is identical and the resulting sound is similar,
it is plausible to use a single sample for all syn-
thetic notes. To avoid a boring similarity, as a com-
promise a small collection of release samples may
be used. We have observed that the largest varia-
tion among different tangent releases is caused by
the velocity of release, which slightly changes the
rhythm of different noises within the knock. De este modo,
one choice is to gather a collection of tangent re-
leases for different release velocities, and select one
Va¨ lima¨ ki, Laurson, and Erkut
77
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
2
7
1
7
1
1
8
5
3
8
2
7
0
1
4
8
9
2
6
0
3
6
0
6
1
3
3
5
3
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 10. Signals involved
in the synthesis of a single
clavichord tone: (a) excita-
tion signal, (b) string algo-
rithm output, (C) soundbox
sample, (d) end noise sam-
por ejemplo (triggered at about 1
segundo), y (mi) synthetic
tono, which is sum of sig-
nal (b) a (d).
0.5
0
(cid:1)0.5
0.5
0
(cid:1)0.5
0.1
0
(cid:1)0.1
0.1
0
(cid:1)0.1
0.5
0
(cid:1)0.5
0
(a)
(b)
(C)
(d)
(mi)
0.2
0.4
0.6
0.8
Time (segundo)
1
1.2
1.4
1.6
randomly or based on some rule, such as the play-
ing tempo. We are currently using two release sam-
ples, and we slightly randomize the release times of
different keys. More sophisticated but still fairly
simple synthesis models employing physically in-
formed randomization have been proposed by Cook
(1997).
Delay Line Variations and the Flanging Effect
Although the variation of the fundamental fre-
quency in clavichord sounds can be inaudible as
discussed earlier, it is also easy to cause pitch
changes with mechanical aftertouch. Because any
change in the string tension will be different for the
two strings of a pair, a flanging-like effect can ap-
pear also in tones where the pitch change is negli-
gible. Variation of the fundamental frequency can
be simulated in the following way: a decaying con-
trol function, Por ejemplo, a scaled impulse re-
sponse of a leaky integrator (a one-pole filter), es
subtracted from the delay-line length of both string
modelos. This imitates the change of pressure on the
key by the player’s finger right after depressing the
key (or the decrease of tension modulation depth
while the string vibration begins to decay), y
brings about the progression of the fundamental
frequency similar to that shown in Figure 3. Nota
that this is a simpler way of producing a time-
varying pitch than the tension-modulation tech-
nique Tolonen et al. (2000) used previously for the
synthesis of the kantele (Va¨ lima¨ ki et al. 1999; Er-
kut et al. 2002) and the tanbur (Erkut and Va¨ lima¨ ki
2000). The tension-modulation algorithm would re-
quire computing the elongation of the string in real
time and controlling the delay-line length of the
string model according to it.
For the mechanical aftertouch, a more sophisti-
cated control signal is required. The pitch contour
of a note is generated with a help of a pitch scaler
in the same fashion as in Laurson et al. (2001). Si
there is neither an initial pitch glide nor vibrato,
the scaler value is 1. The initial pitch glide is im-
plemented as a ramp starting from a value larger
than 1 and ending at 1 after around 0.1 segundo. (El
initial value depends on the dynamic level of the
current note so that forte playing yields a higher
value than piano playing.) The vibrato control, en
doblar, is realized with separate parameters for rate
and maximum depth, and a temporal envelope for
profundidad (for more details, see Laurson et al. 2001).
A specific feature of the clavichord synthesizer is
that the pitch scaler affects a detuning parameter of
the two string models dynamically. De este modo, a more
drastic pitch drift results in a tone that is more out
of tune. This mimics the imperfect mechanism of
the tangent that pulls the two strings unequally. A
database of detuning parameters was generated by
trial and error. An alternative way would be to
measure detuning parameters from the original re-
cordings, which turns out to be difficult. High-
pitched tones tend to be more detuned than low
unos. The sound resulting from the time-varying
detuning is suggestive of the flanging effect, cual
brings warmth and variation to the synthesis.
Synthesis Example
Cifra 10 presents the components for the synthe-
sis of a single clavichord tone. The excitation sig-
nal shown in Figure 10a is inserted into the two
string algorithms. The name ‘‘commuted synthe-
sis’’ comes from the principle that this excitation
signal includes both the contribution of the excita-
78
Computer Music Journal
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
2
7
1
7
1
1
8
5
3
8
2
7
0
1
4
8
9
2
6
0
3
6
0
6
1
3
3
5
3
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
tion mechanism (the tangent) and the soundbox re-
respuesta. Sin embargo, as can be seen, en nuestro
implementation the input signal contains only the
very beginning of the soundbox response. The tail
of the soundbox response is produced separately us-
ing the sampling-based method.
The summed output signals of the string models
constitute the basic vibrating string component of
the synthetic tone, which is displayed in Figure
10b. The key release occurs at 0.97 segundo; note how
the string tone in Figure 10b decays quickly after
eso. Figure 10c shows the beginning of a five-
second-long soundbox sample, which has been
edited from the impulse response of the low-
frequency end of the bridge. A tangent release sam-
por ejemplo, which is started at the release time, is given in
Figure 10d. Finalmente, Figure 10e presents the sum of
the signals shown in Figures 10b, 10C, and 10d, y
it is the output of the clavichord synthesizer.
Although remaining almost invisible in Figure
10mi, the soundbox sample rings several seconds af-
ter the string tone and the key release sample have
died out. The soundbox sample will also be clearly
audible only after the string tone has been ringing
and decaying for some time, and particularly after
the key has been released. We may note that iden-
tity resynthesis is impossible using the proposed
synthesis model and parameter estimation meth-
probabilidades. Sin embargo, the obtained similarity is con-
sidered to be sufficient for high-quality synthesis.
This is confirmed by musical examples produced
with the synthesizer.
Musically Interesting Modifications
The proposed synthesizer structure allows the user
to modify the timbre in numerous ways. muchos de
the possible variations have a clear intuitive inter-
pretation. Por ejemplo, varying the gain gloop of the
loop filter affects the decay time, but otherwise
the timbre remains unchanged. Sin embargo, varying
the loop filter coefficient aloop changes the decay
time at different frequencies, resulting in a curious
evolution of the spectrum over time. The attack
sharpness parameter and the gain of the note-off
noise also enable meaningful and useful controls.
Exaggerated detuning of the two string models for
each voice leads to a low-quality—or possibly a
very old—clavichord. As a consequence of the
above parametric modifications, the synthetic
tones will still be reminiscent of the clavichord.
Extending the range of an instrument is fascinat-
ing and useful in the case of the acoustic guitar.
Design of a synthetic ‘‘super guitar’’ that has a
wide range, almost like that of a grand piano, tiene
been documented recently (Laurson, Va¨ lima¨ ki, y
Erkut 2002). While an arbitrary change of pitch is
easy in a waveguide synthesizer (simply vary the
length of a delay line), the loop filter parameters
and excitation signals should be extracted from re-
cordings, but for non-existing fundamental frequen-
cíes, they are unavailable. The extension of the
pitch range thus involves extrapolation problems
that must be solved somehow. We are planning
tests on extending the range of the proposed clavi-
chord synthesizer.
Naturalmente, it is also possible to turn the clavi-
chord synthesizer into a previously unheard virtual
instrument. Por ejemplo, modifying or replacing
the signals in the sample databases allows dramatic
variations. Exploring all such transformations was
not included in the goals of this study, and the po-
tential of these modifications thus remains mostly
unknown.
Software Implementation of the Synthesizer
The real-time implementation of the proposed clav-
ichord synthesizer has been realized using a
PatchWork (Laurson 1996) user-library called
PWSynth (Laurson and Kuuskankare 2001). El
high-level part of PWSynth is based on Lisp and
CLOS, but the low-level and time-critical DSP-
routines have been implemented in C. El sistema
can be played either from musical notation and
control software called Expressive Notation Pack-
edad (ENP, described in Kuuskankare and Laurson
2001; Laurson et al. 2001), or from a MIDI key-
board.
The starting point for the clavichord implemen-
tation was to use a guitar synthesizer implemented
earlier (Laurson et al. 2001). These systems have
Va¨ lima¨ ki, Laurson, and Erkut
79
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
2
7
1
7
1
1
8
5
3
8
2
7
0
1
4
8
9
2
6
0
3
6
0
6
1
3
3
5
3
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
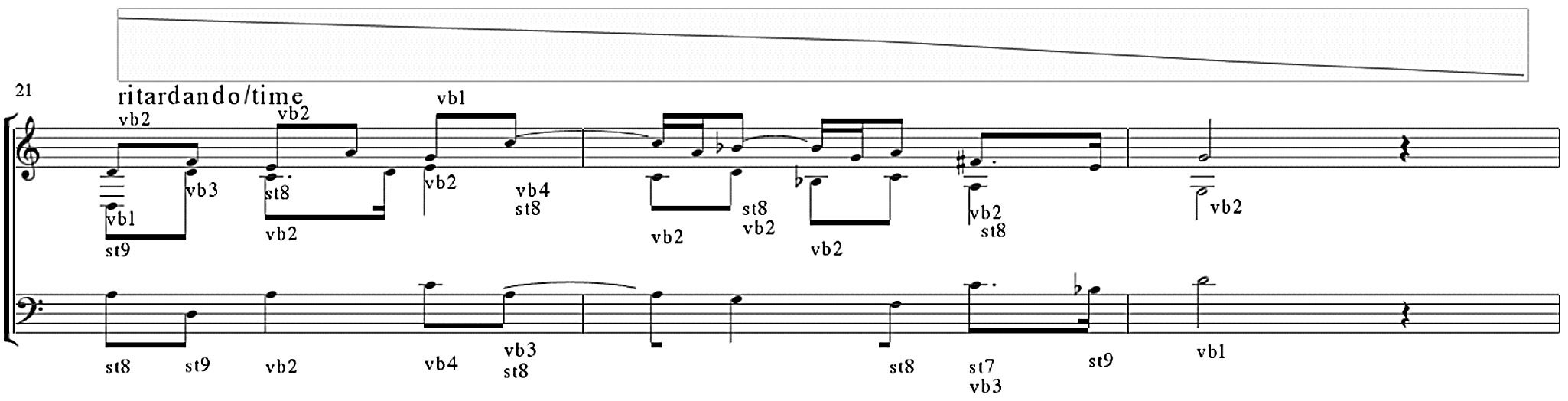
Cifra 11. ENP screenshot
from the final cadence of
Par le regard de vos beaux
yeux by Guillaume Dufay.
several features in common. Both use basically the
same dual-polarization string model, although in
the case of the clavichord, it models a pair of
strings and not the orthogonal polarizations of a
single string. The database of samples—needed for
the excitation signals and the noise effects in the
clavichord simulation—could be used in both cases
in a similar way.
The main difference between the implementa-
tions is the fact that the clavichord consists of 51
strings, while the classical guitar has only six. A
create a synthesizer that could be used in real time,
we designed a voice-allocation algorithm that al-
lows us to effectively play typical pieces of the
clavichord repertoire. We found that a synthesizer
for six simultaneous strings could be played in real
time on a Macintosh G3 400 MHz portable com-
puter. This is sufficient for a large percentage of old
keyboard music. Nuevo, faster computers will allow
playing more voices simultaneously.
The control information for the clavichord syn-
thesizer is calculated from an ENP input score. El
user enters first the basic musical information (es decir.,
pitches and rhythms) of the piece using the graphi-
cal front-end of ENP. After this, the user typically
adds expressions and tempo functions that allow
fine tuning of the timing information in the score.
También, one can include expressions specific to the
clavichord, such as the amount of vibrato to be ap-
plied to a given note. Además, a special rule
modifies the end time of notes (es decir., the time when
the player lifts the fingers from the keyboard). Este
was done to make the performance more lively.
The characteristic noise burst of the instrument
when the fingers are released was found to be es-
sential for the realism of the synthesis.
Cifra 11 shows the three last measures of a
piece by Guillaume Dufay (1400–1474). Besides
pitch and rhythm information, the piece includes
several expression markings that control both vi-
brato (see the labels starting with ‘‘vb’’) and articu-
lación (see labels starting with ‘‘st,’’ which stands
for staccato). The numbers after the expression
markings denote how much vibrato or staccato
should be applied to a given note. This example has
also a special expression containing a tempo func-
ción (see the function above the staff marked with
‘‘ritardando’’ in Figure 11), which controls the
tempo of the piece.
Our current MIDI keyboard implementation is
fairly rudimentary and serves only as a basic tool
para las pruebas. The control parameters of the MIDI
keyboard include key number, key velocity, attack
tiempo, and end time of notes. Además, we use
the MIDI aftertouch parameter to simulate the fin-
ger vibrato effect of the clavichord. A more usable
MIDI implementation would require a keyboard
with polyphonic aftertouch. También, Encontramos eso
the MIDI keyboard at our disposal was not respon-
sive enough when simulating the finger vibrato. A
playable keyboard simulation of the clavichord
model requires more sensitive hardware than what
is commonly available today.
Conclusions and Future Plans
A simplified physical model was proposed for the
synthesis of the clavichord. It follows the principle
of commuted waveguide synthesis, but also uses
many samples obtained by editing and processing
recordings. The excitation signal can be obtained
80
Computer Music Journal
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
2
7
1
7
1
1
8
5
3
8
2
7
0
1
4
8
9
2
6
0
3
6
0
6
1
3
3
5
3
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
by inverse filtering and truncating a recorded clavi-
chord tone. Two coupled digital waveguide string
models are used for synthesizing each voice. A mi-
nor modification to the plucked string model was
introduced to enable control over attack sharpness,
which was found necessary during testing of the
synthesis algorithm. The reverberation caused by
the soundbox that has many resonant modes was
implemented in a computationally economic way
by triggering a soundbox response sample with
each note. The ending of a note requires another
sample to be played, because there must be a
‘‘knocking’’ sound, which is characteristic to the
clavichord. The mechanical aftertouch of the clavi-
chord can be implemented by varying the delay
line lengths of the waveguide string models over
tiempo. When these changes are different for the two
string algorithms modeling a pair of strings, a flang-
ing effect is generated, which is also heard in the
real clavichord.
En el futuro, we plan to develop another version
of the clavichord synthesizer using the direct
physical modeling approach, where the excitation,
strings, and the soundbox have a counterpart in the
modelo. To accomplish this, the sampling-based im-
plementation of the reverberant response of the
soundboard must be replaced with a soundbox
model that filters the output of the string models.
The soundbox can be considered a small reverber-
ant room and be simulated with an artificial rever-
beration algorithm (p.ej., jardinero 1998; Bank 2000).
Además, further measurements of the real in-
strument should be taken. Particularly, the acceler-
ation of the tangent needs to be registered during
the attack of the tone, because this information is
needed for an algorithm simulating the tangent ac-
ción, similar to piano hammer simulations (Bank
2000). This might also reveal the importance of the
tension modulation effect in the sound production
of the clavichord. The tangent modeling algo-
rithm—which will be different from physical mod-
els available for the piano hammer, as Hall (1993)
has pointed out—should be developed to be able to
control the excitation using physical parameters.
Expresiones de gratitud
The work of M. Laurson is part of the project
‘‘Sounding Score—Modeling of Musical Instru-
mentos, Virtual Musical Instruments and their Con-
controlar,’’ and the work of C. Erkut is part of the project
‘‘Technology for Speech and Audio Processing.’’
Both projects are funded by the Academy of Fin-
land. The authors are grateful to Dr. Tero Tolonen
for his contributions in the initial phases of this
estudiar, to Mr. Paulo A. A. Esquef for his help in the
de-noising of the sample databases, and to Mr.
Jonte Knif for his help in the production of musical
examples using the clavichord synthesizer. Special
thanks to Professor Matti Karjalainen who provided
digital photographs of the clavichord and our mea-
surement session.
Referencias
Bank, B. 2000. Physics-Based Sound Synthesis of the Pi-
ano. Report no. 54, Helsinki University of Technology,
Laboratory of Acoustics and Audio Signal Processing,
Espoo, Finland. Available on-line at
www.acoustics.hut.fi/publications/.
Burhans, R. W.. 1973. ‘‘Clavichord Amplification.’’ Jour-
nal of the Audio Engineering Society 21(6):460–463.
Campbell, METRO., and C. Greated. 1987. The Musician’s
Guide to Acoustics. Nueva York: Schirmer Books,
páginas. 234–236.
Cocinar, PAG. R. 1997. ‘‘Physically Informed Sonic Modeling
(PhISM): Synthesis of Percussive Sounds.’’ Computer
Music Journal 21(3):38–49.
Erkut, C., et al. 2000. ‘‘Extraction of Physical and Expres-
sive Parameters for Model-Based Sound Synthesis of
the Classical Guitar.’’ Proceedings of the AES 108th
Convention. Nueva York: Audio Engineering Society.
Erkut, C., and V. Va¨ lima¨ ki. 2000. ‘‘Model-Based Sound
Synthesis of Tanbur, a Turkish Long-Necked Lute.’’
Proceedings of the IEEE International Conference on
Acoustics, Discurso, y procesamiento de señales, volumen. 2. Pis-
cataway, New Jersey: Institute of Electrical and Elec-
tronics Engineers, páginas. 769–772.
Erkut, C., et al. 2002. ‘‘Acoustical Analysis and Model-
Based Sound Synthesis of the Kantele.’’ Journal of the
Acoustical Society of America 112(4):1681–1691.
Fletcher, norte. h., and T. D. Rossing. 1991. The Physics of
Musical Instruments. Nueva York: Editorial Springer.
jardinero, W.. GRAMO. 1998. ‘‘Reverberation Algorithms.’’ In M.
Kahrs and K. Brandenburg, eds. Applications of Digital
Signal Processing to Audio and Acoustics. Dordrecht,
Los países bajos: Desorden, páginas. 85–131.
Va¨ lima¨ ki, Laurson, and Erkut
81
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
2
7
1
7
1
1
8
5
3
8
2
7
0
1
4
8
9
2
6
0
3
6
0
6
1
3
3
5
3
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Sala, D. mi. 1993. ‘‘String Excitation: Piano, Harpsichord
and Clavichord.’’ Proceedings of the 1993 Stockholm
Music Acoustics Conference. Stockholm, Suecia:
Royal Swedish Academy of Music, páginas. 309–314.
Jaffe, D. A., y j. oh. Herrero. 1983. ‘‘Extensions of the
Karplus–Strong Plucked-String Algorithm.’’ Computer
Music Journal 7(2):76–87.
Ja¨ rvela¨ inen, h., and T. Tolonen. 2001. ‘‘Perceptual Toler-
ances for Decay Parameters in Plucked String Synthe-
sis.’’ Journal of the Audio Engineering Society 49(11):
1049–1059.
Ja¨ rvela¨ inen, h., V. Va¨ lima¨ ki, y M. Karjalainen. 2001.
‘‘Audibility of the Timbral Effects of Inharmonicity in
Stringed Instrument Tones.’’ Acoustics Research Let-
ters Online 2(3):79–84.
Ja¨ rvela¨ inen, h., and V. Va¨ lima¨ ki. 2001. ‘‘Audibility of Ini-
tial Pitch Glides in String Instrument Sounds.’’ Pro-
cesiones de la 2001 International Computer Music
Conferencia. San Francisco: International Computer
Music Association, páginas. 282–285.
Karjalainen, METRO., and V. Va¨ lima¨ ki. 1993. ‘‘Model-Based
Analysis/Synthesis of the Acoustic Guitar.’’ Proceed-
ings of the 1993 Stockholm Music Acoustics Confer-
ence. Stockholm, Suecia: Royal Swedish Academy of
Music, páginas. 443–447.
Karjalainen, METRO., V. Va¨ lima¨ ki, and Z. Ja´ nosy. 1993. ‘‘To-
wards High-Quality Sound Synthesis of the Guitar and
String Instruments.’’ Proceedings of the 1993 interna-
tional Computer Music Conference. San Francisco: En-
ternational Computer Music Association, páginas. 56–63.
Karjalainen, METRO., V. Va¨ lima¨ ki, and T. Tolonen. 1998.
‘‘Plucked-String Models: From the Karplus–Strong Al-
gorithm to Digital Waveguides and Beyond.’’ Com-
puter Music Journal, 22(3):17–32.
Kuuskankare, METRO., y M. Laurson. 2001. ‘‘ENP: Musical
Notation Library based on Common Lip and CLOS.’’
Actas de la 2001 International Computer Mu-
sic Conference. San Francisco: International Computer
Music Association, páginas. 131–134.
Laakso, t. I., et al. 1996. ‘‘Splitting the Unit Delay—
Tools for Fractional Delay Filter Design.’’ IEEE Signal
Processing Magazine 13(1):30–60.
Laurson, METRO. 1996. PATCHWORK: A Visual Program-
ming Language and Some Musical Applications. Doc-
toral dissertation, Sibelius Academy, Helsinki,
Finland.
Laurson, METRO., et al. 2001. ‘‘Methods for Modeling Realis-
tic Playing in Acoustic Guitar Synthesis.’’ Computer
Music Journal 25(3):38–49.
Laurson, METRO., y M. Kuuskankare. 2001. ‘‘PWSynth: A
Lisp-based Bridge between Computer Assisted Compo-
sition and Model-based Synthesis.’’ Proceedings of the
2001 International Computer Music Conference. san
Francisco: International Computer Music Association,
páginas. 127–130.
Laurson, METRO., V. Va¨ lima¨ ki, and C. Erkut. 2002. ‘‘Produc-
tion of Virtual Acoustic Guitar Music.’’ Proceedings of
the AES 22nd International Conference on Virtual,
Synthetic, and Entertainment Audio, Nueva York: Au-
dio Engineering Society, páginas. 249–255.
Herrero, j. oh. 1992. ‘‘Physical Modeling Using Digital
Waveguides.’’ Computer Music Journal 16(4): 74–91.
Available on-line at www-ccrma.stanford.edu/(cid:4)jos/
pmudw/.
Herrero, j. oh. 1993. ‘‘Efficient Synthesis of Stringed Musi-
cal Instruments.’’ Proceedings of the 1993 interna-
tional Computer Music Conference. San Francisco:
International Computer Music Association, páginas. 64–71.
Available on-line at www-ccrma.stanford.edu/(cid:4)jos/cs/.
Herrero, j. oh. 1998. ‘‘Principles of Digital Waveguide Mod-
els of Musical Instruments.’’ In M. Kahrs and K. Bran-
denburg, eds. Applications of Digital Signal Processing
to Audio and Acoustics. Dordrecht, Los países bajos:
Desorden, páginas. 417–466.
Herrero, j. o., and S. A. Van Duyne. 1995. ‘‘Commuted Pi-
ano Synthesis.’’ Proceedings of the 1995 Internacional
Computer Music Conference, San Francisco: interna-
tional Computer Music Association, páginas. 319–326.
Thwaites, S., y N. h. Fletcher. 1981. ‘‘Some Notes on
the Clavichord.’’ Journal of the Acoustical Society of
America 69(5):1476–1483.
Tolonen, T., V. Va¨ lima¨ ki, y M. Karjalainen. 2000.
‘‘Modeling of Tension Modulation Nonlinearity in
Plucked Strings.’’ IEEE Transactions on Speech and
Audio Processing 8(3):300–310.
Va¨ lima¨ ki, v., et al. 1996. ‘‘Physical Modeling of Plucked
String Instruments with Application to Real-Time
Sound Synthesis.’’ Journal of the Audio Engineering
Sociedad 44(5):331–353.
Va¨ lima¨ ki, v., et al. 1999. ‘‘Nonlinear Modeling and Syn-
thesis of the Kantele—a Traditional Finnish String In-
strument.’’ Proceedings of the 1999 Internacional
Computer Music Conference. San Francisco: interna-
tional Computer Music Association, páginas. 220–223.
Va¨ lima¨ ki, v., et al. 2000. ‘‘Model-Based Synthesis of the
Clavichord.’’ Proceedings of the 2000 Internacional
Computer Music Conference. San Francisco: interna-
tional Computer Music Association, páginas. 50–53.
Weinreich, GRAMO. 1977. ‘‘Coupled Piano Strings.’’ Journal of
the Acoustical Society of America 62(6):1474–1484.
82
Computer Music Journal
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
/
2
7
1
7
1
1
8
5
3
8
2
7
0
1
4
8
9
2
6
0
3
6
0
6
1
3
3
5
3
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3